Mechanical Properties Regulation of Invar36 Alloy Metastructures Manufactured by Laser Powder Bed Fusion
Abstract
1. Introduction
2. Materials and Methods
2.1. Invar36 Alloy Powder
2.2. Lattice Structure Design
2.3. Lattice Structure Preparation
2.4. Testing and Characterization
3. Results
3.1. Formation Quality
3.2. Mechanical Properties
3.2.1. Macroscopic Deformation
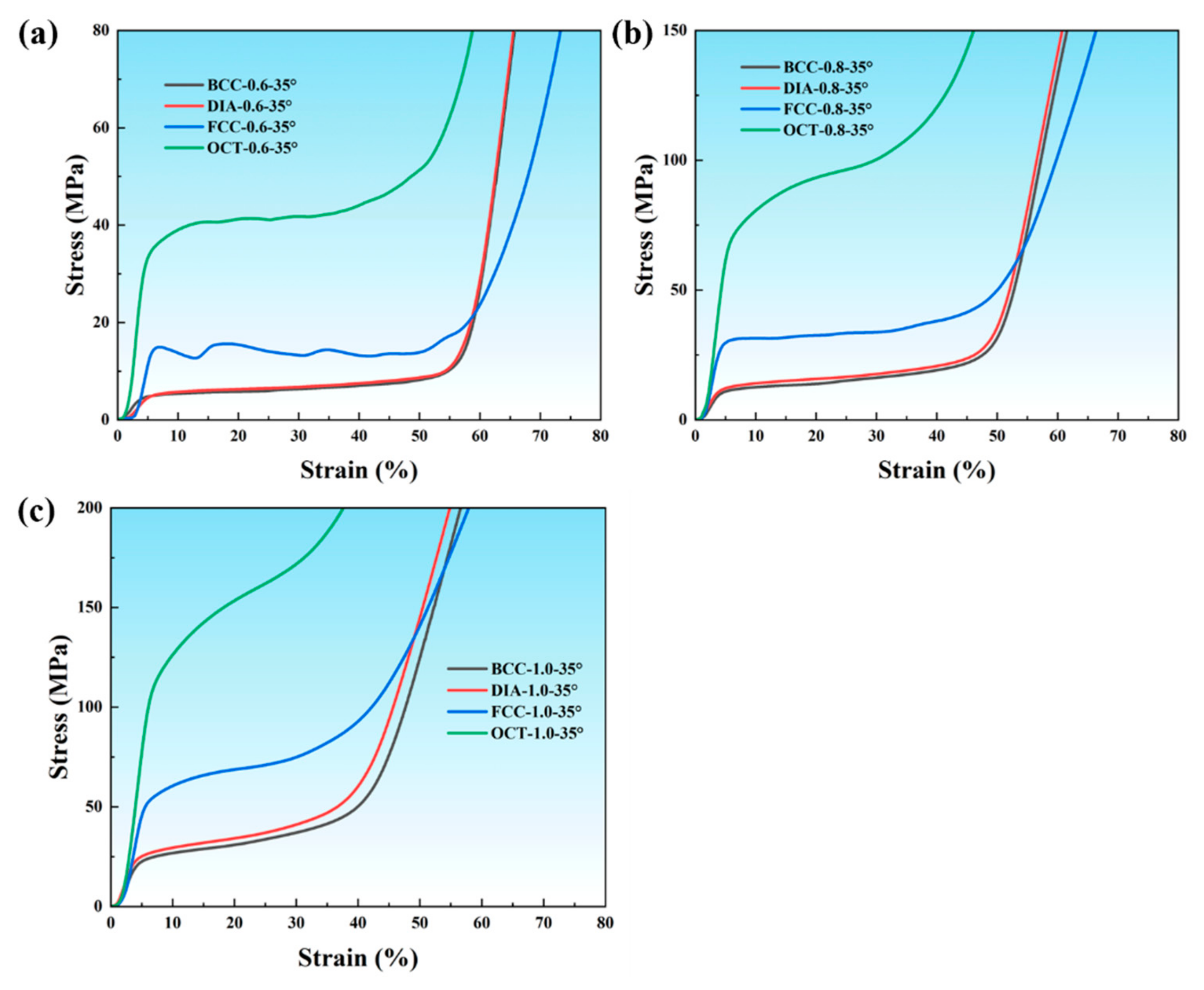
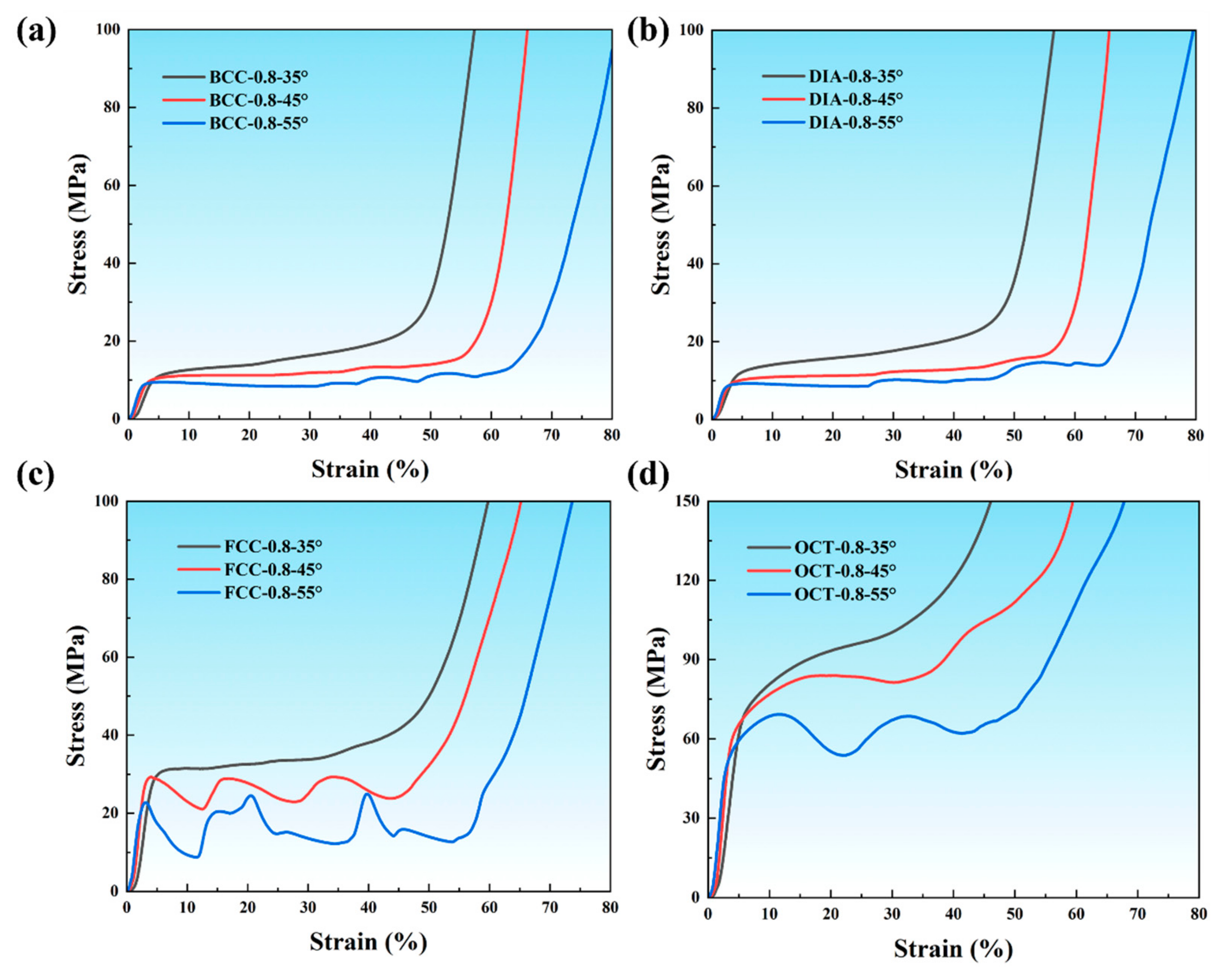
3.2.2. Stress–Strain Curve
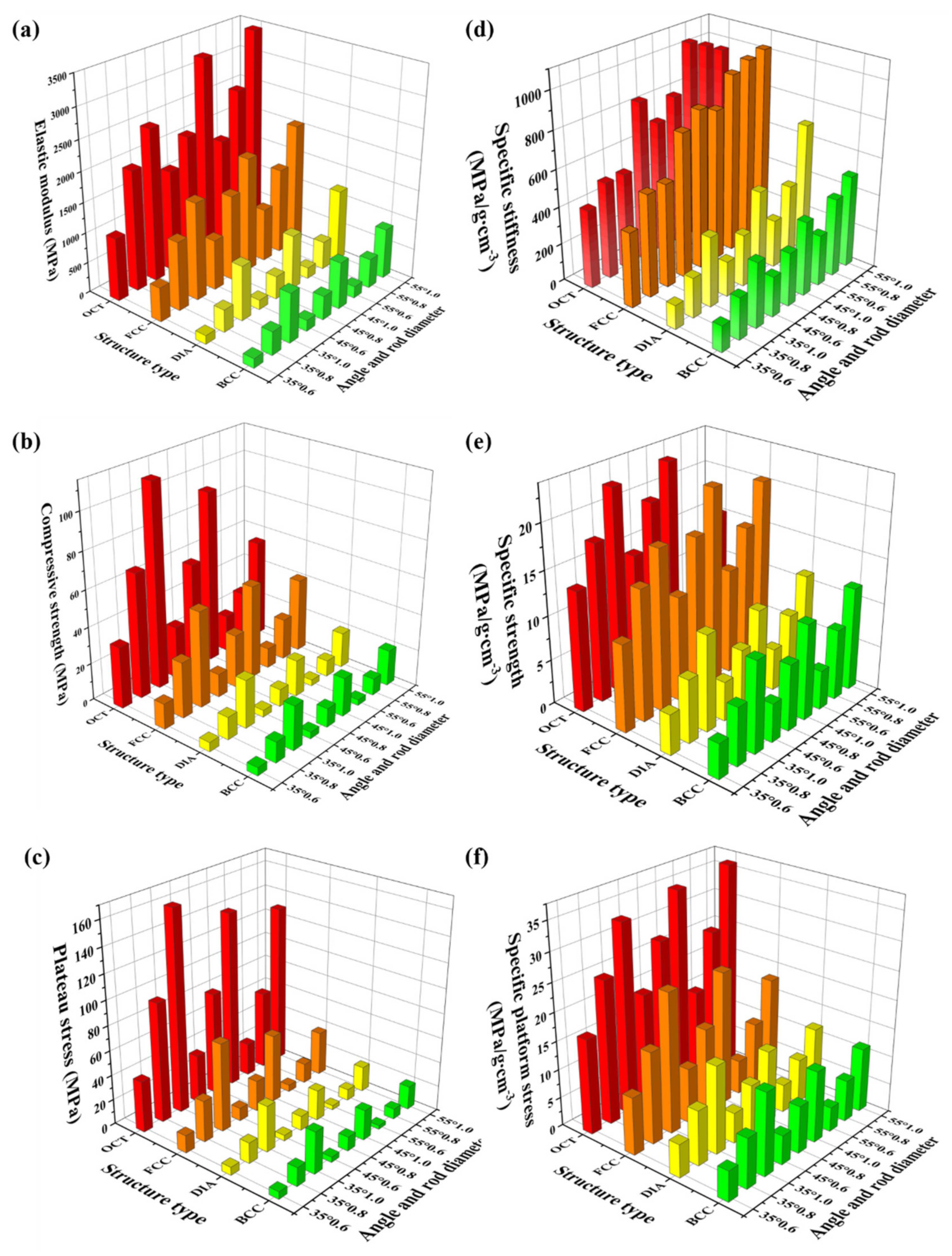
3.2.3. Specific Stiffness, Specific Compressive Stress, and Specific Plateau Stress
3.3. Energy Absorption Performance
4. Discussion
4.1. Layered Deformation Behavior in Lattice Structures
4.2. Impact of Structural Design on Performance
4.2.1. Impact of Lattice Architecture on Performance
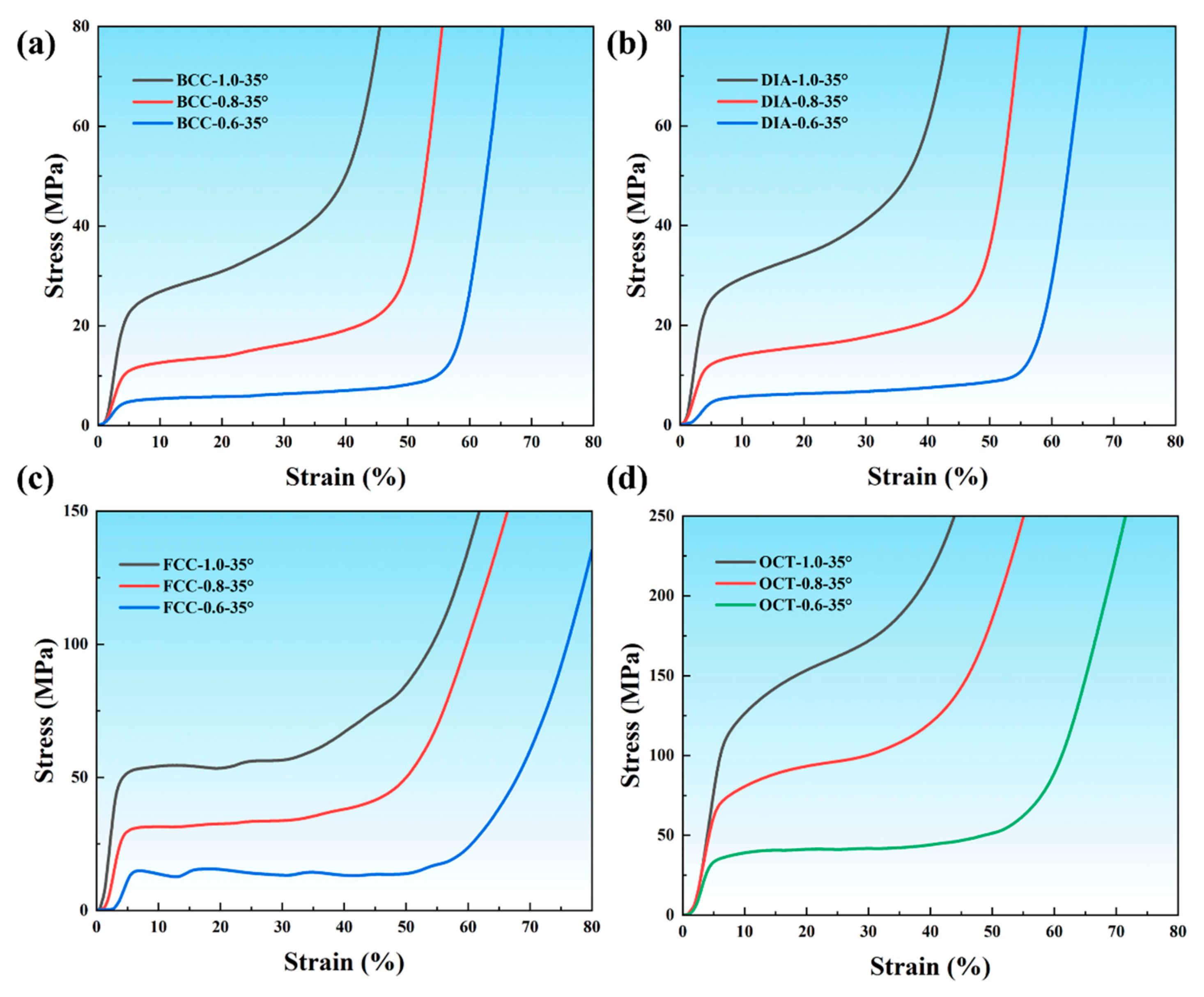
4.2.2. Impact of Rod Diameter on Performance
4.2.3. Impact of Inclination Angles on Performance
5. Conclusions
- The combination of LPBF technology and Invar36 alloy demonstrates excellent compatibility, enabling the precise fabrication of lattice structures. This synergy retains the unique mechanical properties of Invar36 alloy lattice structures, such as being lightweight (lowest apparent density 0.714 g·cm−3 at DIA architecture with 55° inclination angle, 0.6 mm strut diameter), high stiffness (highest stiffness 3429.89 MPa at OCT structure with 55° inclination angle, 1.0 mm strut diameter), and high strength (highest strength 110.65 MPa at OCT structure with 35° inclination angle, 1.0 mm strut diameter).
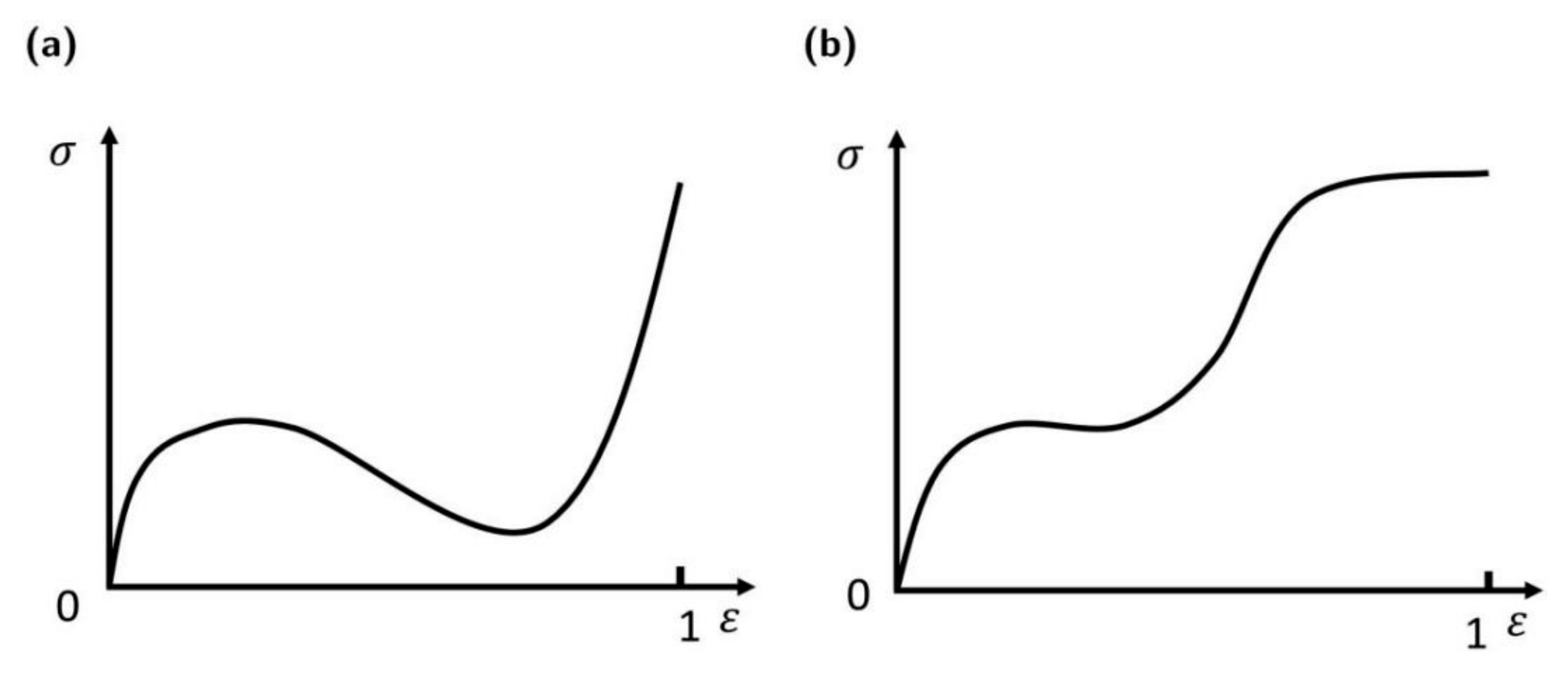
- The stress–strain curves during compression exhibit two distinct behaviors: hardening and softening trends. The hardening trend is predominantly observed in bending-dominated structures (BCC, DIA), where stress gradually increases with strain, struts progressively converge to form self-contact, and the deformation process remains stable. Conversely, the softening trend is more common in stretch-dominated structures (FCC, OCT), characterized by a rapid decline in stress after reaching a peak, localized structural failure due to stress concentration at nodes, and an unstable deformation process.
- The mechanical properties of lattice structures based on Invar36 alloys are strongly influenced by their architectural configuration, strut diameter, and inclination angle. In general, the OCT structure demonstrates the highest mechanical performance, followed by FCC, with BCC and DIA structures exhibiting comparatively lower strength. Additionally, increasing the strut diameter significantly enhances mechanical properties. As the inclination angle increases, the deformation mode gradually shifts from stretch-dominated to bending-dominated behavior.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cahn, R.W. An Unusual Nobel Prize. Notes Rec. R. Soc. 2005, 59, 145–153. [Google Scholar]
- Harner, L.L. Invar at 100 years. Adv. Mater. Process. 1997, 151, 31–34. [Google Scholar]
- Huang, G.; He, G.; Gong, X.; He, Y.; Liu, Y.; Huang, K. Additive manufacturing of Invar 36 alloy. J. Mater. Res. Technol. 2024, 30, 1241–1268. [Google Scholar]
- Sahoo, A.; Medicherla, V.R.R. Fe-Ni Invar alloys: A review. Mater. Today Proc. 2021, 43, 2242–2244. [Google Scholar]
- Chen, Y.; Wang, W.; Yang, Z.; Yan, J.; Chen, X.; Wang, R.; Ran, M. Microstructure and mechanical properties of B4C reinforced Invar 36 composites fabricated by laser powder bed fusion. Compos. Commun. 2025, 53, 102202. [Google Scholar]
- Bekir, A.; Mehmet, K.; Fuat, E. The puzzling thermal expansion behavior of invar alloys: A review on process-structure-property relationship. Crit. Rev. Solid State Mater. Sci. 2024, 49, 254–307. [Google Scholar]
- Chinchanikar, S.; Shaikh, A.A. A Review on Machine Learning, Big Data Analytics, and Design for Additive Manufacturing for Aerospace Applications. J. Mater. Eng. Perform. 2022, 31, 6112–6130. [Google Scholar]
- Ashby, M.F.; Evans, A.; Fleck, N.A.; Gibson, L.J.; Hutchinson, J.W.; Wadley, H.N.G.; Delale, F. Metal Foams: A Design Guide. Appl. Mech. Rev. 2001, 54, B105–B106. [Google Scholar]
- Ashby, M.F. The properties of foams and lattices, Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2006, 364, 15–30. [Google Scholar]
- Abdulhadi, H.S.; Fadeel, A.; Alwattar, T.A.; Mian, A. Developing scaling laws to predict compressive mechanical properties and determine geometrical parameters of modified BCC lattice structures. Eng. Rep. 2022, 5, e12566. [Google Scholar]
- Li, N.; Pang, S.; Chen, S.; Liu, Y.; Aiyiti, W.; Chen, Z. Design and application of hybrid lattice metamaterial structures with high energy absorption and compressive resistance. J. Mater. Res. Technol. 2024, 33, 7100–7112. [Google Scholar]
- Park, S.J.; Lee, J.H.; Yang, J.; Heogh, W.; Kang, D.; Yeon, S.M.; Kim, S.H.; Hong, S.; Son, Y.; Park, J. Lightweight injection mold using additively manufactured Ti-6Al-4V lattice structures. J. Manuf. Process. 2022, 79, 759–766. [Google Scholar]
- Sun, Z.; Gong, Y.; Tian, Y.; Lang, J.; Zhang, J.; Zhao, L.; Hu, N. Design and mechanical properties of layered gradient lattice structures based on additive manufacturing. Addit. Manuf. Front. 2025, 4, 200188. [Google Scholar]
- Li, P.Y.; Ma, Y.E.; Sun, W.B.; Qian, X.; Zhang, W.; Wang, Z.H. Fracture and failure behavior of additive manufactured Ti6Al4V lattice structures under compressive load. Eng. Fract. Mech. 2021, 244, 107537. [Google Scholar]
- Kaur, M.; Yun, T.G.; Han, S.M.; Thomas, E.L.; Kim, W.S. 3D printed stretching-dominated micro-trusses. Mater. Des. 2017, 134, 272–280. [Google Scholar]
- Wu, Z.-J.; Li, F.-M.; Zhang, C. Vibration band-gap properties of three-dimensional Kagome lattices using the spectral element method. J. Sound Vib. 2015, 341, 162–173. [Google Scholar]
- Ataee, A.; Li, Y.; Fraser, D.; Song, G.; Wen, C. Anisotropic Ti-6Al-4V gyroid scaffolds manufactured by electron beam melting (EBM) for bone implant applications. Mater. Des. 2018, 137, 345–354. [Google Scholar]
- Campanelli, S.L.; Casalino, G.; Contuzzi, N.; Ludovico, A.D. Taguchi Optimization of the Surface Finish Obtained by Laser Ablation on Selective Laser Molten Steel Parts. Procedia CIRP 2013, 12, 462–467. [Google Scholar] [CrossRef]
- Wang, X.W.; Ho, J.Y.; Leong, K.C. An experimental investigation of single droplet impact cooling on hot enhanced surfaces fabricated by selective laser melting. Int. J. Heat Mass Transf. 2018, 120, 652–670. [Google Scholar]
- Huang, S.; Liu, H.; Du, L.; Gong, L.; Xie, Y.; Kong, Q.; Yao, Z. Effects of different post-processing temperatures on the microstructure and mechanical properties of TiC-Ni cermets fabricated by selective laser melting. Int. J. Refract. Met. Hard Mater. 2025, 128, 107097. [Google Scholar]
- Fu, J.; Li, H.; Song, X.; Fu, M.W. Multi-scale defects in powder-based additively manufactured metals and alloys. J. Mater. Sci. Technol. 2022, 122, 165–199. [Google Scholar]
- Chen, W.; Yang, J.; Kong, H.; Helou, M.; Zhang, D.; Zhao, J.; Jia, W.; Liu, Q.; He, P.; Li, X. Fatigue behaviour and biocompatibility of additively manufactured bioactive tantalum graded lattice structures for load-bearing orthopaedic applications. Mater. Sci. Eng. C 2021, 130, 112461. [Google Scholar]
- Xiao, Z.; Yu, W.; Fu, H.; Deng, Y.; Wu, Y.; Zheng, H. Recent progress on microstructure manipulation of aluminium alloys manufactured via laser powder bed fusion. Virtual Phys. Prototyp. 2023, 18, e2125880. [Google Scholar] [CrossRef]
- Jing, C.; Zhu, Y.; Wang, J.; Wang, F.; Lu, J.; Liu, C. Investigation on Morphology and Mechanical Properties of Rod Units in Lattice Structures Fabricated by Selective Laser Melting. Materials 2021, 14, 3994. [Google Scholar] [CrossRef]
- Han, Z.; Guo, F.; Zhang, Q.; Wen, W.; Yu, G. Numerical Simulation and Experimental Analysis of Compressive Mechanical Properties of Metal Material Lattice for Additive Manufacturing. In Proceedings of the IEEE 18th Conference on Industrial Electronics and Applications (ICIEA), Ningbo, China, 18–22 August 2023; pp. 733–738. [Google Scholar]
- He, G.; Peng, X.; Zhou, H.; Huang, G.; Xie, Y.; He, Y.; Liu, H.; Huang, K. Superior Mechanical Properties of Invar36 Alloy Lattices Structures Manufactured by Laser Powder Bed Fusion. Materials 2023, 16, 4433. [Google Scholar] [CrossRef]
- Huang, G.; He, G.; Peng, X.; He, Y.; Chen, H.; Huang, K.; Liu, Y. Effect of processing parameters on the microstructure, mechanical properties and thermal expansion behavior of Invar 36 alloy manufactured by laser powder bed fusion. Mater. Sci. Eng. A 2024, 897, 146329. [Google Scholar] [CrossRef]
- Huang, G.; He, G.; Liu, Y.; Huang, K. Anisotropy of microstructure, mechanical properties and thermal expansion in Invar 36 alloy fabricated via laser powder bed fusion. Addit. Manuf. 2024, 82, 104025. [Google Scholar]
- ISO 13314:2011; Mechanical Testing of Metals. Ductility Testing. Compression Test for Porous and Cellular Metals. ISO: Geneva, Switzerland, 2012.
- Deshpande, V.S.; Ashby, M.F.; Fleck, N.A. Foam topology: Bending versus stretching dominated architectures. Acta Mater. 2001, 49, 1035–1040. [Google Scholar]
- Miltz, J.; Gruenbaum, G. Evaluation of Cushioning Properties of Plastic Foams from Compressive Measurements. Polym. Eng. Sci. 1981, 21, 1010–1014. [Google Scholar]
- Chen, W.; Nardhi, D. Experimental study of crush behaviour of sheet aluminium foam-filled sections. Int. J. Crashworthiness 2000, 5, 447–468. [Google Scholar] [CrossRef]
- Hazeli, K.; Babamiri, B.B.; Indeck, J.; Minor, A.; Askari, H. Microstructure-topology relationship effects on the quasi-static and dynamic behavior of additively manufactured lattice structures. Mater. Des. 2019, 176, 107826. [Google Scholar]
- Hairi, Z.; Hao, Z.; Zuoxin, Z.; Huizhong, Z.; Xiaoyu, Z.; Jianzhong, Y.; Hongshuai, L.; Fusheng, H. Energy absorption diagram characteristic of metallic self-supporting 3D lattices fabricated by additive manufacturing and design method of energy absorption structure. Int. J. Solids Struct. 2021, 226–227, 111082. [Google Scholar]
- Geng, X.; Lu, Y.; Liu, C.; Li, W.; Yue, Z. Fracture characteristic analysis of cellular lattice structures under tensile load. Int. J. Solids Struct. 2019, 163, 170–177. [Google Scholar] [CrossRef]
- Huang, Y.; Xue, Y.; Wang, X.; Han, F. Mechanical behavior of three-dimensional pyramidal aluminum lattice materials. Mater. Sci. Eng. A 2017, 696, 520–528. [Google Scholar] [CrossRef]
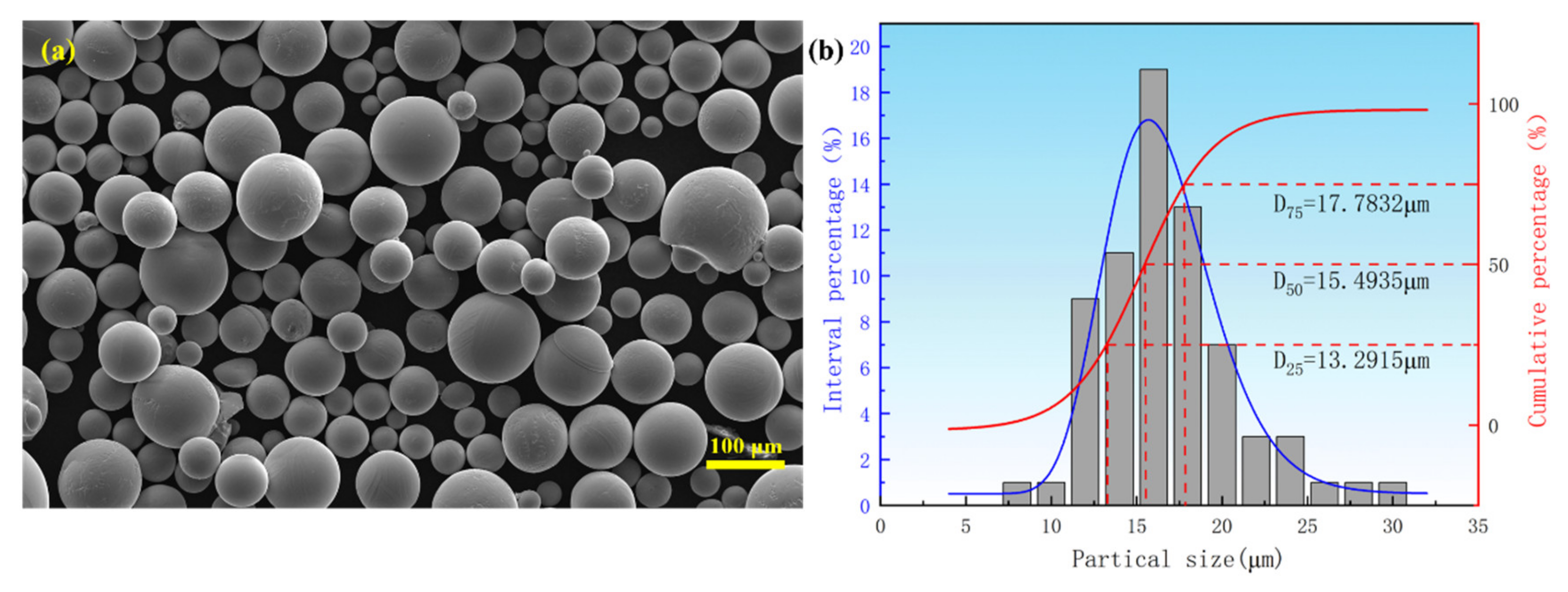
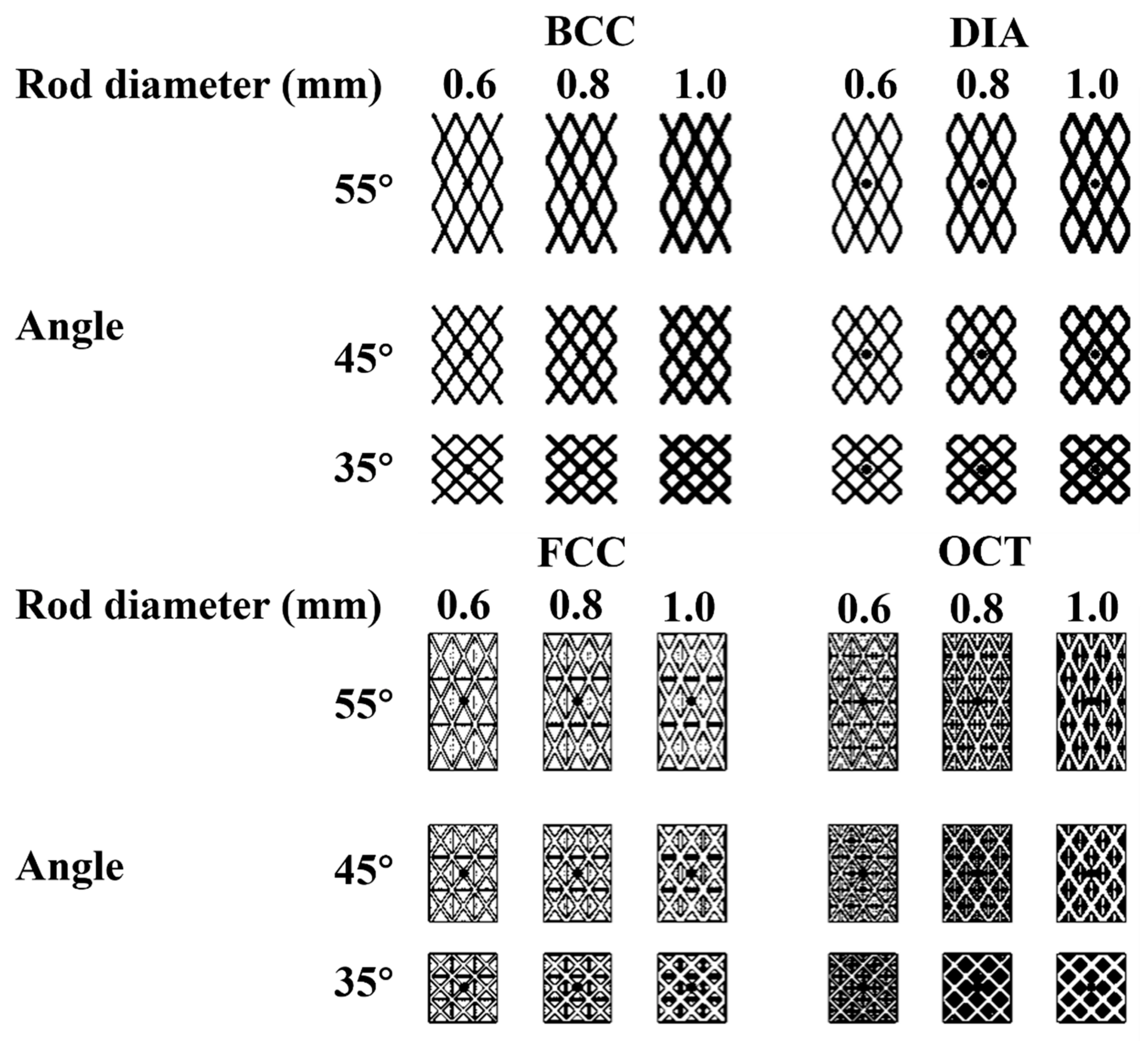






| Elements | C | Si | Mn | P | Ni | S | Cr | Co | O |
|---|---|---|---|---|---|---|---|---|---|
| wt.% | 0.011 | 0.13 | 0.29 | 0.004 | 35.8 | 0.002 | 0.005 | 0.03 | 0.000284 |
| Structure | Dip Angle | Stem Diameter (mm) | Apparent Density (g·cm−3) | Relative Density |
|---|---|---|---|---|
| BCC | 35° | 0.6 | 1.124 | 19.28% |
| 0.8 | 1.722 | 30.96% | ||
| 1.0 | 2.338 | 46.17% | ||
| 45° | 0.6 | 0.848 | 13.89% | |
| 0.8 | 1.377 | 24.51% | ||
| 1.0 | 1.946 | 38.81% | ||
| 55° | 0.6 | 0.715 | 11.57% | |
| 0.8 | 1.158 | 19.97% | ||
| 1.0 | 1.682 | 32.41% | ||
| DIA | 35° | 0.6 | 1.121 | 19.28% |
| 0.8 | 1.731 | 30.96% | ||
| 1.0 | 2.420 | 45.56% | ||
| 45° | 0.6 | 0.852 | 14.30% | |
| 0.8 | 1.368 | 24.92% | ||
| 1.0 | 1.934 | 35.95% | ||
| 55° | 0.6 | 0.714 | 11.57% | |
| 0.8 | 1.169 | 19.39% | ||
| 1.0 | 1.727 | 27.49% | ||
| FCC | 35° | 0.6 | 1.408 | 26.87% |
| 0.8 | 2.068 | 38.53% | ||
| 1.0 | 2.903 | 51.34% | ||
| 45° | 0.6 | 1.077 | 20.83% | |
| 0.8 | 1.663 | 31.45% | ||
| 1.0 | 2.342 | 42.48% | ||
| 55° | 0.6 | 0.925 | 16.49% | |
| 0.8 | 1.428 | 24.88% | ||
| 1.0 | 2.002 | 32.41% | ||
| OCT | 35° | 0.6 | 2.477 | 42.64% |
| 0.8 | 3.832 | 59.58% | ||
| 1.0 | 4.863 | 70.68% | ||
| 45° | 0.6 | 1.978 | 35.13% | |
| 0.8 | 3.010 | 49.02% | ||
| 1.0 | 4.049 | 60.87% | ||
| 55° | 0.6 | 1.703 | 31.54% | |
| 0.8 | 2.504 | 44.56% | ||
| 1.0 | 3.575 | 56.08% |
| Structure | Dip Angle | Rod Diameter (mm) | Elastic Modulus (MPa) | Compressive Strength (MPa) | Plateau Stress (MPa) |
|---|---|---|---|---|---|
| BCC | 35° | 0.6 | 157.85 | 4.46 | 6.03 |
| 0.8 | 387.75 | 11.26 | 15.09 | ||
| 1.0 | 814.92 | 24.08 | 33.80 | ||
| 45° | 0.6 | 182.89 | 3.70 | 4.35 | |
| 0.8 | 394.26 | 10.29 | 11.41 | ||
| 1.0 | 773.67 | 20.99 | 24.32 | ||
| 55° | 0.6 | 194.93 | 3.16 | 3.06 | |
| 0.8 | 487.25 | 9.21 | 8.42 | ||
| 1.0 | 834.24 | 19.60 | 18.94 | ||
| DIA | 35° | 0.6 | 144.50 | 5.10 | 6.52 |
| 0.8 | 372.16 | 12.33 | 16.62 | ||
| 1.0 | 907.38 | 26.22 | 37.24 | ||
| 45° | 0.6 | 161.18 | 3.80 | 4.56 | |
| 0.8 | 382.97 | 9.46 | 11.56 | ||
| 1.0 | 899.46 | 19.92 | 24.53 | ||
| 55° | 0.6 | 183.84 | 3.39 | 3.50 | |
| 0.8 | 467.53 | 8.92 | 9.06 | ||
| 1.0 | 1193.26 | 19.40 | 20.30 | ||
| FCC | 35° | 0.6 | 565.99 | 13.87 | 14.20 |
| 0.8 | 1141.04 | 30.44 | 33.28 | ||
| 1.0 | 1615.83 | 52.40 | 71.26 | ||
| 45° | 0.6 | 836.97 | 12.74 | 10.47 | |
| 0.8 | 1420.42 | 29.05 | 25.09 | ||
| 1.0 | 1900.66 | 51.33 | 55.16 | ||
| 55° | 0.6 | 888.19 | 11.01 | 5.58 | |
| 0.8 | 1430.40 | 22.72 | 16.07 | ||
| 1.0 | 2049.92 | 40.65 | 35.87 | ||
| OCT | 35° | 0.6 | 1045.70 | 33.63 | 41.40 |
| 0.8 | 1994.16 | 68.05 | 96.52 | ||
| 1.0 | 2525.92 | 110.65 | 162.26 | ||
| 45° | 0.6 | 1697.78 | 28.94 | 39.08 | |
| 0.8 | 2139.08 | 59.00 | 83.20 | ||
| 1.0 | 3285.65 | 94.07 | 142.03 | ||
| 55° | 0.6 | 1803.18 | 20.15 | 26.81 | |
| 0.8 | 2536.14 | 28.96 | 63.63 | ||
| 1.0 | 3429.89 | 54.01 | 129.12 |
| Structure | Dip Angle | Rod Diameter (mm) | Specific Stiffness (MPa/g·cm−3) | Specific Compressive Stress (MPa/g·cm−3) | Specific Plateau Stress (MPa/g·cm−3) |
|---|---|---|---|---|---|
| BCC | 35° | 0.6 | 140.38 | 3.97 | 5.36 |
| 0.8 | 225.18 | 6.54 | 8.76 | ||
| 1.0 | 348.52 | 10.30 | 14.46 | ||
| 45° | 0.6 | 215.77 | 4.37 | 5.13 | |
| 0.8 | 286.22 | 7.47 | 8.28 | ||
| 1.0 | 397.64 | 10.79 | 12.50 | ||
| 55° | 0.6 | 272.74 | 4.42 | 4.28 | |
| 0.8 | 420.67 | 7.95 | 7.27 | ||
| 1.0 | 495.89 | 11.65 | 11.26 | ||
| DIA | 35° | 0.6 | 128.85 | 4.55 | 5.81 |
| 0.8 | 214.96 | 7.12 | 9.60 | ||
| 1.0 | 374.95 | 10.83 | 15.39 | ||
| 45° | 0.6 | 189.15 | 4.46 | 5.35 | |
| 0.8 | 280.02 | 6.92 | 8.45 | ||
| 1.0 | 465.02 | 10.30 | 12.68 | ||
| 55° | 0.6 | 257.33 | 4.75 | 4.90 | |
| 0.8 | 399.95 | 7.63 | 7.75 | ||
| 1.0 | 690.77 | 11.23 | 11.75 | ||
| FCC | 35° | 0.6 | 402.06 | 9.85 | 10.09 |
| 0.8 | 551.67 | 14.72 | 16.09 | ||
| 1.0 | 556.60 | 18.05 | 24.55 | ||
| 45° | 0.6 | 776.98 | 11.83 | 9.72 | |
| 0.8 | 854.14 | 17.47 | 15.09 | ||
| 1.0 | 811.44 | 21.91 | 23.55 | ||
| 55° | 0.6 | 960.06 | 11.90 | 6.03 | |
| 0.8 | 1001.39 | 15.91 | 11.25 | ||
| 1.0 | 1023.92 | 20.30 | 17.92 | ||
| OCT | 35° | 0.6 | 422.23 | 13.58 | 16.72 |
| 0.8 | 520.43 | 17.76 | 25.19 | ||
| 1.0 | 519.44 | 22.75 | 33.37 | ||
| 45° | 0.6 | 858.18 | 14.63 | 19.75 | |
| 0.8 | 710.70 | 19.60 | 27.64 | ||
| 1.0 | 811.55 | 23.24 | 35.08 | ||
| 55° | 0.6 | 1059.11 | 11.84 | 15.75 | |
| 0.8 | 1012.69 | 11.56 | 25.41 | ||
| 1.0 | 959.43 | 15.11 | 36.12 |
| Structure | Dip Angle | Stem Diameter (mm) | Energy Absorption (mJ/mm3) | Specific Energy Adsorption (J/g) |
|---|---|---|---|---|
| BCC | 35° | 0.6 | 2.97 | 2.64 |
| 0.8 | 7.75 | 4.50 | ||
| 1.0 | 20.25 | 8.66 | ||
| 45° | 0.6 | 2.19 | 2.58 | |
| 0.8 | 5.72 | 4.15 | ||
| 1.0 | 12.08 | 6.21 | ||
| 55° | 0.6 | 1.62 | 2.27 | |
| 0.8 | 4.49 | 3.88 | ||
| 1.0 | 10.03 | 5.96 | ||
| DIA | 35° | 0.6 | 3.13 | 2.79 |
| 0.8 | 8.55 | 4.94 | ||
| 1.0 | 23.43 | 9.68 | ||
| 45° | 0.6 | 2.24 | 2.63 | |
| 0.8 | 5.76 | 4.21 | ||
| 1.0 | 12.41 | 6.42 | ||
| 55° | 0.6 | 1.77 | 2.48 | |
| 0.8 | 4.66 | 3.99 | ||
| 1.0 | 10.62 | 6.15 | ||
| FCC | 35° | 0.6 | 6.42 | 4.56 |
| 0.8 | 16.50 | 7.98 | ||
| 1.0 | 36.82 | 12.68 | ||
| 45° | 0.6 | 4.44 | 4.12 | |
| 0.8 | 12.51 | 7.52 | ||
| 1.0 | 28.01 | 11.96 | ||
| 55° | 0.6 | 2.81 | 3.04 | |
| 0.8 | 7.95 | 5.57 | ||
| 1.0 | 17.57 | 8.78 | ||
| OCT | 35° | 0.6 | 19.65 | 7.93 |
| 0.8 | 48.75 | 12.72 | ||
| 1.0 | 78.22 | 16.09 | ||
| 45° | 0.6 | 18.30 | 9.25 | |
| 0.8 | 39.89 | 13.25 | ||
| 1.0 | 70.37 | 17.38 | ||
| 55° | 0.6 | 13.46 | 7.91 | |
| 0.8 | 30.51 | 12.18 | ||
| 1.0 | 58.66 | 16.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, J.; Yan, J.; Peng, X.; He, G.; Huang, K. Mechanical Properties Regulation of Invar36 Alloy Metastructures Manufactured by Laser Powder Bed Fusion. Metals 2025, 15, 773. https://doi.org/10.3390/met15070773
Feng J, Yan J, Peng X, He G, Huang K. Mechanical Properties Regulation of Invar36 Alloy Metastructures Manufactured by Laser Powder Bed Fusion. Metals. 2025; 15(7):773. https://doi.org/10.3390/met15070773
Chicago/Turabian StyleFeng, Jianyu, Jialei Yan, Xiaoqiang Peng, Gening He, and Ke Huang. 2025. "Mechanical Properties Regulation of Invar36 Alloy Metastructures Manufactured by Laser Powder Bed Fusion" Metals 15, no. 7: 773. https://doi.org/10.3390/met15070773
APA StyleFeng, J., Yan, J., Peng, X., He, G., & Huang, K. (2025). Mechanical Properties Regulation of Invar36 Alloy Metastructures Manufactured by Laser Powder Bed Fusion. Metals, 15(7), 773. https://doi.org/10.3390/met15070773




