Abstract
Aluminum, boron, and titanium microalloyed into high-strength low-alloy boron steel exhibit a complex interplay, competing for nitrogen, with titanium demonstrating the highest affinity, followed by boron and aluminum. This competition affects the formation and distribution of nitrides, impacting the microstructure and mechanical properties of the steel. Titanium protects boron from forming BN and facilitates the nucleation of acicular ferrite, enhancing toughness. The segregation of boron to grain boundaries, rather than its precipitation as boron nitride, promotes the formation of martensite and thus the through-hardenability. Aluminum nitride is critical in controlling grain size through a pronounced pinning effect. In this study, we employ energy- and wavelength-dispersive X-ray spectroscopy and computer-aided particle analysis to analyze the phase content of 12 high-purity vacuum induction-melted samples. The primary objective of this study is to correctly describe the microstructural evolution in the Fe-Al-B-Ti-C-N system using the Calphad approach, with special emphasis on correctly predicting the dissolution temperatures of nitrides. A multicomponent database is constructed through the incorporation of available binary and ternary descriptions, employing the Calphad approach. The experimental findings regarding the solvus temperature of the involved nitrides are employed to validate the accuracy of the thermodynamic database. The findings offer a comprehensive understanding of the relative phase stabilities and the associated interplay among the involved elements Al, B, and Ti in the Fe-rich corner of the system. The type and size distribution of the stable nitrides in microalloyed steel have been demonstrated to exert a substantial influence on the properties of the material, thereby rendering accurate predictions of phase stabilities of considerable relevance.
1. Introduction
High-strength low-alloy (HSLA) boron steels are widely recognized for their enhanced mechanical properties, which are achieved through the precise control of their microstructure [1]. Reaching the full potential of alloying elements in microalloyed steel is dependent on correctly understanding the variables processing, thermodynamics, and kinetics [2] to reach the desired mechanical properties with reasonable costs [1]. The addition of boron to microalloyed steel has been shown to enhance through-hardenability. Furthermore, the formation of bainite and martensite is promoted by alloying the steel with only about ten wt.-ppm of boron [3,4,5]. The phenomenon referred to as the ‘boron effect’ has been observed to enhance through-hardenability rather than hardness [6]. The underlying mechanism of this advantageous effect involves the retention of boron in solid solution in the matrix, thereby preventing the formation of boron nitride (BN) [7]. In order to protect the steel from the occurrence of this second phase formation, i.e., binding the nitrogen instead of BN, aluminum or titanium are utilized [7]. Titanium, with its high affinity for nitrogen [8], primarily forms titanium nitrides (TiN), which are known to refine the grain structure and improve toughness [9]. Aluminum nitride (AlN) has been shown to be particularly effective in controlling grain size due to its pronounced pinning effect, which is known to inhibit grain growth [10]. The interplay between these elements and their respective roles in the nitride stabilization is critical in determining the final microstructure and mechanical properties of the steel. The interactive role of Al, B, and Ti in the formation and dissolution of nitride precipitates, as well as the associated content of boron in solid solution for the consolidation of martensite, is a subject of considerable concern [7].
In their study, Wang et al. [8] examined the precipitation of AlN, BN, and TiN in boron-bearing steel by using available solubility product descriptions from the literature for describing the stability of the nitrides, concluding that the precipitation of TiN occurs predominantly before the precipitation of BN and AlN. In a related study, Gontijo et al. [11] report on the effects of combined addition of B and Ti in microalloyed steel. The authors find that the formation of TiN is preferential over BN and AlN with regard to ductility behavior. This phenomenon occurs due to segregated B at grain boundaries, which retards the formation of ferrite films at the austenite grain boundaries. To date, a detailed investigation of the competing stabilities of the nitrides from Al, B, and Ti in microalloyed steel, either experimental or simulated, is lacking.
The objective of this study is to apply Calphad [12] in order to elucidate and validate the thermodynamic behavior and microstructural evolution of microalloyed steels containing aluminum, boron, and titanium nitrides in the Fe-rich Fe-Al-B-Ti-C-N system. Experimentally, a combination of advanced analytical techniques, including energy-dispersive X-ray spectroscopy (EDS) in combination with computer-aided EDS and wavelength-dispersive X-ray spectroscopy, is employed to analyze 12 high-purity vacuum induction-melted samples. Furthermore, the material is subjected to annealing under equilibrium-like durations in a dilatometer at varying temperatures. This procedure is employed to ascertain the solvus temperatures of the implicated precipitates. The experimental results are used to validate the accuracy of the integration of binary and ternary reassessments for multi-component microalloyed steel [13,14,15,16,17] in the thermodynamic multi-component database ME-Fe_CDLIPE2.0.2.tdb [18]. Particular emphasis is put on the solvus temperatures (Tsol) of the relevant nitrides as a function of varying chemical compositions in the Fe-rich side in diluted systems. We provide an assessed Gibbs energy description of the BN phase, giving high weight to an accurate solubility description.
The alloying of Al, B, and Ti influences the properties of the material and determines the type and distribution of the stable nitrides. These nitrides subsequently influence the characteristics of the material. The utilization of Al for deoxidation in steel was predominant until the discovery regarding the pivotal influence of AlN precipitates on steel properties. The ability of AlN to impede austenite grain coarsening through the pinning of grain boundaries [19] is well-documented. Conversely, the presence of excessive primary AlN has been shown to induce embrittlement [10,20]. The stoichiometric phase [21] AlN possesses a hexagonal wurtzite structure with a space group of P63mc. Upon cooling, AlN begins to become stable in the austenite (γ) region of microalloyed steel, predominantly nucleating heterogeneously at grain boundaries [10] due to a high volumetric misfit of 70% between the γ-matrix and AlN-precipitate [10,22,23]. In the ferrite (α) phase, the thermomechanical processing route and the nominal Al and N contents [24,25,26,27] are pivotal factors in determining the initial phase, representing metastable cubic rock-salt structured AlN, with a size ranging from 5 to 10 nanometers. This metastable AlN can subsequently be converted into the stable hexagonal AlN modification [28].
The “boron effect” has been demonstrated to be beneficial; however, it only occurs when solute B atoms are present at grain boundaries, which makes the formation of BN a matter of significant concern. BN occurs as hexagonal BN type (Pearson symbol hP4 [29]) in steel [7] and the nucleation of BN has been reported to occur at austenite grain boundaries [30]. The size of the BN precipitates, ranging from 5 to 30 µm, is reported to be dependent on the time–temperature profile of the applied heat treatments [31]. However, this size range is too coarse to have any beneficial effect on the properties of the material [7].
Titanium exhibits a strong affinity for carbon and nitrogen, which leads to the formation of TiN and TiC precipitates. TiN nucleates as face-centered cubic (fcc) phase, often referred to as MX phase, with M being Ti, V, or Nb and X being C and N [2]. The high thermal and chemical stability of the carbonitride results in a high Tsol of the precipitates, even at low fractions of Ti [32]. Carbonitrides have been shown to impede grain growth and recrystallization, which in turn alters the transformation characteristics and improves the properties of the material [9]. The beneficial influence of Ti precipitates is only possible in fully killed steels that have undergone deoxidation with Al due to the strong deoxidizing characteristics and the subsequent formation of titanium oxide [33].
Abnormal grain growth (AGG) in steel is a phenomenon in which certain grains grow significantly larger than others during heat treatment processes such as annealing [34]. This can result in a bimodal grain size distribution that affects the properties of the material. AGG typically occurs in steel at elevated temperatures after the dissolution of precipitates such as Nb or V carbonitrides, which are known to exert a strong solute drag effect on grain boundary mobility [35,36,37].
2. The Thermodynamics of the Fe-C-N-A-B-Ti System in the Fe-Rich Corner in Microalloyed Steel
Typically, the available binary and ternary phase diagrams of a multi-component system encompass the broad spectrum of compositions well, though they do not concentrate on a specific composition space corner. In the case of microalloyed steel with diluted fractions of certain elements, this can result in substantial discrepancies between the predicted and observed phase stability [38]. It is therefore imperative to accurately delineate the thermodynamics and phase boundaries of the constituent phases within the dilute microalloying range to ensure the efficacy of thermokinetic simulations with high predictive capabilities. This study employs available thermodynamic descriptions of binary and ternary systems, combining them into a comprehensive thermodynamic database. The objective of the database setup is to accurately predict the phase stabilities for the Fe-rich side of the multicomponent system Fe-C-N-Al-B-Ti, with a particular focus on the interaction of Al, B, and Ti with nitrogen. This particularly evaluates whether the approach of combining binary and ternary thermodynamics, while keeping further extension to the quaternary and quinary subsystems and beyond ideal (i.e., without additional multi-component excess Gibbs energies optimizations) yields sufficient predictive power for technological alloys, which would be represented by low deviations between experimental data and calculated results.
2.1. Calphad Modeling
For the establishment of the thermodynamic database, the CALPHAD (CALculation of PHAse Diagrams) approach [12,39] is used. In multi-component systems, it is essential to characterize the thermodynamics of all lower-order systems accurately. For pure components, the thermodynamic data is taken from Dinsdale [40]. The Redlich–Kister–Muggianu model for the Gibbs excess energy description for the phases liquid (L), bcc_A2 (bcc, ferrite, α-Fe), and fcc_A1 (fcc, austenite, γ-Fe) is used. The liquid phase uses a random substitutional solution model. Phases bcc and fcc are described by a regular solution model. Carbides and nitrides are described with sublattice models. The following section provides a critical review of the composing subsystems.
2.2. Subsystems with Relevance in Microalloyed Steel
Fe-based databases are determined by the binary systems containing Fe, i.e., Fe-C, Fe-N, Fe-B, Fe-Ti, and Fe-Al. Intrinsic stabilities of non-ferrous nitrides and carbo-nitrides are relevant, so the Al-N, Al-C, Al-Ti, Ti-C, Ti-N, and B-N systems are added. The Fe-C system, actually representing the steel matrix for the precipitation, is of significant importance to the iron and steel industry, as evidenced by the extensive reviews conducted [13,41,42]. The assessment by Gustafson [13] has gained considerable recognition within Calphad databases [43]. In addition to the conventional liquid, bcc, and fcc phases, several iron carbides have been identified, with Fe3C (cementite) [13,44] being the sole metastable carbide. In fact, competitive nitrogen solubility in iron, versus nitride stabilization, is relevant, and thus also the Fe-N system, with the description by Frisk proving reliable [14]. A similar question concerns boron solubility in the steel matrix, versus boride stabilization, and in this context the Fe-B system, which has been evaluated by various researchers [45,46,47,48], with some providing thermodynamic calculations [46,49,50,51]. The primary difference among models lies in the site of boron dissolution within steel phases. Boron can be considered the smallest substitutional element [15,49], the largest interstitial element [50], or a mixed substitutional-interstitial element in bcc-Fe and fcc-Fe [45,52,53,54]. Raghavan [55] gives a brief review of experimental data for the extension to the Fe-B-N system. Tomashik [56] provides an up-to-date review of the available data and claims that ternary phases do not occur. Fountain and Chipman [57] demonstrate a decrease in nitrogen solubility with increasing boron content. The Fe-B, Fe-B-N, and Fe-B-C system has previously been evaluated and in part re-optimized by the present author [58], determining the influence of boron on the solvus temperature of BN, and the liquidus and solidus temperatures of the system. The descriptions of these systems are taken as suggested by Führer et al. [58]. The description of the Al-N system is taken from Saunders [59]. In a recent publication [27], the Fe-Al-N-C system is reassessed for the Fe-rich corner in dilute systems, with particular emphasis on accurate thermodynamic description of the AlN phase. Ti-carbonitrides, which are classified as part of the MX-class [60], are modeled as a FCC solid solution. The model parameters are defined in such a way as to allow for the separation between the austenitic steel phase and the carbo-nitride (MX) phase in the Fe-base system. The multi-component model is expressed as (Fe, Ti)(C, N, Va) within the compound energy formalism.
The binary subsystem description for Ti-C is adopted from the Matcalc steel database [61]. The parameters for Fe-Ti and Ti-N are taken from Lee [16]. In the context of the simulation, the ternary subsystem that has been determined to be of major importance is composed of Fe-Al-C and Fe-Al-N, as delineated by Chin et al. and Hillert and Jonsson [62]. The ternary extension to Fe-Ti-C system is taken from Jacob et al. [60]. Table 1 provides a summary of the subsystems used for describing the Fe-C-N-Al-B-Ti system.

Table 1.
Summary of binary and ternary subsystems used in the present study.
2.3. Gibbs Energy Description of the BN-Phase
The solubility product, K, defines the concentration product between B and N in weight percent, where BN is dissolved in the steel matrix at a given temperature. Solubility products are then plotted logarithmically, log(K), as a function of temperature. The lower the log(K), the lower the respective concentrations of B and N at which BN is completely dissolved.
Due to decreasing element concentrations with decreasing log(K) values, a higher sensitivity of the experimental detection method is required. In general, conducting an experimental investigation of the slope of the solubility product at low concentrations poses a significant challenge. Conversely, BN precipitation occurs at higher concentrations of B and N than given by K. It is self-evident that log(K) is typically lower at lower temperatures: the phase boundary between the steel matrix phase and the precipitate at low temperatures is usually at more dilute compositions than at higher temperatures. As illustrated in Figure 1, a comparison is presented between the experimentally evaluated solubility products [57,66,67] (full lines) and the calculated ones [68,69,70] (dotted lines) in the austenite.

Figure 1.
Full and dashed lines show a comparison of solubility products log(K) = log[B(wt.-%)·N(wt.-%)] in the austenite from experiments from the literature, adapted from Refs. [57,66,67], and assessed thermodynamic descriptions, adapted from Refs. [68,69,70], respectively. The red dotted line shows the result of the newly assessed description. Black crosses are the experimental results from Führer et al. adapted from Ref. [58]. (For the interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article).
The available descriptions can be divided into two groups, with higher and lower solubility product values. Führer et al. [58] provide a comprehensive overview of the substantial discrepancy between the two groups. Importantly, the groups are defined by their approach to either correctly describing thermodynamic quantities, such as enthalpy of formation ∆Hf, entropy S298, and heat capacity Cp298, or correctly depicting solubility limits. Usually, microscopic dissolution observation should be consistent with the thermodynamic properties of a phase, controlling this behavior, as it could be seen for AlN [27]. However, the authors [58] have demonstrated that, in order to accurately depict the phase stability and thermodynamic quantities of the BN phase, for consistency between dissolution and thermodynamic properties, it is imperative to take into account the pronounced segregation tendency of B atoms, in conjunction with the Calphad-type thermodynamic description. In this work, an alternative Gibbs energy description of the BN phase is presented. The objective of this description is to provide a comprehensive characterization of the experimentally accessible solubility products, which involves the pronounced segregation tendency of B atoms, illustrated in Equation (1),
It should be noted that this parameter proposal inevitably leads to different predicted thermodynamics of the BN phase. This results in deviations from the experimental values of Dworkin et al. [71] for enthalpy of formation (ΔHf), entropy (S298), and heat capacity (Cp298) of approximately 25 kJmol−1, 4 Jmol−1K−1, and < 0.1 Jmol−1K−1, respectively. The BN phase is regarded as fully stoichiometric (B)(N). For a more thorough examination of the BN phase description and a deeper discussion about the pertinent subsystems that contain boron, please refer to the extant literature [58,63].
3. Materials and Sample Characterization
3.1. Composition
In the present study, we used the Fe-Al-B-C-N alloying system with 4 and 5 variations in the B and Al contents from 0 to 0.083 wt.-% and from 0 to 0.4 wt.-%, respectively. In the Fe-Al-B-Ti-C-N system, the Ti microalloying content is varied from 0 to 0.042 wt.-% in four variations. The alloying of the material was carried out with high precision in a vacuum induction melting furnace, followed by a casting and forging process and a homogenizing annealing treatment at 1000 °C for ten hours in a vacuum furnace. The resulting composition of the elements C, Al, B, Ti, Mn, and S was measured by optical emission spectroscopy (OES) Thermofisher Type 4460 (Thermo Fisher Scientific, Waltham, MA, USA) and the N fraction by the LECO method [72,73] (Leco ON 736, LECO Corporation, St. Joseph, MO, USA) (see Table 2) with an uncertainty of five ppm and seven ppm, respectively. The numbers in the sample designations indicate the boron fraction in wt.-ppm and the Al and Ti fractions in tens of wt.-ppm. The sample geometries were cylindrical with Ø 5 mm and a height of 10 mm for EDS particle analysis. The stability of precipitates, e.g., AlN, in which Al can form oxides, can be influenced to a significant degree by the presence of impurities. Thus, particularly in the case of phase evaluation in microalloying steels, the utilization of vacuum induction melting for sample preparation is mandatory. It has been demonstrated to result in a significant reduction in impurity levels (see Table 2), with oxygen levels measured in parts per million (wt.). Due to the extremely low impurity levels, the influence of impurity elements on the stability of AlN, BN, and TiN is considered negligible.

Table 2.
Composition of the alloys produced using vacuum induction melting (wt..-%). Numbers in the sample labeling present boron in wt.-ppm and Al and Ti in tens of wt.-ppm.
3.2. Methods
3.2.1. Microstructure Analysis
The analysis of the resulting microstructures, focusing on AlN, BN, and TiN precipitates, was conducted using a ZEISS SIGMA scanning electron microscope (SEM) (carl zeiss microscopy gmbh, Oberkochen, Germany) equipped with a field emission gun operating at an electron beam voltage of 10 kV and a working distance of 10 mm. The chemical analysis was facilitated by EDS, while wavelength-dispersive spectroscopy (WDS) was employed for elements B and N with a low ordering number. The EDS detector utilized was an Octane elect super with a 70 mm2 detector size, while the WDS spectrometer was an EDAX Lambdaplus WDS [74] model (EDAX Inc., Mahwah, NJ, USA). The backscatter electron mode (BSE) in the SEM offers a favorable mass contrast for the precipitates, given their comparatively low atomic masses relative to Fe. For good statistical power, either 50 sections were observed manually in the SEM or computer-aided particle analysis was used. The former austenite grain size was revealed by using the etching reagent PM1998 [75]. The Tsol of the precipitates of the alloys from Table 2 were evaluated by annealing the samples at different temperatures in a Bähr dilatometer type 805 under a vacuum atmosphere with alteration steps of 30 °C for 30 min and then quenching them down to room temperature to “freeze” the microstructure. The temperature curve of the heat treatments is shown in Figure 2. A temperature resolution of 30 K was selected as a compromise between high resolution and the minimization of necessary experiments. It should be noted that unless otherwise specified, all heat treatments are assumed to have undergone heating and cooling rates of 70 K/s and 100 K/s, respectively.
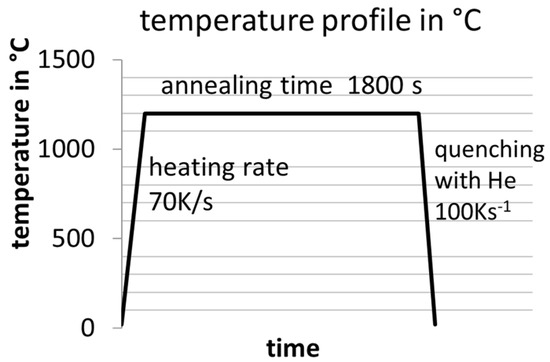
Figure 2.
Applied temperature–time profile in a Bähr dilatometer type 805 under vacuum conditions for determining Tsol of the nitrides.
3.2.2. EDS—Particle Analysis
In addition to the manual analysis of precipitates in the SEM, the computer-aided EDS particle analysis method (PA) [27] was employed. The analysis was conducted using a JEOL JSM-7800F scanning electron microscope (JEOL, Akishima, Japan) with a field emission gun at an operation voltage of 12 kV and an “Oxford X-MAXN” EDS detector (Oxford Instruments, Abingdon, UK) with a 50 mm2 detector size for the computer-aided EDS particle analysis (PA). The primary advantage of PA was the acquisition of substantial statistical data concerning precipitates, including their distribution at interfaces, mean particle size and distribution, and phase fractions. Notably, PA effectively addresses the challenge posed by small and sparse precipitates, particularly those of AlN [27]. The evaluation of particles was conducted in accordance with the methodology outlined by Führer et al. [27]. The salient characteristics of this approach are as follows: the lower detection limit is 60 nm, and the determination of particles is facilitated by their chemical composition. However, this approach is encumbered by the difficulty of detecting light elements with EDS, which introduces a degree of uncertainty. In contrast, the substantial expanse of the investigative domain, in conjunction with the implementation of automated evaluation methodologies, facilitates the consideration of a considerable array of precipitates. Consequently, this approach engenders the generation of reliable statistics concerning precipitate distributions. The particles are then identified using certain composition boundaries, as outlined in Table 3. For AlN and MnS, the recommendation for the selection limit proposed by Führer et al. [27] is adhered to. The presence of BN is indicated by the detection of boron or nitrogen. The solubility of other elements is minimal, and thus, the detection of BN is a reliable indicator of the presence of these elements. BN contains light elements but possesses a substantial diameter, a property that enables its detection through particle analysis. Given the classification of TiN as a carbonitride, the high solubility of carbon must be considered. Given the fact that carbon and nitrogen are light elements and titanium is more readily detected with EDS, the detection of titanium is sufficient for marking a particle as TiN. Upon the satisfaction of all criteria, the spatial coordinates, mean ECD, surface fraction, and precipitate size distribution of the particles are determined.

Table 3.
Selection limits for precipitates AlN, BN, TiN, MnS, and Al2O3 after particle analysis. Boundary conditions for elements are given in wt.-%.
4. Results
4.1. Initial Microstructure
Figure 3 shows the microstructure of the alloy with different B fractions after annealing in a vacuum furnace at 1000 °C for 10 h, followed by cooling to room temperature at 90 K/min and etching with Nital. The results clearly demonstrate a correlation between an increase in grain size and an increase in B fraction between 22 and 44 wt.-ppm boron alloying. This phenomenon has been well-documented in the literature concerning B-alloyed steel and is attributed to the absence of AlN, which is known for its strong grain boundary pinning force, due to the formation of the more stable BN. Conversely, BN is too coarse to have any influence on grain growth [7]. Figure 3 reveals no discernible influence on the grain size between parts a and b for 0 and 22 wt.-ppm. As demonstrated in Table 4 and Figure 4 experimental and thermodynamic equilibrium simulation results, respectively, it is shown that AlN is stable at 1000 °C for alloys Al29B0 and Al29B22 and thus effectively retards grain growth. This indicates that the correct prediction of phase relations is highly relevant for interpretations of the according microstructure.

Figure 3.
Microstructure of the samples after homogenization annealing in the vacuum furnace at 1000 °C for 10 h and subsequent cooling to room temperature with 90 K/min for the alloys with varying B fraction. Etching agent: Nital 5%. Magnification: ×25.

Table 4.
Experimental and computed T sol of AlN and BN in the Fe-C-N-Al-B system.
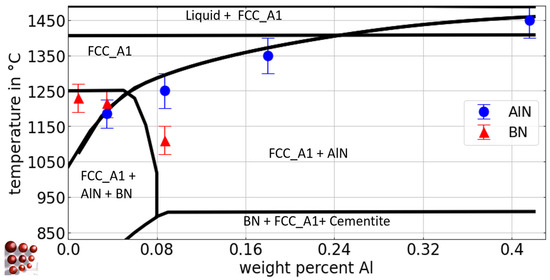
Figure 4.
Calculated pseudo-binary Fe-Al phase diagram with 0.5 wt.-% C, 79 wt.-ppm N, and 21 wt.-ppm B for the austenite region of the Fe-C-N-Al-B system, ME-Fe_CDLIPE2.0.2.tdb. The blue circles and the red triangles mark the experimental results with error bars for the Tsol of AlN and BN for the alloys B21Al0, B19Al35, B21Al88, B21Al180, and B21Al416, respectively. (For the interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article).
4.2. Interrelation of AlN and BN Within Fe-C-N-Al-B
4.2.1. Solvus—Temperature of AlN and BN
In Table 4, the experimental results of Tsol for AlN and BN precipitates using EDS/WDS analysis after annealing at different temperatures are presented, considering various Al and B concentrations, along with the associated range of error. The assessment of Tsol for AlN with low Al fractions and varying B content, i.e., alloys Al29B0, Al29B22, and Al36B44, poses significant challenges due to the low phase fraction and small diameter of AlN [10,27]. Utilizing the outcomes derived from EDS particle analysis and acknowledging the microstructure that has undergone homogenization annealing at 1000 °C (Figure 3b,c), it can be deduced that Tsol of alloy Al36B44 is approximately 970 °C. This determination is substantiated by the considerable augmentation in the affected grain size that has been observed following homogenization annealing, as evidenced by the comparative analysis in Figure 3b,c. The solubility of BN in the alloys with varying B fraction ranges from 1200 °C to 1215 °C, as BN is present at 1200 °C but not at 1235 °C or higher temperatures, in any of the investigated alloys. In alloys with a fixed B content and varying Al fractions, a decrease in the Tsol of BN is observed, with complete suppression of BN formation at concentrations greater than 0.9 wt.-%. Tsol of AlN at temperatures above 1300 °C (alloys B21Al180, B21Al416) is associated with a higher degree of uncertainty, primarily due to the challenges associated with conducting heat treatment experiments at such elevated temperatures, particularly the difficulty of achieving stable connection of the thermocouple on the sample surface.
For alloys B21Al180 and B21Al416, we therefore employ thermodynamic equilibrium simulation in order to discuss the accuracy of experimentally determined T sol. Figure 5 shows an SE image (a) and the EDS mapping of Al (b) and Mn (c) for alloy B21Al88 after annealing at 1100 °C for 1800 s. The concentrations of Al in part b reveal the presence of AlN particles with a size in the range of several hundred nanometers.

Figure 5.
SE image (a) and chemical analysis mapping for Al and Mn (b,c) utilizes EDS to examine AlN precipitates in the size range of several hundred nanometers in alloy B21Al88 after annealing at 1100 °C for 1800 s.
Figure 6 shows the chemical analysis by EDS of AlN and MnS precipitates located along each other in the alloy B21Al88 after annealing at 1180 °C for 1800 s. The EDS mappings (a, b, c, d) in Figure 6 give more details on the distribution of Al, N, Mn and S atoms, showing the actual size of the precipitate and the positioning of the two precipitates along each other. A close nesting between MnS and AlN is evident. AlN precipitates are found in the size range of approx. 100 nm, which is close to the lower resolution limit for PA up to 1 µm. A clear dependence of the AlN particle size on the Al fraction in the alloy is observed, with AlN particles being smaller than 300 nm in alloy B21Al35 and reaching particle diameters larger than 1 µm in alloy B21Al88. Co-precipitation of AlN and MnS in microalloyed steel has been reported by [27,76] and is also observed in this study, see Figure 6. AlN precipitates in the size of 100 nm are not found with a solubility of Mn, as shown in Figure 5.

Figure 6.
Chemical analysis mapping for S, Mn, Al, and N (a–d) utilizes EDS to examine an AlN precipitate alongside a MnS precipitate in alloy B21Al88 after annealing at 1180 °C for 1800 s.
The occurrence of two distinct peaks in the distribution of AlN diameters is evident. As demonstrated in Figure 5, the formation of small AlN particles with diameters of approximately 100 nm occurs during processing at lower temperatures. In contrast, the formation of larger AlN particles occurs at higher temperatures, with the nucleation being initiated at these elevated temperatures. As the aluminum composition increases, the solvus temperature of the aluminum nitride (AlN) also increases. Consequently, the size of the particles increases as well, due to the higher diffusivities that occur at higher temperatures.
Figure 7 shows a corresponding EDS/WDS analysis of a BN precipitate (b), typically located at an austenite grain boundary, in alloy Al36B44 after annealing for 1800 s at 1200 °C. The spectrum (a) from the WDS analysis shows the presence of N.
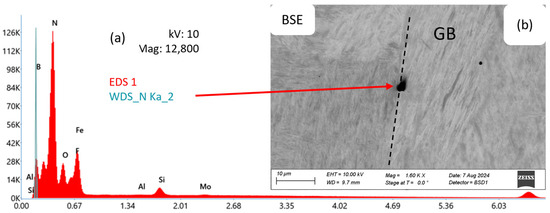
Figure 7.
SEM-BSE image of a BN precipitate (b) at a grain boundary (GB). Chemical analysis of a BN precipitate using EDS and WDS (a) for alloy Al36B44 after annealing for 1800 s at 1200 °C. B is detected using WDS.
From the analysis in the SEM, it can be concluded that BN precipitates appear as roundish features in the range of 1–5 µm and are predominantly nucleated at grain boundaries, as reported in the literature [7,31].
The protection of boron from nitrogen by excess aluminum is controversial. According to the review by Sharma et al. [7], it is believed that AlN dissolves at high temperatures, allowing the N to recombine with B. However, this study shows that AlN remains stable at high temperatures. In a system with 21 wt.-ppm B and 83 wt.-ppm N, an Al fraction greater than 0.09 wt.-% is sufficient to completely suppress BN. As a rule of thumb for the preferential precipitation of AlN over the formation of BN, an Al/N ratio of 20 is found for a B fraction of 21 wt.-ppm.
4.2.2. Pseudo-Binary Fe-Al and Fe-B Phase Diagram Within the Fe-N-C-Al-B System
As illustrated in Figure 4, the pseudo-binary Fe-Al diagram for the system Fe-C-N-Al-B with 0.5 wt.-% C, 79 wt.-ppm N, and 21 wt.-ppm B for the austenite region is calculated using the thermodynamic database ME-Fe_CDLIPE2.0.2.tdb [18].
The blue circles and red triangles represent the experimental results from Section 4.2.1 for the Tsol of AlN and BN, respectively. The Tsol of BN for the alloys B21Al0, B19Al35, and B21Al88 lies within a narrow range, as evidenced by the experimental results. From a thermodynamic perspective, the higher affinity of boron for nitrogen compared to aluminum [8,77] elucidates the amount of aluminum necessary to restrict the solubility of BN in austenite [7], with approximately 0.09 wt.-% required to entirely impede BN formation. Figure 8 shows the pseudo-binary Fe-B diagram for the Fe-rich side of the system Fe-C-N-Al-B with 0.5 wt.-% C, 79 wt.- ppm N, and 0.03 wt.-% Al for the austenite region. These calculations are derived from the thermodynamic database ME-Fe_CDLIPE2.0.2.tdb [18]. The blue circles and red triangles represent the experimental results from Section 4.2.1 for Tsol of AlN and BN, respectively.
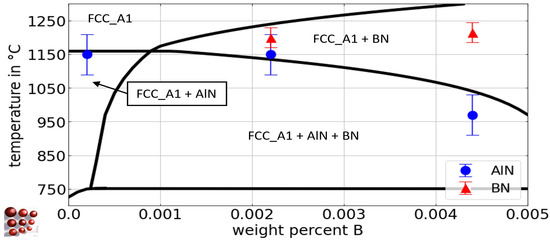
Figure 8.
Calculated pseudo-binary Fe-B phase diagram with 0.5 wt.-% C, 79 wt.-ppm N, and 0.03 wt.-% Al for the austenite region of the Fe-C-N-Al-B system, ME-Fe_CDLIPE2.0.2.tdb. The blue circles and the red triangles mark the experimental results with error bars for the Tsol of AlN and BN for the alloys Al29B0, Al29B22, and Al36B44. (For the interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article).
As the boron fraction increases, the stability of BN begins to manifest at approximately 4 wt.-ppm B. The presence of competing phases, AlN and BN, leads to a reduction in AlN precipitates with an increase in boron content, owing to the formation of BN. At B concentrations greater than 50 wt.-ppm, AlN is completely dissolved.
This work definitively shows that AlN and BN are competing phases. An increase in either aluminum or boron content favors the formation of the corresponding phase, AlN or BN. The BN phase is generally more stable than AlN due to the strong affinity of boron for nitrogen, depending on the relative concentrations of Al, B, and N.
4.3. Interrelation of AlN, BN, and TiN Within Fe-C-N-Al-B-Ti
4.3.1. Experiment
In Table 5, the experimental findings concerning the Tsol of the precipitate phases AlN, BN, and TiN for the alloys exhibiting variable titanium concentrations are presented. The data shows the strong affinity of Ti for N, as evidenced by the observation that a mere 0.03 wt.-% Ti is enough to entirely impede the formation of AlN and BN. This phenomenon, consequently, facilitates the advantageous effect of safeguarding B for the desired “boron-effect” outcome. There is no evidence of mixing between the AlN, BN, and TiN phases in the EDS mapping. The determination of Tsol for TiN is achieved through the integration of thermodynamic equilibrium simulation with experimental evaluation. In the case of alloy Al36B25Ti0, no TiN is detected, whereas in all other alloys containing Ti, TiN is found. The high solubility temperature of TiN, which is approximately 1430 °C or higher, renders dissolution experiments in the dilatometer unfeasible. In Figure 9, an exemplary corresponding EDS analysis of a TiN precipitate in alloy Al42B38Ti30 after annealing at 1300 °C for 1200 s is shown, yielding a spectrum (a) that substantiates the presence of Ti and N. The EDS mappings (b, c, d, and e) provide further insight into the distribution of the Ti, N, Fe, and C atoms, respectively, and demonstrate the actual size of the precipitate. The size of the detected TiN precipitates ranges from 100 nm (lower detection limit) to several µm.

Table 5.
Experimental and computed Tsol of AlN, BN, and TiN in the Fe-C-N-Al-B-Ti system. The values for TiN are taken from thermodynamic equilibrium simulation.
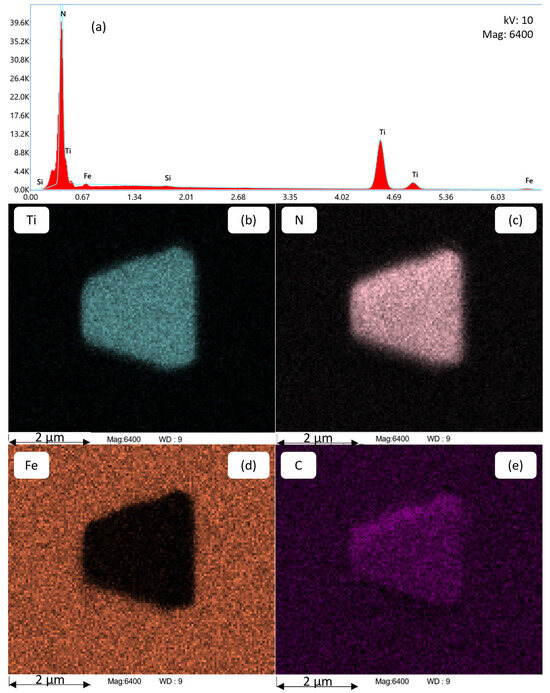
Figure 9.
Chemical analysis of a TiN precipitate using EDS (a) in alloy Al42B38Ti30 after annealing at 1300 °C for 1200 s. The EDS mappings in (b–e) show the distribution of Ti, N, Fe, and C atoms, respectively.
As illustrated in Figure 10, the results of the particle analysis for alloy Al42B38Ti30 after annealing at 1000 °C for 10,000 s indicate the presence of TiN and MnS. The blue and red dots denote the positions of these two phases, respectively. The precipitate size in the plot is multiplied by 20 to enhance the visibility of the particles. The absence of BN and AlN in the present measurement further suggests that AlN and BN are not stable within the alloy and annealing temperature under investigation. The diameter of titanium nitride (TiN) is distributed over a wide range, from a mere hundred nanometers to several micrometers. The formation of large TiN precipitates is hypothesized to occur at elevated temperatures or primarily from the liquid phase [78]. Small TiN particles are thought to nucleate as secondary precipitates from the solid state at lower temperatures during the subsequent production process.
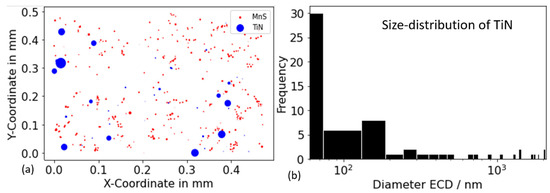
Figure 10.
Results of particle analysis for alloy Al42B38Ti30 after annealing at 1000 °C for 10,000 s. (a) Position of the TiN (blue) and MnS (red) precipitates. The precipitate size in the plot is multiplied by 20 to make the particles more easily visible. (b) Distribution of the TiN precipitates diameter.
Figure 11 shows the resulting austenite grain size after annealing at 1000 °C for 500 s and 10,000 s, respectively. A profound bimodal grain size distribution can be observed, indicating the abnormal grain growth behavior. This behavior is explained by the absence of grain boundary pinning AlN precipitates. A similar effect is reported by Roy et al. [37] and Monschein et al. [35] in HSLA steel, where the dissolution of second-phase particles at higher soaking temperatures is reported to allow AGG. In the alloys without Ti alloying, AGG was not observed, further supporting the theory that the lack of AlN leads to AGG.
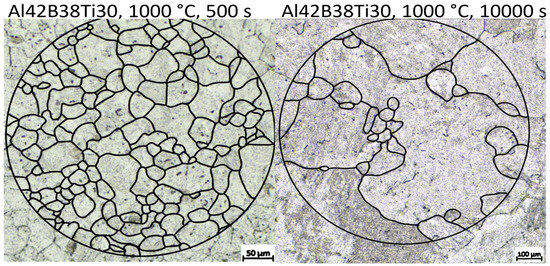
Figure 11.
Comparison of the resulting austenite grain size for alloy Al42B38Ti30 after annealing at 1000 °C for 500 s and 10,000 s, respectively. Etching is performed with PM1998, adapted from Ref. [75]. Black lines are drawn to highlight the PAGB.
4.3.2. Pseudo-Binary Fe-Ti Phase Diagram Within the Fe-N-C-Al-B-Ti System
Figure 12 shows a calculated pseudo-binary Fe-Ti diagram for the Fe-rich side with 0.5 wt.-% C, 79 wt.-ppm N, 0.03 wt.-% Al, and 36 wt.-ppm B for the austenite region of the Fe-C-N-Al-B-Ti system, using the thermodynamic database ME-Fe_CDLIPE2.0.2.tdb [18]. The blue circles, red triangles, and green stars represent the experimental results from Section 4.2.1 for the Tsol of TiN, BN, and AlN, respectively. However, small discrepancies between simulation results and experimental data are observed, and they are attributed to experimental evaluation uncertainties, primarily due to resolution limits and the complex interactions with numerous degrees of freedom in the multicomponent system. In fact, the calibration of such interactions can be achieved, but we prefer to accept deviations due to the high doubt of the appropriate physical base for their modeling. The collective analysis of the simulation results indicates a reasonable agreement between the simulations and the experimental observations, suggesting a satisfactory overall outcome.
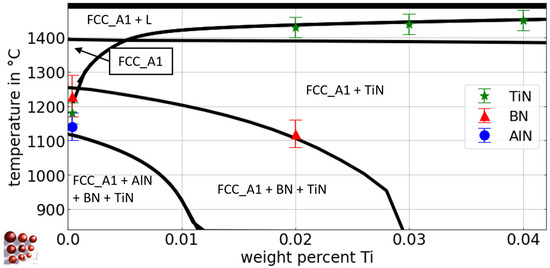
Figure 12.
Calculated pseudo-binary Fe-Ti phase diagram with 0.5 wt.-% C, 79 wt.- ppm N, 0.03 wt.-% Al, and 36 wt.-ppm B for the austenite region of the Fe-C-N-Al-B-Ti system, ME-Fe_CDLIPE2.0.2.tdb. The blue circles, red triangles, and green stars mark the experimental results with error bars for the Tsol of TiN, BN, and AlN for the alloys Al36B25Ti0, Al38B36Ti20, Al42B38Ti30, and Al44B39Ti42. (For the interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article).
5. Summary
Our experimental investigation of high-purity vacuum induction-melted alloys confirms that Ti, B, and Al exhibit decreasing affinities to nitrogen, forming nitrides in microalloyed steel. In the competitive interaction with aluminum, in the Fe-C-N-Al-B system with approximately 80 wt-ppm N and 20 wt.-ppm B, increasing the Al content to 0.09 wt.-% effectively inhibits the formation of BN, in contrast to previous understanding of the negligible protective role of Al at high temperatures. AlN is found to heterogeneously nucleate on MnS. Titanium proves to be very effective in blocking the formation of other nitrides. The presence of 0.02 wt.-% Ti completely blocks the formation of AlN and shifts the Tsol of BN by 150 °C. The addition of 0.03 wt.-% Ti is sufficient to suppress the formation of both BN and AlN, in steel with approximately 50 wt.-ppm N. By integrating available binary and ternary descriptions into a thermodynamic database, we predict the stabilities of the multicomponent system Fe-C-N-Al-B-Ti. A new Gibbs energy description of the BN phase is presented, which provides a comprehensive characterization of the experimentally accessible solubility products. Overall, considering the simulation results for nitride phase boundaries, the outcomes are satisfying, as reflected by a reasonable agreement between the simulations and experimental observations. This further confirms the control by the thermodynamics of binary and ternary subsystems, since the extension to quaternaries, quinaries, and the multi-component steel system studied has been considered ideal, and the applicability of the steel database, being optimized by new experimental data in the Fe-rich corner for dilute microalloyed steel is confirmed.
In alloys with even a small amount of Ti, abnormal grain growth behavior is observed. This inhomogeneous grain growth is attributed to the absence of AlN precipitates, which are known to retard grain boundary movement.
Author Contributions
Conceptualization, M.F. and E.P.-K.; methodology, M.F., C.S. and E.P.-K.; software, M.F. and E.P.-K.; investigation, M.F. and C.S.; writing—original draft preparation, M.F.; writing—review and editing, M.F., S.Z., C.S. and E.P.-K.; visualization, M.F.; supervision, E.P.-K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Christian Doppler Forschungsgesellschaft in the framework of the CD-Laboratory of Interfaces and Precipitation Engineering (CDL-IPE).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The financial support from the Austrian Federal Ministry for Digital and Economic Affairs and the National Foundation for Research, Technology, and Development is gratefully acknowledged. The authors acknowledge TU Wien Bibliothek for financial support through its Open Access Funding Programme. The financial support, as well as the provision of sample material by voestalpine Forschungsservicegesellschaft, is gratefully acknowledged by the authors.
Conflicts of Interest
Author Sabine Zamberger was employed by the company Voestalpine Forschungsservicegesellschaft Donawitz GmbH. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Baker, T.N. Microalloyed Steels. Ironmak. Steelmak. 2016, 43, 264–307. [Google Scholar] [CrossRef]
- e Silva, A.C. Challenges and opportunities in thermodynamic and kinetic modeling microalloyed HSLA steels using computational thermodynamics. Calphad 2020, 68, 101720. [Google Scholar] [CrossRef]
- Habu, R.; Miyata, M.; Tamukai, S.; Sekino, S. Improvement of Hardenability of Steel Containing Aluminum and Boron by Double Quenching. Trans. Iron Steel Inst. Jpn. 1983, 23, 176–183. [Google Scholar] [CrossRef]
- Kawamura, K.; Otsubo, T.; Furukawa, T. Relationship between the Hardenability of Steel and the “Effective Boron” in Steel. Trans. Iron Steel Inst. Jpn. 1976, 16, 545–550. [Google Scholar] [CrossRef]
- McMahon, C.J. The role of solute segregation in promoting the hardenability of steel. Met. Trans. A 1980, 11, 531–535. [Google Scholar] [CrossRef]
- Wipp, D. Boron Influence on Microstructural Evolution and Mechanical Properties in Micro-Alloyed Carbon Steels: Precipitation and Segregation Behavior. Ph.D. Thesis, Technische Universität Wien, Vienna, Austria.
- Sharma, M.; Ortlepp, I.; Bleck, W. Boron in Heat-Treatable Steels: A Review. Steel Res. Int. 2019, 90, 1900133. [Google Scholar] [CrossRef]
- Wang, W.S.; Zhu, H.Y.; Sun, J.; Lei, J.L.; Duan, Y.Q.; Wang, Q. Thermodynamic analysis of BN, AlN AND TiN Precipitation in boron-bearing steel. Metalurgija 2019, 58, 199–202. [Google Scholar]
- Baker, T.N. Titanium microalloyed steels. Ironmak. Steelmak. 2019, 46, 1–55. [Google Scholar] [CrossRef]
- Wilson, F.G.; Gladman, T. Aluminium nitride in steel. Int. Mater. Rev. 1988, 33, 221–286. [Google Scholar] [CrossRef]
- Gontijo, M.; Chakraborty, A.; Webster, R.F.; Ilie, S.; Six, J.; Primig, S.; Sommitsch, C. Thermomechanical and Microstructural Analysis of the Influence of B- and Ti-Content on the Hot Ductility Behavior of Microalloyed Steels. Metals 2022, 12, 1808. [Google Scholar] [CrossRef]
- Kaufman, L.; Bernstein, H. Computer Calculation of Phase Diagrams with Special Reference to Refractory Metals; Academic Press Inc.: New York, NY, USA, 1970. [Google Scholar]
- Gustafson, P. A thermodynamic evaluation of the Fe-C system. Calphad 1985, 259–267. [Google Scholar] [CrossRef]
- Frisk, K. A thermodynamic evaluation of the Cr-N, Fe-N, Mo-N and Cr-Mo-N systems. Calphad 1991, 15, 79–106. [Google Scholar] [CrossRef]
- Miettinen, J.; Visuri, V.-V.; Fabritius, T.; Vassilev, G. Thermodynamic Description of Ternary Fe-B-X Systems. Part 7: Fe-B-C. Arch. Met. Mater. 2020, 65, 923–933. [Google Scholar] [CrossRef]
- Lee, B.-J. Thermodynamic assessment of the Fe-Nb-Ti-C-N system. Met. Mater. Trans. A 2001, 32, 2423–2439. [Google Scholar] [CrossRef]
- Chin, K.-G.; Lee, H.-J.; Kwak, J.-H.; Kang, J.-Y.; Lee, B.-J. Thermodynamic calculation on the stability of (Fe, Mn) 3AlC carbide in high aluminum steels. J. Alloy. Compd. 2010, 505, 217–223. [Google Scholar] [CrossRef]
- Povoden-Karadeniz, E. (Ed.) Thermodynamic Database “ME-Fe_CDLIPE2.0.2.tdb. Unpublished work. 2025. [Google Scholar]
- Rios, P.R.; da Fonseca, G.S. Grain Boundary Pinning by Particles. Mater. Sci. Forum 2010, 638–642, 3907–3912. [Google Scholar] [CrossRef]
- Radis, R.; Kozeschnik, E. Kinetics of AlN Precipitation in Microalloyed Steel. Model. Simul. Mater. Sci. Eng. 2010, 18, 55003. [Google Scholar] [CrossRef]
- Wriedt, H.A. The Al−N (Aluminum-Nitrogen) System. Bull. Alloy. Phase Diagr. 1986, 7, 329–333. [Google Scholar] [CrossRef]
- Bruls, R.; Hintzen, H.; de With, G.; Metselaar, R.; van Miltenburg, J. The temperature dependence of the Grüneisen parameters of MgSiN2, AlN and β-Si3N4. J. Phys. Chem. Solids 2001, 62, 783–792. [Google Scholar] [CrossRef]
- Lu, X.-G.; Selleby, M.; Sundman, B. Assessments of molar volume and thermal expansion for selected bcc, fcc and hcp metallic elements. Calphad 2005, 29, 68–89. [Google Scholar] [CrossRef]
- Sennour, M.; Esnouf, C. Contribution of Advanced Microscopy Techniques to Nano-Precipitates Characterization: Case of AlN Precipitation in Low-Carbon Steel. Acta Mater. 2003, 51, 943–957. [Google Scholar] [CrossRef]
- Gao, N.; Baker, T.N. Austenite Grain Growth Behaviour of Microalloyed Al-V-N and Al-V-Ti-N Steels. ISIJ Int. 1998, 38, 744–751. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Wang, Y.; Zhao, A. Precipitation of AlN and MnS in Low Carbon Aluminium-Killed Steel. J. Iron Steel Res. Int. 2012, 19, 51–56. [Google Scholar] [CrossRef]
- Führer, M.; Zamberger, S.; Povoden-Karadeniz, E. Experimental determination of AlN in microalloyed steel and thermodynamic analysis. Calphad 2024, 88, 102790. [Google Scholar] [CrossRef]
- Massardier, V.; Guétaz, V.; Merlin, J.; Soler, M. Kinetic and Microstructural Study of Aluminium Nitride Precipitation in a Low Carbon Aluminium-Killed Steel. Mater. Sci. Eng. A 2003, 355, 299–310. [Google Scholar] [CrossRef]
- Pearson, W.B.; Villars, P.; Calvert, L.D. Pearson’s Handbook of Crystallographic Data for Intermetallic Phases; ASM International: Materials Park, OH, USA, 1986. [Google Scholar]
- Suzuki, S.; Tanino, M. Role of Grain Boundary Segregation in Austenite Decomposition of Low-Alloyed Steel. Mater. Sci. Forum 2007, 558–559, 965–970. [Google Scholar] [CrossRef]
- Sakuraya, K.; Okada, H.; Abe, F. Influence of Heat Treatment on Formation Behavior of Boron Nitride Inclusions in P122 Heat Resistant Steel. ISIJ Int. 2006, 46, 1712–1719. [Google Scholar] [CrossRef]
- Jonsson, S. Assessment of the Fe-Ti-C system, calculation of the Fe-TiN system, and prediction of the solubility limit of Ti(C,N) in liquid Fe. Met. Mater. Trans. B 1998, 29, 371–384. [Google Scholar] [CrossRef]
- ASM Handbook Committee. High-Strength Structural and High-Strength Low-Alloy Steels. In Properties and Selection: Irons, Steels and High Performance Alloys, 10th ed.; ASM Metals Handbook; ASM: Metals Park, OH, USA, 1990; Volume 1, pp. 403–423. [Google Scholar]
- Najafkhani, F.; Kheiri, S.; Pourbahari, B.; Mirzadeh, H. Recent Advances in the Kinetics of Normal/Abnormal Grain Growth: A Review. Arch. Civ. Mech. Eng. 2021, 21, 29. [Google Scholar] [CrossRef]
- Monschein, S.; Ragger, K.S.; Zügner, D.; Fasching, J.; Schnitzer, R. Influence of the Ti Content on the Grain Stability and the Recrystallization Behavior of Nb-Alloyed High-Strength Low-Alloyed Steels. Steel Res. Int. 2022, 93, 2200094. [Google Scholar] [CrossRef]
- Su, C.; Zhao, G.; Xiao, H.; Lan, Y.; Huang, F. Abnormal Grain Growth of Hi-B Steel in the Secondary Recrystallization. Met. Microstruct. Anal. 2018, 7, 608–617. [Google Scholar] [CrossRef]
- Roy, S.; Karmakar, A.; Mukherjee, S.; Kundu, S.; Srivastava, D.; Chakrabarti, D. Effect of starting microstructure on austenite grain sizes developed after reheating of HSLA steel. Mater. Sci. Technol. 2014, 30, 1142–1153. [Google Scholar] [CrossRef]
- Lang, D.; Povoden-Karadeniz, E.; Schatte, J.; Knabl, W.; Clemens, H.; Primig, S. Thermodynamic evaluation of the Mo-rich corner of the Mo-Hf-C system including O impurities. J. Alloy. Compd. 2017, 695, 372–381. [Google Scholar] [CrossRef]
- Saunders, N.; Miodownik, A.P. CALPHAD (Calculation of Phase Diagrams): A Comprehensive Guide, Transferred to Digital Print; Pergamon Materials Series: Pergamon, Turkey, 1998. [Google Scholar]
- Dinsdale, A. SGTE Data for Pure Elements. Calphad 1991, 15, 317–425. [Google Scholar] [CrossRef]
- Chipman, J. Thermodynamics and phase diagram of the Fe-C system. Met. Trans. 1972, 3, 55–64. [Google Scholar] [CrossRef]
- Göhring, H.; Leineweber, A.; Mittemeijer, E. A thermodynamic model for non-stoichiometric cementite; the Fe–C phase diagram. Calphad 2016, 52, 38–46. [Google Scholar] [CrossRef]
- Naraghi, R.; Selleby, M.; Ågren, J. Thermodynamics of stable and metastable structures in Fe–C system. Calphad 2014, 46, 148–158. [Google Scholar] [CrossRef]
- Hallstedt, B.; Djurovic, D.; von Appen, J.; Dronskowski, R.; Dick, A.; Körmann, F.; Hickel, T.; Neugebauer, J. Thermodynamic properties of cementite. Calphad 2010, 34, 129–133. [Google Scholar] [CrossRef]
- Van Rompaey, T.; Kumar, K.H.; Wollants, P. Thermodynamic optimization of the B–Fe system. J. Alloy. Compd. 2002, 334, 173–181. [Google Scholar] [CrossRef]
- Chart, T.G. CECA, Research Project No.7210, CA/3/303; Comission des Communautès Europèennes: Brussels, Belgium, 1981. [Google Scholar]
- Massalski, T.B. (Ed.) Binary Alloys Phase Diagrams, 2nd ed.; ASM International: Metals Park, OH, USA, 1990. [Google Scholar]
- Kubaschewski, O. Iron–Binary Phase Diagrams; Springer: Berlin, Germany, 1982. [Google Scholar]
- Hallemans, B.; Wollants, P.; Roos, J.R. Thermodynamic Reassessment and Calculation of the Fe-B Phase Diagram. Int. J. Mater. Res. 1994, 85, 676–682. [Google Scholar] [CrossRef]
- Ohtani, H.; Hasebe, M.; Ishida, K.; Nishizawa, T. Calculation of Fe-C-B ternary phase diagram. Trans. Iron Steel Inst. Jpn. 1988, 28, 1043–1050. [Google Scholar] [CrossRef]
- Kaufman, L.; Uhrenius, B.; Birnie, D.; Taylor, K. Coupled pair potential, thermochemical and phase diagram data for transition metal binary systems-VII. Calphad 1984, 8, 25–66. [Google Scholar] [CrossRef]
- Lucci, A.; Della Gatta, G.; Venturello, G. On the Solubility of Boron in High-Purity Alpha-Iron. Met. Sci. J. 1969, 3, 14–17. [Google Scholar] [CrossRef]
- Brodowsky, H.; Wernicke, H.-J. Activity coefficients and the α-γ transition lines in Fe-B alloys. Calphad 1984, 8, 159–162. [Google Scholar] [CrossRef]
- Brown, A.; Garnish, J.D.; Honeycombe, R.W.K. The Distribution of Boron in Pure Iron. Met. Sci. 1974, 8, 317–324. [Google Scholar] [CrossRef]
- Raghavan, V. B-Fe-N (boron-iron-nitrogen). J. Phase Equilibria Diffus. 1993, 14, 619–620. [Google Scholar] [CrossRef]
- Tomashik, V. Boron—Iron—Nitrogen: Iron systems: Phase diagrams, crystallographic and thermodynamic data. Landolt-Börnstein—Group IV Phys. Chem. 2008, 457–471. [Google Scholar] [CrossRef]
- Fountain, R.W.; Chipman, J. Solubility and Precipitation of Boron Nitride in Iron-Boron Alloys; Union Carbide Metals Co.: Niagara Falls, NY, USA, 1962; Volume 224. [Google Scholar]
- Führer, M.; Zamberger, S.; Shan, Y.; Helml, L.; Srikakulapu, K.; Schnitzer, R.; Kozeschnik, E.; Povoden-Karadeniz, E. Influence of Boron Grain Boundary Segregation on the Thermodynamics of the Fe-C-B-N System; unpublished manuscript; Institue of materials science and technology: TU Wien, Vienna, Austria, 2025. [Google Scholar]
- Saunders, N. COST 507: Thermochemical database for light metal alloys. Light Met. 1998, 2, 23–27. [Google Scholar]
- Jacob, A.; Sobotka, E.; Povoden-Karadeniz, E. Thermodynamic modeling of multicomponent MX phases (M = Nb, Ti, V; X = C, N) in steel. Calphad 2025, 88, 102795. [Google Scholar] [CrossRef]
- Povoden-Karadeniz, E. mc_fe_v2.061. 2023. Available online: https://www.matcalc.at/images/stories/Download/Database/mc_fe_v2061.tdb (accessed on 23 August 2023).
- Hillert, M.; Jonsson, S. An Assessment of the Al-Fe-N System. Met. Trans. A 1992, 23, 3141–3149. [Google Scholar] [CrossRef]
- Miettinen, J.; Vassilev, G. Thermodynamic Description of Ternary Fe-B-X Systems. Part 1: Fe-B-Cr. Arch. Met. Mater. 2014, 59, 601–607. [Google Scholar] [CrossRef]
- Seierstein, M. System Al–Fe. COST507. In Thermochemical Database for Light Metal Alloys; Ansara, I., Dinsdale, A.T., Rand, M.H., Eds.; European Commission: Luxembourg; Office for Official Publications: Washington, DC, USA, 1998; p. 234. [Google Scholar]
- Witusiewicz, V.; Bondar, A.; Hecht, U.; Rex, S.; Velikanova, T. The Al–B–Nb–Ti system. J. Alloy. Compd. 2008, 465, 64–77. [Google Scholar] [CrossRef]
- Maneschi, B.A.S. Analysis of Nitrides in Boron Steels by Extraction of Nonmetallic Phases; MET ITAL: New York, NY, USA, 1966. [Google Scholar]
- Turkdogan, E.T. Causes and effects of nitride and carbonitride precipitation in HSLA steels in relation to continuous casting. In Proceedings of the 70th Steelmaking Conference Proceedings, Pittsburgh, PA, USA, 29 March–1 April 1987. [Google Scholar]
- Sridar, S.; Kumar, R.; Kumar, K.H. Thermodynamic Modelling of Al-B-N System. Calphad 2019, 65, 291–298. [Google Scholar] [CrossRef]
- Wen, H.; Lukas, H.-L. Thermochemical Database for Light Metal Alloys; Ansara, I., Dinsdale, A.T., Rand, M.H., Eds.; European Communities: Luxembourg, 1998; Volume 2, System B-N; pp. 65–68. [Google Scholar]
- Thermo-Calc Software. CALPHAD Methodology—Thermo-Calc Software. 2023. Available online: https://thermocalc.com/about-us/methodology/the-calphad-methodology/ (accessed on 5 April 2024).
- Dworkin, A.S.; Sasmor, D.J.; Van Artsdalen, E.R. The Thermodynamics of Boron Nitride; Low-Temperature Heat Capacity and Entropy; Heats of Combustion and Formation. J. Chem. Phys. 1954, 22, 837–842. [Google Scholar] [CrossRef]
- LECO Corporation. LECO. Available online: https://de.leco.com/ (accessed on 7 February 2025).
- Law, C.A. Treatise of Petroleum Geology/Handbook of Petroleum Geology: Exploring for Oil and Gas Traps. Chapter 6: Evaluating Source Rocks; AAPG Special Volumes; AAPG: Tulsa, OK, USA, 1999. [Google Scholar]
- Lambda WDS Spectrometers|EDAX. Available online: https://www.edax.com/products/wds/lambda-wds-analysis-system. (accessed on 8 August 2024).
- Schacht, E.; Richter, J. Erfahrungen mit Ätzmitteln zum Nachweis der ehemaligen Austenitkorngrenzen in Stählen / Experiences with Etching Reagents to Show Former Austenite Grain Boundaries in Steels. Pr. Met. 1998, 35, 384–395. [Google Scholar] [CrossRef]
- Lückl, M. Kinetics Simulation of MnS Precipitation in Electrical Steel. Steel Res. Int. 2016, 87, 271–275. [Google Scholar] [CrossRef]
- Wang, Y.-N.; Bao, Y.-P.; Wang, M.; Zhang, L.-C.; Chen, Y.-N. Basic Research on Precipitation and Control of BN Inclusions in Steel. Met. Mater. Trans. B 2013, 44, 1144–1154. [Google Scholar] [CrossRef]
- Schneider, A.; Stallybrass, C.; Konrad, J.; Kulgemeyer, A.; Meuser, H.; Meimeth, S. Formation of primary TiN precipitates during solidification of microalloyed steels—Scheil versus DICTRA simulations. Int. J. Mater. Res. 2008, 99, 674–679. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).