Kinetics Study of the Hydrogen Reduction of Limonite Ore Using an Unreacted Core Model for Flat-Plate Particles
Abstract
1. Introduction
2. Materials and Experimental Methods
2.1. Materials
2.2. Experimental Method
3. Kinetic Analysis Method
3.1. Chemical Reactions
3.2. Conventional Kinetic Analysis
3.3. Unreacted Core Model (UCM) for Flat-Plate Particles
3.3.1. Basic Assumptions
- It is assumed that the particle bed retains a constant shape and volume throughout the reaction, disregarding any expansion or contraction of the iron ore powder particles.
- The impact of internal structural changes within the porous packed particle bed is disregarded.
- It is assumed that the diffusion of solid products entails equimolar counter-diffusion between the reducing gas and the product gas under isothermal and isobaric conditions. Volume flow rate variations resulting from diffusion are omitted.
- It is assumed that the reaction occurring within the particles is a first-order, isothermal, and irreversible reaction.
- The entire reduction process attained a quasi-steady state.
3.3.2. Mathematical Model and Calculation Process
4. Results and Discussion
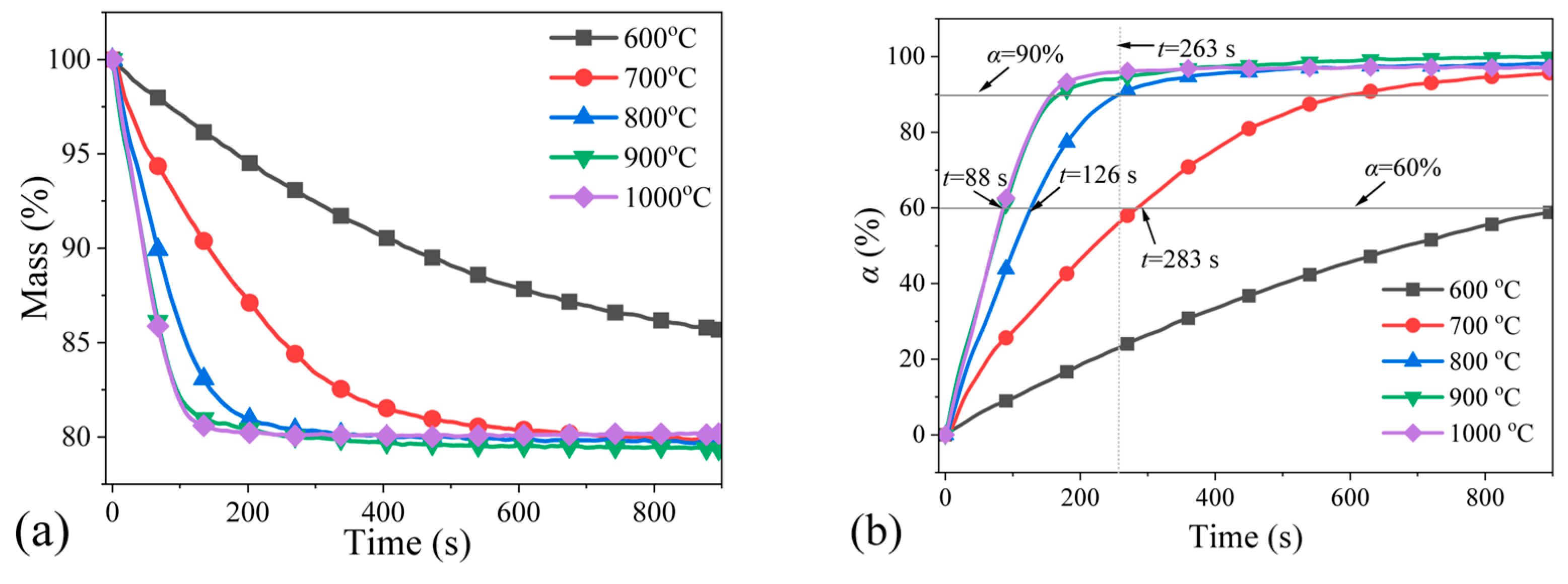
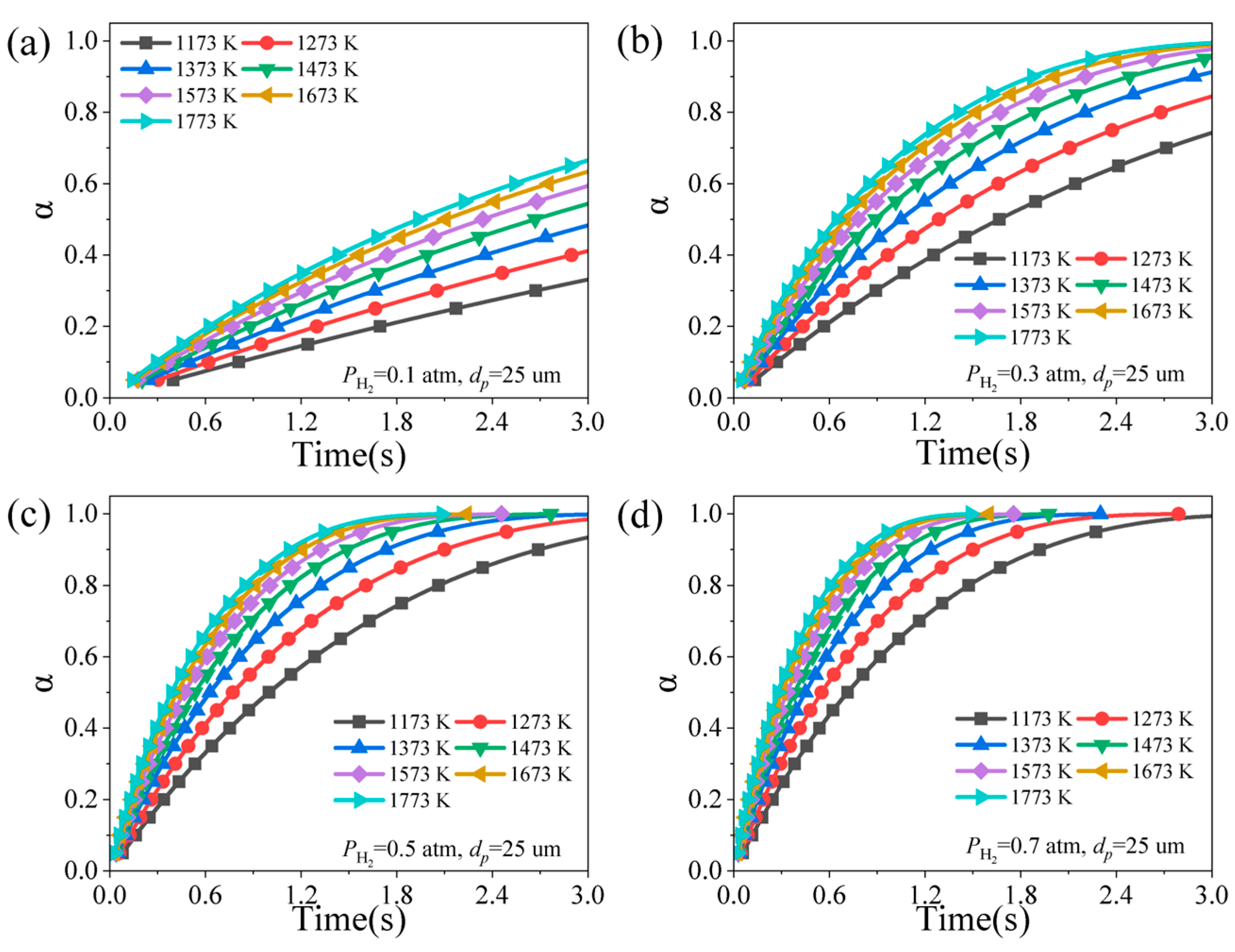
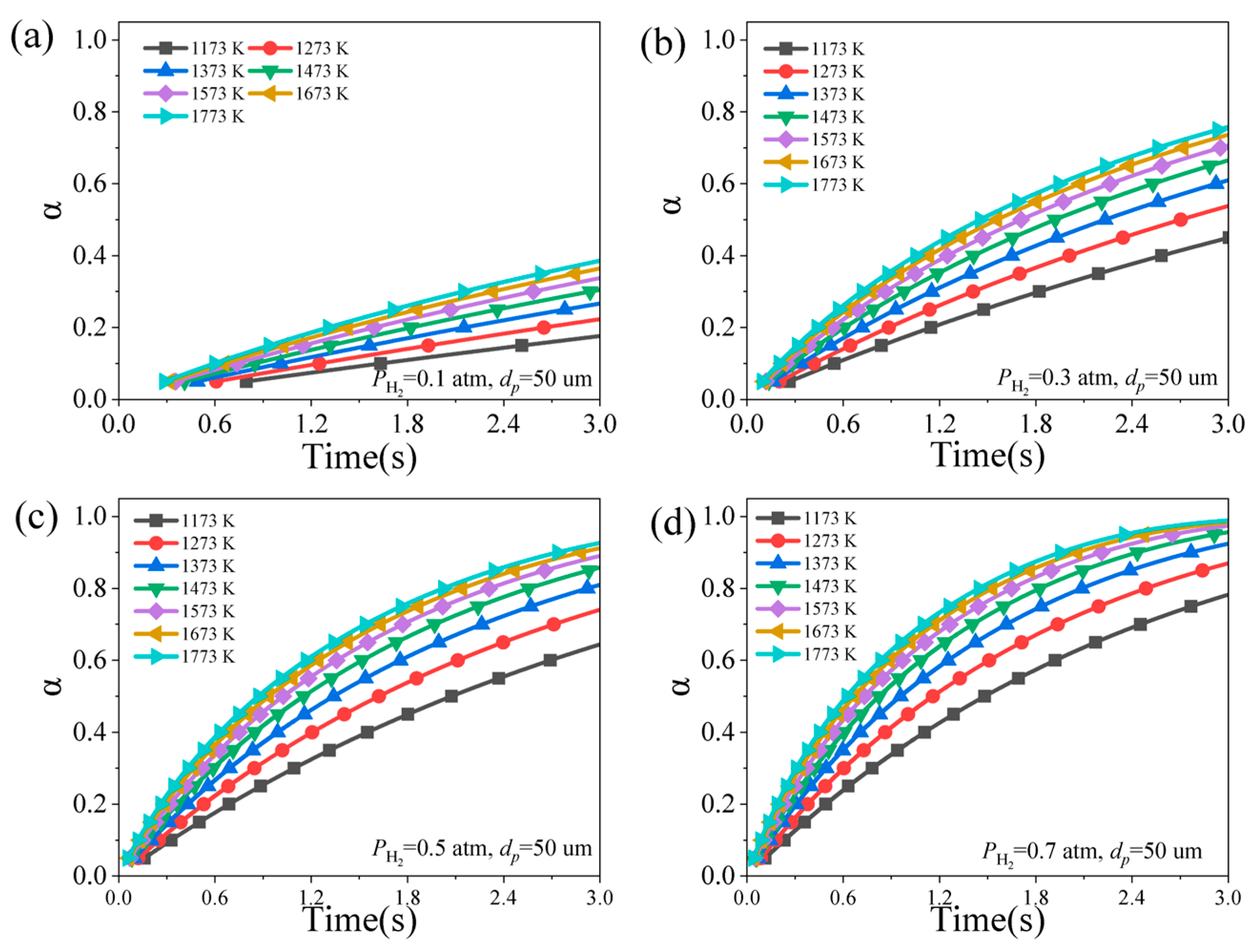
4.1. Effect of Reduction Temperature
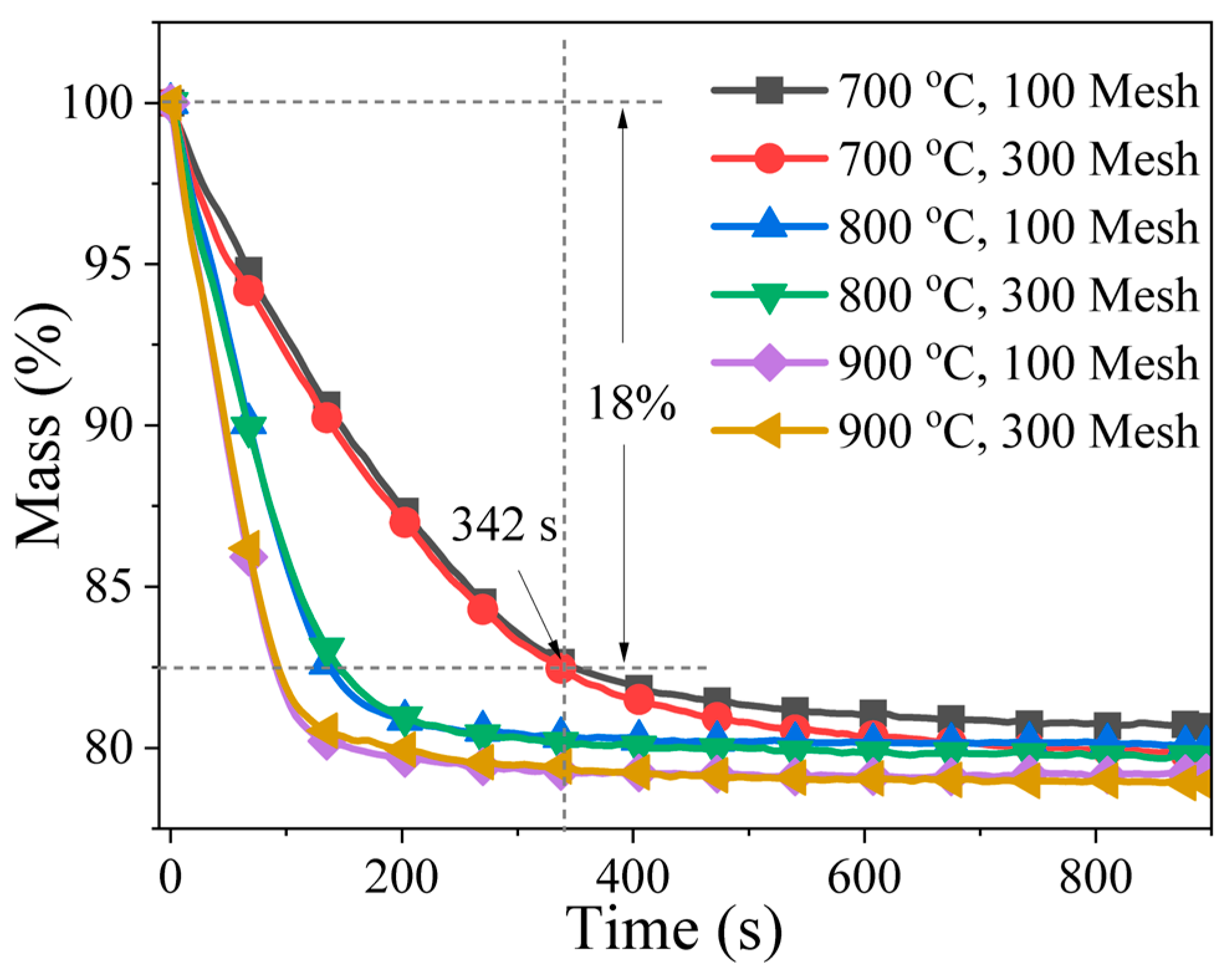
4.2. Effect of Particle Size
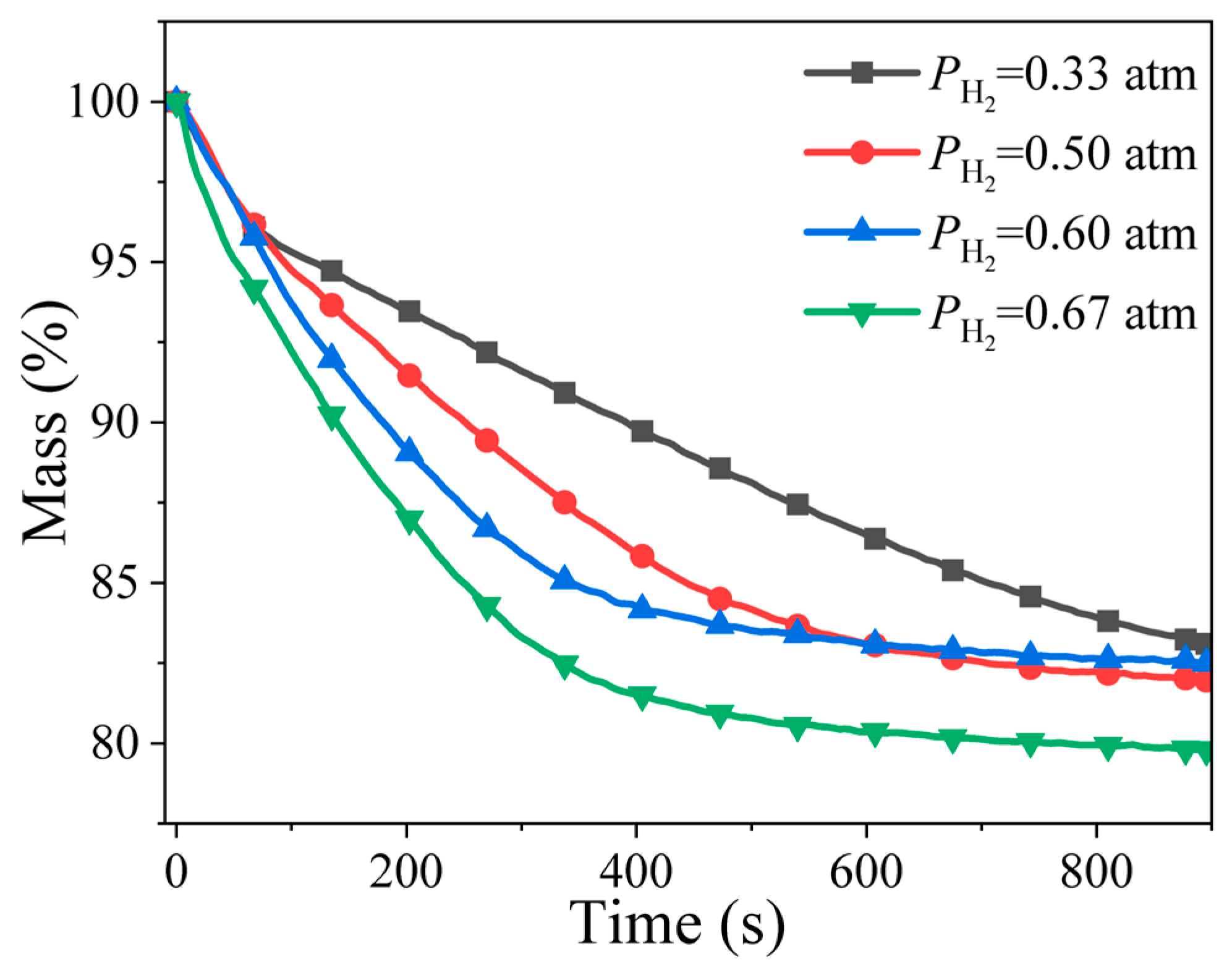
4.3. Effect of Hydrogen Partial Pressure
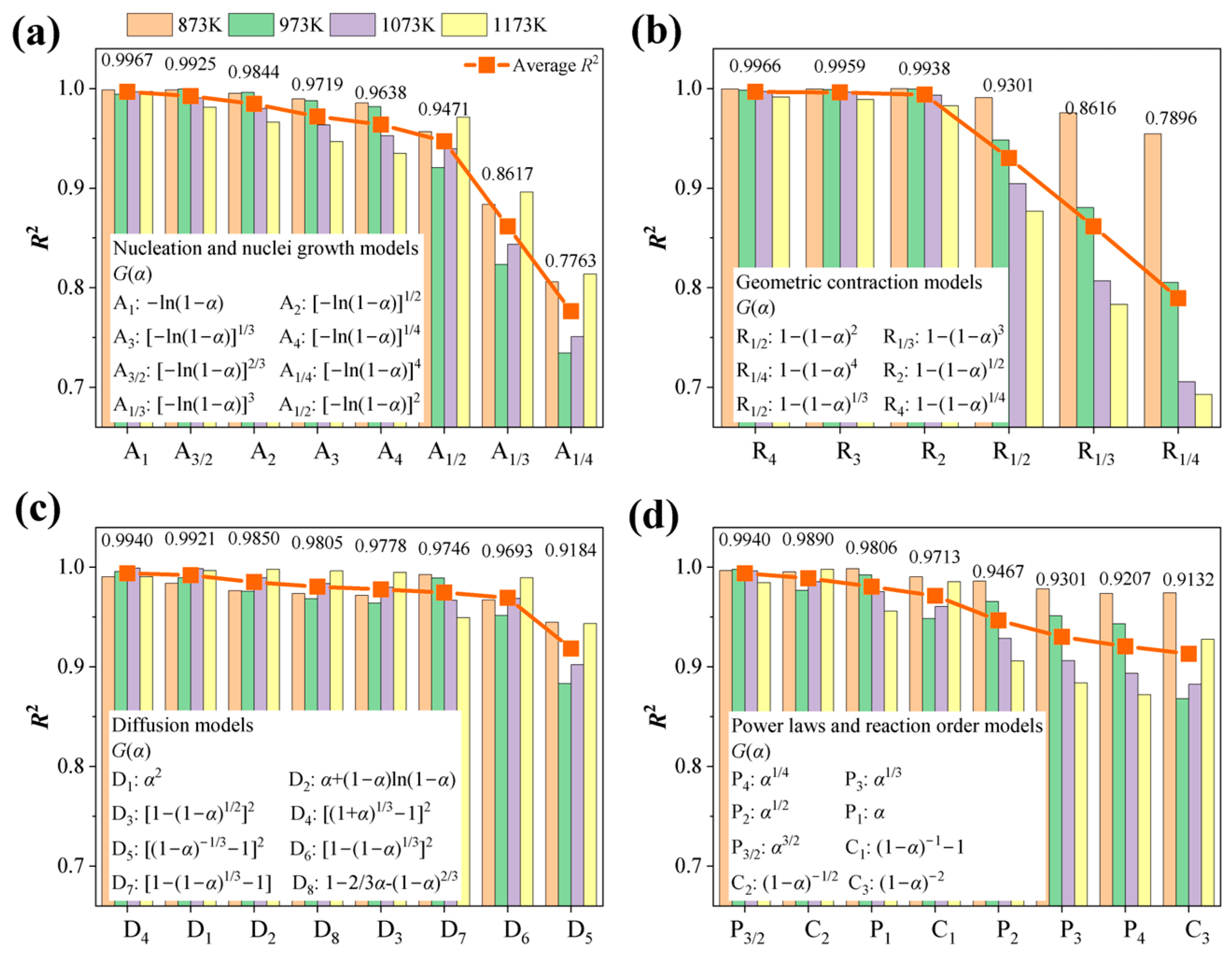
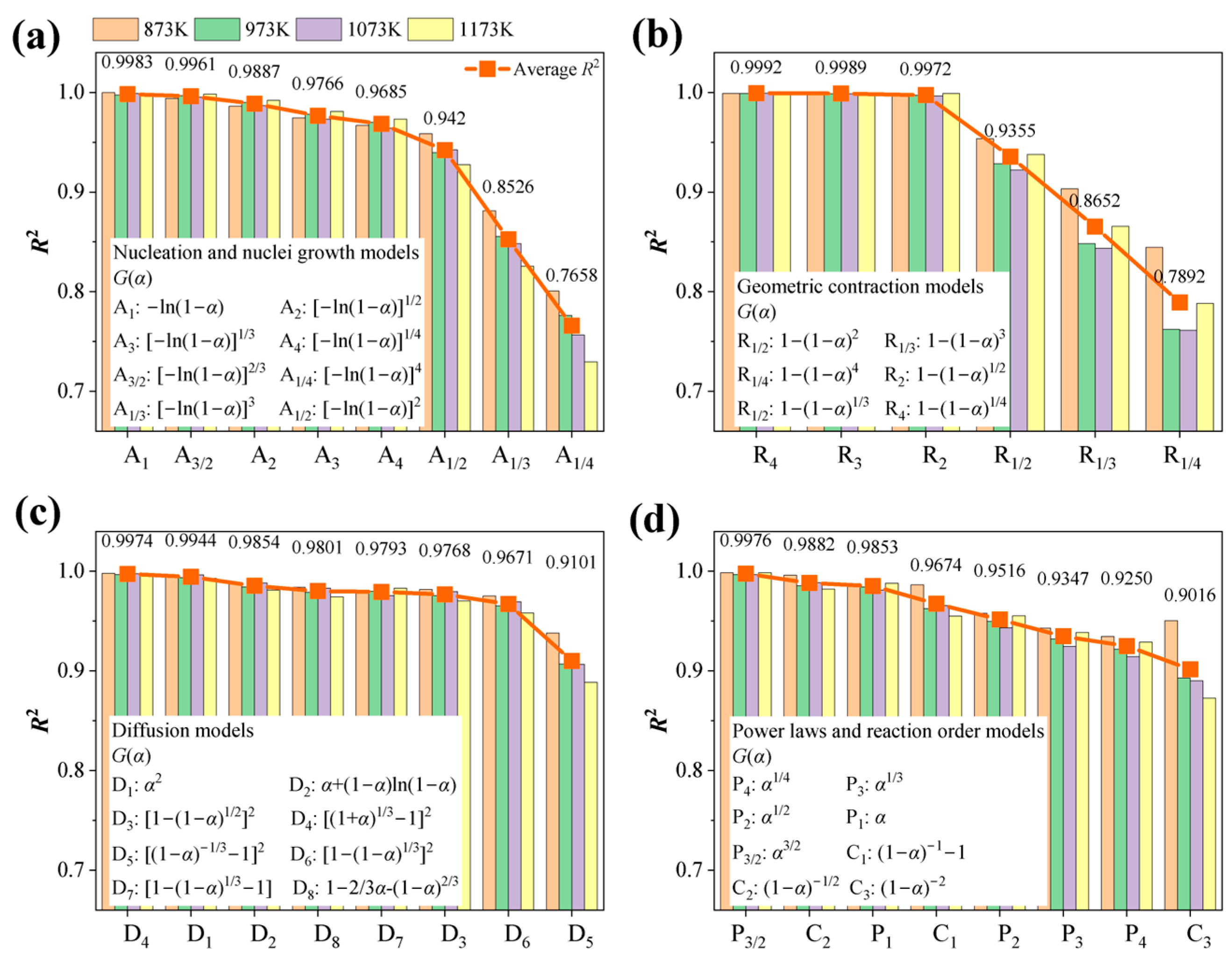
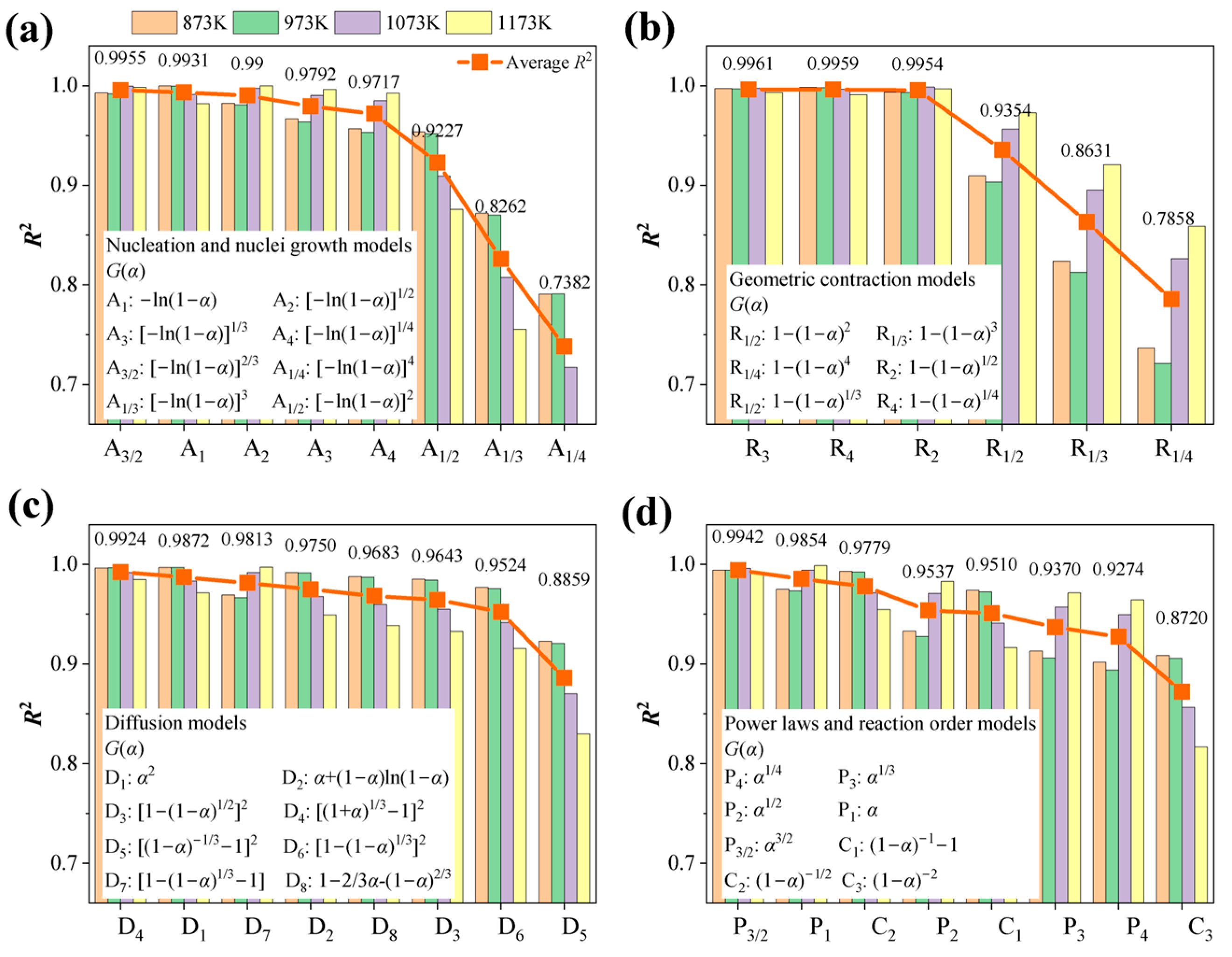
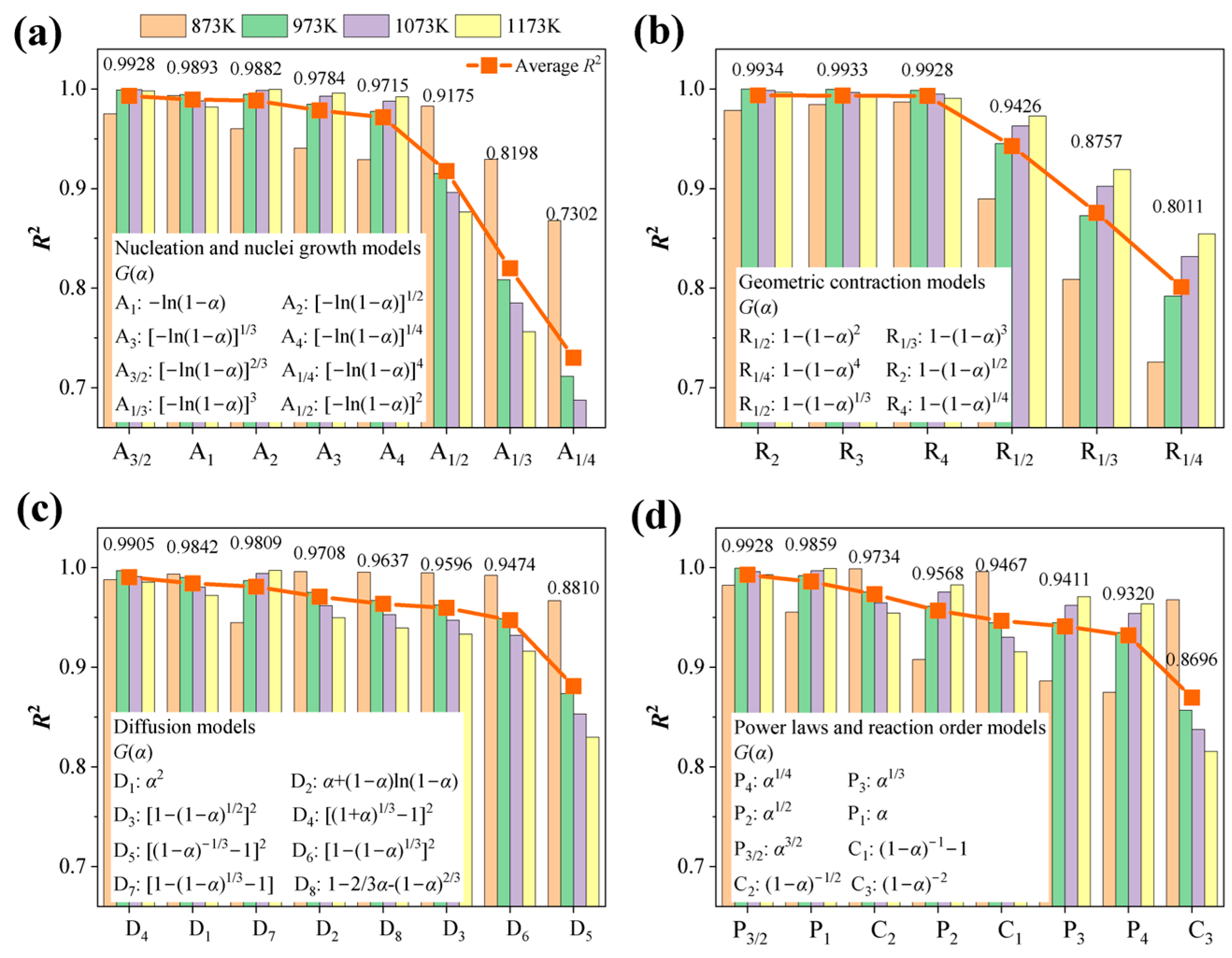
4.4. Mechanism Functions Analysis
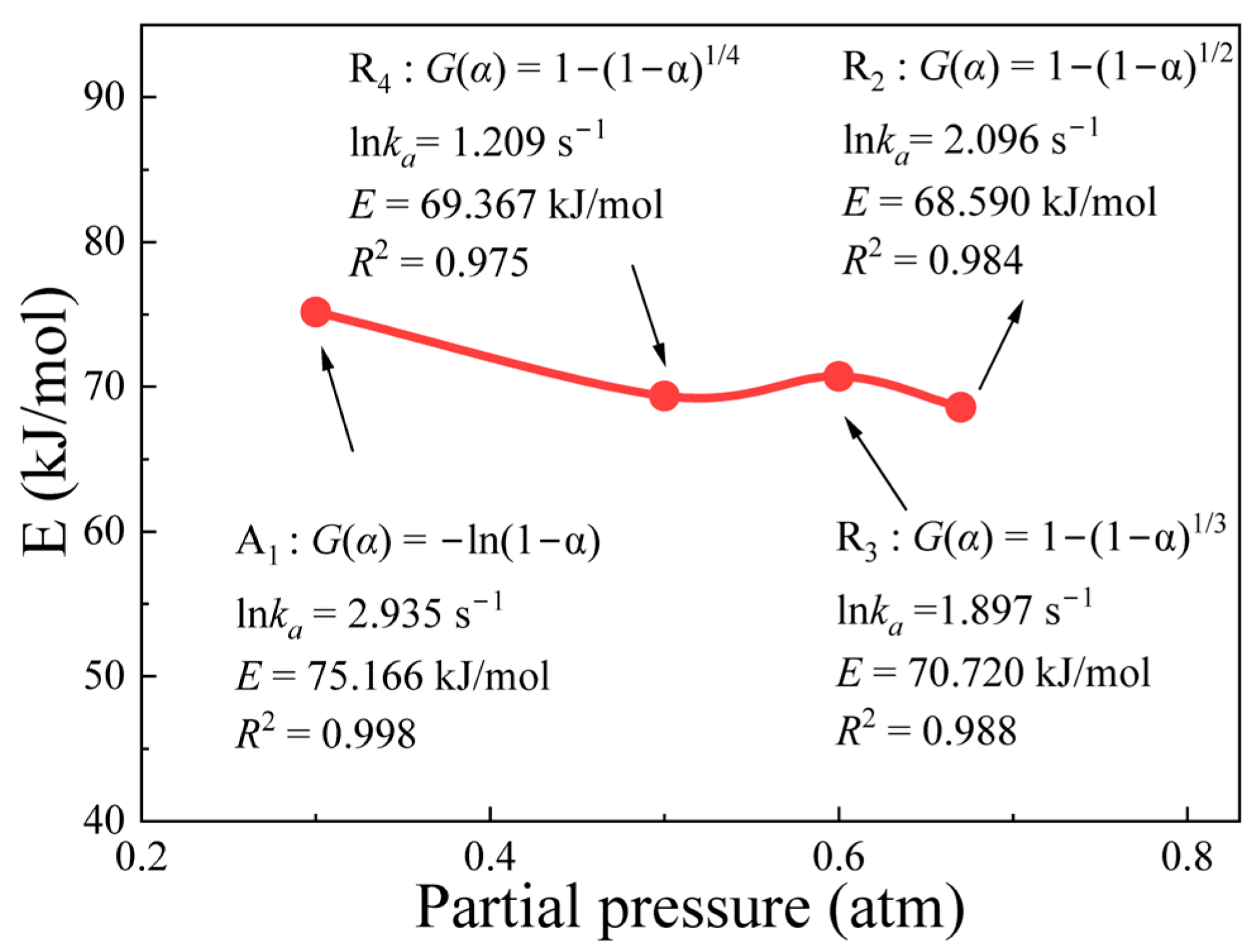
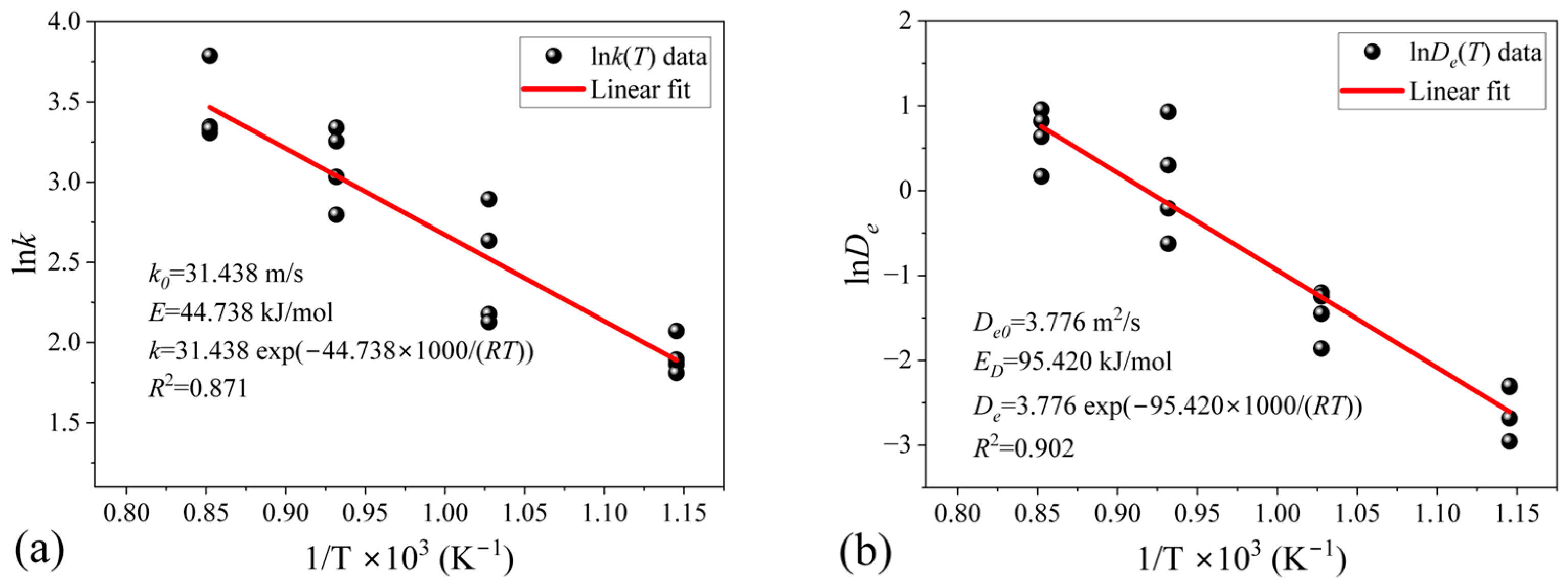
4.5. Determination of Intrinsic Kinetic Parameters
4.6. The Prediction of Reduction Degree
4.7. The Prediction of Reduction Time
5. Conclusions
- (1)
- The hydrogen reduction process of limonite particles is affected by multiple factors, including temperature, heating rate, hydrogen partial pressure, and particle size. Elevating the reduction temperature markedly accelerates the reduction reaction rate, whereas an increase in the heating rate shifts the reduction reaction to occur at higher temperatures. Furthermore, a rise in hydrogen partial pressure promotes a greater degree of reduction for limonite particles.
- (2)
- Based on the isothermal thermal analysis kinetic principles, the mechanism functions for limonite particles in reduction atmospheres with varying hydrogen concentrations were determined. The research findings reveal that hydrogen partial pressure significantly impacts the kinetic mechanism throughout the entire reduction process, despite the relatively minor differences in activation energy (ranging from 68.590 kJ·mol−1 to 75.166 kJ·mol−1). At low hydrogen partial pressures (0.33 atm), the kinetic mechanism of the limonite hydrogen reduction reaction predominantly follows the nucleation and nuclei growth model A1 (). At an intermediate hydrogen partial pressure of 0.50 atm, the reduction reaction is primarily governed by the geometric contraction model (R4, 1−(1−α)1/4). At a slightly higher intermediate hydrogen partial pressure of 0.60 atm, the reaction mechanism further transforms into the geometric contraction model (R3, −ln(1−α)). Under high hydrogen partial pressures (0.67 atm), the reduction reaction reverts to a geometric contraction model (R2, −ln(1−α)1/2).
- (3)
- Based on the UCM for flat-plate particles, the kinetic parameters for the hydrogen reduction of limonite were determined. The reaction activation energy is 44.738 kJ/mol, and the pre-exponential factor is 31.438 m/s. The rate constant for the hydrogen reduction of limonite is .
- (4)
- Contour plots were constructed to predict the reaction time and temperature required for the complete reduction of limonite particles of various sizes to Fe metal particles under hydrogen partial pressures ranging from 0.1 to 1.0 atm. These findings can offer valuable guidance for optimizing the hydrogen-based flash reduction process of limonite.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, K.H.; Deng, J.Y.; Wang, G.; Zhou, Q.; Xu, J. Utilization and impacts of hydrogen in the ironmaking processes: A review from lab-scale basics to industrial practices. Int. J. Hydrog. Energy 2021, 46, 26646–26664. [Google Scholar] [CrossRef]
- Shangguan, F.Q.; Zhou, J.C.; Wang, H.F.; Li, X. Climate change and decarbonization development of steel industry. Iron Steel 2021, 56, 1–6. [Google Scholar] [CrossRef]
- He, K.; Wang, L.; Li, X.Y. Review of the energy consumption and production structure of China’s steel industry: Current situation and future development. Metals 2020, 10, 302. [Google Scholar] [CrossRef]
- Shahabuddin, M.; Brooks, G.; Rhamdhani, M.A. Decarbonisation and hydrogen integration of steel industries: Recent development, challenges and technoeconomic analysis. J. Clean. Prod. 2023, 395, 136391. [Google Scholar] [CrossRef]
- Yue, Q.; Chai, X.C.; Zhang, Y.J.; Wang, Q.; Wang, H.; Zhao, F.; Ji, W.; Lu, Y. Analysis of iron and steel production paths on the energy demand and carbon emission in China’s iron and steel industry. Environ. Dev. Sustain. 2023, 25, 4065–4085. [Google Scholar] [CrossRef]
- Wei, N.; Liu, S.N.; Jiao, Z.S.; Li, X.-C. A possible contribution of carbon capture, geological utilization, and storage in the Chinese crude steel industry for carbon neutrality. J. Clean. Prod. 2022, 374, 133793. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Jiao, K.X.; Zhang, J.L.; Guo, Z. A review on low carbon emissions projects of steel industry in the world. J. Clean. Prod. 2021, 306, 127259. [Google Scholar] [CrossRef]
- Küster, F.; Scharm, C.; An, F.; Reinmöller, M.; Volkova, O.; Richter, A.; Guhl, S.; Gräbner, M. Direct reduction of iron ore pellets by N2/H2 mixture: In-situ investigation and modelling of the surface temperature during reduction progression. Miner. Eng. 2024, 215, 108827. [Google Scholar] [CrossRef]
- Elsherbiny, A.A.; Qiu, D.J.; Wang, K.; Li, M.; Ahmed, M.; Hammam, A.; Zhu, Y.; Song, W.; Galal, A.M.; Chen, H.; et al. Parametric study on hematite pellet direct reduction by hydrogen. Powder Technol. 2024, 435, 119434. [Google Scholar] [CrossRef]
- Fei, Y.; Guan, X.P.; Kuang, S.B.; Yu, A.; Yang, N. A review on the modeling and simulation of shaft furnace hydrogen metallurgy: A chemical engineering perspective. ACS Eng. Au 2024, 4, 145–165. [Google Scholar] [CrossRef]
- Boretti, A. The perspective of hydrogen direct reduction of iron. J. Clean. Prod. 2023, 429, 139585. [Google Scholar] [CrossRef]
- Ye, S.X.; Xie, Z.Y.; Wang, Y.; Wu, W.; Wang, R.; Zhang, Y.; Lu, X. New insights into the influence of hydrogen on important parameters of blast furnace. J. Clean. Prod. 2023, 425, 139042. [Google Scholar] [CrossRef]
- Metolina, P.; Ribeiro, T.R.; Guardani, R. Hydrogen-based direct reduction of industrial iron ore pellets: Statistically designed experiments and computational simulation. Int. J. Min. Met. Mater 2022, 29, 1908–1921. [Google Scholar] [CrossRef]
- Wang, L.; Guo, P.M.; Kong, L.B.; Zhao, P. Industrial application prospects and key issues of the pure-hydrogen reduction process. Int. J. Min. Met. Mater 2022, 29, 1922–1931. [Google Scholar] [CrossRef]
- Souza Filho, I.R.; Springer, H.; Ma, Y.; Mahajan, A.; da Silva, C.C.; Kulse, M.; Raabe, D. Green steel at its crossroads: Hybrid hydrogen-based reduction of iron ores. J. Clean. Prod. 2022, 340, 130805. [Google Scholar] [CrossRef]
- Zhao, J.; Zuo, H.B.; Wang, Y.J.; Wang, J.; Xue, Q. Review of green and low-carbon ironmaking technology. Ironmak. Steelmak. 2020, 47, 296–306. [Google Scholar] [CrossRef]
- Abdul Quader, M.; Ahmed, S.; Dawal, S.Z.; Nukman, Y. Present needs, recent progress and future trends of energy-efficient Ultra-Low Carbon Dioxide (CO2) Steelmaking (ULCOS) program. Renew. Sust. Energ. Rev. 2016, 55, 537–549. [Google Scholar] [CrossRef]
- Sun, M.; Pang, K.; Barati, M.; Meng, X. Hydrogen-based reduction technologies in low-carbon sustainable ironmaking and steelmaking: A review. J. Sustain. Metall. 2024, 10, 10–25. [Google Scholar] [CrossRef]
- Khani, M.; Ale Ebrahim, H.; Habibzadeh, S. A comprehensive random pore model kinetic study of hematite to iron reduction by hydrogen. Chem. Eng. Sci. 2023, 281, 119116. [Google Scholar] [CrossRef]
- Lyu, B.B.; Wang, G.; Yang, F.; Zuo, H.; Xue, Q.; Wang, J. Kinetic analysis of isothermal and non-Isothermal reduction of iron ore fines in hydrogen atmosphere. Metals 2022, 12, 1754. [Google Scholar] [CrossRef]
- Ali, M.L.; Fradet, Q.; Riedel, U. Kinetic mechanism development for the direct reduction of single hematite pellets in H2/CO atmospheres. Steel Res. Int. 2022, 93, 2200043. [Google Scholar] [CrossRef]
- Li, P.; Li, Y.; Yu, J.; Gao, P.; Han, Y. Kinetics and microstructural changes during fluidized reduction of magnetite with hydrogen at low temperatures. Int. J. Hydrog. Energy 2022, 47, 31140–31151. [Google Scholar] [CrossRef]
- Elzohiery, M.; Fan, D.Q.; Mohassab, Y.; Sohn, H.Y. Kinetics of hydrogen reduction of magnetite concentrate particles at 1623-1873 K relevant to flash ironmaking. Ironmak. Steelmak. 2021, 48, 485–492. [Google Scholar] [CrossRef]
- Wang, R.R.; Zhang, J.L.; Liu, Y.R.; Zheng, A.-Y.; Liu, Z.-J.; Liu, X.-L.; Li, Z.-G. Thermal performance and reduction kinetic analysis of cold-bonded pellets with CO and H2 mixtures. Int. J. Min. Met. Mater. 2018, 25, 752–761. [Google Scholar] [CrossRef]
- Elzohiery, M.; Sohn, H.Y.; Mohassab, Y. Kinetics of hydrogen reduction of magnetite concentrate particles in solid state relevant to flash ironmaking. Steel Res. Int. 2017, 88, 1600133. [Google Scholar] [CrossRef]
- Chen, F.; Mohassab, Y.; Jiang, T.; Sohn, H.Y. Hydrogen reduction kinetics of hematite concentrate particles relevant to a novel flash ironmaking process. Metall. Mater. Trans. B 2015, 46, 1133–1145. [Google Scholar] [CrossRef]
- Song, S.; Lu, S.; Lopez-Valdivieso, A. Magnetic separation of hematite and limonite fines as hydrophobic flocs from iron ores. Miner. Eng. 2002, 15, 415–422. [Google Scholar] [CrossRef]
- Lu, Y.; Wei, Z.; Wang, Y.; Zhang, J.; Li, G.; Zhang, Y. Research on the characteristics and kinetics of direct reduction of limonite ore fines under CO atmosphere in a rotary drum reactor. Powder Technol. 2019, 352, 240–250. [Google Scholar] [CrossRef]
- Tang, Z.; Li, P.; Gao, P.; Li, Y.; Han, Y. Minerals phase transformation by hydrogen reduction technology: A new approach to recycle iron from refractory limonite for reducing carbon emissions. Adv. Powder Technol. 2022, 33, 103870. [Google Scholar] [CrossRef]
- Jin, J.; Zhu, X.; Li, P.; Han, Y. Clean utilization of limonite ore by suspension magnetization roasting technology. Minerals 2022, 12, 260. [Google Scholar] [CrossRef]
- Wu, F.; Cao, Z.; Wang, S.; Zhong, H. Novel and green metallurgical technique of comprehensive utilization of refractory limonite ores. J. Clean. Prod. 2018, 171, 831–843. [Google Scholar] [CrossRef]
- Zhu, X.; Han, Y.; Liu, P.; Li, Y. Reduction mechanism of the porous hematite in limonite ore magnetization roasting. Miner. Process. Extr. Metall. Rev. 2024, 45, 85–90. [Google Scholar] [CrossRef]
- de Alvarenga Oliveira, V.; de Jesus Taveira Lana, R.; Da Silva Coelho, H.C.; Brigolini, G.J.S.; dos Santos, C.G. Kinetic studies of the reduction of limonitic nickel ore by hydrogen. Metall. Mater. Trans. B 2020, 51, 1418–1431. [Google Scholar] [CrossRef]
- Liu, P.; Zhu, X.; Han, Y.; Li, Y.; Gao, P. Fluidization magnetization roasting of limonite ore using H2 as a reductant: Phase transformation, structure evolution, and kinetics. Powder Technol. 2023, 414, 118107. [Google Scholar] [CrossRef]
- Sun, Y.; Zhu, X.; Han, Y.; Li, Y.; Gao, P. Iron recovery from refractory limonite ore using suspension magnetization roasting: A pilot-scale study. J. Clean. Prod. 2020, 261, 121221. [Google Scholar] [CrossRef]
- GB/T 6003.1-2022; Test Sieves-Technical Requirements and Testing-Part 1: Test Sieves of Metal Wire Cloth. Standards Press of China: Beijing, China, 2022.
- Dilmaç, N. Isothermal and non-isothermal reduction kinetics of iron ore oxygen carrier by CO: Modelistic and model-free approaches. Fuel 2021, 296, 120707. [Google Scholar] [CrossRef]
- Kwon, E.; Lee, J.; Han, J. Modified unreacted core model for reduction of manganese ore by CO gas. Met. Mater. Int. 2022, 28, 1517–1524. [Google Scholar] [CrossRef]
- Gou, L. Iron Ore Reduction Kinetics Model Considering Multicomponent Gas Diffusion. Master’s Thesis, Northeastern University, Shenyang, China, 2018. [Google Scholar]
- Yuan, Z.; Sohn, H.Y.; Olivas-Martinez, M. Re-oxidation Kinetics of Flash-Reduced Iron Particles in H2-H2O(g) Atmosphere Relevant to a Novel Flash Ironmaking Process. Metall. Mater. Trans. B 2013, 44, 1520–1530. [Google Scholar] [CrossRef]
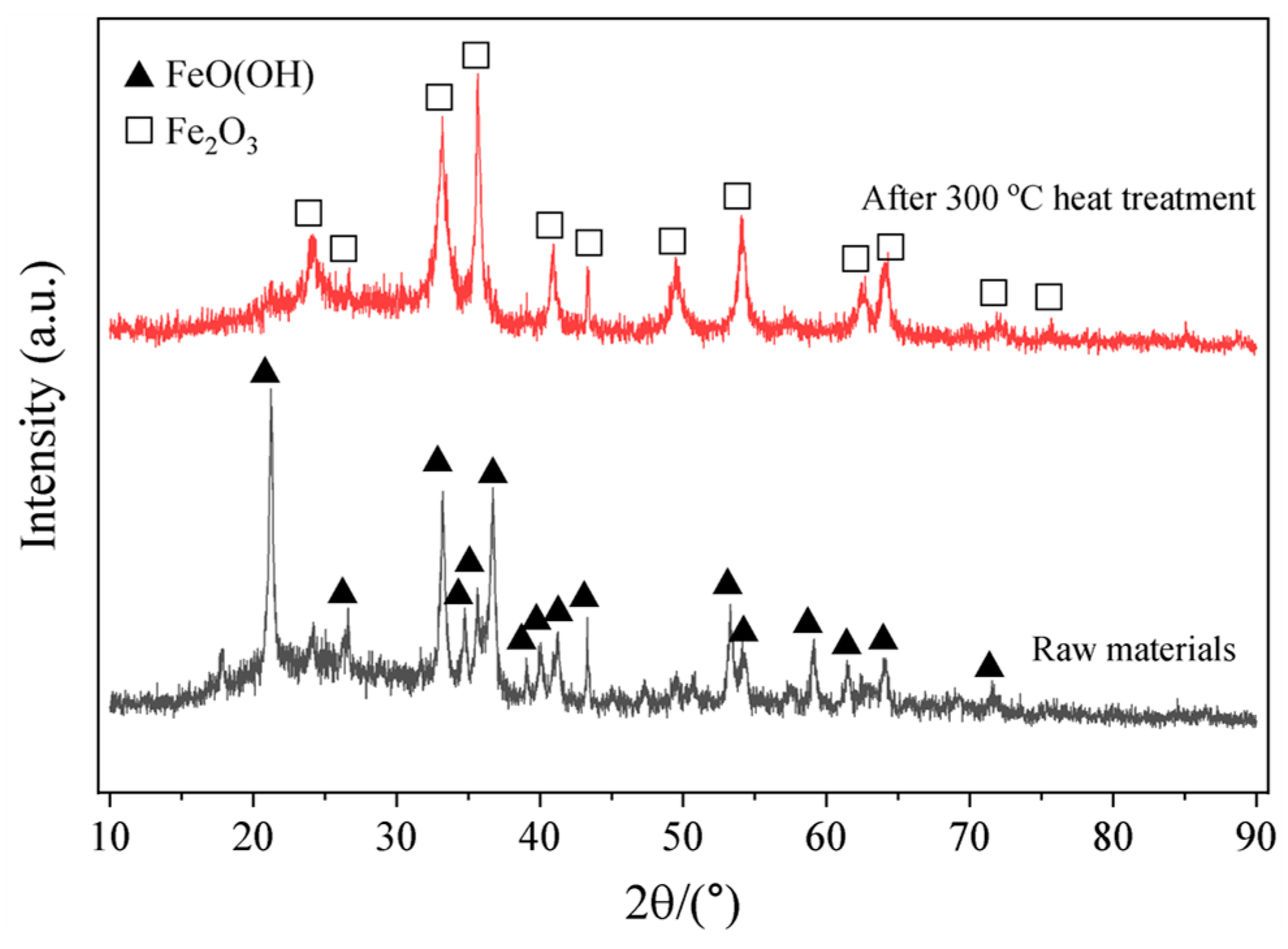
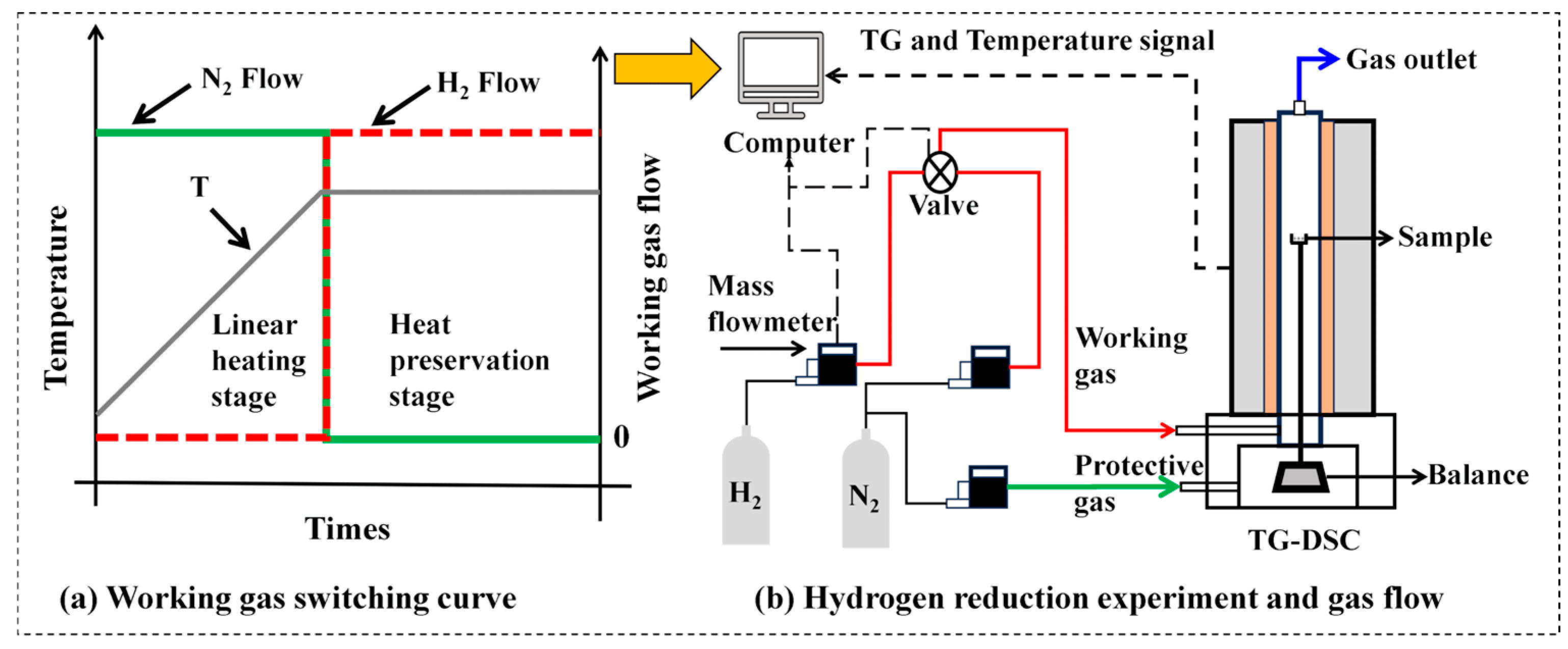
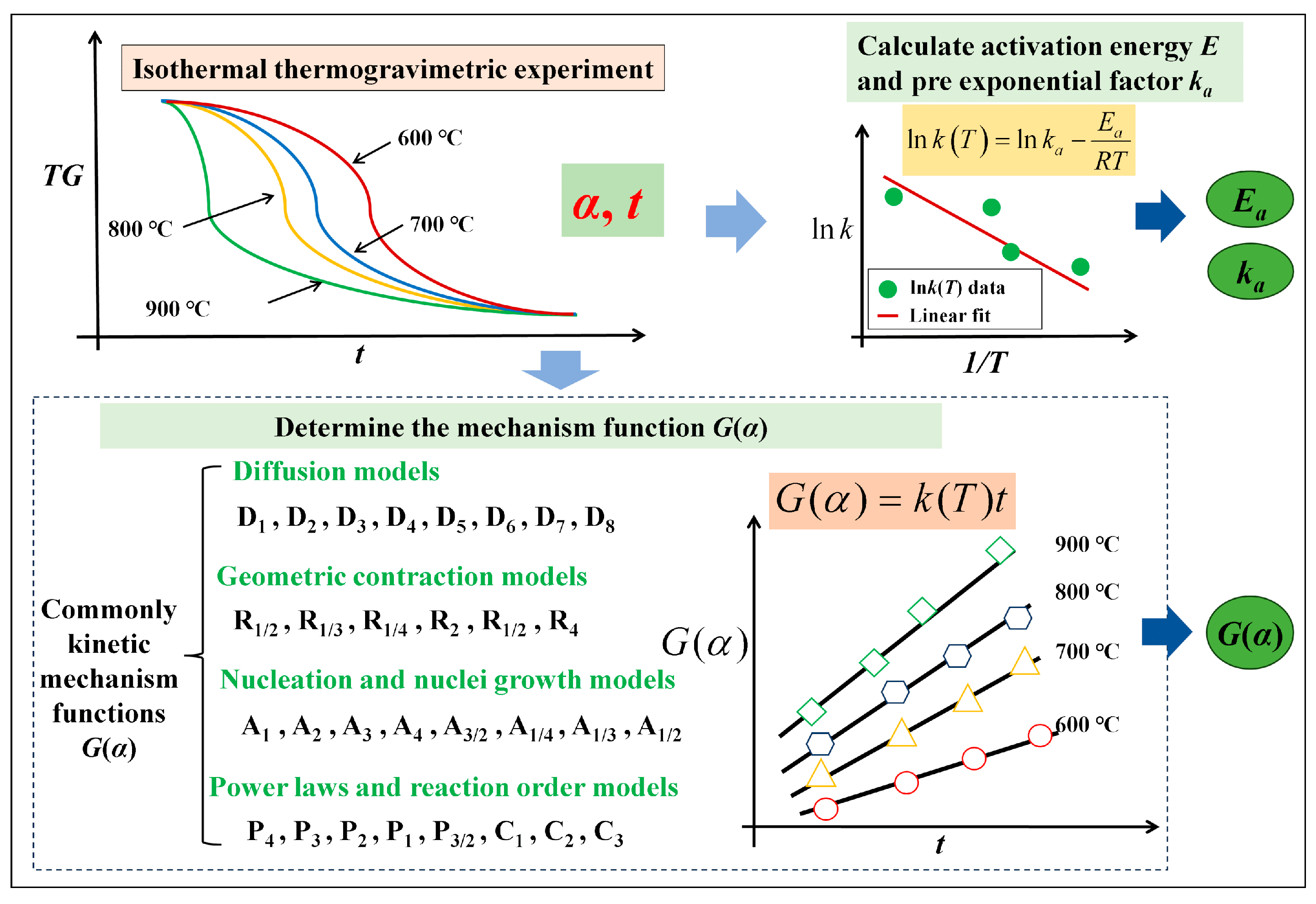
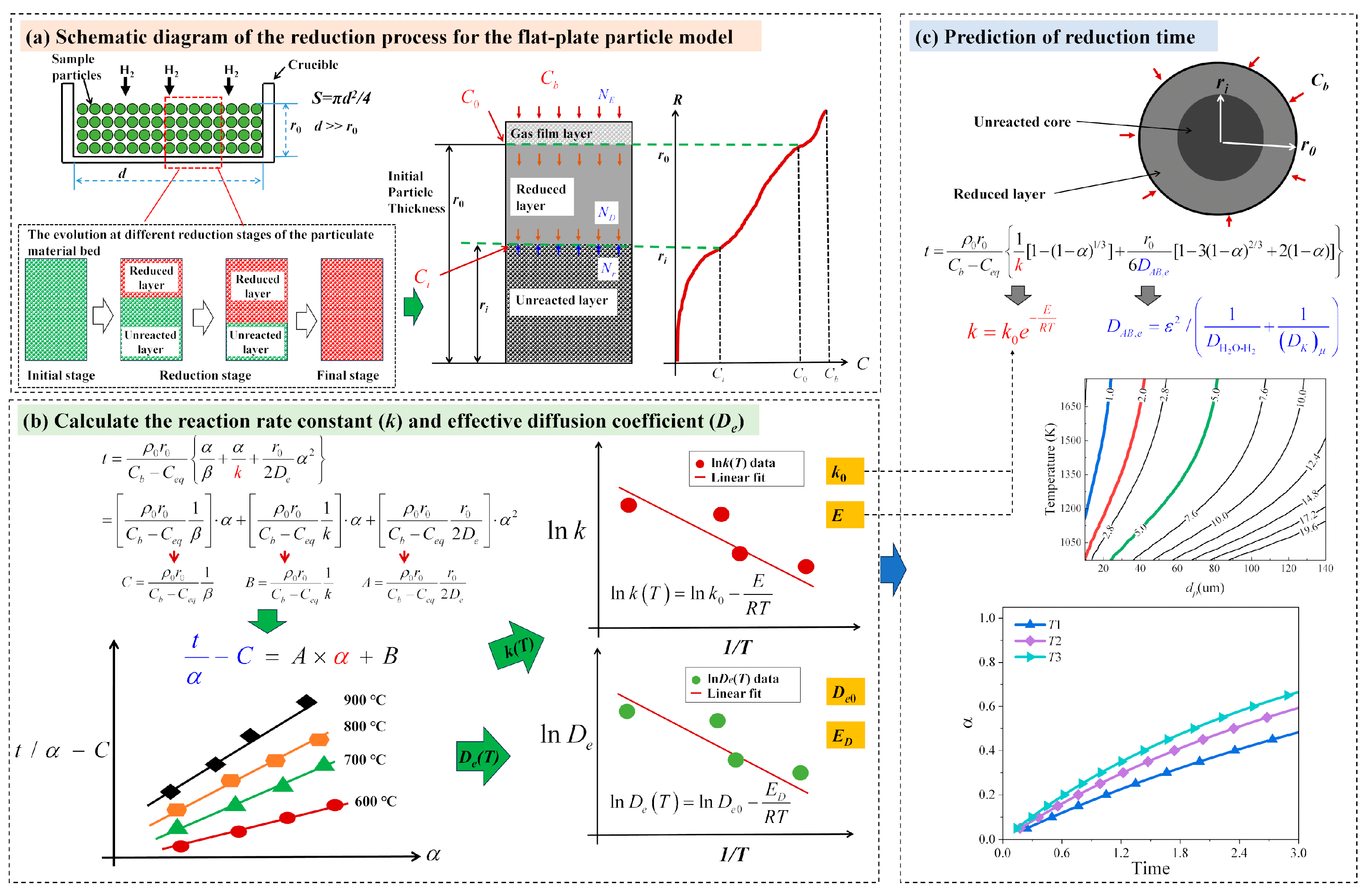

| Compostion | TFe | Fe2O3 | SiO2 | CaO | MgO | Al2O3 | P2O5 | SO3 | Na2O | TiO2 | MnO | Co3O4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Content (wt%) | 62.35 | 89.15 | 6.19 | 0.10 | 0.18 | 3.56 | 0.12 | 0.12 | 0.20 | 0.13 | 0.07 | 0.15 |
| Hydrogen Partial Pressure (atm) | Flow Rate of the Protective Gas (N2) (mL·min−1) | Flow Rate of the Working Gas (H2) (mL·min−1) | Total Flow Rate of the Mixed Gas (mL·min−1) | Total Gas Pressure (atm) |
|---|---|---|---|---|
| 0.33 | 40 | 20 | 60 | 1.0 |
| 0.50 | 40 | 40 | 80 | 1.0 |
| 0.60 | 40 | 60 | 100 | 1.0 |
| 0.67 | 40 | 80 | 120 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Yi, T.; Li, J.; Li, M.; Liu, F.; Wang, J. Kinetics Study of the Hydrogen Reduction of Limonite Ore Using an Unreacted Core Model for Flat-Plate Particles. Metals 2025, 15, 678. https://doi.org/10.3390/met15060678
Huang J, Yi T, Li J, Li M, Liu F, Wang J. Kinetics Study of the Hydrogen Reduction of Limonite Ore Using an Unreacted Core Model for Flat-Plate Particles. Metals. 2025; 15(6):678. https://doi.org/10.3390/met15060678
Chicago/Turabian StyleHuang, Jindi, Tao Yi, Jing Li, Mingzhou Li, Fupeng Liu, and Jinliang Wang. 2025. "Kinetics Study of the Hydrogen Reduction of Limonite Ore Using an Unreacted Core Model for Flat-Plate Particles" Metals 15, no. 6: 678. https://doi.org/10.3390/met15060678
APA StyleHuang, J., Yi, T., Li, J., Li, M., Liu, F., & Wang, J. (2025). Kinetics Study of the Hydrogen Reduction of Limonite Ore Using an Unreacted Core Model for Flat-Plate Particles. Metals, 15(6), 678. https://doi.org/10.3390/met15060678








