In Situ Investigation of Deformation Mechanisms and Stress Evolution in Mg-3Al-1Zn (AZ31) Alloy Using Synchrotron X-Ray Microdiffraction
Abstract
1. Introduction
2. Materials and Methods
2.1. Material Preparation and Characterization
2.2. In Situ Synchrotron X-Ray Microdiffraction
2.3. Simulation of Elastic Strain/Stress Tensor
3. Results
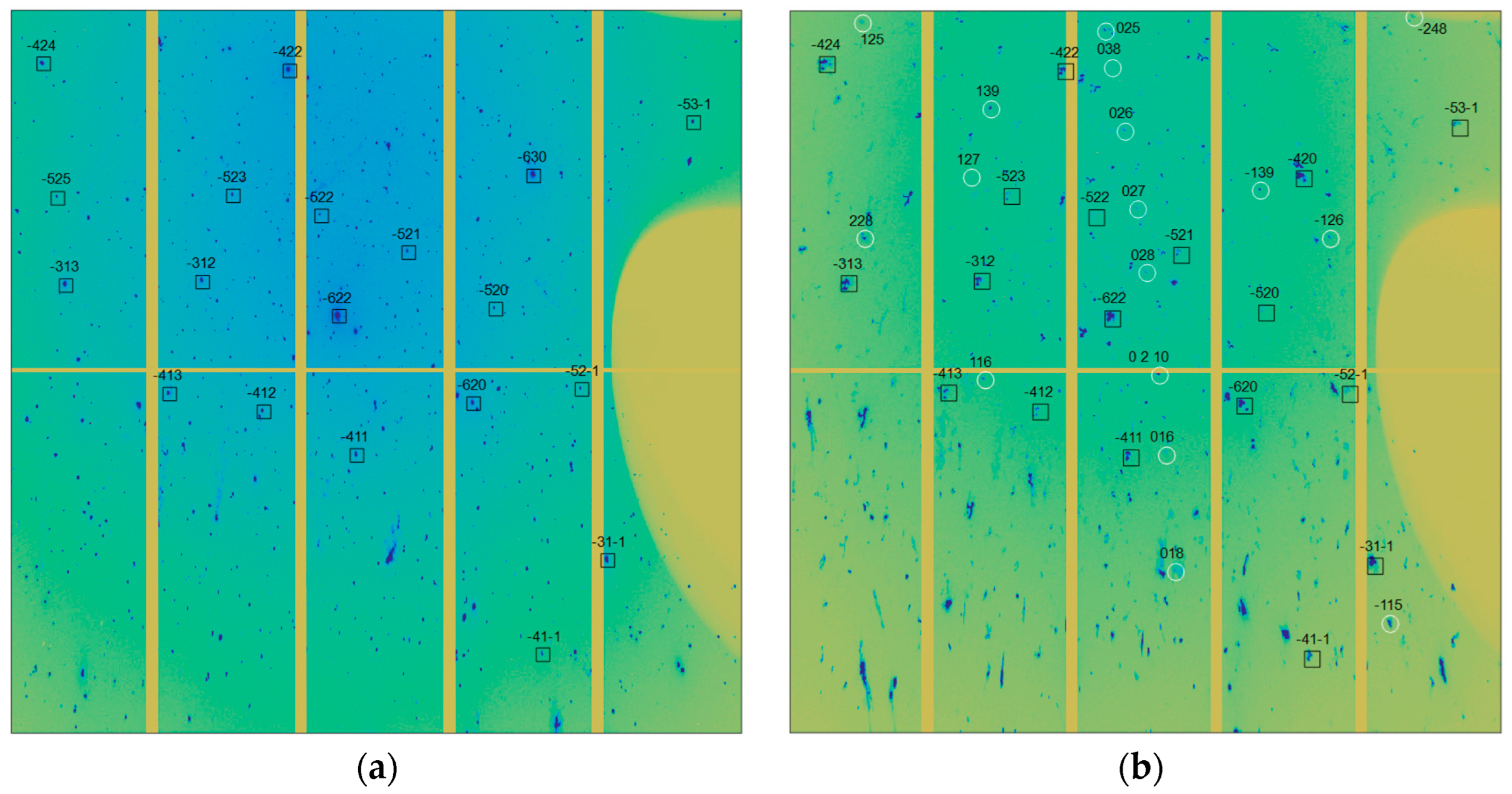
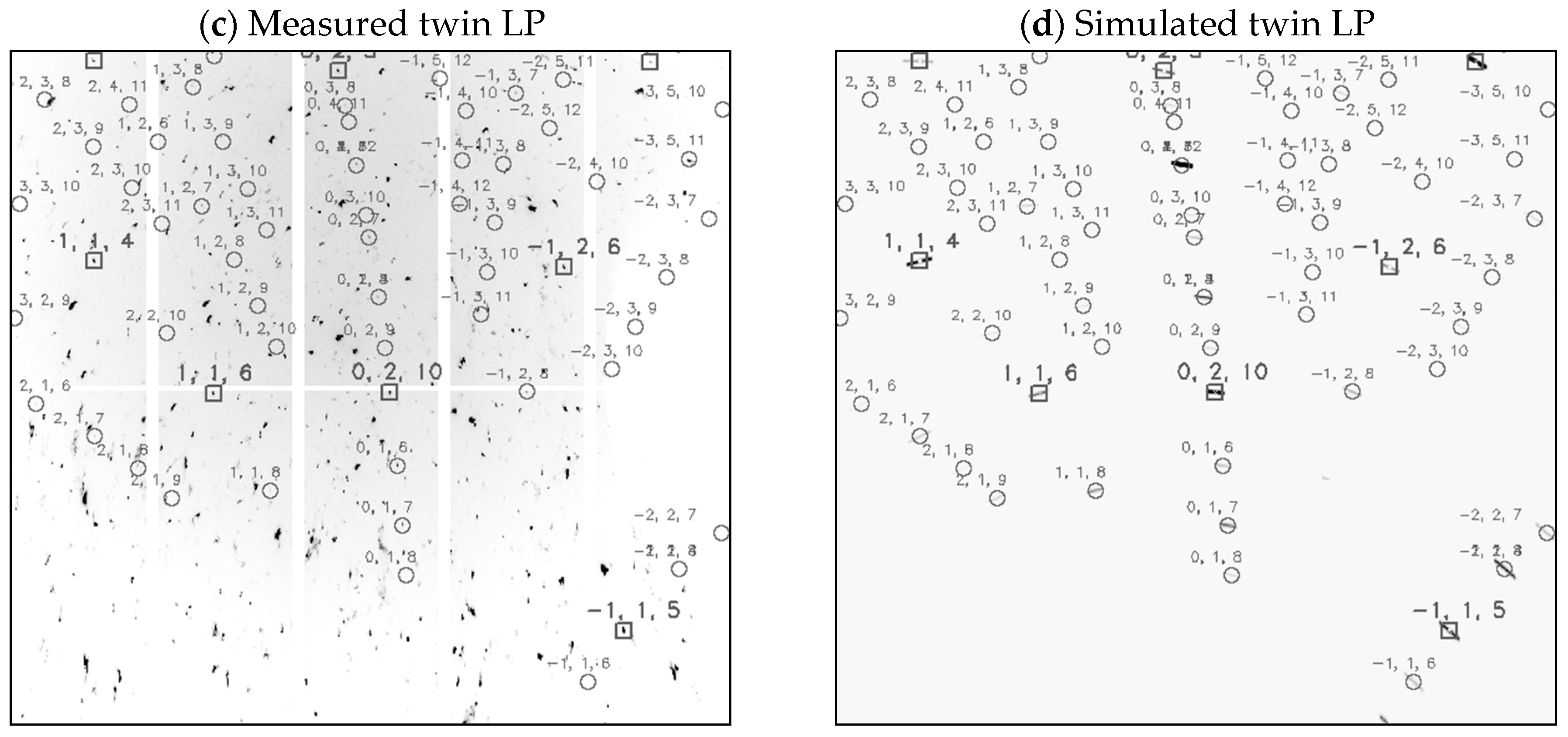
3.1. Parents and Twins Indexation
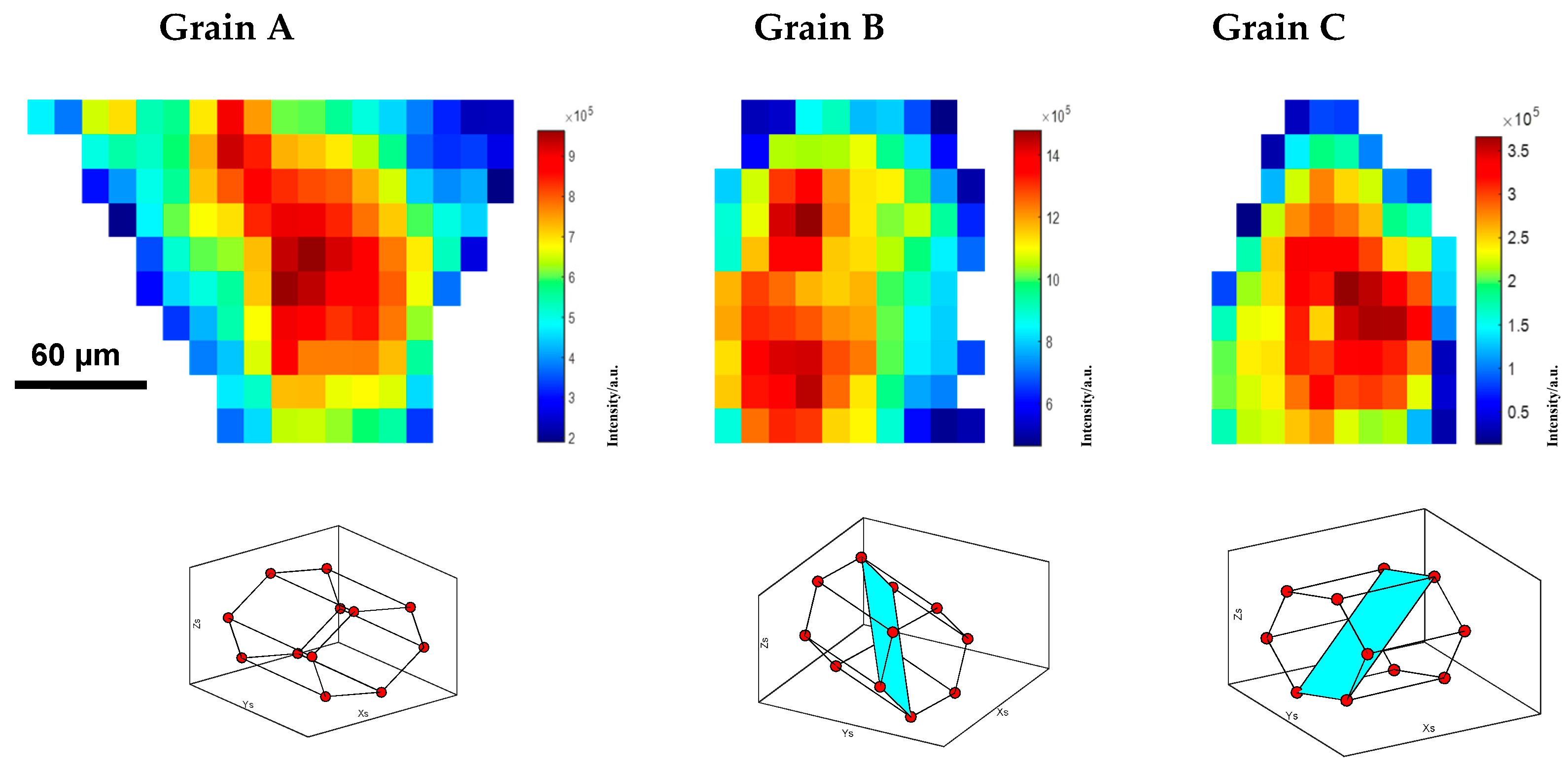
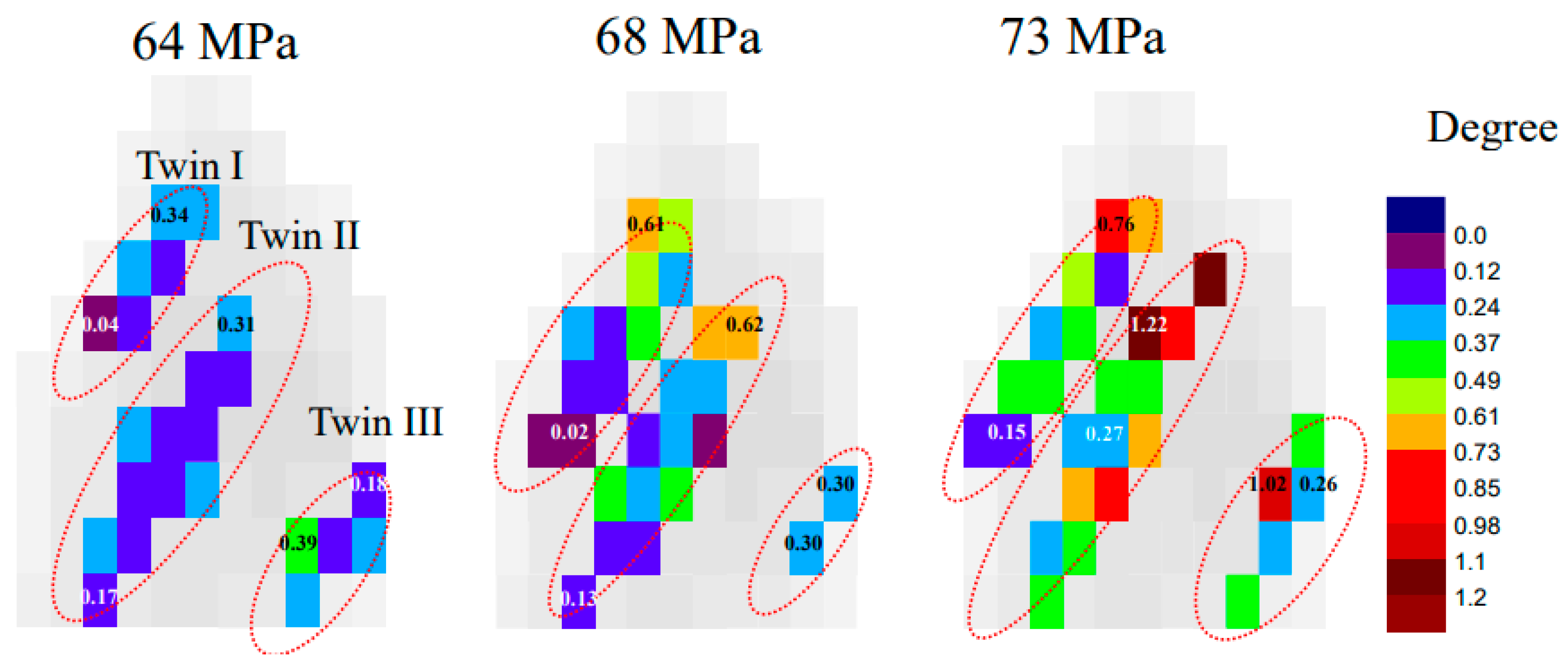
3.2. Orientation Fluctuation of Grains and Twins
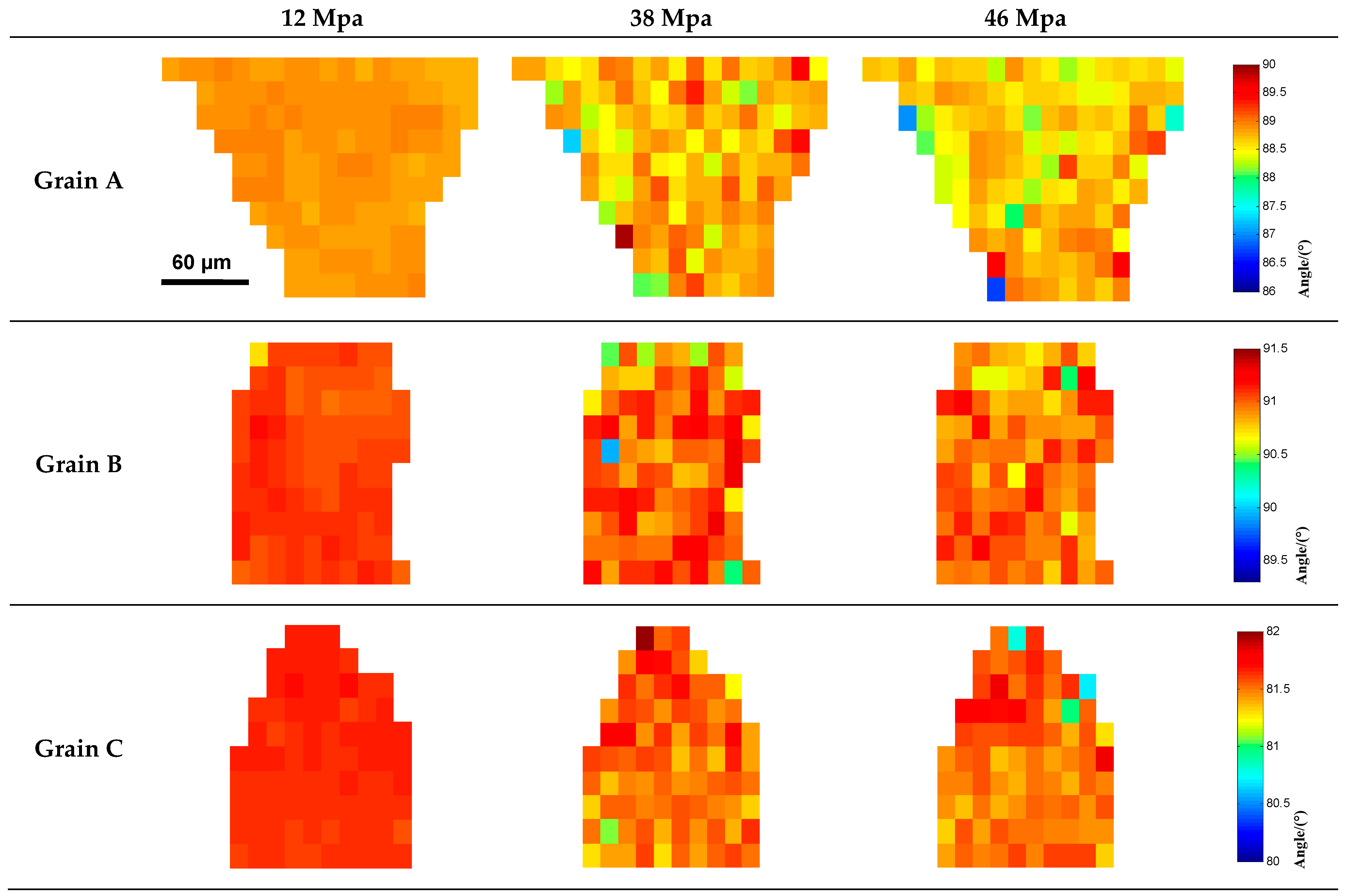
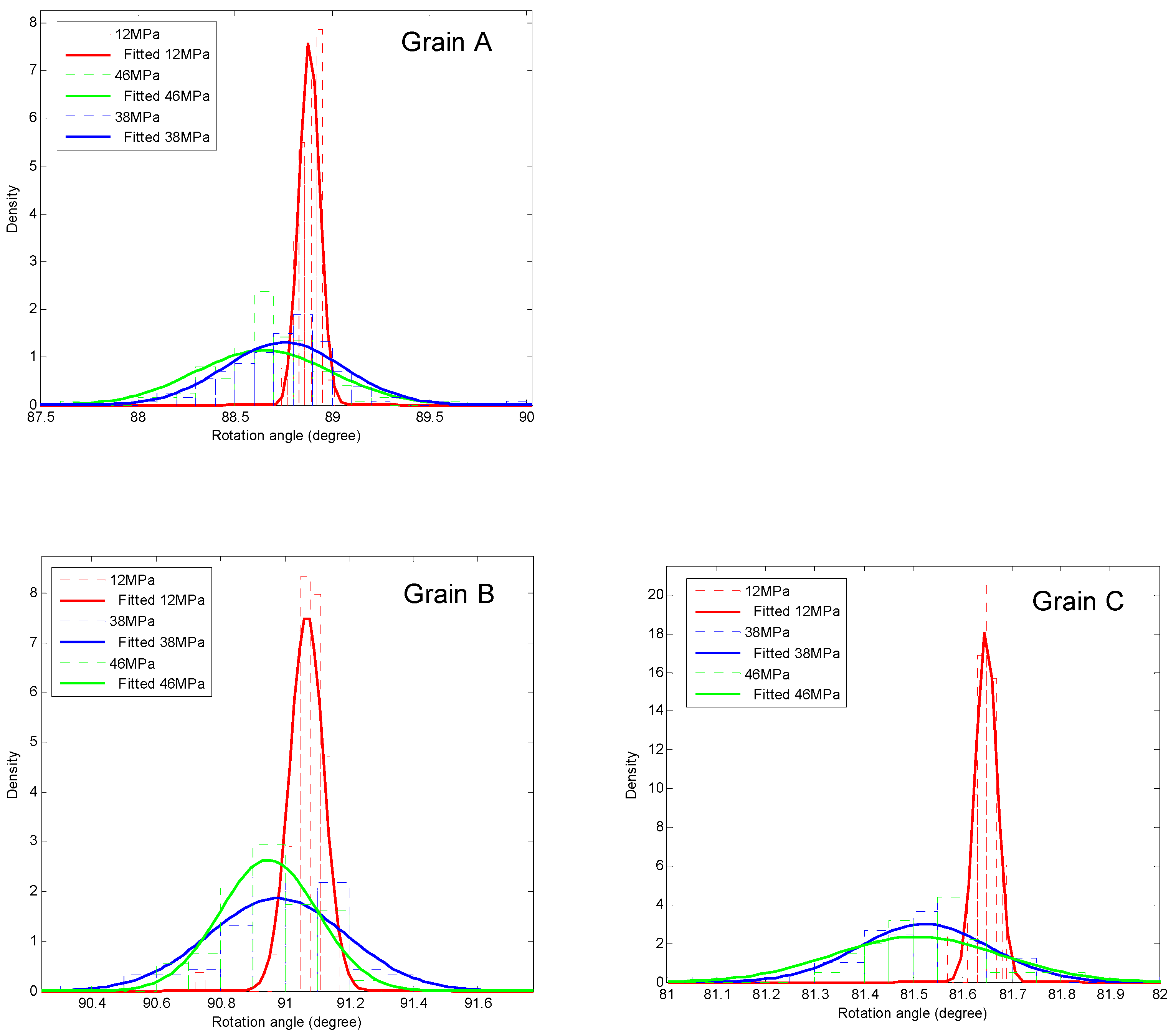
3.3. Mosaic Spread and Deformation Modes
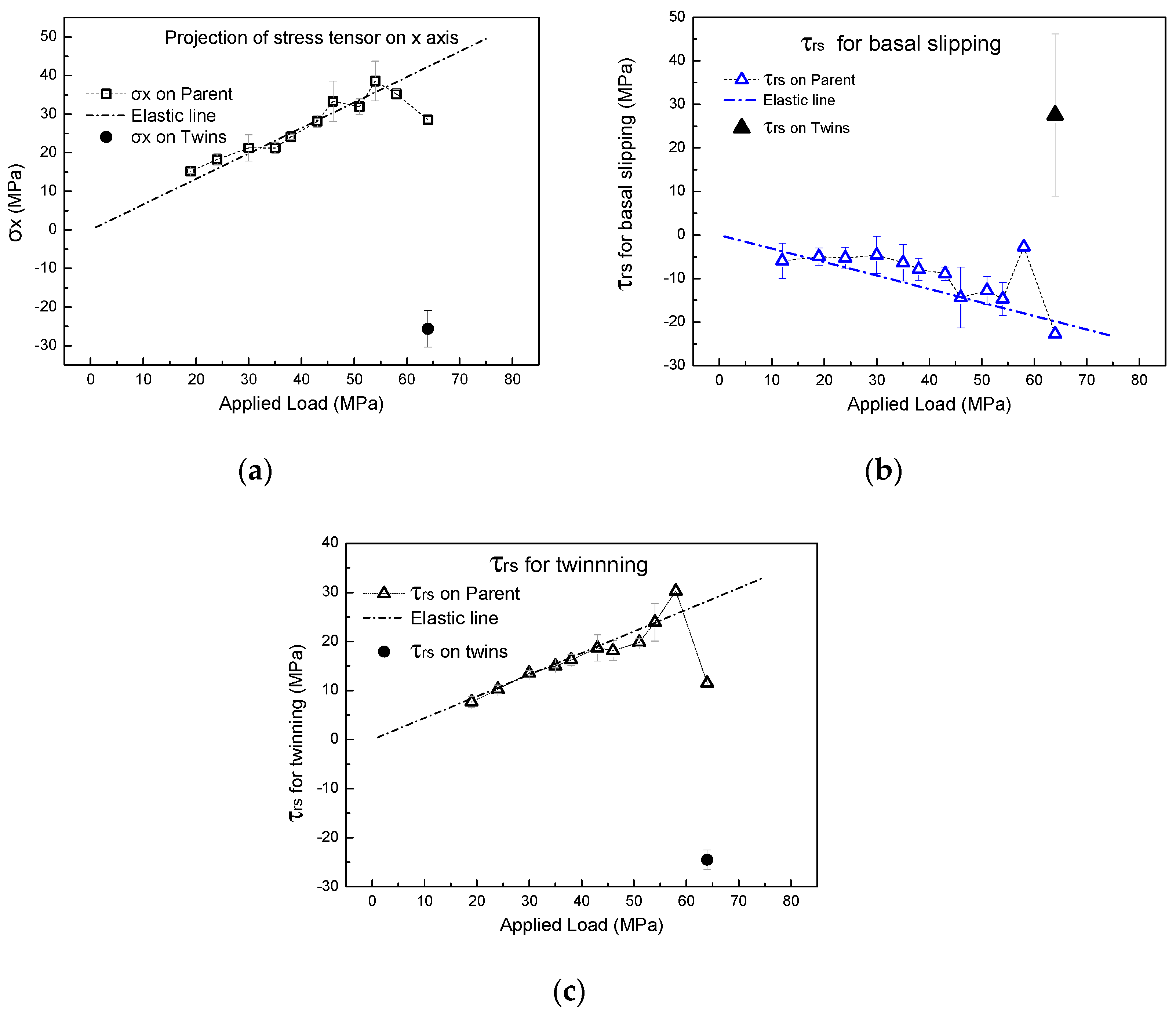
3.4. Stress and Strain Evolution
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, J.; Zhu, Z.; Han, S.; Gu, Y.; Zhu, Z.; Zhang, H. Evolution, limitations, advantages, and future challenges of magnesium alloys as materials for aerospace applications. J. Alloy. Compd. 2024, 1008, 176707. [Google Scholar] [CrossRef]
- Nie, J.F.; Zhu, Y.M.; Liu, J.Z.; Fang, X.Y. Periodic segregation of solute atoms in fully coherent twin boundaries. Science 2013, 340, 957–960. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Zheng, J.; He, Q.; Li, T.; Shou, H.; Yin, D.; Bai, S.; Jiang, B.; Pan, F. Achieving superior strength and ductility synergy of WE54 alloy via combined dislocation introduction and twinning. J. Mater. Sci. Technol. 2025, 227, 174–191. [Google Scholar] [CrossRef]
- Zhao, L.; Zhu, W.; Chen, W.; Zhao, X.; Yan, C.; Hong, R.; Jin, Z. An insight into mechanical response and twinning behavior of bimodal textured AZ31 magnesium alloy under quasi-static and high strain rate compression. J. Mater. Res. Technol. 2023, 27, 4692–4705. [Google Scholar] [CrossRef]
- Lentz, M.; Risse, M.; Schaefer, N.; Reimers, W.; Beyerlein, I.J. Strength and ductility with {1011}–{1012}double twinning in a magnesium alloy. Nat. Commun. 2016, 7, 11068. [Google Scholar] [CrossRef]
- Abdolvand, H.; Daymond, M.R. Internal strain and texture development during twinning: Comparing neutron diffraction measurements with crystal plasticity finite-element approaches. Acta Mater. 2024, 60, 2240–2248. [Google Scholar] [CrossRef]
- Cheng, J.; Bong, H.J.; Qiao, H.; Hu, X.; Sun, X.; Ghosh, S.; Wu, P. Comparison of three state-of-the-art crystal plasticity based deformation twinning models for magnesium alloys. Comput. Mater. Sci. 2022, 210, 111480. [Google Scholar] [CrossRef]
- Lynch, P.A.; Kunz, M.; Tamura, N.; Barnett, M.R. Time and spatial resolution of slip and twinning in a grain embedded within a magnesium polycrystal. Acta Mater. 2014, 78, 203–212. [Google Scholar] [CrossRef]
- Kada, S.R.; Lynch, P.A.; Kimpton, J.A.; Barnett, M.R. In-situ X-ray diffraction studies of slip and twinning in the presence of precipitates in AZ91 alloy. Acta Mater. 2016, 119, 145–156. [Google Scholar] [CrossRef]
- Baczmański, A.; Kot, P.; Wroński, S.; Wróbel, M.; Wroński, M.; Pilch, J.; Muzyka, M.; Wierzbanowski, K.; Zhao, Y.; Le Joncour, L.; et al. Direct diffraction measurement of critical resolved shear stresses and stress localisation in magnesium alloy. Mater. Sci. Eng. A 2021, 801, 140400. [Google Scholar] [CrossRef]
- Kot, P.; Wroński, M.; Baczmański, A.; Ludwik, A.; Wroński, S.; Wierzbanowski, K.; Scheffzük, C.; Pilch, J.; Farkas, G. A novel method of experimental determination of grain stresses and critical resolved shear stresses for slip and twin systems in a magnesium alloy. Measurement 2023, 221, 113469. [Google Scholar] [CrossRef]
- Shin, K.S.; Wang, L.; Bian, M.; Choi, S.; Komissarov, A.; Bazhenov, V. Effects of temperature on critical resolved shear stresses of slip and twining in Mg single crystal via experimental and crystal plasticity modeling. J. Magnes. Alloys 2023, 11, 2027–2041. [Google Scholar] [CrossRef]
- Lynch, P.A.; Stevenson, A.W.; Liang, D.; Parry, D.; Wilkins, S.; Madsen, I.C.; Bettles, C.; Tamura, N.; Geandier, G. In-Situ White Beam Microdiffraction Study of the Deformation Behavior in Polycrystalline Magnesium Alloy During Uniaxial Loading. AIP Conf. Proc. 2007, 879, 1751–1754. [Google Scholar]
- Tamura, N. XMAS: A Versatile Tool for Analyzing Synchrotron X-ray Microdiffraction Data. In Strain and Dislocation Gradients from Diffraction; Imperial College Press: London, UK, 2014; pp. 125–155. [Google Scholar]
- Ting, T.C.T. Invariants of anisotropic elastic constants. Q. J. Mech. Appl. Math. 1987, 40, 431–448. [Google Scholar] [CrossRef]
- Barnett, M.R.; Wang, J.; Kada, S.R.; de Vaucorbeil, A.; Stevenson, A.; Fivel, M.; Lynch, P.A. Grain scale bursts of plasticity in Mg-4Zn via high energy X-rays: Towards twin observation in real-time. Acta Mater. 2024, 264, 119549. [Google Scholar] [CrossRef]
- Barabash, R.I.; Ice, G.E.; Pang, J.W.L. Gradients of geometrically necessary dislocations from white beam microdiffraction. Mater. Sci. Eng. A 2005, 400–401, 125–131. [Google Scholar] [CrossRef]
- Poshadel, A.; Dawson, P.; Johnson, G. Assessment of deviatoric lattice strain uncertainty for polychromatic X-ray microdiffraction experiments. J. Synchrotron Radiat. 2012, 19, 237–244. [Google Scholar] [CrossRef]
- Joo, H.D.; Kim, J.S.; Kim, K.H.; Tamura, N.; Koo, Y.M. In situ synchrotron X-ray microdiffraction study of deformation behavior in polycrystalline coppers during uniaxial deformations. Scr. Mater. 2004, 51, 1183–1186. [Google Scholar] [CrossRef]
- Barabash, R.I.; Ice, G.E.; Liu, W.J.; Barabash, O.M. Polychromatic microdiffraction characterization of defect gradients in severely deformed materials. Micron 2009, 40, 28–36. [Google Scholar] [CrossRef]
- Clausen, B.; Tomé, C.N.; Brown, D.W.; Agnew, S.R. Reorientation and stress relaxation due to twinning: Modeling and experimental characterization for Mg. Acta Mater. 2008, 56, 2456–2468. [Google Scholar] [CrossRef]
- Garcés, G.; Oñorbe, E.; Pérez, P.; Klaus, M.; Genzel, C.; Adeva, P. Influence of SiC particles on compressive deformation of magnesium matrix composites. Mater. Sci. Eng. A 2012, 533, 119–123. [Google Scholar] [CrossRef]
- Aydiner, C.C.; Bernier, J.V.; Clausen, B.; Lienert, U.; Tome, C.N.; Brown, D.W. Evolution of stress in individual grains and twins in a magnesium alloy aggregate. Phys. Rev. B 2009, 80, 024113. [Google Scholar] [CrossRef]
- Muránsky, O.; Barnett, M.R.; Luzin, V.; Vogel, S. On the correlation between deformation twinning and Lüders-like deformation in an extruded Mg alloy: In situ neutron diffraction and EPSC.4 modelling. Mater. Sci. Eng. A 2010, 527, 1383–1394. [Google Scholar] [CrossRef]





| (VI) six {}<> slips | |
| (V) six {}<> slips | |
| (IV) six {}<> slips | |
| (III) six {}<> slips | |
| (I) three basal slips | (II) three prismatic slips |
| Deformation Mode | {} Twin | Basal Slips | {} Slips | {} Slips | {} Slips | {} Slips | {} Slips | {} Slips | {} Twin |
|---|---|---|---|---|---|---|---|---|---|
| Grain A | −0.033 | 0.033 | 0.499 | 0.452 | 0.336 | 0.366 | 0.430 | 0.466 | −0.033 |
| Grain B | 0.096 | 0.405 | 0.388 | 0.478 | 0.446 | 0.378 | 0.409 | 0.285 | 0.096 |
| Grain C | 0.456 | 0.276 | 0.045 | 0.151 | 0.466 | 0.431 | 0.493 | 0.456 | 0.456 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Li, L.; Wang, Y.; Ye, T.; Tang, C. In Situ Investigation of Deformation Mechanisms and Stress Evolution in Mg-3Al-1Zn (AZ31) Alloy Using Synchrotron X-Ray Microdiffraction. Metals 2025, 15, 675. https://doi.org/10.3390/met15060675
Cao Y, Li L, Wang Y, Ye T, Tang C. In Situ Investigation of Deformation Mechanisms and Stress Evolution in Mg-3Al-1Zn (AZ31) Alloy Using Synchrotron X-Ray Microdiffraction. Metals. 2025; 15(6):675. https://doi.org/10.3390/met15060675
Chicago/Turabian StyleCao, Yuxin, Li Li, Yong Wang, Tuo Ye, and Changping Tang. 2025. "In Situ Investigation of Deformation Mechanisms and Stress Evolution in Mg-3Al-1Zn (AZ31) Alloy Using Synchrotron X-Ray Microdiffraction" Metals 15, no. 6: 675. https://doi.org/10.3390/met15060675
APA StyleCao, Y., Li, L., Wang, Y., Ye, T., & Tang, C. (2025). In Situ Investigation of Deformation Mechanisms and Stress Evolution in Mg-3Al-1Zn (AZ31) Alloy Using Synchrotron X-Ray Microdiffraction. Metals, 15(6), 675. https://doi.org/10.3390/met15060675





