A Novel Method to Predict Phase Fraction Based on the Solidification Time on the Cooling Curve
Abstract
1. Introduction
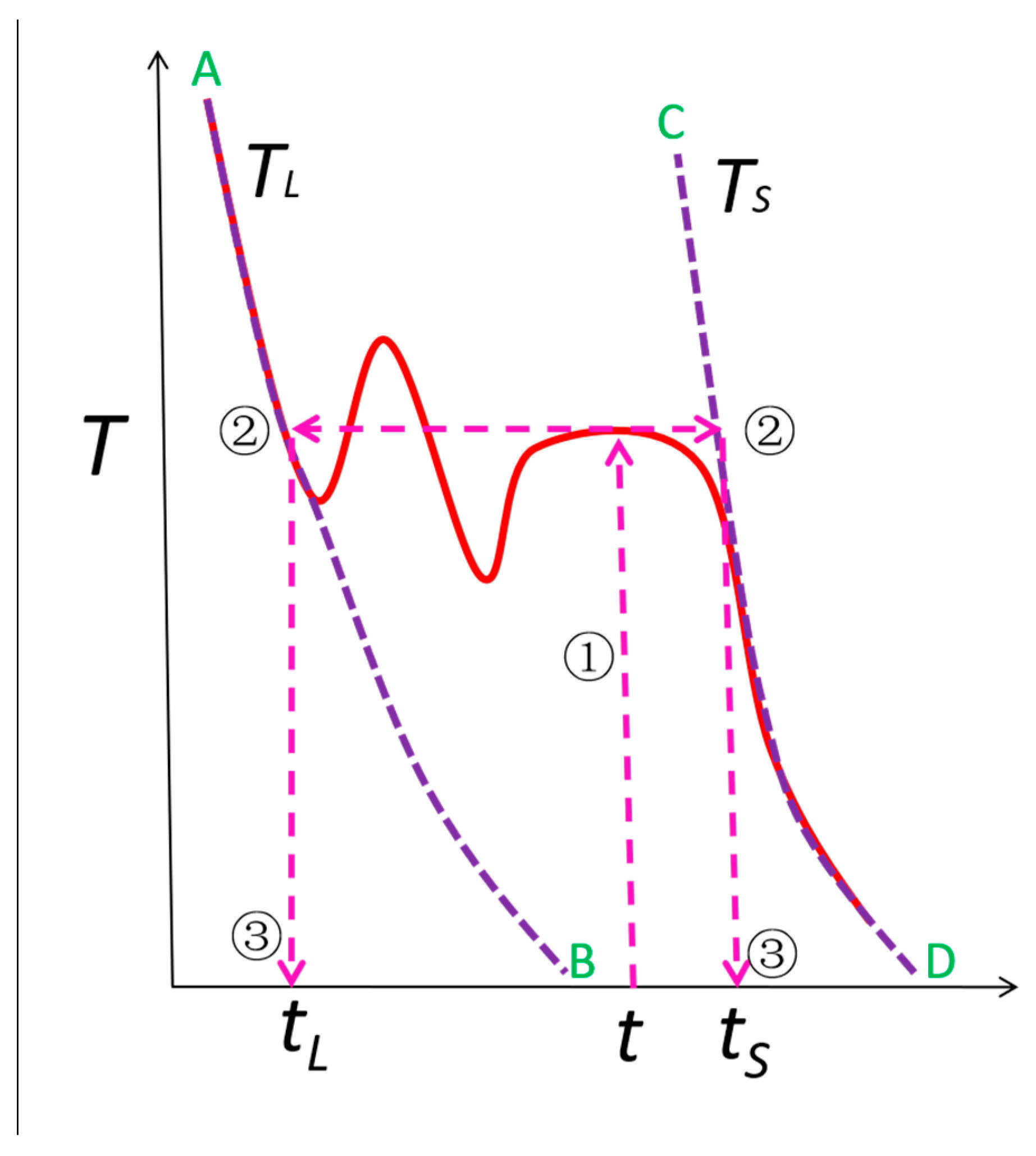
2. Method Description
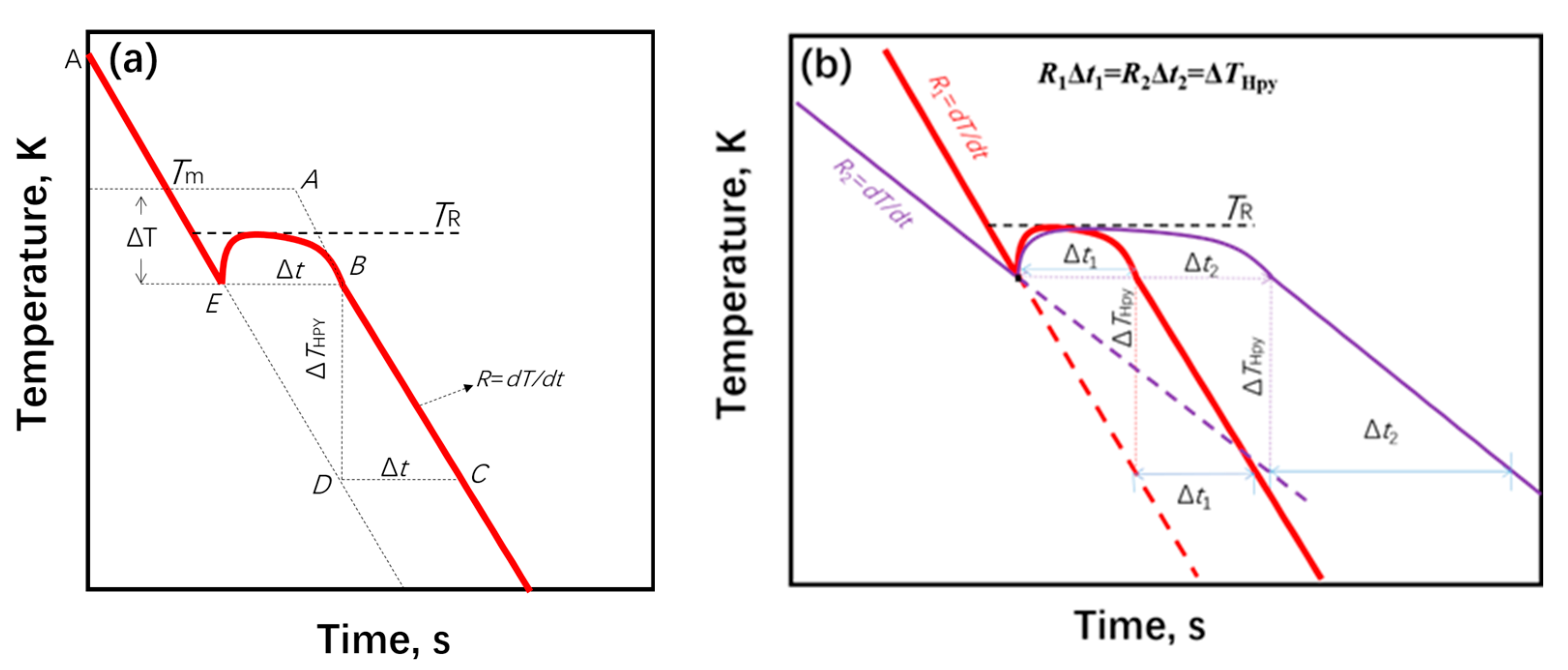
2.1. Phase Fraction Prediction Method
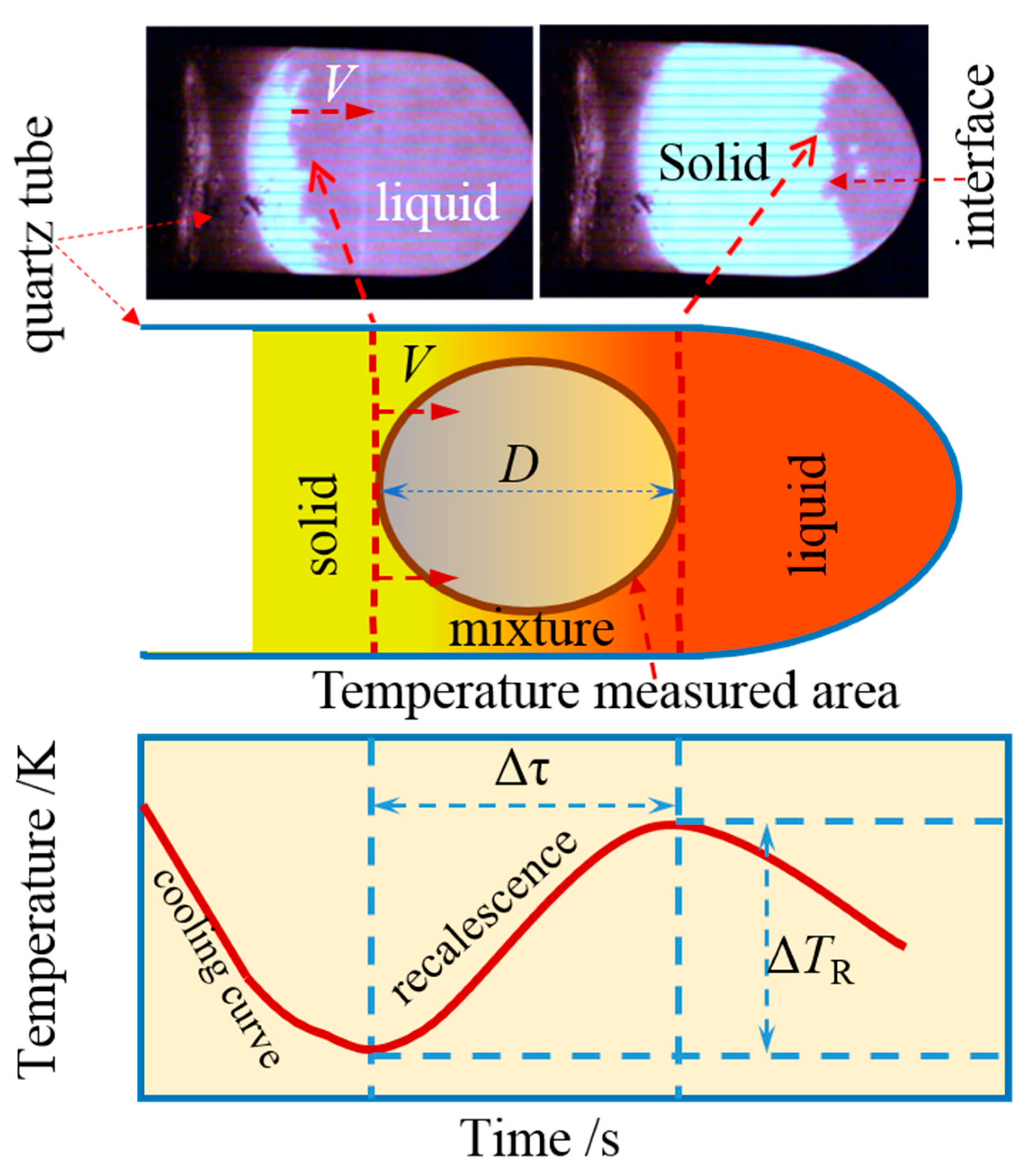
2.2. Microstructure Measurement Method
- (1)
- The image is covered by the boxes of L × L;
- (2)
- The number of boxes containing primary phase (including that full of primary phase and that partially filled with primary phase) is counted as α;
- (3)
- The box number is counted, only containing the primary phase as αf;
- (4)
- The fraction of the primary phase is calculated as follows:
3. Experimental
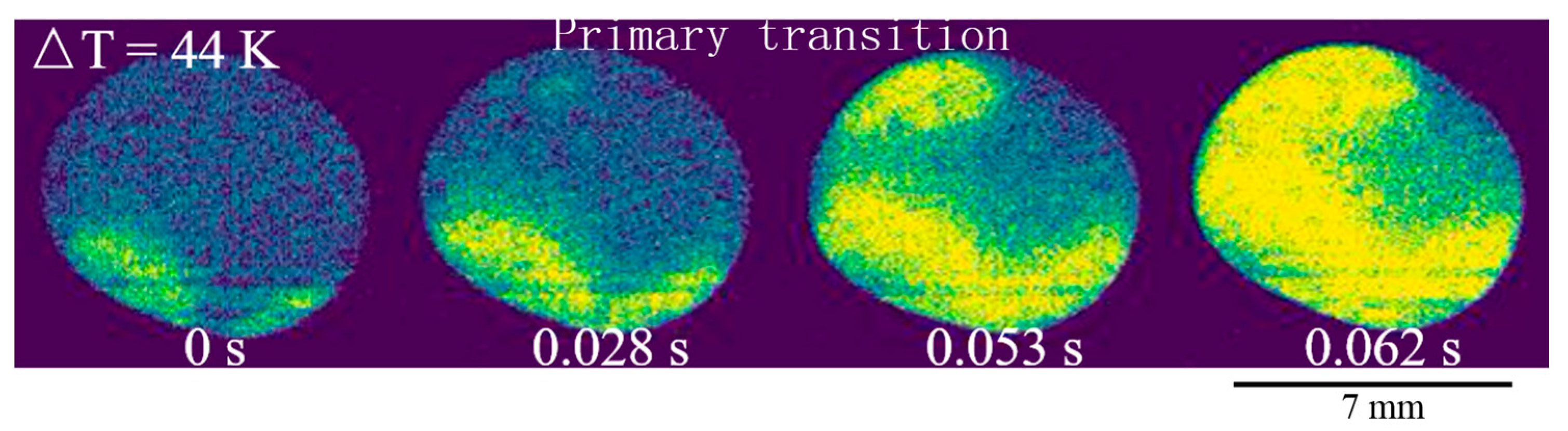
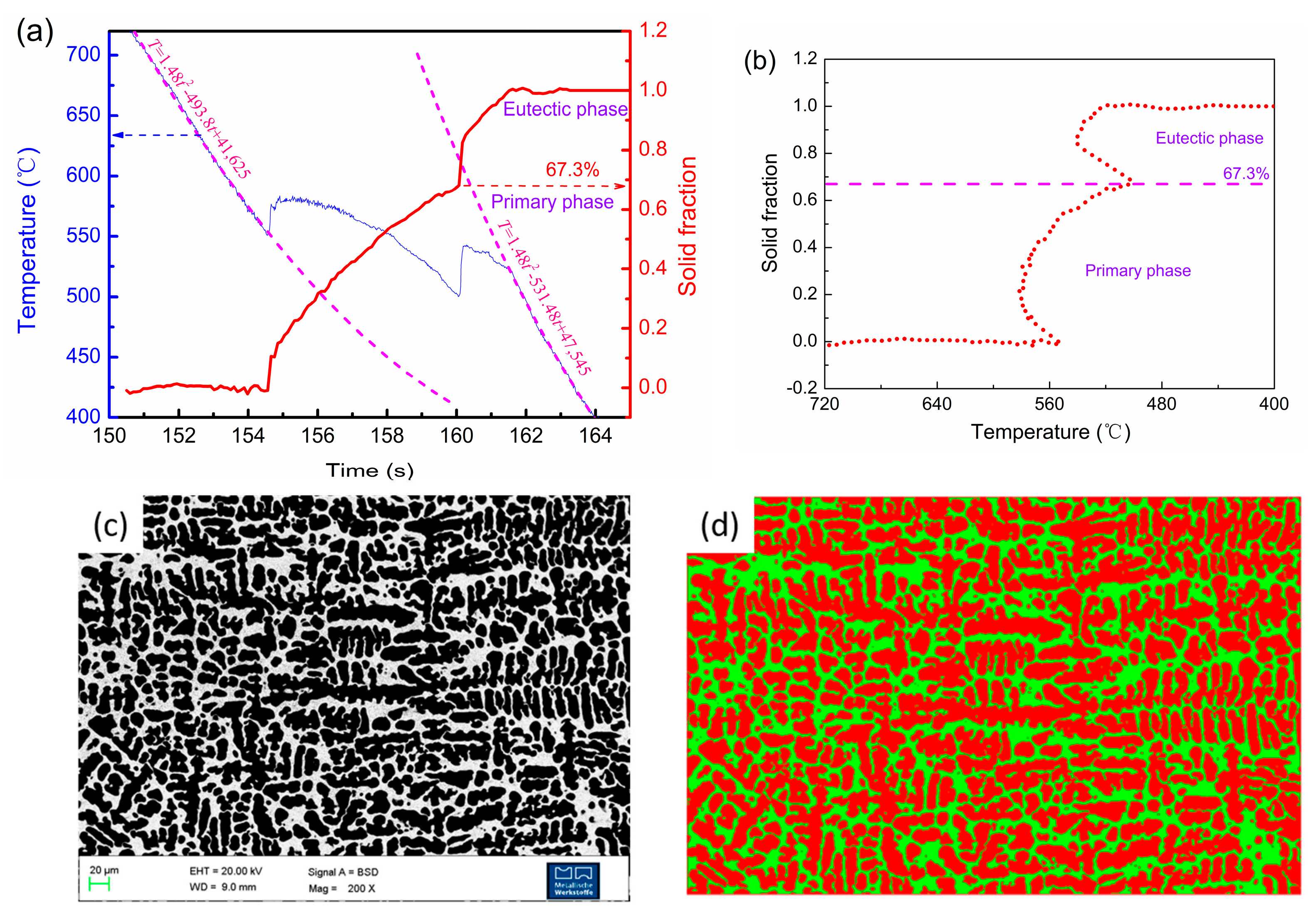
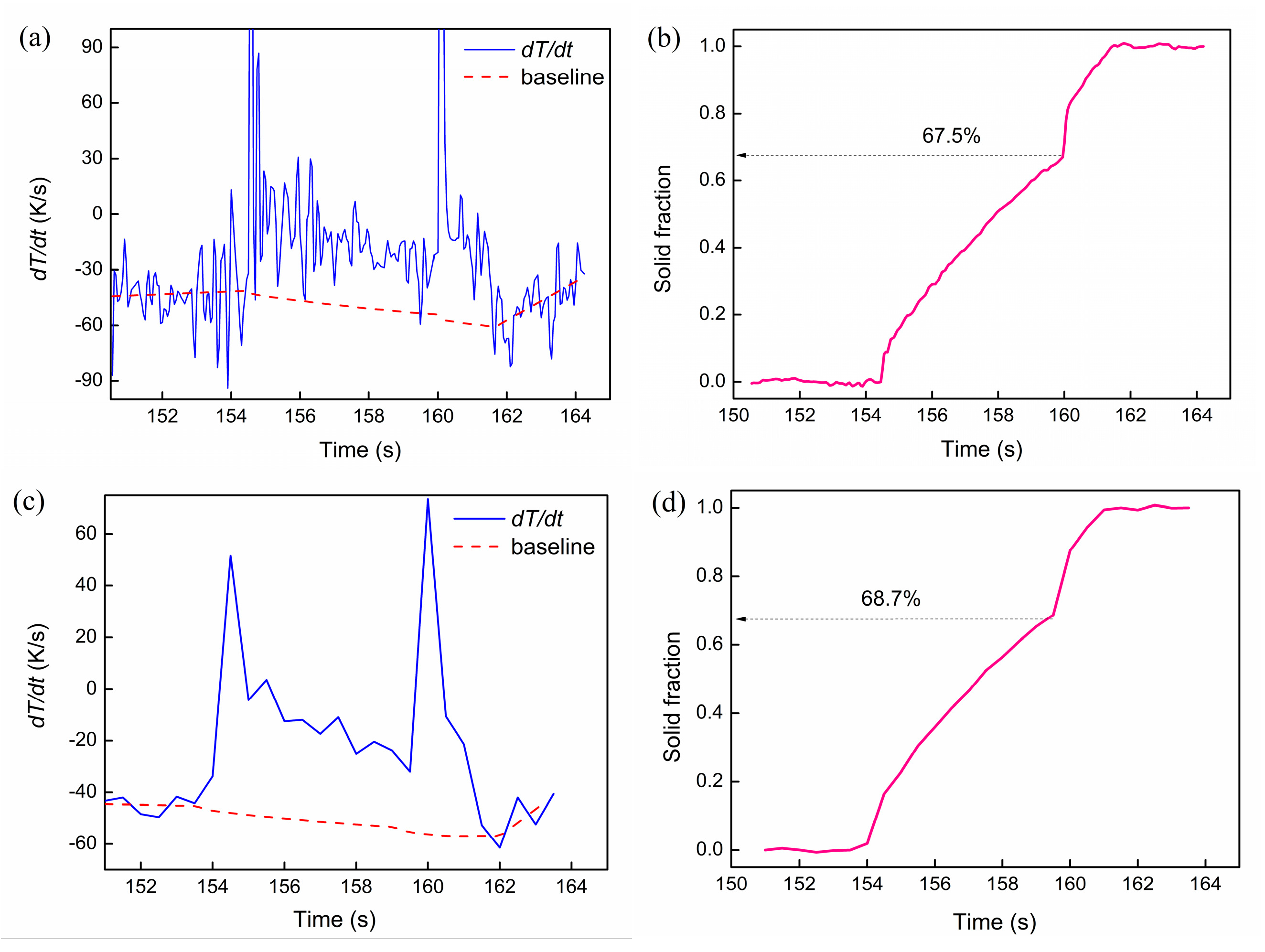
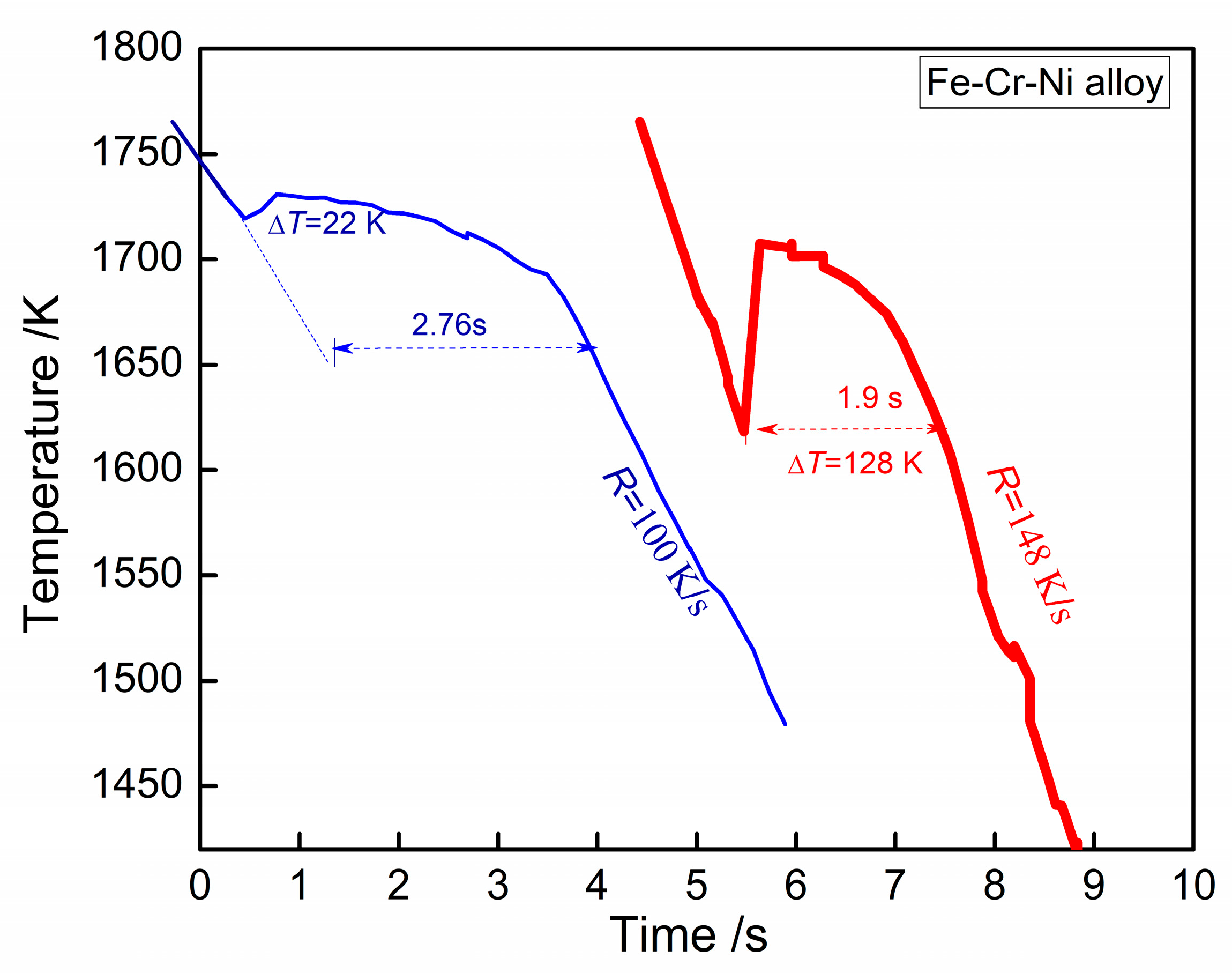
4. Results
5. Discussions
5.1. Effect of the Fitting Coefficient
5.2. Solidification Fraction
5.3. Solidification Rate
5.4. Solidification Plateau Time
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, P.; Hu, Z.; Zhao, Y.; Huang, Q. Investigation on the solidification course of Al–Si alloys by using a numerical Newtonian thermal analysis method. Mater. Res. Express 2017, 4, 126511. [Google Scholar] [CrossRef]
- Kweon, E.S.; Roh, D.H.; Kang, D.Y.; Stefanescu, D.M. The Use of Thermal Analysis for Generation of Fraction Solid Evolution in Ai-Si Alloys. Int. J. Met. 2025, 19, 1–18. [Google Scholar] [CrossRef]
- Isidorio, D.K.M.; Filho, J.d.C.P.; Uddagiri, M.; NouraniNiaki, K.; Shchyglo, O.; Steinbach, I. Super duplex stainless steel fabricated by arc-based directed energy deposition: Microstructure evolution and phase field solidification simulation. Mater. Des. 2025, 254, 114027. [Google Scholar] [CrossRef]
- Kamiyama, T.; Hirano, K.; Sato, H.; Ono, K.; Suzuki, Y.; Ito, D.; Saito, Y. Application of Machine Learning Methods to Neutron Transmission Spectroscopic Imaging for Solid–Liquid Phase Fraction Analysis. Appl. Sci. 2021, 11, 5988. [Google Scholar] [CrossRef]
- Malamud, F.; Alvarez, M.V.; Santisteban, J.; Strobl, M. Wavelength-resolved neutron transmission analyses of textured materials. Mater. Charact. 2025, 223, 114969. [Google Scholar] [CrossRef]
- Sato, H.; Kusumi, A.; Shiota, Y.; Hayashida, H.; Su, Y.; Parker, J.D.; Watanabe, K.; Kamiyama, T.; Kiyanagi, Y. Visualising Martensite Phase Fraction in Bulk Ferrite Steel by Superimposed Bragg-edge Profile Analysis of Wavelength-resolved Neutron Transmission Imaging. ISIJ Int. 2022, 62, 2319–2330. [Google Scholar] [CrossRef]
- Guarda, D.; Martinez-Garcia, J.; Fenk, B.; Schiffmann, D.; Gwerder, D.; Stamatiou, A.; Worlitschek, J.; Mancin, S.; Schuetz, P. New liquid fraction measurement methodology for phase change material analysis based on X-ray computed tomography. Int. J. Therm. Sci. 2023, 194, 108585. [Google Scholar] [CrossRef]
- Kamath, R.R.; Nandwana, P.; Ren, Y.; Choo, H. Solidification texture, variant selection, and phase fraction in a spot-melt electron-beam powder bed fusion processed Ti-6Al-4V. Addit. Manuf. 2021, 46, 102136. [Google Scholar] [CrossRef]
- Cruz, H.; Gonzalez, C.; Juárez, A.; Herrera, M.; Juarez, J. Quantification of the microconstituents formed during solidification by the Newton thermal analysis method. J. Mater. Process. Technol. 2006, 178, 128–134. [Google Scholar] [CrossRef]
- Schumacher, P.; Pogatscher, S.; Starink, M.J.; Schick, C.; Mohles, V.; Milkereit, B. 2015 Quench-induced precipitates in Al–Si alloys: Calorimetric determination of solute content and characterisation of microstructure. Thermochim. Acta 2015, 602, 63–73. [Google Scholar] [CrossRef]
- Hernandez, F.R.; Sokolowski, J.H. Thermal analysis and microscopical characterization of Al–Si hypereutectic alloys. J. Alloys Compd. 2006, 419, 180–190. [Google Scholar] [CrossRef]
- Farahany, S.; Idris, M.H.; Ourdjini, A.; Faris, F.; Ghandvar, H. Evaluation of the effect of grain refiners on the solidification characteristics of an Sr-modified ADC12 die-casting alloy by cooling curve thermal analysis. J. Therm. Anal. Calorim. 2015, 119, 1593–1601. [Google Scholar] [CrossRef]
- Fras, E.; Kapturkiewicz, W.; Burbielko, A.; Lopez, H.F. A new concept in thermal analysis of castings. Trans. Am. Foundrymen’s Soc. 1993, 101, 505–511. [Google Scholar]
- Emadi, D.; Whiting, L.V.; Djurdjevic, M.; Kierkus, W.T.; Sokolowski, J. Comparison of newtonian and fourier thermal analysis techniques for calculation of latent heat and solid fraction of aluminum alloys. Metall. Mater. Eng. 2018. [Google Scholar] [CrossRef]
- Xu, J.; Liu, F.; Xu, X.; Chen, Y. Determination of solid fraction from cooling curve. Metall. Mater. Trans. A 2012, 43, 1268–1276. [Google Scholar] [CrossRef]
- Dediaeva, E.; Padalko, A.; Akopyan, T.; Suchkov, A.; Fedotov, V. Barothermography and microstructure of the hypoeutectic and eutectic alloys in Al–Si system. J. Therm. Anal. Calorim. 2015, 121, 485–490. [Google Scholar] [CrossRef]
- Gibbs, J.W.; Kaufman, M.J.; Hackenberg, R.E.; Mendez, P.F. Cooling curve analysis to determine phase fractions in solid-state precipitation reactions. Metall. Mater. Trans. A 2010, 41A, 2216–2223. [Google Scholar] [CrossRef]
- Djurdjevic, M.B.; Odanovic, Z.; Talijan, N. Characterization of the solidification path of AlSi5Cu (1–4 wt.%) alloys using cooling curve analysis. JOM 2011, 63, 51–57. [Google Scholar] [CrossRef]
- Stefanescu, D.M.; Upadhya, G.; Bandyopadhyay, D. Heat transfer-solidification kinetics modeling of solidification of castings. Metall. Trans. A 1990, 21A, 997–1000. [Google Scholar] [CrossRef]
- Roberts-Austen, W.C. Surfusion in Metals and Alloys. Nature 1898, 58, 619–621. [Google Scholar] [CrossRef][Green Version]
- Patel, S.; Reddy, P.; Kumar, A. A methodology to integrate melt pool convection with rapid solidification and undercooling kinetics in laser spot welding. Int. J. Heat Mass Transf. 2021, 164, 120575. [Google Scholar] [CrossRef]
- He, H.; Yao, Z.; Li, X.; Xu, J. Rapid Solidification of Invar Alloy. Materials 2023, 17, 231. [Google Scholar] [CrossRef] [PubMed]
- Galenko, P.K.; Toropova, L.V.; Alexandrov, D.V.; Phanikumar, G.; Assadi, H.; Reinartz, M.; Paul, P.; Fang, Y.; Lippmann, S. Anomalous kinetics, patterns formation in recalescence, and final microstructure of rapidly solidified Al-rich Al-Ni alloys. Acta Mater. 2022, 241, 118384. [Google Scholar] [CrossRef]
- An, H.; Chua, B.-L.; Saad, I.; Liew, W.Y.H. Effect of Co on Solidification Characteristics and Microstructural Transformation of Nonequilibrium Solidified Cu-Ni Alloys. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2024, 39, 444–453. [Google Scholar] [CrossRef]
- Yang, W.; Liu, F.; Wang, H.; Chen, Z.; Yang, G.; Zhou, Y. Prediction of the maximal recalescence temperature upon rapid solidification of bulk undercooled Cu70Ni30 alloy. J. Alloys Compd. 2009, 470, L13–L16. [Google Scholar] [CrossRef]
- Mullis, A.M.; Clopet, C.R. On the Origin of Anomalous Eutectic Growth from Undercooled Melts: Why Re-melting is not a Plausible Explanation. Acta Mater. 2018, 145, 186–195. [Google Scholar] [CrossRef]
- Gandin, C.A.; Mosbah, S.; Volkmann, T.; Herlach, D.M. Experimental and numerical modeling of equiaxed solidification in metallic alloys. Acta Mater. 2008, 56, 3023–3035. [Google Scholar] [CrossRef]
- Xu, J.; Jian, Z.; Lian, X. An application of box counting method for measuring phase fraction. Measurement 2017, 100, 297–300. [Google Scholar] [CrossRef]
- Niu, T.; Xu, J.; Yao, Z.; Jian, Z.; Galenko, P.K. Density Testing Method for Undercooling Solidification of High-Temperature Metal Melts. Crystals 2023, 13, 1502. [Google Scholar] [CrossRef]
- Tang, P.; Hu, Z.; Zhao, Y.; Huang, Q. Calculation of phase transformation latent heat based on cooling curves in end-quench test and its application in nickel-based superalloy. Trans. Nonferrous Met. Soc. China 2022, 32, 1718–1727. [Google Scholar]
- Xu, J.; Xiao, Y.; Jian, Z. Observe the temperature curve for solidification from high-speed video image. J. Therm. Anal. Calorim. 2021, 146, 2273–2277. [Google Scholar] [CrossRef]
- Farahany, S.; Ourdjini, A.; Idris, M.H.; Shabestari, S.G. Computer-aided cooling curve thermal analysis of near eutectic Al–Si–Cu–Fe alloy. J. Therm. Anal. Calorim. 2013, 114, 705–717. [Google Scholar] [CrossRef]
- Toshihiko, K. Undercooling and Rapid Solidification of Fe-Cr-Ni Ternary Alloys. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1994. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Fang, Y.; Yang, T.; Yang, C. A Novel Method to Predict Phase Fraction Based on the Solidification Time on the Cooling Curve. Metals 2025, 15, 652. https://doi.org/10.3390/met15060652
Xu J, Fang Y, Yang T, Yang C. A Novel Method to Predict Phase Fraction Based on the Solidification Time on the Cooling Curve. Metals. 2025; 15(6):652. https://doi.org/10.3390/met15060652
Chicago/Turabian StyleXu, Junfeng, Yindong Fang, Tian Yang, and Changlin Yang. 2025. "A Novel Method to Predict Phase Fraction Based on the Solidification Time on the Cooling Curve" Metals 15, no. 6: 652. https://doi.org/10.3390/met15060652
APA StyleXu, J., Fang, Y., Yang, T., & Yang, C. (2025). A Novel Method to Predict Phase Fraction Based on the Solidification Time on the Cooling Curve. Metals, 15(6), 652. https://doi.org/10.3390/met15060652







