Advanced Cut-Edge Characterization Methods for Improved Sheared-Edge Damage Evaluation in High-Strength Sheet Steels
Abstract
1. Introduction
2. Materials and Methods
2.1. Sheet Punching
2.2. Cut-Edge Investigation and Shear-Affected Zone
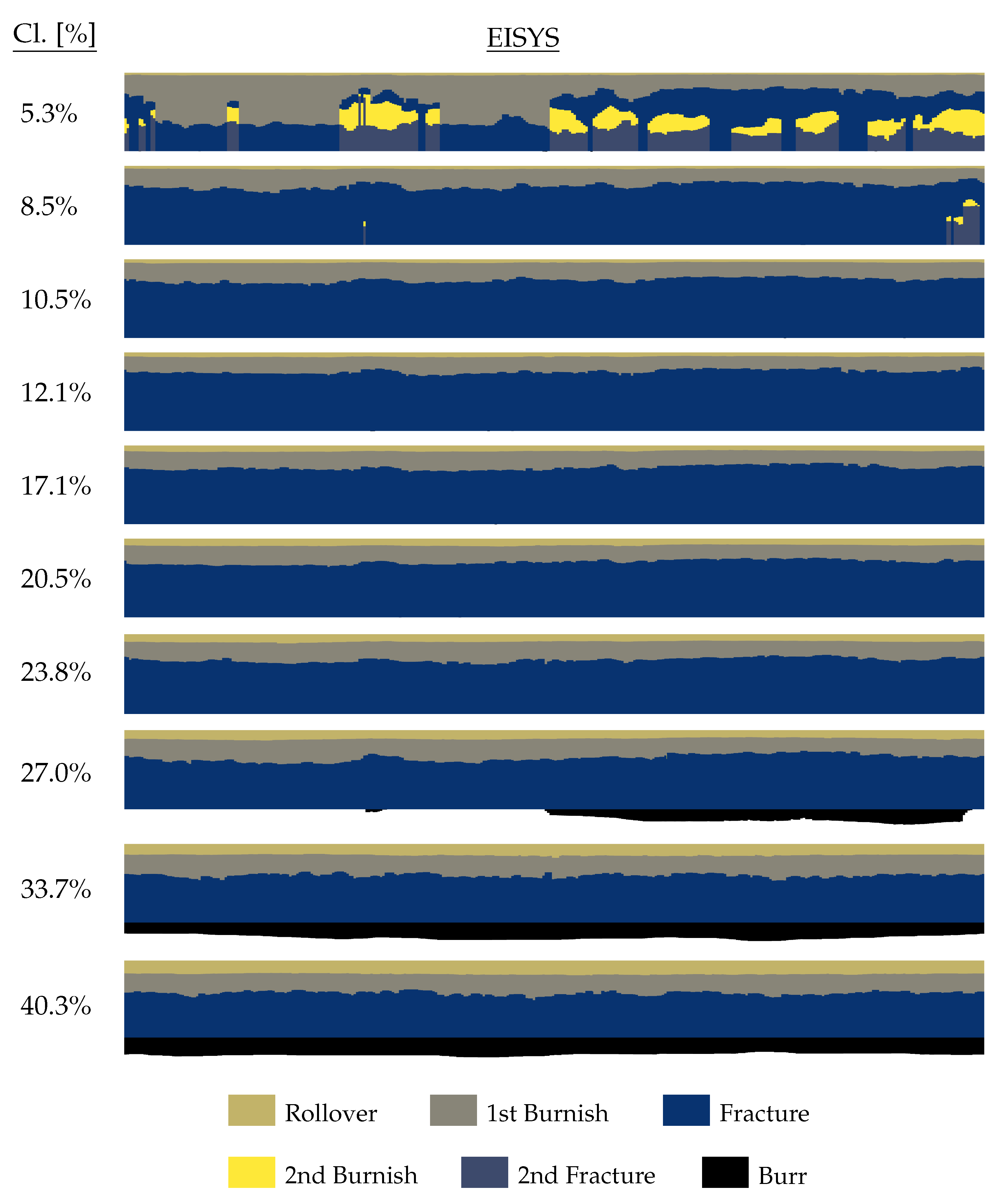
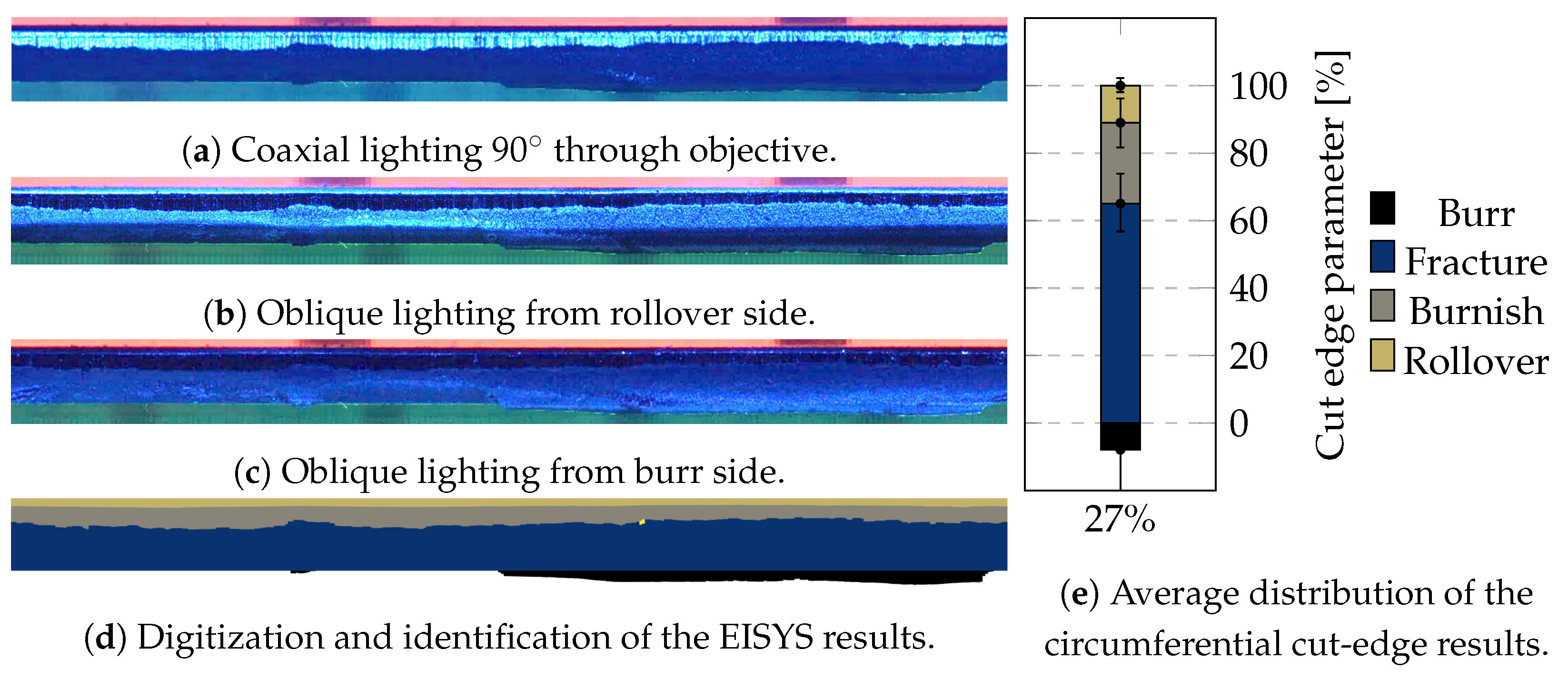
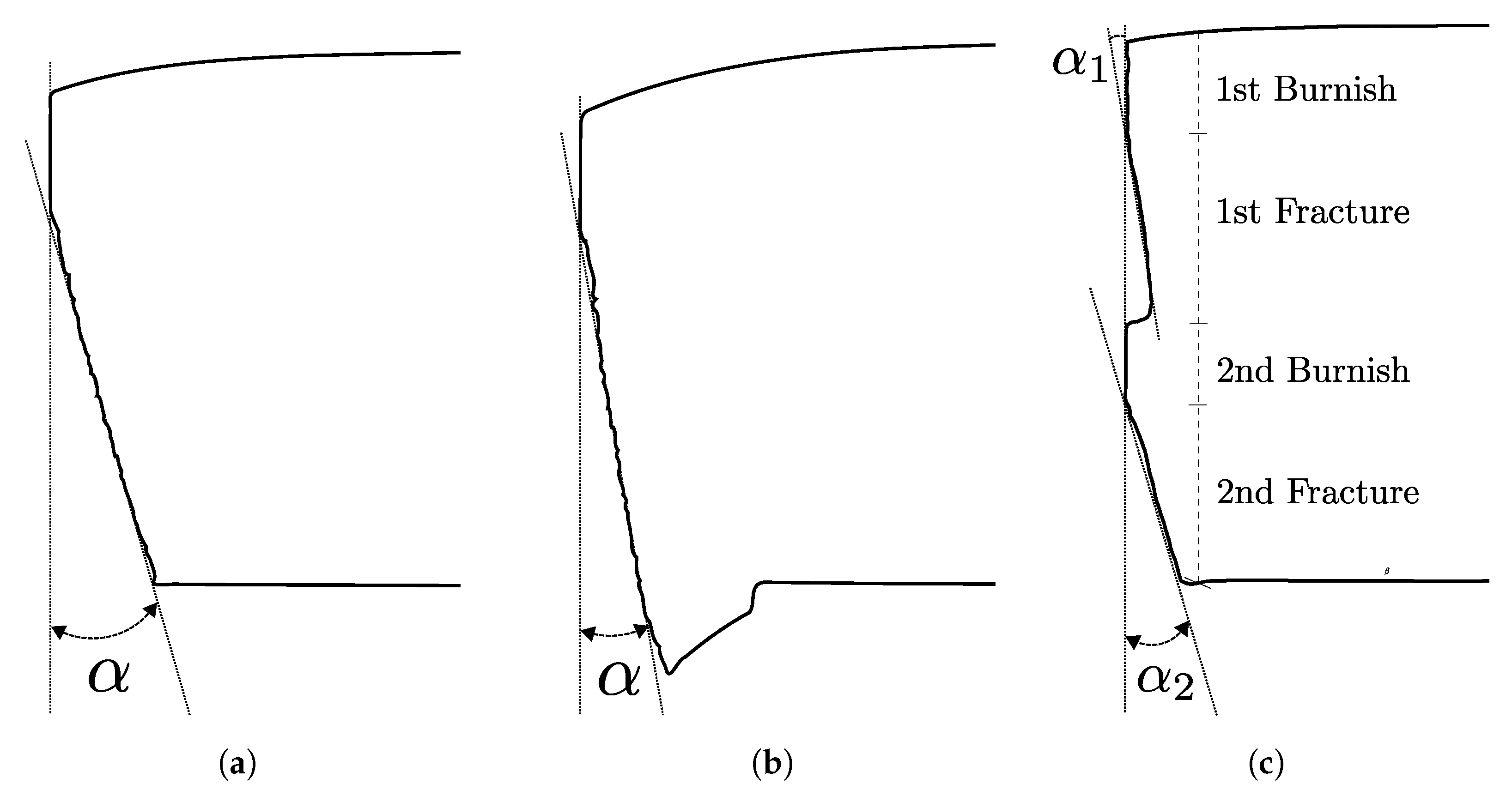
2.2.1. Two-Dimensional Optical EISYS Methodology
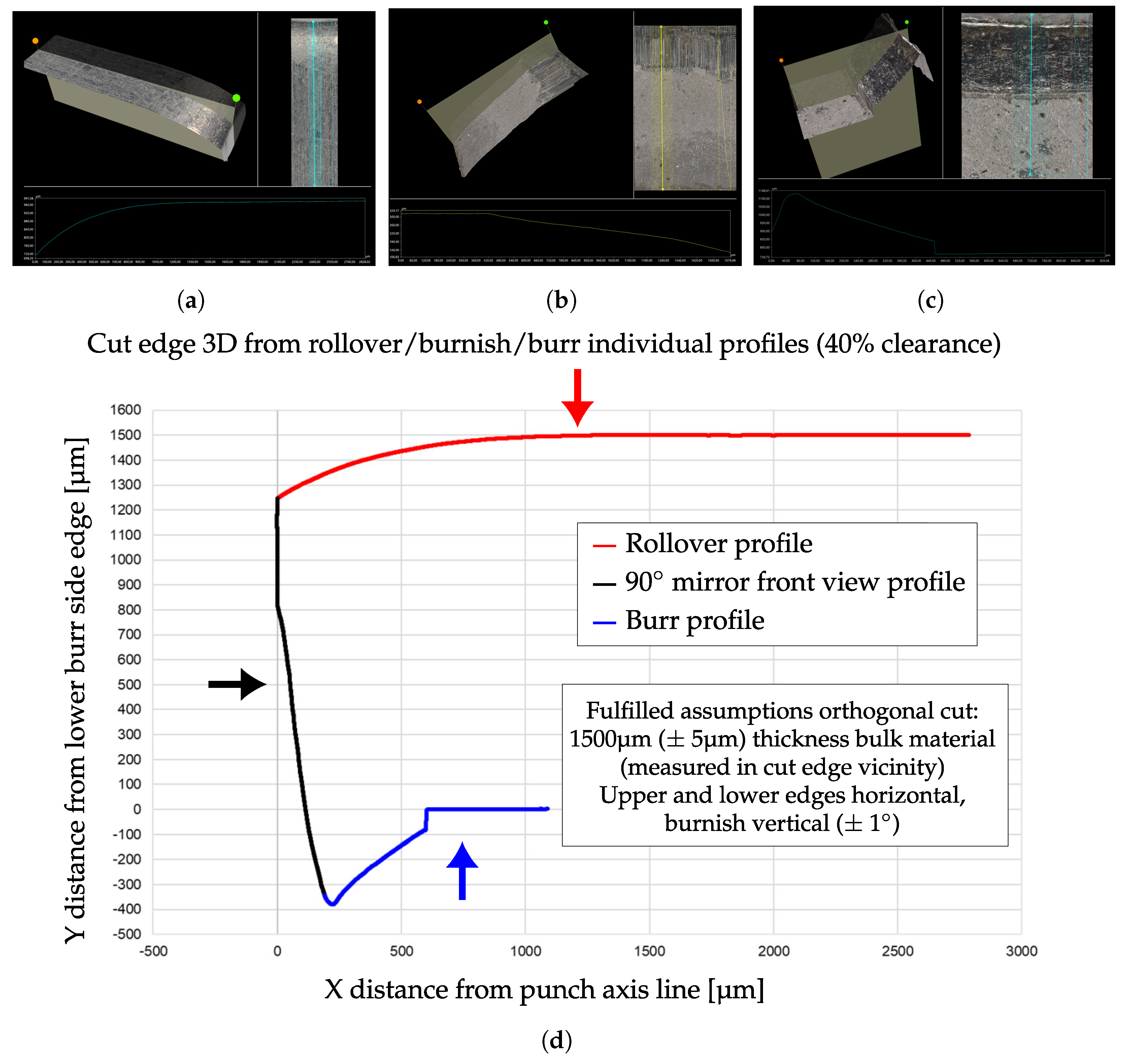
2.2.2. Three-Dimensional Stereo Optical Cut Edge Methodology
2.2.3. Metallographic Cut-Edge Investigation—Vickers Hardness Measurement
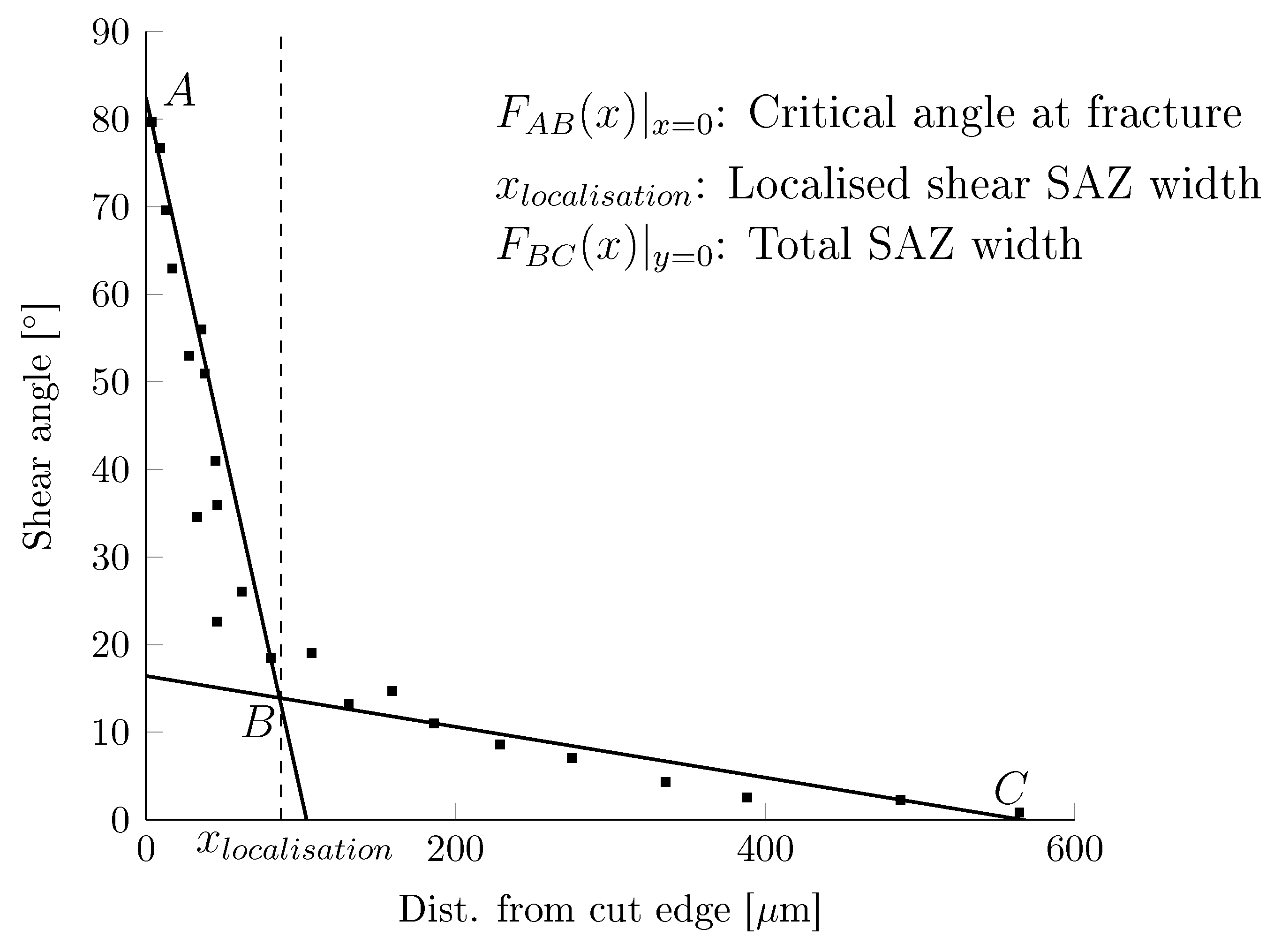
2.2.4. Metallographic Cut-Edge Investigation—Grain Shear Angle Analysis
3. Results
4. Discussion
5. Conclusions
- A thorough understanding of cut-edge parameters (such as nominal vs. effective clearance, hole perimeter coaxiality, and punch tool wear) is essential for accurately interpreting laboratory material test results, particularly for assessments of edge crack sensitivity, hydrogen embrittlement, and fatigue involving cut-edge conditions. Laboratory testing under these conditions is meaningful only when preceded by comprehensive 2D and 3D punch edge characterization as an integral part of the testing protocol. This approach is necessary to distinguish intrinsic material properties from cutting process effects, preventing misinterpretations of material behavior. Also, in industrial forming lines, where circumferential variation in the cut hole edge may occur, cut-edge investigation considering the cut-edge’s perimeter is required. This can be achieved with the 2D panoramic optical EISYS or by the non-destructive 3D optical cut-edge profile determination testing methods developed within this work.
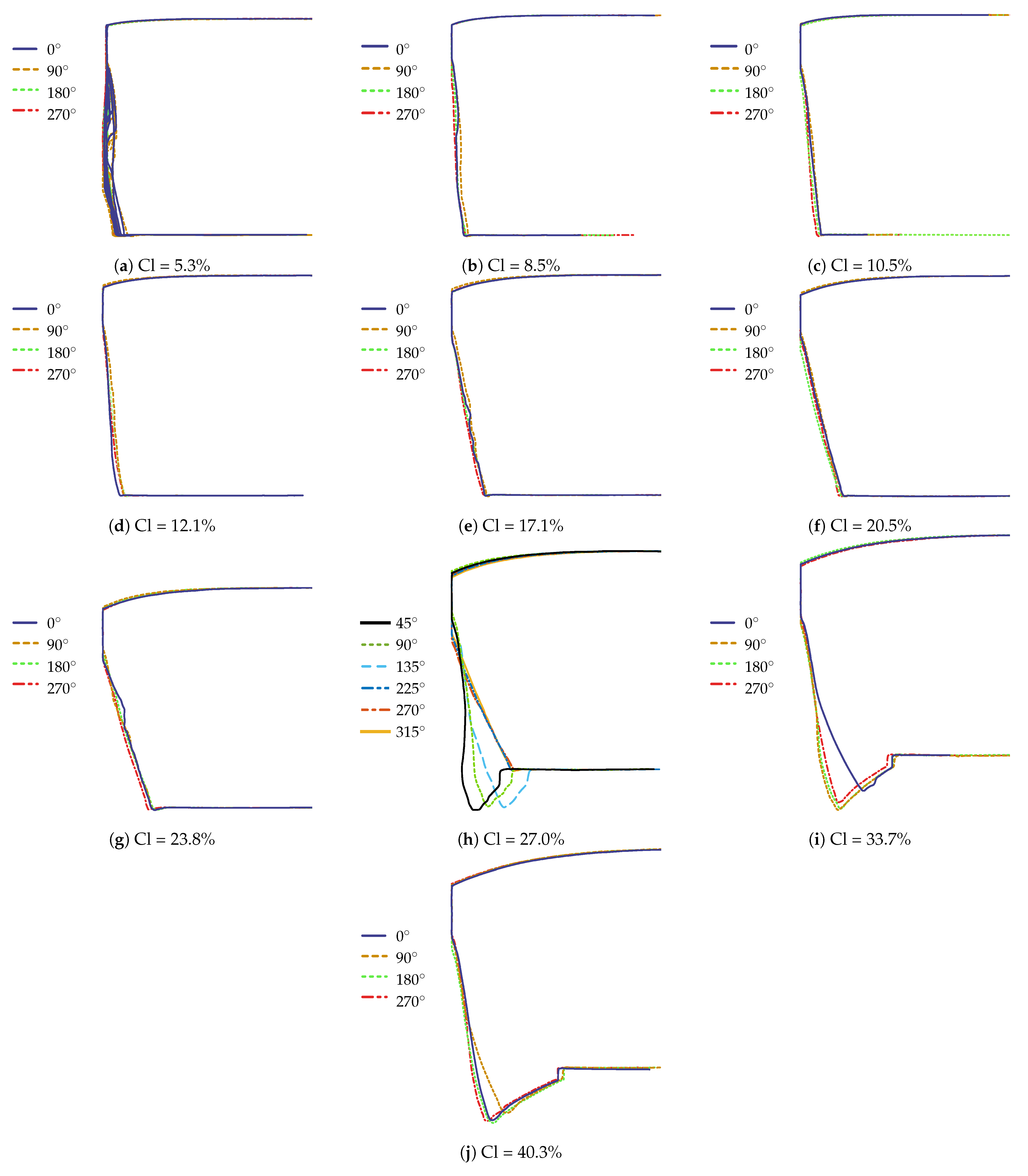
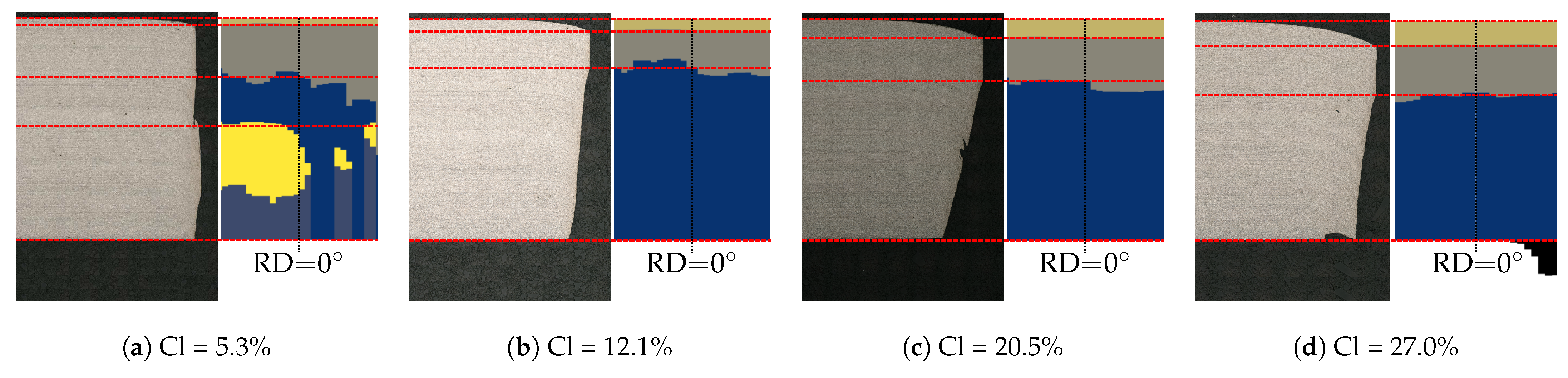
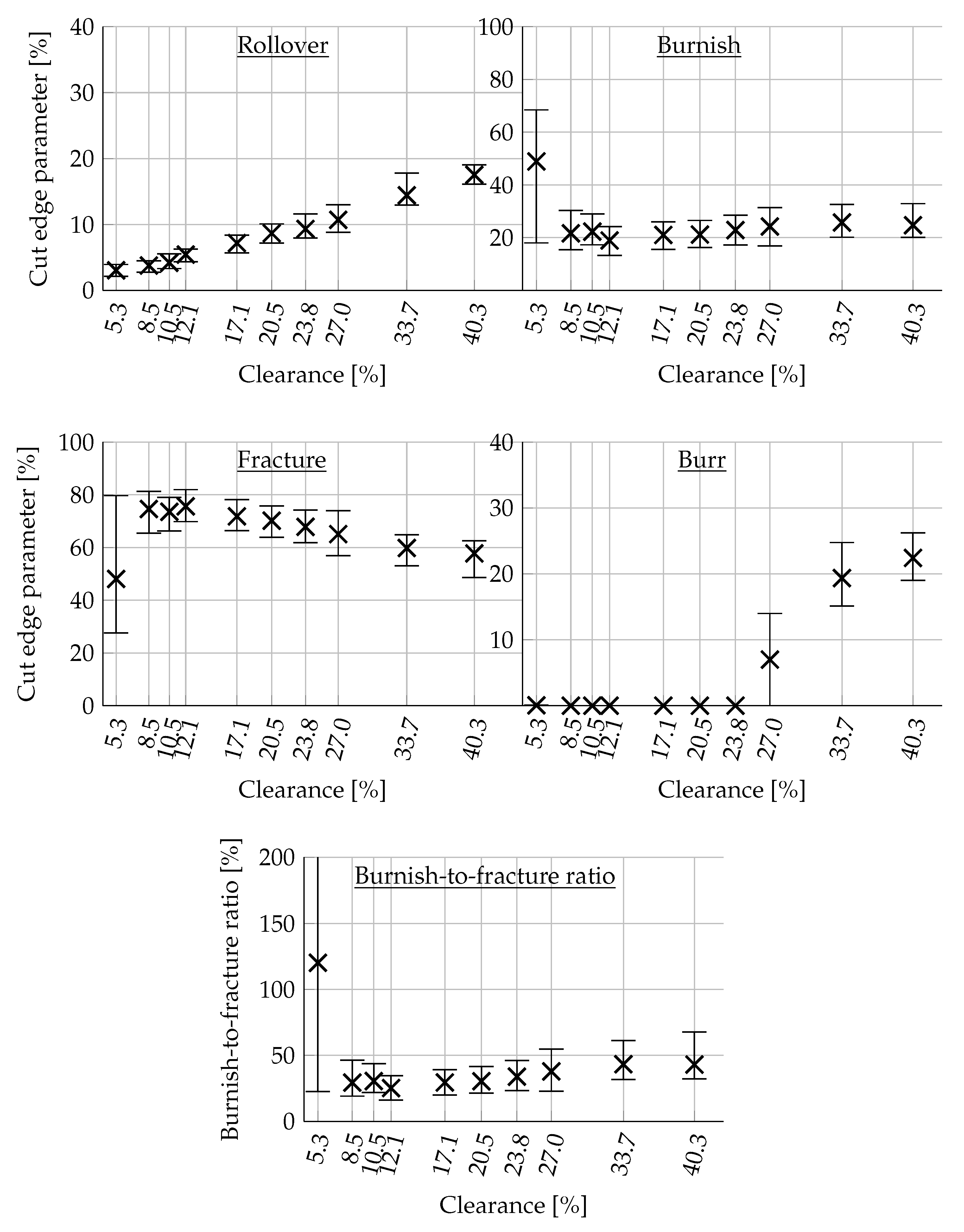
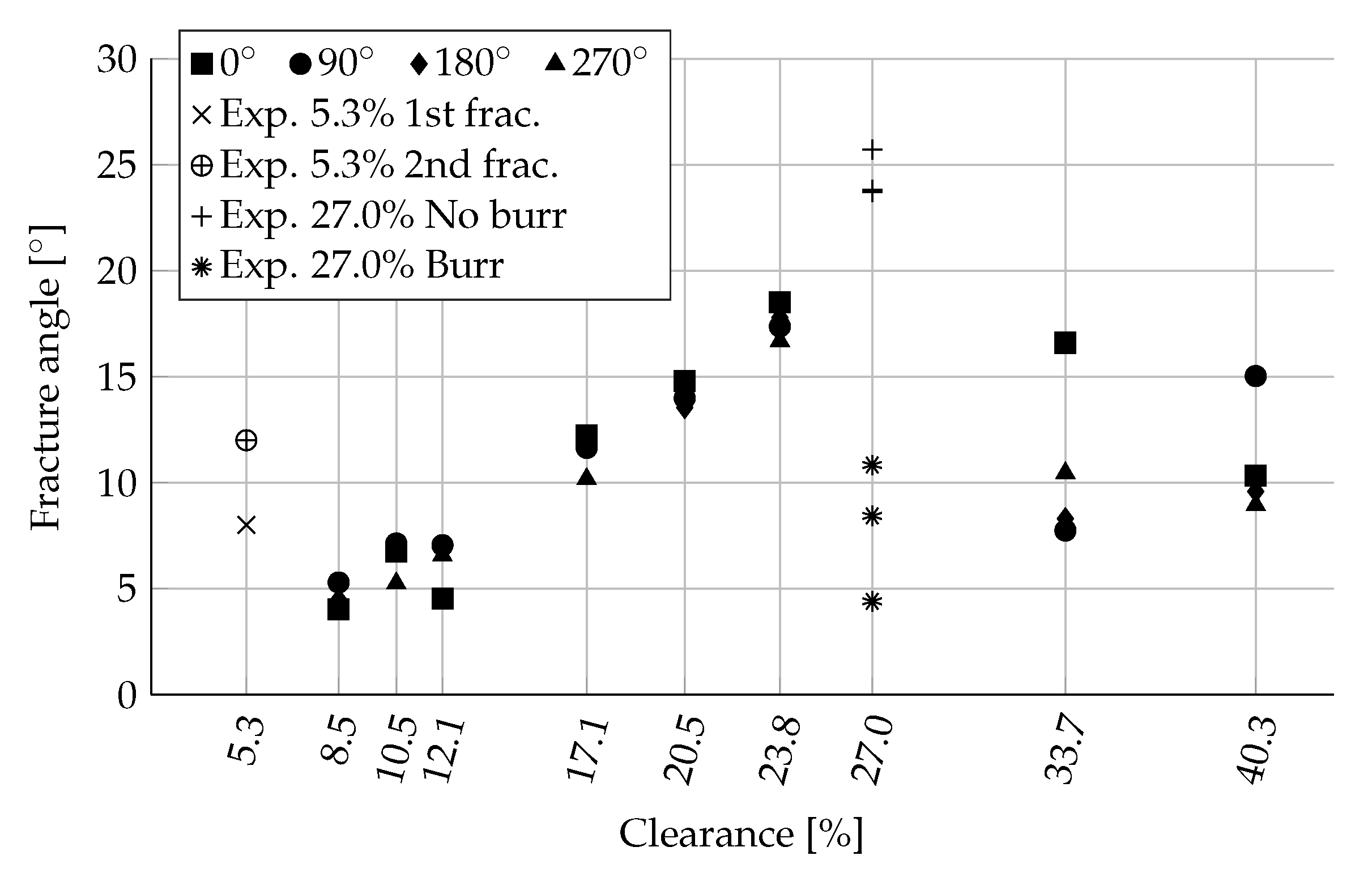
- Investigating the effect of varying the cutting clearance on cut-edge morphology showed that both optical cut-edge investigation methods were useful for detecting the characteristic cut-edge parameters. The results show the appearance of secondary burnish formation at ≈5% and burr formation at ≥ 27% cutting clearance (for sharp tools). In between, smooth fracture zones were detected, with a minimum burnish-to-fracture ratio of 12–15% cutting clearance.
- The 3D optical cut-edge profiling technique is still quite time-consuming. The feasibility has been proven in this investigation for a significantly high number of profiles. A mechanical device for tilting and rotating of the sample could allow for an automatization of an optical high resolution 3D cut-edge profile determination technique in the future. However, the Keyence stereo 3D microscope mirror technique employs simple equipment set-up and minimal post-processing requirements, making it comparably affordable and computationally efficient.
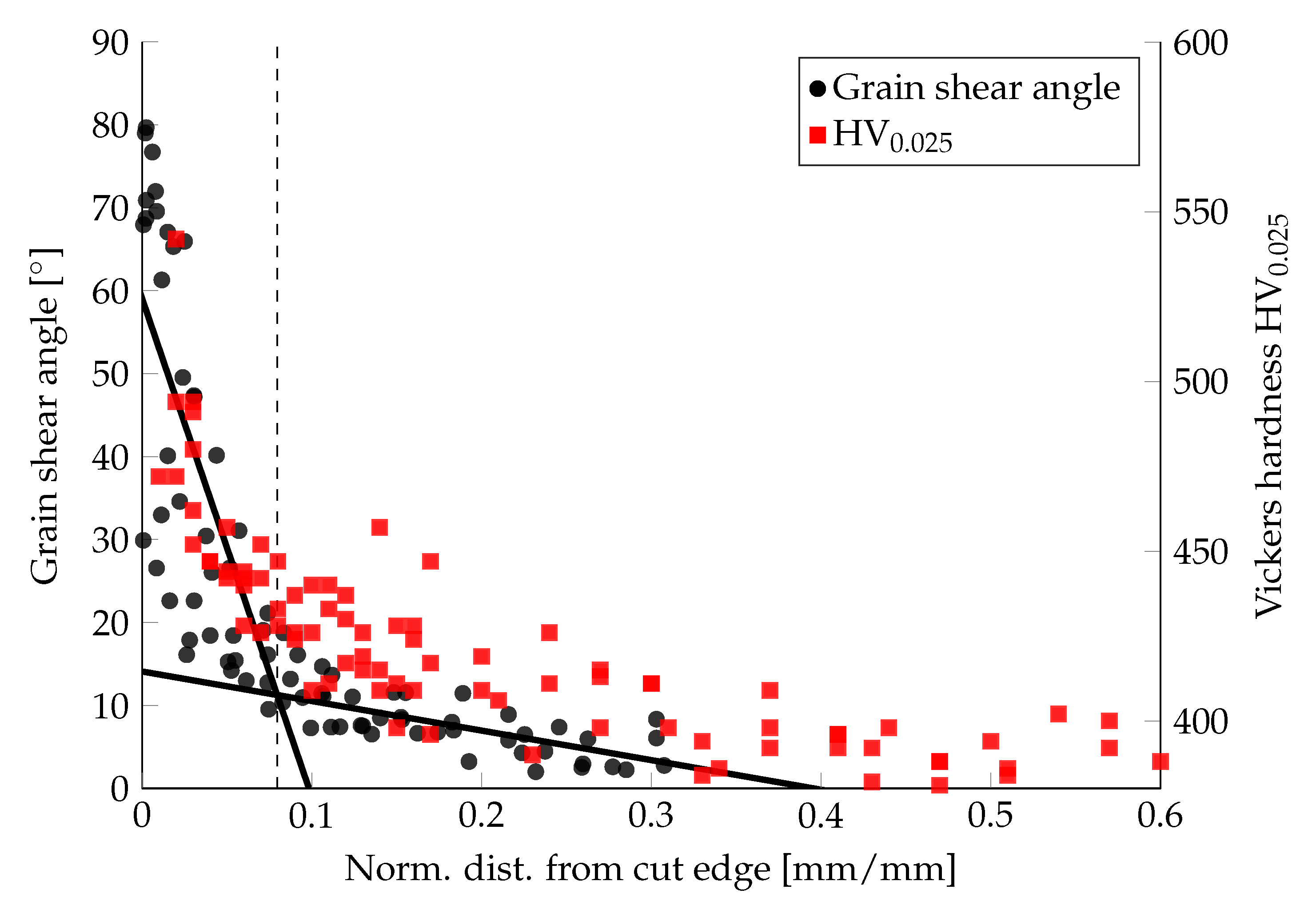
- Due to the narrow shear localization tendency of the CP1000HD grade evaluated in this work, it is concluded that grain shear angle measurement is the preferred method over hardness indentation for AHSS grades since grain shear angle measurements are able to give high-resolution results in the immediate 5 to 10 µm cut-edge vicinity. This is of particularly acute relevance for 1200 MPa strength AHSS with an even sharper strain localization tendency.
- The SAZ grain orientation technique was manually implemented in a time-consuming and tedious manner. It should be further developed according to state-of-the-art image analysis tools. Two-dimensional high-resolution mapping of cut-edge SAZ shear angle would be a valuable addition to Vickers hardness mapping. The shear angle from microstructural measurements allows for a direct physical comparison of experimentally derived shear and Von Mises effective strain results with finite element simulations, as well as material flow motion investigations in shear cutting operations.
- The presented optical techniques provide the data foundation needed for AI and ML to reliably monitor shear processes in-line, enabling real-time edge damage assessment and supporting process optimization in Industry 4.0 environments.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| AE | Acoustic Emission |
| AHSS | Advanced High-Strength Steel |
| AI | Artificial Intelligence |
| Cl | Clearance |
| CP | Complex Phase |
| DIC | Digital Image Correlation |
| DP | Dual Phase |
| EBSD | Electron Backscatter Diffraction |
| EISYS | Edge Inspection System |
| HET | Hole Expansion Test |
| HV | Vickers Hardness |
| LOM | Light Optical Microscopy |
| LVDT | Linear Variable Differential Transformer |
| ML | Machine Learning |
| Norm. dist. | Normalized Distance |
| SAZ | Shear-Affected Zone |
| SEM | Scanning Electron Microscopy |
| UTS | Ultimate Tensile Strength |
Appendix A
References
- Wu, X.; Bahmanpour, H.; Schmid, K. Characterization of mechanically sheared edges of dual phase steels. J. Mater. Process. Technol. 2012, 212, 1209–1224. [Google Scholar] [CrossRef]
- Shi, M.F.; Chen, X. Prediction of Stretch Flangeability Limits of Advanced High Strength Steels Using the Hole Expansion Test; SAE Technical Paper 2007-01-1693; SAE International: Warrendale, PA, USA, 2007. [Google Scholar] [CrossRef]
- Konieczny, A.; Henderson, T. On Formability Limitations in Stamping Involving Sheared Edge Stretching; SAE Technical Paper 2007-01-0340; SAE International: Warrendale, PA, USA, 2007. [Google Scholar] [CrossRef]
- Dykeman, J.; Malcolm, S.; Yan, B.; Chintamani, J.; Huang, G.; Ramisetti, N.; Zhu, H. Characterization of Edge Fracture in Various Types of Advanced High Strength Steel; SAE Technical Paper 2011-01-1058; SAE International: Warrendale, PA, USA, 2011. [Google Scholar] [CrossRef]
- Frómeta, D.; Tedesco, M.; Calvo, J.; Lara, A.; Molas, S.; Casellas, D. Assessing edge cracking resistance in AHSS automotive parts by the Essential Work of Fracture methodology. J. Phys. Conf. Ser. 2017, 896, 012102. [Google Scholar] [CrossRef]
- Shih, H.C.; Chiriac, C.; Shi, M.F. The effects of AHSS shear edge conditions on edge fracture. In Proceedings of the ASME 2010 International Manufacturing Science and Engineering Conference, MSEC 2010, Erie, PA, USA, 12–15 October 2010; Volume 1, pp. 599–608. [Google Scholar] [CrossRef]
- Lara, A.; Picas, I.; Casellas, D. Effect of the cutting process on the fatigue behaviour of press hardened and high strength dual phase steels. J. Mater. Process. Technol. 2013, 213, 1908–1919. [Google Scholar] [CrossRef]
- Stahl, J.; Pätzold, I.; Golle, R.; Sunderkötter, C.; Sieurin, H.; Volk, W. Effect of one- And two-stage shear cutting on the fatigue strength of truck frame parts. J. Manuf. Mater. Process. 2020, 4, 52. [Google Scholar] [CrossRef]
- Thomas, D.J.; Whittaker, M.T.; Bright, G.W.; Gao, Y. The influence of mechanical and CO2 laser cut-edge characteristics on the fatigue life performance of high strength automotive steels. J. Mater. Process. Technol. 2011, 211, 263–274. [Google Scholar] [CrossRef]
- Shiozaki, T.; Tamai, Y.; Urabe, T. Effect of residual stresses on fatigue strength of high strength steel sheets with punched holes. Int. J. Fatigue 2015, 80, 324–331. [Google Scholar] [CrossRef]
- Gustafsson, D.; Parareda, S.; Munier, R.; Olsson, E. High cycle fatigue life estimation of punched and trimmed specimens considering residual stresses and surface roughness. Int. J. Fatigue 2024, 186, 108384. [Google Scholar] [CrossRef]
- Drexler, A.; Bergmann, C.; Manke, G.; Kokotin, V.; Mraczek, K.; Leitner, S.; Pohl, M.; Ecker, W. Local hydrogen accumulation after cold forming and heat treatment in punched advanced high strength steel sheets. J. Alloys Compd. 2021, 856, 158226. [Google Scholar] [CrossRef]
- Sheng, Z.; Guo, X.; Prahl, U.; Bleck, W. Shear and laser cutting effects on hydrogen embrittlement of a high-Mn TWIP steel. Eng. Fail. Anal. 2020, 108, 104243. [Google Scholar] [CrossRef]
- Levy, B.; Van Tyne, C.J. Review of the Shearing Process for Sheet Steels and Its Effect on Sheared-Edge Stretching. J. Mater. Eng. Perform. 2012, 21, 1205–1213. [Google Scholar] [CrossRef]
- Cui, Z.; Bhattacharya, S.; Green, D.; Alpas, A. Mechanisms of die wear and wear-induced damage at the trimmed edge of high strength steel sheets. Wear 2019, 426–427, 1635–1645. [Google Scholar] [CrossRef]
- Magliaro, J.; Cui, Z.; Shirzadian, S.; Green, D.E.; Altenhof, W.; Alpas, A.T. Evaluating die wear-induced edge quality degradation in trimmed DP980 steel sheets from in situ force response monitoring. Wear 2023, 524–525, 204792. [Google Scholar] [CrossRef]
- Diaz-Infante, D.; Narayanan, A.; Groseclose, A.; Altan, T. FE Simulations of Piercing and Trimming of AL and AHSS Alloys. In Forming the Future; Daehn, G., Cao, J., Kinsey, B., Tekkaya, E., Vivek, A., Yoshida, Y., Eds.; The Minerals, Metals & Materials Series; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Nasheralahkami, S.; Golovashchenko, S.; Malek, C.; Rugh, E.; Kowalsky, D.; Zhou, W. Sheared Edge Stretchability of Steels Suitable for Automotive Applications; Technical Paper 2017-01-1708; SAE International: Warrendale, PA, USA, 2017. [Google Scholar] [CrossRef]
- Nothhaft, K.; Suh, J.; Golle, M.; Picas, I.; Casellas, D.; Volk, W. Shear cutting of press hardened steel: Influence of punch chamfer on process forces, tool stresses and sheared edge qualities. Prod. Eng. 2012, 6, 413–420. [Google Scholar] [CrossRef]
- So, H.; Fasmann, D.; Hoffmann, H.; Golle, R.; Schaper, M. An investigation of the blanking process of the quenchable boron alloyed Steel 22MnB5 before and after hot stamping process. J. Mater. Process. Technol. 2012, 212, 437–449. [Google Scholar] [CrossRef]
- Chumrum, P.; Koga, N.; Premanond, V. Experimental investigation of energy and punch wear in piercing of advanced high-strength steel sheet. Int. J. Adv. Manuf. Technol. 2015, 79, 1035–1042. [Google Scholar] [CrossRef]
- Mishra, D.; Awasthi, U.; Pattipati, K.R.; Bollas, G.M. Tool wear classification in precision machining using distance metrics and unsupervised machine learning. J. Intell. Manuf. 2025, 36, 331–355. [Google Scholar] [CrossRef]
- Shanbhag, V.V.; Rolfe, B.F.; Arunachalam, N.; Pereira, M.P. Investigating galling wear behaviour in sheet metal stamping using acoustic emissions. Wear 2018, 414–415, 31–42. [Google Scholar] [CrossRef]
- Yoon, J.; Han, H.; Kang, B.; Kim, Y. Investigation of stamping tool wear initiation at microscopic level using acoustic emission sensors. Key Eng. Mater. 2019, 794, 285–294. [Google Scholar] [CrossRef]
- Martinez-Gonzalez, E.; Picas, I.; Casellas, D.; Romeu, J. Detection of crack nucleation and growth in tool steels using fracture tests and acoustic emission. Meccanica 2015, 50, 1155–1166. [Google Scholar] [CrossRef]
- Sandin, O.; Larour, P.; Hammarberg, S.; Kajberg, J.; Casellas, D. The influence of cut edge heterogeneity in complex phase steel sheet edge cracking: An experimental and numerical investigation. Eng. Fract. Mech. 2025, 322, 111176. [Google Scholar] [CrossRef]
- Yoon, J.I.; Jung, J.; Joo, S.; Song, T.J.; Chin, K.G.; Seo, M.; Kim, S.J.; Lee, S.; Kim, H.S. Correlation between fracture toughness and stretch-flangeability of advanced high strength steels. Mater. Lett. 2016, 180, 322–326. [Google Scholar] [CrossRef]
- Habibi, N.; Mathi, S.; Beier, T.; Könemann, M.; Münstermann, S. Effects of Microstructural Properties on Damage Evolution and Edge Crack Sensitivity of DP1000 Steels. Crystals 2022, 12, 845. [Google Scholar] [CrossRef]
- Khalilabad, M.M.; Perdahcıoğlu, S.; Atzema, E.; Boogaard, T.v.d. Initiation and growth of edge cracks after shear cutting of dual-phase steel. Int. J. Adv. Manuf. Technol. 2023, 127, 2327–2341. [Google Scholar] [CrossRef]
- ISO6507-1:2023; Metallic Materials—Vickers Hardness Test—Part 1: Test Method. International Organization for Standardization: Geneva, Switzerland, 2013.
- Dalloz, A.; Besson, J.; Gourgues-Lorenzon, A.F.; Sturel, T.; Pineau, A. Effect of shear cutting on ductility of a dual phase steel. Eng. Fract. Mech. 2009, 76, 1411–1424. [Google Scholar] [CrossRef]
- Upadhya, S.; Staupendahl, D.; Heuse, M.; Tekkaya, A.E. Improved failure prediction in forming simulations through pre-strain mapping. AIP Conf. Proc. 2018, 1960, 090013. [Google Scholar] [CrossRef]
- Pätzold, I.; Stahl, J.; Golle, R.; Volk, W. Reducing the shear affected zone to improve the edge formability using a two-stage shear cutting simulation. J. Mater. Process. Technol. 2023, 313, 117872. [Google Scholar] [CrossRef]
- Pathak, N.; Butcher, C.; Worswick, M.J. Experimental Techniques for Finite Shear Strain Measurement within Two Advanced High Strength Steels. Exp. Mech. 2019, 59, 125–148. [Google Scholar] [CrossRef]
- Li, H.; Venezuela, J.; Qian, Z.; Zhou, Q.; Shi, Z.; Yan, M.; Knibbe, R.; Zhang, M.; Dong, F.; Atrens, A. Hydrogen fracture maps for sheared-edge-controlled hydrogen-delayed fracture of 1180 MPa advanced high-strength steels. Corros. Sci. 2021, 184, 109360. [Google Scholar] [CrossRef]
- Rahmaan, T.; Abedini, A.; Butcher, C.; Pathak, N.; Worswick, M.J. Investigation into the shear stress, localization and fracture behaviour of DP600 and AA5182-O sheet metal alloys under elevated strain rates. Int. J. Impact Eng. 2017, 108, 303–321. [Google Scholar] [CrossRef]
- ISO16630:2017; Metallic Materials–Sheet and Strip–Hole Expanding Test. International Organization for Standardization: Geneva, Switzerland, 2017.
- Levin, E.; Larour, P.; Heuse, M.; Staupendahl, D.; Clausmeyer, T.; Tekkaya, A.E. Influence of cutting tool stiffness on edge formability. IOP Conf. Ser. Mater. Sci. Eng. 2018, 418, 012061. [Google Scholar] [CrossRef]
- Larour, P.; Hinterdorfer, J.; Wagner, L.; Freudenthaler, J.; Grünsteidl, A.; Kerschbaum, M. Stretch flangeability of AHSS automotive grades versus cutting tool clearance, wear, angle and radial strain gradients. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1238, 012041. [Google Scholar] [CrossRef]
- Wang, K.; Ayoub, G.; Kridli, G. Effect of Trimming Process Parameters on Sheared Edge Geometry and Stretch Limit: An Experimental Investigation. J. Mater. Eng. Perform. 2020, 29, 5933–5949. [Google Scholar] [CrossRef]
- Jeong, K.; Jeong, Y.; Lee, J.; Won, C.; Yoon, J. Prediction of Hole Expansion Ratio for Advanced High-Strength Steel with Image Feature Analysis of Sheared Edge. Materials 2023, 16, 2847. [Google Scholar] [CrossRef]
- Feistle, M.; Golle, R.; Volk, W. Edge crack test methods for AHSS steel grades: A review and comparisons. J. Mater. Process. Technol. 2022, 302, 117488. [Google Scholar] [CrossRef]
- Paetzold, I.; Dittmann, F.; Feistle, M.; Golle, R.; Haefele, P.; Hoffmann, H.; Volk, W. Influence of shear cutting parameters on the fatigue behavior of a dual-phase steel. J. Phys. Conf. Ser. 2017, 896, 012107. [Google Scholar] [CrossRef]
- Yoshino, M.; Toji, Y.; Takagi, S.; Hasegawa, K. Influence of sheared edge on hydrogen embrittlement resistance in an ultra-high strength steel sheet. ISIJ Int. 2014, 54, 1416–1425. [Google Scholar] [CrossRef]
- Hu, X.; Sun, X.; Raghavan, K.; Comstock, R.J.; Ren, Y. Linking constituent phase properties to ductility and edge stretchability of two DP 980 steels. Mater. Sci. Eng. A 2020, 780, 139176. [Google Scholar] [CrossRef]
- Hartmann, C.; Volk, W. Digital image correlation and optical flow analysis based on the material texture with application on high-speed deformation measurement in shear cutting. In Proceedings of the International Conference on Digital Image & Signal Processing, Oxford, UK, 29–30 April 2019. [Google Scholar]
- Hartmann, C.; Weiss, H.A.; Lechner, P.; Volk, W.; Neumayer, S.; Fitschen, J.H.; Steidl, G. Measurement of strain, strain rate and crack evolution in shear cutting. J. Mater. Process. Technol. 2021, 288, 116872. [Google Scholar] [CrossRef]
- Bauer, A.; Volk, W.; Hartmann, C. Application of Fractal Image Analysis by Scale-Space Filtering in Experimental Mechanics. J. Imaging 2022, 8, 230. [Google Scholar] [CrossRef]
- Wu, X.; Bahmanpour, H. Characterization of Mechanically Sheared Edges of Dual Phase Steels. 2010. Available online: https://www.a-sp.org/wp-content/uploads/2020/08/Characterization-of-Mechanically-Sheared-Edges-of-DP-Steels-Final-Report.pdf (accessed on 12 May 2025).
- Frómeta, D.; Cuadrado, N.; Rehrl, J.; Suppan, C.; Dieudonné, T.; Dietsch, P.; Calvo, J.; Casellas, D. Microstructural effects on fracture toughness of ultra-high strength dual phase sheet steels. Mater. Sci. Eng. A 2021, 802, 140631. [Google Scholar] [CrossRef]
- Al-Rubaye, A.D.G.; Alali, M. A method to measure and visualize strain distribution via nanoindentation measurements. Mater. Today Proc. 2021, 44, 383–390. [Google Scholar] [CrossRef]
- Pavlina, E.J.; Van Tyne, C.J. Correlation of Yield strength and Tensile strength with hardness for steels. J. Mater. Eng. Perform. 2008, 17, 888–893. [Google Scholar] [CrossRef]
- Sarrionandia, X.; Nieves, J.; Bravo, B.; Pastor-López, I.; Bringas, P.G. An Objective Metallographic Analysis Approach Based on Advanced Image Processing Techniques. J. Manuf. Mater. Process. 2023, 7, 17. [Google Scholar] [CrossRef]
- Moske, J.; Kutlu, H.; Steinmeier, A.; Groenewold, P.; Santos, P.; Kuijper, A.; Weinmann, A.; Groche, P. Inline Wear Detection in High-Speed Progressive Dies Using Photometric Stereo. In Proceedings of the MATEC Web of Conferences, Lisbon, Portugal, 1–5 June 2025; Volume 408, p. 01031. [Google Scholar] [CrossRef]
- Kerschbaum, M.; Ebbichl, R. Method and device for determining the break area of a sample. European Patent EP3904867B9, 17 August 2022. [Google Scholar]
- Görz, M.; Schenek, A.; Vo, T.Q.; Riedmüller, K.R.; Liewald, M. Determining the residual formability of shear-cut sheet metal edges by utilizing an ML based prediction model. Mater. Res. Proc. 2024, 41, 1799–1806. [Google Scholar] [CrossRef]
- Li, W.; Vittorietti, M.; Jongbloed, G.; Sietsma, J. Microstructure–property relation and machine learning prediction of hole expansion capacity of high-strength steels. J. Mater. Sci. 2021, 56, 19228–19243. [Google Scholar] [CrossRef]














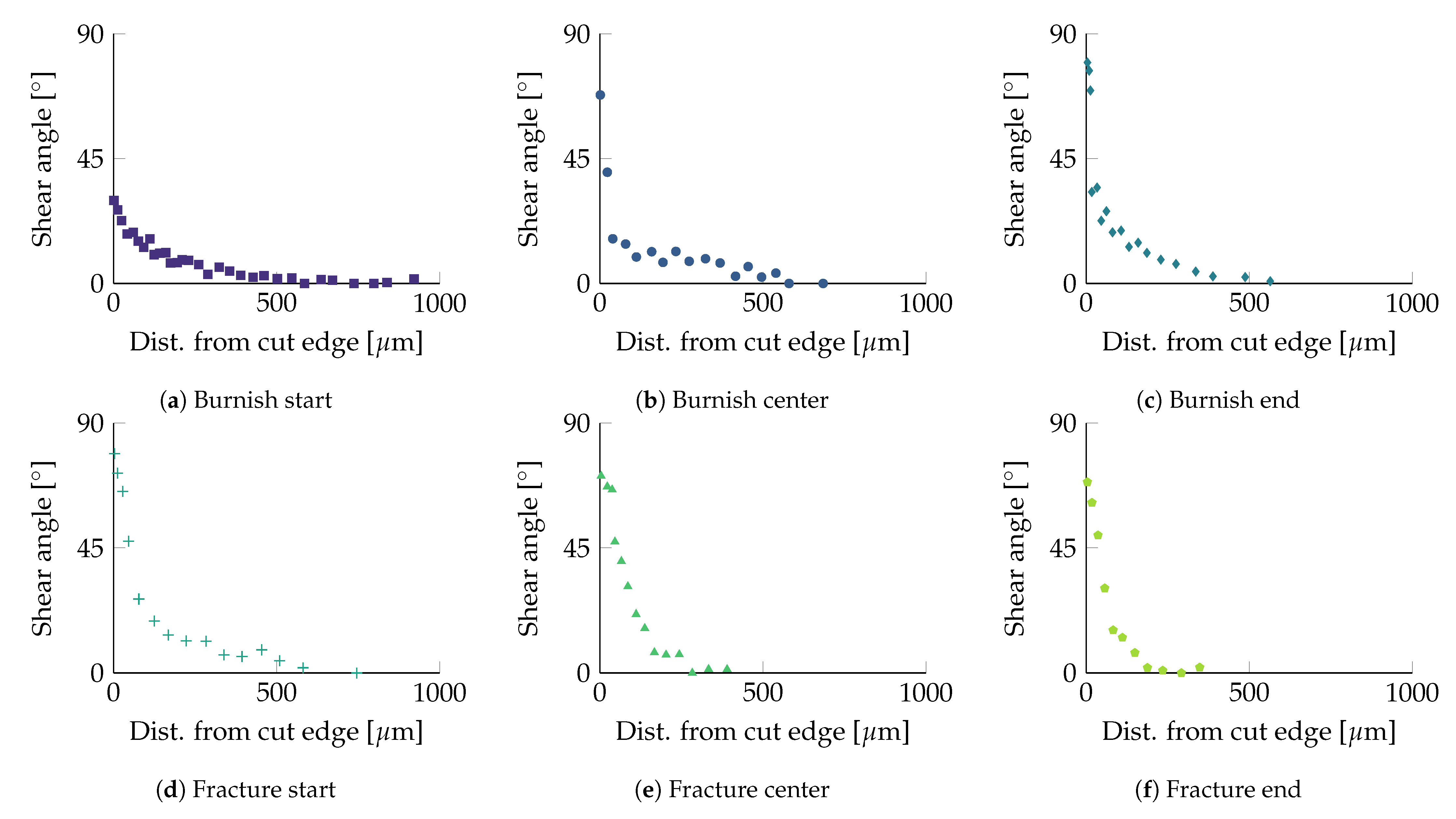
| RD | [MPa] | [MPa] | [%] | [%] | [-] | [-] |
|---|---|---|---|---|---|---|
| 893 | 1052 | 7.3 | 11.1 | 0.071 | 0.91 | |
| 905 | 1052 | 7.0 | 10.6 | 0.068 | 1.02 | |
| 909 | 1062 | 7.1 | 10.7 | 0.068 | 0.96 |
| Cl [%] | 5.3 | 8.5 | 10.5 | 12.1 | 17.1 | 20.5 | 23.8 | 27.0 | 33.7 | 40.3 |
| [mm] | 10.16 | 10.25 | 10.31 | 10.36 | 10.51 | 10.61 | 10.71 | 10.81 | 11.01 | 11.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Larour, P.; Sandin, O.; Casellas, D. Advanced Cut-Edge Characterization Methods for Improved Sheared-Edge Damage Evaluation in High-Strength Sheet Steels. Metals 2025, 15, 645. https://doi.org/10.3390/met15060645
Larour P, Sandin O, Casellas D. Advanced Cut-Edge Characterization Methods for Improved Sheared-Edge Damage Evaluation in High-Strength Sheet Steels. Metals. 2025; 15(6):645. https://doi.org/10.3390/met15060645
Chicago/Turabian StyleLarour, Patrick, Olle Sandin, and Daniel Casellas. 2025. "Advanced Cut-Edge Characterization Methods for Improved Sheared-Edge Damage Evaluation in High-Strength Sheet Steels" Metals 15, no. 6: 645. https://doi.org/10.3390/met15060645
APA StyleLarour, P., Sandin, O., & Casellas, D. (2025). Advanced Cut-Edge Characterization Methods for Improved Sheared-Edge Damage Evaluation in High-Strength Sheet Steels. Metals, 15(6), 645. https://doi.org/10.3390/met15060645







