Next Article in Journal
Continuous Fabrication Process of Aluminum Foam from Foaming to Press Forming
Previous Article in Journal
Influence of Microstructure and Texture on Tensile Properties of an As-Rolled Ti2AlNb-Based Alloy
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 15
Issue 6
10.3390/met15060632
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Data Science in Order and Disorder of High-Entropy Materials

by
Jiasheng Wang
1,2,
Jianzhong Jiang
2,
Peter K. Liaw
3,
Guihong Geng
4 and
Yong Zhang
1,2,*
1
State Key Laboratory for Advanced Metals and Materials, University of Science and Technology Beijing, Beijing 100083, China
2
School of Materials Science and Engineering, Fujian Fuyao University of Science and Technology, Fuzhou 350109, China
3
Department of Materials Science and Engineering, The University of Tennessee, Knoxville, TN 37996, USA
4
Department of Materials Science and Engineering, Northern University for Nationalities, Yinchuan 750030, China
*
Author to whom correspondence should be addressed.
Metals 2025, 15(6), 632; https://doi.org/10.3390/met15060632
Submission received: 7 May 2025 / Revised: 30 May 2025 / Accepted: 2 June 2025 / Published: 3 June 2025
Browse Figures
Versions Notes

Abstract

:
In recent years, high-entropy materials (HEMs) have garnered significant attention due to their unique multi-principal element compositions, which endow them with remarkable properties distinct from traditional materials. The order and disorder in HEMs are particularly complex, influenced by factors such as temperature, pressure, and composition, and are closely related to their mechanical and physical properties. This review systematically summarizes the progress in understanding the order and disorder in HEMs, with a focus on the role of data science in this field. We introduce the basic concepts of order and disorder and the related research in HEMs, discuss the nonlinear behaviors of HEMs, and elaborate on the relevant applications of data science, including analysis by machine learning, molecular dynamics simulations, and Monte Carlo simulations. Challenges and future directions are also explored, aiming to provide comprehensive insights into materials science.

1. Introduction

In the past few decades, high-entropy materials (HEMs) have emerged as a new class of materials that have attracted extensive attention from researchers in the field of materials science, whose unique composition design endows them with a series of characteristics that are distinct from traditional materials [1,2,3].
The concept of HEMs originated from the principle of entropy in thermodynamics [4]. When multiple elements are combined in a high-entropy alloy (HEA), the configurational entropy of the system is significantly increased. According to the principle of thermodynamics, the system tends to approach the state with the maximum entropy, which promotes the formation of a simple and stable solid-solution structure. This is the so-called “high-entropy effect” [5,6]. In addition, HEMs also exhibit the “cocktail effect”, which means that they can combine the excellent properties of multiple elements [7], such as high strength, high hardness, good corrosion resistance, and excellent high-temperature stability, giving them excellent comprehensive performance in extreme environments [8,9,10].
The order–disorder transformation in traditional materials usually follows a relatively simple pattern [11]. For instance, in many traditional alloys, during the solidification process or heat treatment, the atoms gradually arrange themselves in an orderly manner, forming a regular crystal structure, which is a process from disorder to order [12]. This transformation is mainly driven by factors, such as temperature and energy, aiming to minimize the free energy of the system [13]. However, the order–disorder transformation in HEMs is much more complex and diverse [14]. HEMs can not only transform from disorder to order but also show the reverse process, i.e., from order to disorder. This unique transformation behavior is closely related to their complex multi-elemental compositions, strong atomic interactions, and thermomechanical treatments [15]. For example, under certain external conditions, such as high temperatures, high pressures, or specific chemical environments, the originally ordered atomic arrangements in HEMs may be disrupted, leading to an increase in the degree of disorder. On the contrary, through appropriate heat treatments or other processing methods, the disordered atoms in HEMs can also be rearranged to form an ordered structure [16,17].
The rapid development of data science has brought new opportunities and challenges to the study of HEMs [18]. Data-driven methods can effectively deal with the massive and complex data generated in the research of HEMs, such as the relationship between compositions, structures, and properties [19]. By collecting and analyzing a large amount of experimental data and simulation results, data science can help us quickly discover hidden patterns and correlations in HEMs and then predict and optimize their properties [20]. For example, machine learning (ML) algorithms can be used to establish models to predict the phase structures and properties of HEMs based on their compositions and processing parameters, providing important guidance for the design and development of new HEMs [21].
The main purpose of this review is to systematically summarize the research progress of the order and disorder in HEMs and deeply analyze the key role of data science in this field. Firstly, the basic concepts of order and disorder in materials will be introduced, followed by a detailed discussion of the order–disorder transformation and the accompanying nonlinear law in HEMs. Later, the rising role of data science in the study of order and disorder in HEMs will be elaborated on. Finally, the challenges and future development directions in this field will be explored, aiming to provide a comprehensive understanding and reference for researchers engaged in HEMs and related fields.

2. Order–Disorder Transitions in High-Entropy Materials

2.1. Ordering and Disordering of Materials

Ordering and disordering are fundamental processes in materials science that are closely related to the crystal structures and properties of materials [22]. Understanding these processes is crucial for exploring the potential of HEMs.
In materials, the concept of ordering refers to the regular arrangement of atoms in a crystal lattice. When atoms are in an ordered state, they form a specific crystal structure with a high degree of symmetry [23]. For example, in the face-centered-cubic (FCC) structure, atoms are arranged at the corners and the centers of each face of a cube, resulting in a highly symmetrical and densely packed structure. This type of order is commonly seen in metals such as Ni, Cu, and Al, which exhibit excellent mechanical properties, such as high strength and ductility, due to the regular arrangement of atoms and the efficient packing of atomic planes [24]. Conversely, disordering represents a state where atoms are randomly distributed within the crystal lattice, lacking a long-range ordered arrangement [25]. For instance, in the amorphous Si, the atoms are arranged in a more disordered manner compared to crystalline Si, leading to different electrical and optical properties [26]. The degree of disordering can be influenced by various factors, e.g., temperatures, pressures, and compositions [27]. The transformation between ordering and disordering is often accompanied by changes in the crystal structure and has important implications for the properties of materials [28]. Understanding and controlling the ordering and disordering processes in materials is therefore essential for tailoring their properties for specific applications.

2.2. Order–Disorder Transitions in High-Entropy Alloys

The interplay between ordering and disordering in HEAs is particularly complex and intriguing [14]. From a crystallographic perspective, order–disorder transitions in HEAs are closely linked to their crystal structures. In FCC-structured HEAs, the disorder-to-order transition often involves the formation of superlattices, which change the crystal symmetry and significantly influence physical properties such as electrical and thermal conductivity. For example, in an FCC-structured NiCoFeCr alloy, superlattice formation led to a 15% increase in electrical resistivity and a 10% decrease in thermal conductivity [29]. In BCC-structured HEAs, order–disorder transitions are associated with the redistribution of atoms with different sizes and electronegativities. The ordered state results in a more regular atomic arrangement, reducing lattice distortion and modifying the alloy’s electronic structure, which in turn affects its mechanical properties. For instance, in a BCC-structured MoNbTaW alloy, short-range order (SRO) increased the Peierls stress from 2.47 GPa in the disordered state to 2.91 GPa, enhancing dislocation friction and strengthening the alloy [30].
High configurational entropy in HEAs stabilizes the disordered state of atoms, preventing the formation of simple ordered structures typically seen in traditional materials [31]. This inherent disorder can lead to novel properties, such as enhanced mechanical strength, improved corrosion resistance, and unique electronic behaviors [32]. However, under specific conditions, e.g., specific heat treatment or external stress, partial ordering can occur, tailoring the properties of HEAs for specific applications [33]. For example, the CoCrFeMnNi HEA exhibits a disordered FCC solid-solution structure at elevated temperatures, with atoms randomly distributed. As the temperature decreases, a significant transformation occurs, and SRO emerges in the FCC lattice under specific cooling conditions, leading to a more ordered local structure. Chen et al. [34] used high-resolution transmission electron microscopy (HRTEM) and atom-probe tomography to reveal that SRO regions, ranging from a few nanometers to tens of nanometers, form within the alloy. These regions exhibit distinct clustering patterns, with Cr atoms clustering with Ni and Co atoms, as shown by Zhang et al. [35]. This clustering phenomenon forms SRO structures that significantly impact the mechanical properties of the alloy. SRO enhances the alloy’s strength and hardness by modifying dislocation movement and strengthening lattice resistance. Ordered regions create obstacles for dislocation motion, increasing yield strength and hardness. Additionally, SRO influences deformation mechanisms such as twinning and slip, affecting ductility and toughness. The degree of SRO can be tailored through thermomechanical processing, such as aging treatments at specific temperatures, which promote SRO formation [35]. This tunability offers a promising approach to optimize the performance of the CoCrFeMnNi and other HEAs for various engineering applications.
Meanwhile, HEAs with refractory elements, such as Nb, Ta, Mo, and W, exhibit significantly more complex order–disorder transitions. During the solidification process, the large differences in the atomic size and diffusion rate among these refractory elements lead to a highly intricate initial solid-solution structure [36]. As the alloy undergoes further heat treatment, the atoms undergo a complex rearrangement process, which may result in the formation of ordered intermetallic compounds. For instance, in the TiZrNbTa-model alloy, Zhao et al. [37] revealed the formation of ω and ω-like phases during annealing through atomic-scale high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) imaging and first-principles calculations. Upon annealing at 1300 °C, the alloy develops a hierarchical microstructure with colony boundaries composed of bcc-1, bcc-2, and ω/ω-like phases, as shown in Figure 1a–c. The bcc-1 phase is enriched in Nb and Ta, while the bcc-2 and ω/ω-like phases are enriched in Zr, as shown in Figure 1d–f. These phases form ordered layered structures within the bcc matrix, with atomic arrangements transitioning from the (111) bcc planes to a non-close-packed hexagonal ω structure through self-adaptive atomic shuffling. Further strain analysis indicates that these phases are semi-coherent with the bcc matrix, with significant strain fields at the interfaces, as shown in Figure 1g,h. This order–disorder transition involves not only compositional partitioning based on atomic diffusion and displacive transformations but also the formation of ordered superstructures and collective displacements of atomic layers induced by strain.
In addition, the ZrNbTiAl HEA represents a particularly remarkable case, exhibiting a unique reverse transformation phenomenon: transitioning from an ordered state to a disordered state. Initially, through precise preparation processes, the ZrNbTiAl HEA can form an ordered crystal structure, such as a specific ordered intermetallic compound phase. However, when subjected to extreme conditions like high-temperature and high-pressure treatments or specific chemical treatments, the ordered atomic arrangement can be disrupted. As described by Gao et al. [15], in the high-Al-content Zr40Ti28Nb12Al20 refractory HEA, a phase transformation from the ordered B2 phase to a disordered BCC + B2 microstructure has been observed. The as-cast alloy exhibits a single-ordered B2 structure. After undergoing a series of thermomechanical treatments, a phase transformation occurs, as demonstrated in Figure 2a. In addition to the B2 phase, a BCC phase emerges in the rolled sample after annealing at various temperatures, and the diffraction peaks of the B2 phase split, indicating the decomposition of the B2 phase into a B2 + BCC structure. The microstructural evolution begins with the decomposition of the B2 phase into Al-rich and Al-poor regions. Bright-field (BF) TEM images of annealed samples (Figure 2b) reveal numerous spherical or ellipsoidal precipitates dispersed in the matrix. The number density and size of these precipitates vary with annealing conditions, consistent with the process of the B2-phase decomposition and coarsening. Subsequently, the coarsening of the aluminum-rich B2 precipitates continuously consumes Al and Zr atoms from the solid solution, leading to the depletion of aluminum and zirconium in the matrix (Figure 2d). This depletion drives the matrix to gradually transform from an ordered B2 structure to a disordered BCC structure, ultimately resulting in a single BCC matrix phase with dispersed spherical B2 precipitates (Figure 2c). This phase transformation not only enhances the tensile ductility of the refractory HEA but also maintains its high specific strength. The as-cast sample is completely brittle, with a relatively low ultimate strength of only 512 MPa. After warm rolling, the strength increases significantly, but ductility remains limited. However, after annealing at 923 K for 30 min to induce the phase transformation, the elongation at break increases to approximately 3.4%, while the strength is still maintained at a high level (an ultimate strength of 1713 MPa).
In summary, the order–disorder transitions in HEAs are complex phenomena that are governed by multiple factors. Different compositions give rise to distinct initial states and transition paths, and a thorough understanding of these transitions is essential for optimizing the properties of HEAs and expanding their application horizons.

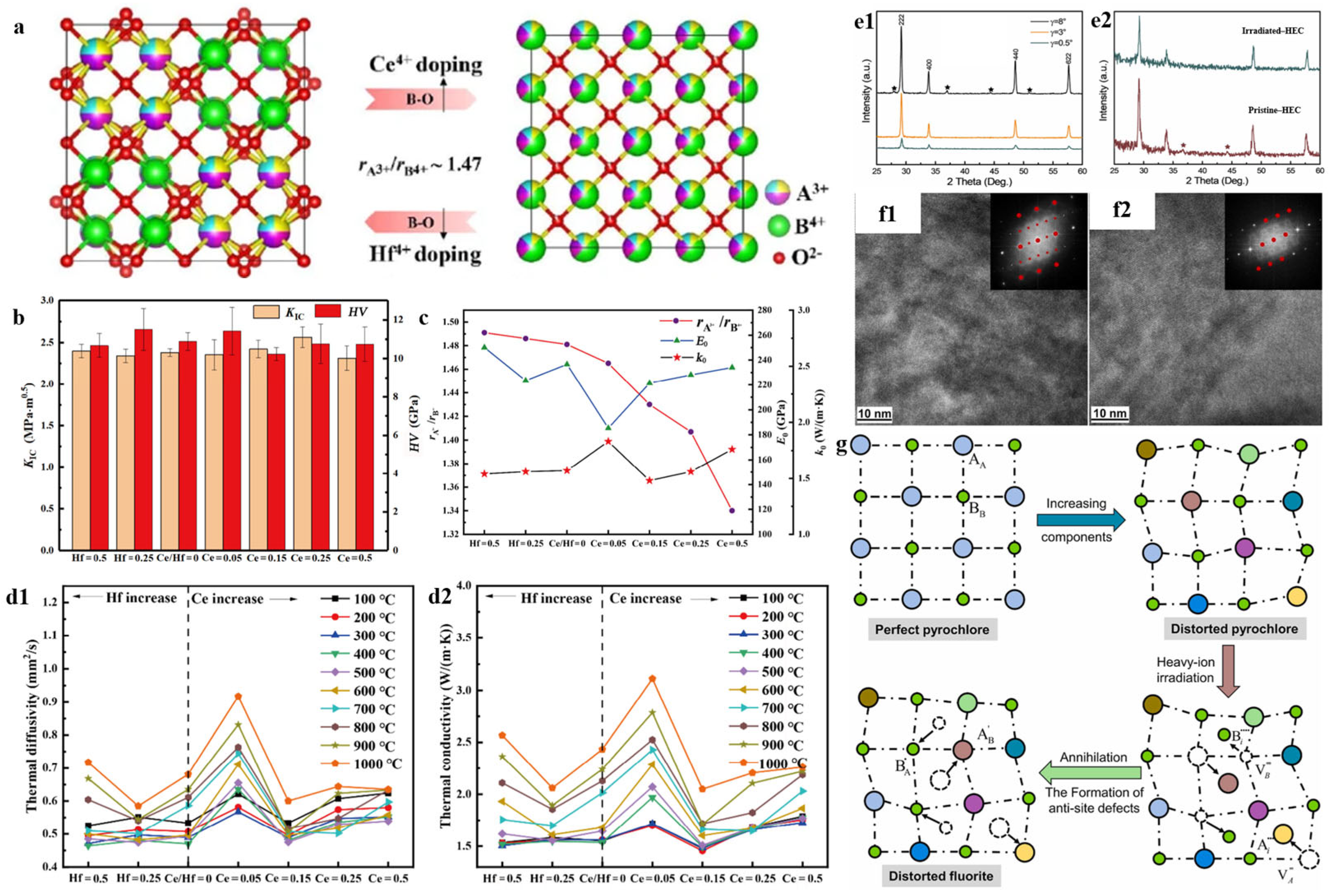
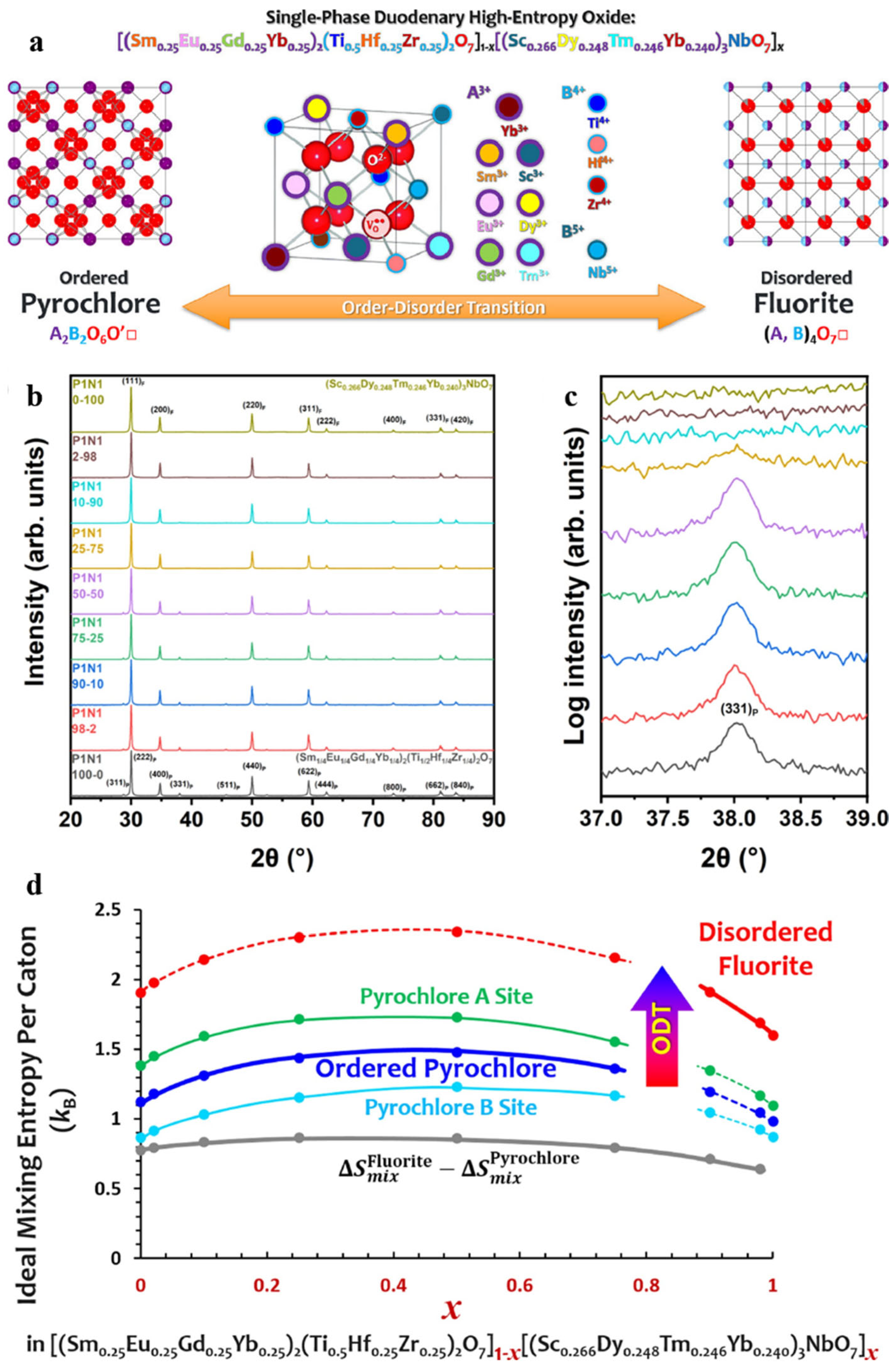
2.3. Order–Disorder Transitions in High-Entropy Ceramics

In the captivating realm of high-entropy ceramics (HECs), the order–disorder transitions exhibit unique characteristics that are distinct from those in alloys and exert a significant impact on their mechanical and thermophysical properties. It is evident that the HEAs mainly rely on the rearrangement of metal atoms in the lattice for order–disorder transitions, and the driving forces mainly include temperature, stress, and chemical potential differences. In HECs, due to the presence of non-metallic elements and complex chemical bonds, the order–disorder transitions are more influenced by factors such as lattice distortion, oxygen vacancy concentration, and chemical reactions.
For instance, Zhu et al. [38] investigated the impact of order–disorder transitions on the mechanical and thermophysical properties of dual-phase A2B2O7-type HECs by substituting Hf4+ and Ce4+ on B-sites (Zr4+), and identified r A 3 + / r B 4 + = 1.47 as the critical value for the order–disorder transition-phase boundary, as shown in Figure 3a. The high-entropy effect stabilized the modulus (E0 ≈ 230 GPa, Figure 3b) while enhancing mechanical properties (HV ≈ 10 GPa, KIC ≈ 2.3 MPa·m0.5, Figure 3c). The order–disorder transition also enhanced the phonon-scattering coefficient, leading to a relatively lower thermal conductivity [1.48–1.51 W·(m·K)−1 at 100–500 °C, Figure 3d1,d2]. The study proposes a novel composition design principle, highlighting the potential of HECs for high-temperature insulation. Additionally, another significant study by Xu et al. [39] explored the structural and mechanical response of high-entropy (La0.2Ce0.2Nd0.2Sm0.2Gd0.2)2Zr2O7 pyrochlore to heavy-ion irradiation, which demonstrated that the high-entropy oxide (HEO) maintained crystallinity after being irradiated by 9.0 MeV Au3+ ions at a fluence of 4.5 × 1015 ions/cm2. The irradiation-induced order–disorder transition from a pyrochlore to a defective fluorite structure occurred, which was demonstrated by Figure 3e1,e2,f, but no irradiation-induced segregation was observed at grain boundaries. The mechanical properties, including nano-hardness and Young’s modulus, were improved after irradiation. It highlights the superior irradiation resistance of high-entropy pyrochlore, making it a promising candidate for immobilizing the high-level radioactive waste and for use in advanced nuclear reactor systems. Meanwhile, Wright et al. [40] synthesized a series of duodenary (11 metals + oxygen) HEOs by mixing different fractions of a five-cation fluorite-structured niobate and a seven-cation pyrochlore, as demonstrated by Figure 4a. All compositions exhibited single high-entropy phases of either a disordered fluorite or ordered pyrochlore structure, as shown in Figure 4b. An order–disorder transition was evident with the changing composition (Figure 4c,d), accompanied by a reduction in thermal conductivity. Moreover, abrupt increases in Young’s modulus were observed at low mixing concentrations near both endmembers, resulting in higher E/k ratios compared to both endmembers. The present work suggests a new route to tailor HECs via controlling cation ordering vs. disordering, offering significant opportunities for optimizing material properties.
In summary, the induction of the order-disorder transitions in HECs can be achieved through the composition design and environmental condition adjustment, which is crucial for optimizing the performance of HECs in high-temperature, high-strength, and functional applications. Future we should focus on further exploring the mechanisms of these transitions and developing new HEC compositions with characteristics required for specific applications.

2.4. Nonlinear Law in High-Entropy Materials

HEMs exhibit distinct physical and mechanical properties from traditional alloys due to their unique multi-principal element system. This phenomenon, known as the “cocktail effect” [41], originates from the synergistic interactions among elements in the multi-principal element system, causing the physical responses to deviate from linear laws. In conventional single-principal element alloys, the predictable atomic arrangement allows linear superposition principles, such as Vegard’s law [42] or Matthiessen’s rule [43], to effectively estimate material properties. However, in HEMs, the maximization of entropy, combined with the equimolar dissolution of five or more principal elements, induces significant lattice distortion [44] and forms a heterogeneous structure characterized by chemical short-range order (CSRO) and topological disorder [45]. This multi-scale disorder breaks the translational symmetry assumption in conventional solid-state physics [46], resulting in the nonlinear evolution of electronic band structures, phonon spectra, and magnetic-exchange interactions. Specifically, the nonlinear behavior of HEMs can be explained by the following aspects.
Firstly, from the perspective of mechanical properties, the traditional solid-solution strengthening theory (such as the Labusch–Nabarro model [47]) is based on the elastic interaction between a single solute atom and a dislocation, whose strengthening increment has a linear relationship with the solute concentration. However, it fails to describe the CoCrFeMnNi HEA, where an experimentally measured yield strength reaches 1 GPa [48], 200–300% higher than theoretical predictions. This nonlinear enhancement stems from multi-element synergies: dynamic-strain partitioning caused by shear-modulus differences confines dislocation movement to localized modulus fluctuation zones; strong electronic interactions between CSRO-derived nanoclusters and extended dislocation cores exponentially increase pinning-energy barriers; crucially, the high configuration entropy (ΔSconfig ≈ 1.61R, R is the gas constant [6]) thermodynamically stabilizes these metastable disordered structures by reducing the Gibbs free energy (ΔG = ΔH − TΔS).
In addition, electronic transport behaviors similarly defy classical theories. While Nordheim’s law [49] predicts resistivity proportional to solute concentration squared, AlCoCrFeNi HEAs exhibit an electrical resistivity in the range of 160–188 μΩ·cm [50], an order of magnitude higher than conventional alloys. This anomaly originates from the electronic-state reconstruction induced by multi-element disorder [51]: potential field fluctuations from chemical disorder shorten electron mean free paths to atomic spacing scales, satisfying the Ioffe–Regel localization criterion [52].
Furthermore, nonmonotonic–magnetic evolution in the FeCoNi(AlSi)x HEA system further evidences ubiquitous nonlinear responses. As the content of Al and Si increases, the coercivity shows irregular changes, particularly when the coercivity significantly increases at x = 0.3 [53]. This nonlinear behavior is related to chemical disorder and changes in the crystal structure.
The “cocktail effect” in HEMs fundamentally reshapes material behaviors through multi-element synergies. It shows significant nonlinear characteristics and challenges and expands the application scope of classical theories. Therefore, a deep understanding of the essence of the synergistic effect of multiple principal elements in HEMs not only helps reveal the physical mechanism of their nonlinear behaviors but also provides important guidance for designing the next generation of high-performance materials. Data science provides a new approach for quantitatively analyzing such nonlinear characteristics. By building data-driven models, the multi-element interactions and complex microstructural features of HEAs can be taken into account, enabling more accurate prediction of their properties.

3. The Rising Role of Data Science

In recent years, data-driven approaches have emerged as powerful tools in materials science, especially for studying HEMs [54,55]. These approaches offer several advantages, such as accelerating the discovery process, reducing experimental costs, and providing insights into complex material behaviors that are difficult to obtain through traditional methods alone [56,57]. By leveraging extensive data from experiments, simulations, and theoretical calculations, researchers can gain a deeper understanding of material properties and behaviors [58,59]. Notably, data-driven methods have enabled accurate analysis of the order and disorder in HEMs, significantly enhancing our ability to design and optimize these complex materials.

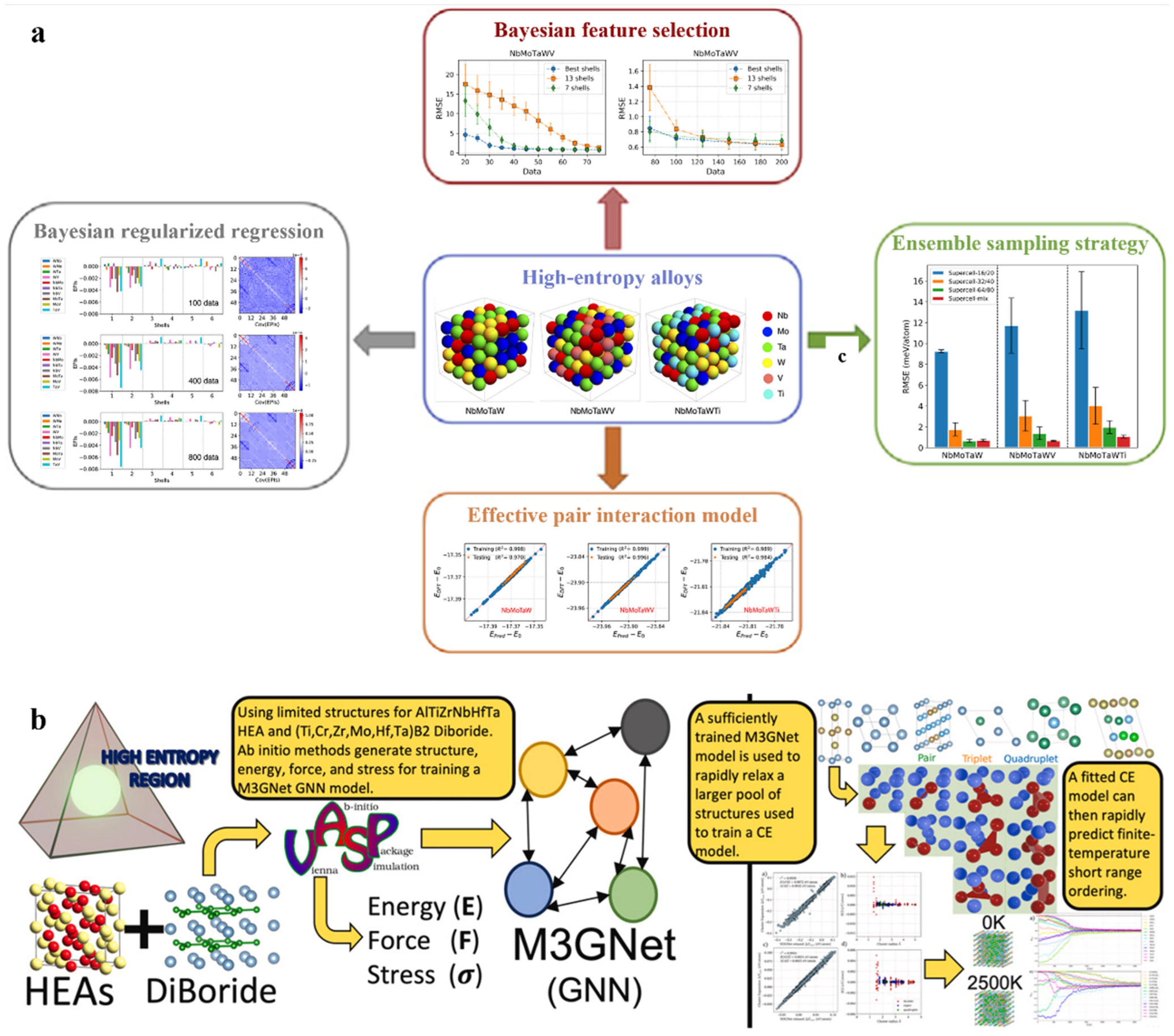
3.1. Machine Learning

ML has played a key role in the research of order and disorder in HEMs, especially in constructing efficient models and accelerating calculations [60,61]. One notable application is the use of Bayesian regression models to predict the configurational energy of HEAs. Zhang et al. [62] developed a robust data-driven framework based on Bayesian approaches to accurately predict the configurational energy of HEAs, such as NbMoTaW, NbMoTaWV, and NbMoTaWTi, as shown in Figure 5a. Bayesian regularized regression shows plots with data series for 100, 400, and 800 data points. These plots display coefficients related to shells and correlations, helping to establish a regression model. Bayesian feature selection plots the Root-Mean-Square Error (RMSE) against the number of data points. Different-colored lines represent various shell configurations, aiding in determining the optimal features for the model. The bar charts in the Ensemble sampling strategy display the RMSE values for different supercell configurations, which helps in assessing uncertainties through multiple sampling methods. The regression lines in the effective pair interaction model illustrate the relationship between calculated and reference energies. The high R-squared values (e.g., training R2= 0.998) indicate a good fit of the model for predicting configurational energy. From above, this method not only improves the accuracy of predictions but also effectively quantifies the uncertainties associated with the effective pair interaction (EPI) parameters. The Bayesian information criterion was employed for feature selection, which helped in identifying the optimal number of coordination shells to be considered in the EPI model. This approach demonstrated significant improvements in predicting order–disorder transitions, especially when dealing with limited datasets. Additionally, graph neural network (GNN) models perform excellently in handling data with complex network structures and can effectively capture the complex relationships between nodes. Vazquez et al. [63] used the GNN model combined with cluster expansion (CE) methods to investigate the chemical ordering in HEMs, which leveraged the M3GNet network to significantly reduce the computational load associated with generating the training data through density functional theory (DFT) calculations, as shown in Figure 5b. This hybrid ML-CE approach enabled the sampling of thousands of structures and fitting of a CE model with an RMSE below 10 meV·atom−1. The method was validated in the (Ti, Cr, Zr, Mo, Hf, Ta)B2 diboride system and the AlTiZrNbHfTa HEA system, demonstrating its effectiveness in predicting SRO and phase stability. Furthermore, Santos-Florez et al. [30] employed an ML potential trained with a neural network, using bispectrum coefficients as descriptors, to delve into the effects of SRO on the elasticity, vibrational modes, plasticity, and strength of the BCC MoNbTaW HEA. The findings revealed a significant attractive interaction between Mo-Ta pairs, leading to the formation of locally ordered B2 clusters. These clusters are temperature-dependent, and their number increases with the addition of Nb. SRO contributes to an increase in high-frequency phonon modes, introducing additional lattice friction for dislocation motion, thereby enhancing the alloy’s strength. While SRO has a minimal impact on elastic constants, it significantly affects other properties, highlighting its importance in the alloy’s strengthening mechanisms. The research elucidates HEA strengthening mechanisms and guides compositional design for property optimization.

3.2. Molecular Dynamics Simulations

Molecular dynamics (MD) simulations, which describe atomic motion trajectories by solving Newton’s equations of motion, have been extensively applied to non-equilibrium processes [64]. They are particularly useful for studying the order and disorder in HEMs. For instance, in non-equilibrium simulations, the dynamic evolution laws of CSRO can be extracted by analyzing atomic trajectory data. Akter et al. [65] used MD simulations to investigate the effects of grain boundaries (GBs) and CSRO on the mechanical properties of NiCoCr multi-principal element alloys (MPEAs), as shown in Figure 6a1,a2. They demonstrated that the presence of various grain boundaries and CSRO significantly affects the mechanical properties of NiCoCr MPEAs by analyzing lattice distortion, elastic constants, and other mechanical parameters. Meanwhile, the elastic moduli show an increasing trend with grain boundaries and CSRO, indicating enhanced rigidity. Moreover, the addition of CSRO and GBs was shown to have a significant impact on the ductility and fracture toughness of the MPEAs. SRO has been identified as a key factor influencing the mechanical and thermodynamic properties of HEMs. Similarly, Hasan et al. [66] investigated the SRO effects on the thermodynamic behavior of AlxCoCrFeNi HEAs using MD simulations and DFT calculations, as shown in Figure 6b. They found that SRO significantly affects the lattice thermal conductivity, coefficient of thermal expansion, and bulk modulus of the HEAs. Specifically, the presence of SRO leads to a higher lattice thermal conductivity and bulk modulus, while the coefficient of thermal expansion is reduced. This research highlights the importance of SRO in tailoring the properties of HEAs for specific applications.

3.3. Monte Carlo Simulations

Monte Carlo (MC) is a statistical mechanics method, which explores the equilibrium properties of a system through random sampling [67] and is well-suited for studying order and disorder in HEMs. Alvarado et al. [68] developed a methodology to predict the SRO and thermodynamic properties in chemically complex systems, specifically focusing on the WTaCrVHf quinary alloy. They used the CE method combined with DFT and MC simulations to study the effect of Hf addition on the stability of disordered states. The results showed that the addition of Hf significantly modifies the SRO, particularly at intermediate to low temperatures, which matches experimental observations, as presented in Figure 6c. It demonstrates the potential of using data science techniques to predict and optimize the SRO in HEMs for enhanced material performance. Moreover, Liu et al. [69] employed a data-driven framework to construct effective Hamiltonians for studying the thermodynamics of HEAs through canonical MC simulations. They employed a linear-scaling self-consistent multiple-scattering method to calculate configurational energy from first principles, which significantly improved computational efficiency. The EPI model was used to build the energy model, and Bayesian ridge regression was applied to determine the EPI parameters. The resulting effective Hamiltonians were highly accurate and robust, with RMSEs as low as 0.019, 0.044, and 0.099 mRy for MoNbTaW, MoNbTaVW, and MoNbTaTiW, respectively. Meanwhile, it provided valuable insights into the order–disorder transitions and their effects on the specific heat and short-range order parameters. For example, structural snapshots of MoNbTaW at different temperatures (Figure 6d) depict that at 101 K, MoNbTaW segregates into two phases, with Mo and Ta forming B2 structures. As the temperature increases to 304 K, some Nb and W atoms move into the Mo-Ta phase, partially breaking the B2 structure. At 2000 K, the ordered structure vanishes completely, forming a random solid solution. The specific heat curves of MoNbTaW, MoNbTaVW, and MoNbTaTiW (Figure 6e) revealed two major phase-transition peaks. The first transition occurs near room temperature (T1) and is mainly due to W and Nb, while the second transition at an elevated temperature (T2) is caused by the other elements. These findings suggest that the random phases provide good ductility, while the ordered precipitates enhance strength by impeding dislocation movement. The addition of V in the MoNbTaVW significantly increases T2, resulting in a higher abundance of ordered precipitates and thus reduced ductility compared to MoNbTaW and MoNbTaTiW.
Metals 15 00632 g006
Figure 6. Computational models of (a1) random and (a2) CSRO for NiCoCr MPEAs. Reprinted with permission from Ref. [65], copyright 2023, Elsevier. (b) Structure, SRO effect, and thermodynamic properties of AlxCoCrFeNi HEAs. Reprinted with permission from Ref. [66], copyright 2024, Elsevier. (c) Atomic arrangement and elemental concentration distribution at 300 K of the W0.31Ta0.34Cr0.05V0.37Hf0.03 HEA obtained through (c1) MC simulations and (c2) experiments. Reprinted with permission from Ref. [68], copyright 2023, Elsevier. (d) Snapshots of the structure of MoNbTaW at (d1) 101 K, (d2) 304 K, and (d3) 2000 K. (e) The specific heats of (e1) MoNbTaW, (e2) MoNbTaVW, and (e3) MoNbTaTiW. Reprinted with permission from Ref. [69], copyright 2021, Elsevier.
Figure 6. Computational models of (a1) random and (a2) CSRO for NiCoCr MPEAs. Reprinted with permission from Ref. [65], copyright 2023, Elsevier. (b) Structure, SRO effect, and thermodynamic properties of AlxCoCrFeNi HEAs. Reprinted with permission from Ref. [66], copyright 2024, Elsevier. (c) Atomic arrangement and elemental concentration distribution at 300 K of the W0.31Ta0.34Cr0.05V0.37Hf0.03 HEA obtained through (c1) MC simulations and (c2) experiments. Reprinted with permission from Ref. [68], copyright 2023, Elsevier. (d) Snapshots of the structure of MoNbTaW at (d1) 101 K, (d2) 304 K, and (d3) 2000 K. (e) The specific heats of (e1) MoNbTaW, (e2) MoNbTaVW, and (e3) MoNbTaTiW. Reprinted with permission from Ref. [69], copyright 2021, Elsevier.
Metals 15 00632 g006
The contributions of different data science methods (ML/MD/MC) to the analysis of the order–disorder mechanism are summarized in Table 1. In summary, the applications of data science in HEMs, especially in analyzing order and disorder, have opened up new avenues for the development and utilization of these materials, promising to bring about more efficient and effective material design and engineering in the future.

4. Synergistic Insights and Future Perspectives

4.1. Current Understanding and Achievements

The integration of data science with the study of order and disorder in HEMs has significantly advanced our understanding of their composition–structure relationships, structure–property connections, and influencing factors. Data-driven approaches have revealed that specific combinations and proportions of elements play a decisive role in determining initial crystal structures and the tendency of order–disorder transitions [70]. For instance, alloys with higher atomic-size mismatch are more likely to exhibit complex disordered structures initially, requiring stringent thermal or mechanical treatments to transition to ordered states.
In terms of structure–property relationships, ML models have effectively predicted how changes in the order–disorder state affect mechanical, physical, and chemical properties. These models indicate that increased ordering enhances material strength by resisting dislocation movement, though excessive ordering can lead to brittle intermetallic compounds, reducing ductility [71].
Data science has also improved our understanding of transformation-influencing factors. By analyzing temperature, pressure, and external fields, researchers can establish accurate models for predicting transformation conditions, uncovering new correlations between these factors and transformation kinetics [72].

4.2. Challenges and Limitations

Despite the significant progress made in the integration of data science and HEM research, several challenges and limitations remain.
One of the primary challenges lies in data acquisition. Obtaining accurate and comprehensive experimental data for HEMs is a complex task. The synthesis of HEMs often requires precise control over multiple elements and processing conditions, and even slight variations can lead to significant differences in material properties [73]. For example, different fabrication techniques such as arc-melting, spark plasma sintering, and additive manufacturing can result in distinct microstructures, defect levels, element distribution uniformity, and local order degree, which directly influence mechanical performance.
Moreover, the integration of big data from various sources is also a formidable challenge. HEM research generates data from a wide range of experimental techniques, such as XRD, electron microscopy, mechanical testing, and computational simulations. Each data source has its format, resolution, and level of detail, making it difficult to combine and analyze them effectively [62].
In terms of model construction, developing models that can accurately describe the complex order–disorder transitions in HEMs is still a major hurdle. HEMs have complex multi-element compositions and strong atomic interactions, which result in highly nonlinear and complex behaviors. Current ML models and theoretical models often struggle to capture these complex relationships accurately [74]. Additionally, many advanced ML models, such as deep neural networks, are considered “black boxes” due to their lack of interpretability, making it difficult to understand the physical mechanisms behind the predictions [75].
Furthermore, there is a lack of standardized datasets that include both compositional and process parameters. Most studies focus only on alloy composition and ignore critical aspects such as heat treatment history, cooling rates, and forming processes, which significantly affect the final material properties [76]. This gap limits the ability of current models to generalize across different fabrication routes and hinders the development of robust design frameworks.
The accuracy of model predictions also has limitations. Although data-driven models can provide valuable insights, they are often based on assumptions and simplifications due to the complexity of HEMs [77]. For example, in some models predicting the mechanical properties of HEMs, the influence of both local atomic environments and the presence of defects may not be fully considered. As a result, the predicted properties may deviate from the actual experimental values, especially when dealing with complex real-world scenarios involving thermal cycles, residual stresses, or anisotropic microstructures.

4.3. Future Directions

Looking ahead, I believe that the integration of data science and HEM research will be a transformative pathway for uncovering novel phenomena and enabling advanced applications. One of the most pressing needs is the development of more accurate multi-scale models that can effectively bridge atomic-level interactions with macroscopic material properties. In my view, this requires not only computational innovation but also a rethinking of how we represent disorder across scales. For instance, while traditional methods like cluster expansion or special quasi-random structures have been useful in capturing configurational energy landscapes, they may fall short when applied to systems with extreme chemical complexity or dynamic disorder. Therefore, exploring new modeling paradigms, such as hybrid quantum–classical approaches or machine learning potentials trained on physically meaningful descriptors, could offer a more robust framework for predicting order–disorder transitions under varying thermodynamic conditions.
I also see great value in fusing interdisciplinary knowledge to enrich our understanding of HEMs. From a physics perspective, there is still much to learn about the fundamental mechanisms driving short-range order and its impact on mechanical and thermal behavior. Chemically, the synthesis of HEMs often involves competing enthalpic and entropic effects that are not yet fully captured by existing models. And from a data science standpoint, the challenge lies not just in handling large datasets but in designing algorithms that can incorporate physical constraints and guide the discovery process intelligently. This suggests an opportunity to develop domain-specific machine learning architectures that go beyond generic neural networks and instead reflect the symmetry, conservation laws, and thermodynamic principles inherent in materials systems.
A key future direction involves explicitly incorporating fabrication-related parameters into data-driven models. These include laser power, scanning speed, feeding rate, and temperature history in additive manufacturing, as well as annealing time and pressure in bulk alloy processing [78]. By integrating these process variables into the feature space, one can build physics-informed surrogate models that better reflect the real-world behavior of HEMs. For example, recent work has shown that process parameters can be directly correlated to final microstructural features such as grain structures, porosity, and geometrical distortion through data-driven surrogate modeling.
Another direction I find particularly exciting is the potential for real-time monitoring and adaptive control of material properties during processing. With the emergence of in situ characterization techniques, we can now observe structural evolution at the atomic level as it happens. In my opinion, integrating these real-time data streams into predictive models could lead to the creation of intelligent feedback loops, whereby processing parameters are dynamically adjusted based on observed microstructural changes. This would mark a shift from reactive to proactive materials engineering, allowing us to fine-tune performance characteristics on the fly.
Finally, I believe that the future of HEM discovery lies in the synergy between high-throughput experimentation and data-driven design. While automated platforms can rapidly generate and test thousands of compositions, their full potential can only be realized if paired with smart data analysis tools. In particular, I advocate for the use of active learning strategies that prioritize experiments likely to yield the most informative results. This approach not only accelerates discovery but also ensures that limited resources are used efficiently, especially in cases where experimental or computational costs are high.
Challenges and future directions in the order and disorder of HEM research are summarized in Figure 7. I envision a future where data science becomes deeply embedded in the materials design loop—not merely as a tool for summarizing known trends, but as a driver of new hypotheses, a facilitator of cross-disciplinary insight, and a partner in the co-evolution of theory, experiment, and application.

5. Summary

The ordering and disordering processes in materials, especially in HEMs, are complex and fascinating phenomena. They are not only related to the basic crystal structure and atomic arrangement of materials but also have a profound impact on the physical and mechanical properties of materials. Understanding these processes through data science is of great significance for the design, development, and application of HEMs.

Author Contributions

J.W.: data curation, investigation, writing—original draft preparation, writing—review and editing; J.J.: funding acquisition, methodology, writing—review and editing; P.K.L.: formal analysis, methodology, validation, writing—review and editing; G.G.: data curation, methodology, supervision, writing—review and editing; Y.Z.: conceptualization, supervision, writing—original draft, writing—review and editing. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zhang, Y.; Zuo, T.T.; Tang, Z.; Gao, M.C.; Dahmen, K.A.; Liaw, P.K.; Lu, Z.P. Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 2013, 61, 1–93. [Google Scholar] [CrossRef]
  2. Li, W.; Xie, D.; Li, D.; Zhang, Y.; Gao, Y.; Liaw, P.K. Mechanical behavior of high-entropy alloys. Prog. Mater. Sci. 2021, 118, 100777. [Google Scholar] [CrossRef]
  3. George, E.P.; Raabe, D.; Ritchie, R.O. High-entropy alloys. Nat. Rev. Mater. 2019, 4, 515–534. [Google Scholar] [CrossRef]
  4. Liu, C.; Li, S.; Zheng, Y.; Xu, M.; Su, H.; Miao, X.; Liu, Y.; Zhou, Z.; Qi, J.; Yang, B.; et al. Advances in high entropy oxides: Synthesis, structure, properties and beyond. Prog. Mater. Sci. 2024, 148, 101385. [Google Scholar] [CrossRef]
  5. Tsai, M.; Yeh, J. High-entropy alloys: A critical review. Mater. Res. Lett. 2014, 2, 107–123. [Google Scholar] [CrossRef]
  6. Miracle, D.; Senkov, O. A critical review of high entropy alloys and related concepts. Acta Mater. 2016, 122, 448–511. [Google Scholar] [CrossRef]
  7. Hsu, W.; Tsai, C.; Yeh, A.; Yeh, J. Clarifying the four core effects of high-entropy materials. Nat. Rev. Chem. 2024, 8, 471–485. [Google Scholar] [CrossRef]
  8. Han, L.; Zhu, S.; Rao, Z.; Scheu, C.; Ponge, D.; Ludwig, A.; Zhang, H.; Gutfleisch, O.; Hahn, H.; Li, Z.; et al. Multifunctional high-entropy materials. Nat. Rev. Mater. 2024, 9, 846–865. [Google Scholar] [CrossRef]
  9. Wyatt, B.C.; Nemani, S.K.; Hilmas, G.E.; Opila, E.J.; Anasori, B. Ultra-high temperature ceramics for extreme environments. Nat. Rev. Mater. 2023, 9, 773–789. [Google Scholar] [CrossRef]
  10. Xi, R.; Li, Y. Recent advances in the performance and mechanisms of high-entropy alloys under low- and high-temperature conditions. Coatings 2025, 15, 92. [Google Scholar] [CrossRef]
  11. Šíma, V. Order-disorder transformations in materials. J. Alloys Compd. 2004, 378, 44–51. [Google Scholar] [CrossRef]
  12. Pfeiler, W.; Sprušil, B. Atomic ordering in alloys: Stable states and kinetics. Mater. Sci. Eng. A 2002, 324, 34–42. [Google Scholar] [CrossRef]
  13. Luo, Q.; Guo, Y.; Liu, B.; Feng, Y.; Zhang, J.; Li, Q.; Chou, K. Thermodynamics and kinetics of phase transformation in rare earth-magnesium alloys: A critical review. J. Mater. Sci. Technol. 2020, 44, 171–190. [Google Scholar] [CrossRef]
  14. Yan, X.; Liaw, P.K.; Zhang, Y. Order and disorder in amorphous and high-entropy materials. Metall. Mater. Trans. A 2021, 52, 2111–2122. [Google Scholar] [CrossRef]
  15. Gao, K.; Chu, Y.; Zhou, W.; Tian, Y.; Zhang, Y.; Li, Y. Phase inversion in a lightweight high Al content refractory high-entropy alloy. J. Mater. Sci. Technol. 2023, 150, 124–137. [Google Scholar] [CrossRef]
  16. Wang, X.; Wang, Y. Disorder-order transition in multiprincipal element alloy: A free energy perspective. Phys. Rev. Mater. 2023, 7, 033606. [Google Scholar] [CrossRef]
  17. Lokhande, V.; Malavekar, D.; Kim, C.; Vinu, A.; Ji, T. Order within disorder: Unveiling the potential of high entropy materials in energy storage and electrocatalysis. Energy Storage Mater. 2024, 72, 103718. [Google Scholar] [CrossRef]
  18. Lu, Z.; Ma, D.; Liu, X.; Lu, Z. High-throughput and data-driven machine learning techniques for discovering high-entropy alloys. Commun. Mater. 2024, 5, 76. [Google Scholar]
  19. Yao, Y.; Dong, Q.; Brozena, A.; Luo, J.; Miao, J.; Chi, M.; Wang, C.; Kevrekidis, I.G.; Ren, Z.J.; Greeley, J.; et al. High-entropy nanoparticles: Synthesis-structure-property relationships and data-driven discovery. Science 2022, 376, eabn3103. [Google Scholar] [CrossRef]
  20. Cui, K.; Qiao, J.; Liaw, P.K.; Zhang, Y. Data driving design of high-entropy alloys for lightweight and dynamic applications. Sci. China Phys. Mech. Astron. 2024, 67, 227101. [Google Scholar] [CrossRef]
  21. Meng, H.; Yu, H.; Zhuang, L.; Chu, Y. Data-driven acceleration of high-entropy ceramic discovery. Matter 2024, 7, 2646–2649. [Google Scholar] [CrossRef]
  22. Nix, F.C.; Shockley, W. Order-Disorder transformations in alloys. Rev. Mod. Phys. 1938, 10, 1–71. [Google Scholar] [CrossRef]
  23. Wu, X.; Wang, Z.; Yang, F.; Gao, R.; Liang, C.; Tey, M.K.; Li, X.; Pohl, T.; You, L. Dissipative time crystal in a strongly interacting Rydberg gas. Nat. Phys. 2024, 20, 1389–1394. [Google Scholar] [CrossRef]
  24. Çiftci, Y.; Çolakoğlu, K. Mechanical stability and elastic properties of some FCC metals: A many-body potential applications. Math. Comput. Appl. 2003, 8, 295–302. [Google Scholar] [CrossRef]
  25. Zhou, Z.Y.; Yang, Q.; Yu, H.B. Toward atomic-scale understanding of structure-dynamics-properties relations for metallic glasses. Prog. Mater. Sci. 2024, 145, 101311. [Google Scholar] [CrossRef]
  26. Deringer, V.L.; Bernstein, N.; Csányi, G.; Mahmoud, C.B.; Ceriotti, M.; Wilson, M.; Drabold, D.A.; Elliott, S.R. Origins of structural and electronic transitions in disordered silicon. Nature 2021, 589, 59–64. [Google Scholar] [CrossRef]
  27. Zhang, F.; Lou, H.; Cheng, B.; Zeng, Z.; Zeng, Q. High-pressure induced phase transitions in high-entropy alloys: A review. Entropy 2019, 21, 239. [Google Scholar] [CrossRef]
  28. Tian, L.; Levämäki, H.; Eriksson, O.; Kokko, K.; Nagy, Á.; Délczeg-Czirják, E.K.; Vitos, L. Density functional theory description of the order-disorder transformation in Fe-Ni. Sci. Rep. 2019, 9, 8172. [Google Scholar] [CrossRef]
  29. Bag, P.; Su, Y.; Kuo, Y.; Lai, Y.; Wu, S. Physical properties of face-centered cubic structured high-entropy alloys: Effects of NiCo, NiFe, and NiCoFe alloying with Mn, Cr, and Pd. Phys. Rev. Mater. 2021, 5, 085003. [Google Scholar] [CrossRef]
  30. Santos-Florez, P.A.; Dai, S.; Yao, Y.; Yanxon, H.; Li, L.; Wang, Y.; Zhu, Q.; Yu, X. Short-range order and its impacts on the BCC MoNbTaW multi-principal element alloy by the machine-learning potential. Acta Mater. 2023, 255, 119041. [Google Scholar] [CrossRef]
  31. Fernández-Caballero, A.; Fedorov, M.; Wróbel, J.; Mummery, P.; Nguyen-Manh, D. Configurational entropy in multicomponent alloys: Matrix formulation from ab initio based Hamiltonian and application to the FCC Cr-Fe-Mn-Ni system. Entropy 2019, 21, 68. [Google Scholar] [CrossRef] [PubMed]
  32. Huang, X.; Miao, J.; Luo, A.A. Order-disorder transition and its mechanical effects in lightweight AlCrTiV high entropy alloys. Scr. Mater. 2021, 210, 114462. [Google Scholar] [CrossRef]
  33. Kumar, T.S.; Chauhan, L.; Chakravarthy, K.; Chelvane, A.; Shanmugasundaram, T. The improved galvanic corrosion resistance of a eutectic high entropy alloy through heat treatment. J. Mater. Res. 2022, 37, 4211–4221. [Google Scholar] [CrossRef]
  34. Chen, X.; Wang, Q.; Cheng, Z.; Zhu, J.; Jiang, L. Direct observation of chemical short-range order in a medium-entropy alloy. Nature 2021, 592, 712–716. [Google Scholar] [CrossRef]
  35. Zhang, R.; Zhao, S.; Ding, J.; Chong, Y.; Jia, T.; Ophus, C.; Asta, M.; Ritchie, R.O.; Minor, A.M. Short-range order and its impact on the CrCoNi medium-entropy alloy. Nature 2020, 581, 283–287. [Google Scholar] [CrossRef]
  36. Udayakumaran, G.; Gandhi, T.K.; Raju, R.; Bansal, R.; Kukade, J.; Barpha, V.; Saxena, K.K.; Panchal, S.M.; Bhavani, B. Study of phase equilibrium of refractory high-entropy alloys using the atomic size difference concept for turbine blade applications. High Temp. Mater. Proc. 2024, 43, 20240006. [Google Scholar] [CrossRef]
  37. Zhao, X.; Li, S.; Jiang, J.; Bai, J.; Xie, H.; Pan, H.; Tian, Y.; Ren, Y.; Teng, C.; Wu, L.; et al. Polytypic omega/omega-like transformation in a refractory high-entropy alloy. Acta Mater. 2022, 238, 118207. [Google Scholar] [CrossRef]
  38. Zhu, J.; Wei, M.; Xu, J.; Yang, R.; Meng, X.; Zhang, P.; Yang, J.; Li, G.; Gao, F. Influence of order-disorder transition on the mechanical and thermophysical properties of A2B2O7 high-entropy ceramics. J. Adv. Ceram. 2022, 11, 1222–1234. [Google Scholar] [CrossRef]
  39. Xu, L.; Niu, M.; Wang, H.; Su, L.; Gao, H.; Zhuang, L. Response of structure and mechanical properties of high entropy pyrochlore to heavy ion irradiation. J. Eur. Ceram. Soc. 2022, 42, 6624–6632. [Google Scholar] [CrossRef]
  40. Wright, A.J.; Wang, Q.; Hu, C.; Yeh, Y.; Chen, R.; Luo, J. Single-phase duodenary high-entropy fluorite/pyrochlore oxides with an order-disorder transition. Acta Mater. 2021, 211, 116858. [Google Scholar] [CrossRef]
  41. Pickering, E.J.; Jones, N.G. High-entropy alloys: A critical assessment of their founding principles and future prospects. Int. Mater. Rev. 2016, 61, 183–202. [Google Scholar] [CrossRef]
  42. Denton, A.R.; Ashcroft, N.W. Vegard’s law. Phys. Rev. A 1991, 43, 3161–3164. [Google Scholar] [CrossRef] [PubMed]
  43. Schwerer, F.; Conroy, J.; Arajs, S. Matthiessen’s rule and the electrical resistivity of iron-silicon solid solutions. J. Phys. Chem. Solids 1969, 30, 1513–1525. [Google Scholar] [CrossRef]
  44. Kumar, N.; Waghmare, U.V. Entropic stabilization and descriptors of structural transformation in high entropy alloys. Acta Mater. 2023, 255, 119077. [Google Scholar] [CrossRef]
  45. Yang, Y.; Jia, Z.; Zhang, X.; Liu, Y.; Wang, Q.; Li, Y.; Shao, L.; Di, S.; Kuang, J.; Sun, L.; et al. Chemical short-range order in multi-principal element alloy with ordering effects on water electrolysis performance. Mater. Today 2023, 72, 97–108. [Google Scholar] [CrossRef]
  46. Yu, P.Y.; Cardona, M.; Sham, L.J. Fundamentals of Semiconductors: Physics and materials properties. Phys. Today 1997, 50, 76–77. [Google Scholar] [CrossRef]
  47. Zhang, H.; Cai, D.; Sun, X.; Huang, H.; Lu, S.; Wang, Y.; Hu, Q.; Vitos, L.; Ding, X. Solid solution strengthening of high-entropy alloys from first-principles study. J. Mater. Sci. Technol. 2022, 121, 105–116. [Google Scholar] [CrossRef]
  48. Wang, Y.; Li, D.; Yang, J.; Jin, J.; Zhang, M.; Wang, X.; Li, B.; Hu, Z.; Gong, P. Effect of grain size on the tribological behavior of CoCrFeMnNi high entropy alloy. Materials 2023, 16, 1714. [Google Scholar] [CrossRef]
  49. Rossiter, P.L. The Electrical Resistivity of Metals and Alloys; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
  50. Zhao, C.; Li, J.; He, Y.; Wang, J.; Wang, W.Y.; Kou, H.; Wang, J. Effect of strong magnetic field on the microstructure and mechanical-magnetic properties of AlCoCrFeNi high-entropy alloy. J. Alloys Compd. 2019, 820, 153407. [Google Scholar] [CrossRef]
  51. Yeh, J.; Chen, S.; Lin, S.; Gan, J.; Chin, T.; Shun, T.; Tsau, C.; Chang, S. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
  52. John, S.; Rangarajan, R. Optimal structures for classical wave localization: An alternative to the Ioffe-Regel criterion. Phys. Rev. B 1988, 38, 10101–10104. [Google Scholar] [CrossRef] [PubMed]
  53. Zhang, Y.; Zuo, T.; Cheng, Y.; Liaw, P.K. High-entropy alloys with high saturation magnetization, electrical resistivity and malleability. Sci. Rep. 2013, 3, 1455. [Google Scholar] [CrossRef] [PubMed]
  54. Liu, S.; Yang, C. Machine learning design for high-entropy alloys: Models and algorithms. Metals 2024, 14, 235. [Google Scholar] [CrossRef]
  55. Elkatatny, S.; Abd-Elaziem, W.; Sebaey, T.A.; Darwish, M.A.; Hamada, A. Machine-learning synergy in high-entropy alloys: A review. J. Mater. Res. Technol. 2024, 33, 3976–3997. [Google Scholar] [CrossRef]
  56. Pyzer-Knapp, E.O.; Pitera, J.W.; Staar, P.W.J.; Takeda, S.; Laino, T.; Sanders, D.P.; Sexton, J.; Smith, J.R.; Curioni, A. Accelerating materials discovery using artificial intelligence, high performance computing and robotics. Npj Comput. Mater. 2022, 8, 84. [Google Scholar] [CrossRef]
  57. Qi, J.; Fan, X.; Hoyos, D.I.; Widom, M.; Liaw, P.K.; Poon, J. Integrated design of aluminum-enriched high-entropy refractory B2 alloys with synergy of high strength and ductility. Sci. Adv. 2024, 10, eadq0083. [Google Scholar] [CrossRef]
  58. Ren, W.; Zhang, Y.; Wang, W.; Ding, S.; Li, N. Prediction and design of high hardness high entropy alloy through machine learning. Mater. Des. 2023, 235, 112454. [Google Scholar] [CrossRef]
  59. Gao, T.; Gao, J.; Yang, S.; Zhang, L. Data-driven design of novel lightweight refractory high-entropy alloys with superb hardness and corrosion resistance. npj Comput. Mater. 2024, 10, 256. [Google Scholar] [CrossRef]
  60. Wen, C.; Zhang, Y.; Wang, C.; Huang, H.; Wu, Y.; Lookman, T.; Su, Y. Machine-learning-assisted compositional design of refractory high-entropy alloys with optimal strength and ductility. Engineering 2024, 46, 214–223. [Google Scholar] [CrossRef]
  61. Liu, X.; Zhang, J.; Pei, Z. Machine learning for high-entropy alloys: Progress, challenges and opportunities. Prog. Mater. Sci. 2022, 131, 101018. [Google Scholar] [CrossRef]
  62. Zhang, J.; Liu, X.; Bi, S.; Yin, J.; Zhang, G.; Eisenbach, M. Robust data-driven approach for predicting the configurational energy of high entropy alloys. Mater. Des. 2019, 185, 108247. [Google Scholar] [CrossRef]
  63. Vazquez, G.; Sauceda, D.; Arróyave, R. Deciphering chemical ordering in high entropy materials: A machine learning-accelerated high-throughput cluster expansion approach. Acta Mater. 2024, 276, 120137. [Google Scholar] [CrossRef]
  64. Kadupitiya, J.C.S.; Fox, G.C.; Jadhao, V. Solving Newton’s equations of motion with large timesteps using recurrent neural networks based operators. Mach. Learn. Sci. Technol. 2022, 3, 025002. [Google Scholar] [CrossRef]
  65. Akter, R.; Khan, M.; Nobin, M.N.M.; Ali, M.S.; Hossain, M.M.; Rahaman, M.Z.; Ali, M.L. Effects of grain boundary and chemical short-range order on mechanical properties of NiCoCr multi-principal element alloys: A molecular dynamics simulations. Mater. Today Commun. 2023, 36, 106630. [Google Scholar] [CrossRef]
  66. Hasan, M.A.A.; Shin, S.; Liaw, P.K. Short-range order effects on the thermodynamic behavior of AlCoCrFeNi high-entropy alloys. Comput. Mater. Sci. 2024, 239, 112980. [Google Scholar] [CrossRef]
  67. Carreño, J.C.L.; Del Valle, E.; Laussy, F.P. Frequency-resolved Monte Carlo. Sci. Rep. 2018, 8, 6975. [Google Scholar]
  68. Alvarado, A.M.; Lee, C.; Wróbel, J.S.; Sobieraj, D.; Nguyen-Manh, D.; Poplawsky, J.D.; Fensin, S.J.; Martinez, E.; El-Atwani, O. Predicting short-range order evolution in WTaCrVHf refractory high-entropy alloys. Scr. Mater. 2023, 233, 115506. [Google Scholar] [CrossRef]
  69. Liu, X.; Zhang, J.; Yin, J.; Bi, S.; Eisenbach, M.; Wang, Y. Monte Carlo simulation of order-disorder transition in refractory high entropy alloys: A data-driven approach. Comput. Mater. Sci. 2020, 187, 110135. [Google Scholar] [CrossRef]
  70. Yang, T.; Zhao, Y.L.; Tong, Y.; Jiao, Z.B.; Wei, J.; Cai, J.X.; Han, X.D.; Chen, D.; Hu, A.; Kai, J.J.; et al. Multicomponent intermetallic nanoparticles and superb mechanical behaviors of complex alloys. Science 2018, 362, 933–937. [Google Scholar] [CrossRef]
  71. Lederer, Y.; Toher, C.; Vecchio, K.S.; Curtarolo, S. The search for high entropy alloys: A high-throughput ab-initio approach. Acta Mater. 2018, 159, 364–383. [Google Scholar] [CrossRef]
  72. Ren, F.; Pandolfi, R.; Van Campen, D.; Hexemer, A.; Mehta, A. On-the-fly data assessment for high-throughput X-ray diffraction measurements. ACS Comb. Sci. 2017, 19, 377–385. [Google Scholar] [CrossRef] [PubMed]
  73. Li, Q.; Sheng, H.; Ma, E. Strengthening in multi-principal element alloys with local-chemical-order roughened dislocation pathways. Nat. Commun. 2019, 10, 3563. [Google Scholar] [CrossRef] [PubMed]
  74. Dai, F.; Wen, B.; Sun, Y.; Xiang, H.; Zhou, Y. Theoretical prediction on thermal and mechanical properties of high entropy (Zr0.2Hf0.2Ti0.2Nb0.2Ta0.2)C by deep learning potential. J. Mater. Sci. Technol. 2020, 43, 168–174. [Google Scholar] [CrossRef]
  75. Yao, Y.; Huang, Z.; Xie, P.; Lacey, S.D.; Jacob, R.J.; Xie, H.; Chen, F.; Nie, A.; Pu, T.; Rehwoldt, M.; et al. Carbothermal shock synthesis of high-entropy-alloy nanoparticles. Science 2018, 359, 1489–1494. [Google Scholar] [CrossRef]
  76. Soni, V.K.; Sinha, A.K. Effect of alloying elements, phases and heat treatments on properties of high-entropy alloys: A review. Trans. Indian Inst. Met. 2023, 76, 897–914. [Google Scholar] [CrossRef]
  77. Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef]
  78. Steingrimsson, B.; Fan, X.; Kulkarni, A.; Kulkarni, A.; Gao, M.C.; Liaw, P.K. Machine learning and data analytics for design and manufacturing of high-entropy materials exhibiting mechanical or fatigue properties of interest. In High-Entropy Materials: Theory, Experiments, and Applications; Springer International Publishing: Cham, Switzerland, 2022; pp. 115–238. [Google Scholar]
Metals 15 00632 g001
Figure 1. (a–c) Structural characterization analysis of the colony boundaries in the furnace-cooled TiZrNbTa0.75 HEA. (a,b) Bright-field TEM images of the colony boundaries. (c1–c3) Selected area electron diffraction (SAED) analysis for the colony boundary presented in (b), indicating that the colony boundary is composed of bcc–1, bcc–2, and ω-like phases. (c4–c6) Local parts in (b) are further enlarged, and the corresponding atomic-scale HAADF-STEM images of the bcc–1, bcc–2, and ω-like phases are provided in (c4), (c5), and (c6), respectively. The electron beam is parallel to [111]bcc–1 (c1,c4), [110]bcc–2 (c2,c5), and [ 1 ¯ 2 1 ¯ 0]ω (c3,c6). (d–f) STEM-EDS analysis results of the colony boundaries in the furnace-cooled HEA. HAADF-STEM images (d1,e1,f1) and the corresponding EDS mapping images related to the elements Ti (d2,e2,f2), Zr (d3,e3,f3), Nb (d4,e4,f4), and Ta (d5,e5,f5). (g,h) Structural details of the bcc–1/bcc–2 and bcc–1/ω/ω–like interfaces. Atomic-scale HAADF-STEM images of the bcc−1/bcc–2 (g1) and bcc-1/ω/ω-like (h1) interfaces. The corresponding inverse FFT images showing the misfit dislocations present in the bcc-1/bcc-2 (g2) and bcc–1/ω/ω–like (h2) interfaces, which are obtained by masking the (10 1 ¯ )bcc–1/(10 1 ¯ )bcc–2 and (10 1 ¯ )bcc–1/(2 1 ¯ 1 ¯ 0)ω diffractions (indicated by cyan circles) in the inserted FFT patterns. (g3,h3) GPA strain maps (εxx) calculated in the directions normal to the (10 1 ¯ )bcc–1/bcc–2 (g2) and (10 1 ¯ )bcc–1/(2 1 ¯ 1 ¯ 0)ω (h2) showing the compression and extension strain fields around the misfit dislocations. The HAADF-STEM images overlapped with the εxx strain maps in (g4) and (h4), respectively. The symbol “⊥” represents a misfit dislocation. Reprinted with permission from Ref. [37], copyright 2022, Elsevier.
Figure 1. (a–c) Structural characterization analysis of the colony boundaries in the furnace-cooled TiZrNbTa0.75 HEA. (a,b) Bright-field TEM images of the colony boundaries. (c1–c3) Selected area electron diffraction (SAED) analysis for the colony boundary presented in (b), indicating that the colony boundary is composed of bcc–1, bcc–2, and ω-like phases. (c4–c6) Local parts in (b) are further enlarged, and the corresponding atomic-scale HAADF-STEM images of the bcc–1, bcc–2, and ω-like phases are provided in (c4), (c5), and (c6), respectively. The electron beam is parallel to [111]bcc–1 (c1,c4), [110]bcc–2 (c2,c5), and [ 1 ¯ 2 1 ¯ 0]ω (c3,c6). (d–f) STEM-EDS analysis results of the colony boundaries in the furnace-cooled HEA. HAADF-STEM images (d1,e1,f1) and the corresponding EDS mapping images related to the elements Ti (d2,e2,f2), Zr (d3,e3,f3), Nb (d4,e4,f4), and Ta (d5,e5,f5). (g,h) Structural details of the bcc–1/bcc–2 and bcc–1/ω/ω–like interfaces. Atomic-scale HAADF-STEM images of the bcc−1/bcc–2 (g1) and bcc-1/ω/ω-like (h1) interfaces. The corresponding inverse FFT images showing the misfit dislocations present in the bcc-1/bcc-2 (g2) and bcc–1/ω/ω–like (h2) interfaces, which are obtained by masking the (10 1 ¯ )bcc–1/(10 1 ¯ )bcc–2 and (10 1 ¯ )bcc–1/(2 1 ¯ 1 ¯ 0)ω diffractions (indicated by cyan circles) in the inserted FFT patterns. (g3,h3) GPA strain maps (εxx) calculated in the directions normal to the (10 1 ¯ )bcc–1/bcc–2 (g2) and (10 1 ¯ )bcc–1/(2 1 ¯ 1 ¯ 0)ω (h2) showing the compression and extension strain fields around the misfit dislocations. The HAADF-STEM images overlapped with the εxx strain maps in (g4) and (h4), respectively. The symbol “⊥” represents a misfit dislocation. Reprinted with permission from Ref. [37], copyright 2022, Elsevier.
Metals 15 00632 g001
Metals 15 00632 g002
Figure 2. (a) Crystal structure evolution with annealing. (a1) XRD patterns of the as-cast, as-rolled, and rolled samples with different thermomechanical treatments. Three phases of BCC, B2, and Al3Zr5 were observed after annealing. (a2,a3) Detailed scans at the (110) peak of the B2/BCC phase for the rolled samples that were isochronally and isothermally annealed, respectively. The splitting in these two peaks became clearer with the annealing process. (b) Morphologies of BCC and B2 phases. (b1) BF TEM image along the direction of the as-cast sample, showing that it is a single-phase structure. Rolled samples after annealing at (b2) 923 K for 6 min, (b3) 923 K for 30 min, and (b4) 1073 K for 30 min, showing continuous coarsening of the B2 precipitates. (c) Phase transition process of the matrix. High-resolution TEM images of the matrix in (c1) the as-cast and (c2,c3) rolled samples after annealing at 923 K for (c2) 6 min and (c3) 30 min. The corresponding SAED patterns confirmed (c1) a single B2 structure, (c2) a mixture of B2 and BCC phases, and (c3) a single BCC structure. (d) Elemental changes in the precipitation process. (d1) HAADF image in the BCC/B2 region of rolled samples after annealing at 923 K for 30 min. The elemental distribution of (d2) Al, (d3) Nb, (d4) Ti, and (d5) Zr. Reprinted with permission from Ref. [15], copyright 2022, Elsevier.
Figure 2. (a) Crystal structure evolution with annealing. (a1) XRD patterns of the as-cast, as-rolled, and rolled samples with different thermomechanical treatments. Three phases of BCC, B2, and Al3Zr5 were observed after annealing. (a2,a3) Detailed scans at the (110) peak of the B2/BCC phase for the rolled samples that were isochronally and isothermally annealed, respectively. The splitting in these two peaks became clearer with the annealing process. (b) Morphologies of BCC and B2 phases. (b1) BF TEM image along the direction of the as-cast sample, showing that it is a single-phase structure. Rolled samples after annealing at (b2) 923 K for 6 min, (b3) 923 K for 30 min, and (b4) 1073 K for 30 min, showing continuous coarsening of the B2 precipitates. (c) Phase transition process of the matrix. High-resolution TEM images of the matrix in (c1) the as-cast and (c2,c3) rolled samples after annealing at 923 K for (c2) 6 min and (c3) 30 min. The corresponding SAED patterns confirmed (c1) a single B2 structure, (c2) a mixture of B2 and BCC phases, and (c3) a single BCC structure. (d) Elemental changes in the precipitation process. (d1) HAADF image in the BCC/B2 region of rolled samples after annealing at 923 K for 30 min. The elemental distribution of (d2) Al, (d3) Nb, (d4) Ti, and (d5) Zr. Reprinted with permission from Ref. [15], copyright 2022, Elsevier.
Metals 15 00632 g002
Metals 15 00632 g003
Figure 3. (a) Order–disorder transition in HECs. (b) Vickers hardness (HV) and fracture toughness (KIC) of HECs. (c) Effect of B-site doping on the radius ratio of A3+ to B4+ ( r A 3 + / r B 4 + ), unreduced modulus (E0), and dense thermal conductivity (k0) of HECs. Thermophysical properties of HECs: (d1) thermal diffusivity; (d2) thermal conductivity. Reprinted with permission from Ref. [38], copyright 2021, Springer. The gazing incident angle XRD patterns of (e1) the HEC at the different grazing incidence angles after irradiation; (e2) pristine and irradiated HEC at the grazing incidence angles of 0.5°. The peaks related to the superlattice of the pyrochlore structure are noted with stars. The HRTEM images and the corresponding SAED patterns of the HEC (f1) before and (f2) after irradiation. (g) The structural evolution of perfect pyrochlore after increasing components and heavy-ion irradiation. Reprinted with permission from Ref. [39], copyright 2022, Elsevier.
Figure 3. (a) Order–disorder transition in HECs. (b) Vickers hardness (HV) and fracture toughness (KIC) of HECs. (c) Effect of B-site doping on the radius ratio of A3+ to B4+ ( r A 3 + / r B 4 + ), unreduced modulus (E0), and dense thermal conductivity (k0) of HECs. Thermophysical properties of HECs: (d1) thermal diffusivity; (d2) thermal conductivity. Reprinted with permission from Ref. [38], copyright 2021, Springer. The gazing incident angle XRD patterns of (e1) the HEC at the different grazing incidence angles after irradiation; (e2) pristine and irradiated HEC at the grazing incidence angles of 0.5°. The peaks related to the superlattice of the pyrochlore structure are noted with stars. The HRTEM images and the corresponding SAED patterns of the HEC (f1) before and (f2) after irradiation. (g) The structural evolution of perfect pyrochlore after increasing components and heavy-ion irradiation. Reprinted with permission from Ref. [39], copyright 2022, Elsevier.
Metals 15 00632 g003
Metals 15 00632 g004
Figure 4. (a) Schematic illustration of the ordered pyrochlore and disordered defect fluorite structures and the associated order–disorder transition. (b) XRD spectra of the P1N1 series and (c) the evolution of the (331) pyrochlore superstructure peak. The evolution of the pyrochlore superstructure peak is plotted on a logarithmic intensity scale. (d) Computed ideal configurational entropies of mixing per cation for both ordered pyrochlore and disordered fluorite phases for the P1N1 series. Reprinted with permission from Ref. [40], copyright 2021, Elsevier.
Figure 4. (a) Schematic illustration of the ordered pyrochlore and disordered defect fluorite structures and the associated order–disorder transition. (b) XRD spectra of the P1N1 series and (c) the evolution of the (331) pyrochlore superstructure peak. The evolution of the pyrochlore superstructure peak is plotted on a logarithmic intensity scale. (d) Computed ideal configurational entropies of mixing per cation for both ordered pyrochlore and disordered fluorite phases for the P1N1 series. Reprinted with permission from Ref. [40], copyright 2021, Elsevier.
Metals 15 00632 g004
Metals 15 00632 g005
Figure 5. (a) Bayesian approaches for predicting the configurational energy of NbMoTaW, NbMoTaWV, and NbMoTaWTi HEAs. In the center of the figure, three models of HEAs are displayed, representing NbMoTaW, NbMoTaWV, and NbMoTaWTi, respectively, with different-colored spheres indicating elements like Nb, Mo, Ta, W, V, and Ti. Arrows lead from the HEA models to four key components. The top, bottom, left, and right components correspond to Bayesian feature selection, effective pair interaction model, Bayesian regularized regression, and Ensemble sampling strategy, respectively. Reprinted with permission from Ref. [62], copyright 2020, Elsevier. (b) The flowchart of the accelerated high-throughput CE M3GNet GNN model is used to analyze the chemical orderliness of HEMs. The ab initio method was used to generate energy data for HEAs and diborides to train the M3GNet model. The relaxed structures from the M3GNet model are then used to train the cluster expansion model, ultimately enabling rapid prediction of short-range order at finite temperatures. Reprinted with permission from Ref. [63], copyright 2024, Elsevier.
Figure 5. (a) Bayesian approaches for predicting the configurational energy of NbMoTaW, NbMoTaWV, and NbMoTaWTi HEAs. In the center of the figure, three models of HEAs are displayed, representing NbMoTaW, NbMoTaWV, and NbMoTaWTi, respectively, with different-colored spheres indicating elements like Nb, Mo, Ta, W, V, and Ti. Arrows lead from the HEA models to four key components. The top, bottom, left, and right components correspond to Bayesian feature selection, effective pair interaction model, Bayesian regularized regression, and Ensemble sampling strategy, respectively. Reprinted with permission from Ref. [62], copyright 2020, Elsevier. (b) The flowchart of the accelerated high-throughput CE M3GNet GNN model is used to analyze the chemical orderliness of HEMs. The ab initio method was used to generate energy data for HEAs and diborides to train the M3GNet model. The relaxed structures from the M3GNet model are then used to train the cluster expansion model, ultimately enabling rapid prediction of short-range order at finite temperatures. Reprinted with permission from Ref. [63], copyright 2024, Elsevier.
Metals 15 00632 g005
Metals 15 00632 g007
Figure 7. Challenges and future directions in order and disorder HEM research.
Figure 7. Challenges and future directions in order and disorder HEM research.
Metals 15 00632 g007
Table 1. Contributions of different data science methods to the analysis of order–disorder.
Table 1. Contributions of different data science methods to the analysis of order–disorder.
MethodAccuracyScaleCostScene
MLHighAtomMediumFast prediction, uncertainty quantification
MDMediumAtomHighDynamic evolution, micro-mechanism
MCMediumAtomMediumBalance property, phase transition
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, J.; Jiang, J.; Liaw, P.K.; Geng, G.; Zhang, Y. Data Science in Order and Disorder of High-Entropy Materials. Metals 2025, 15, 632. https://doi.org/10.3390/met15060632

AMA Style

Wang J, Jiang J, Liaw PK, Geng G, Zhang Y. Data Science in Order and Disorder of High-Entropy Materials. Metals. 2025; 15(6):632. https://doi.org/10.3390/met15060632

Chicago/Turabian Style

Wang, Jiasheng, Jianzhong Jiang, Peter K. Liaw, Guihong Geng, and Yong Zhang. 2025. "Data Science in Order and Disorder of High-Entropy Materials" Metals 15, no. 6: 632. https://doi.org/10.3390/met15060632

APA Style

Wang, J., Jiang, J., Liaw, P. K., Geng, G., & Zhang, Y. (2025). Data Science in Order and Disorder of High-Entropy Materials. Metals, 15(6), 632. https://doi.org/10.3390/met15060632

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop