Magnetic Pulse Welding of Dissimilar Materials: Weldability Window for AA6082-T6/HC420LA Stacks

Abstract

Magnetic pulse welding (MPW) is a promising solid-state joining process that utilizes electromagnetic forces to create high-speed, impact-like collisions between two metal components. This welding technique is widely known for its ability to join dissimilar metals, including aluminum, steel, and copper, without the need for additional filler materials or fluxes. MPW offers several advantages, such as minimal heat input, no distortion or warping, and excellent joint strength and integrity. The process is highly efficient, with welding times typically ranging from microseconds to milliseconds, making it suitable for high-volume production applications in sectors including automotive, aerospace, electronics, and various other industries where strong and reliable joints are required. It provides a cost-effective solution for joining lightweight materials, reducing weight and improving fuel efficiency in transportation systems. This contribution concerns an application for the automotive sector (body-in-white) and specifically examines the welding of AA6082-T6 aluminum alloy with HC420LA cold-rolled micro-alloyed steel. One of the main aspects for MPW optimization is the determination of the process window that does not depend on the equipment used but rather on the parameters associated with the physical mechanisms of the process. It was demonstrated that process windows based on contact angle versus output voltage diagrams can be of interest for production use for a given component (shock absorbers, suspension struts, chassis components, instrument panel beams, next-generation crash boxes, etc.). The process window based on impact pressures versus impact velocity for different impact angles, in addition to not depending on the equipment, allows highlighting other factors such as the pressure welding threshold for different temperatures in the impact zone, critical transition speeds for straight or wavy interface formation, and the jetting/no jetting effect transition. Experimental results demonstrated that optimal welding conditions are achieved with impact velocities between 900 and 1200 m/s, impact pressures of 3000–4000 MPa, and impact angles ranging from 18–35°. These conditions correspond to optimal technological parameters including gaps of 1.5–2 mm and output voltages between 7.5 and 8.5 kV. Successful welds require mean energy values above 20 kJ and weld specific energy values exceeding 150 kJ/m². The study establishes critical failure thresholds: welds consistently failed when gap distances exceeded 3 mm, output voltage dropped below 5.5 kV, or impact pressures fell below 2000 MPa. To determine these impact parameters, relationships based on Buckingham’s π theorem provide a viable solution closely aligned with experimental reality. Additionally, shear tests were conducted to determine weld cohesion, enabling the integration of mechanical resistance isovalues into the process window. The findings reveal an inverse relationship between impact angle and weld specific energy, with higher impact velocities producing thicker intermetallic compounds (IMCs), emphasizing the need for careful parameter optimization to balance weld strength and IMC formation.

1. Introduction

The development of elements composed of dissimilar materials is booming. The automotive sector is one of the industries that shows the greatest interest, being able to benefit from the development of dissimilar joints, especially with regard to using lighter elements such as high-strength aluminum instead of heavier ones. Different companies have shown interest in replacing steel parts with another, lighter component in the bodies and chassis, body-in-white (BIW). Companies such as Honda and Fiat [1,2] are considering replacing BIW steel parts with aluminum alloys with adequate mechanical characteristics. By using these alloys, the overall weight of the vehicle is reduced, as well as fuel consumption and, therefore, harmful gases such as CO₂ into the atmosphere. In addition to improving the environmental conditions, it allows compliance with current and increasingly restrictive environmental legislation [3], both national and international.

The joining of dissimilar materials, including steel and aluminum, by welding has been studied in the last decade [1,4,5]. The challenges are linked to the differences in (i) the melting temperature of aluminum (660 °C) and iron (1538 °C); (ii) densities (2.69 and 7.8 g/cm^3, respectively, for aluminum and iron) leading to macroscale segregation and poor mechanical properties of the joint [6,7,8]; (iii) thermal conductivity and rates of thermal expansion of aluminum and steel. Therefore, it is necessary to optimize accurately the process parameters to obtain an adequate union of both materials.

Techniques such as laser welding, ultrasonic welding, and electromagnetic pulse welding offer the opportunity to control the joining process [1,9] and, therefore, to join these two materials, overcoming the difficulties that may arise. Likewise, the energy efficiency of these processes and the ability to automate make them a plausible solution for the automotive sector.

In the case of laser welding, a high-intensity beam is focused on a specific point, heating it up and producing a fusion of the materials. Lasers have a high power density and travel speed and low heat input, thus enabling welds to be made that would not be possible with other fusion methods.

Ultrasonic welding (USW) is a solid-state welding process that uses high-frequency mechanical vibrations to generate friction and heat between the faying surfaces of two materials, causing them to plastically deform and form a metallurgical bond. This process is particularly well suited for joining dissimilar materials, such as aluminum and steel, due to its ability to produce sound welds without the need for filler materials or fusion. However, the process is limited to a maximum thickness of materials of around 3 mm, and is best suited for joints with simple geometries, such as lap joints or spot welds [10].

Electromagnetic welding is a solid-state process generated at high-impact speed [11]. The pressure generated by the electromagnetic field is the reason for the formation of a solid-state cold weld. The MPW process is free of emissions such as fumes, spatter, and heat that are typically produced during conventional welding techniques. Due to these differences, this type of weld presents advantages over conventional welding processes [12], as follows:

−

It is possible to achieve welded joints of dissimilar materials, unlike fusion welding where the ability of these to be welded must be taken into account. In this way, materials such as titanium, aluminum, and magnesium can be welded, even if their capacity to be welded is very low despite the fact that they are of great interest due to their mechanical properties.

−

There are no heat-affected zones (HAZ), so the materials maintain the original mechanical properties; this means that the resulting parts do not have fragile areas. However, galvanic coupling exists and the intermetallic compounds (IMCs) can act as a buffer between steel and aluminum. It is therefore important to be able to control the nature and thickness of these IMCs to maintain their mechanical properties while avoiding corrosion.

This welding process is also a green process or at least not harmful to the environment due to the fact that it does not emit any gas resulting from combustion in the process, which is common in fusion welding. However, it also has its limitations, such as:

−

A limit in the thickness of the plates or sheets that can be welded (≤6 mm).

−

The moving plate, which is driven against the other plate at a high speed, must be electrically conductive and, depending on this capacity, it will be necessary to apply more or less discharge energy to reach the weld. The electrical resistivity of the material in contact with the electromagnetic coil is one of the key parameters of the process. In general, the most prominent alloys in the automotive, aeronautical, and biomedical sectors are materials with high electrical resistivity, which are not favorable for this process. The use of low electrical resistivity, such as an aluminum or copper alloy pusher, is then a solution.

The objectives of this work were to (i) define the process window of MPW independently of the geometry of the coil and of the relative position of the components to weld; (ii) associate the process window values of the cohesion energy of the welded joint; and (iii) evaluate the quantity of intermetallic compounds generated by the process and its influence on the properties of the welded joint. Different studies concerning MPW, explosion welding, etc. [4,5,8,9,13,14] showed that for a weld to exist between two solid bodies it was necessary to exceed a threshold pressure. So, the impact pressures, associated with the impact velocity and the impact angle, are therefore the physical parameters that will control the process.

2. Literature Review of the Magnetic Pulse Welding Process (MPW)

Solid-state welding depends on the pressure generated between the elements to be welded. This pressure can be applied in different ways (mechanical, electromagnetic, explosive wave, etc.). This study focused on the application of pressure through an impact at high speed, caused in the particular case of MPW, by an electromagnetic pulse (Figure 1 and Figure 2) and applied to both flat and cylindrical parts [13,14,15,16].

To carry out electromagnetic impact welding, an electrical installation is required, made up of a bank of capacitors, an electromagnetic coil, and an optional tooling to shape the material that was accelerated against it [11,17] (Figure 2). It should be mentioned that the coils can have an infinite number of different shapes. They can be both flat and cylindrical, which allows significant flexibility when configuring the type of welding that is desired. The capacitor bank contains a transformer that adapts the low-voltage electricity supply to a high-voltage one to charge the capacitor bank.

The capacitor bank is connected to an electromagnetic coil and discharges through it a large current of a few kilo-amps. This discharge creates an oscillating electromagnetic field (Figure 2) that in turn induces currents in the nearby conductive material (the moving plate in the case of this project). The currents in the piece or moving material are those that, when reacting with the oscillating electromagnetic field, generate the Lorentz forces, responsible for the deformation of the piece. In the same way that Lorentz forces are generated, the material is also instantly heated by the Joule effect, but the sheet as a whole does not at any time approach the melting temperature or undergo any metallurgical transformation [18]. These forces generate a deformation at high speed, which causes the deformed part to impact with a very high amount of energy against the part to be welded.

High-speed impact welds have a permanent joint only a few microns wide [18]. The experimental research works developed in MPW are mainly oriented to understand how the micrometer-scale junction is generated.

2.1. Welded Interface

Different studies [18,19] suggested that the temperature generated at the interface due to the impact at high speeds and consequent pressure was well below the melting temperature of the elements to be welded. On the other hand, the formation of intermetallic compounds was considered unlikely, assuming that the welding was induced by the impact pressure and totally ruling out the effect of heating.

A study by Aizawa et al. [20] found evidence of fusion and solidification at the interface of the two welded surfaces, in contradiction to previous postulates. A very high temperature increase was identified in the interface but, due to its instantaneous nature, it was not enough to spread throughout the part and its effect was located in the intermediate layer between the two welded sheets. The welding was considered to be due to the combination of magnetic pressure and heating by the Joule effect. The solid-state reaction at the junction interface could induce the formation of intermetallic phases, with the observation of localized fused points at the junction interface not being common and not being a prerequisite for the formation of intermetallic compounds.

In impact welding, the interface area of the joint shows a wavy morphology, characterized by a pattern similar to “Velcro”, where the two joined plates are mechanically interlocked (Figure 3). This wavy interface occurs with all impact methods. However, the length and amplitude of the waves tend to vary depending on the process by which the weld was performed. Psyk and Raoelison [21,22] associated the wave morphology of the junction with the process parameters of discharge energy and impact velocity.

The works developed by Lee and Li [23,24] in MPW joints of steel and aluminum alloys pointed out the existence of an intermediate layer at the interface of the joint. Research by other groups again found the existence of an inhomogeneous layer at the weld interface [21]. Other researchers such as Zhang et al. [25] raised the existence of concentrations of intermetallic phases in the case of a wavy interface (Figure 4).

When a low-energy discharge is realized for the welding operation, a thin phase of intermetallic is generated. When the energy level of the discharge is increased, the thickness of the intermetallic phase increases, resulting in the generation of cracks, voids, and pores. Psyk [21] presented results in which the existence of micro fractures was confirmed if the selected discharge energy level was too high.

2.2. Outstanding Parameters of the Process

MPW process parameters can be divided into technological parameters (gap, overlap, cantilever, discharge energy or output voltage, discharge pulse frequency, and skin depth), which depend on the equipment used to perform the weld, and physical parameters (impact pressure, velocity, and angle), which are independent of the equipment. An operator can directly modify the technological parameters but not the physical parameters. The geometric parameters (gap, overlap, cantilever) are defined in Figure 5.

2.2.1. Gap Between Joining Surfaces

The gap or distance between the surfaces to be welded is very important. In this space, the launched and moving material (the one closest to the coil) will increase its acceleration after being electromagnetically driven towards the surface against which it will impact and be welded. This parameter affects the collision conditions, the level of impact pressure generated in the same, and, consequently, the formation of the weld. The higher this parameter is, the greater the acceleration and impact pressure reached are. The limiting aspect of the increase in gap resides in the ability to guide the material uniformly during the path between discharge and impact, being able to deflect the moving material and generate the weld in unwanted areas.

2.2.2. Overlap

The overlap is the distance the flyer overlaps with the coil. It is the part where the Laplace forces are generated and that is projected towards the other material to be welded or the target material.

2.2.3. Cantilever

The cantilever is the free length of the flyer that determines the angle of impact.

2.2.4. Discharge Voltage or Energy

Regarding the discharge energy, a command console allows its adjustment, and it is a prominent input parameter. The discharged energy can be expressed as follows:

$$Energy={\displaystyle \frac{1}{2}}C{U}^2$$

(1)

where Energy is the discharge energy (J), C is the total capacity of the generator (F), and U is the discharge voltage (V).

This energy, stored in the capacitors, is channeled into the coil and is responsible for generating an electromagnetic field that is translated into a magnetic pulse in the sheet. The energy required depends on the materials to be welded. To obtain an equivalent bond level, the required level of energy to discharge will be lower for moving materials with low electrical resistivity. The use of an energy level below the threshold marked for each application and its corresponding specific conditions will not generate enough momentum to achieve the joint between the materials. In the case in which the maximum threshold is exceeded, as mentioned above, the thickness of the intermetallic layer increases, generating defects such as cracks, pores, and voids.

2.2.5. Discharge Pulse Frequency

Another very important parameter that defines how much the magnetic field created by the coil penetrates into the material to be accelerated is the frequency of the discharge pulse. The pulse discharge frequency depends on the parameters of the electromagnetic circuit and varies between 10 and 200 KHz. However, it generally operates between 10 and 20 KHz. The frequency is expressed as follows:

$$f={\displaystyle \frac{1}{2\pi }}\sqrt{{\displaystyle \frac{1}{L_t C}}}$$

(2)

where f is the circuit frequency (Hz), L_t is the total circuit inductance (H), and C is the total generator capacitance (F).

High frequencies are generally recommended for high-strength materials. As a consequence, the pulse discharge frequency can be considered as a requirement for the configuration of the generator and, in turn, for the welding machine. In addition, increasing the frequency reduces the impulse time, which increases the stresses on the material and consequently the dynamic response of the material, leading to a collision of greater energy magnitude.

2.2.6. Skin Depth

The magnetic field creates eddy currents in the sheet closest to the coil. The depth to which the field penetrates is called “skin depth” (δ). The interaction of the eddy current with the magnetic field produces the Lorentz forces that accelerate the moving plate next to the coil against the fixed one, causing them to impact. Therefore, without this “skin depth” it would be impossible to carry out the welding. For an effective collision between both materials, the generated depth must be smaller than the thickness of the moving sheet. The lower the field penetration or “skin depth” is, the higher the energy efficiency of the collision generated is. Equation (3) allows us to quantify this depth:

$$\delta =\sqrt{{\displaystyle \frac{\rho }{\pi f \mu }}}$$

(3)

where δ is the “skin depth” (m), ρ is the electrical resistivity of the material in contact with the coil (Ωm), f is the pulse discharge frequency (Hz), and μ is the flyer magnetic permeability (H/m).

2.2.7. Impact Velocity

This parameter depends on the discharge energy and the gap between surfaces. The force generated by the electromagnetic field accelerates the moving part towards the fixed part in the space between them. When dealing with very high energies, one also works with high speeds. These speeds are of great importance not only because of the momentum itself but also because they create an air blast generated due to the fast launch of the material that cleans the surfaces to be welded and prepares the surface for joining. The oxides existing on the two surfaces to be welded are eliminated through the air blast, and this cleaning of the surfaces creates a favorable condition to generate a permanent joint.

Shotri et al. [26] defined a model linking the impact velocity with the geometrical parameters of the inductor (coil) and the process parameters from a dimensional analysis using the Buckingham π theorem:

$$V_i=\left({\displaystyle \frac{Gap}{e_f}}\right)\sqrt{{\displaystyle \frac{P_i}{{\rho }_f}}}$$

(4)

where V_i is the impact velocity (m/s), Gap is the initial stand-off distance between the two parts to join (m), P_i is the impact pressure (N/m²), and e_f and ρ_f are, respectively, the thickness (m) and the density of the flyer (kg/m³).

This dimensional analysis for the impact pressure and flyer impact velocity was developed considering the effect of the related variables and was employed due to the presence of several physical phenomena and their complex interactions, which cannot always be expressed by closed-form mechanistic relationships.

Similar analytical expressions were reported in the literature [27,28]. However, these relations did not consider the effect of the gap [27] and the flyer thickness [28].

2.2.8. Impact Pressure

A unique aspect of high-velocity deformation is that, when two solid bodies collide with significant velocity, very high pressures are created [29]. The impact pressure $P_i,$ developed when two semi-infinitely elastic bodies, called 1 and 2, collide at an impact velocity $V_i$, is given by the equation:

$$P_i={\displaystyle \frac{{\rho }_1 {\rho }_2 C_1 C_2}{{\rho }_1 {C_1+\rho }_2 C_2}} V_i$$

(5)

where P_i and V_i are, respectively, the impact pressure (N/m²) and the impact velocity (m/s), ρ is the density of the material, and $C$ is the longitudinal wave velocity [23] obtained by:

$$C=\sqrt{{\displaystyle \frac{E}{\rho }}}$$

(6)

where $E$ and ρ represent, respectively, the Young’s Modulus (N/m²) and the density (kg/m³) of the materials to join. Values of $C$ are of the order of 3000 m/s for most structural materials. Even at moderate impact velocities, it is easy to develop pressures large enough to produce plastic deformation. But this relation means that the ratio P_i/V_i is always constant and does not depend on the collision angle or the welding parameters.

To consider that a magnetic pulse weld is successful, the maximum pressure must exceed a threshold [12], defined by the following expression:

$$P_{threshold}=5 HEL$$

(7)

where the Hugoniot Elastic Limit (HEL) is calculated as follows:

$$HEL={\displaystyle \frac{1}{2}} \left({\displaystyle \frac{K}{G}}+{\displaystyle \frac{3}{4}}\right){\sigma }_{\mathrm{y}\mathrm{p}}={\displaystyle \frac{(1-\nu )}{(1-2.\nu )}} {\sigma }_{\mathrm{y}\mathrm{p}}$$

(8)

where K is the compressibility modulus, G is the shear modulus, ν is the Poisson’s coefficient, and σ_yp is the yield stress.

From the Buckingham π theorem, Shotri et al. [26] defined the following relation of the impact pressure with the geometrical parameters of the inductor and the process parameters as follows:

$$P_i={\displaystyle \frac{Energy}{{Overlap}^3}} f \left({\displaystyle \frac{{\mu }_f}{\tau }}\right) \left({\displaystyle \frac{e_c l_{oc}}{w_c^3 l_{rc } L_t}}\right)$$

(9)

where P_i is the impact pressure (N/m²); Energy is the discharged energy (Equation (1)) provided by the generator (J); f is the discharge pulse energy (Hz) (Equation (2)); Overlap is the distance the flyer overlaps with the coil (m) (Figure 5); μ_f and τ are the magnetic permeability (H/m) and the damping constant (s⁻¹) of the flyer; e_c, w_c, l_oc, and l_rc are the thickness (m), width (m), and the active and non-active segments of the flat coil (m); and L_t is the total inductance of the system (H). By using Equation (2) and eliminating L_t, the expression of P_i is:

$$P_i={\displaystyle \frac{Energy}{{Overlap}^3}} f^3 \left({\displaystyle \frac{{\mu }_f}{\tau }}\right) \left({\displaystyle \frac{e_c l_{oc}}{4{\pi }^2 l_{rc } C}}\right)$$

(10)

where C is the capacity of the system (F).

2.2.9. Impact Angle

The impact angle is the angle that the materials form at the point of impact. The angle in Figure 5 is given as the value γ. At the point of contact, a shock wave is created in the two materials in the radial direction. This shock wave creates the previously mentioned jet of air that cleans the surface to be welded.

$$tan\left(Impact angle\right)=tan(\gamma )={\displaystyle \frac{Gap}{Cantilever-Overlap}}$$

(11)

where Gap is the stand-off distance between the parts to join (m), Cantilever is the free length of the flyer (m), and Overlap is the distance the flyer overlaps with the coil (m) (Figure 5).

2.3. Process Window

To determine the welding parameters, it is possible to build a weldability window that can be called a process window. If the machine, the tool, the assembly, the welding configuration, and the materials to be welded are to be defined, this consists, for example, in finding, in the plane (discharge energy, gap), the points that make it possible to carry out a consistent weld [30,31]. These weldability windows are generally obtained by means of numerous tests. While the practical value of these weldability windows is obvious, the fact remains that they are difficult to transfer from one configuration to another. In this context, it may be relevant to construct weldability zones that are functions only of the materials to be assembled and not of the welding configurations.

To construct these physical weldability windows, some authors use simplified analytical models from the explosion welding literature [1], while others attempt to determine them directly by means of tests [32,33]. Experimentally, it is very difficult to directly construct these magnetic pulse weldability windows. In fact, the impact angle and the impact velocity constantly change from the start to the end of the weld, unlike explosion welding, which allows welding conditions to be maintained by controlling the triggering of explosives.

To overcome this difficulty, Groche et al. [34,35] proposed an experimental setup that allows the velocity and impact angle of two material samples to be controlled and varied separately. More recently, Lee et al. [23] proposed using 16 Photon Doppler Velocimetry (PDV) probes to directly measure the change in impact velocity and impact angle during collision welding.

Psyk [9] studied the influence of important adjustable process parameters on the impacting velocity and impacting angle of the joining partners in order to allow a target-oriented process and joint design based on welding windows, which refer to these collision parameters. Additionally, the influences of the adjustable process parameters on the weld quality characterizing the parameters were analyzed. It was concluded that, although welding windows are a valuable tool for selecting reasonable ranges for the process parameters, detailed knowledge about the specific influence of the parameters is indispensable for designing an optimized process.

The bibliography agrees that the definition of the MPW process window is difficult to obtain and specific to the machine and the materials. Weldability depends on the geometry parameters and is specific for each inductor design. However, there is an interesting approach for the welding window, used in explosive welding (EXW), that shows the viability of the process as a function of the impact angle and the impact velocity (Figure 6) [36,37]. Although the exact same factors of wave formation or transition velocity do not apply for MPW, it is a useful tool to determine where the weld will take place.

Collision parameter-based welding windows can be a powerful tool in the design of MPW processes because they are independent from the individual equipment or setup. It was the objective of this work to quantify welding windows for MPW based on the determination of impact pressure, impact velocity, and impact angle. However, their use in practice is complicated because collision parameters cannot be directly adjusted.

3. Materials and Methods

3.1. Materials

Typical materials from the automotive industry were used: AA6082-T6 aluminum alloy (Alu-Stock, Lontana Group, 01015 Vitoria, Spain) and HC420LA low-carbon steel (Vinco, Lontana Group, E-48195 Larrabetzu, Spain). Their properties can be seen in

Table 1. Chemical composition and properties of HC420LA steel. Reprinted from Ref. [38].

	C	Si	Mn	P	S	Al	Nb	Ti
% maximum and minimum by weight	0–0.1	0–0.5	0–1.6	0–0.025	0–0.025	0–0.015	0–0.09	0–0.15
Ultimate Tensile Strength		Yield Tensile Strength			Elongation at Break
470–590 MPa		420–520 MPa			≥17%
Sound speed within the material		3220 m/s			Density		2700 kg/m3

and

Table 2. Chemical composition and properties of AA6082-T6. Reprinted from Ref. [39].

	Si	Fe	Cu	Mn	Mg	Cr	Ti	Other
% maximum and minimum by weight	0.7–1.30	0–0.5	0–0.1	0.4–1.00	0.60–1.20	0–0.015	0–0.09	0–0.15
Ultimate Tensile Strength		Yield Tensile Strength			Elongation at Break		State
290 MPa		250 MPa			10%		T6 at 20 °C
Yield Strength		200 °C			300 °C		400 °C
		240 MPa			132 MPa		65 MPa
Poisson’s coefficient		0.33			Density		2700 kg/m3
Sound speed within the material		3040 m/s

[38,39].

The electromagnetic pulse welding tests were carried out using lapping 50 × 25 × 1 mm³ steel and aluminum specimens. The tests were carried out at the Innovaltech platform in Saint Quentin, France. The equipment used was a 9 Kv/25 kJ (690F) PULSAR MPW system, which provides an impulse current between 250 and 550 kA, a pseudo-frequency in the range of 16 to 18 kHz, and an output voltage between 4 and 9 kV. This system was connected to the coil and to the clapping system in which the steel and aluminum plates that were going to be joined were located. A flat electromagnetic coil was designed for the experiments (Figure 7) due to the nature of the joint to be made. In order to isolate the current discharge through the coil from the metallic elements of the system, the electromagnetic coil was embedded in a block of G10, a laminated material made with fiberglass and epoxy resin whose most outstanding properties for the present application are high mechanical resistance and electrical insulation. This figure also shows the connections required by the coil for its connection to the capacitor bank and the actuator zone. This last area was where the moving plates were positioned and where the magnetic pulse would be generated.

3.2. Process Parameters

Figure 8 schematically shows the three stages that occur in a magnetic pulse welding operation. In the first place, there is the stage prior to the pulse, where the assembly of the different elements of which the system is made up is carried out. In the lower part, the electromagnetic coil will be located. Next, in our case, an AA 1100 aluminum alloy pushing plate was introduced with the same dimensions as the mobile plate or flyer but with a lower electrical resistivity (2.99 × 10⁻⁸ Ωm compared to 0.038 × 10⁻⁶ for the AA6082-T6 alloy). The use of a pusher improves the energy efficiency of the pulses and its use is recommended for applications in which the energy levels required are high, approaching the maximum capacity of the capacitor bank. The limitation in these tests was set by the capacity of the capacitor bank, and the use of a pusher in the tests was necessary. The mobile elements of the experimental tests were the pusher and the mobile plate or flyer made of AA6082-T6. The latter is defined as mobile because it has a lower weight than the steel one and, through the same impulse, the impact speed to be reached will be greater. The HC420LA steel sheet was kept fixed by means of a mooring system.

The two mobile plates were placed on the electromagnetic coil and positioning gauges on the AA6082-T6 plate (first step in Figure 8). The gauges, in addition to maintaining the necessary clearance or distance between the fixed HC 420 LA steel sheet and the AA6082-T6 mobile sheet, fixed the overlap between both sheets. The gap between the two sheets allowed the moving sheet to be accelerated and a higher impact speed to be reached, which translated into a higher impact mechanical pressure.

The second stage of Figure 8 presents a state after the electromagnetic discharge. The pusher plate underwent a repulsion with respect to the coil and pushed the AA6082-T6 plate, accelerating it until it impacted against the fixed steel plate. This impact is what generates significant pressure and allows a solid-state union.

The third stage, the final situation, reproduced the state of the system after the impact. The two sheets that were impacted were permanently joined, and the pusher returned to its original position on the electromagnetic coil.

Three main parameters were studied: discharge energy, gap (distance between sheets), and overlap distance. To establish the process window, experiments were carried out combining the different parameters (

Table 3. Design of experiments for pulse magnetic welding of AA6082-T6 and HC420LA stacks.

Energy (kJ)	5.52	6.99	8.03	10.44	12.42	14.58	16.91	19.41	22.08	24.93	27.95
Gap (mm)	1	1.5	2	2.5	3
Overlap (mm)	6	7	8

). Two kinds of welding windows were proposed, in 2D and 3D diagrams: one based on process parameters (gap, overlap, mean energy, or output voltage) and the other based on collision parameters (pressure, velocity, and impact angle). The collision angle was calculated based on geometrical principles. Measurements with an optical device verified the calculations. The specimens were cut and prepared for the metallographic analysis with an optical microscope.

The discharge energy, gap, and the overlap between plates (Table 3) were analyzed and impact parameters (pressure, velocity, and angle) were calculated from Equations (4), (10) and (11) [26].

3.3. Microstructure Analyses

Micrographic analyses by optical microscopy and/or scanning electron microscopy were carried out in order to highlight the type of adhesion between the two materials (straight or wavy) and the presence of intermetallic compounds and to determine the length of the welded zone (Figure 9).

3.4. Weld Specific Energy Determination

In order to determine the specific adhesion energy of the weld, shear tests were performed using a device developed by Torregaray et al. [40] for material stacks (Figure 10). The specific adhesion energy was determined by integrating the tension force vs. displacement curve and was related to the area of the welded section. The welded area was measured using a Leica DCM 3D confocal microscope.

4. Results

The results of the tests carried out are reported in Appendix A. For each of the 136 test pieces produced, the process parameters used (gap, overlap, cantilevered, voltage, mean energy), the associated physical parameters (impact pressure, impact velocity, and impact angle), the result of the test (welded or not), and the cohesion energy of the weld were indicated. Out of 136 trials, 73 resulted in successful welding (53.7% success rate). The success rate varied significantly with different combinations of the process parameters.

4.1. Process Window Based on Technological Parameters (Output Voltage and Impact Angle)

Smaller gaps (1 mm and 1.5 mm) generally resulted in more successful welds compared to larger gaps (2 mm, 2.5 mm, and 3 mm). For example, with a 1 mm gap, the success rate was higher compared to a 3 mm gap. Overlap values of 6 mm and 7 mm showed better welding results compared to 8 mm. Consistent overlap seemed to be crucial for successful welding. Cantilevered distances of 9 mm and 10 mm were more frequently associated with successful welds. The data suggested that a cantilevered distance of 11 mm was less effective. Higher voltages (8 kV, 8.5 kV, and 9 kV) generally resulted in more successful welds. Lower voltages (5.5 kV, 6 kV, and 6.5 kV) often led to unsuccessful welds. Higher mean energy values (above 20 kJ) tended to result in successful welds. Lower mean energy values (below 15 kJ) often led to unsuccessful welds. For process parameters, the classical welding windows were performed with two variables, collision angle and output voltage or mean energy [1] (Figure 11). For this combination of stacks (HC420LA/AA6082-T6), a typical zone existed where 100% of the samples were welded. A higher output voltage or mean energy was required for welding when the impact angle was low. Similarly, for low average energies and low impact angles, or for high average energies associated with high impact angles, the weld was not realized. This type of process window was dependent on the welding equipment used and, therefore, could not be transposed to other MPW equipment or devices.

4.2. Process Window Based on Physical Parameters

This representation allowed us to visualize the effects of the three physical parameters, speed, pressure, and impact angle, without there being any confusion about different conditions but which ultimately would coincide at the same point of the diagram as in the case of the process window based on the parameters’ impact angle versus output voltage (Figure 12).

High-impact velocities (above 1000 m/s) tend to result in successful welds. Impact angles around 18.43° and 26.57° are more frequently associated with successful welds compared to 33.69° and 45°.

4.3. Process Window Including Adhesion Specific Energy of the Weld

Results of adhesion specific energy are shown in Appendix A. Isovalues of specific adhesion energy are pointed out in Figure 13 and Figure 14. They allowed us to determine the area of the two windows where the process was stable and robust. Successful welds have a wide range of weld specific energy values, but higher values (above 150 kJ/m²) are more common in successful welds.

5. Discussion

5.1. Process Window Based on MPW Technological Parameters

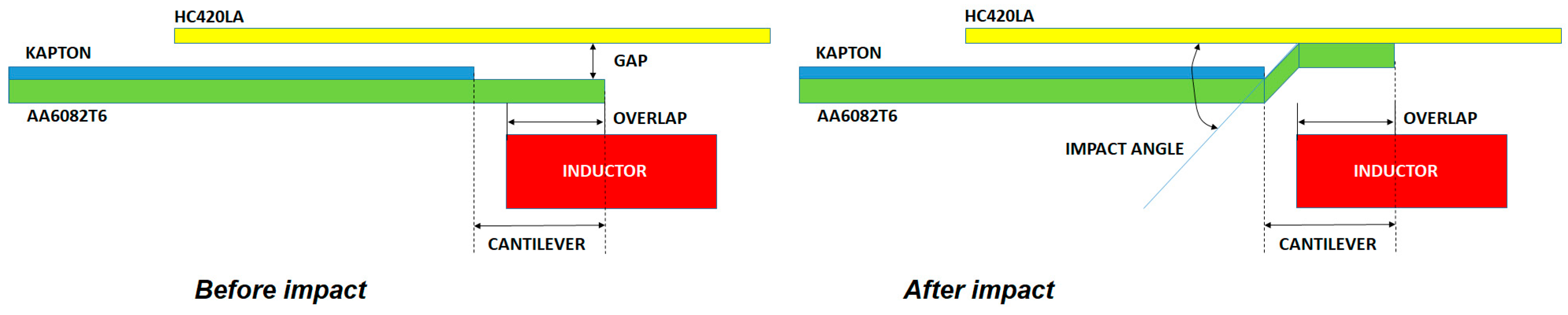
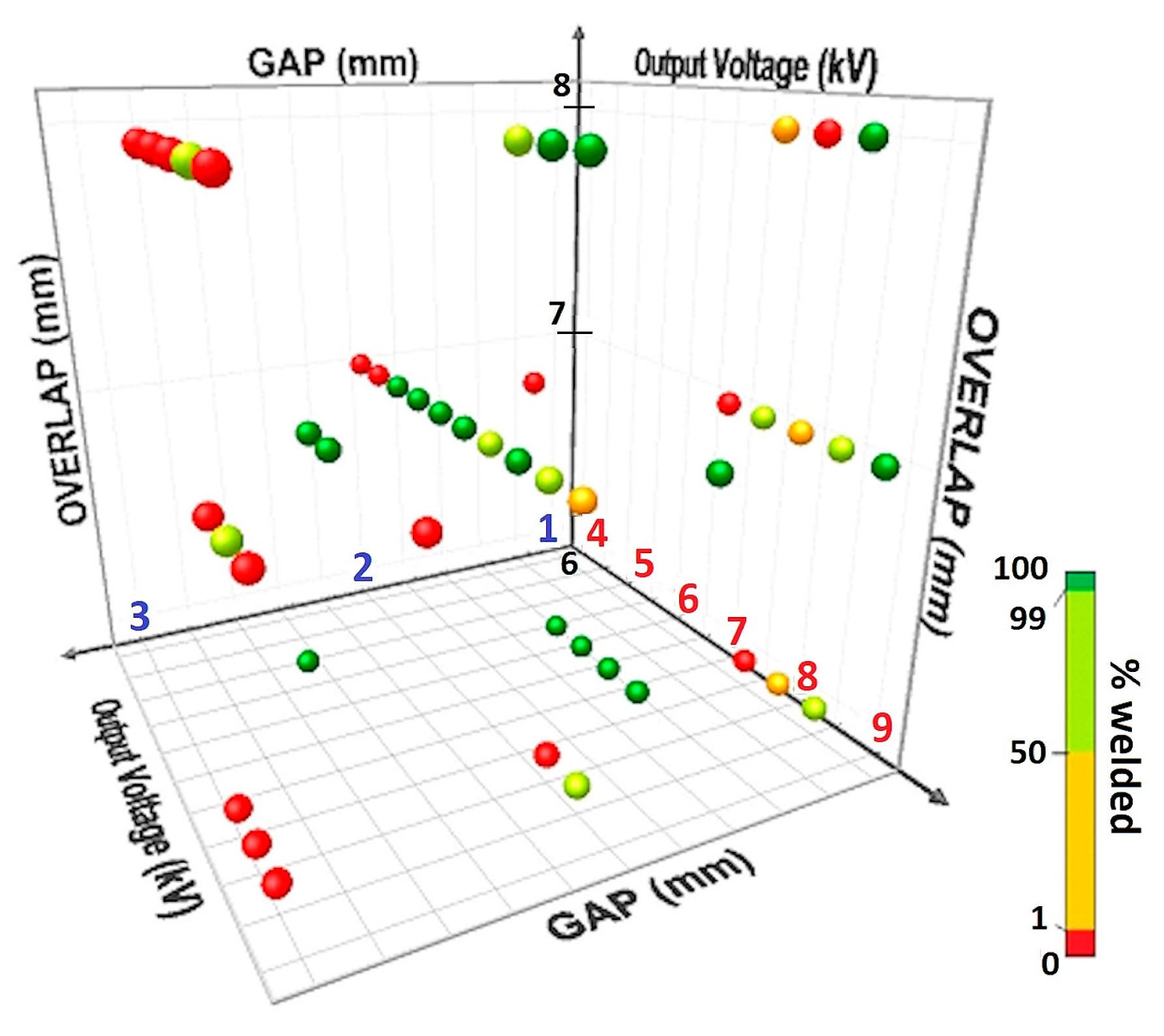
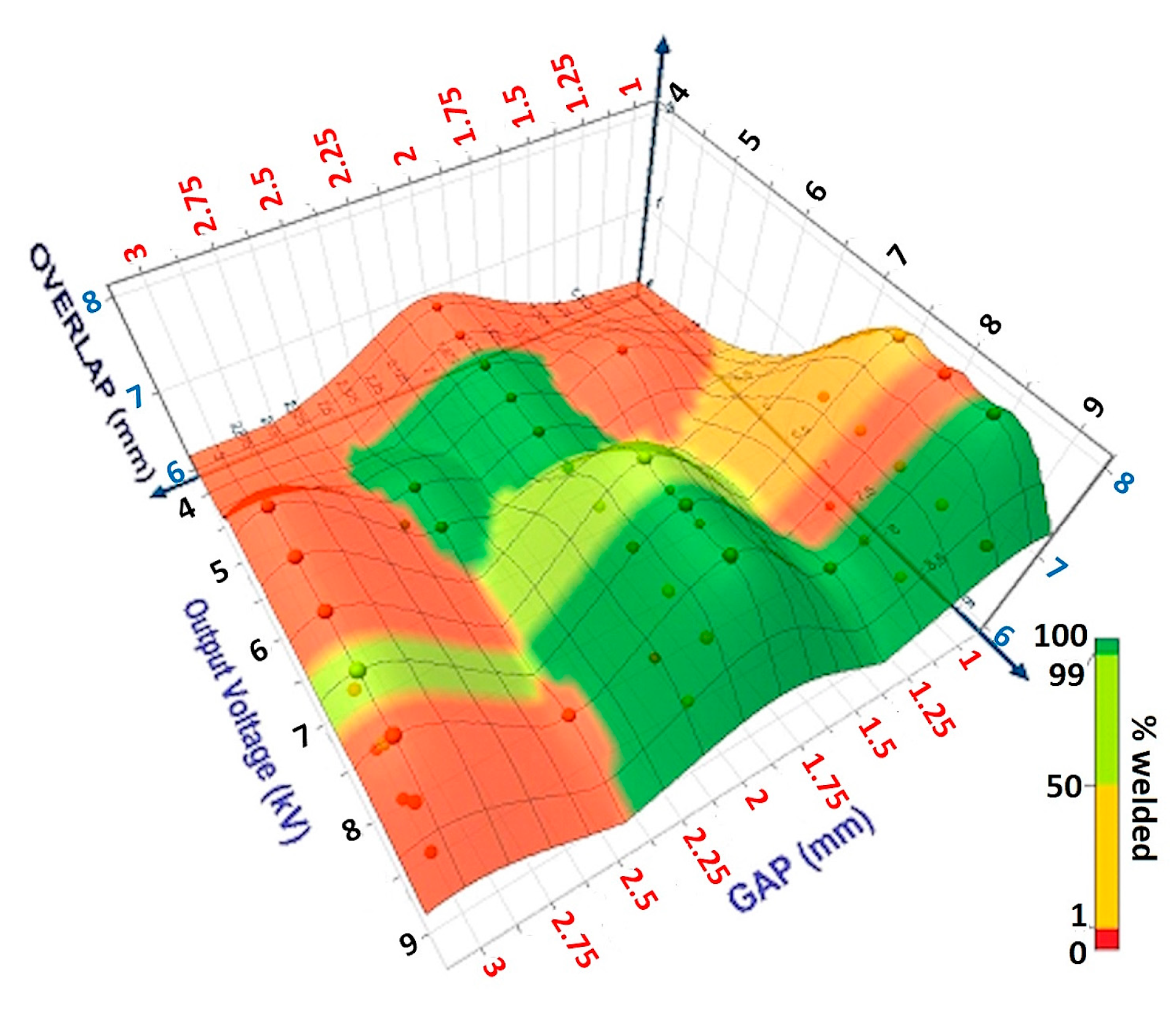
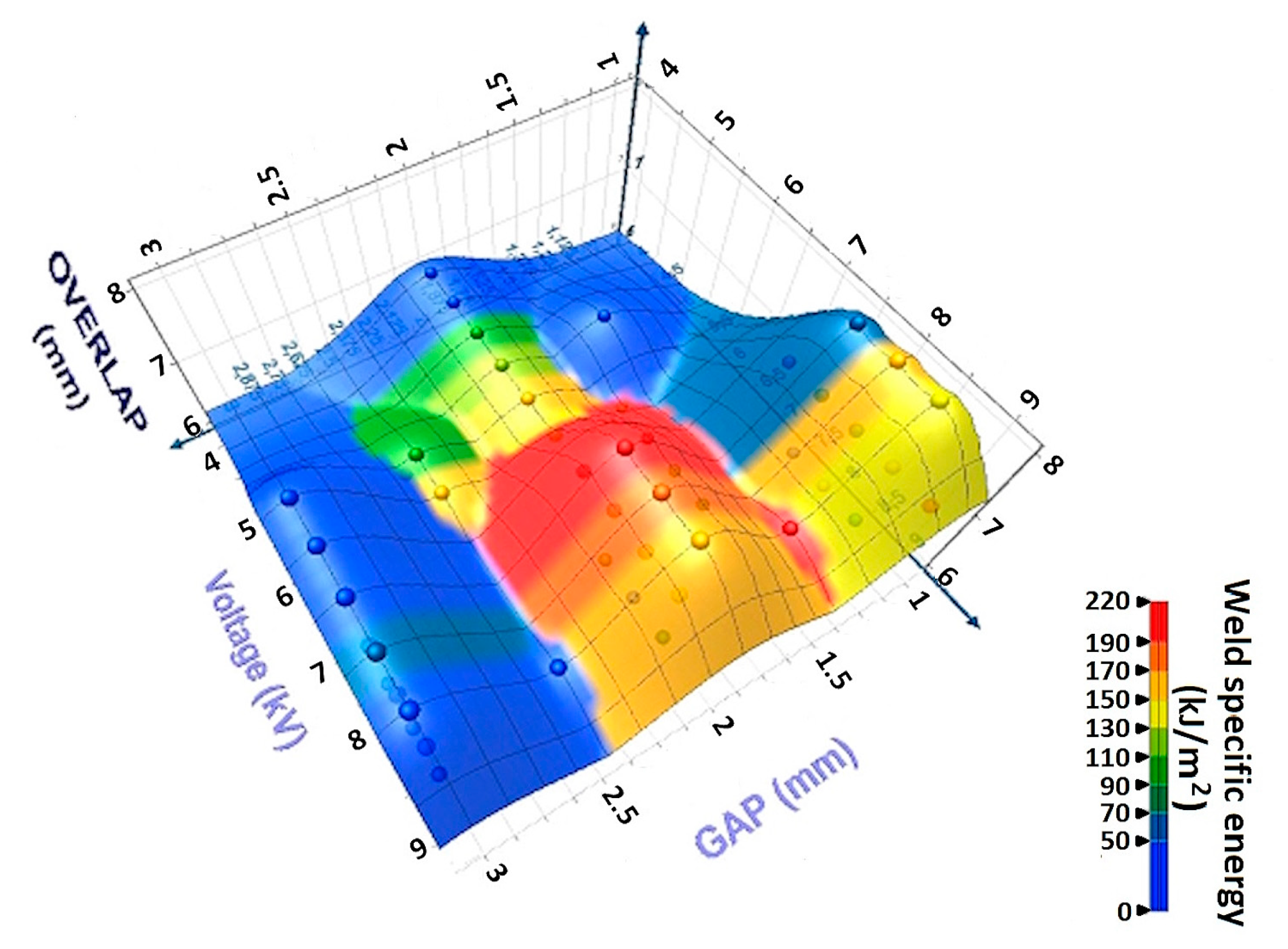
The combination of two parameters gave no real information about the weldability of this process, since different combinations of gap, overlap, and cantilevered can give the same impact angle. A three-parameters window, on the other hand, showed more information (Figure 15) and clearly pointed out the region where the combination of the three parameters (gap, overlap, and output energy) allowed us to reach 100% of the welded samples. However, this type of process window is, again, dependent on the equipment used and cannot be transposed to equipment where the inductor has a different geometry, the LRC circuit has other characteristics, etc. On the other hand, these parameters are directly programmed on the equipment and, therefore, easier to implement at the level of the process. The 3D representation allowed us to point out different parameter combinations where the process was stable and reached 100% of welded samples.

To generate the visualizations, XLSTAT was used. This is a statistical toolbox for Microsoft Excel that significantly extends Excel’s data analysis capabilities. The figures employ “4D plots” as a multivariable visualization technique. They are structured as follows. The three spatial dimensions (X, Y, Z axes) represent three different quantitative variables from technological or physical process parameters. Each sphere in 3D space (fourth dimension in color) represents an additional quantitative variable. In this case, the color tone encodes the numeric outcome of the welded joint’s success or failure.

The technique typically used by XLSTAT to generate surface plots is Inverse Distance Weighting (IDW) interpolation [41]. IDW is a spatial interpolation method that estimates values at unsampled locations based on known data points, assuming that closer points exert more influence. This technique is more computationally efficient than 3D splines, has better handling of irregularly spaced data, and produces visually smooth and interpretable surfaces.

The bibliography does not mention overlap as a factor since most research was performed in a whole overlap configuration. However, if the purpose of the weld is to use it in BIW, a partial overlap is needed to be taken into account. The results showed the importance of overlap in the consideration of the welding first requirement. An analysis of variance (ANOVA) was made for both approaches (process parameters and impact parameters) concerning the percentage of welded stacks depending on the input parameters (technological or physical). The chosen model was a multiple linear regression model including the effects of (i) the main parameters, (ii) the two-by-two interactions of these parameters, and (iii) the quadratic effects of the main parameters. The analysis of variance was repeated until a model was obtained where all the parameters were significant (risk < 10%) with a regression coefficient greater than 0.9. The results for the process parameter approach pointed out the significance of the gap and the interactions between gap and overlap, gap and energy, and overlap and energy (

Table 4. Analysis of variance for the model with technological parameters related to the prediction of percentage of welded parts of HC420LA with AA6082-T6.

Variable		Coefficient			Standard Deviation	t-Value	Risk %
Gap		440.7042			79.7975	5.5228	0.00
Overlap		−89.8196			24.7820	−3.6244	0.08
Gap × Output Voltage		−30.7584			8.2800	−3.7148	0.06
Overlap × Output Voltage		24.2372			5.1067	4.7462	0.00
Output Voltage2		−7.4578			2.3220	−3.2119	0.25
Gap2		−53.5699			10.5086	−5.0977	0.00
Overlap2		−6.9997			3.1064	−2.2534	2.95
Source	Square Sum		DoF	Mean Squares		F-Value	Risk %
Regression	173,536.0837		7	24,790.8691		27.3464	0.00
Résiduals	38,075.0363		42	906.5485
Total	211,611.1200		49	4318.5943
				Regression coefficient R=		0.9056

). This confirmed the importance of the three parameters and that the collision angle, which took into account the gap and the overlap, was not sufficient to properly define the viability zones of the process since different combinations of gap and overlap can result in the same impact angle.

The regression model showed excellent predictive capability with an R-value of 0.9056, indicating that approximately 82% of the variance in welding success percentage is explained by the technological parameters included in the model. The overall F-value of 27.35 with essentially zero risk confirmed the model was highly statistically significant.

Gap emerged as the most influential parameter, with a large positive coefficient (440.7) and the highest t-value (5.52). This suggests that increasing the gap between materials significantly improves welding success, though this effect is moderated by the negative quadratic term (−53.57), indicating an optimal gap distance beyond which performance declines.

Overlap showed a negative linear effect (−89.82) but a positive quadratic component, suggesting a U-shaped relationship where very small or very large overlaps may be detrimental, with an optimal intermediate range.

Output voltage demonstrated a complex relationship through its interactions and quadratic term. The negative quadratic coefficient (−7.46) suggested diminishing returns or an optimal voltage level.

The model revealed important parameter interactions, including:

• Gap × Output Voltage showed a negative interaction (−30.76), meaning higher voltages may reduce the beneficial effect of increased gap.
• Overlap × Output Voltage showed a positive interaction (24.24), suggesting these parameters work synergistically.

The significant quadratic terms for Gap and Output Voltage, combined with the interaction effects, indicated that this magnetic pulse welding process had well-defined optimal operating windows rather than simple linear relationships. The negative quadratic terms suggested that excessive values of key parameters can be detrimental to welding success.

The low residual variance (906.5) relative to the total variance indicated a good model fit, making this analysis valuable for process optimization and quality control in industrial applications.

5.2. Process Window Based on MPW Physical Parameters

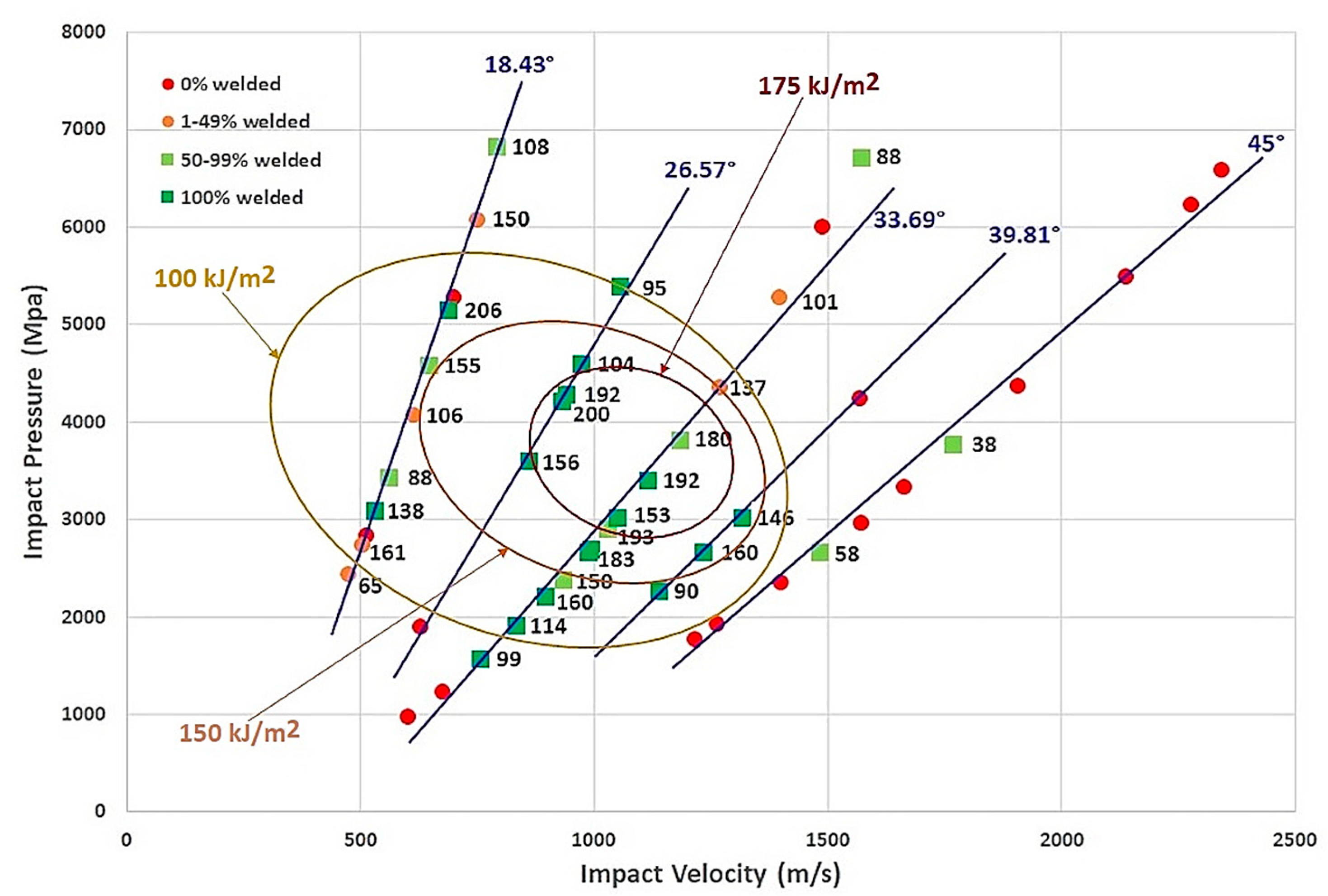
Referring to the works cited above [26], which are based on a physical approach to the MPW process, the parameters that really controlled the weld generation between the two materials were the impact pressure, the impact velocity, and the impact angle. These parameters were independent to the process implemented to perform the MPW and, therefore, allowed us to define a window of the process independently of the MPW equipment used. The only problem was linking these three impact parameters to the different process parameters (gap, overlap, mean energy, frequency, voltage, etc.).

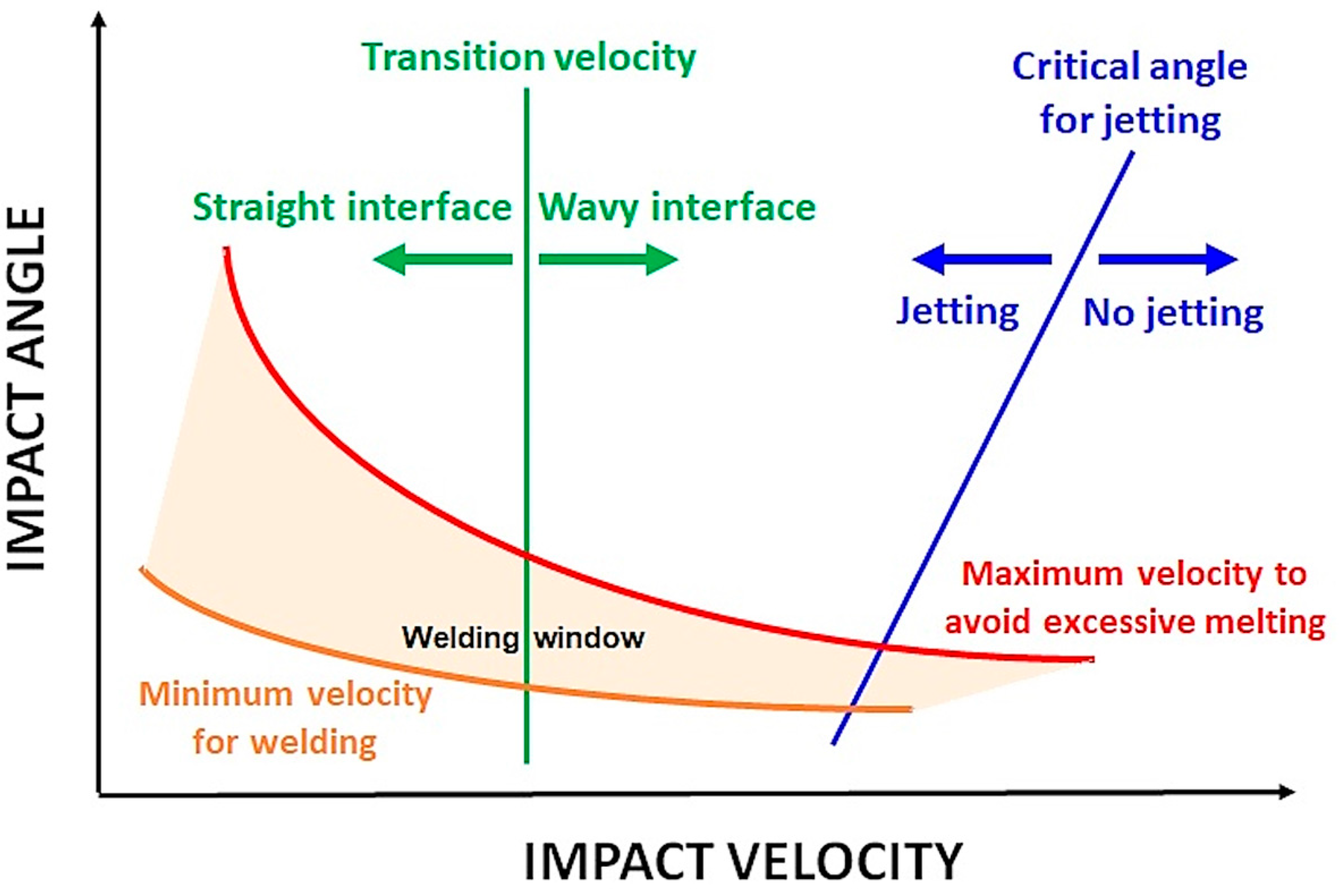
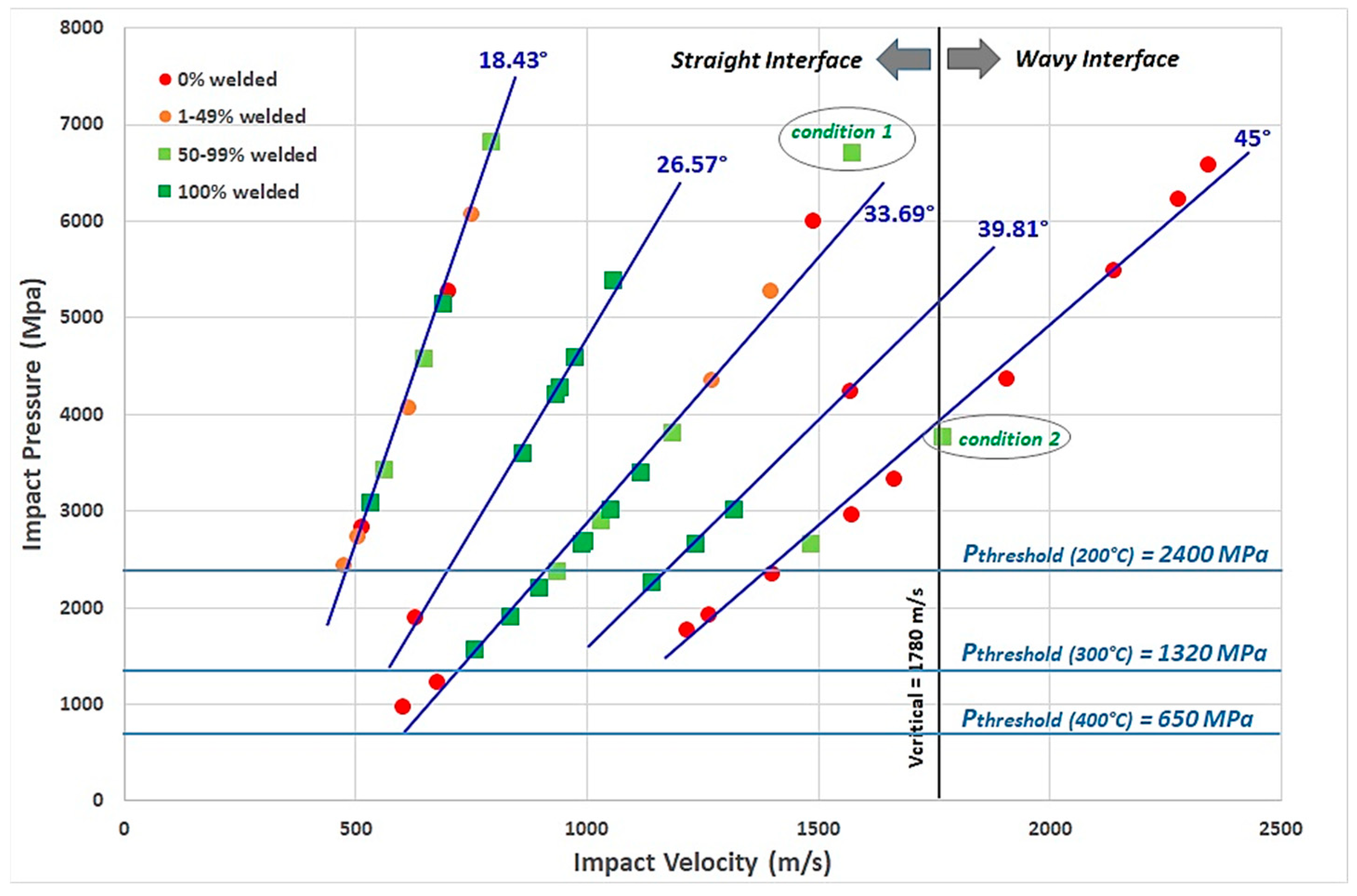
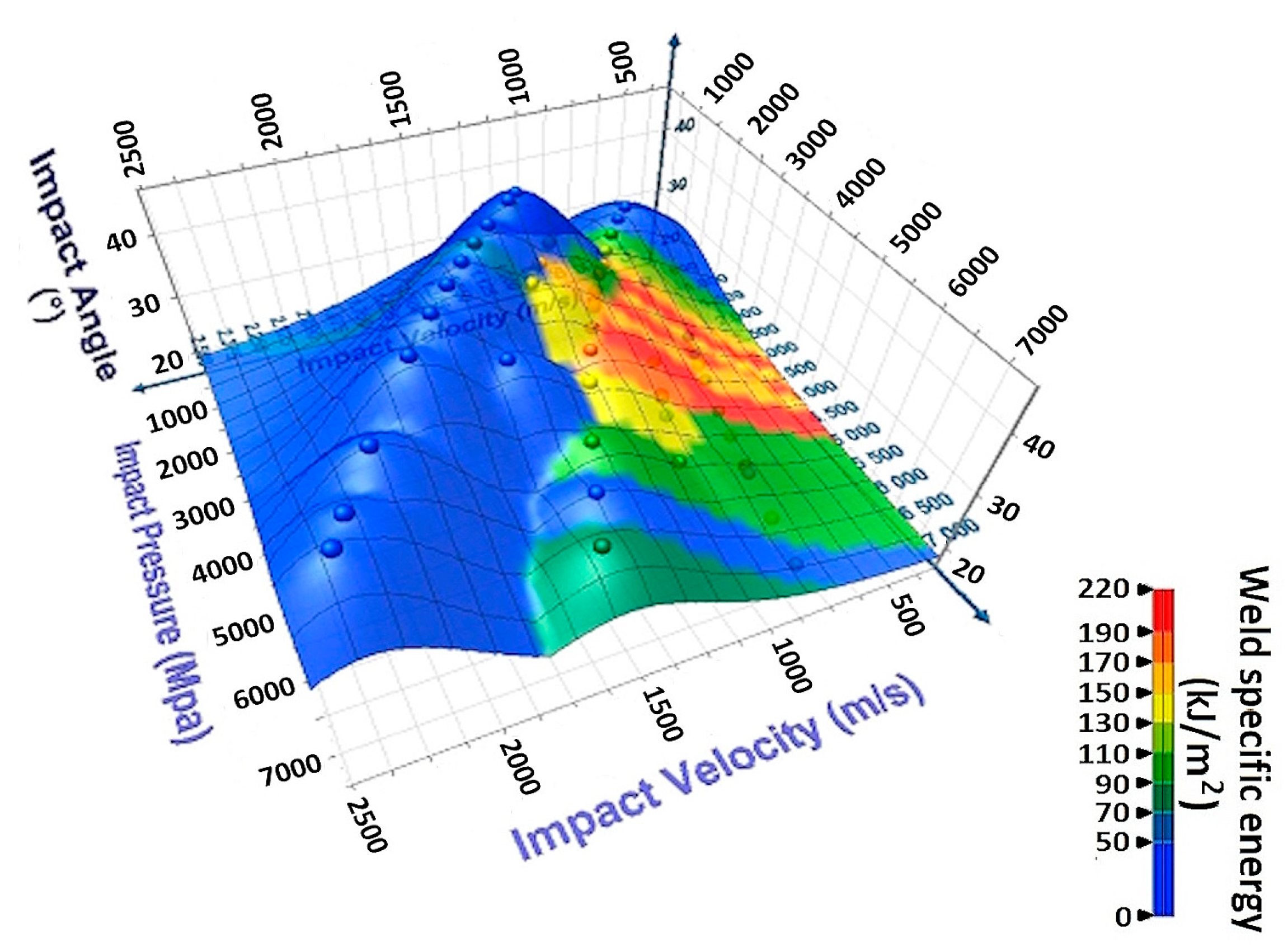
They also allowed us to define different thresholds, guaranteeing the quality of the weld: critical impact speed for a straight or wavy welded interface, threshold pressure to weld the two materials, critical impact velocity to obtain the jetting phenomenon, etc. (Figure 12).

In order to promote the phenomenon of jetting, the collision has to be subsonic compared to the speed of sound in the flyer material. In the case of AA6082-T6, the sound speed in the material was around 3040 m/s. In all the tests, this value was not overcome, which means that the condition of jetting, the ability to clean the surface of both materials, was reached.

The waving morphology of the interface is also a characteristic of high-impact welding processes. This is due to the transition from a laminar to a turbulent flow of the flyer material during the collision. Cowan and Carpenter [42] developed an analytical formula for explosive welding for determining this critical velocity, Vc, by linking wave formation to fluid flow around an obstacle.

$$V_c=\sqrt{{\displaystyle \frac{2.R_{e trans}.(H_{6082T6}+H_{HC420La})}{({\rho }_{A6082T6}+{\rho }_{HC420La})}}}$$

(12)

where R_{e trans} is the critical Reynolds number for transitioning from a laminar to a turbulent flow (~8.9 for aluminum alloys [42]), H is the Vickers hardness (46 HV at 400 °C for A6082 used in this study), and ρ is the density (2700 kg/m³ for A6082 and 7800 kg/m³ for HC420LA). The flyer velocity overcomes a critical collision velocity required for a shear instability to develop for MPW [43]. The value obtained from the experiments and from Equation (12) are in agreement (1780 m/s). Figure 16 points out this difference in hydrodynamic regime for two conditions (noted as condition 1 and condition 2 in Figure 12), where welding was achieved around this critical velocity.

According to Kapil and Sharm [13], the threshold pressure necessary for welding the two plates is defined by Equations (7) and (8), and, using the data in Table 2, we can estimate this minimum pressure being 2400, 1320, and 650 MPa for a temperature of the flyer in the impacted zone, respectively, of 200, 300, and 400 °C.

Kolsky [29] pointed out a linear relation of the impact pressure with the impact velocity (Equation (5)) depending only on the characteristics of the two materials to be welded (density and speed of sound in each of them). Figure 12 confirms this trend by highlighting the important role of the impact angle, with a Pi/Vi ratio which decrease when the impact angle increases (

Table 5. Relation among impact pressure, velocity, and angle.

Impact Angle	18.43°	26.57°	33.69°	39.81°	45°
Pi/Vi (N.s/m3)	13.573 × 106	7.950 × 106	5.902 × 106	4.723 × 106	4.288 × 106
	Pi/Vi = [28.895 × tan2(γ) − 51.601 × tan(γ) + 27.240] × 106 R2 = 0.9845
Pi/Vi (N.s/m3)	6.186 × 106 (from Equation (5))

).

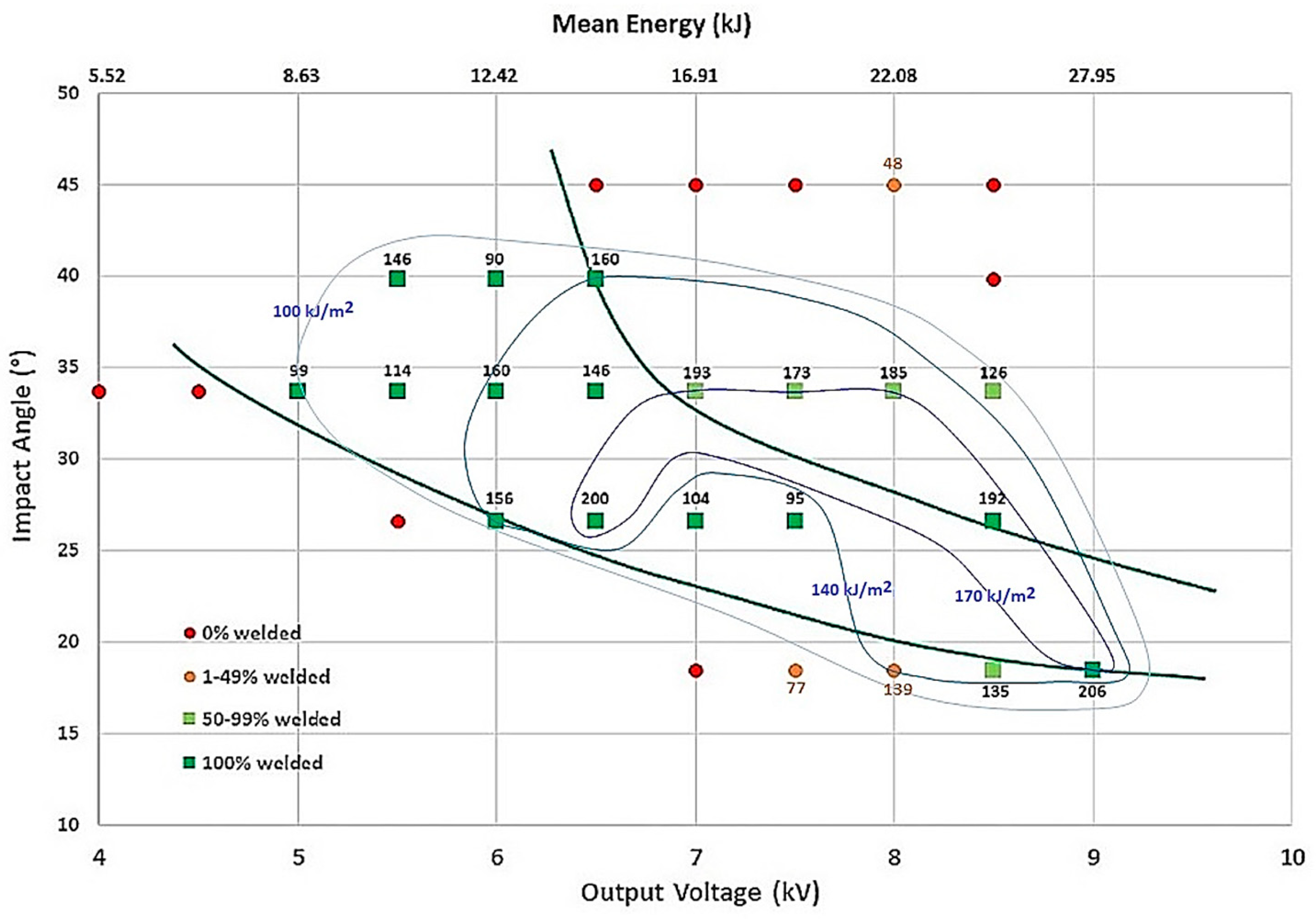
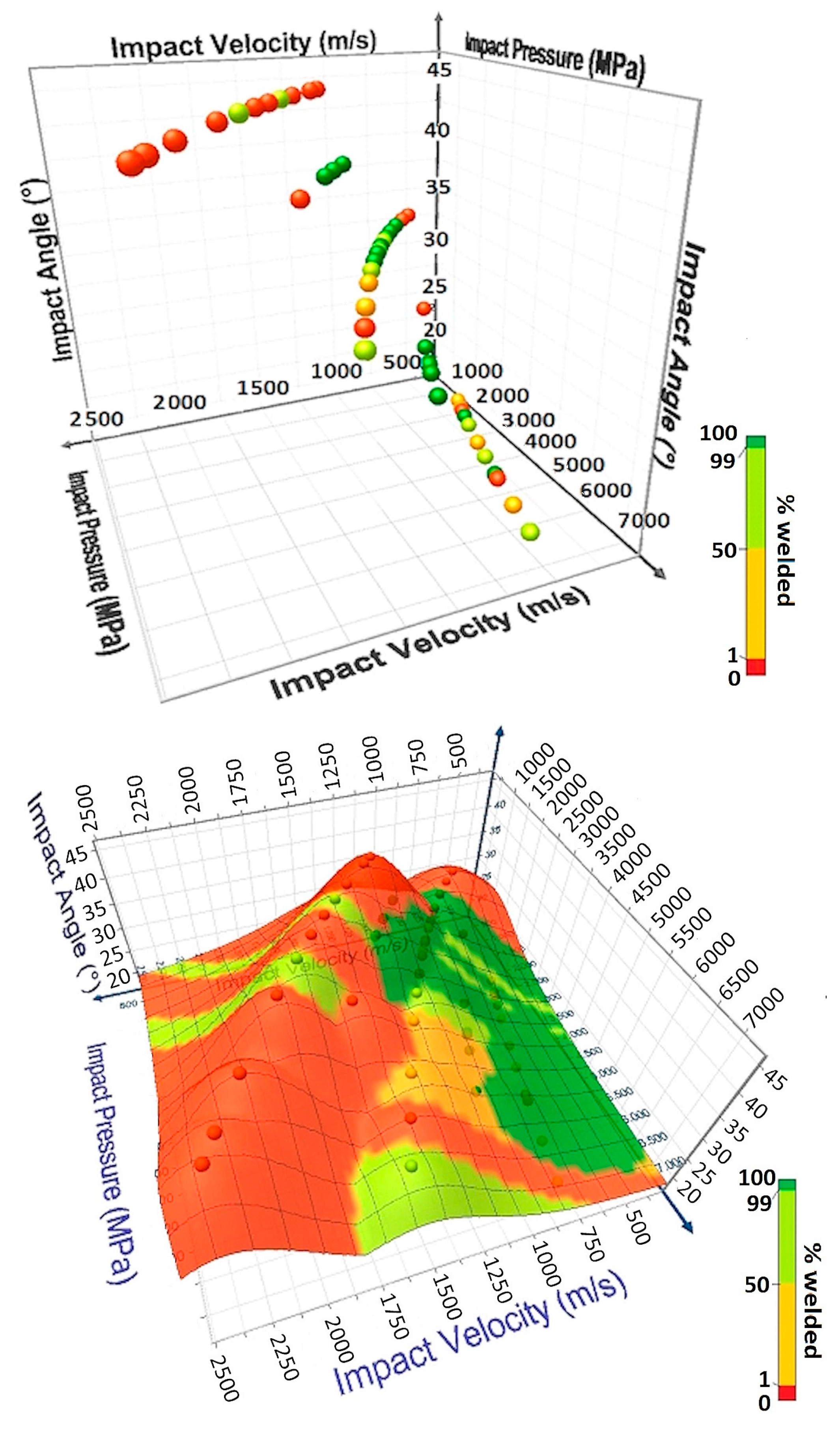
The three-dimensional process window considering the impact parameters is shown in Figure 17. Here, again, two zones can be pointed out where the process was stable and 100% of the welded samples were successfully achieved.

The analysis of variance of the results confirmed that the impact pressure, the impact velocity, and the interaction between impact velocity and impact angle were the significant parameters of the process (

Table 6. Analysis of variance for the model with impact parameters related to the prediction of percentage of welded parts of HC420LA with AA6082-T6.

Variable			Coefficient		Standard Deviation	t-Value	Risk %
Impact Pressure			−0.1945		0.0472	−4.1211	0.02
Impact Velocity			5.8905		1.2237	4.8136	0.00
Impact Angle			−71.0335		17.0303	−4.1710	0.02
Impact Pressure × Impact Angle			−0.0158		0.0036	−4.4333	0.01
Impact Velocity × Impact Angle			−0.1133		0.0263	−4.2997	0.01
Impact Pressure2			0.0000		0.0000	2.9856	0.48
Impact Velocity2			0.0007		0.0002	3.6998	0.06
Impact Angle2			1.3786		0.4313	3.1961	0.27
Source	Square Sum	Degree of Freedom		Mean Squares		F-Value	Risk %
Regression	167,332.3338	8		20,916.5417		22.4106	0.00
Residuals	37,333.2262	40		933.3307
Total	204,665.5600	48		4263.8658
				Regression coefficient R=		0.9042

). This confirmed the results of the bibliography, where it was specified that a minimum pressure is necessary to ensure welding and that a critical speed defines the type of interface obtained (straight or wavy) and highlights the importance of the impact velocity associated with the collision angle. The impact velocity necessary to generate sufficient impact pressure for welding is intrinsically related to the angle at which the collision occurs.

This impact parameter model demonstrated similarly excellent predictive capability with an R-value of 0.9042, explaining approximately 82% of the variance in welding success percentage. The F-value of 22.41 with zero risk confirmed strong statistical significance, indicating that impact parameters are crucial determinants of welding success.

The impact velocity showed the strongest positive influence (coefficient: 5.89, t-value: 4.81), indicating that higher impact velocities significantly improve welding success. The positive quadratic term (0.0007) suggested this beneficial effect continued to increase, though at a diminishing rate.

The impact pressure exhibited a negative linear effect (−0.1945) but with a small positive quadratic component, suggesting an optimal pressure range where too little pressure is ineffective but excessive pressure may also be detrimental to weld quality.

The impact angle demonstrated a strong negative linear coefficient (−71.03) with a positive quadratic term (1.38), indicating a U-shaped relationship. This suggests there was an optimal impact angle, with performance declining as angles deviated significantly from this optimum in either direction.

The model revealed two important negative interactions, as follows:

• Impact Pressure × Impact Angle (−0.0158): higher pressures became less effective at certain angles.
• Impact Velocity × Impact Angle (−0.1133): the benefits of higher velocity were reduced at certain impact angles.

These interactions suggest that parameter optimization must consider the combined effects rather than individual parameter optimization.

The dominance of impact velocity as a positive factor, combined with the complex angle-dependent interactions, indicated that achieving optimal collision dynamics is critical for successful magnetic pulse welding. The negative interaction terms suggested that there are specific combinations of pressure, velocity, and angle that maximize welding success. Interestingly, this impact parameter model (R = 0.9042) performed nearly as well as the technological parameter model (R = 0.9056), suggesting that both the setup parameters and the resulting impact dynamics are equally important for predicting welding success. The similar residual variances indicated both models captured the essential physics of the welding process effectively.

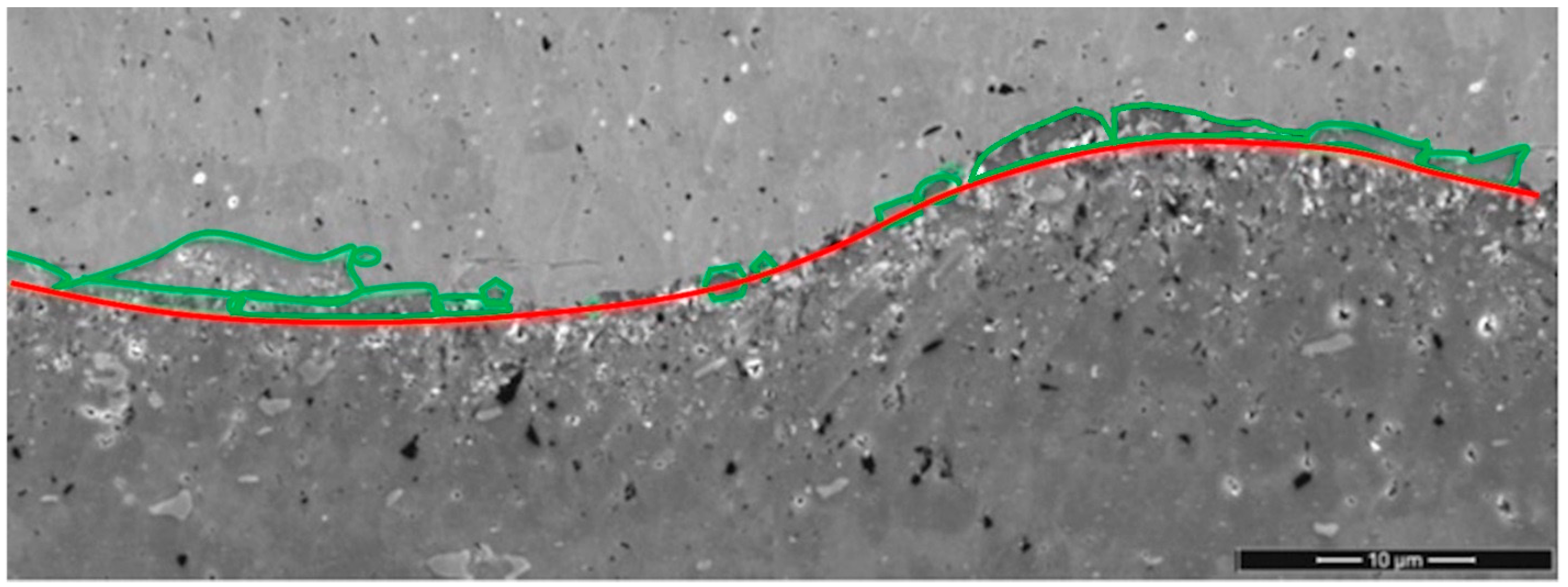
5.3. Influence of Weld Microstructure and Role of Intermetallic Compounds

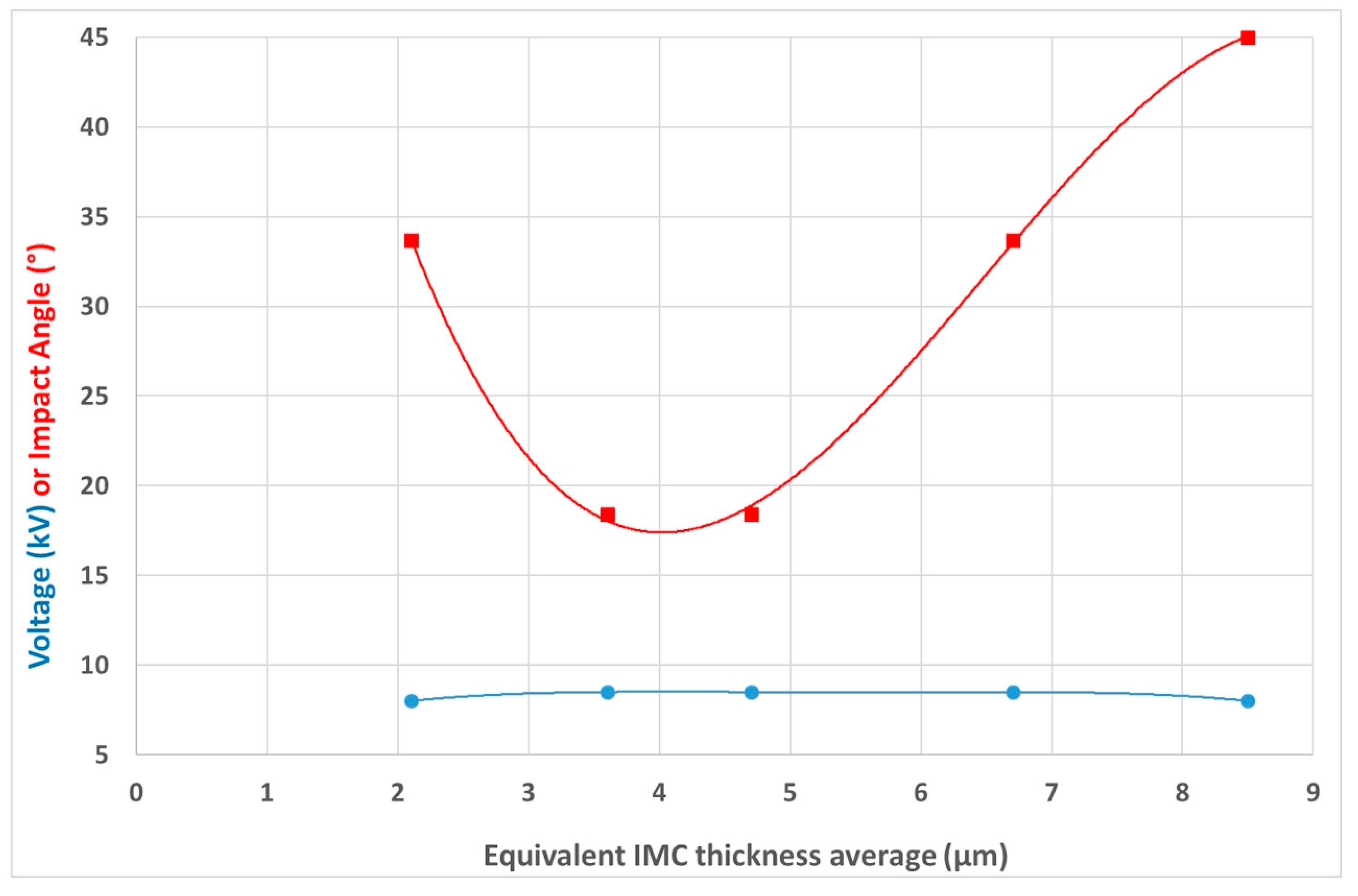
After polishing and chemical etching to highlight the intermetallic compounds, micrographs were made by optical microscopy (Figure 18) and the area occupied by the intermetallic compounds was measured by image analysis using ImageJ154-win-java8 software. It was clear that the specific energy of the welded part depended on the amount of intermetallic compounds created during the process. The higher the quantity of intermetallic compounds (IMCs) at the interface was, the lower the weld specific energy was (Figure 19).

Intermetallic compounds can appear in two different ways. First, as a layer through the whole interface [44] and, second, at the trough of a wave or the nucleus of a vortex [45,46] not exceeding the 5 μm thickness on the cross-section. Even though the interface zone may be a layer or pockets of IMCs, the distribution is usually not uniform [46]. From a performance point of view, continuous IMCs are undesirable, as they can represent a long, continuous brittle path. In contrast, the pocketed intermetallic phases are likely to give acceptable fracture performance. M. Marya et al. related the strength with the intermetallic equivalent layer thickness, with 4–6 μm being the optimum one [47], in good agreement with results of Figure 20. T. Lee et al. suggested that when IMC interfaces are separated by IMC-free interfaces, it can provide an effective barrier to the crack propagation and the overall strength of the weld may not be significantly affected by the IMC found elsewhere along the weld interface [48]. Various authors identified IMC compounds as exhibiting either tongue-shaped Fe₂Al₅ morphology or needle-like FeAl₃ structures [49,50]. SEM-EDS analysis conducted in this study confirmed the presence of tongue-shaped Fe₂Al₅, which aligns with findings from previous research [45,46]. Among the intermetallic compounds, Fe₂Al₅ exhibited the most negative heat of formation at compositions corresponding to the liquidus temperature in the Al-Fe phase diagram.

The analysis revealed a highly significant and strong inverse relationship between weld specific energy and intermetallic compound thickness. The statistical model demonstrated exceptional predictive capability with 97% correlation and less than 1% risk of error (

Table 7. Analysis of variance for the linear model of weld specific energy vs. equivalent IMC thickness.

Variable			Coefficient		Standard Deviation	t-Value	Risk %
Constant			214.6409		15.5062	13.8422	0.08
IMC equivalent thickness			−19.2267		2.7707	−6.9392	0.61
Source	Square Sum	Degree of Freedom		Mean Squares		F-Value	Risk %
Regression	9436.8643	1		9436.8643		48.1525	0.61
Residuals	587.9357	3		195.9786
Total	10,024.8	4		2506.2
				Regression coefficient R=		0.9702

), indicating also that IMC formation became more efficient at lower energy inputs (Figure 21). This finding has important implications for optimizing magnetic pulse welding processes, suggesting that energy consumption can be reduced while maintaining or improving weld quality through better IMC formation.

The model provided a reliable foundation for process control and quality assurance in industrial magnetic pulse welding applications, though expanding the dataset would further strengthen these conclusions.

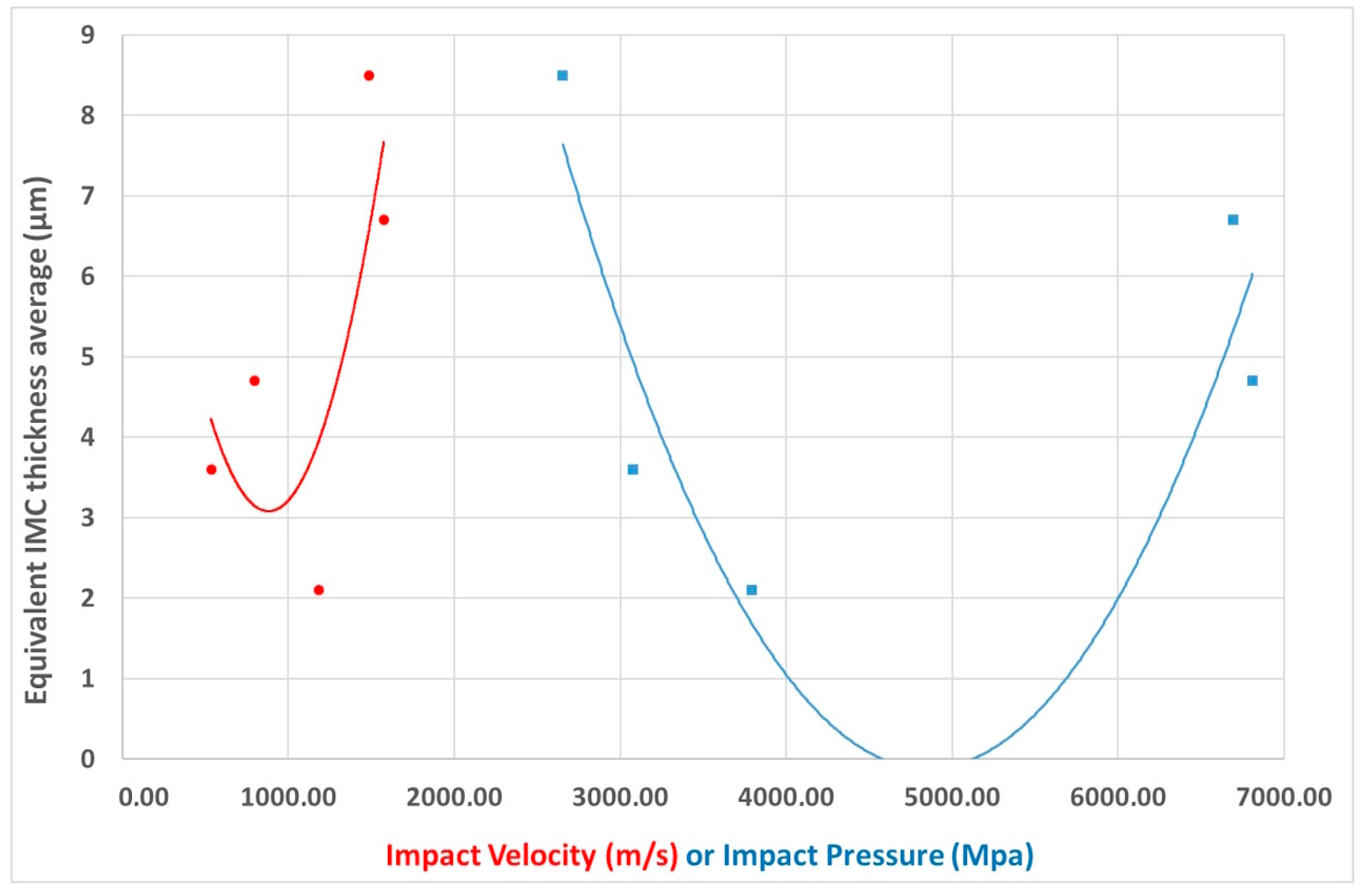
However, the dependence of the level of IMCs with the output energy as mentioned by different researchers (Psyk et al. [21], Lee et al. [23], Zhang et al. [25]) was not so clear and seemed to be related also to the impact angle, as shown in Figure 21.

Concerning its dependence with the physical parameters of the process, it was pointed out that a minimum concentration of IMCs was obtained for an impact velocity in the range of 500 to 1200 m/s, associated to an impact pressure between 3000 and 4000 MPa (Figure 22).

In the different micrographs of the welded zone (Figure 18), a higher concentration of IMCs with a straight interface also appeared, as reported by Zhang et al. [25].

The data suggest that higher impact pressures and velocities, along with optimal impact angles, result in thinner IMC layers, which are desirable for stronger welds. Higher output voltage and weld specific energy values also correlate with thinner IMC layers.

6. Conclusions

In this approach concerning the magnetic impact welding process, we attempted to define the process window in two different ways.

The first approach is based on the use of technological process parameters (gap, overlap, and mean energy or output voltage) and is perfectly suited for use in production. The impact angle versus mean energy or output voltage diagrams are able to define the process window for the equipment used. This diagram must be associated with a 3D diagram to define the parameters (gap and overlap) that are at the origin of the angle of impact. They highlight the importance of the overlap factor for all applications of this type, in particular, in the automotive sector for body-in-white (BIW) applications. On the other hand, the results cannot be transposed directly to other stack thicknesses or equipment where the geometry of the inductor, the LRC values, and the frequency of the electromagnetic circuit are different.

The second approach is based on the use of impact parameters (velocity, pressure, and angle of impact), which are the basis of the physics of the process. Using the relationships defined by Shotri et al. [26] from Buckingham’s π theorem, these parameters can be determined independently of the dimensions of the parts to be welded, of the generator, of the LRC circuit, and of the geometry of the inductor used. The process window, based on these parameters, can therefore be used regardless of the equipment. The 2D or 3D window from the impact pressure as a function of the impact velocity for different impact angle is therefore the right tool to understand the different mechanisms generating the weld. It allows us to locate the threshold pressure as defined by the Hugoniot relation, the critical speed of change in type of weld (straight or wavy) from the Cowan and Carpenter relation, and the subsonic speed limit associated with the phenomenon of jetting/no jetting.

The strength of the weld is strongly related to the content of IMCs generated during the process. Thinner IMCs generally correspond to higher weld specific energy. There is an inverse relationship between impact angle and weld specific energy. Higher angles generally result in lower weld energy.

Higher impact velocities tend to produce thicker intermetallic compounds (IMCs).

For successful welding, the optimal process parameters include a gap of 1 mm to 1.5 mm, an overlap of 6 mm to 7 mm, a cantilevered distance of 9 mm to 10 mm, and a voltage of 8 kV to 9 kV.

Higher mean energy values (above 20 kJ) and weld specific energy values (above 150 kJ/m²) are crucial for successful welds.

In terms of physical parameters, the optimum conditions for a high weld specific energy associated to a probability of 100% or near of joining are obtained for an impact velocity between 900 and 1200 m/s, an impact pressure between 3000 and 4000 MPa, and an impact angle in the range of 18 to 35°.

These conditions correspond to a gap of 1.5 to 2 mm and an output voltage between 7.5 and 8.5 kV.

Welds consistently failed when the gap distances exceeded 3 mm, the output voltage was below 5.5 kV, and the impact pressures were below 2000 MPa.

These findings suggest that controlling the impact angle, pressure, and velocity is crucial for achieving an optimal weld quality while minimizing IMCs’ formation. The trade-off between weld strength (indicated by specific energy) and IMCs’ thickness needs to be carefully balanced for optimal joint properties.

Further experiments should focus on refining the process parameters to achieve consistent welding results with thinner IMC layers. An additional analysis of the microstructure and mechanical properties of the welds can provide deeper insights into the welding process.

However, this analysis provides a comprehensive understanding of the magnetic pulse welding process for AA6082-T6 aluminum alloy with HC420LA steel, highlighting the critical factors that influence welding success and the formation of intermetallic compounds.