High-Speed Bearing Reliability: Analysis of Tapered Roller Bearing Performance and Cage Fracture Mechanisms
Abstract
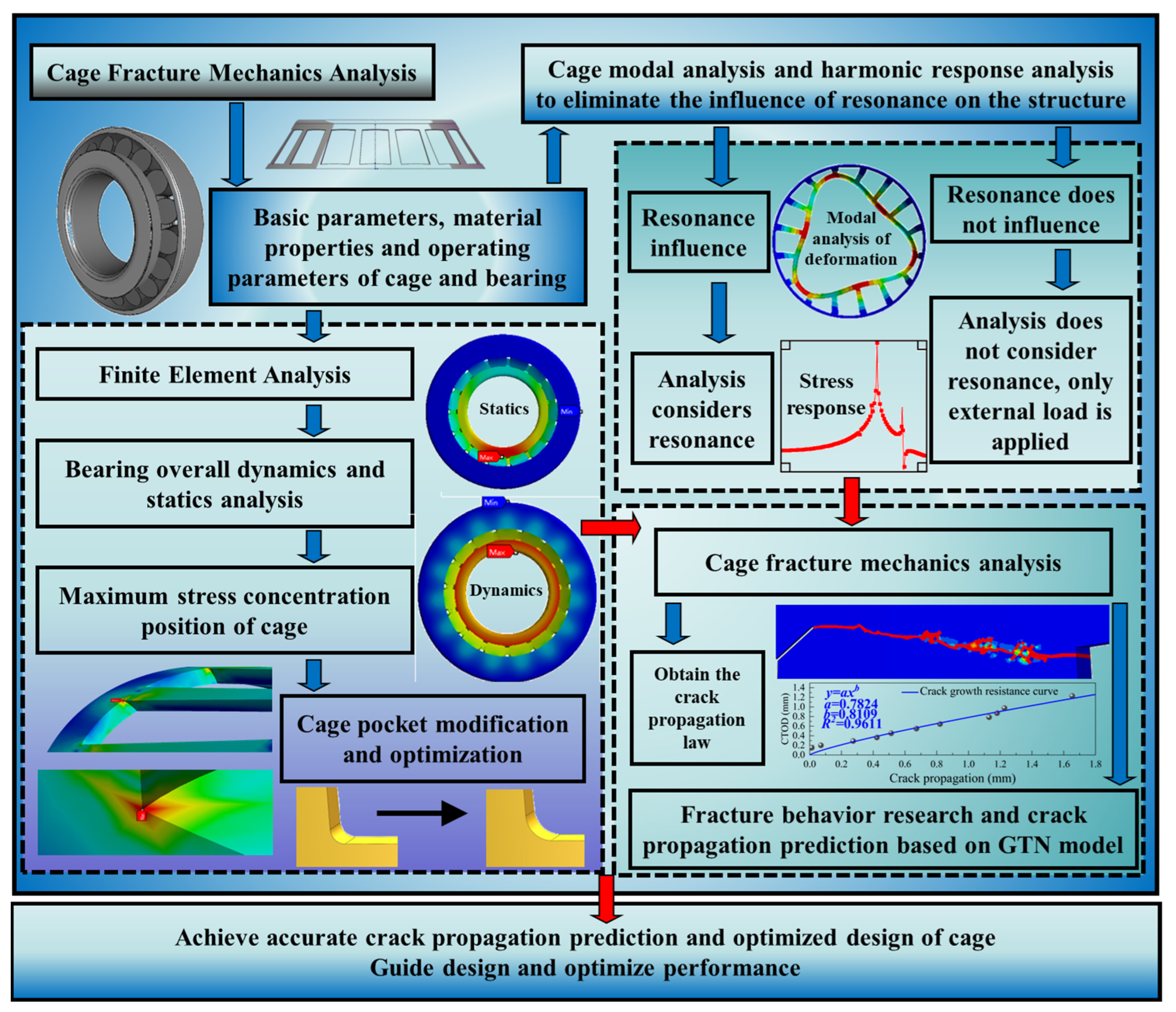
1. Introduction
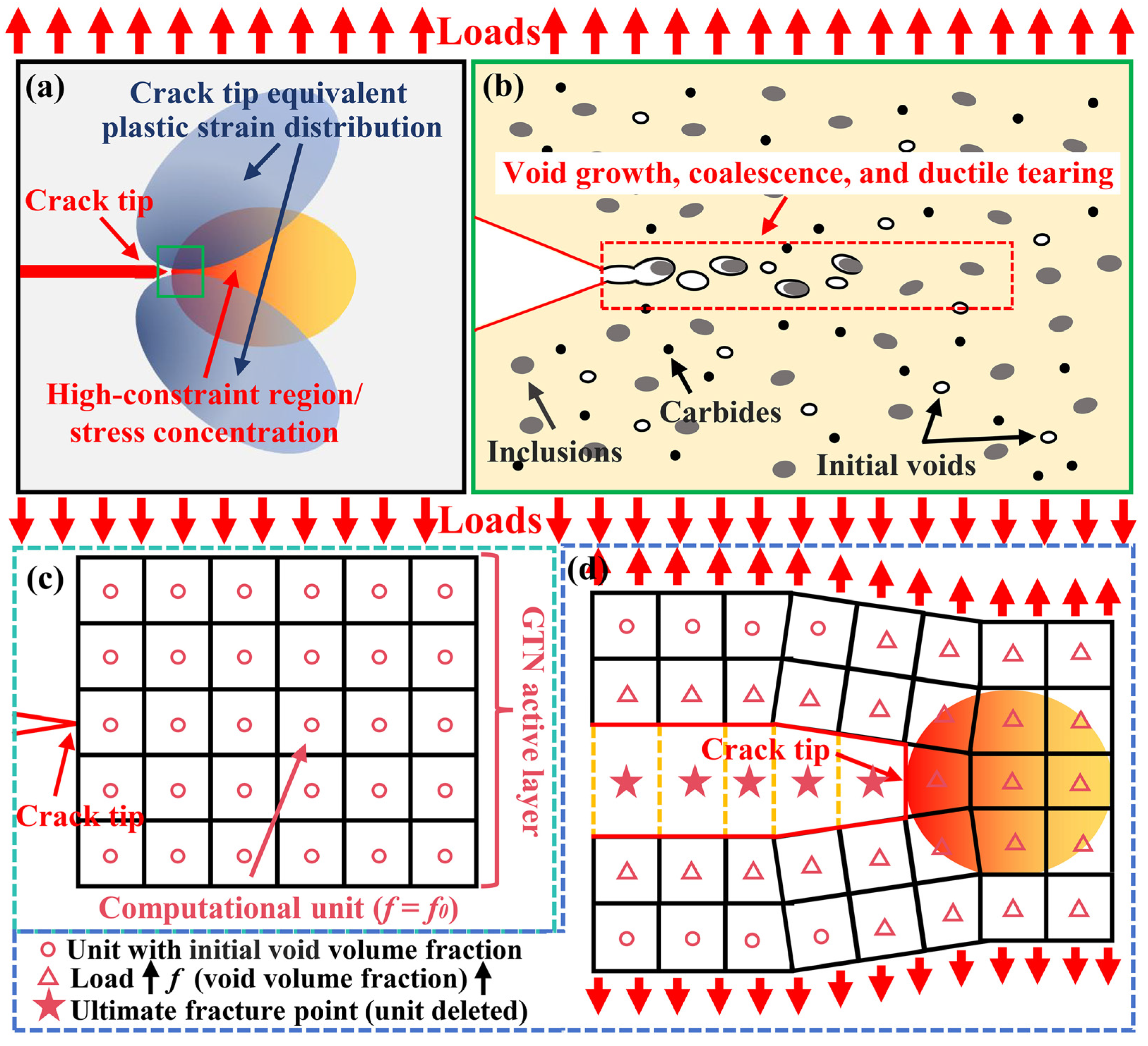
2. Modal Analysis Theory and GTN Microscopic Damage Model
2.1. Modal Analysis Theory
2.2. GTN Model
3. Finite Element Model, Material Properties, and Preprocessing
3.1. Bearing Model and Material Properties
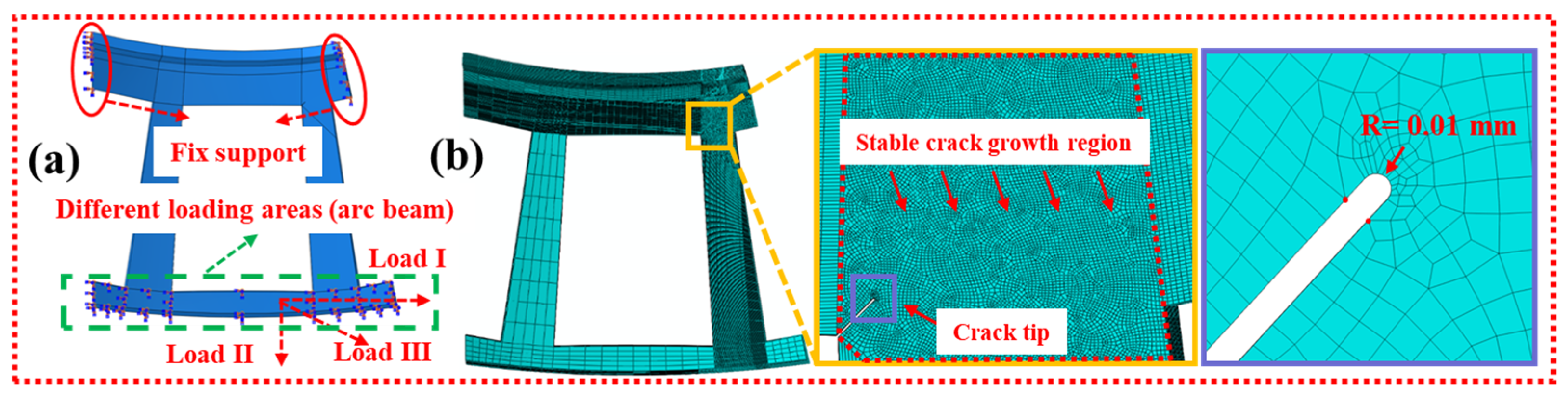
3.2. Finite Element Preprocessing
4. Bearing Static, Dynamic Analysis, and Verification
5. Fracture Analysis of Cage Failure
5.1. Dynamic Characterization: Modal and Harmonic Response Analysis
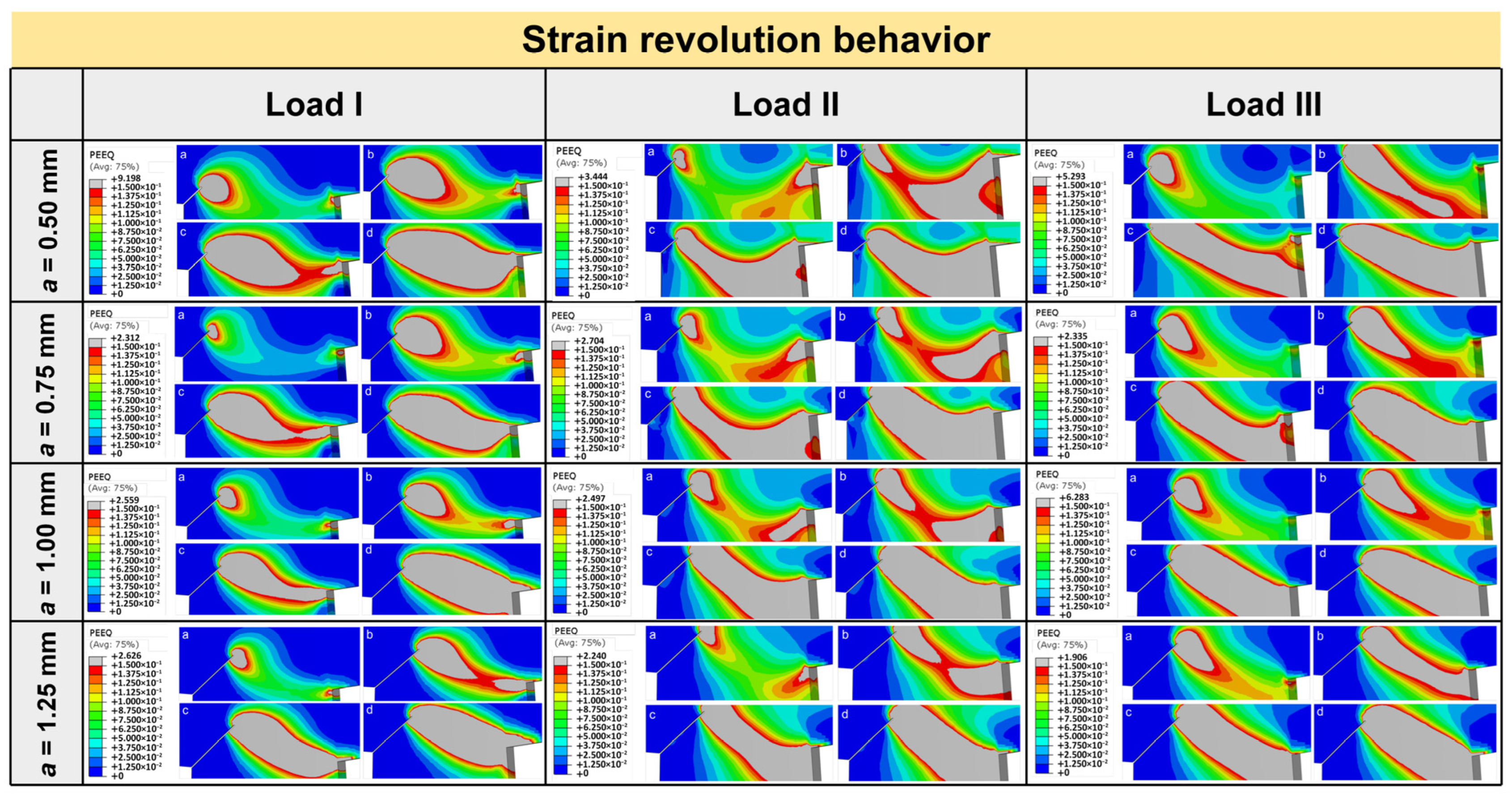
5.2. Fracture Mechanics Analysis: Cage Crack Growth Behavior
6. Cage Pocket Fillet Analysis and Optimized Design
Modal Analysis and Harmonic Response Analysis of the Cage
7. Conclusions
- (1)
- The maximum deformation location is on the inner ring, while the maximum equivalent stress location is at the contact area between the rolling elements and the inner ring.
- (2)
- Under the bearing maximum operational speed, calculations demonstrate that the resonance-induced failure of the cage can be ruled out for this tapered roller bearing configuration. Future work should incorporate more realistic roller profiles with appropriate end reliefs and optimized contact geometry to eliminate artificial stress concentrations and produce more accurate absolute stress values. While the current study’s simplified geometry may overestimate absolute stress values, the relative stress distributions and identified failure mechanisms remain valid.
- (3)
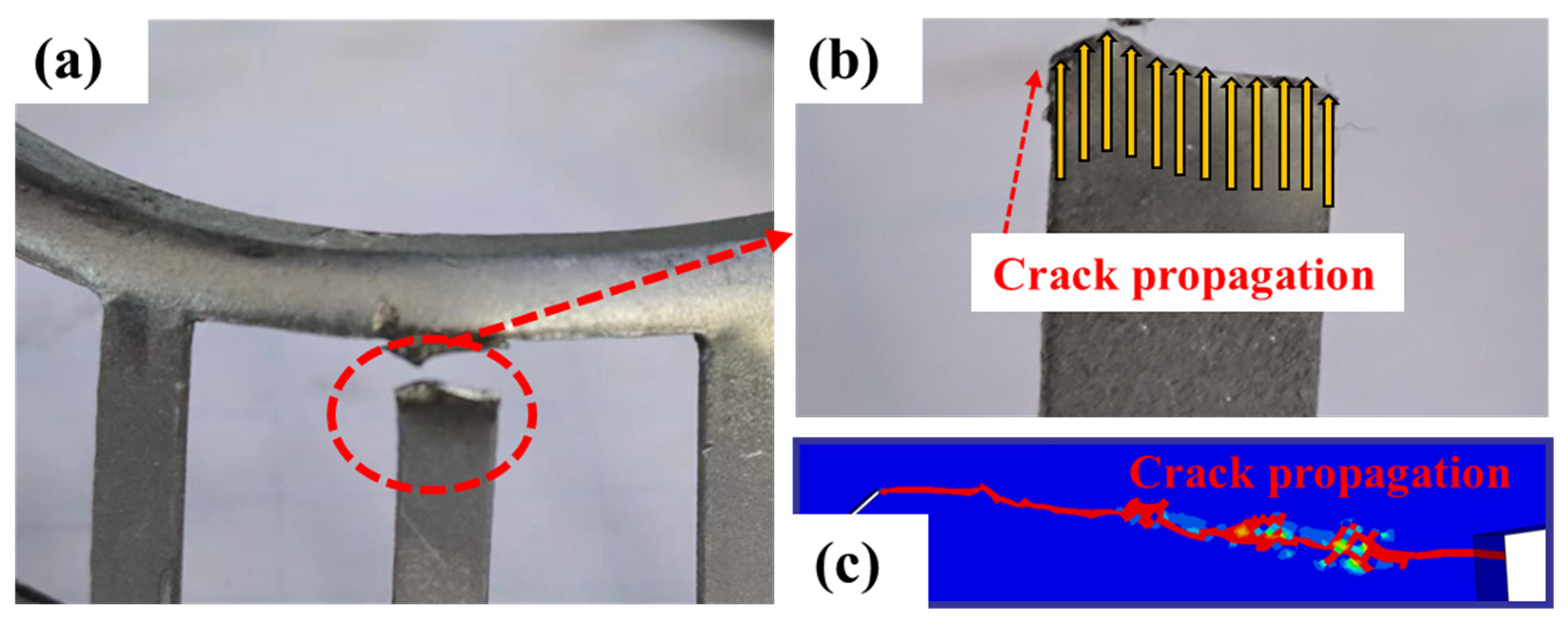
- Crack propagation in the cage predominantly follows a circumferential direction, with crack initiation occurring at the corners of adjacent pocket bridges. These cracks ultimately coalesce, leading to structural failure.
- (4)
- Longitudinal loading (Load II) provides superior fracture toughness and crack growth resistance (peak CTODc: 0.598 mm) due to enhanced plastic strain accumulation, outperforming circumferential (Load I) and coupled loading (Load III).
- (5)
- Fracture toughness decreases with crack depth (CTODc reductions of 66.5%, 20.1%, and 58.4% for Loads I, II, and III, respectively), while crack deflection angles exhibit significant variability only under Load I (35% increase), indicating load-dependent failure mechanisms.
- (6)
- Enhancing the machining precision of the pocket bridge fillet radius effectively reduces stress concentrations, thereby improving the bearing’s durability and extending its service life.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tedric, A.H.; Michael, N. Advanced Concepts of Bearing Technology, 5th ed.; CRC Press: Boca Raton, FL, USA, 2018; pp. 1–20. [Google Scholar]
- Zhang, J.; Fang, B.; Hong, J. Effect of preload on ball-raceway contact state and fatigue life of angular contact ball bearing. Tribol. Int. 2017, 114, 365. [Google Scholar] [CrossRef]
- Hua, R.; Zhu, L. Contact stress FEM analysis of deep groove ball bearing based on ANSYS Workbench. Appl. Mech. Mater. 2014, 574, 21. [Google Scholar]
- Zhang, Y.; Shu, T.; Ding, R. Bearing life prediction based on SPSS and grey prediction model. IOP Conf. Ser. Earth Environ. Sci. 2021, 634, 012054. [Google Scholar] [CrossRef]
- Xu, D.; Zhu, Q.; Zhang, Y. Review of research on detection of bearing subsurface white corrosion defects. Meas. Test. Technol. 2023, 50, 16. [Google Scholar]
- Nahm, S.H.; Jeon, S.K.; Kim, D.K.; Suh, M.S.; Suh, C.M. Very-High-Cycle Fatigue Behaviors for Bearing Steel Microstructural Transformation. Crystals 2024, 14, 1040. [Google Scholar] [CrossRef]
- Sharma, A.; Upadhyay, N.; Kankar, P. Nonlinear dynamic investigations on rolling element bearings: A review. Adv. Mech. Eng. 2018, 10, 168781401876414. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Z. Skidding research of a high-speed cylindrical roller bearing with beveled cage pockets. Ind. Lubr. Tribol. 2020, 72, 969. [Google Scholar] [CrossRef]
- Zheng, J.; Hu, Y. Study on crack propagation of a bearing inner-ring under cyclic loading. Appl. Mech. Mater. 2016, 851, 317. [Google Scholar] [CrossRef]
- Mu, W.; Chen, C. Crystallization of High-Performance Metallic Materials. Crystals 2025, 15, 147. [Google Scholar] [CrossRef]
- Kadin, Y.; Dop, J.; Schaake, R. Modeling of fatigue/creep in polymer cage of large size bearing. Adv. Sci. Technol. 2025, 18, 1583. [Google Scholar]
- Takeshima, K.; Mutoh, K.; Imanishi, K. Mechanisms of cage noise generation in machine tool bearings. Front. Mech. Eng. 2025, 10, 1469546. [Google Scholar] [CrossRef]
- Feng, X.; Zhu, P.; Wang, W. Lubricant seepage behavior of porous polyimide cage materials under sliding contact loading. Tribol. Int. 2025, 204, 110470. [Google Scholar] [CrossRef]
- Zeng, G.; Liang, Z.; Zhao, C. Study on the mass imbalance macro-micro friction and wear characteristics of high-speed angular contact ball bearing cages. Tribol. Int. 2025, 204, 110491. [Google Scholar] [CrossRef]
- Wang, Y.J.; Wang, H.Y.; Yan, J.X.; Wang, B.; Wen, B.G. Cage dynamic analysis of four-point contact ball bearing for high-speed railway traction motor. J. Phys. Conf. Ser. 2024, 2890, 012064. [Google Scholar] [CrossRef]
- Xiao, L.F.; Zheng, Z.B.; Tan, Y.S.; Yang, Z.J.; Zhang, J.W.; Zhou, N.; Yan, J.M.; Li, J.J.; Chen, J.; Wu, Y.X.; et al. Causes and analysis of failure of bearing cage at non-driven end of wind turbine generator. Eng. Fail. Anal. 2025, 167, 108991. [Google Scholar] [CrossRef]
- You, J.Y.; Ma, X.Q.; Liu, C.Y.; Zuo, M.J.; Jin, D.L.; Zhang, H. Measurement and dynamic analysis of the centroid trajectories of angular-contact ball bearing cages. Lubricants 2024, 12, 379. [Google Scholar] [CrossRef]
- Chen, W.B.; Wang, C.; Zhou, G.; Liu, F.B.; Wang, W.Z.; Zhu, P.Z. Molecular Dynamics Simulations of Lubricant Supply in Porous Polyimide Bearing Retainers. Lubricants 2024, 12, 343. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, H.; Wang, J.; Qin, S.; Duan, X.; Duan, M. Study on mechanics and high temperature tribological properties of porous bearing cage material. J. Reinf. Plast. Compos. 2024, 43, 1165. [Google Scholar] [CrossRef]
- Li, H.; Liu, H.; Liu, Y. On the dynamic characteristics of ball bearing with cage broken. Ind. Lubr. Tribol. 2020, 72, 881. [Google Scholar] [CrossRef]
- Wang, B.X.; Fang, W.B.; Yan, R.X.; Qian, S.K. Investigation of oil-air two-phase flow inside angular contact ball bearing with textured cage. J. Shanghai Jiaotong Univ. (Sci.) 2024, 10, 1. [Google Scholar] [CrossRef]
- Chen, H.; Liu, Y.; Liang, H. The cage instability of angular contact ball bearing under high-speed conditions. Mech. Mach. Theory 2024, 197, 105646. [Google Scholar] [CrossRef]
- Su, B.; Li, H.; Zhang, G. Study on cage stability of solid-lubricated angular contact ball bearings in an ultra-low temperature environment. Lubricants 2024, 12, 124. [Google Scholar] [CrossRef]
- ISO 281:2007; Rolling Bearings-Dynamic Load Ratings and Rating Life. International Organization for Standardization: Geneva, Switzerland, 2007.
- Gurson, A.L. Continuum theory of ductile rupture by void nucleation and growth: Part I-Yield criteria and flow rules for porous ductile media. J. Eng. Mater. Technol. 1977, 99, 297. [Google Scholar] [CrossRef]
- Tu, H. The Gurson-Tvergaard-Needleman (GTN) Model. In Numerical Simulation and Experimental Investigation of the Fracture Behaviour of an Electron Beam Welded Steel Joint; Springer: Cham, Switzerland, 2018; pp. 75–95. [Google Scholar]
- Perna, A.S.; Savio, L.; Coppola, M.; Scherillo, F. Investigating Fracture Behavior in Titanium Aluminides: Surface Roughness as an Indicator of Fracture Mechanisms in Ti-48Al-2Cr-2Nb Alloys. Metals 2025, 15, 49. [Google Scholar] [CrossRef]
- Ren, Z.D.; Li, B.Z.; Zhou, Q.Z. Rolling contact fatigue crack propagation on contact surface and subsurface in mixed mode I+II+III fracture. Wear 2022, 506–507, 204459. [Google Scholar] [CrossRef]
- Fu, Z.; Hua, H. Modal Analysis Theory and Application; Shanghai Jiao Tong University Press: Shanghai, China, 2000; pp. 12–80. [Google Scholar]
- Wang, X.; Tan, Y.; Deng, Y. Modal and harmonic response analysis on the irregular arm based on ANSYS Workbench. Mech. Res. Appl. 2024, 37, 108. [Google Scholar]
- Liang, H.; Zhan, R.; Wang, D.P.; Deng, C.Y.; Guo, B.C.; Xu, X.H. Fatigue crack growth under overload/underload in different strength structural steels. J. Constr. Steel Res. 2022, 192, 107213. [Google Scholar] [CrossRef]
- Maziar, K.; Moslemi, H.; Javad, M. Fracture prediction of AA6061-T6 sheet in bending process using Gurson-Tvergaard-Needleman model. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2023, 237, 2506. [Google Scholar]
- Ning, J.A.; Deng, C.Y.; Dai, L.S.; Liu, Q.; Gong, B.M.; Guo, B.C.; Wang, Y.J. Fracture behavior analysis of X80 girth welds considering misaligned and variable-wall-thickness geometric features via modified single-edge notched tensile (MSENT) specimens. Eng. Fract. Mech. 2025, 317, 110910. [Google Scholar] [CrossRef]
- Liang, H.; Wang, D.P.; Deng, C.Y.; Zhan, R. Fatigue crack growth acceleration in S355 steel under a single and periodic underload. Int. J. Fatigue 2022, 158, 106744. [Google Scholar] [CrossRef]
- Hu, W.T.; Gong, B.M.; Chang, Q.; Zhao, Z.F.; Dai, L.S.; Liu, Y. Strain fracture behaviors and crack equivalence of X80 welded joints with non-sharp notches at weld root. Int. J. Pressure Vessels Piping. 2025, 2214, 105414. [Google Scholar] [CrossRef]
- Ning, J.A.; Deng, C.Y.; Wang, Y.J.; Gong, B.M.; Guo, B.C.; Zhao, N.; Dai, L.S. Stress state analysis of root notch for X80 girth welds with variable wall thickness and misalignment geometric features. Int. J. Pressure Vessels Piping. 2023, 206, 105064. [Google Scholar] [CrossRef]
- Harris, T.; Michael, N. Rolling Bearing Analysis; Taylor & Francis: New York, NY, USA, 2006; pp. 33–140. [Google Scholar]
- Cheng, D.X. Bearing. In Mechanical Design Handbook, 6th ed.; China Machine Press: Beijing, China, 2004; Volume 3, pp. 1–193. [Google Scholar]
- Tvergaard, V.; Needleman, A. Analysis of the cup-cone fracture in a round tensile bar. Acta Metall. 1984, 32, 157. [Google Scholar] [CrossRef]
- Hung, N. Computational Design of Rolling Bearings; Springer: Shanghai, China, 2016; pp. 18–100. [Google Scholar]
- Huang, Y. Research on Fatigue Life of High-Speed Train Axle-Box Bearing Under Fluctuant Impact Load. Master’s Thesis, Henan University of Science and Technology, Luoyang, China, 2017; pp. 12–70. [Google Scholar]
- Song, B. Analysis of Mechanical Properties and Fatigue Life of Tapered Roller Bearings. Ph.D. Thesis, Xi’an University Technology, Shannxi, China, 2018; pp. 16–60. [Google Scholar]
- Hung, N. Numerische Auslegung von Wälzlagern; Springer: Asperg, Germany, 2017; pp. 10–110. [Google Scholar]












| Parameter | Value |
|---|---|
| Inner diameter d/mm | 55 |
| Outer diameter D/mm | 120 |
| Inner ring width B/mm | 29 |
| Outer ring width C/mm | 21 |
| Ring diameter d1/mm | 90.2 |
| Roller’s big end diameter/mm | 7 |
| Roller radius/mm | 3.5 |
| Roller length/mm | 25 |
| Rated dynamic load (Cr) | Approximately 245 kN (dynamic load capacity, 1 million revolutions at 90% reliability) |
| Rated static load (Cor) | Approximately 305 kN |
| Limiting speed (oil lubrication) | Approximately 3000 rpm (reduced by approximately 20~30% when grease lubrication is used) |
| Fatigue life | Based on load and lubrication conditions, usually up to tens of thousands of hours |
| Material | Elastic Modulus | Poisson’s Ratio | Density | Yield Strength | Tensile Strength |
|---|---|---|---|---|---|
| GCr15 | 208 GPa | 0.3 | 7.85 g/cm3 | 518.42 MPa | 861.3 MPa |
| Material | Elastic Modulus | Poisson’s Ratio | Density | Yield Strength | Tensile Strength |
|---|---|---|---|---|---|
| 10#Steel. | 206 GPa | 0.3 | 7.9 g/cm3 | 205 MPa | 410 MPa |
| q1 | q2 | q3 | εn | fc | fF | f0 | Sn | |
|---|---|---|---|---|---|---|---|---|
| Value | 1.5 | 1.0 | 2.25 | 0.3 | 0.2 | 0.2 | 0.0005 | 0.1 |
| R = 0 mm | R = 0.25 mm | R = 0.5 mm | R = 0.75 mm | R = 1.0 mm | |
|---|---|---|---|---|---|
| Load F = 500 N | 272.08 | 262.08 | 217.8 | 203.84 | 204.53 |
| Load F = 400 N | 214.37 | 210.27 | 174.24 | 163.07 | 163.63 |
| Load F = 300 N | 164.9 | 157.7 | 130.68 | 123.3 | 122.72 |
| Load F = 200 N | 123.67 | 105.13 | 87.122 | 81.536 | 80.035 |
| Load F = 100 N | 65.989 | 52.566 | 43.561 | 40.768 | 39.489 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Ning, J.; Liang, H.; Yang, M. High-Speed Bearing Reliability: Analysis of Tapered Roller Bearing Performance and Cage Fracture Mechanisms. Metals 2025, 15, 592. https://doi.org/10.3390/met15060592
Li Q, Ning J, Liang H, Yang M. High-Speed Bearing Reliability: Analysis of Tapered Roller Bearing Performance and Cage Fracture Mechanisms. Metals. 2025; 15(6):592. https://doi.org/10.3390/met15060592
Chicago/Turabian StyleLi, Qingsong, Jiaao Ning, Hang Liang, and Muzhen Yang. 2025. "High-Speed Bearing Reliability: Analysis of Tapered Roller Bearing Performance and Cage Fracture Mechanisms" Metals 15, no. 6: 592. https://doi.org/10.3390/met15060592
APA StyleLi, Q., Ning, J., Liang, H., & Yang, M. (2025). High-Speed Bearing Reliability: Analysis of Tapered Roller Bearing Performance and Cage Fracture Mechanisms. Metals, 15(6), 592. https://doi.org/10.3390/met15060592






