Predictive Capability Evaluation of Micrograph-Driven Deep Learning for Ti6Al4V Alloy Tensile Strength Under Varied Preprocessing Strategies
Abstract
1. Introduction
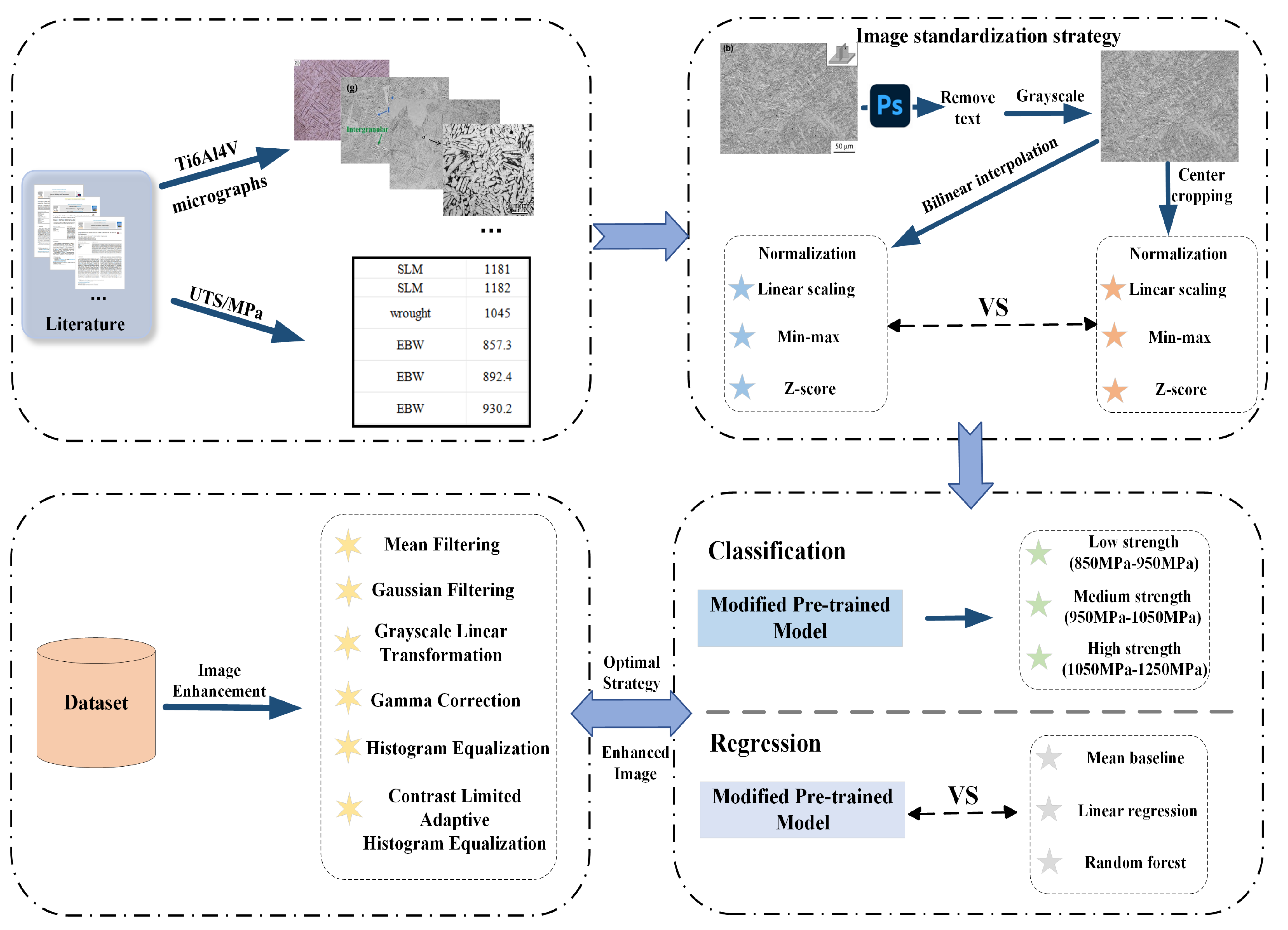
2. Materials and Methods
2.1. Data Collection
2.2. Image Standardization
2.2.1. Color Processing
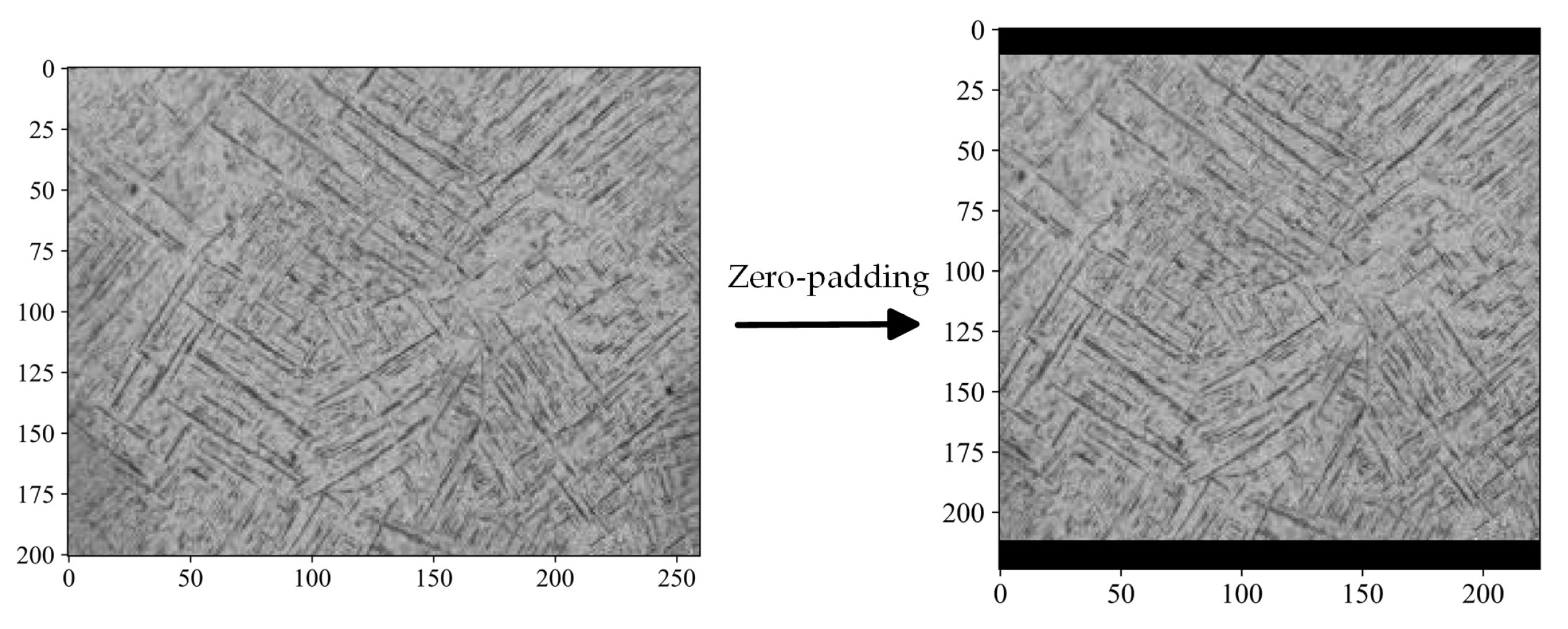
2.2.2. Size Adjustment
- Center cropping
- Bilinear interpolation
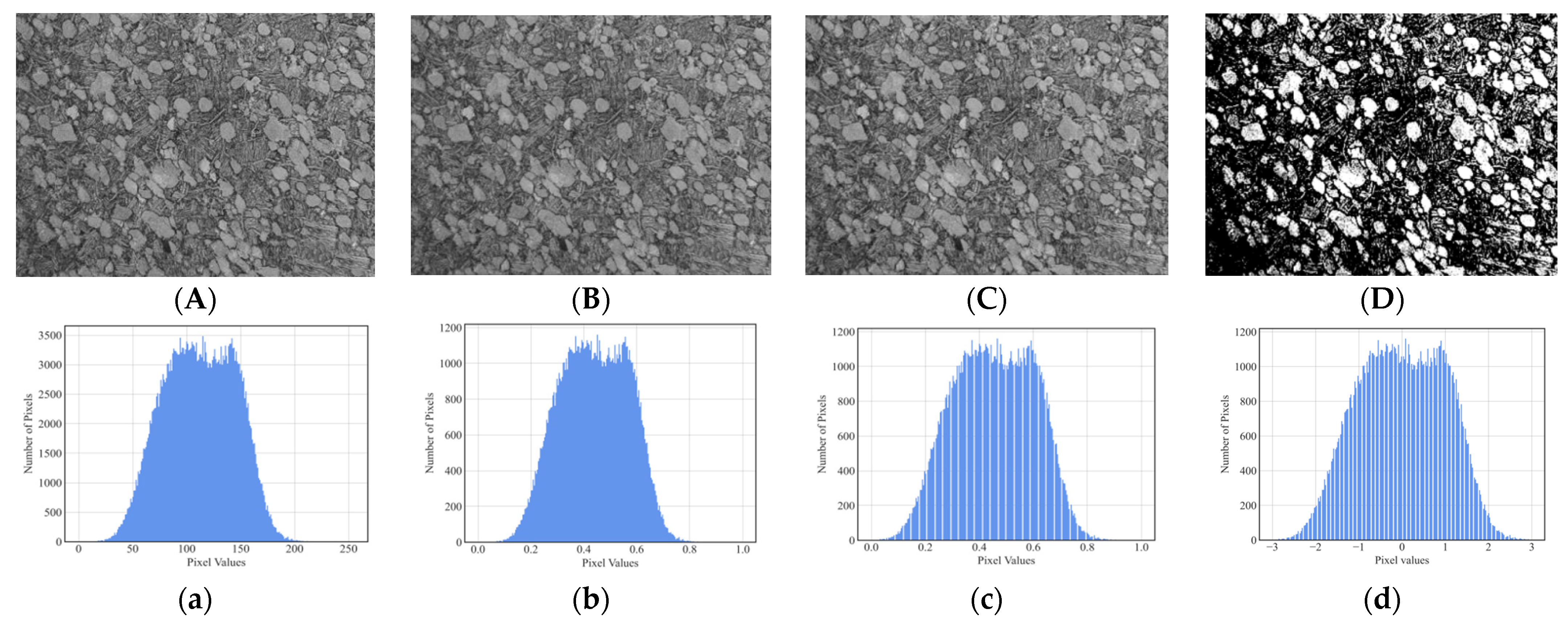
2.2.3. Image Normalization
- Linear scaling
- 2.
- Min–max normalization
- 3.
- Z-score normalization
2.3. Image Enhancement
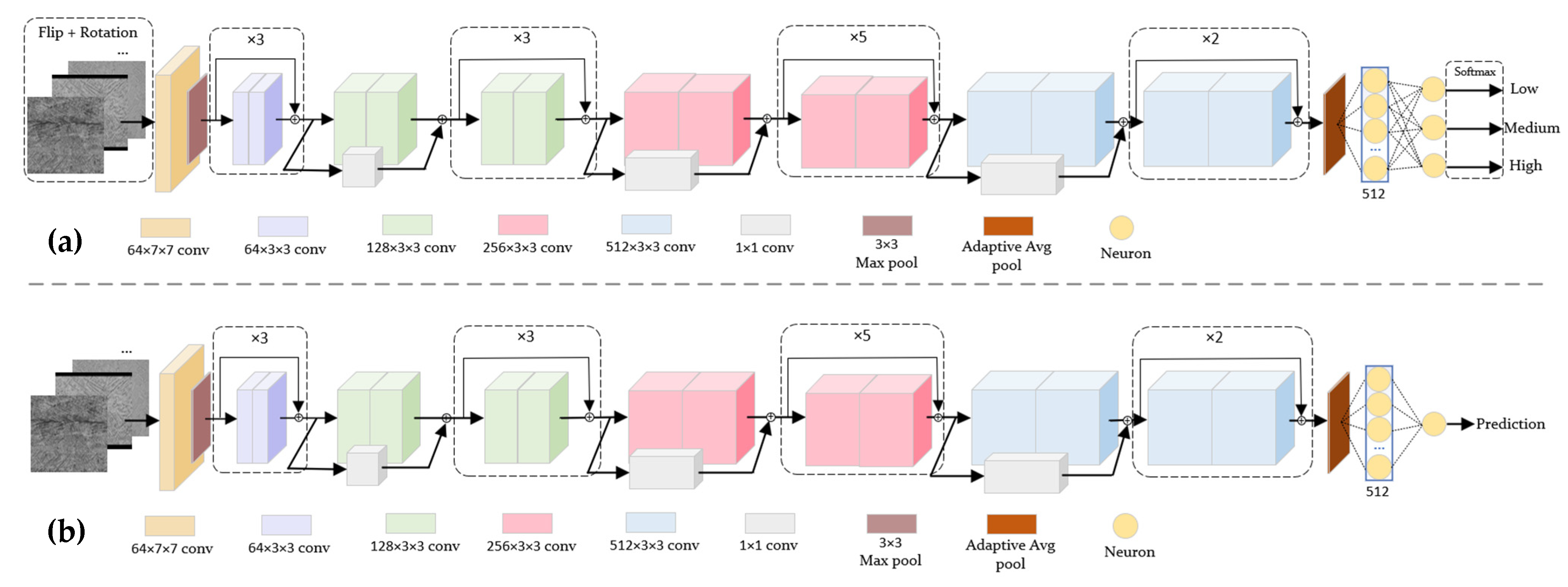
2.4. Models for Classification and Prediction
| Method and Hyperparameter | Configuration |
|---|---|
| Optimizer | Adam |
| Epoch | 200 |
| Early stop patience [29] | 7 |
| Learning rate | 0.0001 |
| Batch size | 8 |
| Initialization of weights in FC | Xavier uniform |
| K-fold cross validation | K = 5, Shuffle = True, random_state = 42 |
| Method and Hyperparameter | Configuration |
|---|---|
| Optimizer | Adam |
| Epoch | 200 |
| Early stop patience | 16 |
| Learning rate | 0.008 |
| Batch size | 8 |
| Initialization of weights in FC | Xavier uniform |
| K-fold cross validation | K = 5, Shuffle = True, random_state = 42 |
| Random Forest | Configuration | |
| n_estimators | 100 | |
| Random state | 42 | |
| GLCM | distance | [1] |
| angles | [0] | |
| Symmetric | True | |
| normed | True | |
| levels | 256 | |
| Extracted features | contrast | |
| energy | ||
| homogeneity | ||
| correlation | ||
3. Results
3.1. Test Results of Classification Model
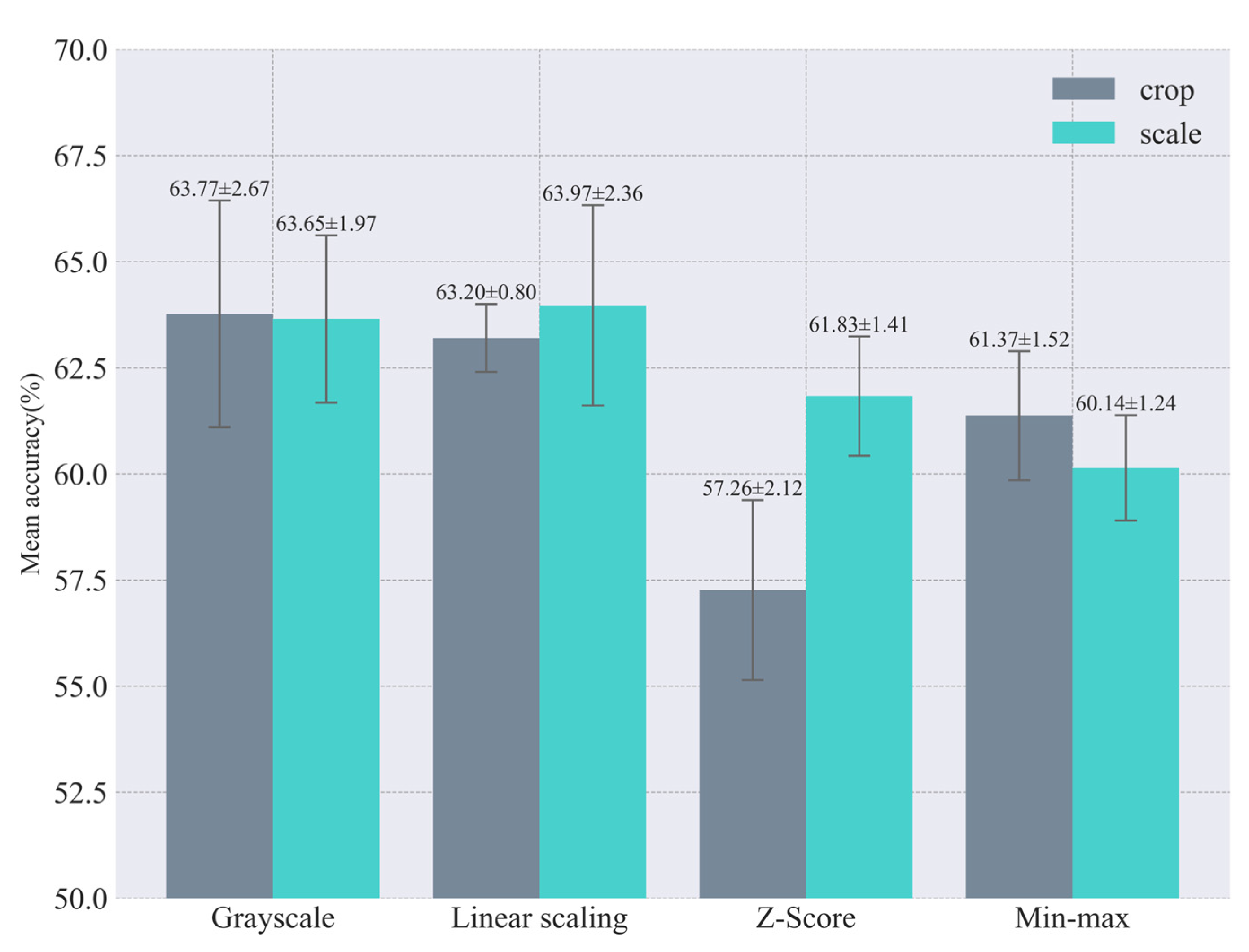
3.1.1. Test Results of Image Standardization
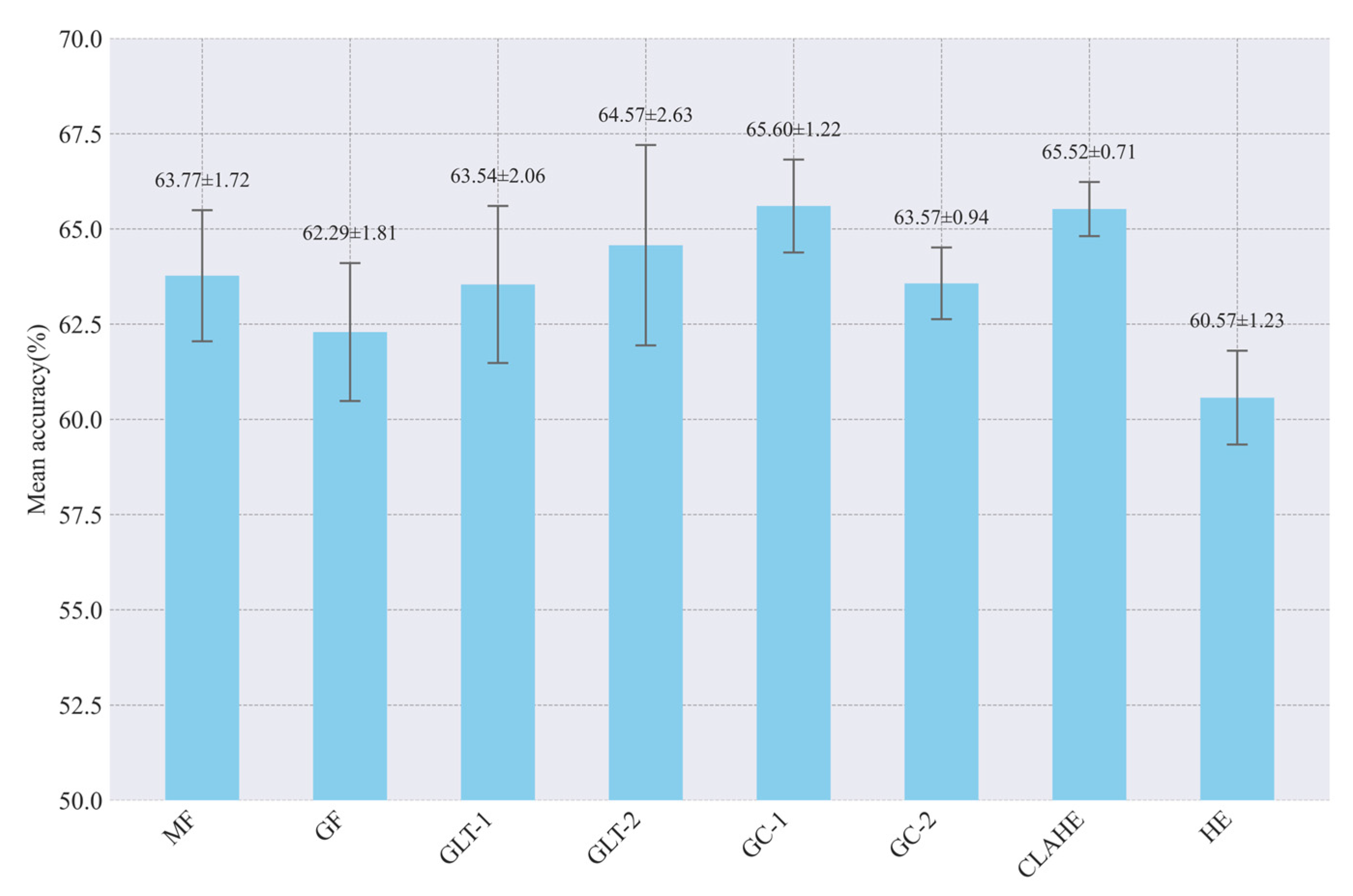
3.1.2. Test Results of Image Enhancement
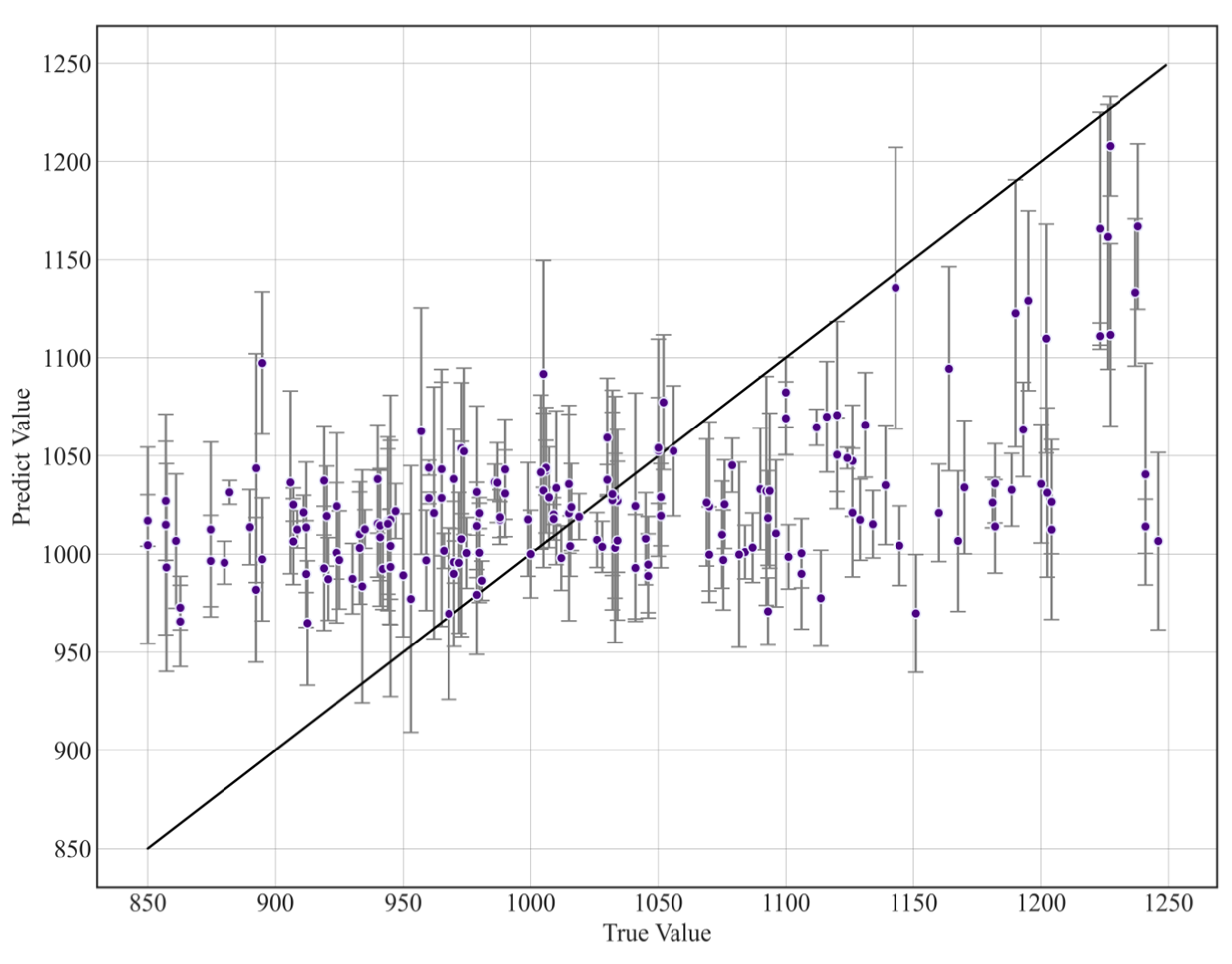
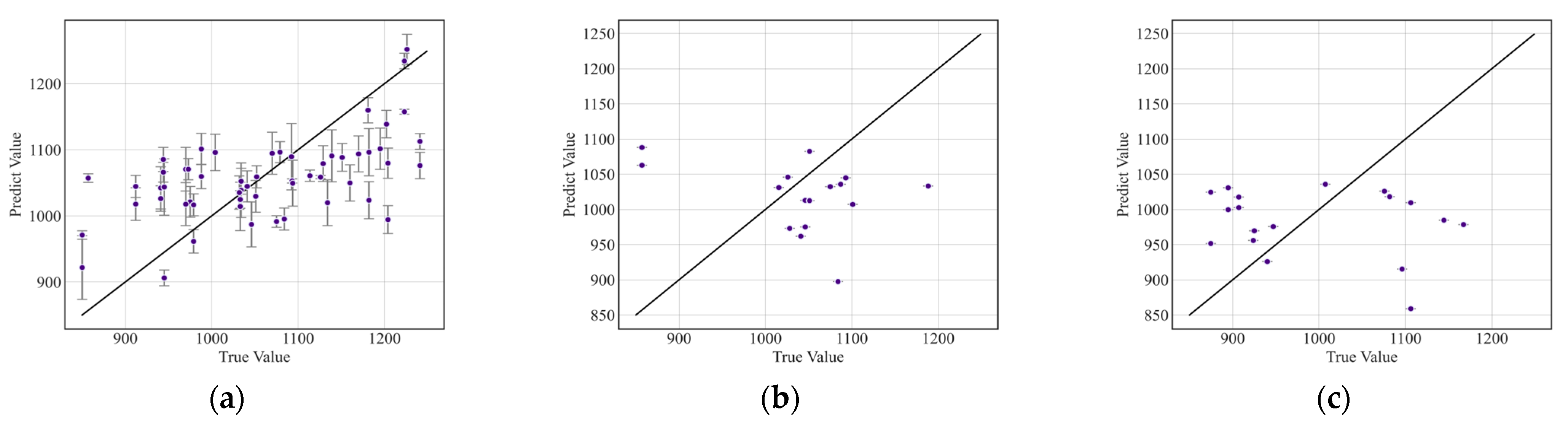
3.2. Test Results of Regression Models
3.2.1. Test Results of Image Standardization
3.2.2. Test Results of Image Enhancement
3.2.3. Test Results of Subsets with Less Heterogeneity
4. Discussion
4.1. Predictive Capability of the Model
4.2. Impact of Size Adjustment and Normalization Methods on Model Performance
4.3. Impact of Image Enhancement Methods on Model Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goyal, V.; Prasad, N.K.; Verma, G. Experimental investigations into corrosion behaviour of DMLS manufactured Ti6Al4V alloy in different biofluids for orthopedic implants. Mater. Today Commun. 2025, 42, 111158. [Google Scholar] [CrossRef]
- Nagalingam, A.P.; Gopasetty, S.K.; Wang, J.; Yuvaraj, H.K.; Gopinath, A.; Yeo, S.H. Comparative fatigue analysis of wrought and laser powder bed fused Ti-6Al-4V for aerospace repairs: Academic and industrial insights. Int. J. Fatigue 2023, 176, 107879. [Google Scholar] [CrossRef]
- Liu, S.; Shin, Y.C. Additive manufacturing of Ti6Al4V alloy: A review. Mater. Des. 2019, 164, 107552. [Google Scholar] [CrossRef]
- Cheng, D.; Gao, F. Research Progress and Application of Laser Welding Technology for Titanium Alloy. Dev. Appl. Mater. 2020, 35, 87–93. [Google Scholar] [CrossRef]
- Shi, X.; Zeng, W.; Sun, Y.; Han, Y.; Zhao, Y.; Guo, P. Microstructure-Tensile Properties Correlation for the Ti-6Al-4V Titanium Alloy. J. Mater. Eng. Perform. 2015, 24, 1754–1762. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Li, B.; Zhang, W.; Xuan, F. Microstructural feature-driven machine learning for predicting mechanical tensile strength of laser powder bed fusion (L-PBF) additively manufactured Ti6Al4V alloy. Eng. Fract. Mech. 2024, 295, 109788. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, M.; Sisson, R.; Li, Y.; Liang, J. A machine-learning model to predict tensile properties of Ti6Al4V parts prepared by laser powder bed fusion with hot isostatic pressing. Mater. Today Commun. 2022, 33, 104205. [Google Scholar] [CrossRef]
- Shen, T.; Zhang, W.; Li, B. Machine learning-enabled predictions of as-built relative density and high-cycle fatigue life of Ti6Al4V alloy additively manufactured by laser powder bed fusion. Mater. Today Commun. 2023, 37, 107286. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, L.; Zhang, Y.; Han, X.; Deveci, M.; Parmar, M. A review of convolutional neural networks in computer vision. Artif. Intell. Rev. 2024, 57, 99. [Google Scholar] [CrossRef]
- Manjunath, J.; Mohana; Madhulika, M.S.; Divya, G.D.; Meghana, R.K.; Apoorva, S. Feature Extraction using Convolution Neural Networks (CNN) and Deep Learning. In Proceedings of the 2018 3rd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bangalore, India, 18–19 May 2018; pp. 2319–2323. [Google Scholar] [CrossRef]
- Murakami, Y.; Furushima, R.; Shiga, K.; Miyajima, T.; Omura, N. Mechanical property prediction of aluminium alloys with varied silicon content using deep learning. Acta Mater. 2025, 286, 120683. [Google Scholar] [CrossRef]
- Pei, X.; Zhao, Y.; Chen, L.; Guo, Q.; Duan, Z.; Pan, Y.; Hou, H. Robustness of machine learning to color, size change, normalization, and image enhancement on micrograph datasets with large sample differences. Mater. Des. 2023, 232, 112086. [Google Scholar] [CrossRef]
- Hashemi, M. Enlarging smaller images before inputting into convolutional neural network: Zero-padding vs. interpolation. J. Big Data 2019, 6, 98. [Google Scholar] [CrossRef]
- Bilal, M.; Ullah, Z.; Mujahid, O.; Fouzder, T. Fast Linde–Buzo–Gray (FLBG) Algorithm for Image Compression through Rescaling Using Bilinear Interpolation. Imaging 2024, 10, 124. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Qin, J.; Zhou, Y.; Zhu, F.; Liu, L.; Shao, L. Normalization Techniques in Training DNNs: Methodology, Analysis and Application. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10173–10196. [Google Scholar] [CrossRef] [PubMed]
- Albert, S.; Wichtmann, B.D.; Zhao, W.; Maurer, A.; Hesser, J.; Attenberger, U.I.; Schad, L.R.; Zöllner, F.G. Comparison of Image Normalization Methods for Multi-Site Deep Learning. Appl. Sci. 2023, 13, 8923. [Google Scholar] [CrossRef]
- Kuran, U.; Kuran, E.C. Parameter selection for CLAHE using multi-objective cuckoo search algorithm for image contrast enhancement. Intell. Syst. Appl. 2021, 12, 200051. [Google Scholar] [CrossRef]
- Wang, H.; Yan, X.; Hou, X.; Li, J.; Dun, Y.; Zhang, K. Division gets better: Learning brightness-aware and detail-sensitive representations for low-light image enhancement. Knowl. -Based Syst. 2024, 299, 111958. [Google Scholar] [CrossRef]
- Sahnoun, M.; Kallel, F.; Dammak, M.; Mhiri, C.; Mahfoudh, K.B.; Hamida, A.B. A comparative study of MRI contrast enhancement techniques based on Traditional Gamma Correction and Adaptive Gamma Correction: Case of multiple sclerosis pathology. In Proceedings of the 2018 4th Inter-national Conference on Advanced Technologies for Signal and Image Processing (ATSIP), Sousse, Tunisia, 21–24 March 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Azizah, L.M.; Kanafiah, S.N.A.B.M.; Jusman, Y.; Raof, R.A.A.; Zin, A.A.M.; Mashor, M.Y. Performance of the H-Butterworth, CLAHE, and HE Methods for Adenocarcinoma Images. In Proceedings of the 2024 International Conference on Information Technology and Computing (ICITCOM), Yogyakarta, Indonesia, 7–8 August 2024; pp. 301–305. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Huang, M. Theory and Implementation of linear regression. In Proceedings of the 2020 International Conference on Computer Vision, Image and Deep Learning (CVIDL), Chongqing, China, 10–12 July 2020; pp. 210–217. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kurniati, F.T.; Sembiring, I.; Setiawan, A.; Setyawan, I.; Huizen, R.R. GLCM-based feature combination for extraction model optimization in object detection using machine learning. J. Ilm. Tek. Elektro Komput. Informatika. 2023, 9, 1196–1205. [Google Scholar] [CrossRef]
- Mao, A.; Mohri, M.; Zhong, Y. Cross-Entropy Loss Functions: Theoretical Analysis and Applications. In Proceedings of the International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023; pp. 23803–23828. [Google Scholar]
- Elharrouss, O.; Mahmood, Y.; Bechqito, Y.; Serhani, M.A.; Badidi, E. Loss Functions in Deep Learning: A Comprehensive Review. arXiv 2025, arXiv:2504.04242. [Google Scholar]
- Foody, G.M. Challenges in the real world use of classification accuracy metrics: From recall and precision to the Matthews correlation coefficient. PLoS ONE 2023, 18, e0291908. [Google Scholar] [CrossRef] [PubMed]
- Domingo, R.A.; Martínez-Fernández, S.; Verdecchia, R. Energy efficient neural network training through runtime layer freezing, model quantization, and early stopping. Comput. Stand. Interfaces 2025, 92, 103906. [Google Scholar] [CrossRef]
- Tsutsui, K.; Terasaki, H.; Uto, K.; Maemura, Y.; Hiramatsu, S.; Hayashi, K.; Moriguchi, K.; Morito, S. A methodology of steel microstructure recognition using SEM images by machine learning based on textural analysis. Mater. Today Commun. 2020, 25, 101514. [Google Scholar] [CrossRef]
- Hai, X.; Cao, S.; Cui, S.; Ma, J.; Gao, K. Image Filter Processing Algorithm Analysis and Comparison. J. Phys. Conf. Ser. 2021, 1820, 012192. [Google Scholar] [CrossRef]




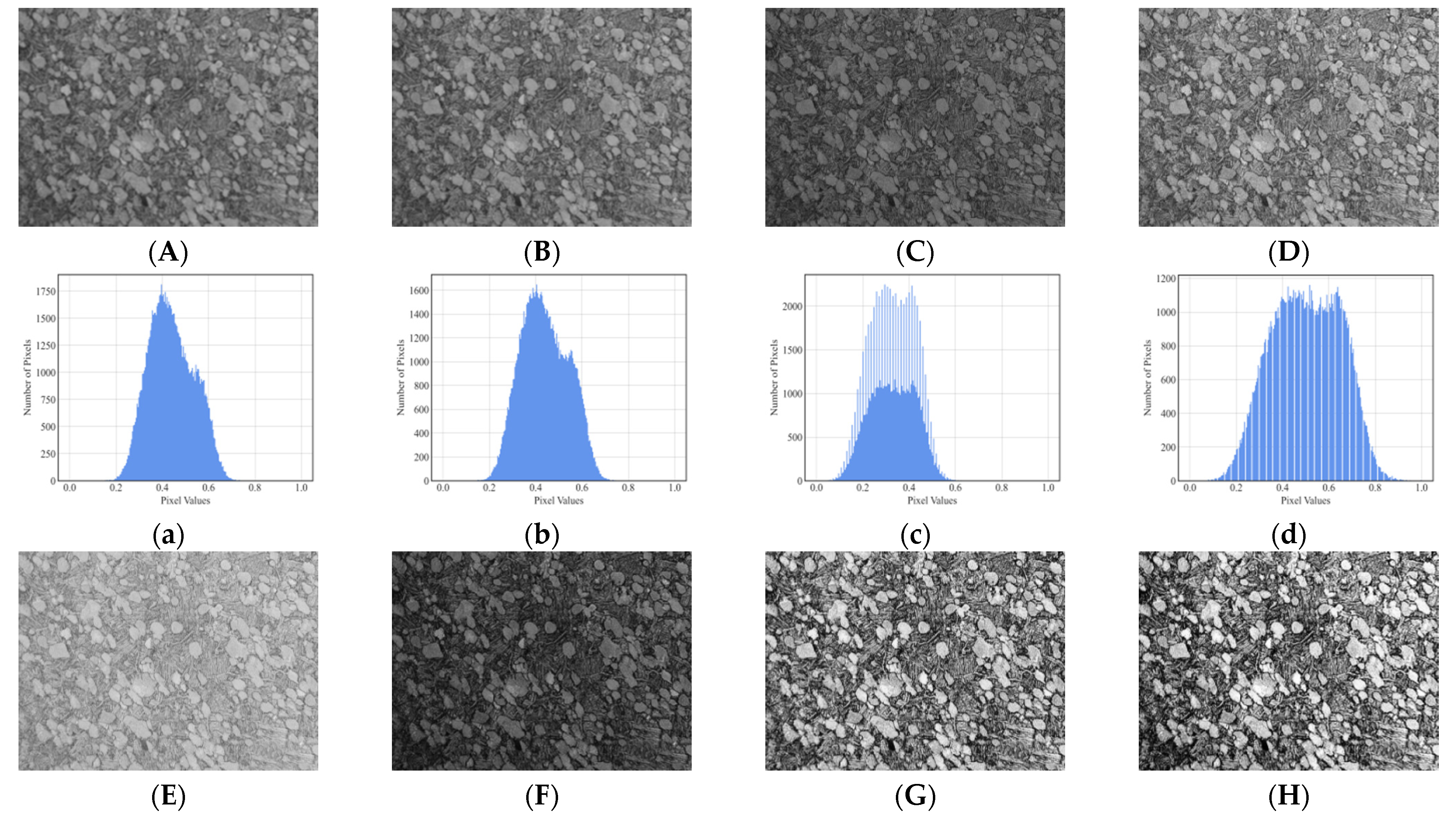

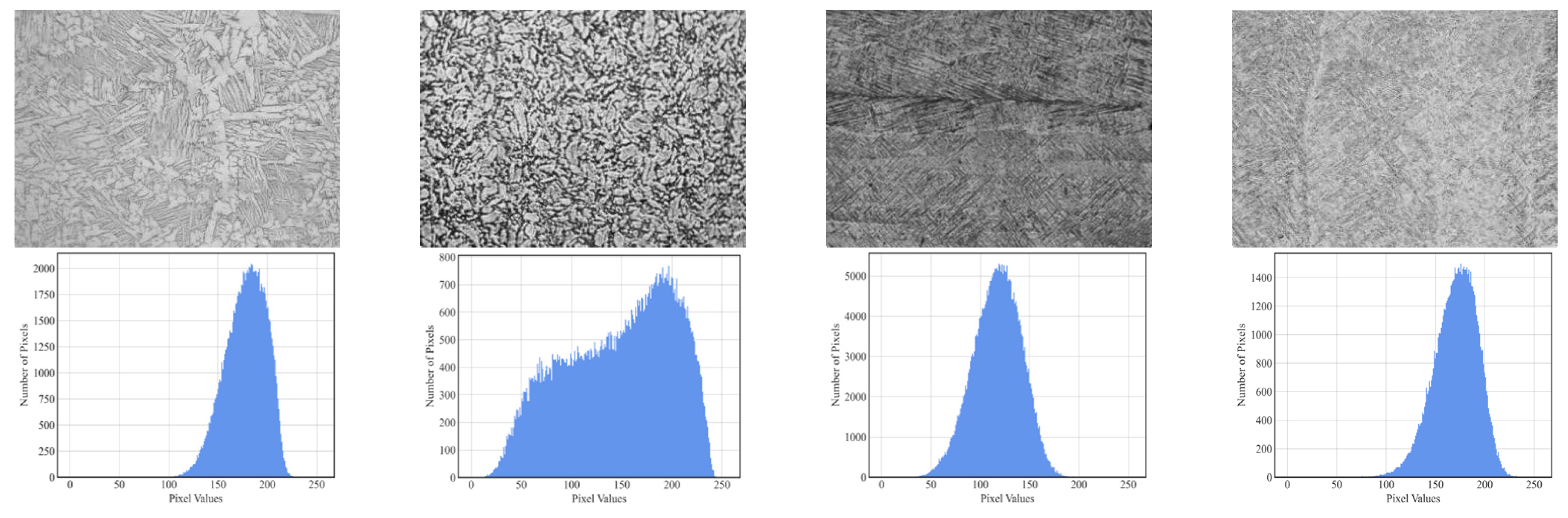


| Method | Role | Parameters |
|---|---|---|
| Mean Filtering (MF) | Remove noise and smooth image | Ksize = (3,3) (Based on OpenCV) |
| Gaussian Filtering (GF) | Remove noise and smooth image | Ksize = (3,3), sigmaX = 0 (Based on OpenCV) |
| Gray Linear Transformation-1 (GLT-1) | Reduce brightness and contrast | Y = kx + b, x represents pixel value, k = 0.75, b = 0 |
| Gray Linear Transformation-2 (GLT-2) | Increase brightness and contrast | Y = kx + b, k = 1.15, b = 0 |
| Gamma Correction-1 (GC-1) | Increase brightness and highlight dark details | Y = xγ, x is divided by 255, x ∈ [0, 1]. γ = 0.5 |
| Gamma Correction-2 (GC-2) | Reduce brightness and highlight bright details | Y = xγ, x ∈ [0, 1]. γ = 1.7 |
| Contrast Limited Adaptive Histogram Equalization (CLAHE) | Enhance local contrasts of the image | clipLimit = 2.0, titleGridsize = (4,4) (Based on OpenCV) |
| Histogram Equalization (HE) | Enhance contrasts and details of the image | Default parameters (Based on OpenCV) |
| Strength Grade | UTS Interval (MPa) | Proportion of Samples (%) |
|---|---|---|
| Low-strength | 28 | |
| Medium-strength | 35 | |
| High-strength | 37 |
| Crop | Scale | Linear Scaling | Min–Max | Z-Score | Mean R2 | Standard Deviation |
|---|---|---|---|---|---|---|
| √ | √ | 0.061 | 0.029 | |||
| √ | √ | 0.111 | 0.017 | |||
| √ | √ | 0.074 | 0.018 | |||
| √ | √ | 0.079 | 0.006 | |||
| √ | √ | 0.061 | 0.031 | |||
| √ | √ | 0.102 | 0.026 | |||
| √ | 0.047 | 0.021 | ||||
| √ | 0.026 | 0.020 | ||||
| Mean baseline | −0.003 | 0 | ||||
| Linear Regression | Random Forest | Crop | Scale | Mean R2 |
|---|---|---|---|---|
| √ | √ | −0.024 | ||
| √ | √ | 0.003 | ||
| √ | √ | −0.028 | ||
| √ | √ | 0.109 | ||
| Mean baseline | −0.003 | |||
| MF | GF | GLT-1 | GLT2-2 | GC-1 | GC-2 | CLAHE | HE | Mean R2 | Standard Deviation |
|---|---|---|---|---|---|---|---|---|---|
| √ | 0.117 | 0.029 | |||||||
| √ | 0.126 | 0.017 | |||||||
| √ | 0.080 | 0.018 | |||||||
| √ | 0.058 | 0.006 | |||||||
| √ | 0.102 | 0.031 | |||||||
| √ | 0.089 | 0.026 | |||||||
| √ | 0.071 | 0.021 | |||||||
| √ | 0.163 | 0.020 | |||||||
| Mean baseline | −0.003 | 0 | |||||||
| MF | GF | GLT-1 | GLT2-2 | GC-1 | GC-2 | CLAHE | HE | Mean R2 |
|---|---|---|---|---|---|---|---|---|
| √ | 0.093 | |||||||
| √ | 0.082 | |||||||
| √ | 0.045 | |||||||
| √ | 0.014 | |||||||
| √ | 0.052 | |||||||
| √ | 0.024 | |||||||
| √ | −0.086 | |||||||
| √ | −0.043 | |||||||
| Mean baseline | −0.003 | |||||||
| MF | GF | GLT-1 | GLT-2 | GC-1 | GC-2 | CLAHE | HE | Mean R2 |
|---|---|---|---|---|---|---|---|---|
| √ | 0.016 | |||||||
| √ | 0.085 | |||||||
| √ | 0.111 | |||||||
| √ | 0.139 | |||||||
| √ | −0.021 | |||||||
| √ | 0.048 | |||||||
| √ | −0.016 | |||||||
| √ | −0.057 | |||||||
| Mean baseline | −0.003 | |||||||
| Subset | Sample Size | Mean R2 | Standard Deviation |
|---|---|---|---|
| SLM-based | 56 | 0.298 | 0.003 |
| DED-based | 16 | 0.360 | 1.47 × 10−5 |
| EBM-based | 18 | 0.329 | 6.66 × 10−5 |
| Subset | Sample Size | Mean R2 |
|---|---|---|
| SLM-based | 56 | 0.137 |
| DED-based | 16 | 0.148 |
| EBM-based | 18 | -0.233 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, Y.; Duan, W. Predictive Capability Evaluation of Micrograph-Driven Deep Learning for Ti6Al4V Alloy Tensile Strength Under Varied Preprocessing Strategies. Metals 2025, 15, 586. https://doi.org/10.3390/met15060586
Xiong Y, Duan W. Predictive Capability Evaluation of Micrograph-Driven Deep Learning for Ti6Al4V Alloy Tensile Strength Under Varied Preprocessing Strategies. Metals. 2025; 15(6):586. https://doi.org/10.3390/met15060586
Chicago/Turabian StyleXiong, Yuqi, and Wei Duan. 2025. "Predictive Capability Evaluation of Micrograph-Driven Deep Learning for Ti6Al4V Alloy Tensile Strength Under Varied Preprocessing Strategies" Metals 15, no. 6: 586. https://doi.org/10.3390/met15060586
APA StyleXiong, Y., & Duan, W. (2025). Predictive Capability Evaluation of Micrograph-Driven Deep Learning for Ti6Al4V Alloy Tensile Strength Under Varied Preprocessing Strategies. Metals, 15(6), 586. https://doi.org/10.3390/met15060586





