Fatigue Life Analysis of Cruciform Specimens Under Biaxial Loading Using the Paris Equation
Abstract
1. Introduction
2. Materials and Methods
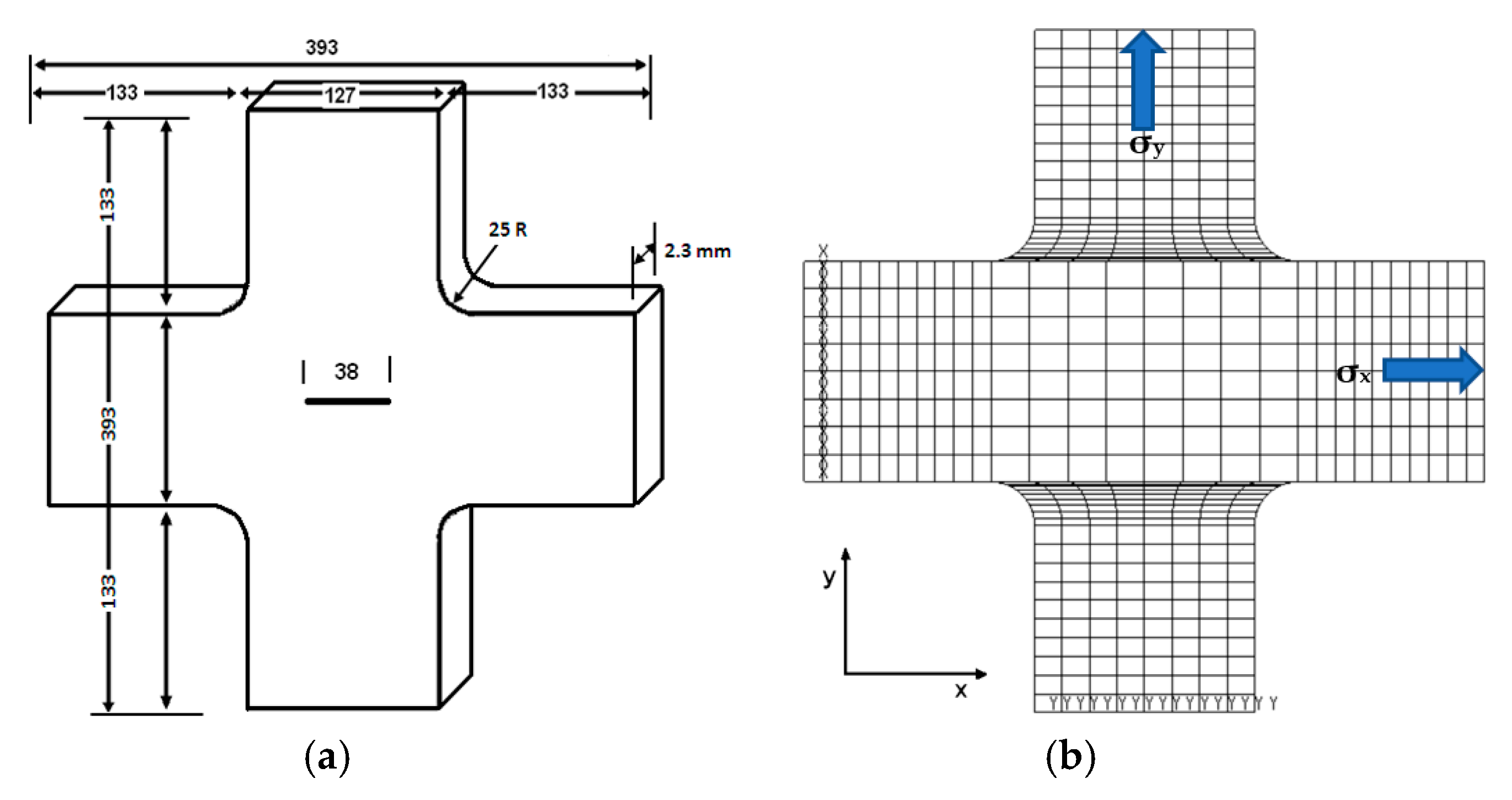
2.1. Specimen Materials and Geometry
2.2. Crack Simulation and Modeling
3. Numerical Calculations
3.1. Biaxial Ratios and Mixed-Mode Stresses
3.2. Paris’ Fatigue Life Calculation and LEFM Method
4. Results and Discussion
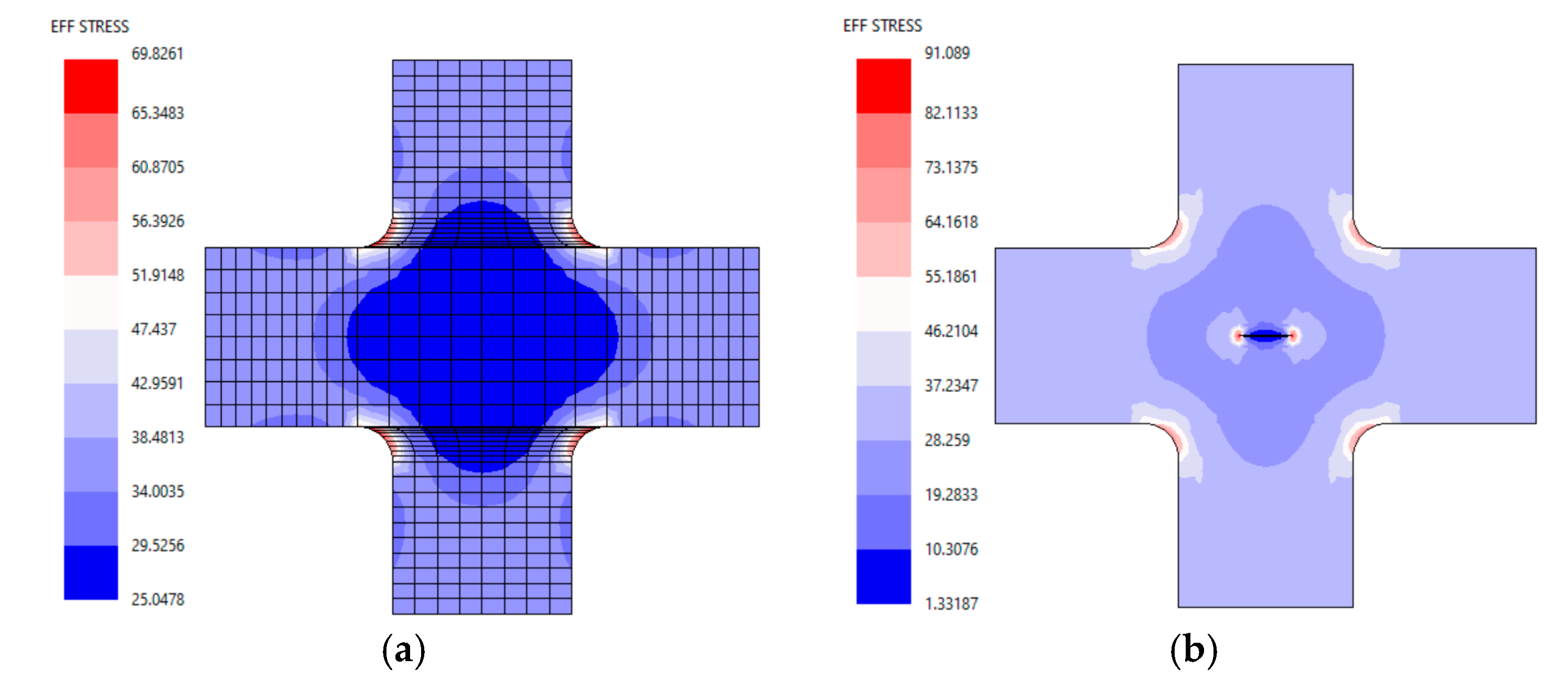
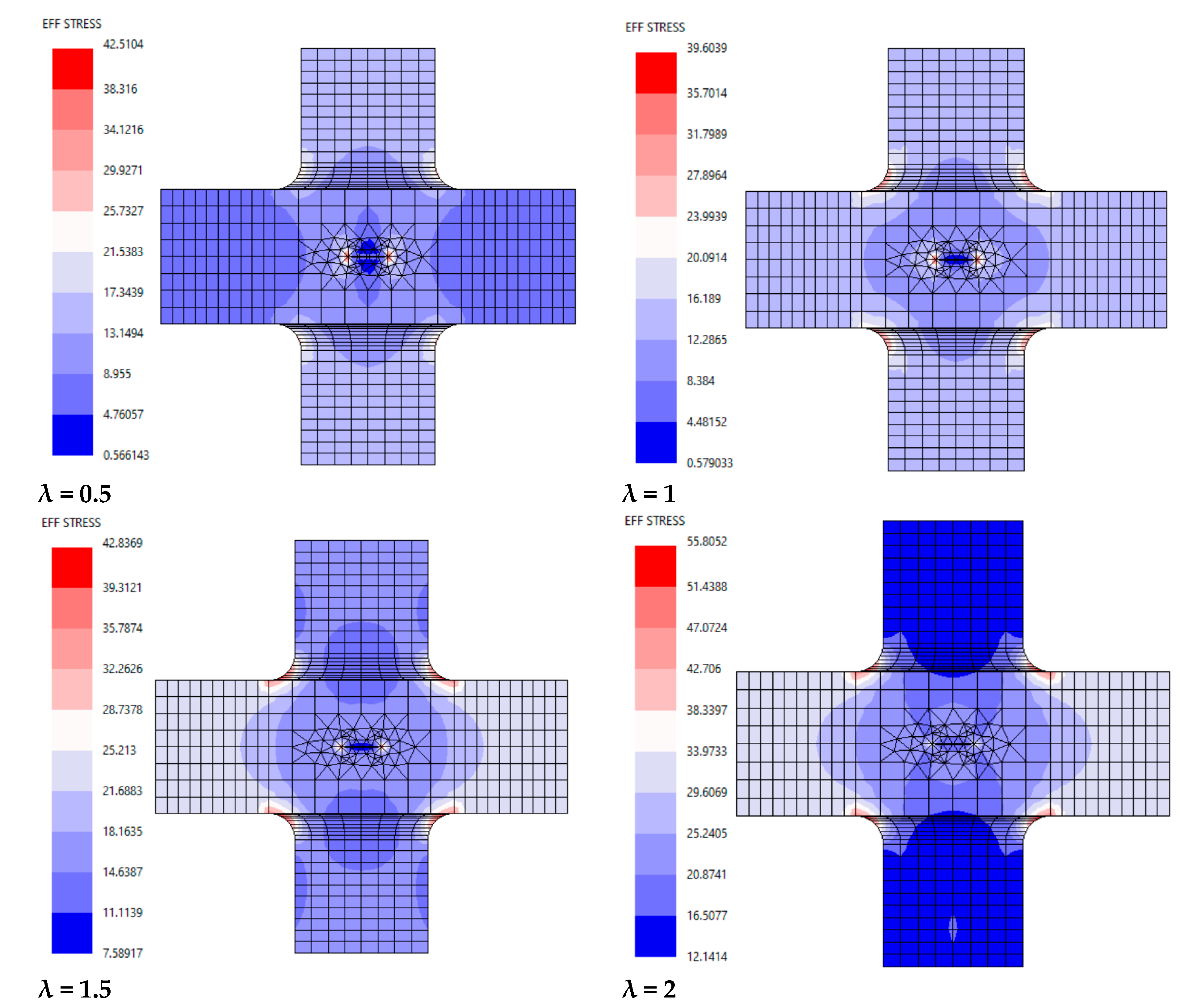
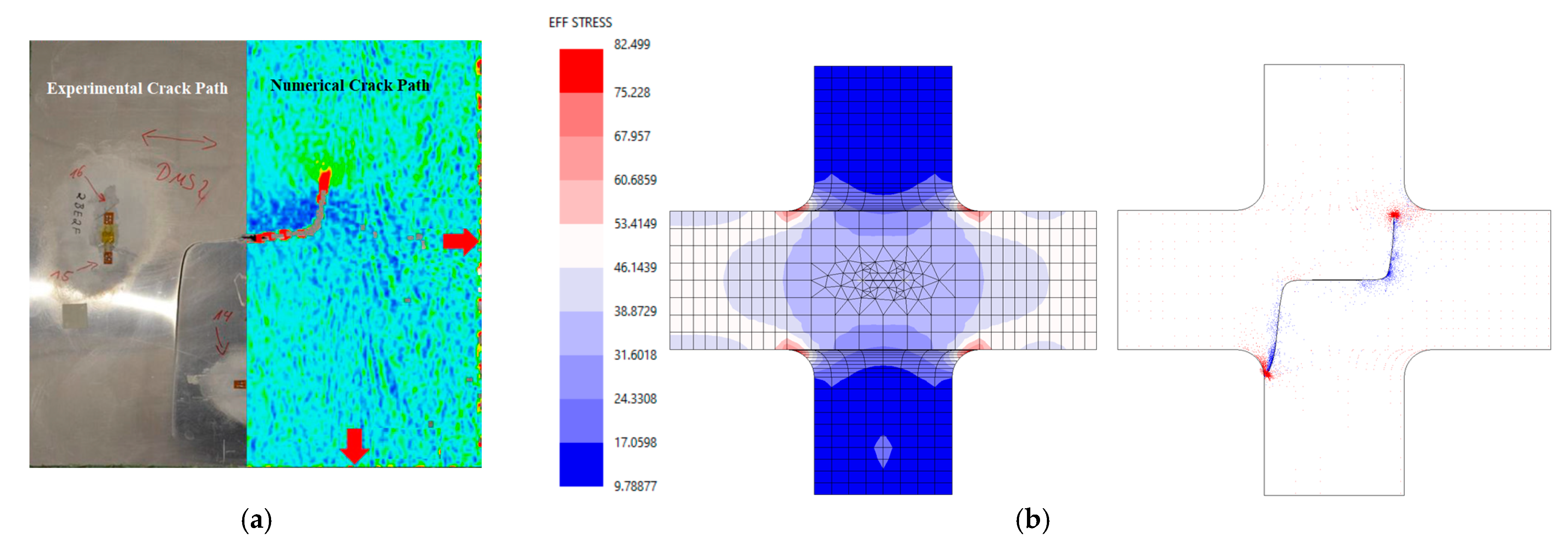
4.1. Effect of Biaxial Loading on Stress Distributions
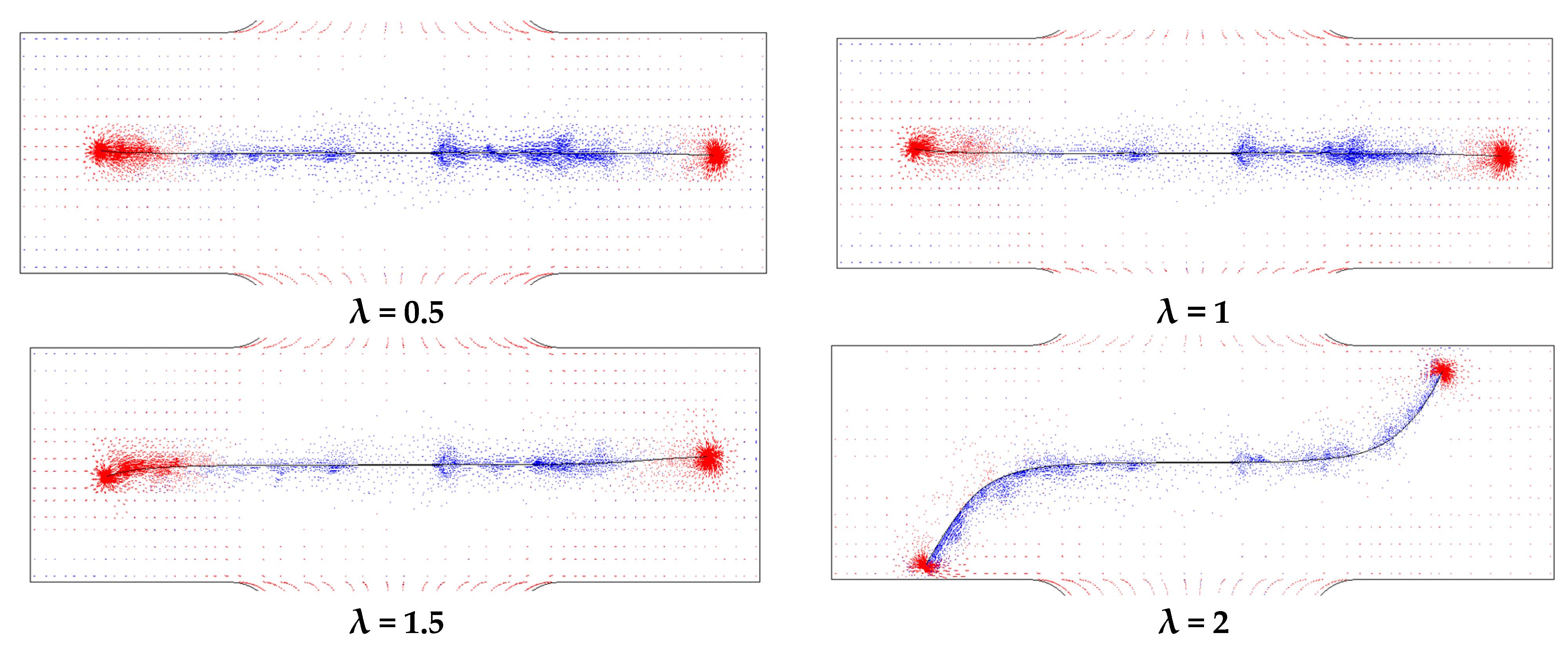
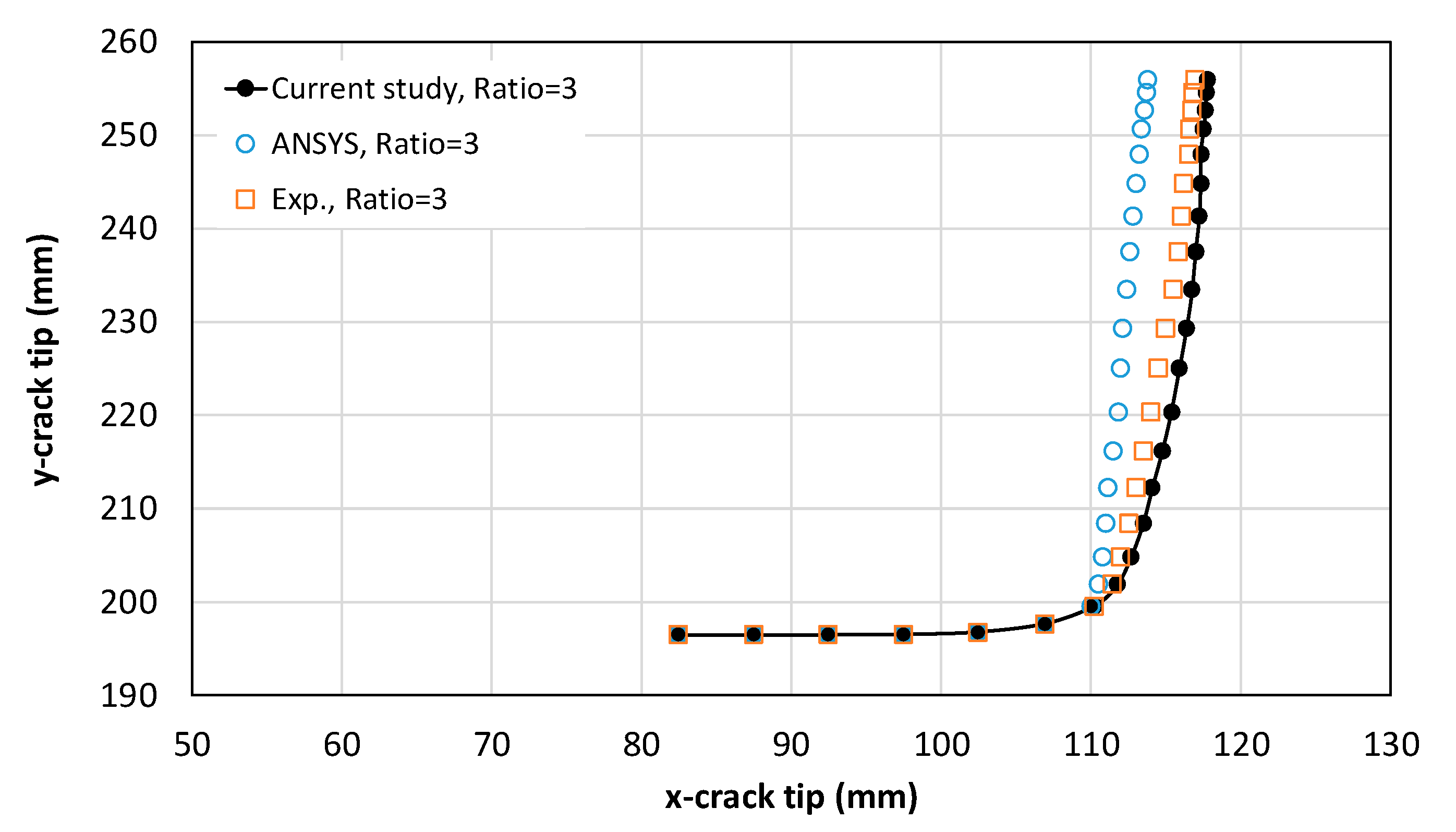
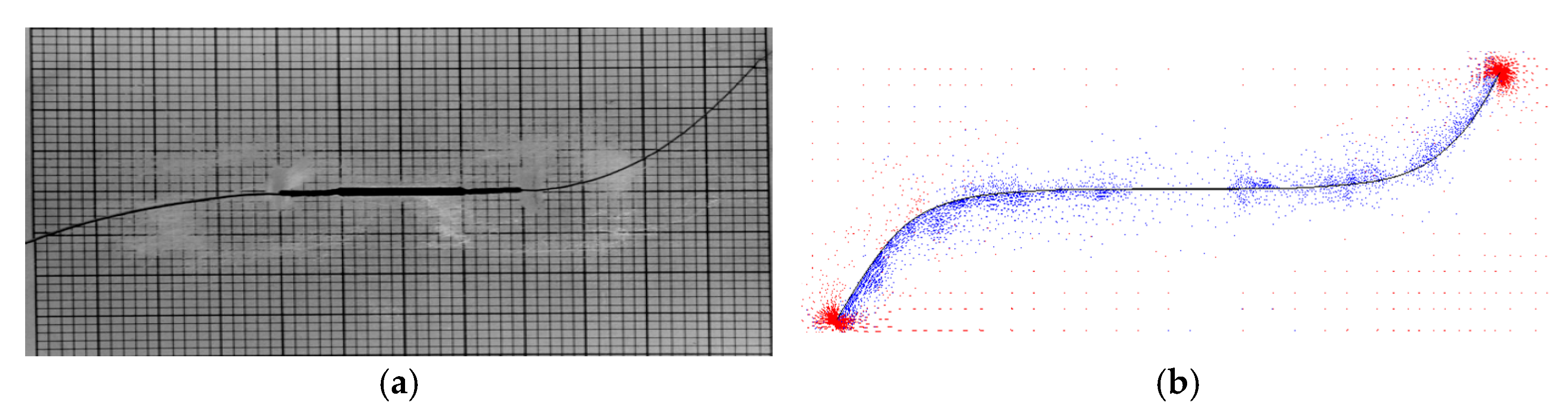
4.2. Effect of Biaxial Loading on Crack Path and Propagation
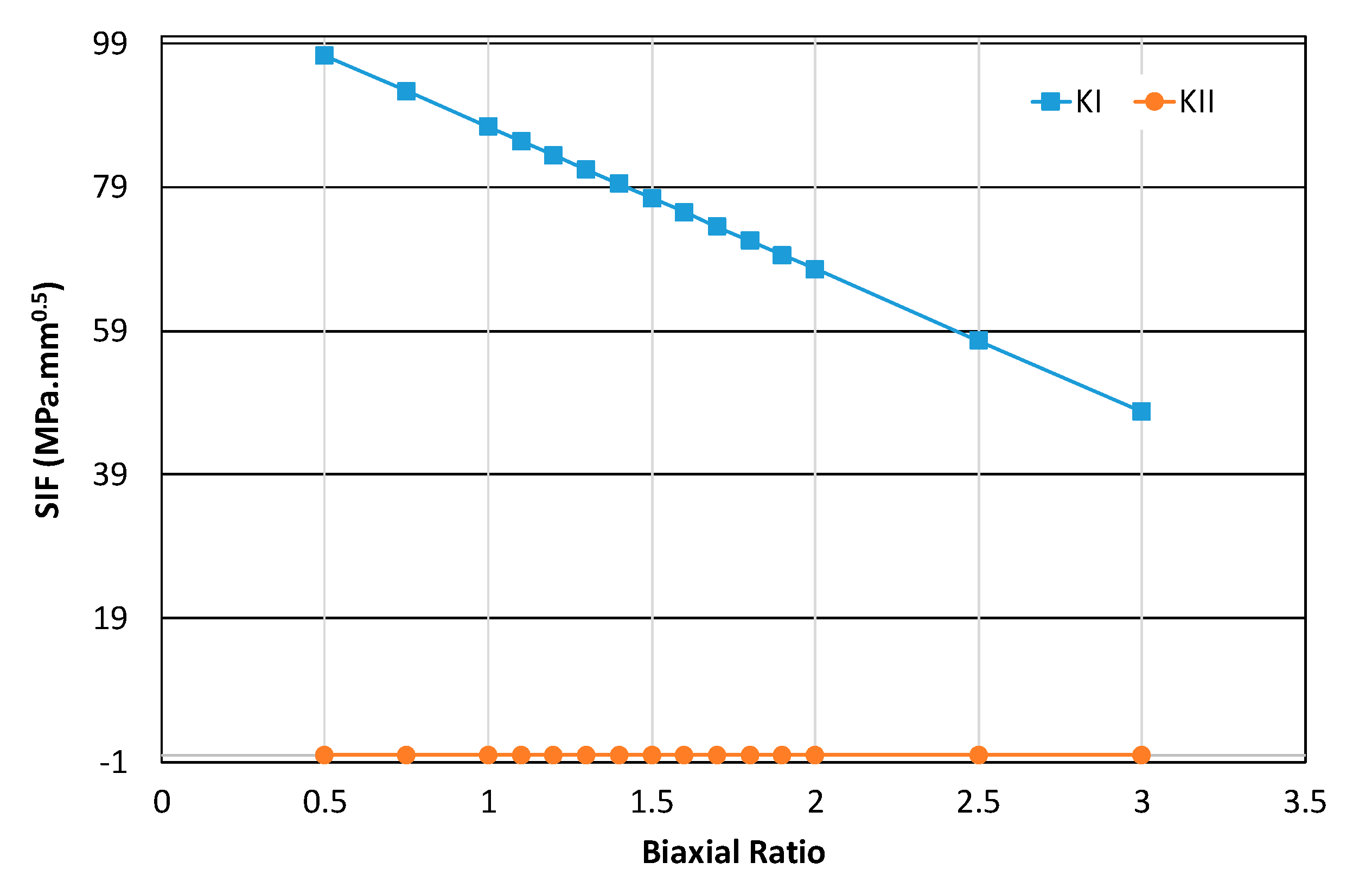
4.3. Effect of Biaxial Loading on Stress Intensity Factors Mode I-II
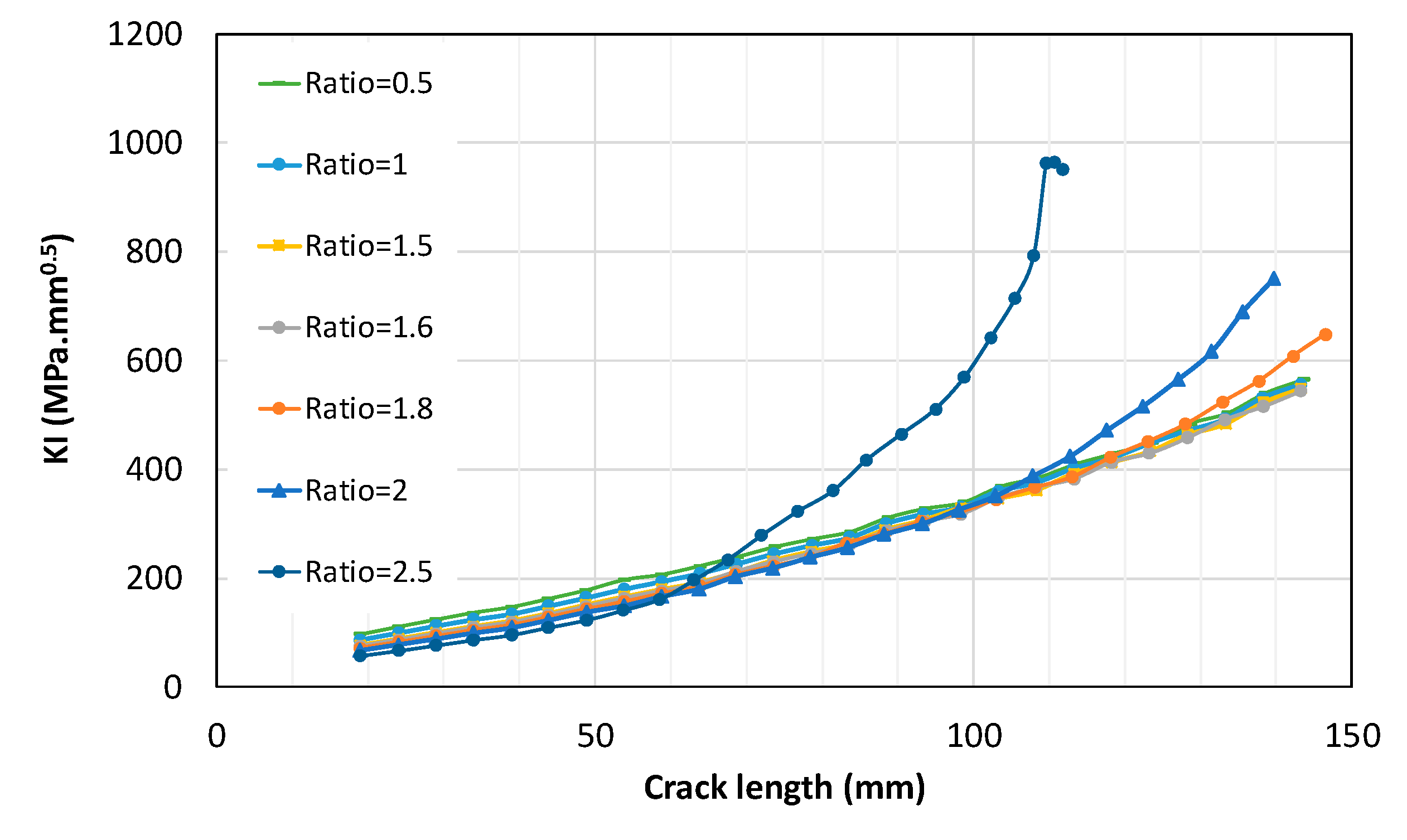
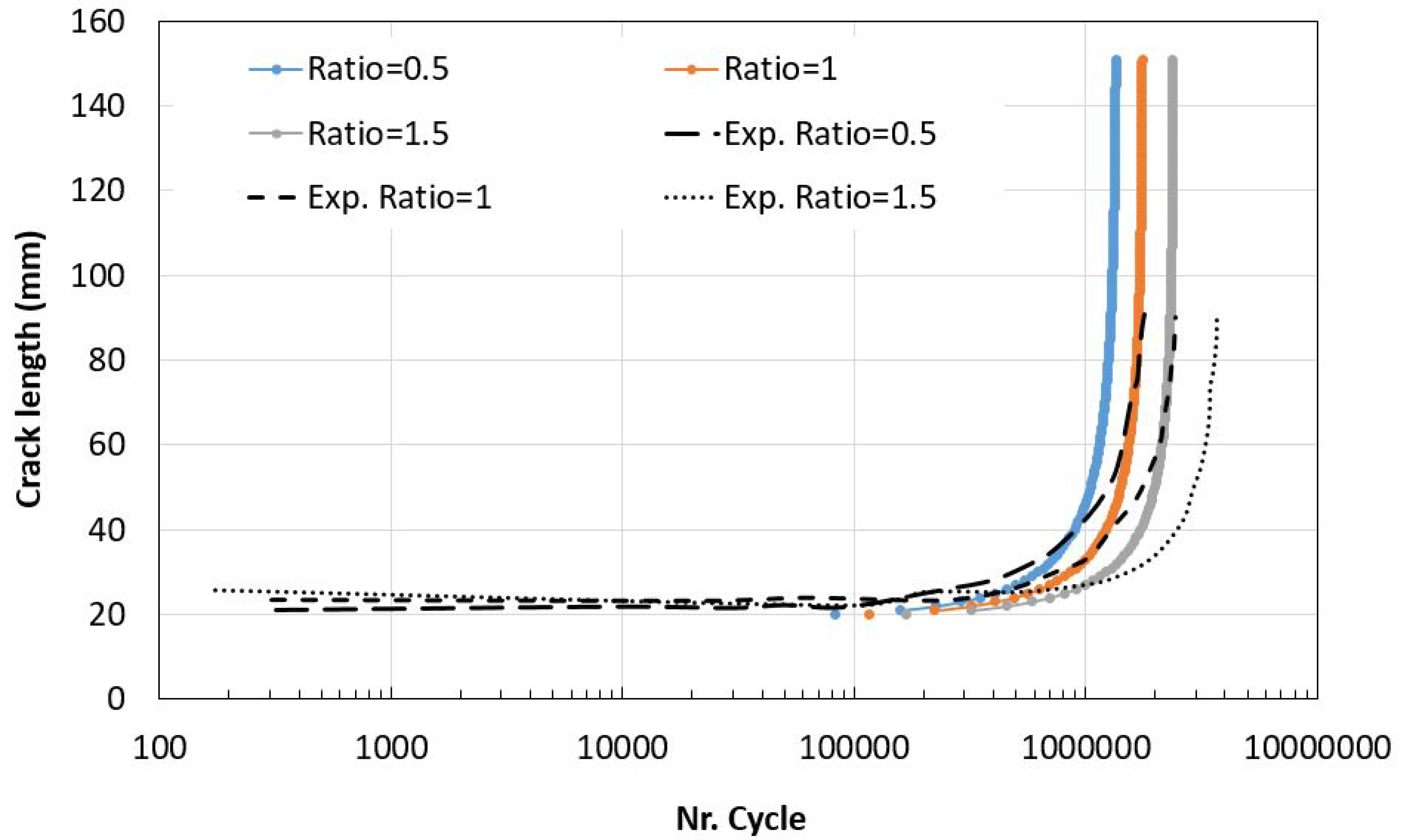
4.4. Fatigue Crack Growth: A Comparative Study
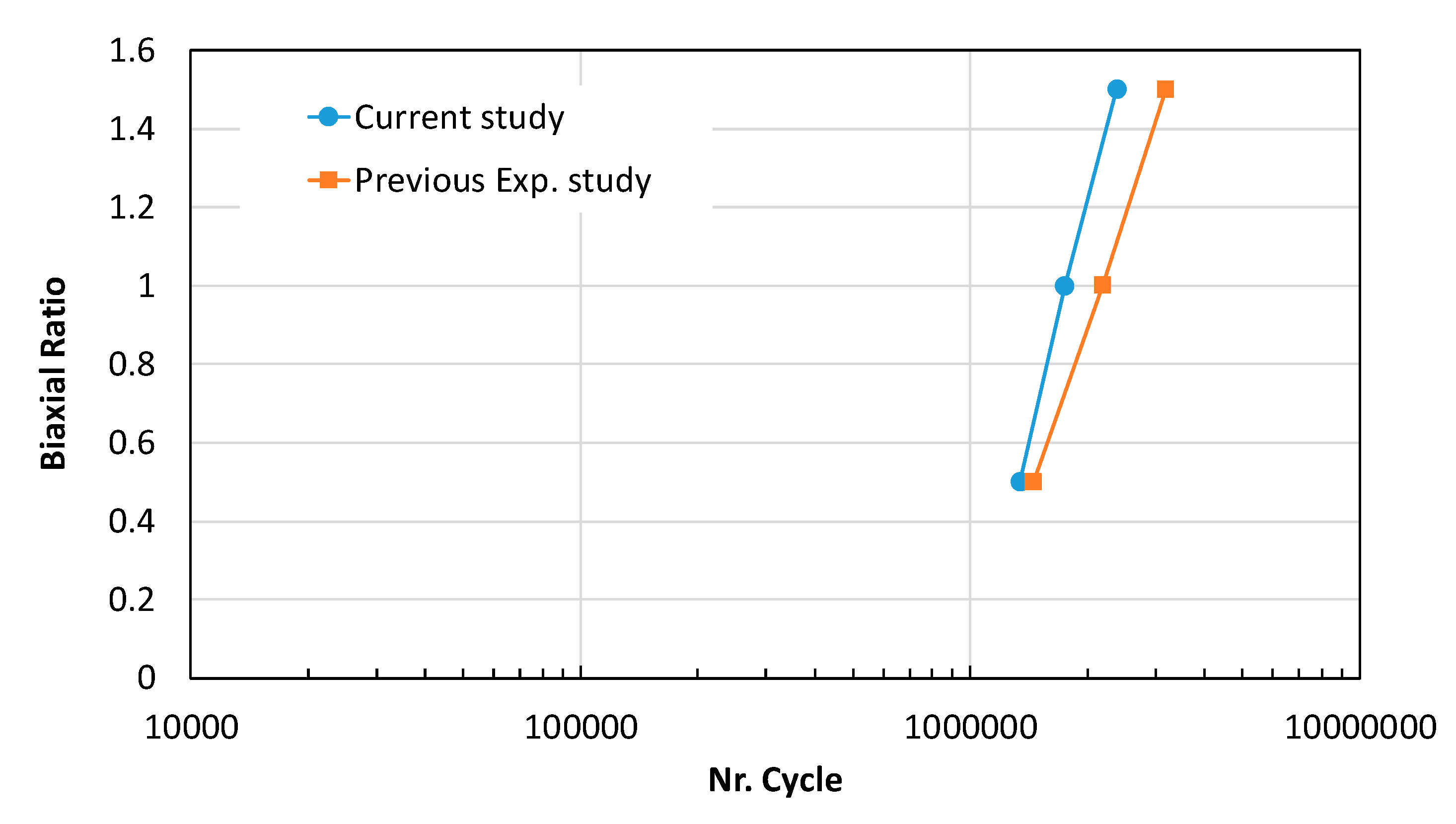
4.5. Fatigue Life and SIF Under High Biaxial Ratios
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Horta Muñoz, S.; Serna Moreno, M.D.C. Advances in Cruciform Biaxial Testing of Fibre-Reinforced Polymers. Polymers 2022, 14, 686. [Google Scholar] [CrossRef] [PubMed]
- Hammouda, M.M.I. Mixed-mode I/II stress intensity factors of a biaxially loaded plate with a central slant frictional crack: An analytical comprehensive solution. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 3501–3513. [Google Scholar] [CrossRef]
- Kikuchi, M.; Sato, T. Fatigue Crack Growth Simulation Under Mode I+II Mixed Mode Condition; The University of Tokyo: Tokyo, Japan, 2004; Volume 47, pp. 403–409. [Google Scholar]
- Lebedev, A.A.; Muzyka, N.R. Design of cruciform specimens for fracture toughness tests in biaxial tension (Review). Strength Mater. 1998, 30, 243–254. [Google Scholar] [CrossRef]
- Radon, J.C.; Leevers, P.S.; Culver, L.E. A simple testing technique for fracture under biaxial stresses: A mechanical-hydraulic machine for biaxial fatigue and ramp loading of precracked plate specimens is described. Preliminary results show that crack behavior in PMMA is independent of the stress acting parallel to the crack plane. Exp. Mech. 1977, 17, 228–232. [Google Scholar] [CrossRef]
- Wu, X.-D.; Wan, M.; Zhou, X.-B. Biaxial tensile testing of cruciform specimen under complex loading. J. Mater. Process. Technol. 2005, 168, 181–183. [Google Scholar] [CrossRef]
- Makinde, A.; Thibodeau, L.; Neale, K.W. Development of an apparatus for biaxial testing using cruciform specimens. Exp. Mech. 1992, 32, 138–144. [Google Scholar] [CrossRef]
- Erdogan, F.; Sih, G.C. On the crack extension in plates under plane loading and transverse shear. J. Basic Eng. 1963, 85, 519–525. [Google Scholar] [CrossRef]
- Liu, J.-Y.; Bao, W.-J.; Zhao, J.-Y.; Zhou, C.-Y. Fatigue Crack Growth Behavior of CP-Ti Cruciform Specimens with Mixed Mode I-II Crack under Biaxial Loading. Materials 2022, 15, 1926. [Google Scholar] [CrossRef]
- Cornell Fracture Group. FRANC2D. English. Cornell University. 2015. Available online: https://cfg.cornell.edu/software/ (accessed on 20 May 2025).
- Al-Mukhtar, A.M.; Biermann, H.; Hübner, P.; Henkel, S. Determination of Some Parameters for Fatigue Life in Welded Joints Using Fracture Mechanics Method. J. Mater. Eng. Perform. 2010, 19, 1225–1234. [Google Scholar] [CrossRef]
- Al-Mukhtar, A.; Biermann, H.; Henkel, S.; Hübner, P. Comparison of the Stress Intensity Factor of Load-Carrying Cruciform Welded Joints with Different Geometries. J. Mater. Eng. Perform. 2010, 19, 802–809. [Google Scholar] [CrossRef]
- Men, M.; Meng, B.; Wan, M. Investigation on the biaxial tensile testing method for metal foil using cruciform specimen. Theor. Appl. Fract. Mech. 2024, 133, 104577. [Google Scholar] [CrossRef]
- Serna Moreno, M.C.; Muñoz, S.H. Experimental evaluation of the use of cruciform specimens for biaxial stability analysis. Compos. Part B Eng. 2024, 286, 111764. [Google Scholar] [CrossRef]
- Baptista, R.; Infante, V.; Madeira, J.F.A. Optimization of a cruciform specimen for fatigue crack growth under in and out-of-phase in-plane biaxial loading conditions. Mech. Adv. Mater. Struct. 2023, 30, 1649–1666. [Google Scholar] [CrossRef]
- Jin, P.; Liu, Z.; Chen, H.; Liu, M.; Wang, X.; Chen, X. Mixed-mode I&II fatigue crack growth behaviors of 16MND5 steel: The role of crack driving forces and crack closure. Int. J. Fatigue 2024, 183, 108228. [Google Scholar] [CrossRef]
- Al-Mukhtar, A.M. Mixed-Mode Crack Propagation in Cruciform Joint using Franc2D. J. Fail. Anal. Prev. 2016, 16, 326–332. [Google Scholar] [CrossRef]
- Shlyannikov, V.N.; Tumanov, A.V.; Zakharov, A.P. The mixed mode crack growth rate in cruciform specimens subject to biaxial loading. Theor. Appl. Fract. Mech. 2014, 73, 68–81. [Google Scholar] [CrossRef]
- Lee, E.U.; Taylor, R.E. Fatigue behavior of aluminum alloys under biaxial loading. Eng. Fract. Mech. 2011, 78, 1555–1564. [Google Scholar] [CrossRef]
- Lee, E.U.; Taylor, R. Biaxial Fatigue of Aluminum Alloy 1100. In Proceedings of the Multiaxial Fatigue, 9th International Conference on Multiaxial Fatigue and Fracture (ICMFF9), Parma, Italy, 7–9 June 2010; pp. 63–82. [Google Scholar]
- Bao, W.-J.; Liu, J.-Y.; Tao, Z.-L.; Zhao, G.-Z.; Zhou, C.-Y. Investigation of Fatigue Crack Growth in TA2 Cruciform Specimen with an Inclined Crack, Considering Stress Ratio and Biaxial Load Ratio. Crystals 2022, 12, 1530. [Google Scholar] [CrossRef]
- Fahem, A.; Kidane, A.; Sutton, M. Loading Rate Effects for Flaws Undergoing Mixed-Mode I/III Fracture. Exp. Mech. 2021, 61, 1291–1307. [Google Scholar] [CrossRef]
- Jahanshahi, S.; Chakherlou, T.N.; Rostampoureh, A.; Aalami, M.R. Evaluating the validity of the cohesive zone model in mixed mode I + III fracture of Al-alloy 2024-T3 adhesive joints using DBM-DCB tests. Int. J. Fract. 2023, 240, 143–165. [Google Scholar] [CrossRef]
- Marsavina, L. Linear Elastic Fracture Mechanics. Compr. Mech. Mater. 2024, 1, 172–191. [Google Scholar] [CrossRef]
- Gao, T.; Yuanzhou, Z.; Ji, B.; Xie, Z. Vision-based fatigue crack automatic perception and geometric updating of finite element model for welded joint in steel structures. Comput.-Aided Civ. Infrastruct. Eng. 2024, 39, 1659–1675. [Google Scholar] [CrossRef]
- Ribeiro, A.S.; de Jesus, A.M.P. Fatigue Behaviour of Welded Joints Made of 6061-T651 Aluminium Alloy. In Aluminium Alloys, Theory and Applications; IntechOpen: London, UK, 2011. [Google Scholar] [CrossRef][Green Version]
- Meguid, S.A. Linear Elastic Fracture Mechanics. In Atomistic and Continuum Fracture Mechanics of Solids; Springer Nature: Cham, Switzerland, 2024; pp. 185–225. [Google Scholar] [CrossRef]
- Hua, W.; Li, J.; Zhu, Z.; Li, A.; Huang, J.; Gan, Z.; Dong, S. A review of mixed mode I-II fracture criteria and their applications in brittle or quasi-brittle fracture analysis. Theor. Appl. Fract. Mech. 2023, 124, 103741. [Google Scholar] [CrossRef]
- Breitbarth, E.; Besel, M. Fatigue crack deflection in cruciform specimens subjected to biaxial loading conditions. Int. J. Fatigue 2018, 113, 345–350. [Google Scholar] [CrossRef]
- Pook, L.P. Five decades of crack path research. Eng. Fract. Mech. 2010, 77, 1619–1630. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, B.; Wang, S.; Huang, M.; Zheng, H.; Xiao, S. Mixed mode (I/II) fatigue crack growth in butt-welded joints using actual stress intensity factors. Theor. Appl. Fract. Mech. 2025, 138, 104894. [Google Scholar] [CrossRef]




| λ | σy | σx |
|---|---|---|
| 1 | 35.7 | 35.7 |
| 1.1 | 35.7 | 39.27 |
| 1.2 | 35.7 | 42.84 |
| 1.3 | 35.7 | 46.41 |
| 1.4 | 35.7 | 49.98 |
| 1.5 | 35.7 | 53.55 |
| 1.6 | 35.7 | 57.12 |
| 1.7 | 35.7 | 60.69 |
| 1.8 | 35.7 | 64.26 |
| 1.9 | 35.7 | 67.83 |
| 2 | 35.7 | 71.4 |
| 2.5 | 35.7 | 89.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Mukhtar, A.; Koenke, C. Fatigue Life Analysis of Cruciform Specimens Under Biaxial Loading Using the Paris Equation. Metals 2025, 15, 579. https://doi.org/10.3390/met15060579
Al-Mukhtar A, Koenke C. Fatigue Life Analysis of Cruciform Specimens Under Biaxial Loading Using the Paris Equation. Metals. 2025; 15(6):579. https://doi.org/10.3390/met15060579
Chicago/Turabian StyleAl-Mukhtar, Ahmed, and Carsten Koenke. 2025. "Fatigue Life Analysis of Cruciform Specimens Under Biaxial Loading Using the Paris Equation" Metals 15, no. 6: 579. https://doi.org/10.3390/met15060579
APA StyleAl-Mukhtar, A., & Koenke, C. (2025). Fatigue Life Analysis of Cruciform Specimens Under Biaxial Loading Using the Paris Equation. Metals, 15(6), 579. https://doi.org/10.3390/met15060579







