Isothermal Oxidation Kinetics of Iron Powders Under Vapor Atmosphere
Abstract
1. Introduction
2. Experiment
2.1. Materials
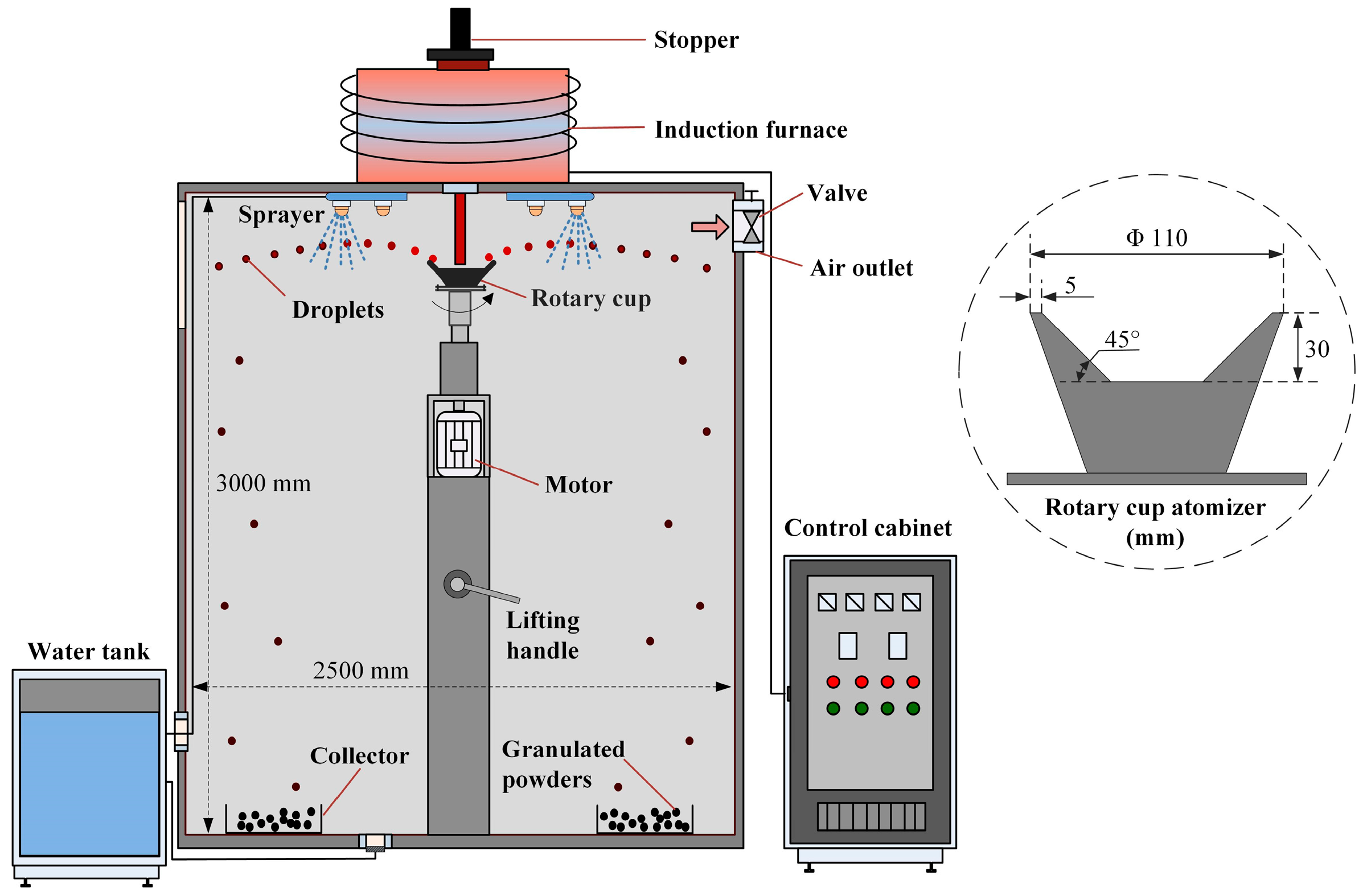
2.2. Granulation Experiment
2.3. Oxidation Characteristics of Granulated Powders
2.4. Isothermal TG Measurements of Pure Iron Powders
3. Results and Discussion
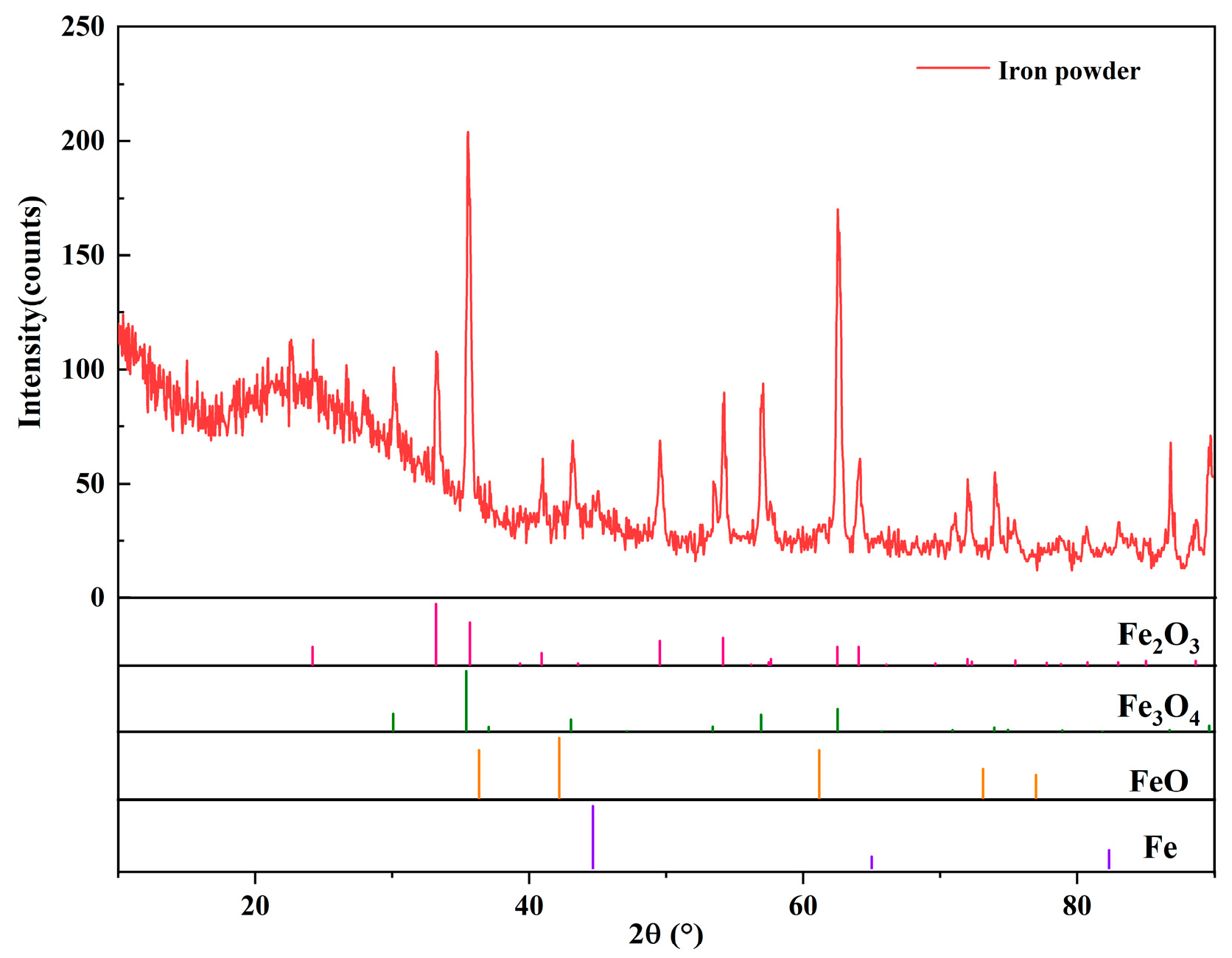
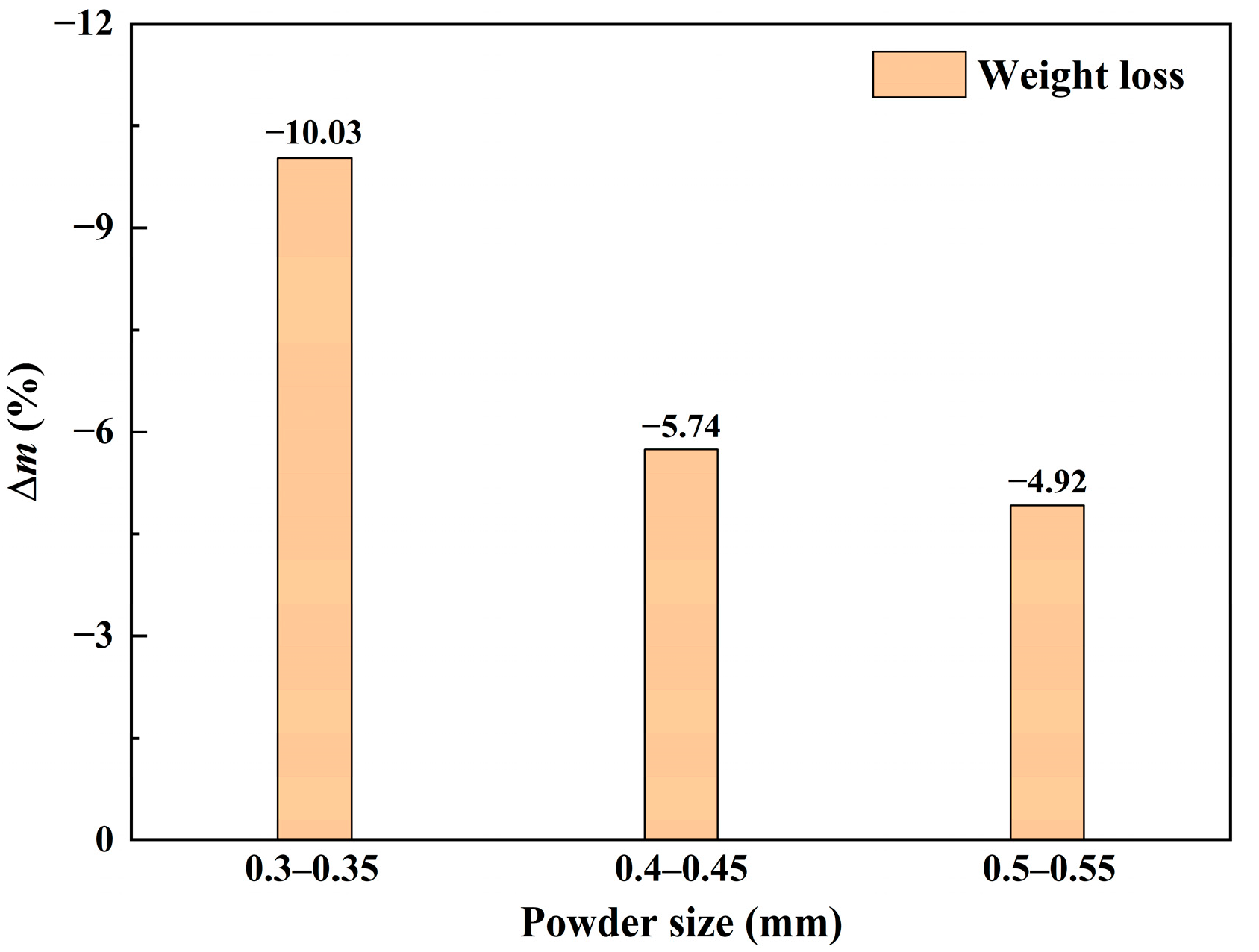
3.1. Oxidation Characteristics of Granulated Powders
3.2. Isothermal TG Analysis of Pure Iron Powders
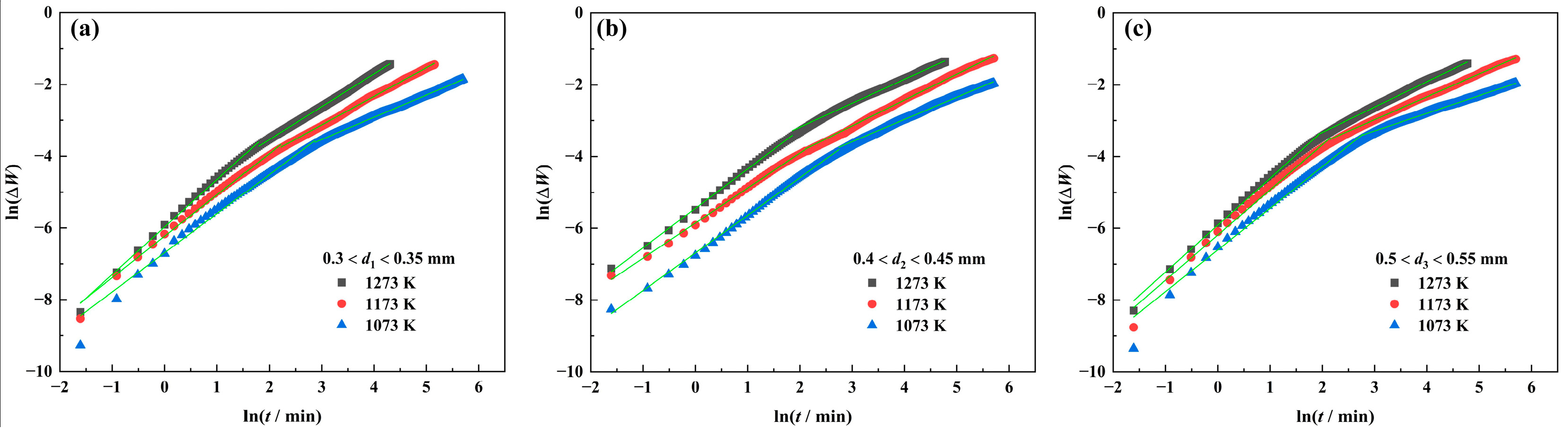
3.2.1. TG Analysis
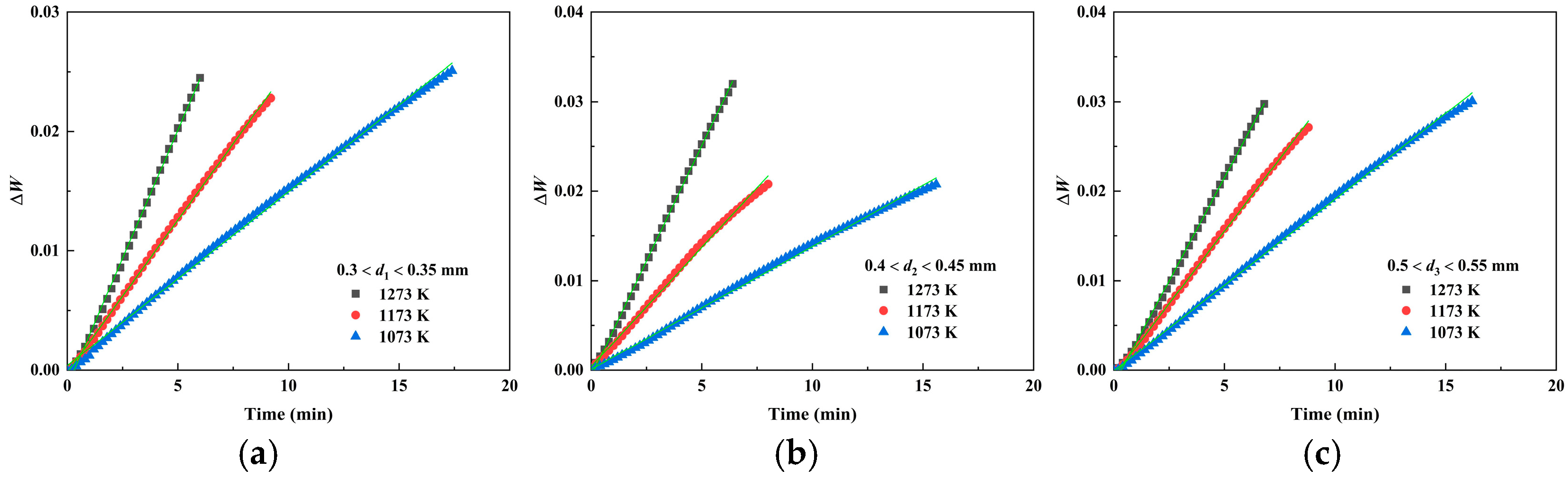
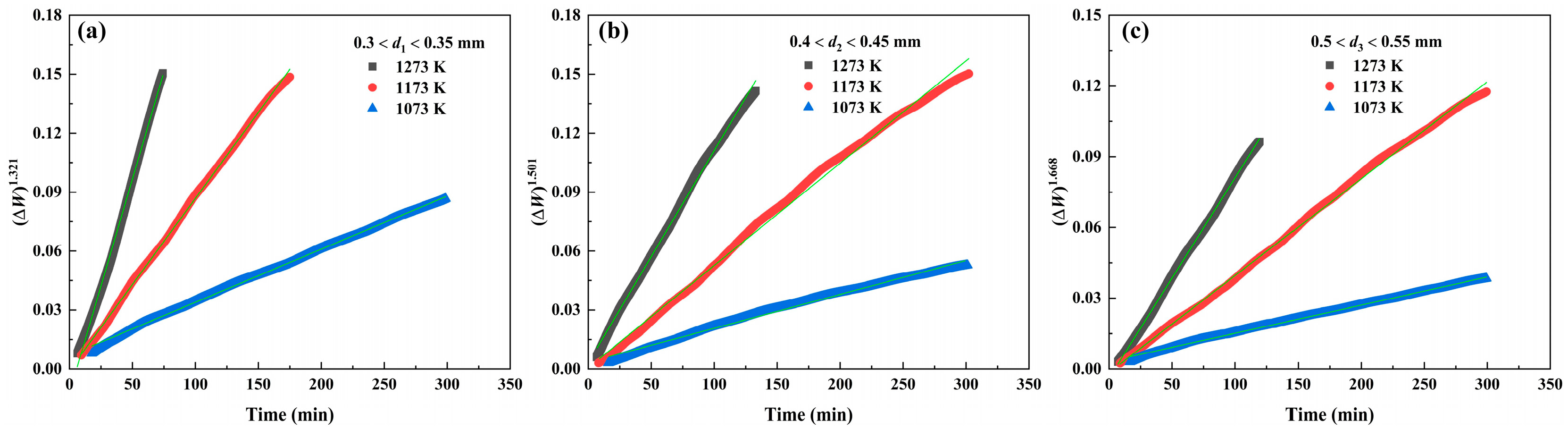
3.2.2. Reaction Mechanism
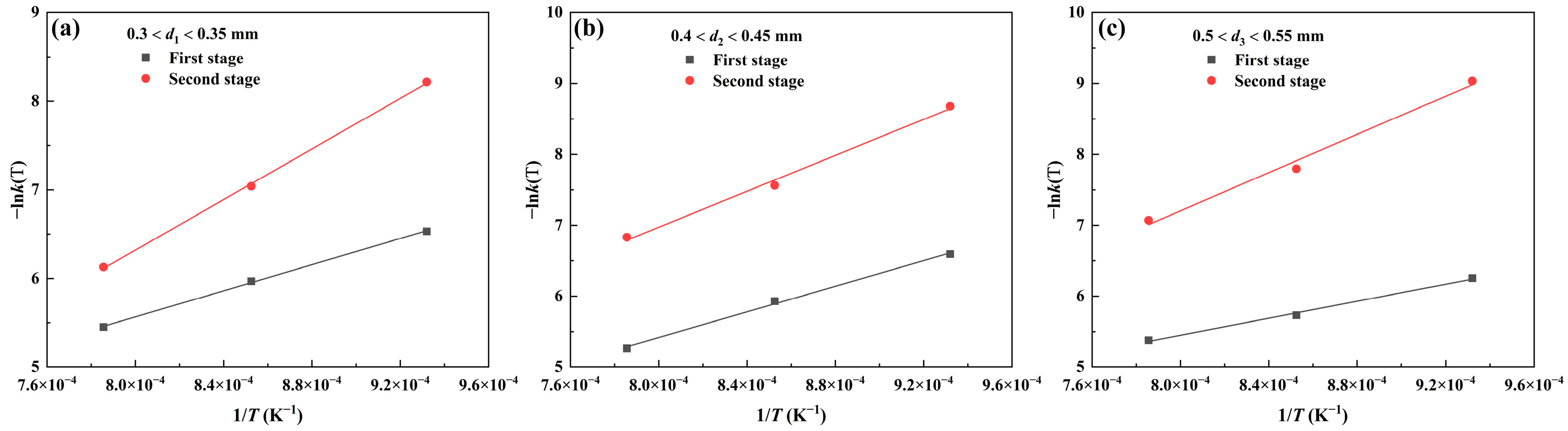
3.2.3. Reaction Activation Energy
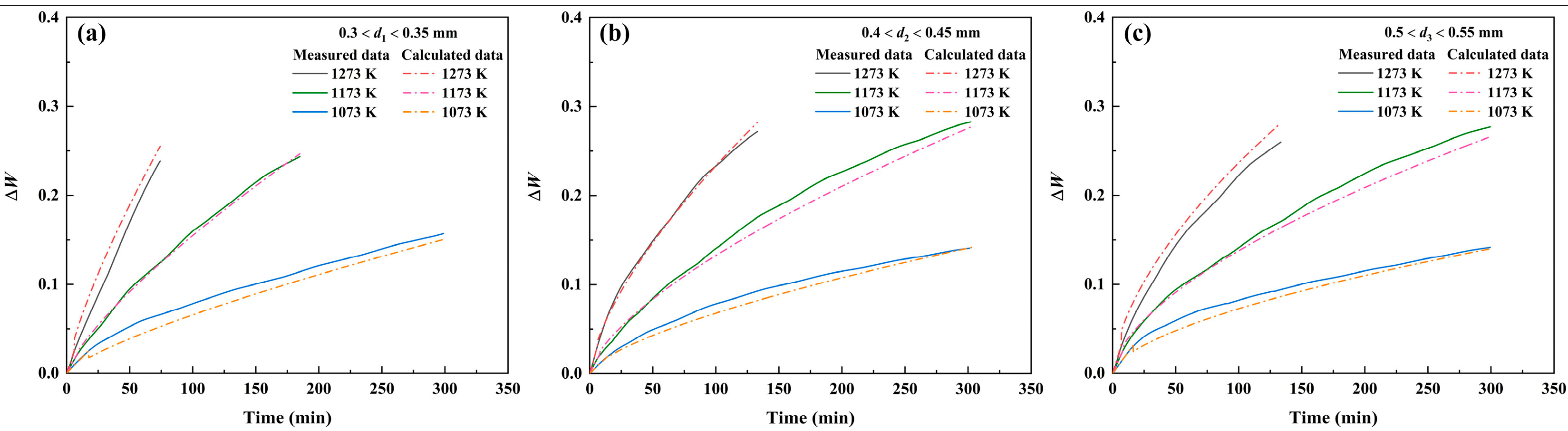
3.2.4. Oxidation Reaction Rate
3.2.5. Discussion
4. Conclusions
- (1)
- An oxide layer formed on the granulated powder outer surface consists of Fe3O4 and Fe2O3.
- (2)
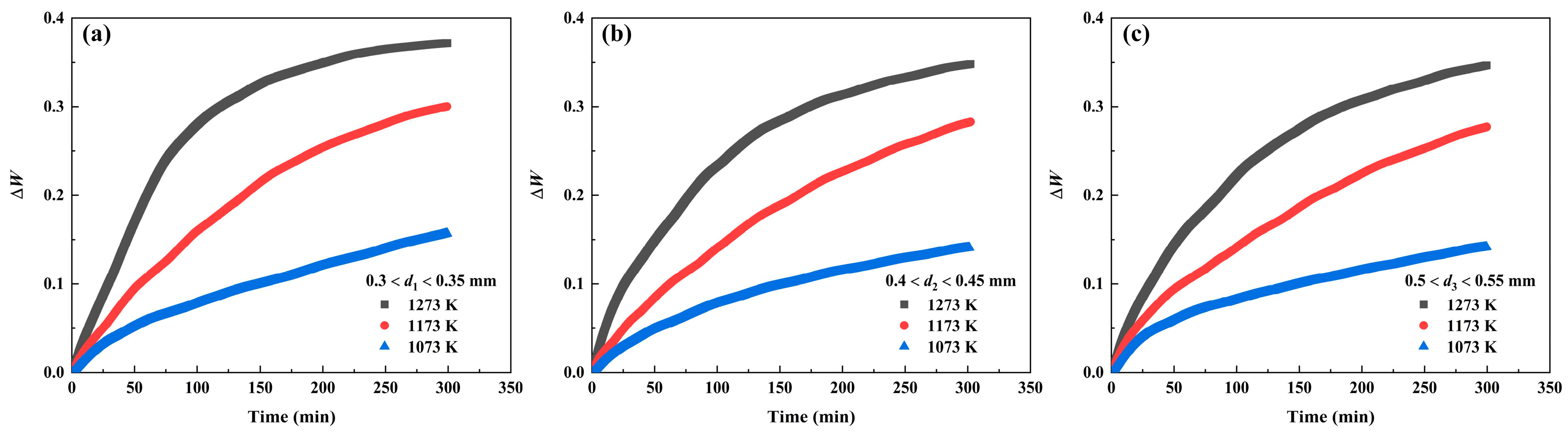
- The oxidation rate of pure iron powders under vapor atmosphere increases with the increasing temperature and decreasing powder size.
- (3)
- The kinetic mechanism of first stage consistent with the linear law, and the rate-controlling step is a chemical reaction; whereas the kinetic mechanism of second stage consistent with the integrated law of line and parabola, and the rate-controlling step include internal diffusion and chemical reaction.
- (4)
- For iron powders in the range of 0.3 mm < d1 < 0.35 mm, 0.4 mm < d2 < 0.45 mm, and 0.5 mm < d3 < 0.55 mm, the reaction activation energy at the first oxidation stage is 61.276, 75.119, and 49.919 KJ/mol; the reaction activation energy at the second oxidation stage is 118.648, 105.354, and 111.968 KJ/mol.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, D.; Chu, J.; Li, J.; Qi, T.; Wang, W. Anti-caking in the production of titanium dioxide using low-grade titanium slag via the NaOH molten salt method. Powder Technol. 2012, 232, 99–105. [Google Scholar] [CrossRef]
- Tian, C. A Novel Approach for comprehensive utilization by leaching pyrite cinder with titanium dioxide waste acid by response surface methodology. ACS Omega 2024, 9, 8510–8519. [Google Scholar] [CrossRef]
- Narayan, R.; Raju, K. Use of calcined clay as part replacement of titanium dioxide in latex paint formulations. J. Appl. Polym. Sci. 2015, 77, 1029–1036. [Google Scholar] [CrossRef]
- Lv, W.; Liu, F.; Chu, M.; Lv, X.; Barati, M. Characterisation of titania slag produced by a novel process: Acidolysis performance. Can. Metall. Q. 2022, 61, 454–463. [Google Scholar] [CrossRef]
- Xiong, X.; Wang, Z.; Wu, F.; Li, X.; Guo, H. Preparation of TiO2 from ilmenite using sulfuric acid decomposition of the titania residue combined with separation of Fe3+ with EDTA during hydrolysis. Adv. Powder Technol. 2013, 24, 60–67. [Google Scholar] [CrossRef]
- Wu, J.; Xu, B.; Dong, Z.; Zhou, Y.; Xu, L.; Li, G.; Jiang, T. Preparation of high-purity reduced iron powder by Höganäs process from ultra-pure magnetite concentrate. J. Cent. South Univ. 2023, 9, 3006–3020. [Google Scholar] [CrossRef]
- Liu, Y.; Niu, S.; Li, F.; Zhu, Y.; He, Y. Preparation of amorphous Fe-based magnetic powder by water atomization. Powder Technol. 2011, 213, 36–40. [Google Scholar] [CrossRef]
- Liu, J.; Dong, Y.; Wang, P.; Zhao, H.; Pang, J.; Li, X.; Zhang, J. Simulation and experiment investigations on fabrication of Fe-based amorphous powders by a novel atomization process equipped with assisted gas nozzles. J. Iron Steel Res. Int. 2022, 30, 1142–1155. [Google Scholar] [CrossRef]
- Huang, Q.; He, W.; Lv, X. Preparation of iron powders with semi-steel by rotary cup atomizer. J. Iron Steel Res. 2020, 32, 563–570. [Google Scholar]
- Mizuochi, T.; Akiyama, T.; Shimada, T.; Kasai, E.; Yagi, J. Feasibility of rotary cup atomizer for slag granulation. ISIJ Int. 2001, 41, 1423–1428. [Google Scholar] [CrossRef]
- Sahoo, K.; Kumar, S. Influence of surface and edge profile of a spinning disc on its atomization characteristics in direct drop mode. Chem. Eng. Sci. 2024, 287, 119743. [Google Scholar] [CrossRef]
- Xie, J.; Zhao, Y.; Dunkley, J. Effects of processing conditions on powder particle size and morphology in centrifugal atomisation of tin. Powder Metall. 2004, 47, 168–172. [Google Scholar] [CrossRef]
- Tan, Y.; Ding, B.; Shi, j.; Yan, H.; Wu, Y.; Wu, J. Modelling the film fragmentation of industrial-scale centrifugal granulation of high-temperature molten slag. Powder Technol. 2023, 426, 118654. [Google Scholar] [CrossRef]
- Liu, J.; Yu, Q.; Duan, W.; Qin, Q. Experimental investigation on ligament formation for molten slag granulation. Appl. Therm. Eng. 2014, 73, 888–893. [Google Scholar] [CrossRef]
- Plookphol, T.; Wisutmethangoon, S.; Gonsrang, S. Influence of process parameters on SAC305 lead-free solder powder produced by centrifugal atomization. Powder Technol. 2011, 214, 506–512. [Google Scholar] [CrossRef]
- Liu, J.; Yu, Q.; Guo, Q. Experimental investigation of liquid disintegration by rotary cups. Chem. Eng. Sci. 2012, 73, 44–50. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, H.; Tan, Y.; Wang, H.; Liao, Q. Analogue experimental study on centrifugal-air blast granulation for molten slag. Appl. Therm. Eng. 2015, 88, 157–164. [Google Scholar] [CrossRef]
- Liu, J.; Yu, Q.; Li, P.; Du, W. Cold experiments on ligament formation for blast furnace slag granulation. Appl. Therm. Eng. 2012, 40, 351–357. [Google Scholar] [CrossRef]
- Tan, Y.; Chen, X.; Jia, M.; Ding, B.; Wu, J.; Qin, Y. Redefining limits: Impact of nozzle diameter on film flow and atomization beyond the synchronizing radius. Chem. Eng. J. 2025, 505, 159816. [Google Scholar] [CrossRef]
- Vourlias, G.; Pistofidis, N.; Chrissafis, K. High-temperature oxidation of precipitation hardening steel. Thermochim. Acta 2008, 478, 28–33. [Google Scholar] [CrossRef]
- Kofstad, P.; Hauffe, K.; Kjllesdal, H.; Siekevitz, P.; Diczfalusy, E. Investigation on oxidation mechanism of titanium. Acta Chem. Scand. 1958, 12, 239–266. [Google Scholar] [CrossRef]
- Chen, R.; Yeun, W. Review of the high-temperature oxidation of iron and carbon steels in air or oxygen. Oxid. Met. 2003, 59, 433–468. [Google Scholar] [CrossRef]
- Yan, R.; Liu, Z.; Chu, M.; Liu, P.; Dang, S.; Li, N.; Li, X. Effect of coke reactivity on reduction behaviours and non-isothermal kinetics of sinter at 1173–1373 K. Ironmak. Steelmak. 2023, 50, 1502–1511. [Google Scholar] [CrossRef]
- Wu, M.; Li, Z.; Huang, J.; Wang, Q.; Li, T.; Yang, S.; He, H.; Jiang, Y. Non-isothermal kinetics of coke and iron ore melting reduction with variable activation energy model. Fuel 2024, 357, 129991. [Google Scholar] [CrossRef]

| Raw Material | Powder Size/mm | Oxidation Temperature/K |
|---|---|---|
| Iron powder 1 | 0.3 < d1 < 0.35 1 | 1073, 1173, 1273 |
| Iron powder 2 | 0.4 < d2 < 0.45 | 1073, 1173, 1273 |
| Iron powder 3 | 0.5 < d3 < 0.55 | 1073, 1173, 1273 |
| Powder Size/mm | Period | n | r | ||||
|---|---|---|---|---|---|---|---|
| 1073 K | 1173 K | 1273 K | 1073 K | 1173 K | 1273 K | ||
| 0.3 < d1 < 0.35 | First stage | 0.917 | 0.868 | 0.756 | 0.993 | 0.996 | 0.998 |
| Second stage | 1.616 | 1.255 | 1.092 | 0.999 | 0.999 | 0.999 | |
| 0.4 < d2 < 0.45 | First stage | 0.953 | 1.024 | 0.912 | 0.999 | 0.999 | 0.999 |
| Second stage | 1.616 | 1.387 | 1.499 | 0.997 | 0.998 | 0.998 | |
| 0.5 < d3 < 0.55 | First stage | 0.861 | 0.794 | 0.765 | 0.993 | 0.994 | 0.998 |
| Second stage | 2.028 | 1.565 | 1.412 | 0.999 | 0.999 | 0.998 | |
| Powder Size/mm | Period | k (10−3) | r | ||||
|---|---|---|---|---|---|---|---|
| 1073 K | 1173 K | 1273 K | 1073 K | 1173 K | 1273 K | ||
| 0.3 < d1 < 0.35 | First stage | 1.46 | 2.56 | 4.29 | 0.999 | 0.999 | 0.999 |
| 0.4 < d2 < 0.45 | First stage | 1.37 | 2.66 | 5.16 | 0.999 | 0.998 | 0.999 |
| 0.5 < d3 < 0.55 | First stage | 1.82 | 3.24 | 4.61 | 0.999 | 0.999 | 0.999 |
| Powder Size/mm | Period | k (10−3) | r | ||||
|---|---|---|---|---|---|---|---|
| 1073 K | 1173 K | 1273 K | 1073 K | 1173 K | 1273 K | ||
| 0.3 < d1 < 0.35 | Second stage | 0.27 | 0.88 | 2.18 | 0.999 | 0.999 | 0.998 |
| 0.4 < d2 < 0.45 | Second stage | 0.17 | 0.52 | 1.08 | 0.996 | 0.999 | 0.999 |
| 0.5 < d3 < 0.55 | Second stage | 0.12 | 0.41 | 0.85 | 0.999 | 0.999 | 0.999 |
| Powder Size/mm | Period | E | A |
|---|---|---|---|
| 0.3 < d1 < 0.35 | First stage | 61,275.58 | 1.39 |
| Second stage | 118,647.83 | 163.60 | |
| 0.4 < d2 < 0.45 | First stage | 75,119.11 | 6.11 |
| Second stage | 105,354.10 | 23.69 | |
| 0.5 < d3 < 0.55 | First stage | 49,918.79 | 0.52 |
| Second stage | 111,967.83 | 35.52 |
| Powder Size/mm | Period | Oxidation Reaction Rate Equations |
|---|---|---|
| 0.3 < d1 < 0.35 | First stage | ΔW = 1.39 exp(−61,275.58/RT) t |
| Second stage | (ΔW)1.321 = 163.60 exp(−118,647.83/RT) t | |
| 0.4 < d2 < 0.45 | First stage | ΔW = 6.11 exp(−75,119.11/RT) t |
| Second stage | (ΔW)1.501 = 23.69 exp(−105,354.10/RT) t | |
| 0.5 < d3 < 0.55 | First stage | ΔW = 0.52 exp(−49,918.79/RT) t |
| Second stage | (ΔW)1.668 = 35.52 exp(−111,967.83/RT) t |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, W.; Chen, J.; Deng, Y.; Yan, Z. Isothermal Oxidation Kinetics of Iron Powders Under Vapor Atmosphere. Metals 2025, 15, 553. https://doi.org/10.3390/met15050553
He W, Chen J, Deng Y, Yan Z. Isothermal Oxidation Kinetics of Iron Powders Under Vapor Atmosphere. Metals. 2025; 15(5):553. https://doi.org/10.3390/met15050553
Chicago/Turabian StyleHe, Wenchao, Jian Chen, Yin Deng, and Zhiming Yan. 2025. "Isothermal Oxidation Kinetics of Iron Powders Under Vapor Atmosphere" Metals 15, no. 5: 553. https://doi.org/10.3390/met15050553
APA StyleHe, W., Chen, J., Deng, Y., & Yan, Z. (2025). Isothermal Oxidation Kinetics of Iron Powders Under Vapor Atmosphere. Metals, 15(5), 553. https://doi.org/10.3390/met15050553






