Optimization of Roll Configuration and Investigation of Forming Process in Three-Roll Planetary Rolling of Stainless Steel Seamless Tubes
Abstract
1. Introduction
2. Simulation Parameter Setting
3. Effect of Roller Rotation Speed on Three-Roll Planetary Rolling Performance
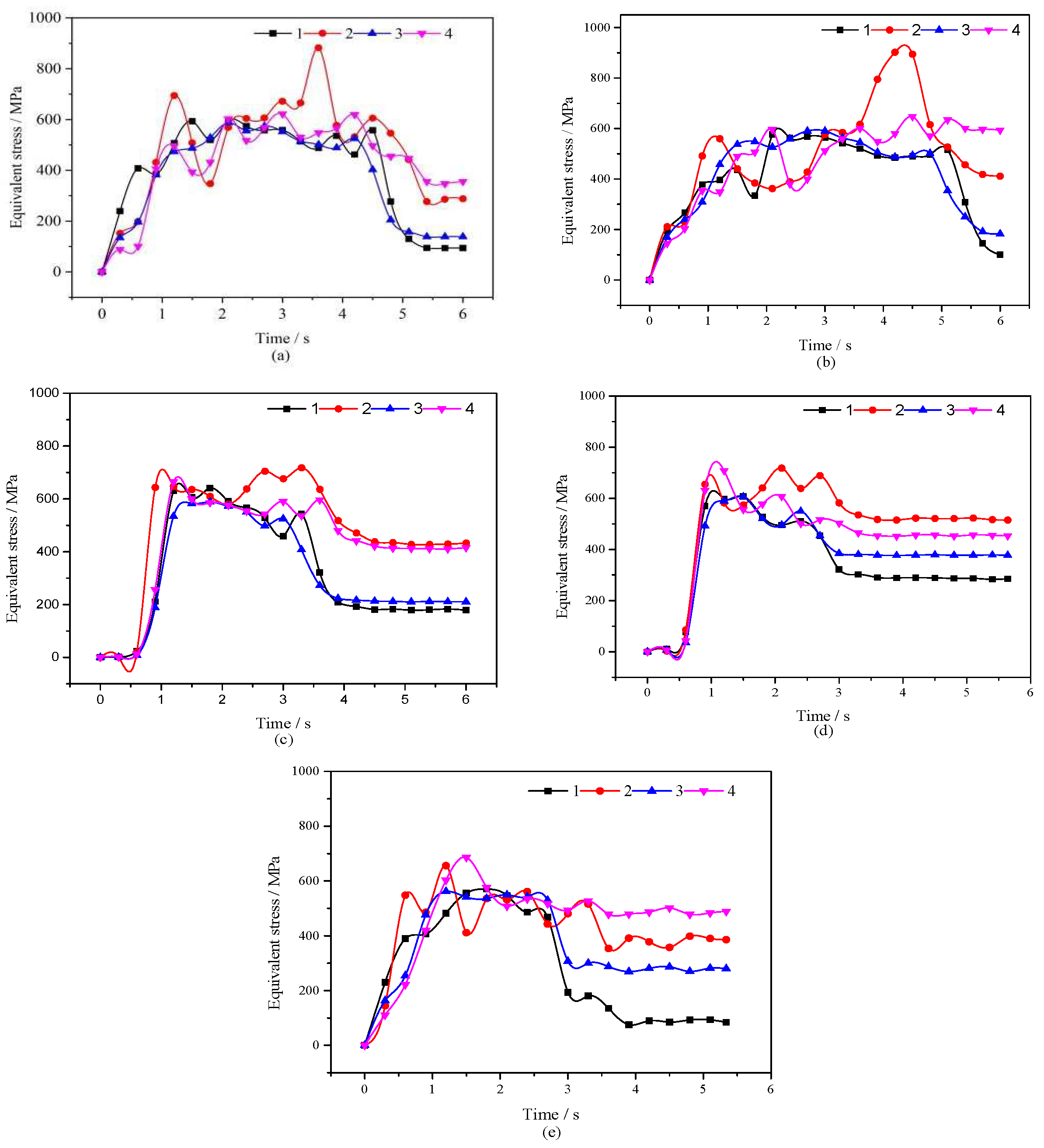
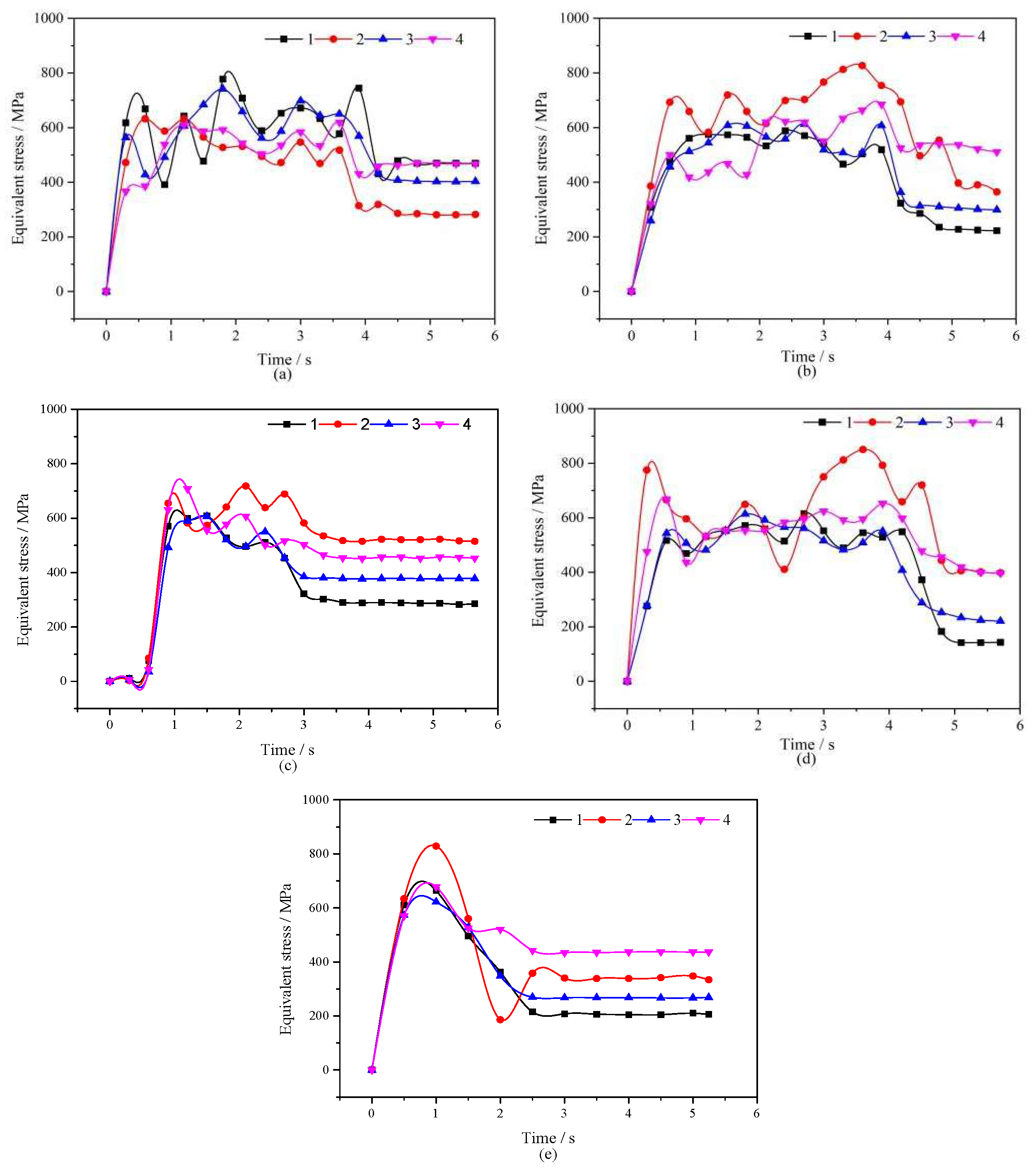
3.1. Equivalent Stress
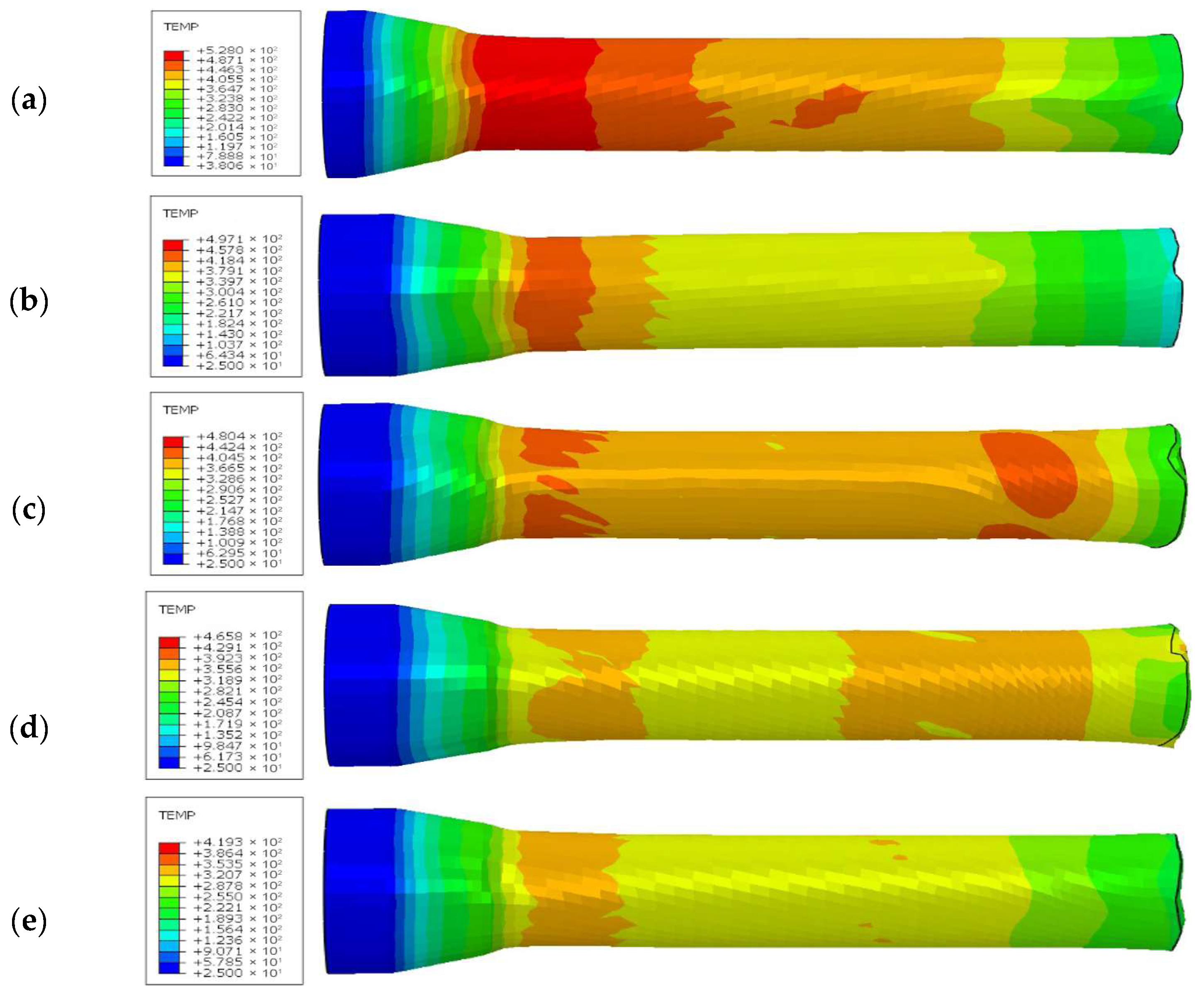
3.2. Deformation Temperature
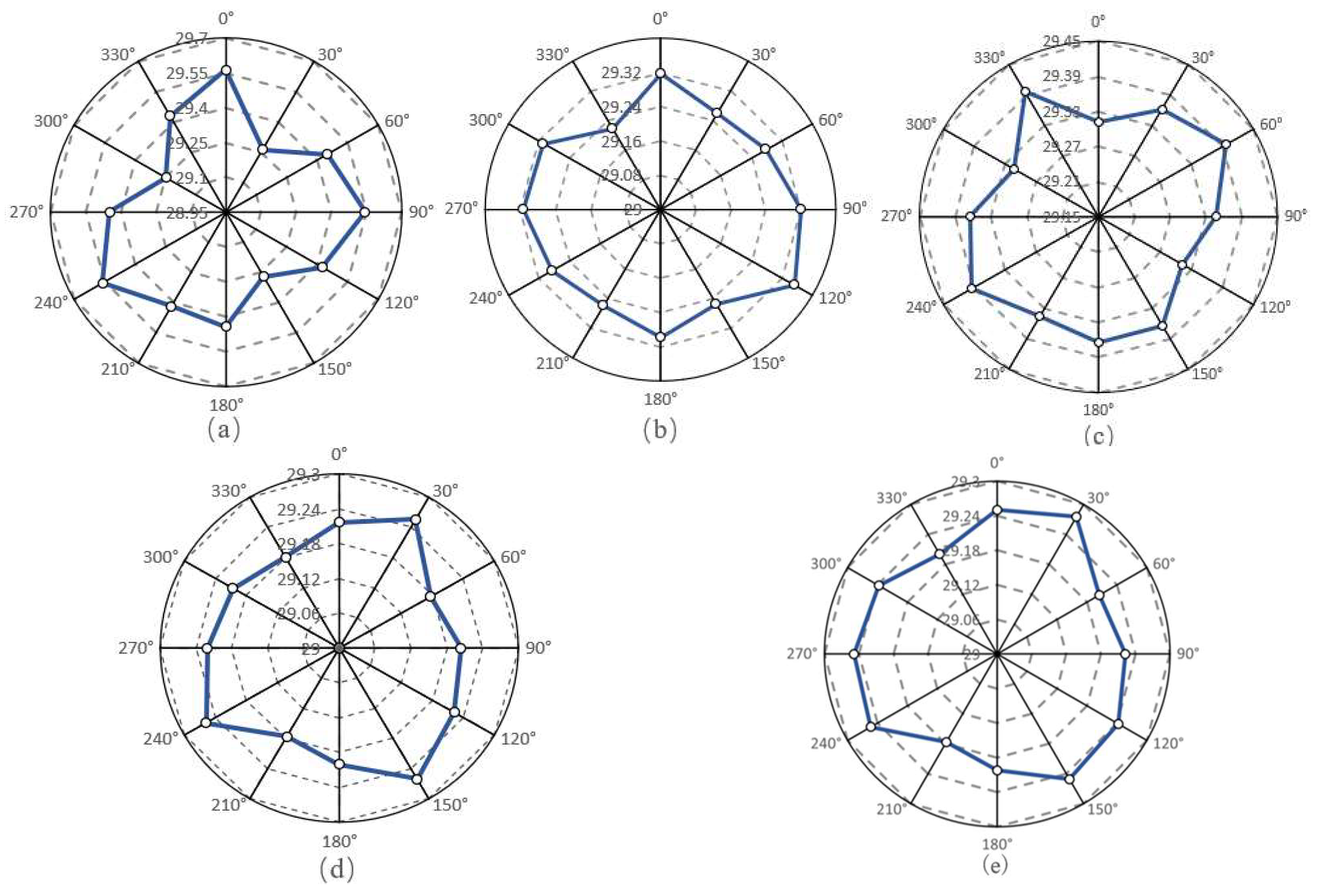
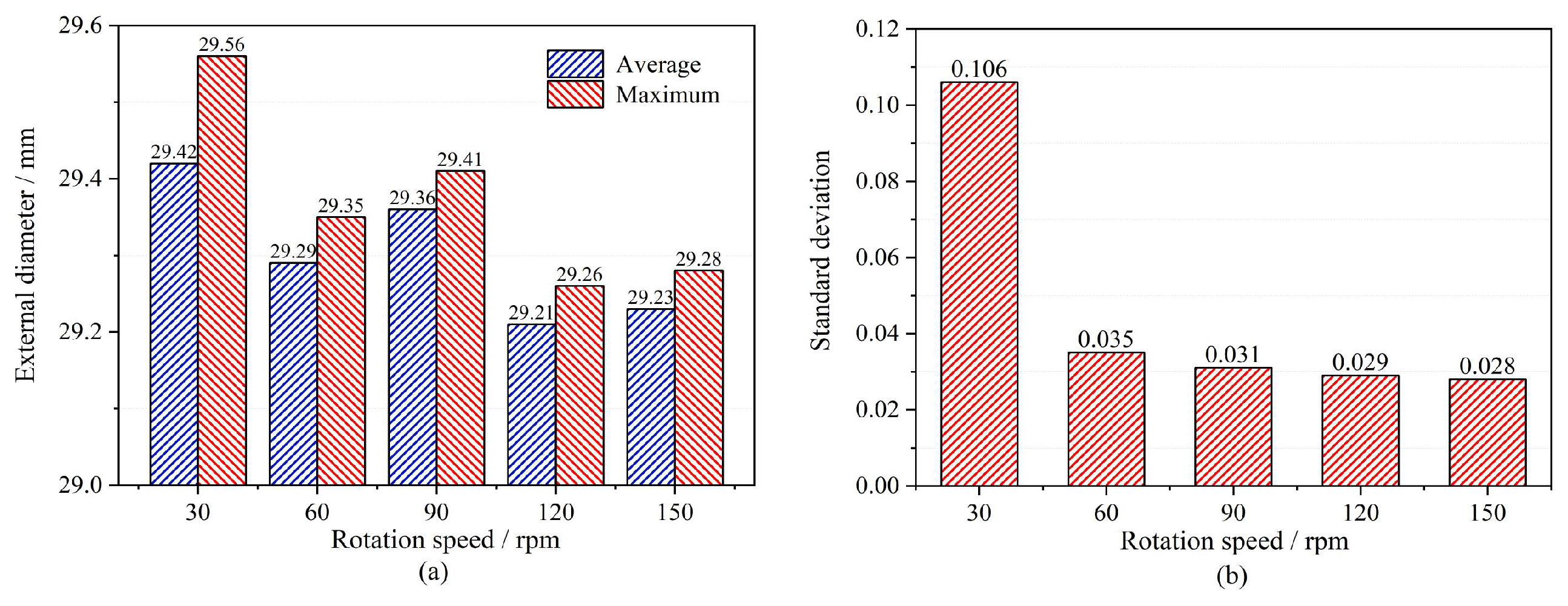
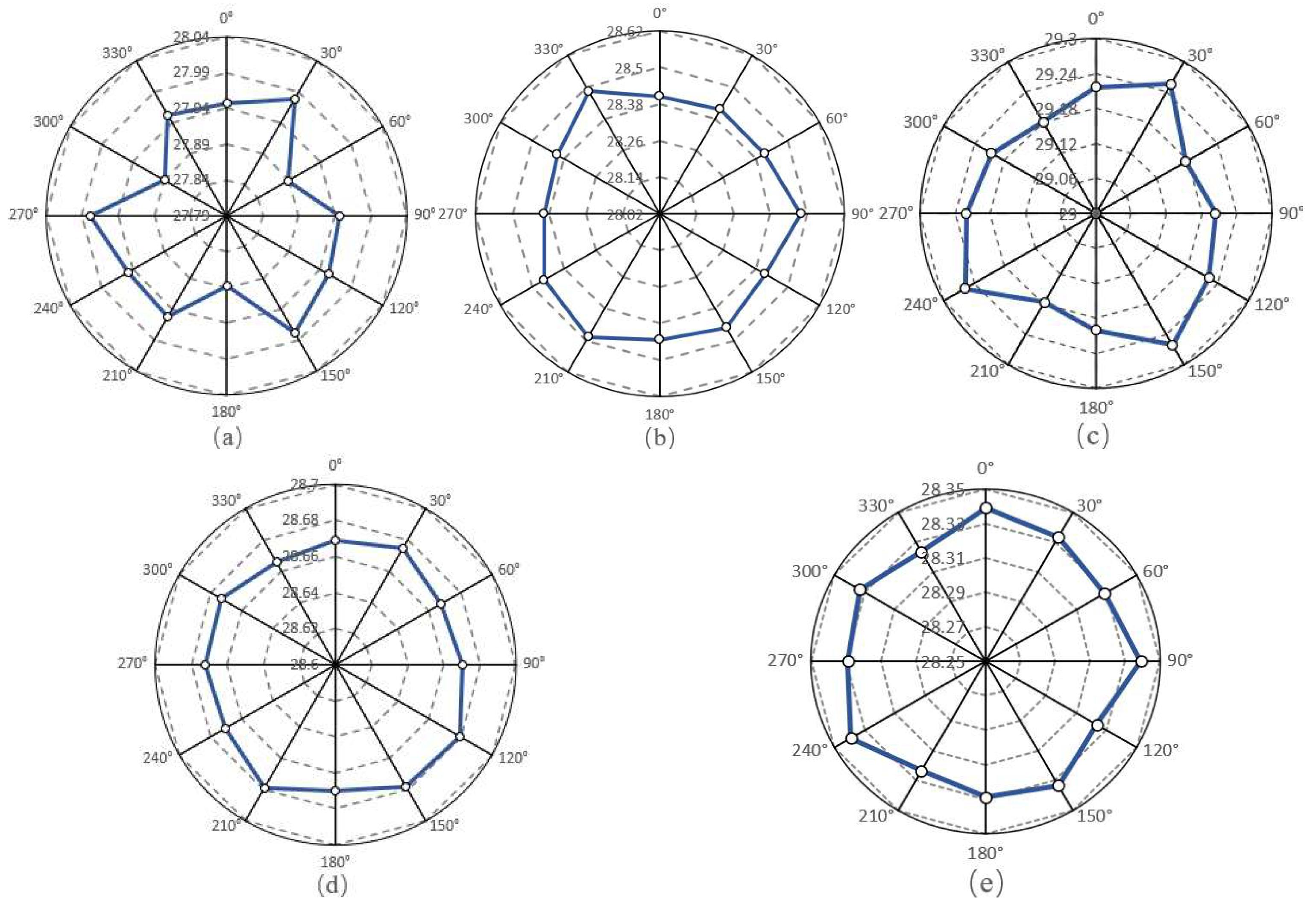
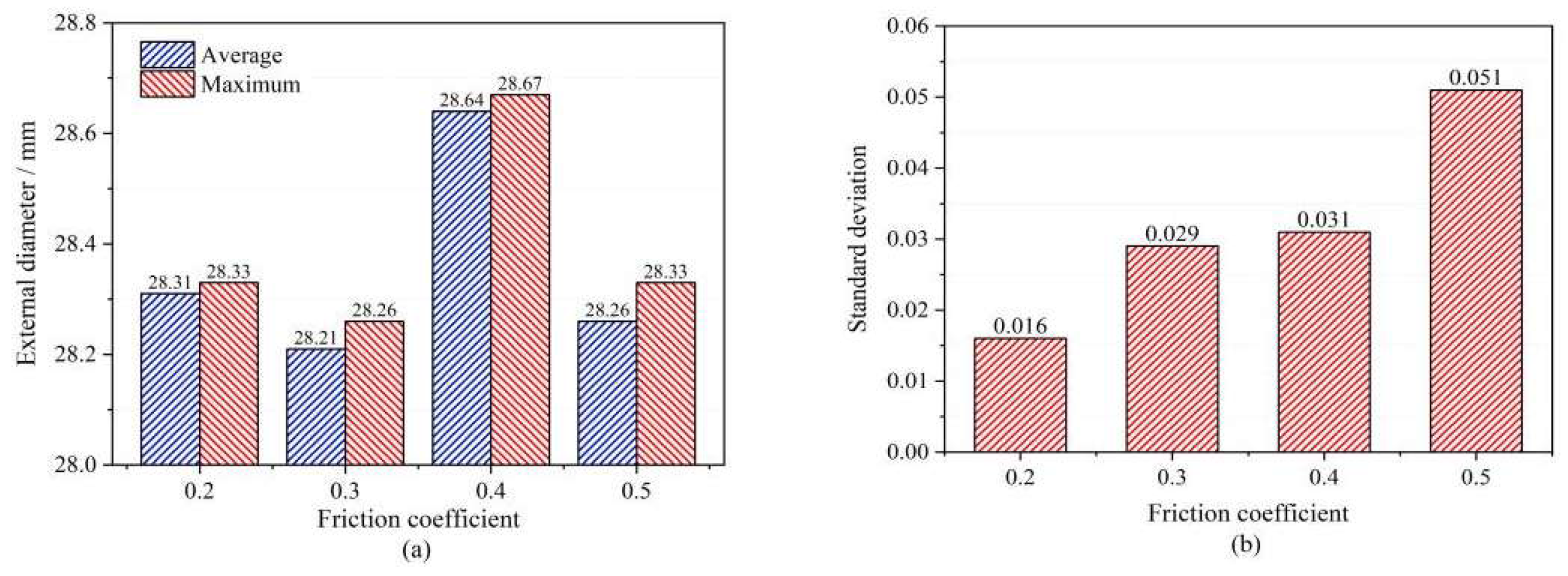
3.3. Roundness
4. Effect of Roller Rotation Speed on Three-Roll Planetary Rolling Performance
4.1. Equivalent Stress
4.2. Deformation Temperature
4.3. Roundness
5. Influence of Friction Coefficient on Three-Roll Planetary Rolling Performance
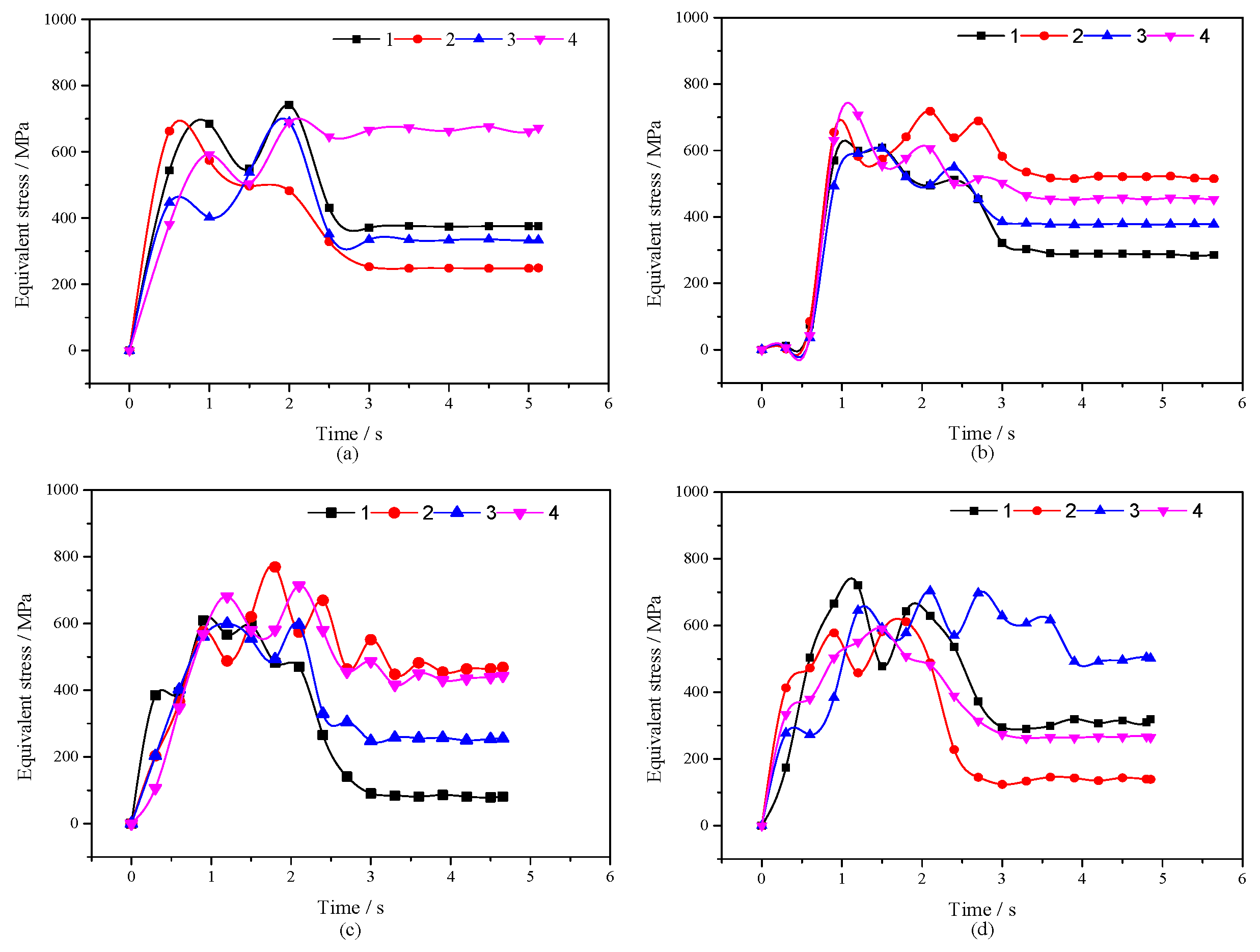
5.1. Stress Distribution Characteristics
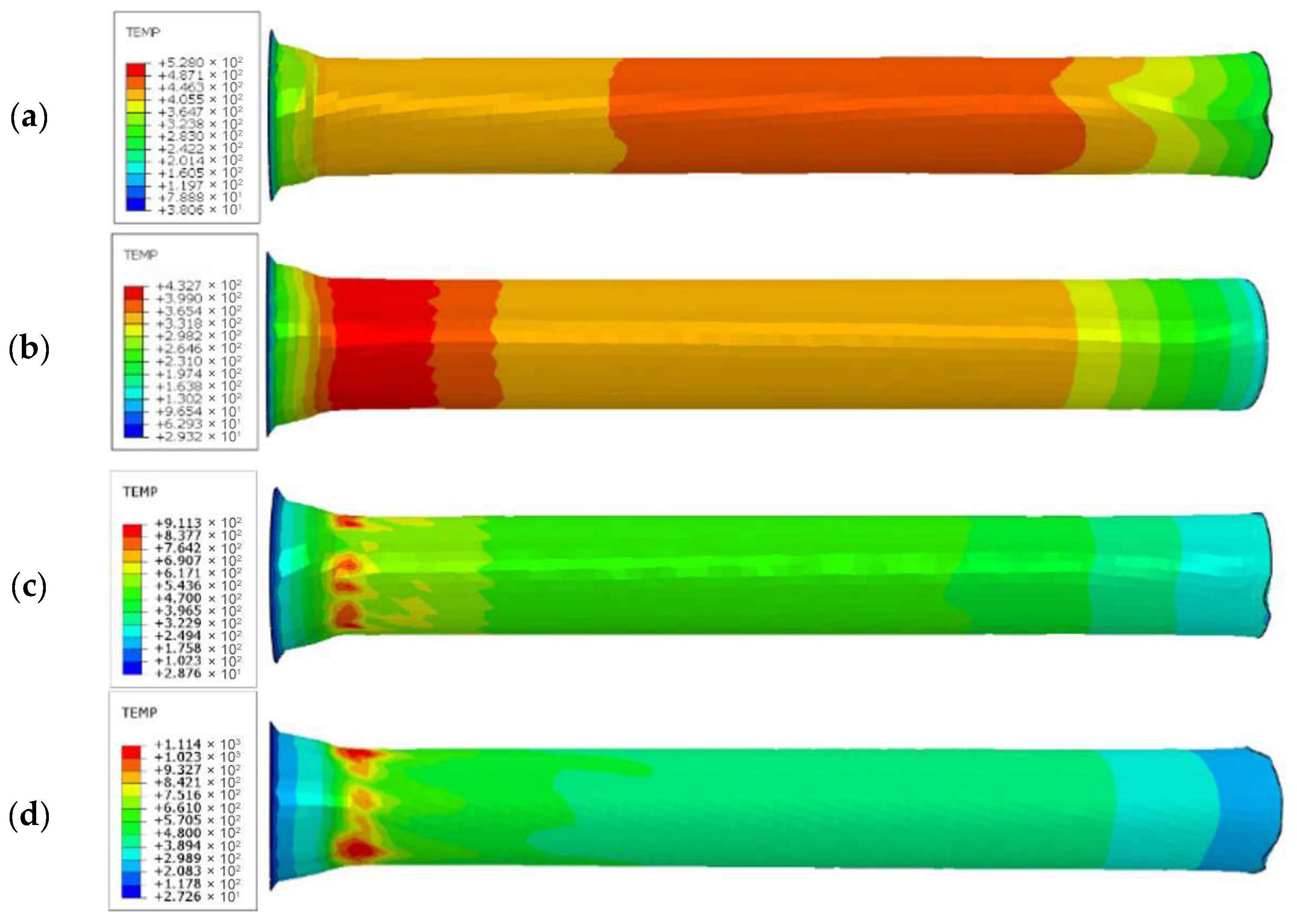
5.2. Deformation Temperature
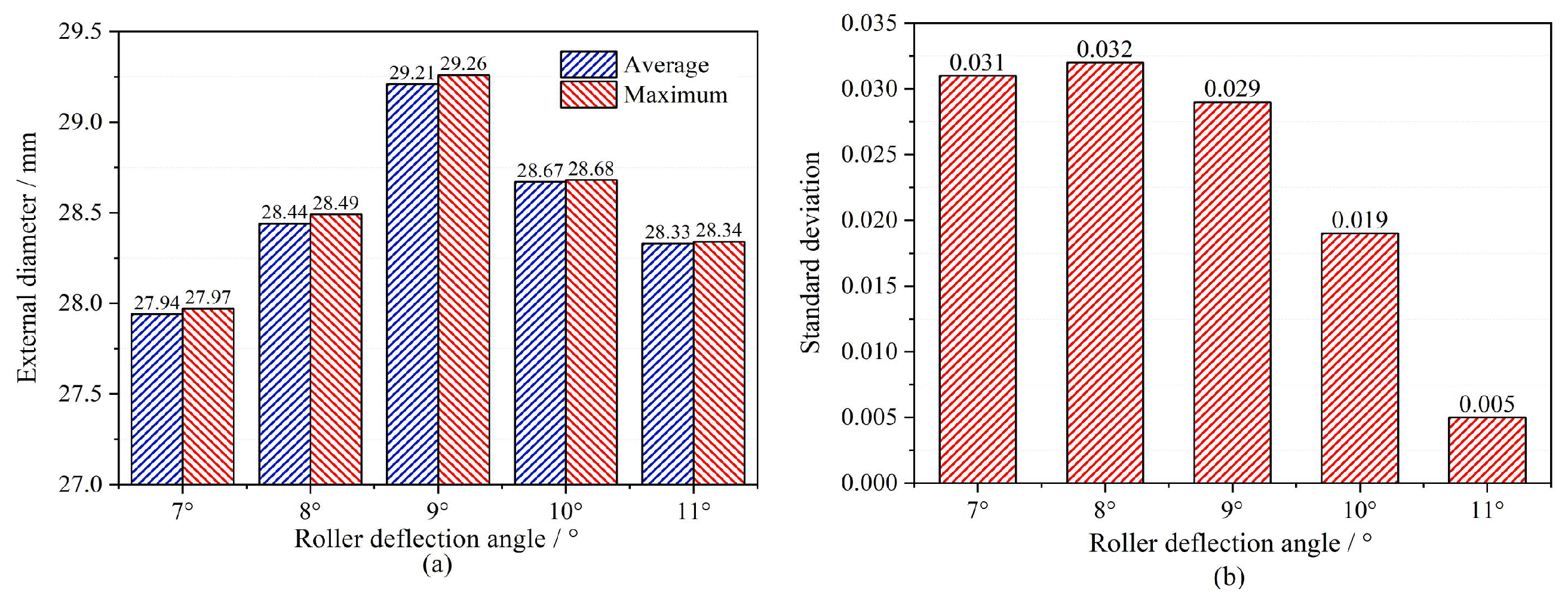
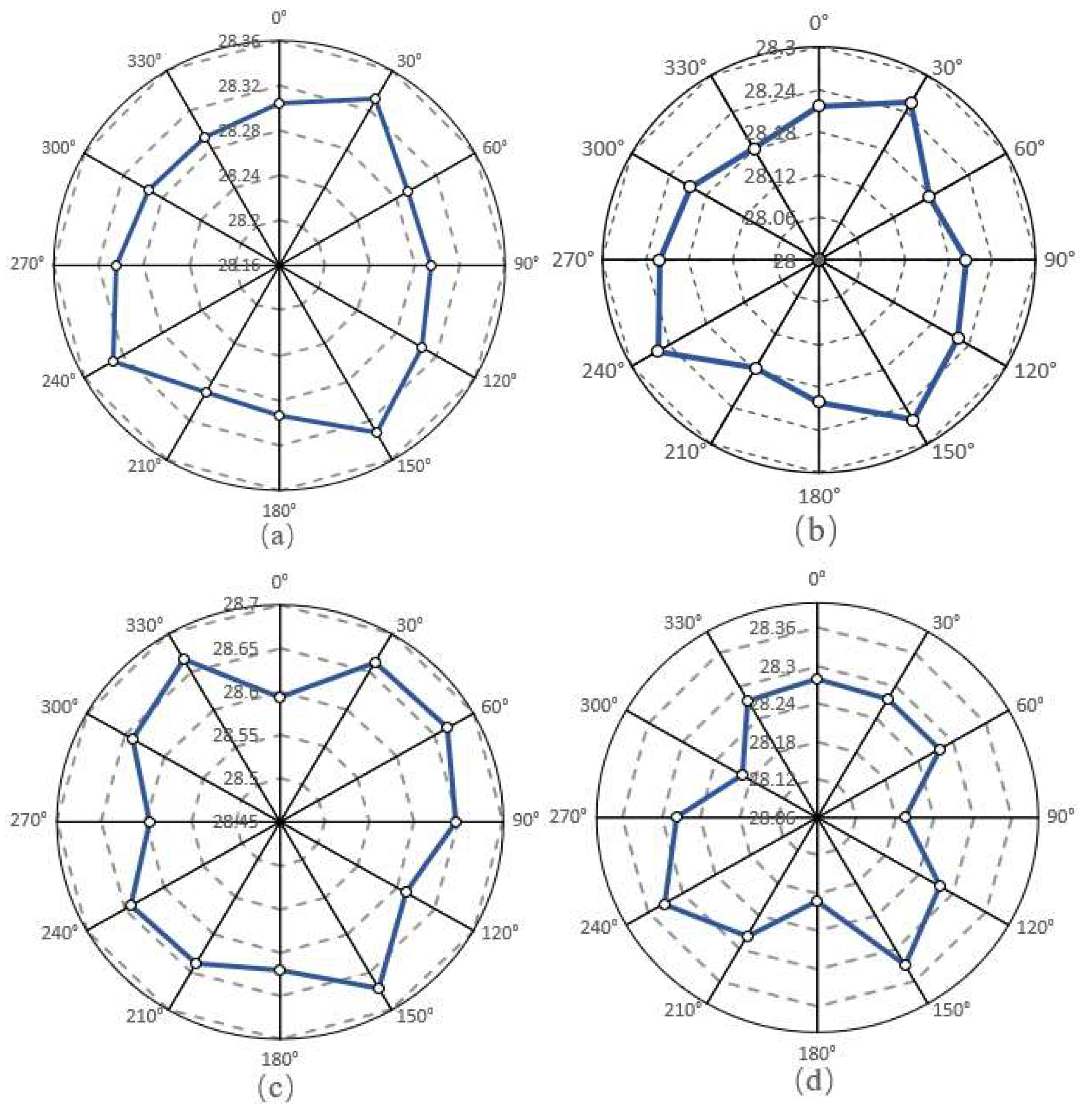
5.3. Roundness
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liang, G.; Tan, J.; Qian, X.; Xiang, Y.; Gou, Z.; Zhang, B.; Chen, T. Interfacial Bonding Properties Experimental Research of 316L Stainless Steel–Carbon Steel Clad Rebar in the Process of Intermediate and Finish Rolling. Metals 2025, 15, 108. [Google Scholar] [CrossRef]
- Sun, Y.Z.; Cao, S.P.; Gao, G. Effects of Extrusion Deformation on the Microstructure and Mechanical Properties of 5083 Seamless Tubes. Light Met. 2024, 33–38. (In Chinese) [Google Scholar] [CrossRef]
- Li, S.B.; Xie, J.-X. Fabrication of Thin-Walled 316L Stainless Steel Seamless Pipes by Extrusion Technology. J. Mater. Process. Technol. 2007, 183, 57–61. [Google Scholar] [CrossRef]
- Li, D.; He, Y.; Guo, L.G.; Shi, L.; Zhang, J.; Zheng, W.D. Microstructure Responses to Key Extrusion Parameters of Large-Scale Thick-Walled 304 Stainless Steel Pipes. Rare Met. Mater. Eng. 2014, 43, 2675–2681. [Google Scholar] [CrossRef]
- Mao, Y.R.; Qiu, C.L.; Gao, X.H. Finite Element Simulation Analysis of Lamination Defects in the Cross-Rolling Piercing Process of Seamless Steel Tubes. J. Steel Roll. 2023, 40, 59–64. (In Chinese) [Google Scholar]
- Wang, X.; Xiao, Z.; Zhou, T.; Jiang, X.F. Deformation Mechanism and Properties Evolution of a Copper Alloy with Ultra-High Strength After Cold Drawing and Subsequent Aging Treatment. Mater. Sci. Eng. A 2024, 912, 146952. [Google Scholar] [CrossRef]
- Li, Q.; Zhou, L.C.; Gao, H.; Wang, J.Y.; Cao, X.; Ma, J.F.; Jiang, J.Q.; Fang, F. Ultra-strong cold-drawn 2507 stainless steel wire with heterogenous microstructure of dual-phase and grain size. J. Mater. Res. Technol. 2024, 33, 6876–6889. [Google Scholar] [CrossRef]
- Fan, X.Y.; Hou, J.P.; Lu, Y.; Wang, S.; Liu, Z.Q.; Duan, Q.Q.; Wang, Q.; Zhang, Z.J.; Zhang, Z.F. Strengthening Mechanisms and Strength Prediction of Directionally Solidified Cu Wire Processed by Cold-Drawing. Mater. Today Commun. 2025, 42, 111421. [Google Scholar] [CrossRef]
- Dai, X.B.; Liu, Z.H.; Xu, Y. PSW Roll Profile Design Based on Matlab. J. Shaoyang Univ. Nat. Sci. Ed. 2016, 13, 76–81. (In Chinese) [Google Scholar]
- Li, L.M.; Zang, Y.; Zhang, Z.Z.; Yao, H.Z.; Zhang, B. Influence of Friction Condition on Copper Tube Planetary Rolling Process. J. Plast. Eng. 2009, 16, 115–119. (In Chinese) [Google Scholar]
- Liu, H.; Zhang, S.H.; Cheng, D.Y. Contact Zone Distribution Between Rolls andWorkpiece in Three-Roll Planetary Rolling. Forg. Stamp. Technol. 2011, 36, 46–49. (In Chinese) [Google Scholar]
- Hwang, Y.M.; Tsai, W.M.; Tsai, F.H.; Her, I. Analytical and Experimental Study on the Spiral Marks of the Rolled Product During Three-Roll Planetary Rolling Processes. Int. J. Mach. Tools Manuf. 2006, 46, 1555–1562. [Google Scholar] [CrossRef]
- Shih, C.K.; Hung, C.H. Experimental and Numerical Analyses on Three-Roll Planetary Rolling Process. J. Mater. Process. Technol. 2003, 142, 702–709. [Google Scholar] [CrossRef]
- Li, B.; Zhang, S.H.; Zhang, G.L.; Zhang, H.Q. Prediction of 3-D Temperature Field of TP2 Copper Tubes in Three-Roll Planetary Rolling Process. J. Mater. Process. Technol. 2008, 205, 370–375. [Google Scholar] [CrossRef]
- Shih, C.K.; Hung, C.H.; Hsu, R.Q. The Finite Element Analysis on Planetary Rolling Process. J. Mater. Process. Technol. 2001, 113, 115–123. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, X.B.; Wang, Z.X.; Xiao, Y.; Gao, X.L.; Zhao, Y.Q. Study on Cooling Process of Copper Tube After Three-Roll Planetary Rolling. Int. Commun. Heat Mass Transf. 2020, 110, 104393. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, J.S.; Wang, Z.; Chen, S.P.; Zhao, Q.H.; Peng, Y.C.; Qu, S.W. Mechanical Behavior Analysis of Roller Shaft in Three-Roll Planetary Rolling Process of Copper Tube. Hot Work. Technol. 2016, 45, 111–115. (In Chinese) [Google Scholar]
- Zeng, Q.L. Study on Metal Flow and Its Stability During Planetary Rolling Process. Ph.D. Thesis, University of Science and Technology Beijing, Beijing, China, 2016. (In Chinese). [Google Scholar]
- Romantsev, B.; Goncharuk, A.; Aleshchenko, A.; Gamin, Y.; Mintakhanov, M. Development of Multipass Skew Rolling Technology for Stainless Steel and Alloy Pipes’ Production. Int. J. Adv. Manuf. Technol. 2018, 97, 3223–3230. [Google Scholar] [CrossRef]
- Mori, K.; Yoshimura, H.; Osakada, K. Simplified Three-Dimensional Simulation of Rotary Piercing of Seamless Pipe by Rigid-Plastic Finite-Element Method. J. Mater. Process. Technol. 1998, 80–81, 700–706. [Google Scholar] [CrossRef]
- Li, L.; Li, J.; Ye, B. Internal Damage Mechanism and Deformation Process Window of a Free-Cutting Stainless Steel Bar Rolled by Three-Roll Planetary Mill. J. Mater. Eng. Perform. 2022, 31, 1187–1194. [Google Scholar] [CrossRef]
- Hu, S.; Wang, C.; Wang, X.; Li, L.; Liu, S. Process Optimization of Planetary Rolling of Bismuth-Containing Austenitic Stainless Steel. J. Mater. Eng. Perform. 2022, 31, 2012–2022. [Google Scholar] [CrossRef]
- Zhou, Y.; Mao, Z.; Liu, Y.; Wang, J. Microstructure Evolution of Copper by Three Roll Planetary Milling. Solid State Phenom. 2018, 279, 44–48. [Google Scholar] [CrossRef]
- Fu, Y.; Cui, J.; Cao, Z. Cracks of Cu-Cr-Zr Alloy Bars Under Planetary Rolling. Rare Met. Mater. Eng. 2015, 44, 567–570. [Google Scholar]
- Zeng, Q.L.; Zang, Y.; Qin, Q. The Effect of Roll with Passive Segment on the Planetary Rolling Process. Adv. Mech. Eng. 2015, 7, 2. [Google Scholar] [CrossRef]
- Kharitonov, E.A.; Romanenko, V.P.; Budnikov, A.S. Pipe Behavior in a Three-Roller Screw-Rolling Mill. Steel Transl. 2014, 44, 769–772. [Google Scholar] [CrossRef]
- Jin, R.; Chu, Z.B. Numerical Simulation of Three-Roll Planetary Rolling Process for 304 Stainless Steel Pipe Blank. Forg. Stamp. Technol. 2024, 49, 59–66. (In Chinese) [Google Scholar]
- Hu, S.D.; Du, Z.H.; Yu, H.; Li, L.X. Process Parameter Optimization for Three-Roll Planetary Rolling of Bismuth-Containing Austenitic Stainless Steel Bars. J. Wuhan Univ. Sci. Technol. 2021, 44, 13–19. (In Chinese) [Google Scholar]
- Du, Z.H. Determination of Process Parameters for Three-Roll Planetary Rolling of Bismuth-Containing Bright Stainless Steel. Master’s Thesis, Wuhan University of Science and Technology, Wuhan, China, 2021. (In Chinese). [Google Scholar]
- Jin, R. Roll Configuration Design and Process Optimization for Three-Roll Planetary Rolling of 304 Stainless Steel Tubes. Ph.D. Thesis, Taiyuan University of Science and Technology, Taiyuan, China, 2024. (In Chinese). [Google Scholar]

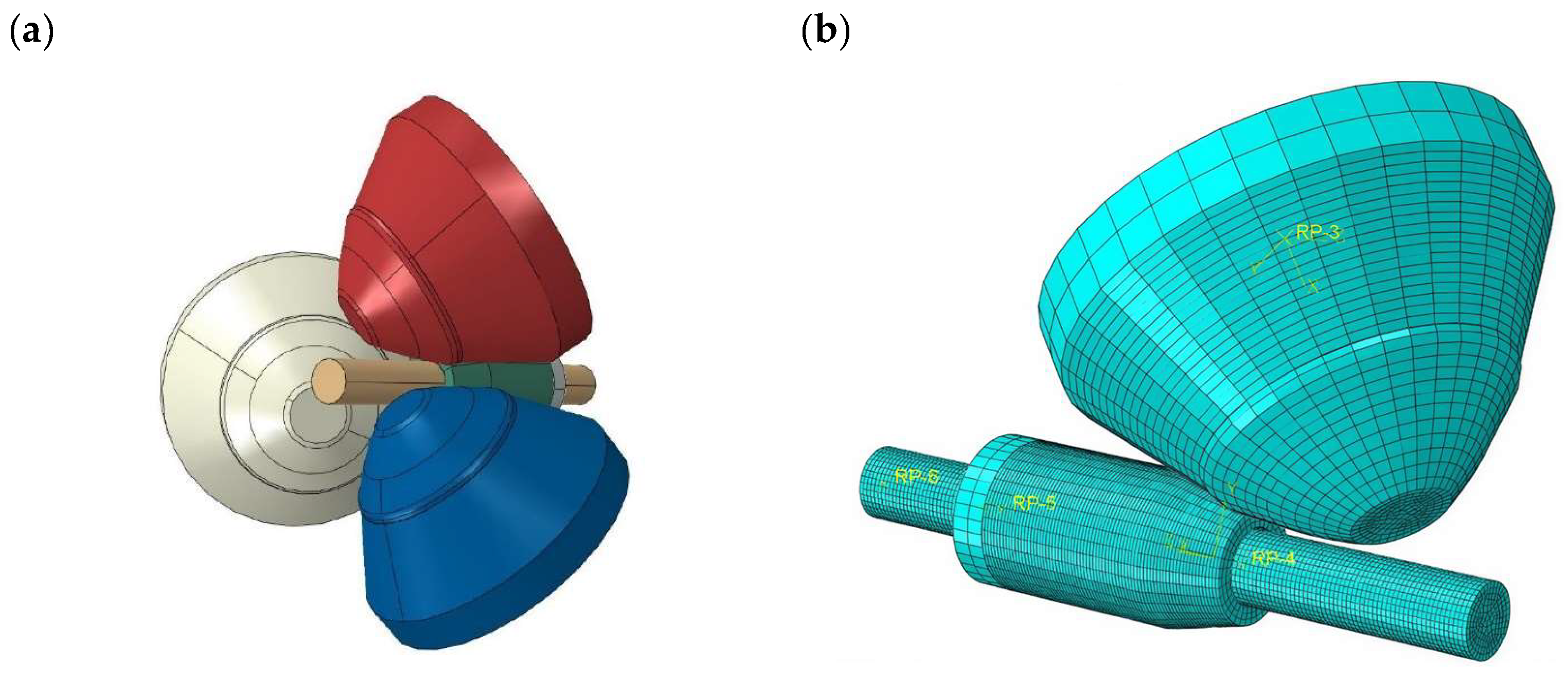
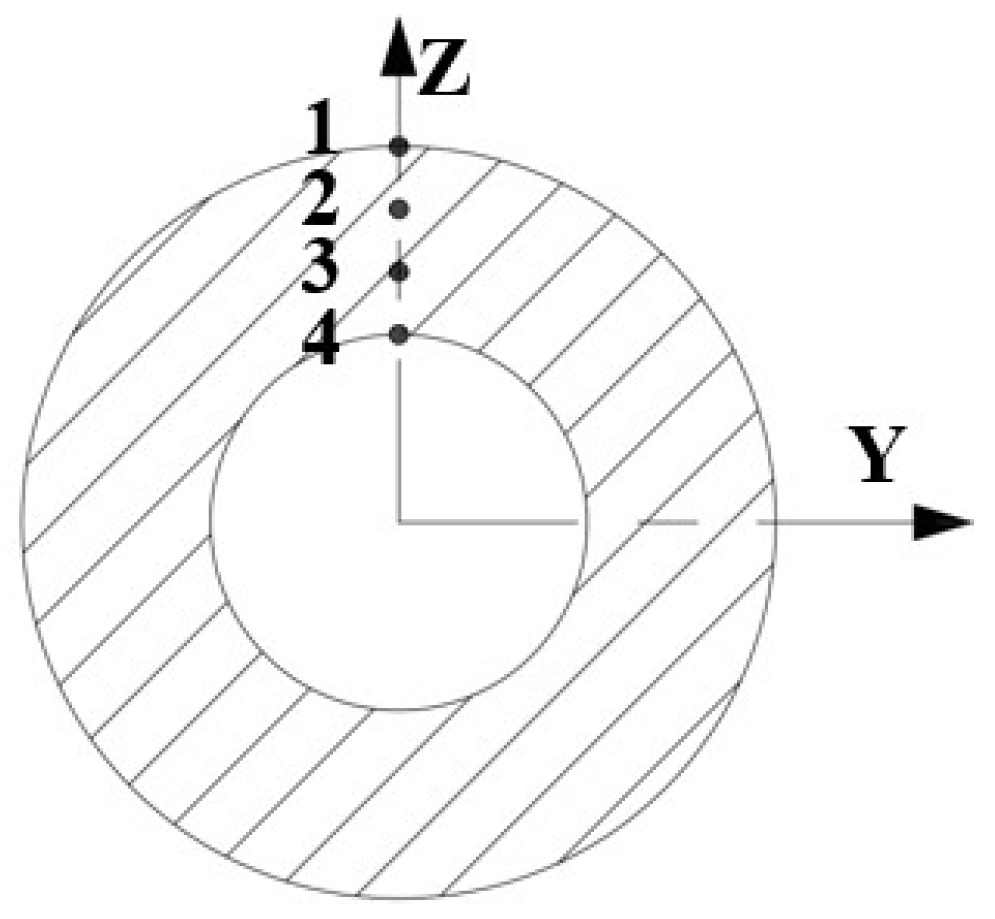


| Density (g·cm−3) | Elastic Modulus (GPa) | Thermal Expansion Coefficient (W·(m·K)−1) | Poisson’s Ratio |
|---|---|---|---|
| 7.93 | 194 | 1.67 | 0.3 |
| Initial OD (mm) | Initial ID (mm) | Final OD (mm) | Final ID (mm) | Reduction (%) |
|---|---|---|---|---|
| 84 | 40 | 50 | 40 | 68 |
| Friction Coefficient (μ) | 0.2 | 0.3 | 0.4 | 0.5 | / |
|---|---|---|---|---|---|
| Roll speed (rpm) | 30 | 60 | 90 | 120 | 150 |
| Roll deflection angle (°) | 7 | 8 | 9 | 10 | 11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Li, T.; Xue, C.; Jin, R.; Chu, Z.; Shuai, M.; Tuo, L. Optimization of Roll Configuration and Investigation of Forming Process in Three-Roll Planetary Rolling of Stainless Steel Seamless Tubes. Metals 2025, 15, 540. https://doi.org/10.3390/met15050540
Ma C, Li T, Xue C, Jin R, Chu Z, Shuai M, Tuo L. Optimization of Roll Configuration and Investigation of Forming Process in Three-Roll Planetary Rolling of Stainless Steel Seamless Tubes. Metals. 2025; 15(5):540. https://doi.org/10.3390/met15050540
Chicago/Turabian StyleMa, Chuanchuan, Tuo Li, Chun Xue, Ri Jin, Zhibing Chu, Meirong Shuai, and Leifeng Tuo. 2025. "Optimization of Roll Configuration and Investigation of Forming Process in Three-Roll Planetary Rolling of Stainless Steel Seamless Tubes" Metals 15, no. 5: 540. https://doi.org/10.3390/met15050540
APA StyleMa, C., Li, T., Xue, C., Jin, R., Chu, Z., Shuai, M., & Tuo, L. (2025). Optimization of Roll Configuration and Investigation of Forming Process in Three-Roll Planetary Rolling of Stainless Steel Seamless Tubes. Metals, 15(5), 540. https://doi.org/10.3390/met15050540





