Constitutive Model for Hot Deformation Behavior of Fe-Mn-Cr-Based Alloys: Physical Model, ANN Model, Model Optimization, Parameter Evaluation and Calibration
Abstract
1. Introduction
2. Materials and Methods
3. Results
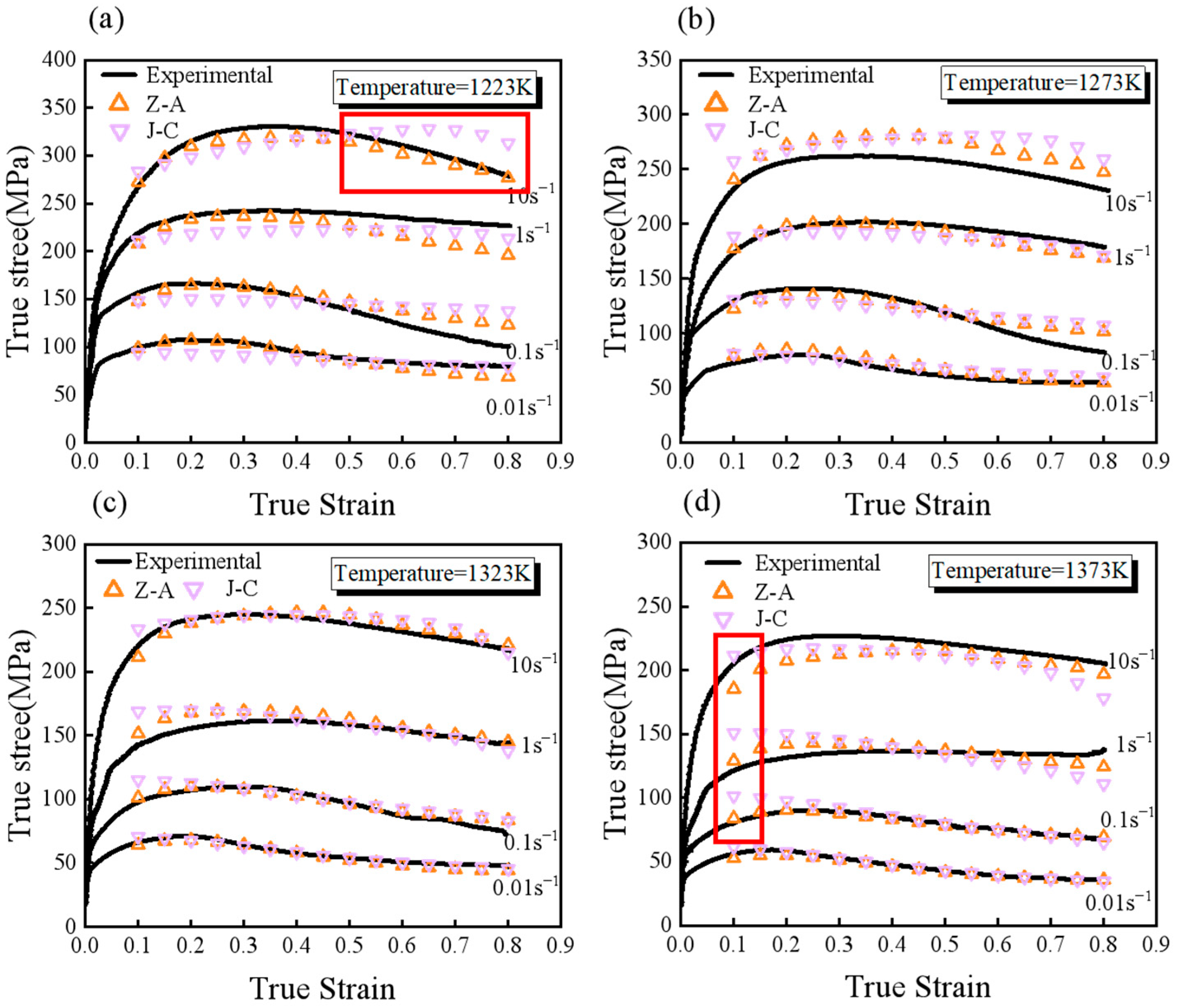
3.1. Flow Behavior
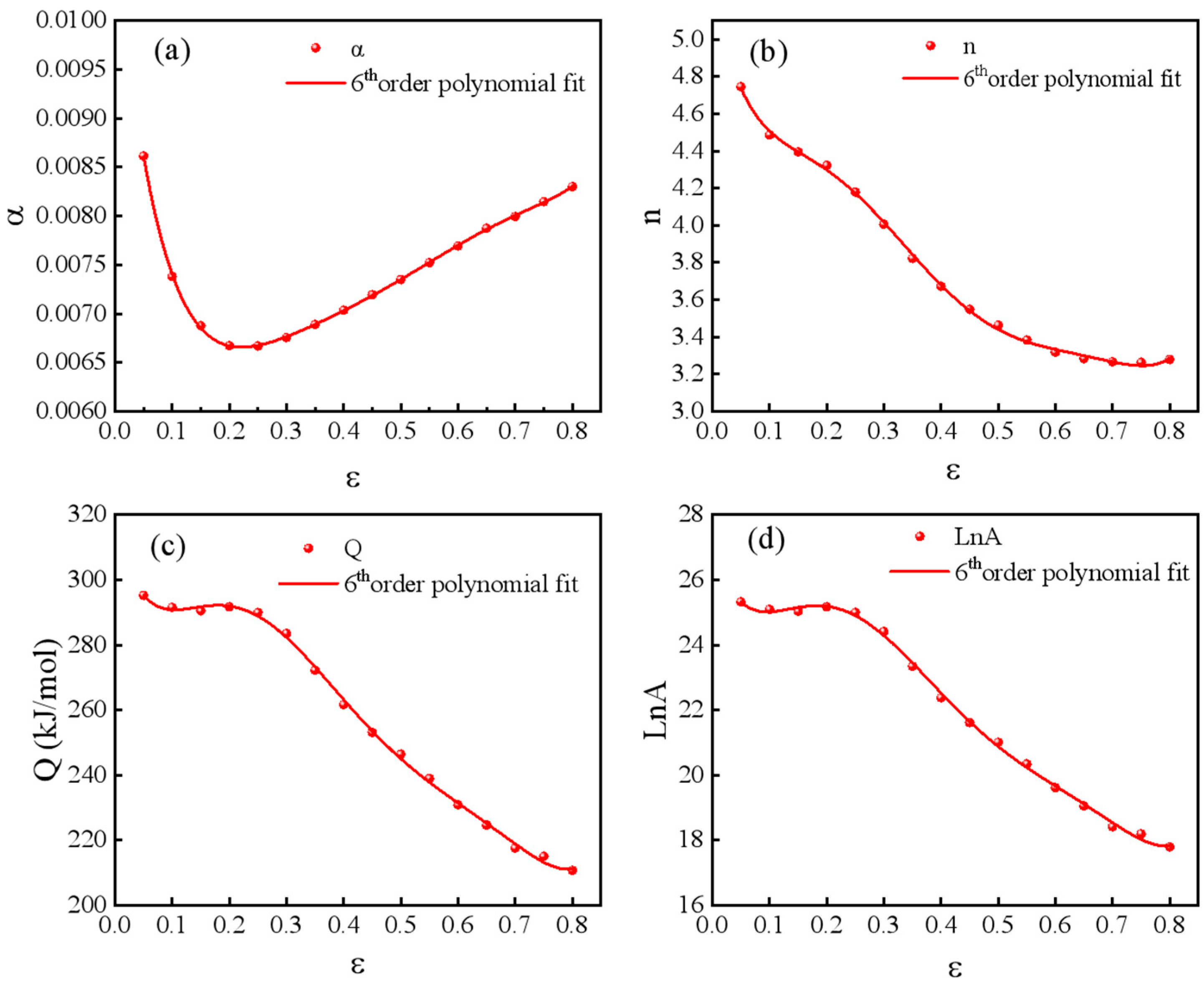
3.2. Establishment and Optimization of Physical Constitutive Models
3.2.1. Arrhenius and Johnson–Cook Constitutive Model
3.2.2. Constitutive Model Fitting Based on Numerical Optimization
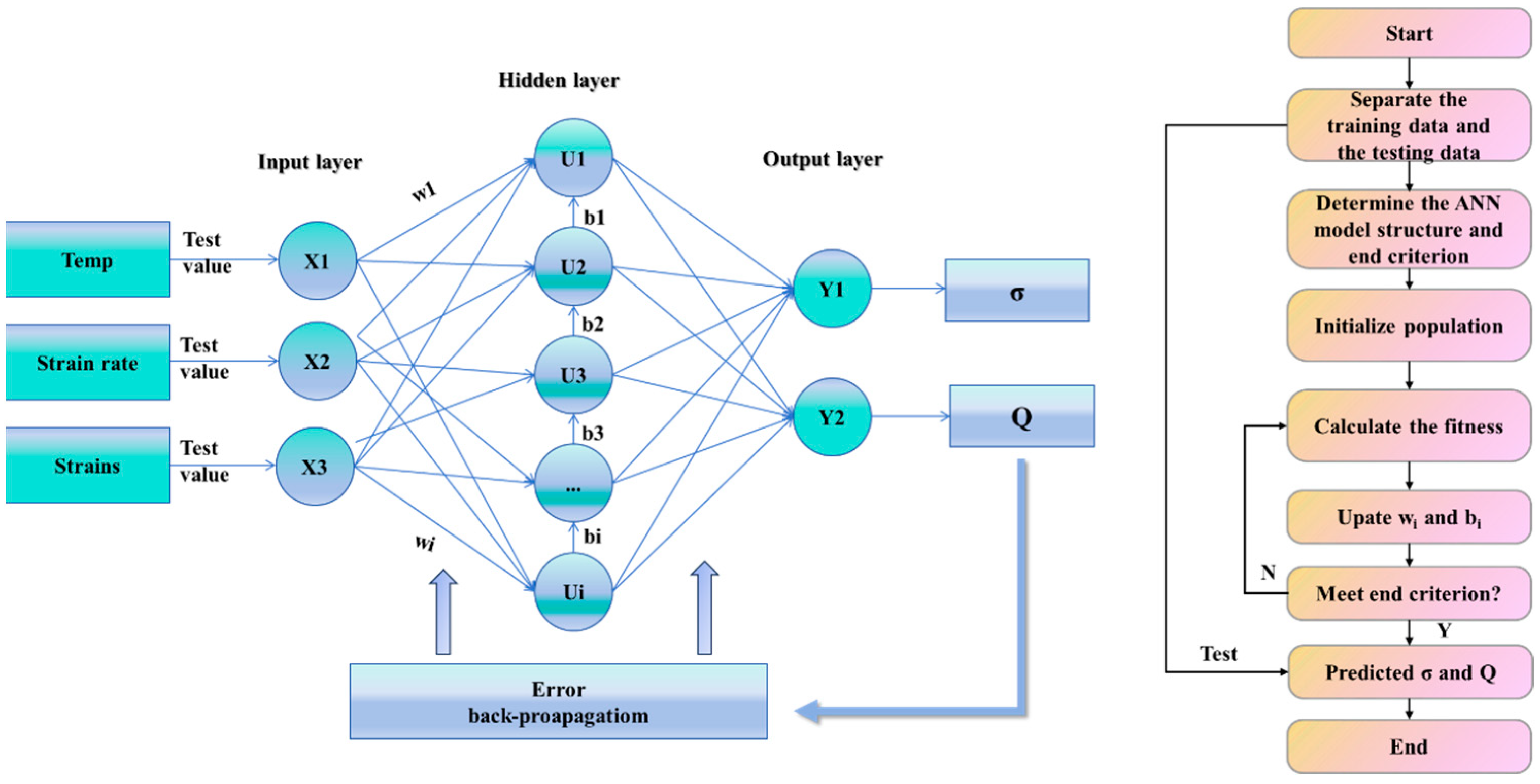
3.3. Establishment and Optimization of ANN Model
3.3.1. ANN Model
3.3.2. Structure Optimization of ANN Model
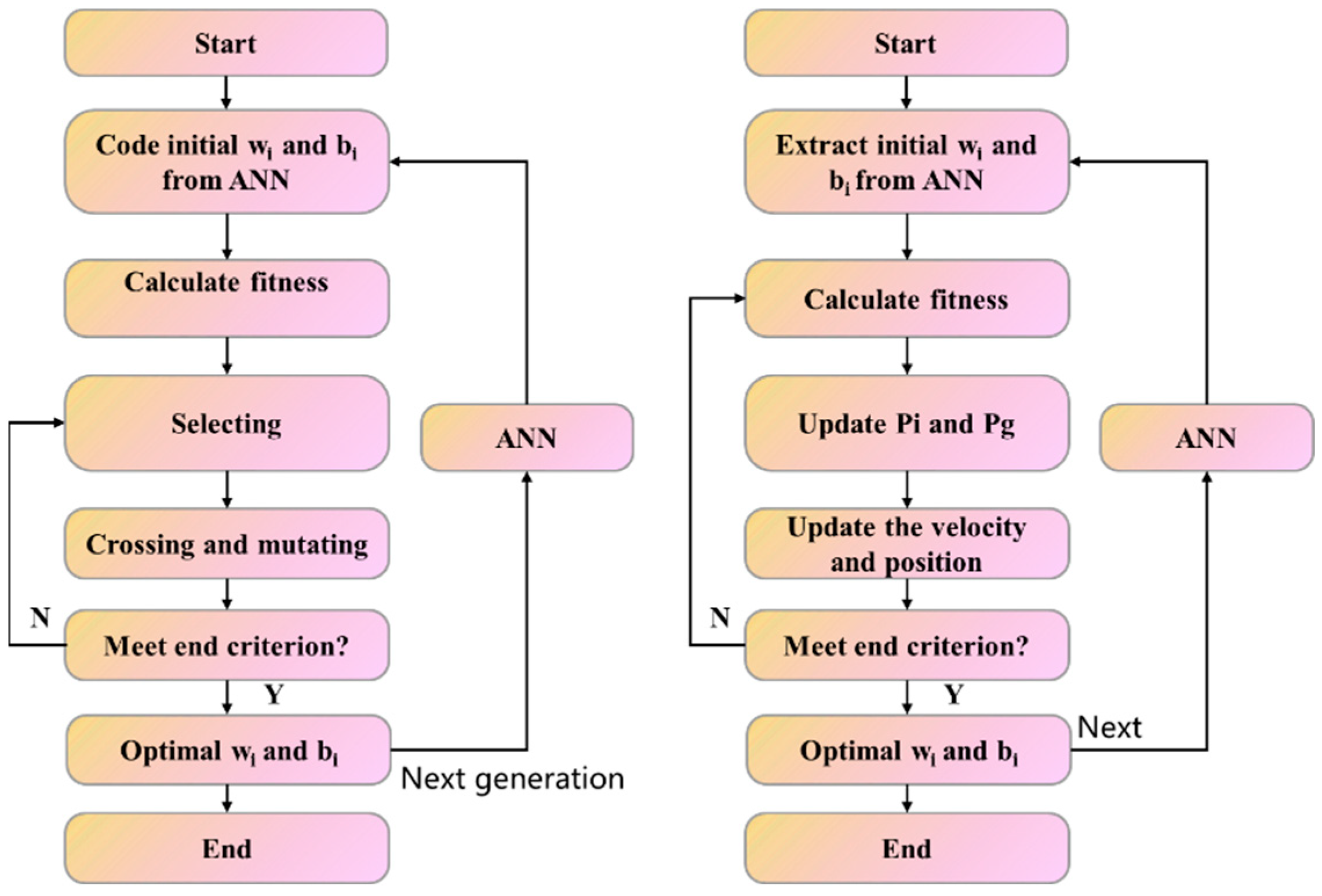
3.3.3. Optimization Algorithm
4. Discussion
4.1. Mathematical Derivation vs. Numerical Optimization vs. Machine Learning
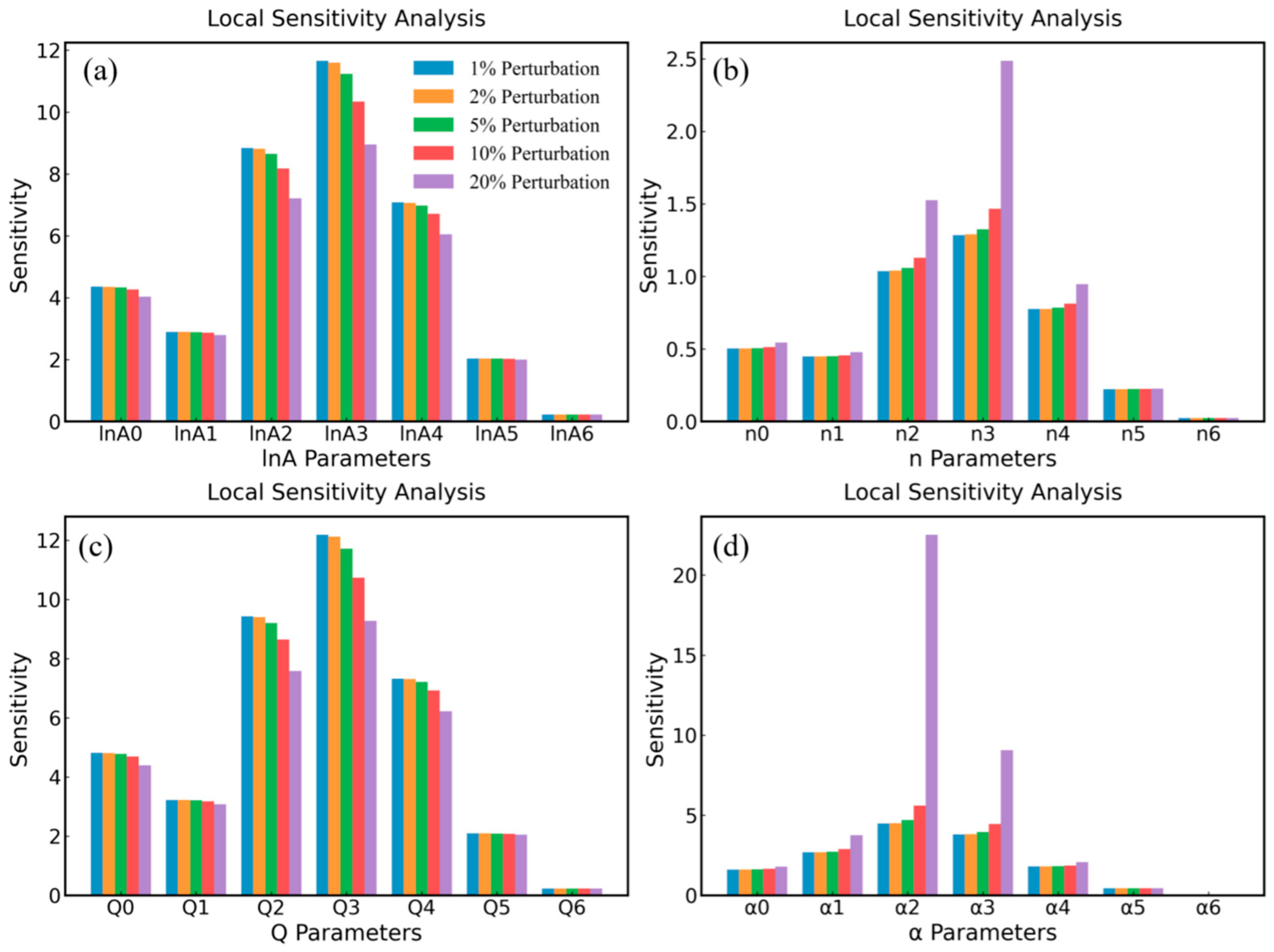
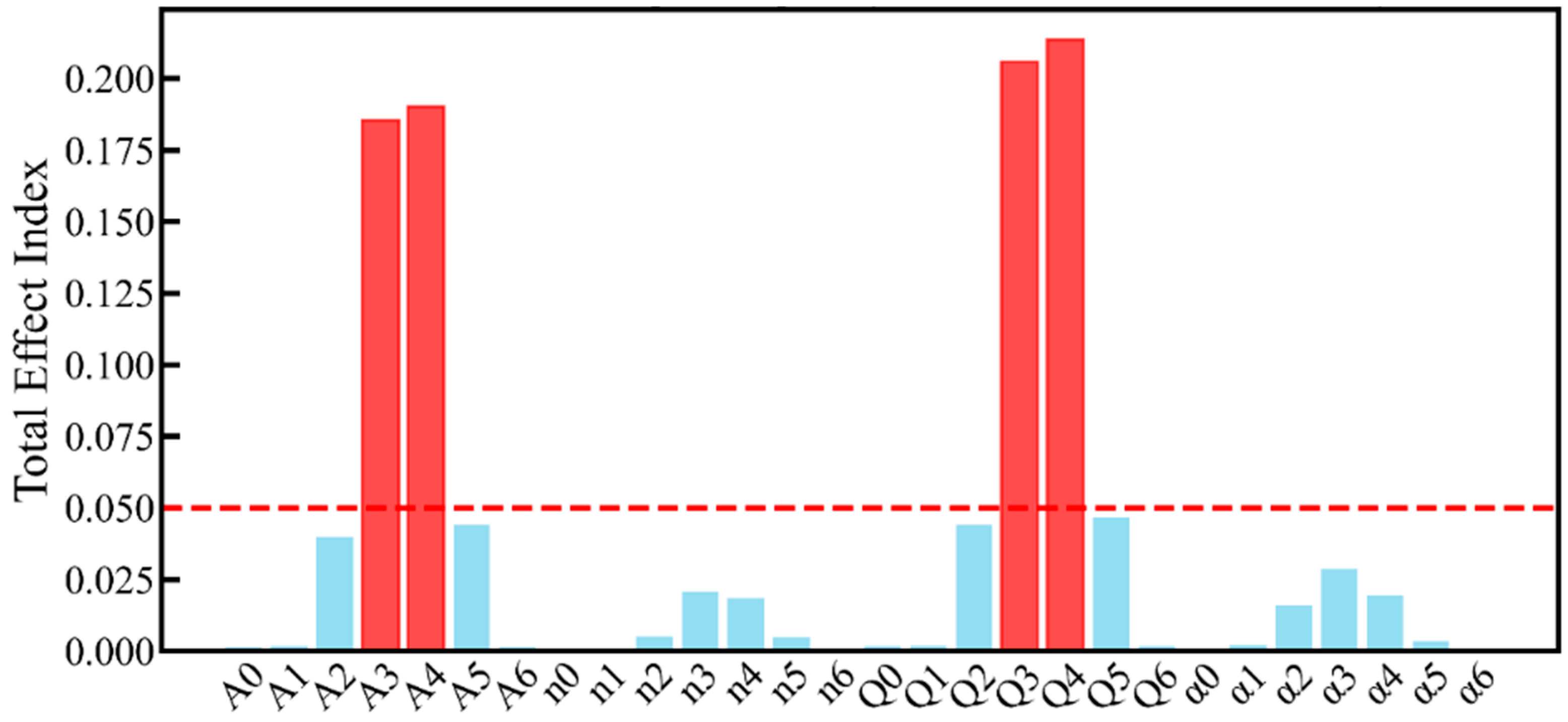
4.2. Sensitivity Analysis of Constitutive Model Parameters
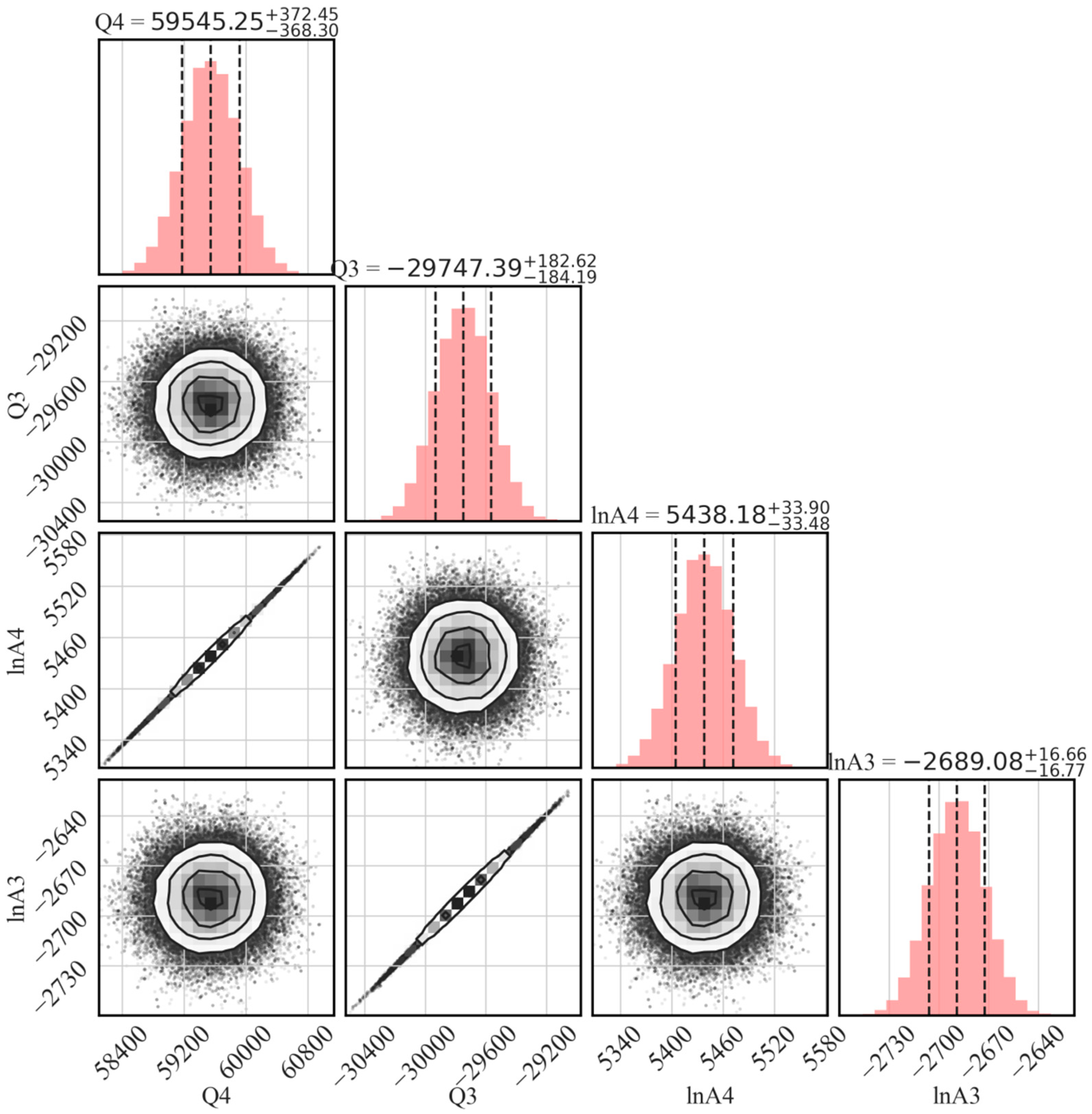
4.3. Parameter Evaluation and Calibration Based on Bayesian Reasoning
5. Conclusions
- (1)
- Traditional physical models (e.g., the Arrhenius model) offer physical interpretability in predicting high-temperature flow behavior but face challenges in parameter solving. Machine learning models (e.g., artificial neural networks), optimized via genetic algorithms, particle swarm optimization, and Bayesian optimization, achieve high-precision nonlinear modeling (R2 = 0.9985, AARE = 3.01%). Numerical optimization, meanwhile, balances rapid parameter fitting with model interpretability. These three methodologies are, respectively, suited for distinct application scenarios: simplified physical modeling, complex nonlinear predictions, and efficient parameter optimization tasks.
- (2)
- The sensitivity analysis method is used to determine the key parameters (lnA3, lnA4, Q3, Q4) of the Arrhenius model which have the greatest influence on rheological behavior. Bayesian inference and MCMC sampling methods are used to quantify the uncertainty of model parameters and analyze the posterior probability density distribution of key parameters, so as to evaluate and calibrate parameters and improve the robustness of the model.
- (3)
- The Bayesian inference method significantly improves model accuracy, raising the correlation coefficient (R2) from 0.942 to 0.983 after parameter calibration. Posterior distribution analysis reveals key physical insights, including strong correlations between activation energy (Q3, Q4) and frequency factors (lnA3, lnA4), while identifying higher uncertainty in low-temperature and high-strain regions. This approach is valuable for both predicting Fe-Mn-Cr alloy deformation behavior and calibrating constitutive models of other metallic materials, with potential for integration with micromechanism modeling to enhance physical consistency and predictive accuracy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khan, S.; Pydi, Y.S.; Mani Prabu, S.S.; Palani, I.A.; Singh, P. Development and Actuation Analysis of Shape Memory Alloy Reinforced Composite Fin for Aerodynamic Application. Sens. Actuators A Phys. 2021, 331, 113012. [Google Scholar] [CrossRef]
- Ghafoori, E.; Wang, B.; Andrawes, B. Shape Memory Alloys for Structural Engineering: An Editorial Overview of Research and Future Potentials. Eng. Struct. 2022, 273, 115138. [Google Scholar] [CrossRef]
- Algamal, A.; Abedi, H.; Gandhi, U.; Benafan, O.; Elahinia, M.; Qattawi, A. Manufacturing, Processing, Applications, and Advancements of Fe-Based Shape Memory Alloys. J. Alloys Compd. 2025, 1010, 177068. [Google Scholar] [CrossRef]
- Vilella, T.; Rodríguez, D.; Fargas, G. Additive Manufacturing of Ni-Free Ti-Based Shape Memory Alloys: A Review. Biomater. Adv. 2024, 158, 213774. [Google Scholar] [CrossRef] [PubMed]
- Pan, M.-M.; Zhang, X.-M.; Zhou, D.; Misra, R.D.K.; Chen, P. Fe–Mn–Si–Cr–Ni Based Shape Memory Alloy: Thermal and Stress-Induced Martensite. Mater. Sci. Eng. A 2020, 797, 140107. [Google Scholar] [CrossRef]
- Cladera, A.; Weber, B.; Leinenbach, C.; Czaderski, C.; Shahverdi, M.; Motavalli, M. Iron-Based Shape Memory Alloys for Civil Engineering Structures: An Overview. Constr. Build. Mater. 2014, 63, 281–293. [Google Scholar] [CrossRef]
- Sajadi, S.A.; Toroghinejad, M.R.; Rezaeian, A.; Ebrahimi, G.R. A Study of Hot Compression Behavior of an as-Cast Fecrcuni2mn2 High-Entropy Alloy. J. Alloys Compd. 2022, 896, 162732. [Google Scholar] [CrossRef]
- Deng, H.; Zheng, Z.; Song, W.; Tan, X.; Liang, X.; Li, H.; Li, H. Constitutive Model and Microstructure Evolution of Thermal Deformation Behavior of in Situ Tib2p/Al-Zn-Mg-Cu Composites with High Zn Content. Mater. Today Commun. 2024, 41, 110308. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, G.; Hou, B.; Wang, W. Deep Learning Coupled Bayesian Inference Method for Measuring the Elastoplastic Properties of Ss400 Steel Welds by Nanoindentation Experiment. Measurement 2025, 242, 116092. [Google Scholar] [CrossRef]
- Zhang, Y.; Hart, J.D.; Needleman, A. Identification of Plastic Properties from Conical Indentation Using a Bayesian-Type Statistical Approach. J. Appl. Mech. 2019, 86, 011002. [Google Scholar] [CrossRef]
- Adarsh, S.H.; Sampath, V. Hot Deformation Behavior of Fe–28ni–17co-11.5al-2.5ta-0.05b (At.%) Shape Memory Alloy by Isothermal Compression. Intermetallics 2019, 115, 106632. [Google Scholar] [CrossRef]
- Rajoria, S.R.; Gulhane, S.; Khan Md, F.; Sahoo, B.N. Hot Deformation Behavior Study of Coarse Grained and Ultrafine Grained Qe22 Magnesium Alloy through Development of Constitutive Analysis and Johnson–Cook Model. J. Alloys Compd. 2025, 1013, 178530. [Google Scholar] [CrossRef]
- Portone, T.; Niederhaus, J.; Sanchez, J.; Swiler, L. Bayesian Model Selection for Metal Yield Models in High-Velocity Impact. Int. J. Impact Eng. 2020, 137, 103459. [Google Scholar] [CrossRef]
- Bernstein, J.; Schmidt, K.; Rivera, D.; Barton, N.; Florando, J.; Kupresanin, A. A Comparison of Material Flow Strength Models Using Bayesian Cross-Validation. Comput. Mater. Sci. 2019, 169, 109098. [Google Scholar] [CrossRef]
- Hamdia, K.M.; Zhuang, X.; He, P.; Rabczuk, T. Fracture Toughness of Polymeric Particle Nanocomposites: Evaluation of Models Performance Using Bayesian Method. Compos. Sci. Technol. 2016, 126, 122–129. [Google Scholar] [CrossRef]
- Ritto, T.G.; Nunes, L.C.S. Bayesian Model Selection of Hyperelastic Models for Simple and Pure Shear at Large Deformations. Comput. Struct. 2015, 156, 101–109. [Google Scholar] [CrossRef]
- Jeong, K.; Lee, K.; Lee, S.; Kang, S.-G.; Jung, J.; Lee, H.; Kwak, N.; Kwon, D.; Han, H.N. Deep Learning-Based Indentation Plastometry in Anisotropic Materials. Int. J. Plast. 2022, 157, 103403. [Google Scholar] [CrossRef]
- Shin, S.; Lee, Y.; Kim, M.; Park, J.; Lee, S.; Min, K. Deep Neural Network Model with Bayesian Hyperparameter Optimization for Prediction of Nox at Transient Conditions in a Diesel Engine. Eng. Appl. Artif. Intell. 2020, 94, 103761. [Google Scholar] [CrossRef]
- Jeong, K.; Lee, H.; Kwon, O.M.; Jung, J.; Kwon, D.; Han, H.N. Prediction of Uniaxial Tensile Flow Using Finite Element-Based Indentation and Optimized Artificial Neural Networks. Mater. Des. 2020, 196, 109104. [Google Scholar] [CrossRef]
- Rivera, D.; Bernstein, J.; Schmidt, K.; Muyskens, A.; Nelms, M.; Barton, N.; Kupresanin, A.; Florando, J. Bayesian Calibration of Strength Model Parameters from Taylor Impact Data. Comput. Mater. Sci. 2022, 210, 110999. [Google Scholar] [CrossRef]
- Madireddy, S.; Sista, B.; Vemaganti, K. A Bayesian Approach to Selecting Hyperelastic Constitutive Models of Soft Tissue. Comput. Methods Appl. Mech. Eng. 2015, 291, 102–122. [Google Scholar] [CrossRef]
- Papadimas, N.; Dodwell, T. A Hierarchical Bayesian Approach for Calibration of Stochastic Material Models. Data-Centric Eng. 2021, 2, e20. [Google Scholar] [CrossRef]
- Battalgazy, B.; Khatamsaz, D.; Ghasemi, Z.; Mallick, D.D.; Arroyave, R.; Srivastava, A. A Bayesian-Based Approach for Constitutive Model Selection and Calibration Using Diverse Material Responses. Acta Mater. 2025, 287, 120796. [Google Scholar] [CrossRef]
- Ryan, S.; Berk, J.; Rana, S.; McDonald, B.; Venkatesh, S. A Bayesian Optimisation Methodology for the Inverse Derivation of Viscoplasticity Model Constants in High Strain-Rate Simulations. Def. Technol. 2022, 18, 1563–1577. [Google Scholar] [CrossRef]
- Aggarwal, A.; Hudson, L.T.; Laurence, D.W.; Lee, C.-H.; Pant, S. A Bayesian Constitutive Model Selection Framework for Biaxial Mechanical Testing of Planar Soft Tissues: Application to Porcine Aortic Valves. J. Mech. Behav. Biomed. Mater. 2023, 138, 105657. [Google Scholar] [CrossRef]
- Haj-Ali, R.; Kim, H.-K.; Koh, S.W.; Saxena, A.; Tummala, R. Nonlinear Constitutive Models from Nanoindentation Tests Using Artificial Neural Networks. Int. J. Plast. 2008, 24, 371–396. [Google Scholar] [CrossRef]
- Ji, H.; Duan, H.; Li, Y.; Li, W.; Huang, X.; Pei, W.; Lu, Y. Optimization the Working Parameters of as-Forged 42crmo Steel by Constitutive Equation-Dynamic Recrystallization Equation and Processing Maps. J. Mater. Res. Technol. 2020, 9, 7210–7224. [Google Scholar] [CrossRef]
- Li, D.Z.; Zhao, X.M.; Zhang, H.L.; Li, J. Flow Stress-Strain Curves and Dynamic Recrystallization Behavior of High Carbon Low Alloy Steels during Hot Deformation. J. Mater. Res. Technol. 2025, 35, 3144–3160. [Google Scholar] [CrossRef]
- He, X.; Liu, L.; Zeng, T.; Yao, Y. Micromechanical Modeling of Work Hardening for Coupling Microstructure Evolution, Dynamic Recovery and Recrystallization: Application to High Entropy Alloys. Int. J. Mech. Sci. 2020, 177, 105567. [Google Scholar] [CrossRef]
- Li, C.; Huang, L.; Zhao, M.; Zhang, X.; Li, J.; Li, P. Influence of Hot Deformation on Dynamic Recrystallization Behavior of 300m Steel: Rules and Modeling. Mater. Sci. Eng. A 2020, 797, 139925. [Google Scholar] [CrossRef]
- He, J.; Hu, M.; Zhou, Z.; Li, C.; Sun, Y.; Zhu, X. Effect of Initial Grain Size on Hot Deformation Behavior and Recrystallization Mechanism of Al-Zn-Mg-Cu Alloy. Mater. Charact. 2024, 212, 114012. [Google Scholar] [CrossRef]
- Karimzadeh, M.; Malekan, M.; Mirzadeh, H.; Saini, N.; Li, L. Hot Deformation Behavior Analysis of as-Cast Cocrfeni High Entropy Alloy Using Arrhenius-Type and Artificial Neural Network Models. Intermetallics 2024, 168, 108240. [Google Scholar] [CrossRef]
- Chen, H.; Huo, Y.; He, T.; Yan, Z.; Li, Z.; Ji, H.; Hosseini, S.R.E.; Wang, Z.; Bian, Z.; Yu, W.; et al. Establishing a Unified Viscoplastic Constitutive Equation for Ea4t Steel: Comparative Analysis with Arrhenius Model. Int. J. Non-Linear Mech. 2024, 166, 104835. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Y.; Huang, Y.; Wang, B.; Wei, W.; Qin, S.; Zhou, H.; Liu, J. The Thermal Deformation Behavior and Processing Map of Tc9 Titanium Alloy. J. Mater. Res. Technol. 2024, 33, 6576–6590. [Google Scholar] [CrossRef]
- Zeng, Z.; Jonsson, S.; Zhang, Y. Constitutive Equations for Pure Titanium at Elevated Temperatures. Mater. Sci. Eng. A 2009, 505, 116–119. [Google Scholar] [CrossRef]
- Li, H.-Y.; Li, Y.-H.; Wang, X.-F.; Liu, J.-J.; Wu, Y. A Comparative Study on Modified Johnson Cook, Modified Zerilli–Armstrong and Arrhenius-Type Constitutive Models to Predict the Hot Deformation Behavior in 28crmnmov Steel. Mater. Des. 2013, 49, 493–501. [Google Scholar] [CrossRef]
- Karkalos, N.E.; Markopoulos, A.P. Determination of Johnson-Cook Material Model Parameters by an Optimization Approach Using the Fireworks Algorithm. Procedia Manuf. 2018, 22, 107–113. [Google Scholar] [CrossRef]
- Meng, Z.; Zhang, C.; Zhang, G.; Wang, K.; Wang, Z.; Chen, L.; Zhao, G. Hot Compressive Deformation Behavior and Microstructural Evolution of the Spray-Formed 1420 Al–Li Alloy. J. Mater. Res. Technol. 2023, 27, 4469–4484. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.-M.; Liu, G. A Modified Johnson–Cook Model for Tensile Behaviors of Typical High-Strength Alloy Steel. Mater. Sci. Eng. A 2010, 527, 6980–6986. [Google Scholar] [CrossRef]
- Fan, M.-R.; Luo, Z.-A.; Liu, Y.-H.; Feng, Y.-Y. Hot Deformation Behavior of 30mnb5v Steel: Phenomenological Constitutive Model, Ensemble Learning Algorithm, Hot Processing Map and Microstructure Evolution. J. Mater. Res. Technol. 2024, 32, 2675–2690. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.; Fan, P.; Zhu, L.; Zhang, K.; Wang, K.; Song, C.; Ren, S. A Creep Life Prediction Model of P91 Steel Coupled with Back-Propagation Artificial Neural Network (Bp-Ann) and Θ Projection Method. Int. J. Press. Vessel. Pip. 2023, 206, 105039. [Google Scholar] [CrossRef]
- Long, J.; Deng, L.; Jin, J.; Zhang, M.; Tang, X.; Gong, P.; Wang, X.; Xiao, G.; Xia, Q. Enhancing Constitutive Description and Workability Characterization of Mg Alloy during Hot Deformation Using Machine Learning-Based Arrhenius-Type Model. J. Magnes. Alloys 2024, 12, 3003–3023. [Google Scholar] [CrossRef]
- Liang, Z.; Yu, F.; Yinyang, W.; Yongdong, X. Constitutive Relationship of (Ti5si3 +Tibw)/Tc11 Composites Based on Bp Neural Network. Mater. Today Commun. 2022, 32, 103973. [Google Scholar] [CrossRef]
- Kareem, S.A.; Anaele, J.U.; Aikulola, E.O.; Olanrewaju, O.F.; Omiyale, B.O.; Falana, S.O.; Oke, S.R.; Bodunrin, M.O. Hot Deformation Behavior of Aluminum Alloys: A Comprehensive Review on Deformation Mechanism, Processing Maps Analysis and Constitutive Model Description. Mater. Today Commun. 2025, 44, 112004. [Google Scholar] [CrossRef]
- Yao, Q.; Dong, P.; Zhao, Z.; Li, Z.; Wei, T.; Wu, J.; Qiu, J.; Li, W. Temperature Dependent Tensile Fracture Strength Model of Rubber Materials Based on Mooney-Rivlin Model. Eng. Fract. Mech. 2023, 292, 109646. [Google Scholar] [CrossRef]
- Banerjee, A.; Dhar, S.; Acharyya, S.; Datta, D.; Nayak, N. Determination of Johnson Cook Material and Failure Model Constants and Numerical Modelling of Charpy Impact Test of Armour Steel. Mater. Sci. Eng. A 2015, 640, 200–209. [Google Scholar] [CrossRef]
- Bouchkira, I.; Latifi, A.M.; Khamar, L.; Benjelloun, S. Global Sensitivity Based Estimability Analysis for the Parameter Identification of Pitzer’s Thermodynamic Model. Reliab. Eng. Amp; Syst. Saf. 2021, 207, 107263. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. Emcee: The Mcmc Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306–312. [Google Scholar] [CrossRef]
- Zhao, Q.; Wu, T.; Zhu, L.; Hong, J. Online Adaptive Selection of Appropriate Learning Functions with Parallel Infilling Strategy for Kriging-Based Reliability Analysis. Comput. Amp Ind. Eng. 2024, 194, 110361. [Google Scholar] [CrossRef]
- Jiang, L.; Fu, H.; Zhang, H.; Xie, J. Physical Mechanism Interpretation of Polycrystalline Metals’ Yield Strength Via a Data-Driven Method: A Novel Hall–Petch Relationship. Acta Mater. 2022, 231, 117868. [Google Scholar] [CrossRef]
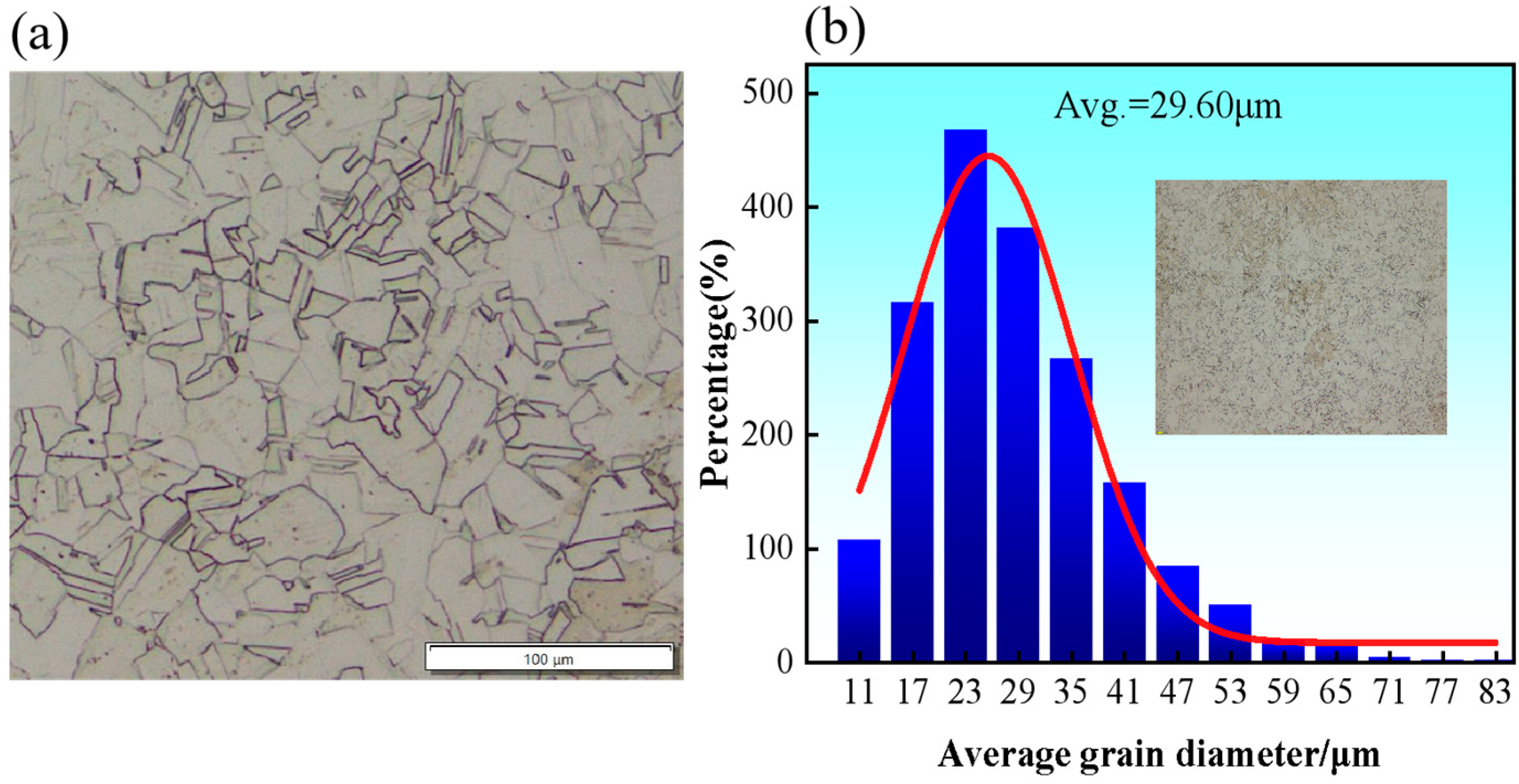
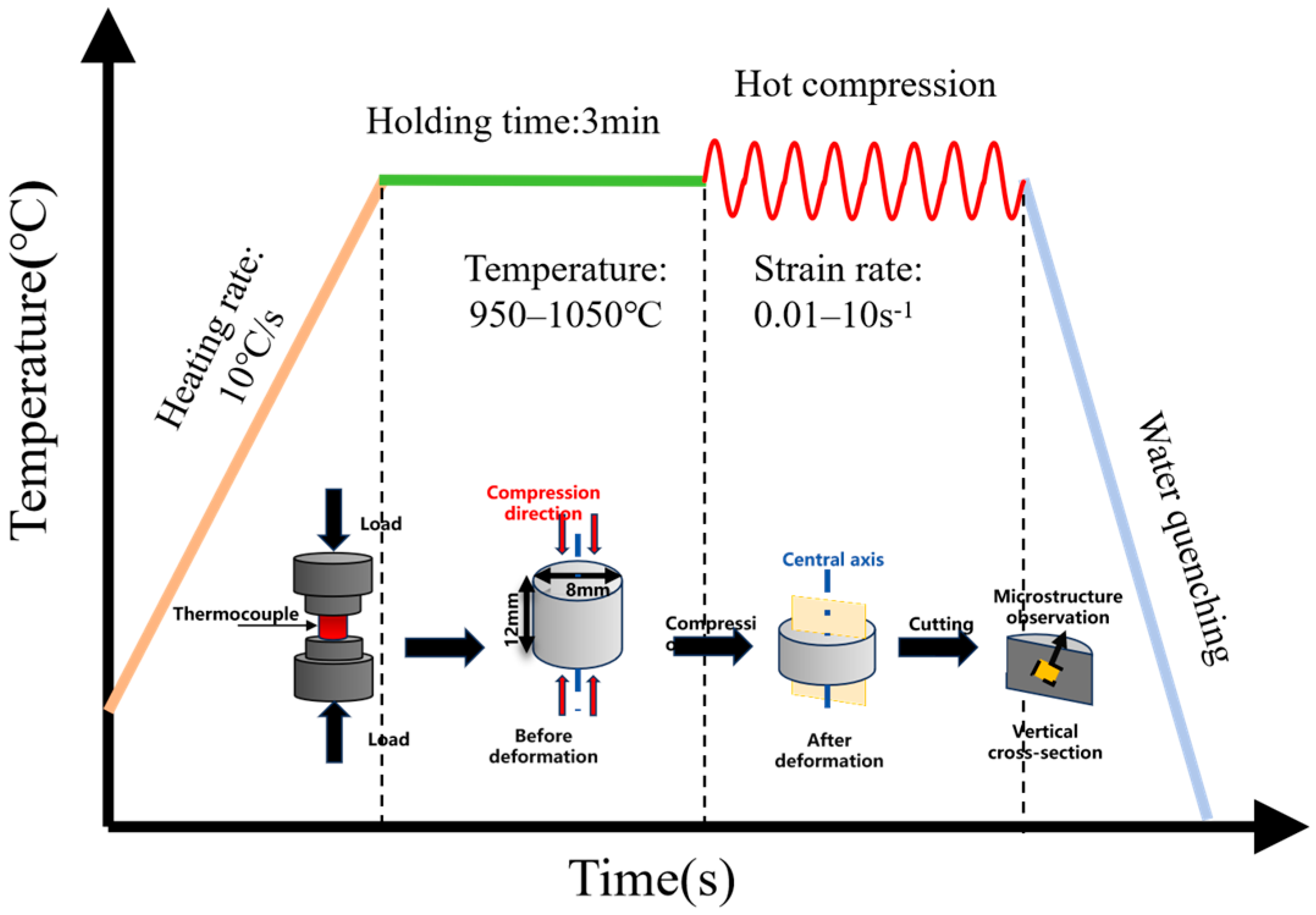
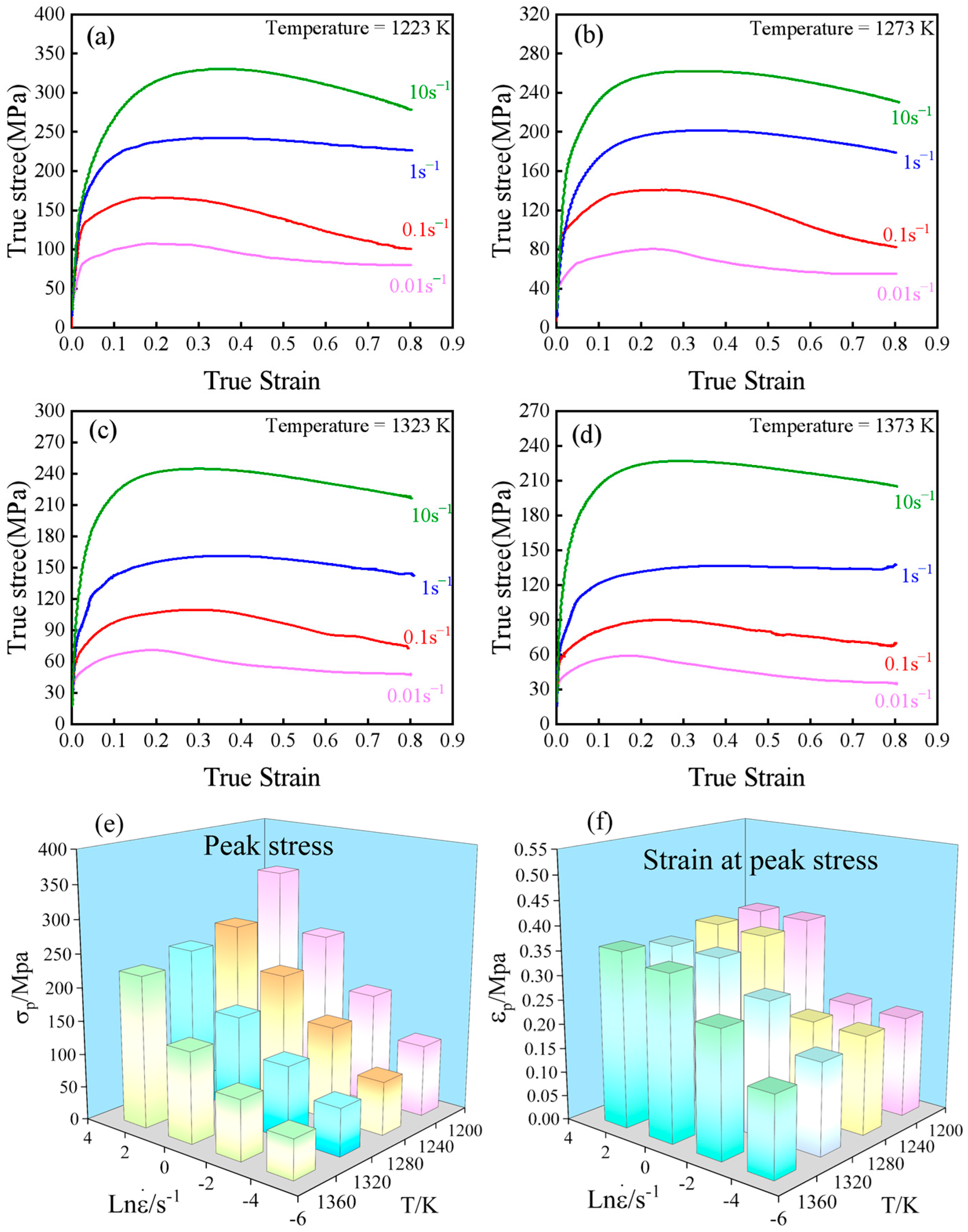
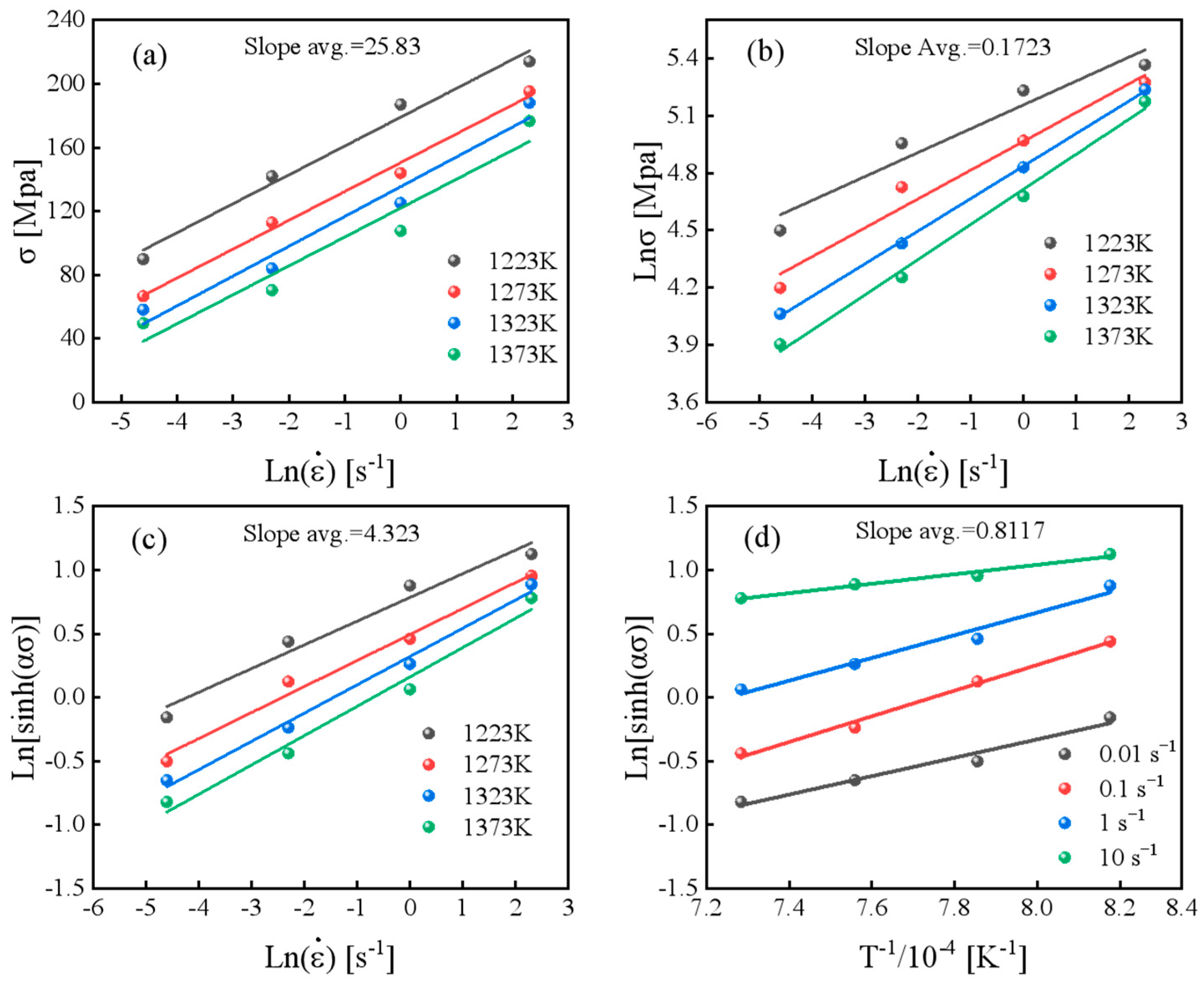




| Test | Mn | Si | Cr | Ni | Cu | Nb | C | Fe |
|---|---|---|---|---|---|---|---|---|
| Fe66Mn15Si5Cr9Ni5 | 14.78 | 4.9 | 9.19 | 5.1 | 0.002 | 0.003 | ≤0.01 | Balance |
| Parameters | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| A | −0.0569 | 1.1087 | 0.7647 | 0.1072 | 1.1580 | 0.9807 |
| n | 1.0579 | 1.783 | 2.823 | 1.314 | 1.091 | 1.715 |
| Q | 0.84578 | 0.176 | 1.266 | 1.249 | 0.795 | 1.261 |
| α | 0.083725 | −0.51288 | 0.59375 | 0.55653 | 1.0432 | 1.0745 |
| Characteristics | Mathematical Derivation | Numerical Optimization | Machine Learning Method |
|---|---|---|---|
| Model Structure | Explicit physical equations | Explicit equations and parameter optimization | Blac-box model |
| Data Requirements | Low | Medium | High |
| Computational Efficiency | High | Medium | Low |
| Interpretability | Strong | Medium | Weak |
| Complex Nonlinear Model | Weak | Medium | Strong |
| Generalization Ability | Low | Medium | High |
| Applicable Scenarios | Simple behavior verification, theoretical derivation | Multi-parameter coupling optimization | Complex multi-field coupling, big data scenarios |
| Rank | Parameter | Sensitivity | Range (Min: Max) |
|---|---|---|---|
| 1 | Q3 | 0.2099 | [−30,057.26: 29,462.06] |
| 2 | Q4 | 0.2096 | [58,952.18: 60,143.14] |
| 3 | A4 | 0.1929 | [5382.57: 5491.31] |
| 4 | A3 | 0.1922 | [−2715.25: −2661.49] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Sun, C.; Liang, H.; Qian, L.; Wang, C. Constitutive Model for Hot Deformation Behavior of Fe-Mn-Cr-Based Alloys: Physical Model, ANN Model, Model Optimization, Parameter Evaluation and Calibration. Metals 2025, 15, 512. https://doi.org/10.3390/met15050512
Xu J, Sun C, Liang H, Qian L, Wang C. Constitutive Model for Hot Deformation Behavior of Fe-Mn-Cr-Based Alloys: Physical Model, ANN Model, Model Optimization, Parameter Evaluation and Calibration. Metals. 2025; 15(5):512. https://doi.org/10.3390/met15050512
Chicago/Turabian StyleXu, Jie, Chaoyang Sun, Huijun Liang, Lingyun Qian, and Chunhui Wang. 2025. "Constitutive Model for Hot Deformation Behavior of Fe-Mn-Cr-Based Alloys: Physical Model, ANN Model, Model Optimization, Parameter Evaluation and Calibration" Metals 15, no. 5: 512. https://doi.org/10.3390/met15050512
APA StyleXu, J., Sun, C., Liang, H., Qian, L., & Wang, C. (2025). Constitutive Model for Hot Deformation Behavior of Fe-Mn-Cr-Based Alloys: Physical Model, ANN Model, Model Optimization, Parameter Evaluation and Calibration. Metals, 15(5), 512. https://doi.org/10.3390/met15050512







