A Theoretical Study of Ordinary Dislocations and Order Twinning in γ-TiAl at Finite Temperatures

Abstract

The generalized planar fault energies of 1/2<110] and 1/6<112] slip directions on {111} planes in $\gamma$-TiAl at temperatures up to 1500 K were predicted through first-principles calculations and quasi-harmonic approximation. The obtained unstable stacking and twinning fault (USF and UTF) energies, as well as superlattice intrinsic and extrinsic stacking fault (SISF and SESF) energies, are consistent with existing theoretical data. Results show that the USF, UTF, SISF, and SESF energies for both slip directions decrease overall as temperature increases. The effect of temperature on the 1/2<110] ordinary dislocation and 1/6<112] order twinning in $\gamma$-TiAl is further analyzed generalized planar fault energies. It is demonstrated that the nucleation of ordinary dislocation and twinning dislocations becomes more favorable with increasing temperature. Furthermore, it is shown that order twinning in $\gamma$-TiAl is more likely to occur at crack tips or grain boundaries, and its twinnability is enhanced at elevated temperatures.

1. Introduction

Alloys based on $\gamma$-TiAl intermetallic compound are widely recognized to be ideal high-temperature structural materials for the aerospace and automotive industries due to their low density, good high-temperature strength, and good oxidation resistance [1,2,3]. However, their inherent brittleness at low temperatures limits their widespread applications [2]. $\gamma$-TiAl-based alloys with the best balance of mechanical properties consist of a single phase $\gamma$ and colonies of ${\alpha }_2$/$\gamma$ lamellae. Undoubtedly, the mechanical properties of these alloys are closely related to the slip and twining characteristics of the $\gamma$-TiAl phase. Deformation of this phase occurs exclusively on {111} planes through the glide of ordinary dislocations with the Burgers vector $\mathbf{b}$ = 1/2<110] and to a lesser extent by order twinning along 1/6<11$\overline{2}$] and by superlattice dislocations with the Burgers vectors $\mathbf{b}$ = 1/2<11$\overline{2}$] and <011], respectively [4]. The relative contributions of these mechanisms to deformation mainly depend on the deformation temperature, the Al concentration, and the content of ternary and higher alloying elements [3]. There is an increasing awareness that the activation of superlattice dislocations is difficult and requires significantly higher shear stresses when compared with ordinary screw dislocations or order twinning. In the past decades, some experimental investigations have indicated that the deformation by ordinary dislocations and order twinning can exist in $\gamma$-TiAl-based alloys over a wide range of temperatures [5]. Therefore, to better understand the plastic deformation of $\gamma$-TiAl-based alloys, it is necessary to explore the influence of temperature on the glide of ordinary dislocations and order twinning in $\gamma$-TiAl.

Generalized planar fault energy (${\gamma }_{\mathrm{GPF}}$) provides fundamental physical information for understanding the plastic deformation mechanisms. Over the last few decades, some research groups have employed first-principles calculations (FPC) to generate the generalized planar fault energy for $\gamma$-TiAl and its alloys and have assessed their deformation behaviors by analyzing the information contained in the ${\gamma }_{\mathrm{GPF}}$ curve [6,7,8,9,10,11,12,13,14,15,16]. Nevertheless, these generalized planar fault energies are all at absolute zero temperature due to the limitations of first-principles calculations. To the best of our knowledge, no experimental or theoretical investigations have reported the effect of temperature on the generalized planar fault energies for $\gamma$-TiAl to date. Due to the nature of quasi-harmonic approximation (QHA), the anharmonic contributions are treated only approximately via the volume dependence of ground state energy and the temperature dependence of the vibrational density of states [17]. By combining the FPC with the QHA, several groups have studied the temperature dependence of the generalized planar fault energies of pure metals and intermetallic compounds, evaluating the influence of temperature on their deformation behaviors [17,18]. Accordingly, the objective of this study is to explore the effect of temperature on the glide of ordinary dislocations and order twinning based on the temperature-dependent generalized planar fault energies for $\gamma$-TiAl, derived from the FPC in combination with the QHA.

2. Methodology

2.1. Thermodynamic Properties [17,18]

Before calculating the generalized planar fault energy of $\gamma$-TiAl at finite temperature, the temperature dependent volume is estimated using first-principles QHA to describe the Helmholtz free energy $F(V,T)$ as a function of volume $\left(V\right)$ and temperature $\left(T\right)$:

$$F(V,T)=E(V,0)+F_{\mathrm{el}}(V,T)+F_{\mathrm{vib}}(V,T).$$

(1)

Here, $E(V,0)$ represents the static energy at 0 K directly obtained from the FPC, and $F_{\mathrm{el}}(V,T)$ signifies the thermal electronic contribution to free energy determined by integrating the electronic density of state (DOS) directly obtained for the FPC, and $F_{\mathrm{vib}}(V,T)$ denotes the vibrational contribution estimated through phonon calculations. The phonon-free energy in the QHA can be expressed as

$$F_{\mathrm{vib}}(V,T)=\sum _{\mathbf{q}\lambda }[1/2\hslash {\omega }_{\mathbf{q}\lambda }+k_{B}T\ln (1-e^{-\hslash {\omega }_{\mathbf{q}\lambda }/k_{B}T})].$$

(2)

Here, $k_B$ denotes Boltzmann’s constant, ℏ is the reduced Planck constant, ${\omega }_{\mathbf{q}\lambda }$ represents the frequency of the $\lambda$-th phonon mode at wave vector $\mathbf{q}$, and the sum is over all wave vectors $\mathbf{q}$ and all three phonon branches $\lambda$ in the first Brillouin zone. The relationship between volume and temperature $\left(T\right(V)$ or $V\left(T\right))$, i.e., the average thermal expansion coefficient is directly estimated from the Helmholtz free energy.

2.2. Generalized Planar Fault Energy

The generalized planar fault energy for $\gamma$-TiAl is defined as the energy per unit area required to create n-layer faults by shearing n successive {111}-layers along a slip direction:

$${\gamma }_{\mathrm{GPF}}=(E_x-E_p)/S.$$

(3)

Here, $E_x$ represents the total energy of the supercells with the top half of atomic planes shifted by a displacement x relative to the bottom half along the slip direction, $E_p$ is the total energy of the perfect supercell, and S denotes the area of the {111} slip plane. To obtain the temperature-dependent ${\gamma }_{\mathrm{GPF}}$, the temperature dependence of the lattice constants $(a,c)$ is estimated based on volume change resulting from temperature variations through the following three steps: (i) predict the volume-dependent static lattice constants $a\left(V\right)$ and $c\left(V\right)$ at 0 K using FPC; (ii) predict the volume change as a function of temperature $V\left(T\right)$, or inversely the $T\left(V\right)$ relation; (iii) based on the above two steps, the temperature dependent lattice constants $a\left(T\right)$ and $c\left(T\right)$ are functions of V, expressed as $a\left(T\right)=a\left(T\right(V\left)\right)$ and $c\left(T\right)=c\left(T\right(V\left)\right)$. Based on the lattice constants $a\left(T\right)$ and $c\left(T\right)$ at a given temperature, a supercell model was constructed using the three basic vectors of $\left[1\overline{1}0\right]$, $\left[11\overline{2}\right]$ and [111] to predict generalized planar fault energy. The supercell model consists of twelve atomic layers with eight atoms per layer and a 15 Å vacuum layer in the [111] direction. For the $1/2\left[1\overline{1}0\right]$ ordinary dislocation, the generalized planar fault energy was estimated by shifting the upper half of layers 7–12 relative to the lower half of layers 1–6 equal to its Burgers vector. For the $1/6\left[11\overline{2}\right]$ order twinning dislocation, the generalized planar fault energy was firstly estimated by shifting the upper half of layers 7–12 relative to the lower half of layers 1–6 by a displacement equal to its Burgers vector, and the upper half of layers 8–12 was shifted immediately relative to the lower half of layers 1–7 by a displacement equal to its Burgers vector. In this work, the generalized planar fault energy was predicted at 0, 300, 600, 900, 1200, and 1500 K, respectively.

2.3. Computational Details

The FPC was conducted using the Vienna ab initio simulation package (VASP) based on density functional theory (DFT) [19,20,21] employing pseudopotentials generated by the projector augmented plane wave (PAW) method [22,23]. The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) potential function was utilized to describe the exchange-correlation effects [24]. A cutoff energy of 550 eV was established, and total energy convergence was ${10}^{-6}$ eV in the electronic self-consistent loop. The Brillouin zone was sampled using the Monkhorst–Pack method [25]. An $8\times 8\times 8$ k-point mesh was employed for the unit cell. Accurate calculations of the total energy and electronic DOS at 0 K were performed for $E(V,0)$ and $F_{\mathrm{el}}(V,T)$ using the linear tetrahedron method with Blöchl corrections [26]. For the ${\gamma }_{\mathrm{GPF}}$, the Brillouin zone was sampled using $4\times 3\times 1$ Monkhorst–Pack k-point grids for all supercell models. Phonon calculations were conducted using the supercell approach, as implemented in the PHONOPY package, which serves as an interface to the VASP [27]. A 32-atom supercell comprising $2\times 2\times 2$ unit cells and an $8\times 8\times 8$ k-point mesh were employed for the calculations. Force constants were computed using density functional perturbation theory (DFPT), as implemented in VASP [19,20,21], and subsequently post-processed by PHONOPY [27]. During the DFPT calculations, total energy convergence was achieved to within ${10}^{-8}$ eV in the electronic self-consistent loop. The phonon spectra for $F_{\mathrm{vib}}(V,T)$ are obtained using the PHONOPY package based on the computed force constants. Additionally, PHONOPY was employed to obtain $F(V,T)$ and other thermodynamic properties. $E(V,0)$ and $F_{\mathrm{vib}}(V,T)$ have been calculated at eleven different volumes. The equilibrium volume at any given temperature is determined by fitting the $F(V,T)$ versus V data points with Vinet equation of state (EOS) [28]. The relations between $F(V,T)$ and V for $\gamma$-TiAl at varying temperatures are illustrated in Figure 1a, showcasing the equilibrium volume at a specific temperature denoted by the solid ball. The evolution of the equilibrium volume with T is depicted in Figure 1b, indicating the thermal expansion of $\gamma$-TiAl attributed to the rise in its equilibrium volume with increasing temperature.

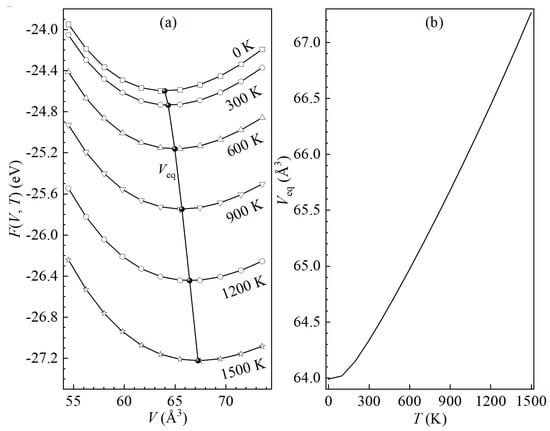
Figure 1. (a) The dependence of Helmholtz free energy $F(V,T)$ on the unit cell volume $\left(V\right)$ and the values of equilibrium volumes $\left(V_{eq}\right)$ for $\gamma$-TiAl at temperatures between 0 and 1500 K with a step of 300 K. (b) The equilibrium volumes as a function of temperature $\left(T\right)$ for $\gamma$-TiAl.

3. Results and Discussion

The generalized planar fault energies along both 1/2[1$\overline{1}$0] and 1/6[11$\overline{2}$] slip directions on (111) plane in $\gamma$-TiAl have been calculated with their displacements normalized by the corresponding Burgers vectors. The absolute zero temperature ${\gamma }_{\mathrm{GPF}}$ curves of both slip directions in $\gamma$-TiAl are shown in Figure 2. It can be seen from Figure 2a that the deformation energy associated with the 1/2[1$\overline{1}$0] direction is zero at the displacement point of unity due to its high symmetry. As a matter of fact, the FPC of the ${\gamma }_{\mathrm{GPF}}$ of stoichiometric $\gamma$-TiAl has also been performed by Wang’s group [6,9,15], Dumitraschkewitz et al. [10], Lee et al. [11], Qi et al. [12], Sheng et al. [13] and Seko [14] based on the PAW and the GGA-PBE, and by Wen and sun [7], and Ji et al. [8] based on the PAW and the GGA parameterized by Perdew and Wang (GGA-PW91), and by Liu et al. [16] based on ultrasoft pseudopotentials and the GGA-PW91. All of theoretical values of ${\gamma }_{\mathrm{USF}}$, ${\gamma }_{\mathrm{SISF}}$, and ${\gamma }_{\mathrm{SESF}}$ from the FPC are presented in Table 1. Overall, our predictions align well with prior calculations [6,7,8,9,10,11,12,13,14,16]. For instance, the ${\gamma }_{\mathrm{USF}}$ value of 898.21 mJ/m² for the 1/2[1$\overline{1}$0] slip direction is well consistent with the theoretical values of 833 and 865 mJ/m² reported by sheng et al. [13] and Liu et al. [16]. The ${\gamma }_{\mathrm{USF}}$ value of 309.63 mJ/m² for the 1/6[11$\overline{2}$] slip direction falls within the previously reported ranges of 256–335 mJ/m² [6,7,8,9,10,13,16]. The ${\gamma }_{\mathrm{USF}}$ and ${\gamma }_{\mathrm{SESF}}$ values of 413.38 and 182.08 mJ/m² for the direction are in excellent agreement with theoretical values of 409 and 182 mJ/m² reported by Wen et al. [7], of 410 and 177 mJ/m² reported by Ji et al. [8] and of 412 and 182 mJ/m² reported by Sheng et al. [13]. Additionally, the theoretical value of ${\gamma }_{\mathrm{SISF}}$ for the 1/6[11$\overline{2}$] slip direction is in accord with other calculated results [6,7,8,9,10,11,12,13,14,16]. Especially, it matches well with the reported results by Wen et al. [7], Ji et al. [8], Dumitraschkewitz et al. [10] and Qi et al. [12].

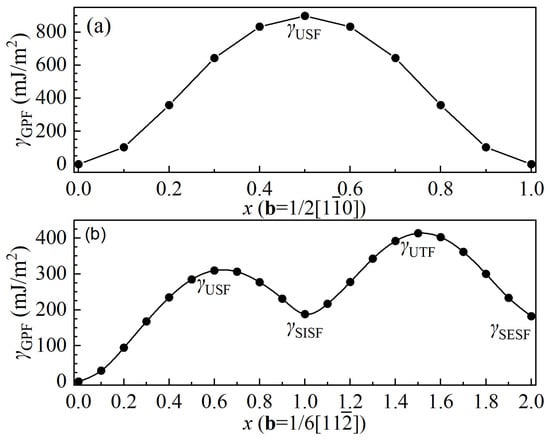
Figure 2. Generalized planar fault energies of (a) 1/2[1$\overline{1}$0](111) and (b) 1/6[11$\overline{2}$](111) slip systems in $\gamma$-TiAl at 0 K. Where, ${\gamma }_{\mathrm{USF}}$, ${\gamma }_{\mathrm{SISF}}$, ${\gamma }_{\mathrm{UTF}}$, and ${\gamma }_{\mathrm{SESF}}$ denote unstable stacking fault energy, superlattice intrinsic stacking fault energy, unstable twinning fault energy, and superlattice extrinsic stacking fault energy, respectively.

Table 1. Unstable stacking fault energy (${\gamma }_{\mathrm{USF}}$, mJ/m²), superlattice intrinsic stacking fault energy (${\gamma }_{\mathrm{SISF}}$, mJ/m²), unstable twinning fault energy (${\gamma }_{\mathrm{UTF}}$, mJ/m²), and superlattice extrinsic stacking fault energy (${\gamma }_{\mathrm{SESF}}$, mJ/m²) of 1/2[1$\overline{1}$0](111) and 1/6[11$\overline{2}$](111) slip systems in $\gamma$-TiAl obtained from first-principles calculations (FPC) and molecular dynamics simulations (MDS).

Method	1/2[1$\overline{1}$0]	1/6[11$\overline{2}$]				Ref.
	${\mathbf{\gamma }}_{\mathbf{USF}}$	${\mathbf{\gamma }}_{\mathbf{USF}}$	${\gamma }_{\mathbf{SISF}}$	${\gamma }_{\mathbf{UTF}}$	${\gamma }_{\mathbf{SESF}}$
FPC	898.21	309.63	188.08	413.38	182.02	this
		332.35	167.11			[6]
		321	184	409	182	[7]
		316	181	410	177	[8]
		332.83	167.11			[9]
		335	188			[10]
			203			[11]
			182			[12]
	833	313	171	412	182	[13]
			194			[14]
		496.07	10.57			[15]
	865	256	137			[16]
MDS			322			[12]
			281, 165, 258			[14]
			129			[29]
			66, 101			[29]
	827	211	68	912		[30]
			88, 93			[31]
			0, 135			[31]

In addition to FPC, molecular dynamics simulation (MDS) of the ${\gamma }_{\mathrm{GPF}}$ of $\gamma$-TiAl was also conducted by Qi et al. [12] with a highly accurate moment tensor potential (MTP); by Secko [14], based on machine learning potential (MLP) with polynominal invariants to represent neighboring atomic density; by Lu et al. [29], based on MLP with a deep neural network method and embedded atom method (EAM) potentials; by Negogi and Janisch [30], based on EAM potentials; and by Pei et al. [31], based on EAM and modified EAM potentials. These simulated results are also presented in Table 1. For the 1/2[1$\overline{1}$0] slip direction, the obtained ${\gamma }_{\mathrm{USF}}$ value of 898.21 mJ/m² from the FPC is larger than that of 827 mJ/m² from the MDS [30]. For the 1/6[11$\overline{2}$] slip direction, the obtained ${\gamma }_{\mathrm{USF}}$ value of 309.63 mJ/m² is also larger than that of 211 mJ/m² from the MDS [30]. On the contrary, the obtained ${\gamma }_{\mathrm{UTF}}$ value of 413.38 mJ/m² from the FPC is much smaller than that of 912 mJ/m² from the MDS [30]. For the ${\gamma }_{\mathrm{SISF}}$, the value of 182.02 mJ/m² obtained from the FPC falls within the ranges of 0-332 mJ/m² determined from the MDS [12,14,29,30,31].

The change of the ${\gamma }_{\mathrm{USF}}$ for the 1/2[1$\overline{1}$0] slip direction with temperature is shown in Figure 3a. From the figure, one can find that the ${\gamma }_{\mathrm{USF}}$ is reduced in the whole with increasing temperature. The variation of the ${\gamma }_{\mathrm{USF}}$, ${\gamma }_{\mathrm{UTF}}$, ${\gamma }_{\mathrm{SISF}}$, and ${\gamma }_{\mathrm{SESF}}$ for the 1/6[11$\overline{2}$] slip direction is shown in Figure 3b. One can also see from the figure that the ${\gamma }_{\mathrm{USF}}$, ${\gamma }_{\mathrm{UTF}}$, ${\gamma }_{\mathrm{SISF}}$, and ${\gamma }_{\mathrm{SESF}}$ are all reduced with increasing temperature. Unfortunately, the ${\gamma }_{\mathrm{GPF}}$ of stoichiometric TiAl at different temperatures has not yet been investigated both experimentally and theoretically. However, experimental studies on nonstoichiometric TiAl have reported the SISF energy of Ti₄₆Al₅₄ as 70-85 mJ/m² at 293 K and 60 mJ/m² at 873 K [32]. Similarly, the SISF energies of the high-Nb TiAl alloy with a composition of Ti-46Al-8.5Nb-0.2W were measured as 77–81 mJ/m² at 298 K and 57–60 mJ/m² at 1273 K [33]. These experimental measurements also indicated a decreasing trend in the ${\gamma }_{\mathrm{SISF}}$ with increasing temperature. It is well known that stoichiometry and alloying elements have an impact on the ${\gamma }_{\mathrm{GPF}}$ and deformation mechanisms of TiAl alloys. Thus, the above change trend may be caused by the combined effect of temperature, Al content and alloying elements. To deeply understand these experimental phenomena, it is necessary to further investigate the impact of Al content and alloying elements on the temperature dependent ${\gamma }_{\mathrm{GPF}}$ of TiAl alloys. Since this study focuses only on pure $\gamma$-TiAl without considering the influence of stoichiometry and alloying elements, the current findings can not explain these experimental phenomena. In spite, the findings of this study are of great significance for future research on the ${\gamma }_{\mathrm{GPF}}$ and deformation mechanisms of real-world alloys. As suggested by Rice [34], the ${\gamma }_{\mathrm{USF}}$ represents the energy barrier for leading dislocation nucleation. Due to the decreased ${\gamma }_{\mathrm{USF}}$ values of both slip directions with temperature rise, the nucleation of both 1/2[1$\overline{1}$0] and 1/6[11$\overline{2}$] leading dislocations become easier with increasing temperature.

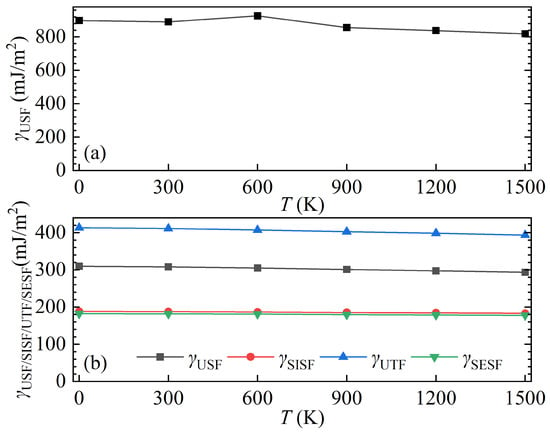
Figure 3. Temperature dependencies of unstable and stable planar fault energies ( ${\gamma }_{\mathrm{USF}}$, ${\gamma }_{\mathrm{SISF}}$, and ${\gamma }_{\mathrm{UTF}}$, ${\gamma }_{\mathrm{SESF}}$) of (a) 1/2[1$\overline{1}$0](111) and (b) 1/6[11$\overline{2}$](111) slip systems in $\gamma$-TiAl.

In grains or lamellae that are unfavorably oriented for the glide of ordinary dislocations, significant constraint stresses can be developed to ensure compatibility with the shape change of adjacent grains. This can easily lead to crack nucleation and failure. In this respect, the activation of mechanical twinning may compensate for the lack of independent glide systems which can operate at comparable stresses and, thus, support the plasticity of polycrystalline materials. Both grain and lamellar boundaries were observed in $\gamma$-TiAl-based alloys as prominent sources of 1/6<112] partial dislocations [8]. Experimental investigations have revealed that the growth of twins occurs mainly through the propagation of 1/6<112] partials on successive {111} planes [35]. Herein, it is emphasized that the activation of deformation modes depends significantly on the nucleation of dislocations. In face-centered cubic (FCC) metals, assuming the nucleation of a 1/6<112> Shockley partial dislocation from a grain boundary, slip deformation means that a leading Shockley partial is followed by a trailing Shockley partial on the same slip plane. The leading and trailing Shockley partial Burgers vectors add up to make a 1/2<110> full dislocation Burgers vector. For deformation twinning, the same leading Shockley partial is followed by a twinning Shockley partial which slips on an adjacent {111} plane. The competition between dislocation slip and deformation twinning is, thus, the competition between the nucleation of a trailing partial and a twinning partial. The (${\gamma }_{\mathrm{USF}}-{\gamma }_{\mathrm{SISF}}$) and (${\gamma }_{\mathrm{UTF}}-{\gamma }_{\mathrm{SISF}}$) represent the energy barrier for trailing and twinning dislocation nucleation, respectively [34]. Therefore, the (${\gamma }_{\mathrm{USF}}-{\gamma }_{\mathrm{SISF}}$) and (${\gamma }_{\mathrm{UTF}}-{\gamma }_{\mathrm{SISF}}$) for the 1/6[11$\overline{2}$] slip direction are further calculated in this study and shown in Figure 4. It can be observed from the figure that both (${\gamma }_{\mathrm{USF}}-{\gamma }_{\mathrm{SISF}}$) and (${\gamma }_{\mathrm{UTF}}-{\gamma }_{\mathrm{SISF}}$) for the slip direction also exhibit a reduction with rising temperature. This finding indicates that the nucleation of trailing and twinning 1/6<11$\overline{2}$] Shockley partials become increasingly favorable as the temperature is elevated.

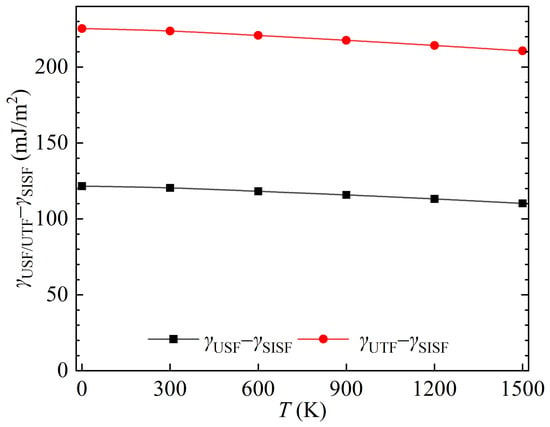
Figure 4. Temperature dependencies of the energy barriers (${\gamma }_{\mathrm{USF}}-{\gamma }_{\mathrm{SISF}}$ and ${\gamma }_{\mathrm{UTF}}-{\gamma }_{\mathrm{SISF}}$) of trailing and twinning 1/6<11$\overline{2}$] dislocations in $\gamma$-TiAl.

Jo et al. [36] proposed a comprehensive theory for the plastic deformation of FCC metals, demonstrating that the ratio (${\gamma }_d$) of ${\gamma }_{\mathrm{ISF}}$ to (${\gamma }_{\mathrm{USF}}-{\gamma }_{\mathrm{ISF}}$) for the trailing 1/6<112> dislocation serves as a primary parameter for characterizing the deformation behavior of FCC metals. The critical values of ${\gamma }_d=-1/2,0,2$ delineate four distinct classes of material deformation: stacking fault only (${\gamma }_d<-1/2$), stacking fault with full slip ($-1/2<{\gamma }_d<0$), full slip with twinning ($0<{\gamma }_d<2$), and full slip only (${\gamma }_d>2$). The predictions on the ratio ${\gamma }_d$ of $\gamma$-TiAl at different temperatures are shown in Figure 5. It can be seen from the figure that the value of ${\gamma }_d$ increases with rising temperature, but it remains within the range of 0 to 2 across temperatures from 0 to 1500 K. This indicates that ordinary dislocation slip and order twinning are both viable deformation modes in $\gamma$-TiAl over the entire temperature range. Based on absolute zero temperature ${\gamma }_{\mathrm{SISF}}$ and ${\gamma }_{\mathrm{USF}}$ shown in Table 1, the ${\gamma }_d$ is calculated as 1.011 [6], 1.343 [7], 1.341 [8], 1.008 [9], 1.279 [10], and 1.151 [16], respectively. Although the present result of 1.547 for the ${\gamma }_d$ is relatively larger than these theoretical values, the ${\gamma }_d$ values from the current and previous calculations are all located between 0 and 2. From the perspective of deformation mode prediction, therefore, our findings are qualitatively consistent with those of previous studies [6,7,8,9,10,16]. Furthermore, the deformation by order twinning and ordinary dislocations can exist in $\gamma$-TiAl-based alloys over a wide range of temperatures [5], which aligns well with our present results.

Figure 5. Temperature dependencies of the ratio (${\gamma }_d$) for the trailing 1/6<11$\overline{2}$] dislocation in $\gamma$-TiAl.

The competition between deformation twinning and dislocation slip in FCC metals can be described by “twinnability”, the ease with which a metal deforms by twinning in competing with dislocation-mediated slip. Three qualitative parameters for predicting twinnability in FCC metals have been developed based on crack tip, grain boundary, and perfect materials without crack tip and grain boundary [37,38,39]. The crack tip twinnability parameter ($T_{\mathrm{B}}$) to quantify the propensity of FCC metals to twin emission as opposed to dislocation emission at a crack tip is defined by Bernstein and Tadmor [37] as

$$T_{\mathrm{B}}=[1.136-0.151{\displaystyle \frac{{\gamma }_{\mathrm{ISF}}}{{\gamma }_{\mathrm{USF}}}}]\sqrt{{\displaystyle \frac{{\gamma }_{\mathrm{USF}}}{{\gamma }_{\mathrm{UTF}}}}}.$$

(4)

Deformation twinning is predicted when $T_{\mathrm{B}}>1$, while dislocation emission is expected when $T_{\mathrm{B}}<1$. The grain boundary twinnability parameter ($T_{\mathrm{A}}$) to compare the propensity of FCC metals to emit either twins or dislocations at grain boundaries was defined by Asao and Suresh [38] as

$$T_{\mathrm{A}}=\sqrt{[1+2(1-{\displaystyle \frac{{\gamma }_{\mathrm{ISF}}}{{\gamma }_{\mathrm{USF}}}})]{\displaystyle \frac{{\gamma }_{\mathrm{USF}}}{{\gamma }_{\mathrm{UTF}}}}}.$$

(5)

A condition $T_{\mathrm{A}}>1$ favors twin emission over the emission of trailing partial dislocation. The parameter ($T_{\mathrm{L}}$) for predicting inherent twinnability in perfect FCC metals is proposed by Li et al. [39], which is expressed as follows:

$$T_{\mathrm{L}}={\displaystyle \frac{6}{\pi }}\arctan [{\displaystyle \frac{2({\gamma }_{\mathrm{USF}}-{\gamma }_{\mathrm{ISF}})}{\sqrt{3}({\gamma }_{\mathrm{UTF}}-{\gamma }_{\mathrm{ISF}})}}-{\displaystyle \frac{1}{\sqrt{3}}}].$$

(6)

Inherent twinning is predicted when $0<T_{\mathrm{L}}<1$. The predictions on the three parameters of $\gamma$-TiAl at different temperatures are shown in Figure 6. It can be seen from the figure that the values of $T_{\mathrm{B}}$,$T_{\mathrm{A}}$, and $T_{\mathrm{L}}$ decrease with rising temperature, indicating the diminishing twinning propensity of $\gamma$-TiAl with temperature rise. Meanwhile, over the temperature range of 0 to 1500 K, both $T_{\mathrm{B}}$ and $T_{\mathrm{A}}$ remain greater than unity, while $T_{\mathrm{L}}$ falls within the range of zero to unity. These suggest that deformation twinning is favored relative to dislocation slip across temperatures of 0 to 1500 K. Temperature dependences of the twinnability parameters for $\gamma$-TiAl are compared with those for FCC Cu and Ni [17], as shown in Figure 7. It can be found from the figure that the change trends in twinnability for $\gamma$-TiAl are same with those for pure Cu and Ni. Meanwhile, at identical temperatures, the TB value for $\gamma$-TiAl is comparable to that of Cu and slightly larger than that of Ni. Its $T_{\mathrm{A}}$ value is relatively smaller than those of Cu and Ni. However, the $T_{\mathrm{L}}$ value for $\gamma$-TiAl is somewhat greater than zero and much less than those of Cu and Ni. As is known, the numbers of twinning systems in $\gamma$-TiAl are only one-third of those in FCC metals owing to its tetragonality. Thus, it is easy to understand that $\gamma$-TiAl exhibits much weaker inherent twinnability than FCC Cu and Ni. These findings suggest that the onset of twinning in $\gamma$-TiAl is more likely to originate from crack tips or grain boundaries. Experimental observations have identified both grain and lamellar boundaries as prominent sources of Shockley partials [8], which is consistent with our results.

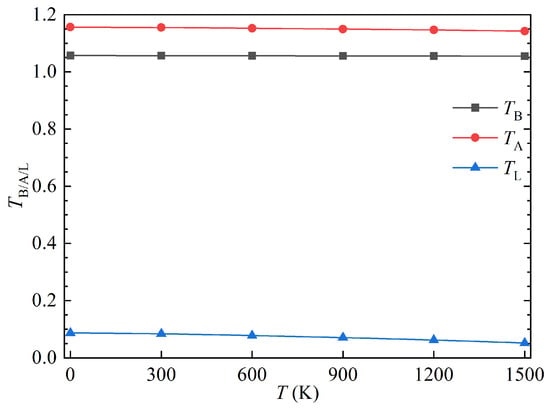
Figure 6. Temperature dependencies of the twinnability parameters ($T_B$, $T_A$ and $T_L$) for $\gamma$-TiAl.

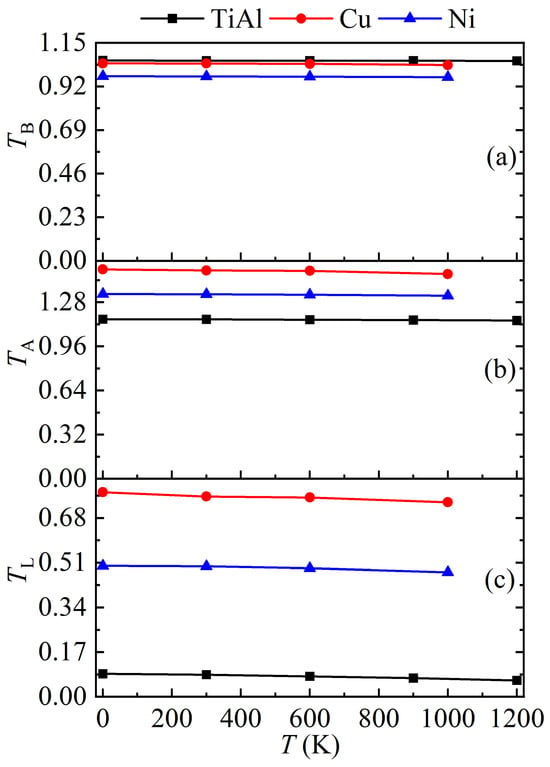
Figure 7. Temperature dependences of the twinnability parameters (a) $T_B$, (b) $T_A$ and (c) $T_L$ for $\gamma$-TiAl and FCC Cu and Ni. Data from [17].

In addition to twinnability, an expression for the critical twinning stress of FCC metals derived from the ${\gamma }_{\mathrm{GPF}}$ has been established by using a dislocation-based twin nucleation model [40]. Assuming a three-layer twin nucleus with a width significantly larger than that of the dislocation core, the critical twinning stress (${\tau }_{\mathrm{crit}}$) is defined as [41,42]

$${\tau }_{\mathrm{crit}}={\displaystyle \frac{5}{18b_{\mathrm{twin}}}}[{\gamma }_{\mathrm{UTF}}+{\displaystyle \frac{({\gamma }_{\mathrm{ESF}}+{\gamma }_{\mathrm{ISF}})}{2}}]-{\displaystyle \frac{2}{9b_{\mathrm{twin}}}}({\gamma }_{\mathrm{USF}}+{\gamma }_{\mathrm{ISF}}).$$

(7)

Here, $b_{\mathrm{twin}}$ represents the Burgers vector associated with the relevant Shockley partial. The predicted values of ${\tau }_{\mathrm{crit}}$ for $\gamma$-TiAl at different temperatures are shown in Figure 8. From the figure, one can find that the ${\tau }_{\mathrm{crit}}$ value for $\gamma$-TiAl decreases from 187.62 to 182.30 MPa with increasing temperature from 0 to 1500 K. This changing trend is also same with those for FCC Cu and Ni [17]. Experimental measurements have shown that the critical resolved shear stress for twinning in Ti₄₄Al₅₆ reduces from 240 to 80 MPa as the temperature rises from 982 to 1350 K [43,44], which qualitatively aligns with our findings. The decrease in critical twinning stress with temperature suggests an increased propensity for twinning in $\gamma$-TiAl at elevated temperatures, which appears to contradict the observations made regarding the twinnability parameters above. This discrepancy may arise from the competitive nature of dislocation-mediated slip and deformation twinning, which is primarily governed by the ratio of twinning to Peierls stresses. It is important to note that both deformation twinning and dislocation slip can be influenced by factors such as composition, strain rate and grain size [44,45]. Because the current twinnability criteria do not fully account for the effects of composition, strain rate, and grain size, the predictions regarding twinnability based on critical twinning stresses can not explain the observed increase in deformation twinning density and the corresponding decrease in dislocation density with rising temperature [44,45].

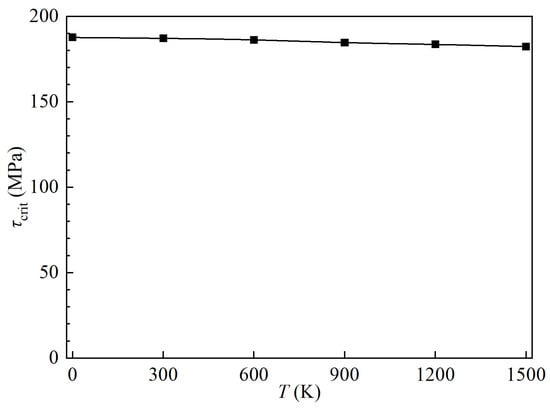
Figure 8. Temperature dependencies of the critical twinning stress for $\gamma$-TiAl.

4. Conclusions

The temperature-dependent generalized planar fault energy curves for the slip systems 1/2<1$\overline{1}$0]{111} and 1/6<11$\overline{2}$]{111} in $\gamma$-TiAl have been determined through a combination of first-principles calculations with the quasi-harmonic approximation. The calculations reveal that, across the temperature range of 0 to 1500 K, the unstable stacking and twinning fault energies and superlattice intrinsic and extrinsic fault energies for both slip systems decrease on the whole with increasing temperature. Further investigations into the effect of temperature on 1/2<1$\overline{1}$0] ordinary and 1/6<11$\overline{2}$] partial dislocation nucleation are conducted based on their temperature-dependent energy barriers. The nucleation of 1/2<1$\overline{1}$0] and 1/6<11$\overline{2}$] leading dislocations is found to be the most favorable within the temperature range of 0 to 1500 K, becoming increasingly easier as the temperature rises. Similarly, the nucleation of 1/6<11$\overline{2}$] trailing and twinning dislocations also shows enhanced feasibility with elevated temperatures. Additionally, we estimate the temperature-dependent twinnability parameters governing the competition between ordinary dislocation slip and order twinning, as well as critical twinning stress, based on the temperature-dependent generalized planar fault energy for the 1/6<11$\overline{2}$] slip direction. The results indicate that the deformation mode in $\gamma$-TiAl consists of ordinary dislocation slip and order twinning throughout the studied temperature range. Furthermore, the onset of order twinning is more likely to occur at crack tips or grain boundaries, with an increasing tendency for twinning as the temperature rises.