Abstract
Lattice materials demonstrate exceptional advantages in lightweight design applications due to their low mass density, high specific strength, and customizable topology. Inspired by the hollow vascular bundle structure of bamboo, this study develops four bio-inspired lattice configurations through two key modifications to conventional body-centered cubic (BCC) structures: Z-axis (loading direction) strut reinforcement and strut hollowing. The specimens were fabricated using AlSi10Mg powder via selective laser melting (SLM) technology, followed by the systematic evaluation of the compressive properties and the energy absorption characteristics. The experimental results reveal that the synergistic combination of Z-strut reinforcement and hollow design significantly enhances both the compressive resistance and the energy absorption capacity. The optimized BCC-5ZH configuration (5 Z-struts with full hollowing) achieves remarkable performance metrics at 0.5 g/cm3 density: yield strength (16.78 MPa), compressive strength (27.91 MPa), and volumetric energy absorption (10.4 MJ/m3). These values represent 236.9%, 283.4%, and 239.3% enhancements, respectively, compared to the reference BCC lattices with an equivalent density. Z-strut integration induces homogeneous stiffness distribution throughout the lattice architecture, while strut hollowing increases the effective moment of inertia. This structural evolution induces a failure mode transition from single shear band deformation to dual X-shaped shear band propagation, resulting in enhanced deformation sequence regulation within the lattice system.
1. Introduction
Lattice structures (or lattice-structured materials) represent a class of porous materials characterized by periodically arranged unit cells. These structures have emerged as promising candidates for impact-resistant applications due to their lightweight nature, high specific strength, and tailorable mechanical properties through controlled relative density and unit cell geometries [1,2,3,4,5,6,7,8]. Advancements in research within this field include refining manufacturing processes, designing hierarchical structures, and integrating multifunctional elements. Bamboo’s natural architecture provides valuable insights for optimizing biomimetic structures. Current investigations into bamboo-inspired lattice structures emphasize a multi-scale optimization framework. Local mechanical properties are modulated at the unit cell scale through parametric biomimetic modelling of individual unit cells, replicating bamboo’s vascular bundle distribution. On the macroscopic scale, hybrid structural configurations are engineered by mimicking bamboo’s load-transfer mechanisms, exemplified by lattice–shell hybrid configurations [9] and functionally graded density distributions [10]. These bio-architected designs exhibit superior energy dissipation efficiency and fracture resistance compared to conventional lattices, providing novel design concepts for protective engineering and energy-absorbing systems [11,12,13,14,15,16,17,18,19,20].
Bamboo, a quintessential natural bio-composite, exhibits exceptional mechanical performance attributed to its unique structural hierarchy. This hierarchical architecture comprises three key features: (1) a central lumen for nutrient transport, (2) a gradient-distributed vascular bundle system along the radial direction, and (3) periodically arranged transverse diaphragms within internodes. Such multi-scale organization endows bamboo with a flexural stiffness 1.3 times greater than steel of equivalent density, significantly outperforming other plant-based structural materials like corn stalks and cork (Figure 1a) [12,21,22,23]. Owing to its lightweight yet high-strength characteristics, bamboo demonstrates remarkable potential in civil engineering applications. Bamboo-inspired structural designs (Figure 1b,c) have enabled the construction of buildings and bridges to achieve surface densities as low as 15–20 kg/m2 while sustaining axial compressive stresses of 10–15 MPa. Notably, these bio-inspired systems exhibit a specific strength exceeding three times that of conventional concrete structures [24]. Bio-architectural ingenuity provides critical guidance for developing lightweight engineering systems through biomimetic design principles.
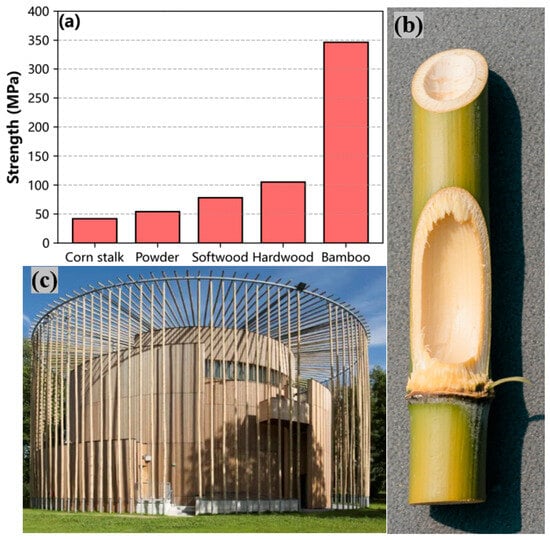
Figure 1.
(a) Comparative strength analysis of natural plant stems; (b) overall and internal structure of bamboo; (c) Hardelot Theatre.
Recent studies demonstrate that unit cell-scale reinforcement strategies significantly enhance compressive and impact-resistant properties. Rehme et al. [25] systematically compared strut-reinforced configurations, revealing that Z-axis reinforcement rods in FCCZ (face-centered cubic with Z-struts) and BCCZ (body-centred cubic with Z-struts) lattices generated 23–41% strength enhancement over conventional BCC (body-centred cubic) topologies. Deng’s team [26] further developed a BCC-4IZ configuration with quadruple Z-strut reinforcement, achieving a 34% improvement in dynamic energy absorption efficiency compared to baseline BCC structures under high-velocity impact loading.
Bamboo-inspired hollow architecture provides innovative solutions to transcend the energy absorption limitations of solid-strut counterparts. Qian Ma’s team [27,28,29] proposed an innovative hybrid-strut strategy combining solid and hollow members in BCC-based lattices, exemplified by their HC_SB (hollow-core/solid-beam) and SC_HB (solid-core/hollow-beam) configurations. Through systematic modulation of vertical struts and horizontal beams, this approach enables controllable deformation mode transition from bending-dominated to stretching-dominated mechanisms. Experimental characterization revealed 32% and 65% simultaneous improvements in tensile strength and toughness. Their work offers pioneering insights for hollow lattice research. Guo et al. [30] engineered a breakthrough partially hollowed BCC (PHBCC) architecture featuring capsule-shaped cavities in strut mid-sections while maintaining solid nodes. This design enhances specific stiffness by 92%, specific strength by 51.9%, and specific energy absorption by 22.8%, addressing the critical issue of node failure in traditional hollow lattices. Zhou et al. [31] engineered a honeycomb-like bamboo-inspired lattice exhibiting 58% and 112% increases in compressive strength and specific energy absorption relative to simple cubic lattices. Zhang’s group [32] pioneered a hollow octet-truss configuration through a face-centred cubic-octahedral (FCC-Oct) hybrid topology, achieving 52% comprehensive performance enhancement over monolithic lattice structures.
This study builds on previous research regarding bamboo-inspired optimization and introduces a coupled design strategy that integrates Z-axis strut reinforcement with strut hollowing. Through parametric configuration innovations, four novel bamboo-inspired lattice structure variants were developed. The work systematically investigates the influence mechanisms of these bio-inspired configurations on the quasi-static compressive properties and energy absorption characteristics of lattice materials. These findings establish a methodological framework for engineering applications in aerospace impact-resistant structures and automotive energy-absorbing devices.
2. Materials and Methods
2.1. Structural Design
This study developed four hollow bamboo-inspired lattice variants based on a body-centred cubic (BCC) parent structure, designated as BCC-4ZPH, BCC-4ZH, BCC-5ZPH, and BCC-5ZH. The three-dimensional unit cell models are illustrated in Figure 2: cross-sectional hollow ratios are precisely controlled through parametric modelling, with Z-strut diameters optimized to maintain equivalent relative density (±3%) compared to baseline BCC lattices. The nomenclature is defined as follows:
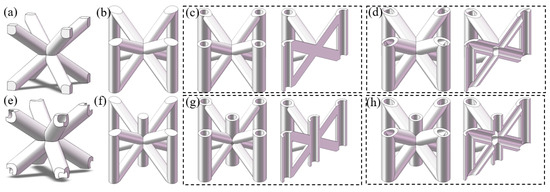
Figure 2.
Three-dimensional models of tested lattice structures: (a) BCC; (b) BCC-4Zl; (c) BCC-4ZPH; (d) BCC-4ZH; (e) BCCH; (f) BCC-5Z; (g) BCC-5ZPH; (h) BCC-5ZH. (The two views within the dashed box belong to the same model.)
- Z: Incorporates vertical (Z-axis) struts into the parent BCC architecture; the numeral preceding “Z” denotes the quantity of added vertical struts (4 or 5);
- H (Hollow): All struts (including original BCC members and Z-struts) exhibit hollow cross-sections;
- PH (Partially Hollow): Only the Z-struts feature hollow morphology, while the original BCC struts remain solid.
The lattice structures were fabricated with a unit cell edge length of 10 mm. Each specimen contained 5 × 5 × 5 periodically arranged unit cells, forming cubic specimens measuring 50 mm × 50 mm × 50 mm. With a constant hollow wall thickness of 0.45 mm, struts’ outer/inner diameters were systematically adjusted within the range of 1.6–2.5 mm, and all configurations maintained identical relative densities (=0.18). Mechanical performance was evaluated by comparative analysis of three key indicators: (1). Yield strength (); (2). Compressive strength (); (3). Specific energy absorption (). The dimensional design parameters of all investigated lattice structures are provided in Table 1.

Table 1.
Lattice structure design parameters.
2.2. Fabrication Methodology
All lattice structures were fabricated via selective laser melting (SLM) technology. The feedstock material was gas-atomized AlSi10Mg powder (particle size: 15–53 μm) supplied by AVIC Maite Additive Technology (Beijing, China) Co., Ltd., and the equipment is manufactured in China. The powder’s chemical composition (Table 2) meets ASTM standards, with a theoretical density of 2.68 g/cm3 for the AlSi10Mg alloy. SLM processing was conducted using an FS271M system (Figure 3a). The equipment comes from Farsoon Technologies Co., Ltd. (Changsha, China), and the equipment is independently developed by the company) with the following parameters: Laser scanning speed: 800 mm/s, Power: 300 W, Hatch spacing: 0.12 mm, Layer thickness: 0.03 mm. The fabrication workflow comprised three stages: (1) CAD modelling of lattice structures using SolidWorks 2022 SP0, (2) STL file conversion and machine parameter optimization, (3) SLM building.

Table 2.
Chemical composition of AlSi10Mg powder (wt.%).

Figure 3.
(a) SLM equipment setup; (b) as-fabricated specimens.
The minimum wall thickness for hollow struts was constrained to 0.45 mm based on equipment specifications to mitigate strut fracture defects during manufacturing. This requirement resulted in standardized hollow strut dimensions with an inner diameter of 1.6 mm, outer diameter of 2.5 mm, and constant wall thickness of 0.45 mm. These geometric parameters ensured equivalent relative density between hollow-strut lattices and their solid-strut counterparts (diameter 2 mm). Representative as-fabricated specimens are shown in Figure 3b. Post-processing involved stress-relief annealing at 275 °C with a controlled heating rate (5 °C/min), followed by 2 h isothermal holding and furnace cooling to room temperature prior to wire EDM cutting for substrate separation.
2.3. Quasi-Static Compression Testing Configuration
Quasi-static compression tests were conducted on an Instron 5985 universal testing machine with a controlled strain rate of 1 × 10⁻3 s⁻¹. The deformation process was monitored using a synchronized digital camera. The upper platen compressed the specimen during loading, while the lower platen remained stationary. All specimens were compressed until full densification, with displacement and load data acquired through the integrated displacement transducer and load cell. Three replicate specimens were prepared per configuration where statistical dispersion analysis was performed on experimental datasets.
The engineering stress () and engineering strain () were calculated using Equation (1):
where:
- F = Applied load (N);
- A0 = Initial cross-sectional area (mm2);
- L1 = Post-test specimen height (mm);
- L0 = Initial specimen height (mm);
- ΔL = Displacement variation (mm).
3. Results and Discussion
3.1. Macroscopic Morphology of Lattice Structures
Figure 4 systematically presents top and front views of six bamboo-inspired lattice specimens (50 mm × 50 mm × 50 mm) fabricated by SLM, with representative configurations shown for BCC-4Z: Figure 4a is top view and Figure 4b is front view. All the as-built structures exhibited no macroscopic defects such as fractures or delamination. The inherent staircase effect in additive manufacturing caused systematic dimensional deviations, resulting in as-built strut diameters exceeding design specifications. Metrological analysis revealed solid strut diameters ranging from 2.0 to 2.2 mm, while hollow struts showed outer diameters of 2.5 to 2.7 mm and inner diameters of 1.6 to 1.8 mm. Measured wall thickness consistently exceeded the 0.45 mm manufacturing threshold. Crucially, all hollow channels remained free from powder adhesion or blockage.

Figure 4.
Top and front views of representative lattice specimens: (a,b) BCC-4Z; (c,d) BCC-4ZH; (e,f) BCC-4ZPH; (g,h) BCC-5Z; (i,j) BCC-5ZH; (k,l) BCC-5ZPH. (The two views within the dashed box belong to the same specimen.).
The apparent density is defined as the ratio of structural mass to total volume. The relative density ρ is calculated by normalizing concerning the base material density ( = 2.68 g/cm3) (Equation (2)):
Table 3 summarizes the measured apparent density () and derived relative density (), showing less than a 5% deviation from design relative density ρ.

Table 3.
Density characteristics of fabricated lattice structures.
3.2. Effects of Bamboo-Inspired Design on Compressive Behavior
The stress–strain curves in this study were obtained through quasi-static compression tests along the [0, 0, 1] direction (Z-axis) of lattice specimens. Mechanical parameters were extracted as defined in Figure 5: the yield strength () was determined via the 0.2% plastic strain offset method, where a line parallel to the elastic modulus was offset by 0.2% strain with the corresponding intersection stress identified as ; the compressive strength () was defined as the first peak stress prior to structural collapse; and the specific energy absorption () was calculated by integrating the area under the stress–strain curve from initial loading to a unified densification strain threshold ( = 0.6) as per Equation (3), ensuring cross-configuration comparability. The strength and energy data presented in the stress–strain curves were calculated based on as-measured specimen dimensions.
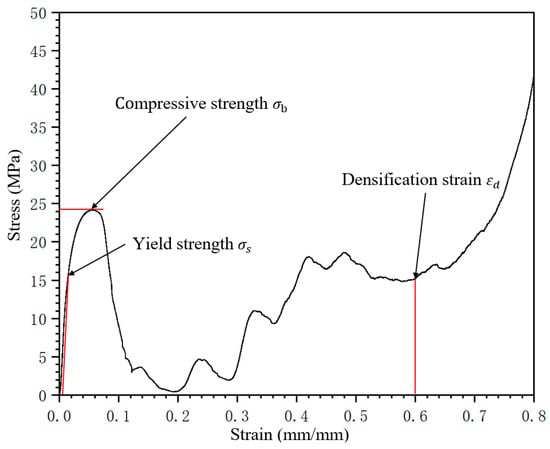
Figure 5.
Schematic illustration of mechanical parameter extraction from stress–strain curves of lattice structures.
All lattice architectures experimentally measured mechanical properties are quantitatively summarized in Table 4, with , , and values reflecting distinct deformation mechanisms governed by biomimetic design features.

Table 4.
Quasi-static mechanical properties of lattice structures.
Figure 6a presents the bar chart comparison of compressive strengths across all lattice configurations, while Figure 6b–d display representative stress–strain curves for three bamboo-inspired design groups. The compressive strength hierarchy derived from Figure 6a reveals the following descending performance ranking: BCC-5ZH > BCC-5ZPH > BCC-5Z > BCC-4ZH > BCC-4ZPH > BCC-4Z > BCCH > BCC.
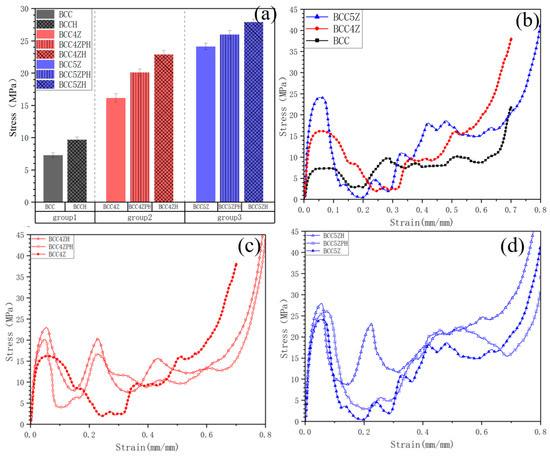
Figure 6.
(a) Bar chart of yield strength comparison for lattice structures; (b) stress–strain curves of BCC-Z series; (c) stress–strain curves of BCC-4Z series; (d) stress–strain curves of BCC-5ZH series.
As evidenced in Figure 6b, Z-strut reinforcement substantially strengthens BCC lattices. The BCC-4Z and BCC-5Z configurations exhibited relative density increases of merely 5.1% and 3.5% compared to the baseline BCC yet demonstrated disproportionate compressive strength () enhancements of 121.8% and 231.5%. Furthermore, the BCC-5Z configuration achieved 49.4% higher than BCC-4Z, indicating that the addition of a Z-direction connection rod has a more significant effect on improving compressive strength in the BCC-5Z configuration.
As shown in Figure 6c,d, strut hollowing demonstrates measurable strengthening effects in BCC-derived lattices. For the BCC, BCC-4Z, and BCC-5Z configurations, transitioning from fully solid to fully hollow struts (corresponding BCCH, BCC-4ZH, and BCC-5ZH) resulted in improvements of 32.8%, 41.7%, and 15.7%, respectively. While the enhancement magnitudes varied, strut hollowing consistently improved compressive performance. To further examine the isolated effect of Z-strut hollowing, we compared partially hollowed Z-struts (BCC-4ZPH) to their fully solid counterparts (BCC-4Z), which showed a 24.4% increase in . In contrast, when applying the same modification in BCC-5ZPH, the improvement was only 7.6% over BCC-5Z. This difference likely arises from the diminishing marginal effects of buckling resistance enhancement. The BCC-5Z configuration features high nodal connectivity and a dense arrangement of Z-struts, which already provide elevated intrinsic buckling resistance. Although Z-strut hollowing increases the sectional moment of inertia I, the additional contribution to critical buckling load increments and strength gains becomes less significant under these pre-existing geometric constraints.
Finally, the synergistic strengthening effects of coupling Z-strut addition and strut hollowing in BCC lattices were investigated. The BCC-5ZH configuration exhibited a 283.4% improvement in over the baseline BCC structure, surpassing the arithmetic sum of individual enhancements from Z-strut reinforcement (BCC-5Z: 231.5%) and full hollowing (BCCH: 32.8%), which totals 264.3%. This nonlinear superposition yielded an additional 19.1% strength gain. Similarly, the combined effect observed in BCC-4ZH, which showed a 214.6% enhancement, surpassed the linear sum of BCC-4Z (121.8%) and BCCH (32.8%) by 60 percentage points (154.6% vs. 214.6%).
This result clearly demonstrates synergistic coupling. The Z-strut reinforcement primarily increases the axial load-bearing capacity through stress redistribution, while strut hollowing enhances buckling resistance by increasing the sectional moment of inertia. This interaction between the two components triggers changes in deformation modes, resulting in mechanical performance enhancements that exceed simple additive predictions.
3.3. Effects of Bamboo-Inspired Design on Energy Absorption
Figure 7a illustrates the relationship between specific energy absorption (SEA) and strain for various lattice configurations. The comparative analysis shows that within specific material series (such as BCC-5Z and BCC-5ZH), the SEA values exhibited significant divergence during the initial stages of plastic deformation (approximately at 0.15). This divergence continued to increase nonlinearly until ε = 0.6, where notable performance differences emerged, such as a 6.5 MJ/m3 enhancement in SEA for BCC-5ZH compared to BCC-5Z. This pattern of divergence is observed despite minimal differences in strength parameters (less than 10% variation in elastic modulus and yield strength). This indicates that the differentiation in energy absorption primarily results from changes in deformation characteristics induced by the topological modifications.
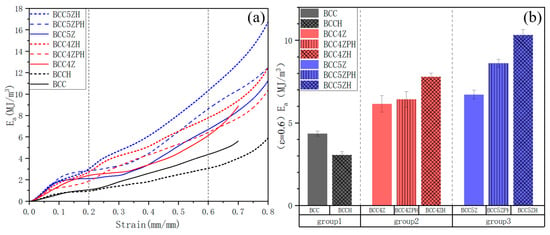
Figure 7.
(a) Energy–strain curves of lattice materials; (b) energy absorption (ε = 0.6).
Analysis of the stress–strain curves in Figure 6b–d confirms that all lattice configurations entered the densification phase at ε = 0.6. Consequently, the column chart ordinate (E0.6) in Figure 7b effectively represents the maximum specific energy absorption (SEA). The SEA hierarchy (descending order: BCC-5ZH > BCC-5ZPH > BCC-4ZH > BCC-5Z > BCC-4ZPH > BCC-4Z > BCC > BCCH) exhibits a strong correlation with compressive strength. The Z-strut reinforced BCC-5Z configuration achieved SEA = 6.7 MJ/m3, representing a 55.8% improvement over the baseline BCC (4.3 MJ/m3), highlighting the efficacy of topological optimization in energy dissipation. Remarkably, the synergistic BCC-5ZH configuration (Z-strut + hollowing) attained SEA = 10.4 MJ/m3—a 141.9% enhancement over BCC—exceeding the arithmetic sum of individual Z-strut (55.8%) and hollowing contributions. This over-linear enhancement quantitatively verifies the nonlinear coupling effects between load-path reinforcement and buckling-resistance optimization.
Notably, Group 1 in Figure 7b reveals an anomalous 12.5% reduction in specific energy absorption (SEA) for the BCCH configuration (2.8 MJ/m3) compared to baseline BCC (3.2 MJ/m3). This counterintuitive phenomenon stems from bending-dominated deformation characteristics inherent to BCC lattices. Hollowing reduces local strut stiffness, lowering plateau stress during intermediate strain regimes ( 0.2–0.6) while simultaneously prolonging the densification regime (BCCH: 0.8 vs. BCC: 0.7). The dual mechanisms synergistically reduce energy absorption in hollow structures relative to solid counterparts within the strain regime of 0.2–0.6. However, complete densification analysis shows BCCH achieves higher cumulative energy absorption (E0.8 = 5.8 MJ/m3) than BCC (E0.7 = 5.6 MJ/m3). These findings collectively demonstrate that the enhancement patterns of Z-strut reinforcement and strut hollowing on energy absorption capacity exhibit congruent optimization trajectories with corresponding strength improvements.
3.4. Effects of Bamboo-Inspired Design on Deformation Characteristics
Figure 8 systematically documents the deformation characteristics of lattice materials during initial compression (ε = 0.1). The comparative panels (a) BCC (b) BCC-4Z and (c) BCC-5Z reveal distinct deformation patterns under identical loading conditions. Red dashed boxes highlight 45° shear bands common to all configurations, while yellow dashed boxes indicate Z-strut axial deformation zones exclusive to reinforced lattices. Metallographic observations demonstrate that BCC-4Z and BCC-5Z configurations exhibit enhanced nodal integrity through Z-strut reinforcement, evidenced by (1) 110% higher compressive stress than baseline BCC (Figure 6 correlation) and (2) homogeneous damage distribution in BCC-5Z versus localized failure in BCC. These visualizations confirm that full nodal reinforcement in BCC-5Z optimizes load transfer efficiency.

Figure 8.
Deformation characteristics of lattice materials under initial compression (ε = 0.1): (a) BCC; (b) BCC-4Z; (c) BCC-5Z.
The viewing angle in Figure 10 and the subsequent deformation processes are designated as View 2 in Figure 9 to facilitate the simultaneous observation of failure characteristics across multiple surfaces. This perspective captures the observations and recordings from the side edge of the specimen.
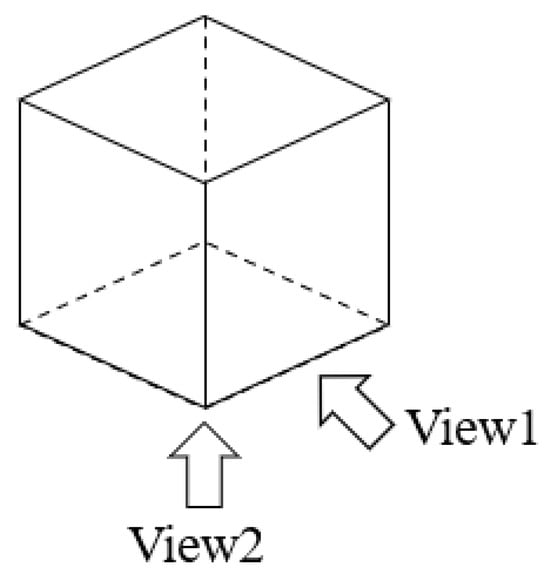
Figure 9.
Two-directional observation of lattice specimen. View1: Positive direction. View2: side edge direction.
Figure 10 and Figure 11 illustrate the evolution of deformation and the failure characteristics of bamboo-inspired BCC-5Z and BCC-4Z lattice structures during quasi-static compression testing. Markers highlight corresponding characteristic points on the stress–strain profiles. Comparative analysis of deformation processes and stress–strain curves in BCC-5Z series and BCC configurations revealed that the divergence in energy absorption and failure characteristics between BCC-5ZH and other configurations predominantly occurred at strain levels of ε = 0.2–0.4. At ε = 0.2, the transition from the yield plateau to the densification regime was accompanied by a secondary peak in BCC-5ZH (① in Figure 10a), contrasting with the descending profiles observed in other configurations (③,⑤,⑦ in Figure 10a). This inflexion point initiated discernible disparities in energy absorption efficiency across configurations. During lateral deformation, BCC-5ZH exhibited dual X-shaped 45° shear bands within individual planes (①), whereas other configurations (③,⑤,⑦) manifested singular 45° shear bands per plane. Notably, intersecting 45° shear bands from distinct planes converged at vertex regions in the BCC lattice (⑦). This phenomenon, consistent with previous findings [16], likely stems from stress concentration intensification caused by geometric imperfections and asymmetric stress distribution, ultimately compromising compressive strength. At ε = 0.4, all configurations exhibited ascending tendencies in stress–strain profiles with intersection points ②, ④, ⑥, coinciding with maximum divergence in specific energy absorption values across configurations. During this deformation phase, progressive shear band propagation and varying failure phenomena (the blue arrow indicates layer-by-layer failure characteristics, while the area within the blue box denotes the characteristic region of shear bands) were observed across configurations. The ε = 0.4–0.6 interval corresponded to stable failure progression, during which stress–strain and energy–strain curves maintained minimal fluctuation. Beyond ε = 0.6, all configurations entered the densification regime with abrupt compressive strength escalation.
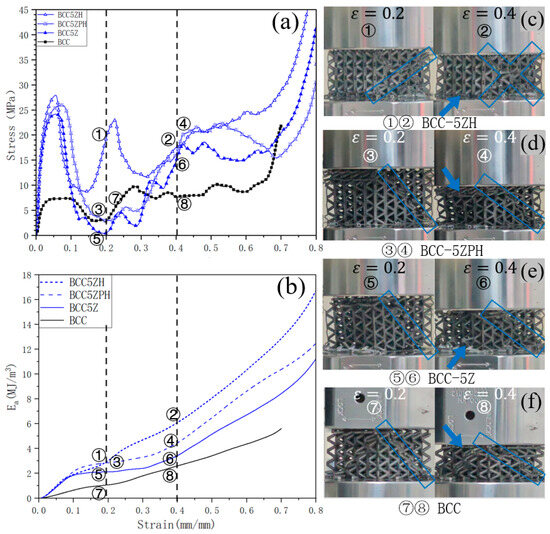
Figure 10.
(a) Stress–strain curves of BCC-5Z series; (b) energy–strain curves of BCC-5Z series; (c–f) the deformation processes of different specimens. (The blue arrow indicates layer-by-layer failure characteristics, while the area within the blue box denotes the characteristic region of shear bands.)
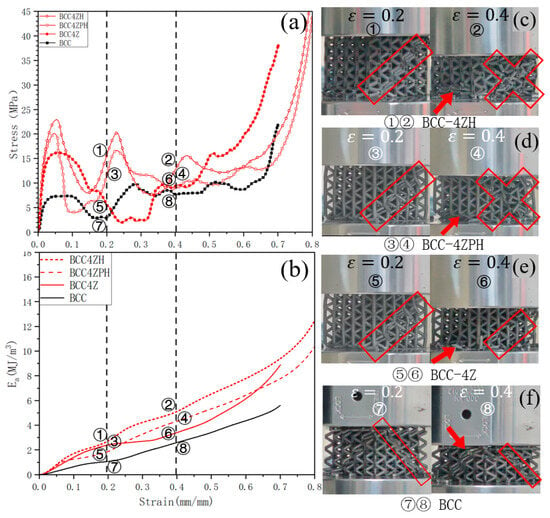
Figure 11.
(a) Stress–strain curves of BCC-4Z series; (b) energy–strain curves of BCC-4Z series; (c–f) the deformation processes of different specimens. (The red arrow indicates layer-by-layer failure characteristics, while the area within the red box denotes the characteristic region of shear bands.)
A comparative analysis of Figure 11 indicates that BCC-4Z series lattice structures exhibited analogous deformation characteristics to those of the BCC-5Z series, with failure zones denoted by red frames and arrows. The critical distinction emerged in the BCC-4ZPH configuration, whose stress–strain curve manifested a secondary peak at ε = 0.2 (③ in Figure 11a), contrasting with the single-peak profile observed in BCC-5ZPH configuration (③ in Figure 10a).
The secondary peak in stress–strain curves signifies that the remaining substructure reassumes load-bearing dominance following localized failure. The emergence of secondary peaks depends on two prerequisites: (1) containment of failure propagation post-localized damage and (2) preserved load-bearing capacity in residual structural components.
Comparative analysis of deformation patterns in Figure 12 reveals that both BCC-4ZH (Figure 12a–d) and BCC-5ZH (Figure 12e–h) configurations exhibit dual-peak characteristics. This mechanical behavior originates from their hollow-strut topology which enables uniform stiffness distribution, enhanced buckling resistance and sufficient structural integrity to sustain secondary load-bearing phases. The failure progression follows three distinct stages: initial localized buckling failure → sequential damage propagation evidenced by shear band bifurcation (transition from single to dual X-shaped shear bands as shown in Figure 12b,c,f,g → cooperative load redistribution through surviving hollow struts, culminating in stress resurgence that generates the secondary peak.


Figure 12.
Deformation evolution of four lattice structures at characteristic strains (ε = 0.1, 0.2, 0.4, 0.6). (a–d) BCC-4ZH; (e–h) BCC-5ZH; (i–l) BCC-4ZPH; (m–p) BCC-5ZPH. (The area within the red dashed line represents the failure characteristics of the specimen.)
The BCC-4ZPH and BCC-5ZPH configurations exhibited stiffness disparity due to exclusive hollow design in Z-oriented struts, predisposing them to accelerated failure propagation. In BCC-4ZPH (Figure 12i–l), partial buckling of Z-struts initiated premature failure, yet preserved nodal spacing maintained structural integrity in residual regions for sustained load-bearing capability. The failure sequence comprised three phases: premature localized buckling → staged propagation (Figure 12j,k) → cooperative load-sharing by residual solid struts → subsequent stress recovery forming secondary peaks. In BCC-5ZPH (Figure 12m–p), Z-struts concentrated at nodal junctions exhibited axial buckling under compression, whereas destruction at nodal junctions induced catastrophic failure propagation. Residual solid struts demonstrated insufficient load redistribution capacity, resulting in progressive stress deterioration, which manifested through three distinct deformation phases: localized buckling onset → rapid failure propagation (Figure 12n,o) → load-bearing incapacity of residual struts → progressive collapse with stress attenuation. The failure characteristics of all four configurations are systematically compared in Table 5.

Table 5.
Comparative analysis of deformation characteristics in bamboo-inspired lattice structures.
In engineering mechanics, hollow cylinders demonstrate superior buckling resistance to solid cylinders at equivalent apparent volumes. Buckling resistance is quantified by the critical buckling load (Pcr), which is defined as the maximum axial load before structural instability. The governing equation derived from Euler’s formula is
where E is Young’s modulus, I is the moment of inertia, L is the original length, and K is the effective length factor (K = 0.5 for fixed-end constraints). Equation (4) reveals a direct proportionality between Pcr and I. The moment of inertia I quantifies the cross-sectional resistance to bending and torsional deformation. Higher I values indicate more excellent deformation resistance. For solid cylinders:
For hollow cylinders:
where D and d denote outer and inner diameters, respectively. At constant volume, hollow configurations generally achieve higher I value. Enhanced buckling resistance strategies include:
- Increasing I;
- Reducing effective length;
- Selecting high-modulus materials;
- Strengthening constraints.
Thus, hollow structures synergistically combine buckling resistance and lightweight advantages. Coupled with Z-strut reinforcement, this generates synergistic performance enhancements in lattice structures.
4. Conclusions
Based on bamboo’s hollow cross-sectional characteristics, this study developed four bamboo-inspired lattice structures (BCC-4ZPH, BCC-4ZH, BCC-5ZPH, and BCC-5ZH). Fabricated via selective laser melting (SLM), their mechanical properties and energy absorption mechanisms were systematically investigated through quasi-static compression tests. The key findings are summarized as follows:
- Z-strut reinforcement significantly enhances yield and compressive strengths: BCC-5Z exhibits a yield strength of 14.38 MPa (188.7% increase over baseline BCCs 4.98 MPa) and 221.5% higher compressive strength.
- The hollow strut design demonstrates dual buckling resistance enhancement and energy absorption improvement mechanisms. This geometry increases the critical buckling load (Pcr) through an enhanced sectional moment of inertia I, significantly improving buckling resistance. Furthermore, hollow structures delay the densification of onset strain and extend the densification duration, ultimately enhancing lattice structures’ specific energy absorption (SEA).
- Synergistic interaction between Z-strut addition and hollow design modifies failure mechanisms: transitioning from single 45° shear bands in solid structures to dual X-shaped 45° shear bands per plane. This topological evolution manifests dual-peak characteristics in stress–strain curves, elevating plateau stress levels and enhancing compressive resistance and energy absorption efficiency. The observed interaction effects require further mechanistic validation through FEA-based modeling in future studies.
Author Contributions
Conceptualization, W.M. and Y.W.; methodology, W.M.; software, W.M. and B.J.; validation, W.M., Q.L. and B.J.; formal analysis, W.M.; investigation, W.M.; resources, Y.W. and Q.L.; data curation, W.M.; writing—original draft preparation, W.M.; writing—review and editing, W.M., Y.W., Q.L. and J.Z.; visualization, W.M.; supervision, Y.W. and J.Z.; project administration, J.Z.; funding acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research is financially supported by the Guangdong Basic and Applied Basic Research Foundation (grant number: 2019A1515110776).
Data Availability Statement
All experimental datasets in this study were generated at the National Key Laboratory of Science and Technology on Materials under Shock and Impact. In compliance with institutional intellectual property protection policies (Article 3.2 of NKLSMSI Data Governance Protocol), interested researchers may submit formal data requests to the corresponding author via their institutional email, along with detailed research objectives and ethical approval documents. Restricted data will be made available within 30 working days upon completion of confidentiality review procedures.
Acknowledgments
During the preparation of this manuscript, the author used Deep Seek-V3 software for formatting and spell-checking purposes. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
Author Qingtang Li was employed by the company Beijing Xinfeng Aerospace Equipment Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SLM | Selective Laser Melting |
| SEA | Specific Energy Absorption |
| EDM | Electrical Discharge Machining |
| BCC | Body-Centered Cubic |
| BCCH | Hollow Body-Centered Cubic |
| BCC-4Z | Body-Centered Cubic with four Z-struts |
| BCC-5Z | Body-Centered Cubic with five Z-struts |
| BCC-4ZH | Hollow Body-Centered Cubic with four Z-struts |
| BCC-5ZH | Hollow Body-Centered Cubic with five Z-struts |
| BCC-4ZPH | Partially Hollow Body-Centered Cubic with four Z-struts |
| BCC-5ZPH | Partially Hollow Body-Centered Cubic with five Z-struts |
References
- Zargarian, A.; Esfahanian, M.; Kadkhodapour, J.; Ziaei-Rad, S.; Zamani, D. On the fatigue behavior of additive manufactured lattice structures. Theor. Appl. Fract. Mech. 2019, 100, 225–232. [Google Scholar] [CrossRef]
- Yu, Z.; Xin, R.; Xu, Z.; Sha, L.; Chen, L.; Zhu, Y.; Liang, P.; Zhang, Z.; Liu, Z.; Cao, Q. Shock-Resistant and Energy-Absorbing Properties of Bionic NiTi Lattice Structure Manufactured by SLM. J. Bionic Eng. 2022, 19, 1684–1698. [Google Scholar] [CrossRef]
- Bai, Y.C.; Gao, J.Y.; Hou, C.X. Topology optimized design and validation of sandwich structures with pure-lattice/solid-lattice infill by additive manufacturing. Compos. Struct. 2023, 319, 117152. [Google Scholar] [CrossRef]
- Maconachie, T.; Leary, M.; Lozanovski, B.; Zhang, X.; Qian, M.; Faruque, O.; Brandt, M. SLM lattice structures: Properties, performance, applications and challenges. Mater. Des. 2019, 183, 108137. [Google Scholar] [CrossRef]
- Jin, N.; Wang, F.; Wang, Y.; Zhang, B.; Cheng, H.; Zhang, H. Effect of structural parameters on mechanical properties of pyramidal Kagome lattice material under impact loading. Int. J. Impact Eng. 2019, 132, 103313. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, J.; Zhang, W.; Gu, X.; Zhou, H. Design and applications of morphing aircraft and their structures. Front. Mech. Eng. 2023, 18, 750–756. [Google Scholar] [CrossRef]
- Wei, Y.L.; Yang, Q.S.; Liu, X.; Tao, R. Multi-bionic mechanical metamaterials: A composite of FCC lattice and bone structures. Int. J. Mech. Sci. 2022, 213, 106857. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.O.; Tuck, C.J.; Ashcroft, I.A.; Wildman, R.D.; Hague, R.J. A mechanical property evaluation of graded density Al-Si10-Mg lattice structures manufactured by selective laser melting. Mater. Sci. Eng. A 2016, 670, 264–274. [Google Scholar] [CrossRef]
- Xiang, J.W.; Du, J.X. Energy absorption characteristics of bio-inspired honeycomb structure under axial impact loading. Mater. Sci. Eng. A 2017, 696, 283–289. [Google Scholar] [CrossRef]
- Liu, S.; Tong, Z.; Tang, Z.; Liu, Y.; Zhang, Z. Bionic design modification of non-convex multi-corner thin-walled columns for improving energy absorption through adding bulkheads. Thin-Walled Struct. 2015, 88, 70–81. [Google Scholar] [CrossRef]
- Mishra, A.K.; Chavan, H.; Kumar, A. Effect of cell size and wall thickness on the compression performance of triply periodic minimal surface based AlSi10Mg lattice structures. Thin-Walled Struct. 2023, 193, 111214. [Google Scholar] [CrossRef]
- Xu, S.; Shen, J.; Zhou, S.; Huang, X.; Xie, Y.M. Design of lattice structures with controlled anisotropy. Mater. Des. 2016, 93, 443–447. [Google Scholar] [CrossRef]
- Wang, C.; Li, Y.; Zhao, W.; Zou, S.; Zhou, G.; Wang, Y. Structure design and multi-objective optimization of a novel crash box based on biomimetic structure. Int. J. Mech. Sci. 2018, 138, 489–501. [Google Scholar] [CrossRef]
- Ma, J.F.; Chen, W.Y.; Zhao, L.; Zhao, D.H. Elastic buckling of bionic cylindrical shells based on bamboo. J. Bionic Eng. 2008, 5, 231–238. [Google Scholar] [CrossRef]
- Zou, M.; Xu, S.; Wei, C.; Wang, H.; Liu, Z. A bionic method for the crashworthiness design of thin-walled structures inspired by bamboo. Thin-Walled Struct. 2016, 101, 222–230. [Google Scholar] [CrossRef]
- Qi, D.; Yu, H.; Liu, M.; Huang, H.; Xu, S.; Xia, Y.; Qian, G.; Wu, W. Mechanical behaviors of SLM additive manufactured octet-truss and truncated-octahedron lattice structures with uniform and taper beams. Int. J. Mech. Sci. 2019, 163, 105091. [Google Scholar] [CrossRef]
- Liu, L.; Kamm, P.; García-Moreno, F.; Banhart, J.; Pasini, D. Elastic and failure response of imperfect three-dimensional metallic lattices: The role of geometric defects induced by selective laser melting. J. Mech. Phys. Solids 2017, 109, 27–41. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rowshan, R.; Abu Al-Rub, R.K. Topology-mechanical property relationship of 3D printed strut, skeletal, and sheet based periodic metallic cellular materials. Addit. Manuf. 2018, 19, 167–183. [Google Scholar] [CrossRef]
- Xiao, L.J.; Li, S.; Feng, G.Z.; Shi, G.Q.; Song, W.D. Research progress on mechanical properties characterization and mesoscopic optimization design of additive manufacturing three-dimensional micro-lattice materials. Chin. J. Solid Mech. 2023, 44, 718–754. [Google Scholar]
- Wu, Y.L. Study on Mechanical Properties of Titanium Alloy 3D Lattice Structures Fabricated by SLM. Master’s Thesis, Chongqing University, Chongqing, China, 2016. [Google Scholar]
- Ling, C.; Cernicchi, A.; Gilchrist, M.D.; Cardiff, P. Mechanical behaviour of additively-manufactured polymeric octet-truss lattice structures under quasi-static and dynamic compressive loading. Mater. Des. 2019, 162, 106–118. [Google Scholar] [CrossRef]
- Zheng, X.; Lee, H.; Weisgraber, T.H.; Shusteff, M.; DeOtte, J.; Duoss, E.B.; Kuntz, J.D.; Biener, M.M.; Ge, Q.; Jackson, J.A.; et al. Ultralight, ultrastiff mechanical metamaterials. Science 2014, 344, 1373–1377. [Google Scholar] [CrossRef]
- Tan, X.P.; Tan, Y.J.; Chow, C.S.; Tor, S.B.; Yeong, W.Y. Metallic powder-bed based 3D printing of cellular scaffolds for orthopaedic implants: A state-of-the-art review on manufacturing, topological design, mechanical properties and biocompatibility. Mater. Sci. Eng. C 2017, 76, 1328–1343. [Google Scholar] [CrossRef] [PubMed]
- Mechtcherine, V.; Bos, F.P.; Perrot, A.; Leal da Silva, W.R.; Nerella, V.N.; Fataei, S.; Wolfs, R.J.M.; Sonebi, M.; Roussel, N. Extrusion-based additive manufacturing with cement-based materials—Production steps, processes, and their underlying physics: A review. Cem. Concr. Res. 2020, 132, 106037. [Google Scholar]
- Rehme, O.; Emmelmann, C. Rapid manufacturing of lattice structures with selective laser melting. In Laser-Based Micropackaging; SPIE: San Diego, CA, USA, 2006. [Google Scholar]
- Deng, H.; Zhao, J.; Wang, C. Bionic design method of a non-uniform lattice structure for a landing footpad. Aerospace 2022, 9, 220. [Google Scholar] [CrossRef]
- Noronha, J.; Leary, M.; Brandt, M.; Qian, M. AlSi10Mg hollow-strut lattice metamaterials by laser powder bed fusion. Mater. Adv. 2024, 5, 3751–3770. [Google Scholar] [CrossRef]
- Noronha, J.; Qian, M.; Leary, M.; Kyriakou, E.; Brandt, M. Hollow-walled lattice materials by additive manufacturing: Design, manufacture, properties, applications and challenges. Curr. Opin. Solid State Mater. Sci. 2021, 25, 100940. [Google Scholar] [CrossRef]
- Noronha, J.; Dash, J.; Downing, D.; Rogers, J.; Qian, M.; Brandt, M.; Leary, M. Ti–6Al–4V hybrid-strut lattice metamaterials: A design strategy for improved performance. Mater. Sci. Eng. A 2024, 911, 146918. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, F.; Li, P.; Li, L.; Zhao, M.; Shi, J.; Zhang, L.; Cai, Y. A partially hollow BCC lattice structure with capsule-shaped cavities for enhancing load-bearing and energy absorption properties. Eng. Struct. 2024, 305, 117777. [Google Scholar] [CrossRef]
- Zhou, W.; Li, M. Compressive properties of functionally graded bionic bamboo lattice structures fabricated by FDM. Materials 2021, 14, 4410. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, B.; Qi, J.; Shi, Y. Designing and additive manufacturing of bamboo-imitated octet-truss lattice structure. J. Huazhong Univ. Sci. Technol. 2022, 50, 34–40. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).