Solid-State Welding of Thin Aluminum Sheets: A Case Study of Friction Stir Welding Alloys 1050 and 5754
Abstract
1. Introduction
2. Materials and Methods
2.1. Material Selection
2.2. Friction Stir Welding Setup
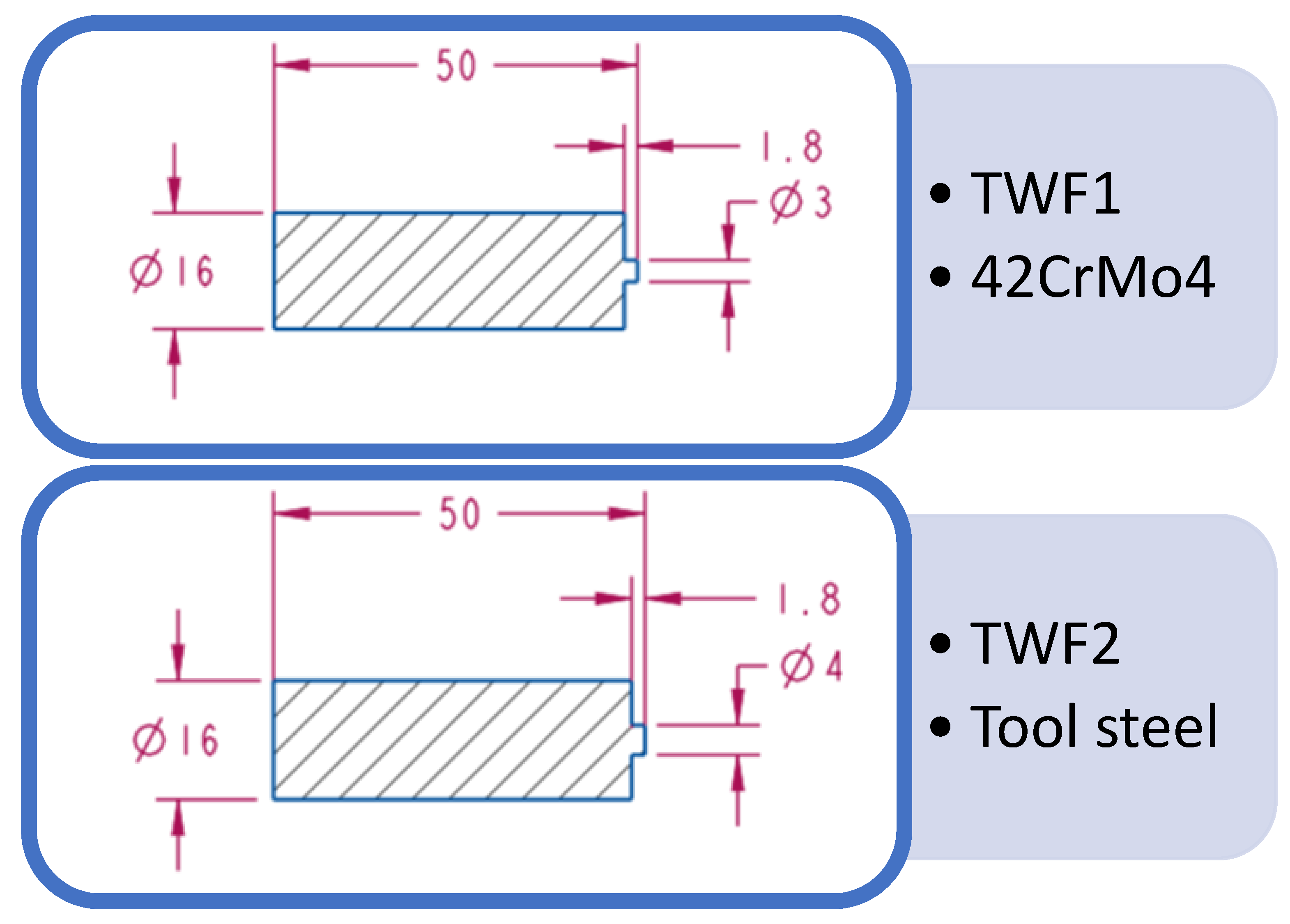
2.2.1. Tool Design
2.2.2. Process Parameters
2.3. Welding
2.4. Tensile Strength Testing
3. Results
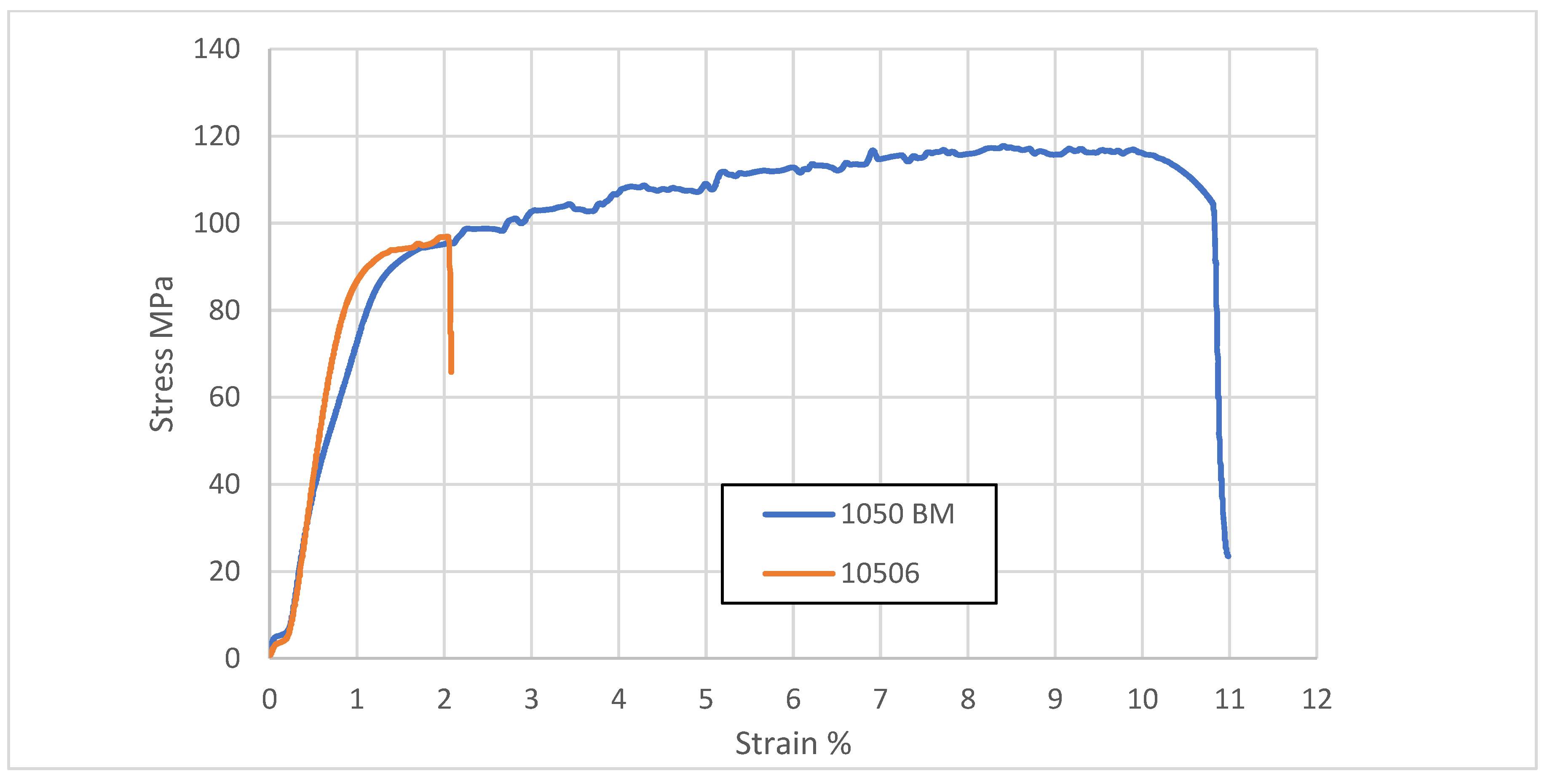
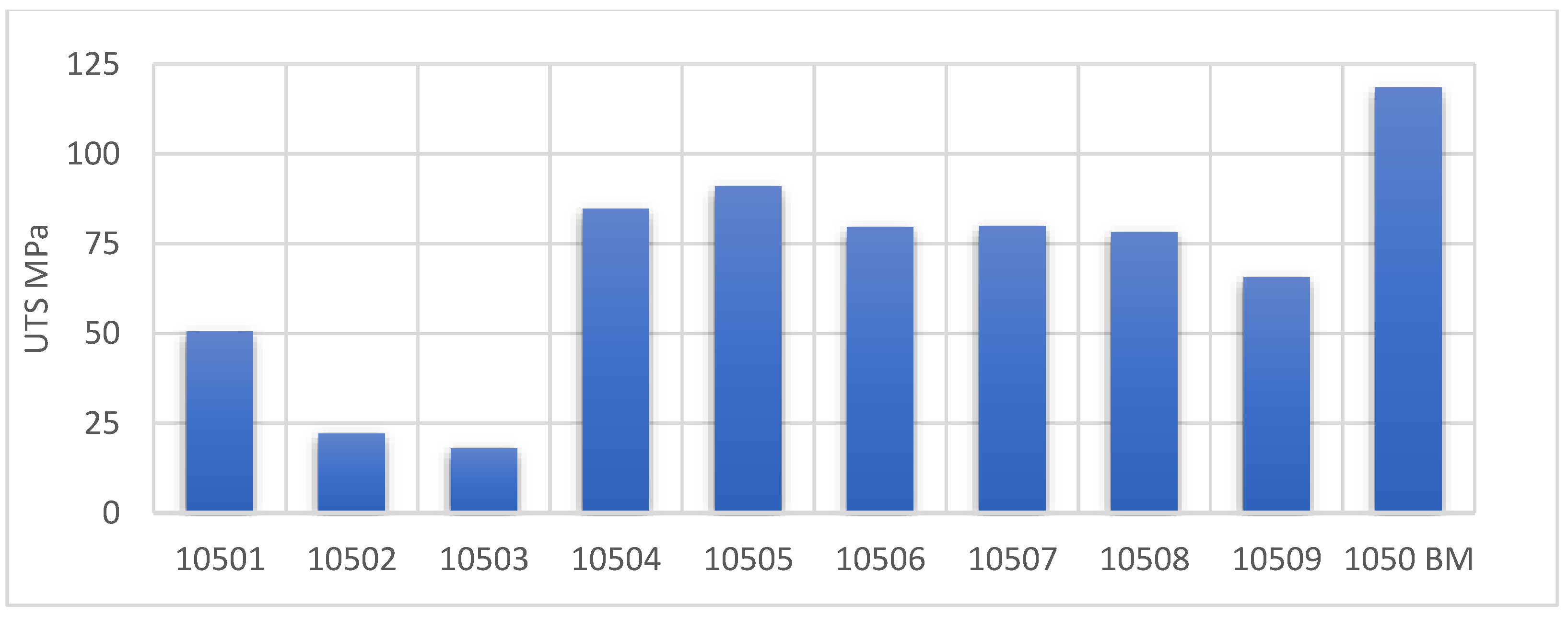
3.1. Friction Stir Welding AA1050
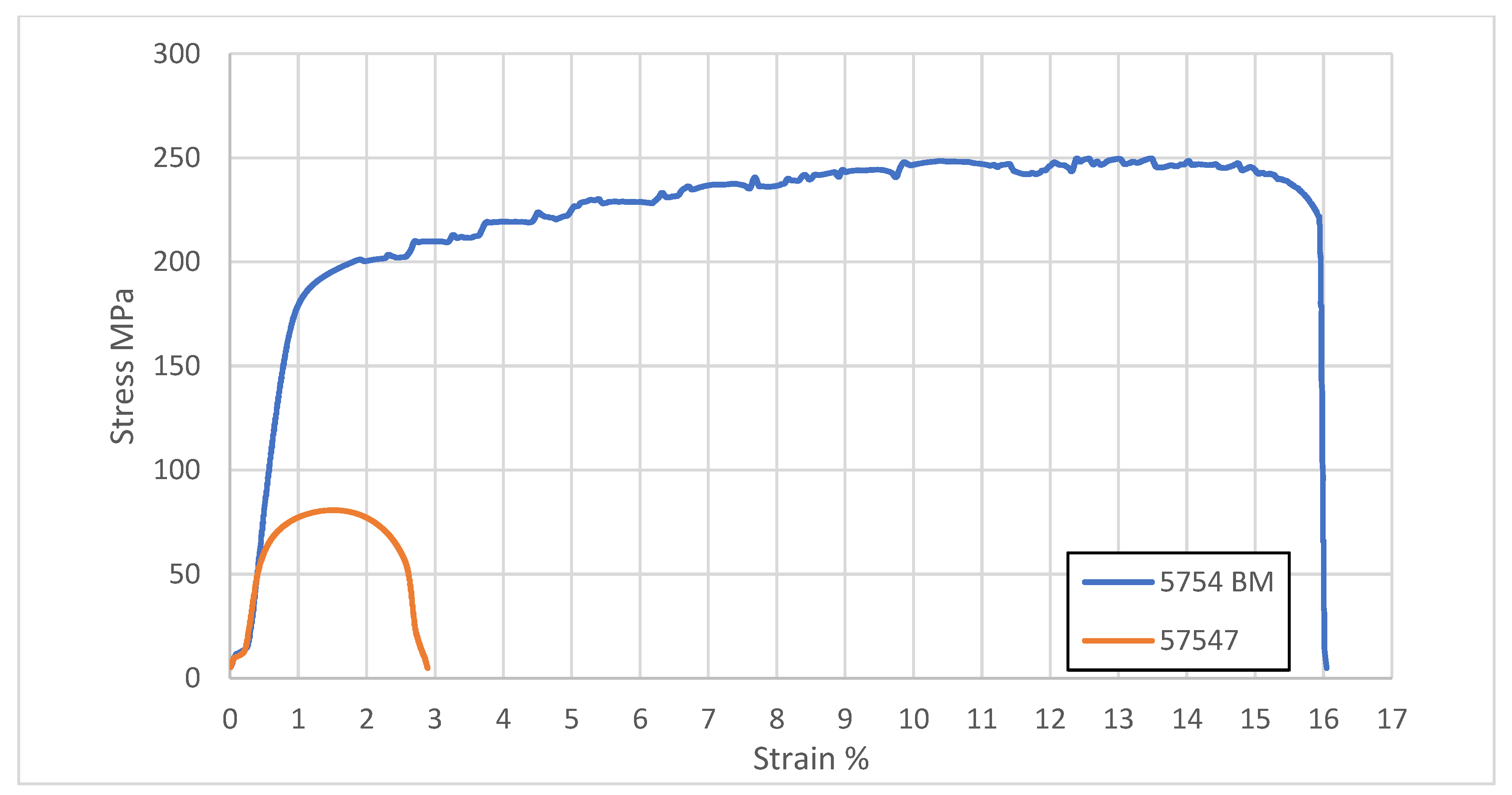
3.2. Friction Stir Welding AA5754
4. Discussion
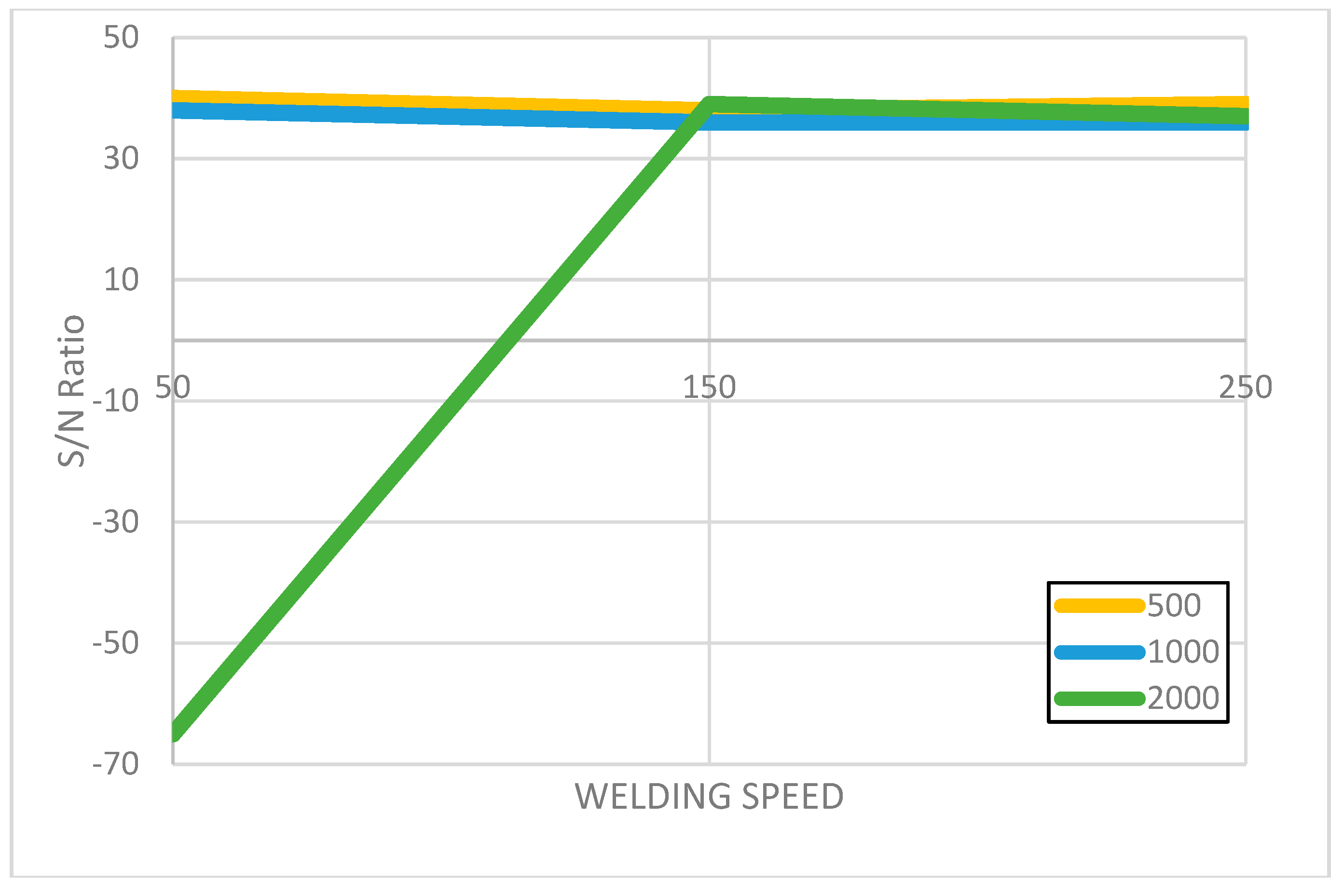
4.1. Enhancement and Evaluation of Welding Parameters for AA1050
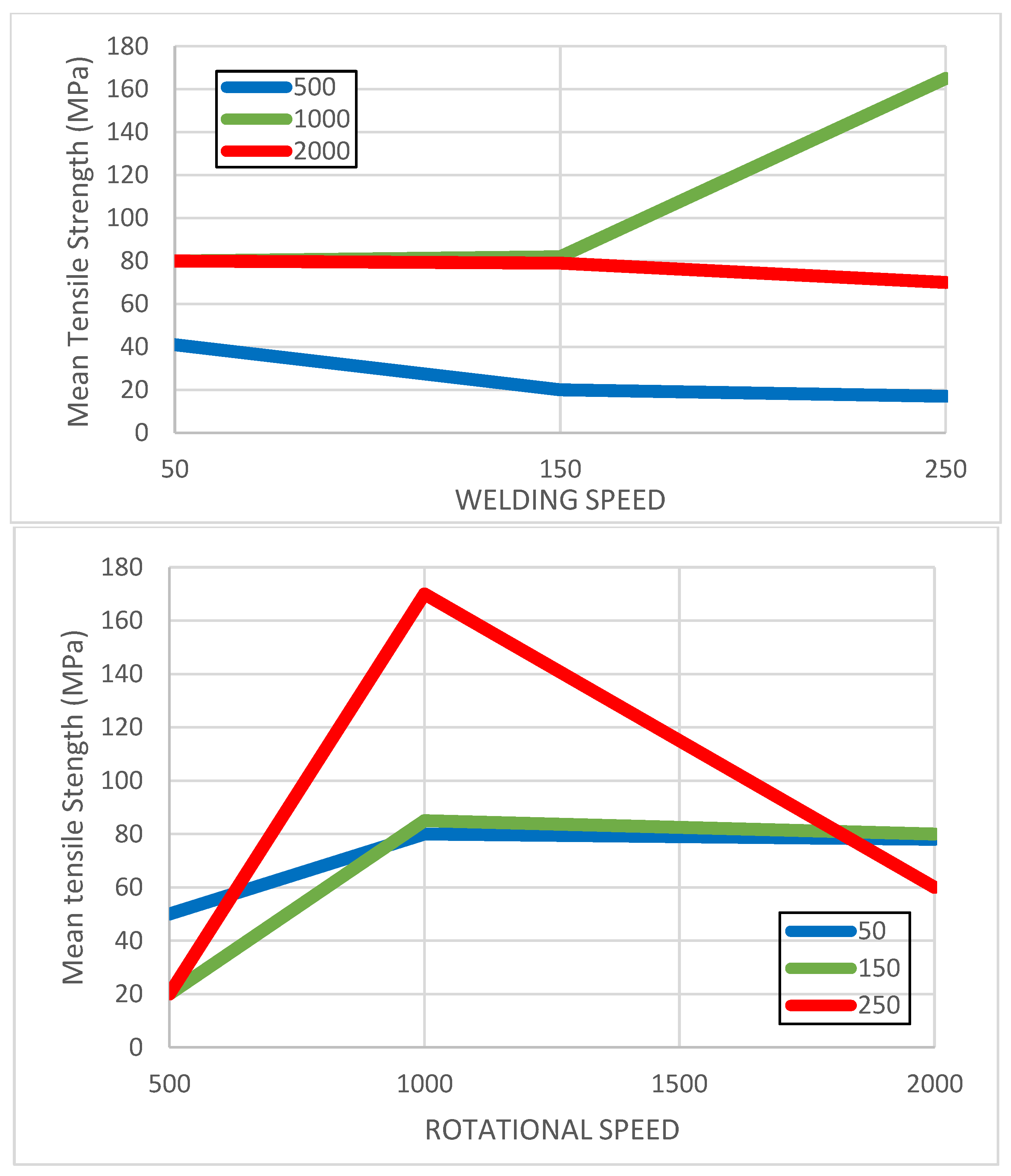
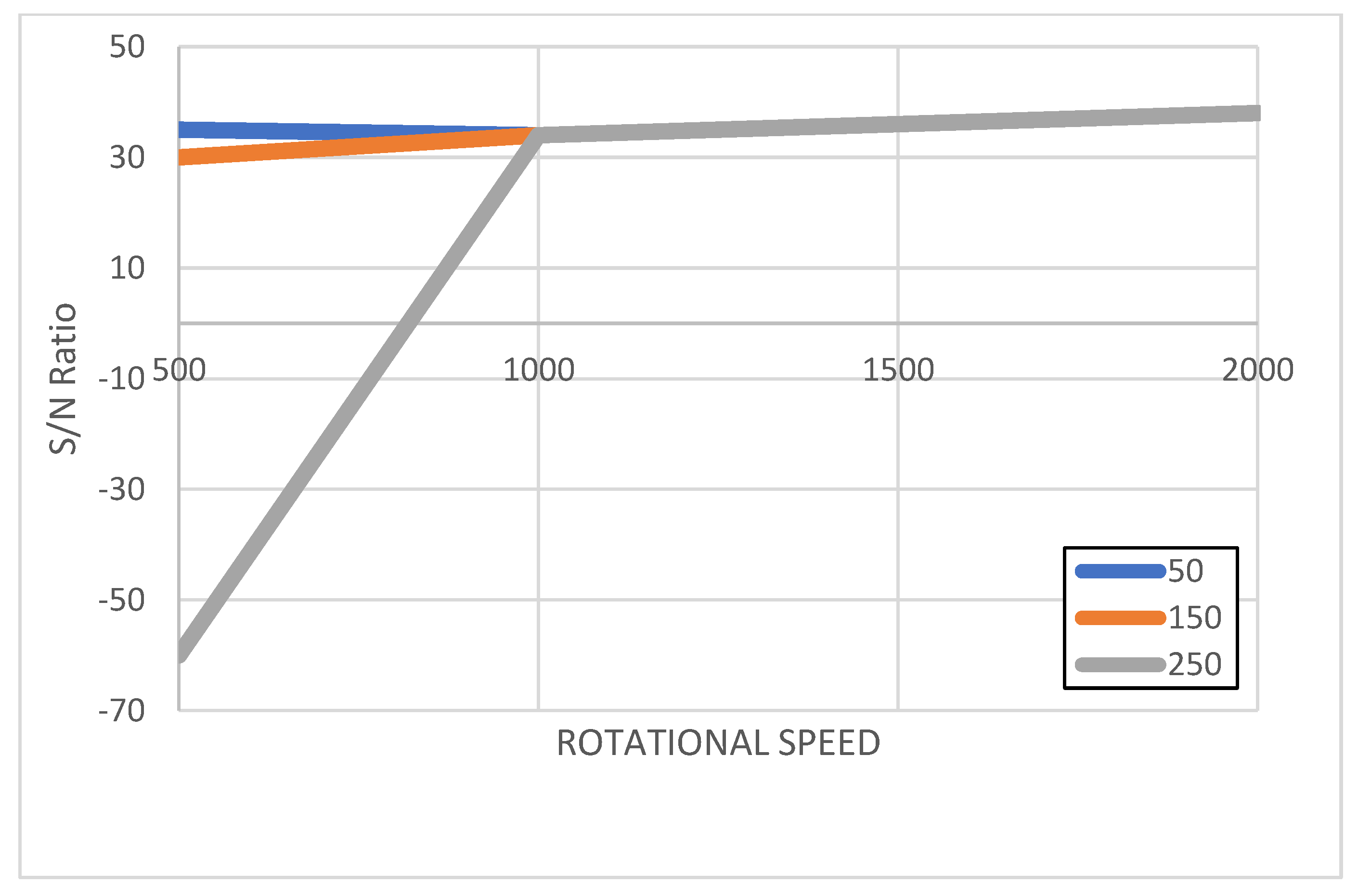
4.2. Enhancement and Evaluation of Welding Parameters for AA5754
5. Conclusions
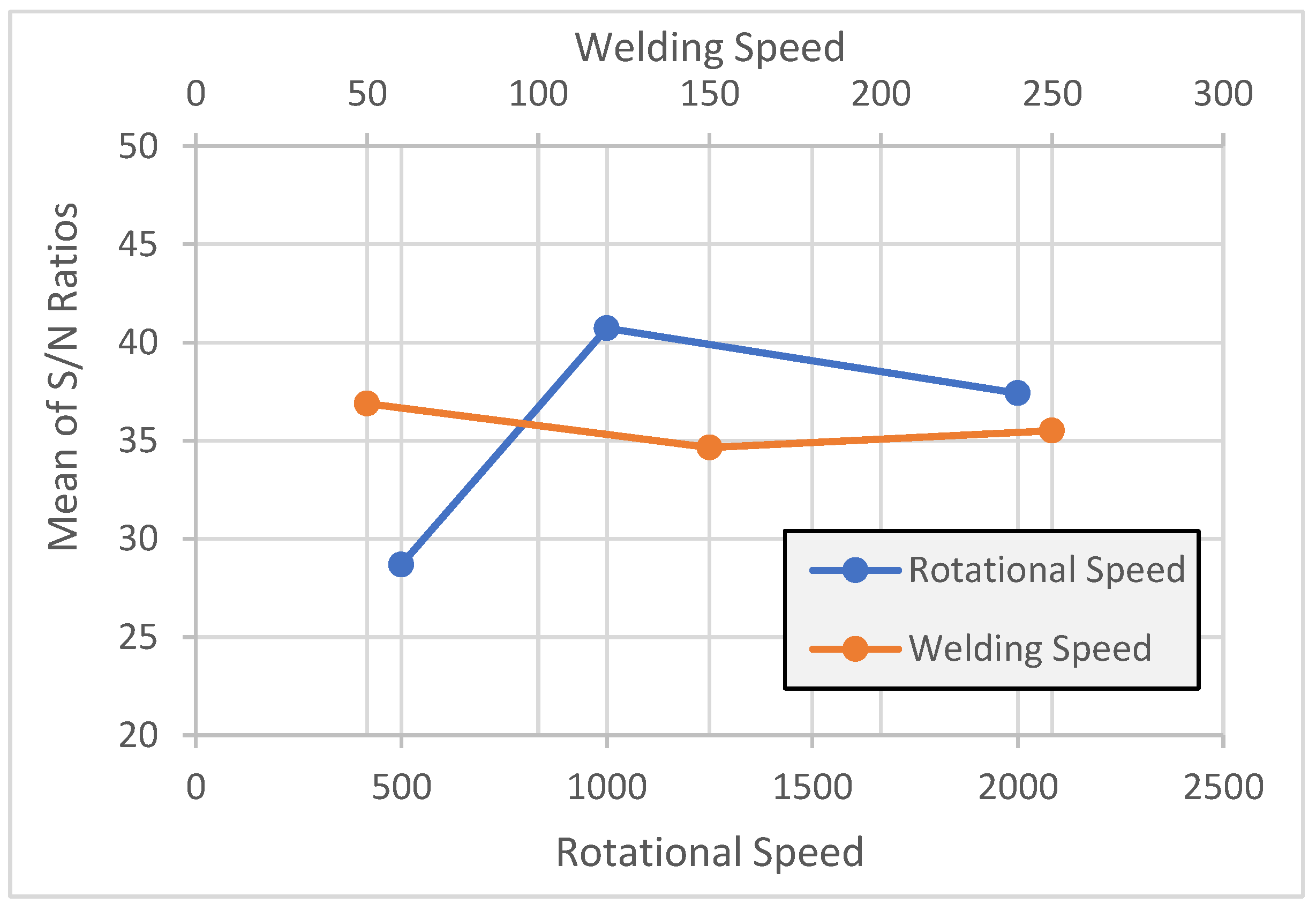
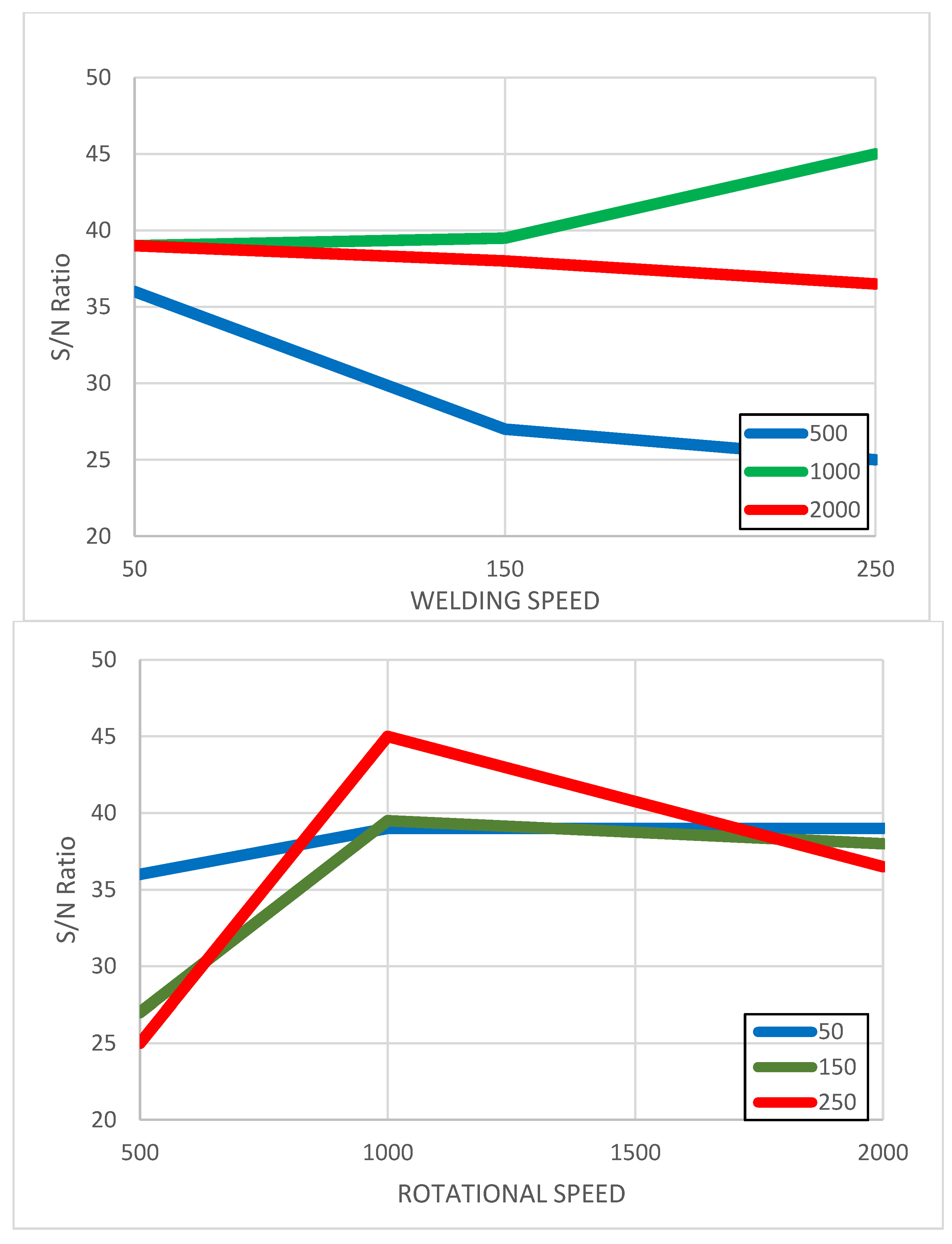
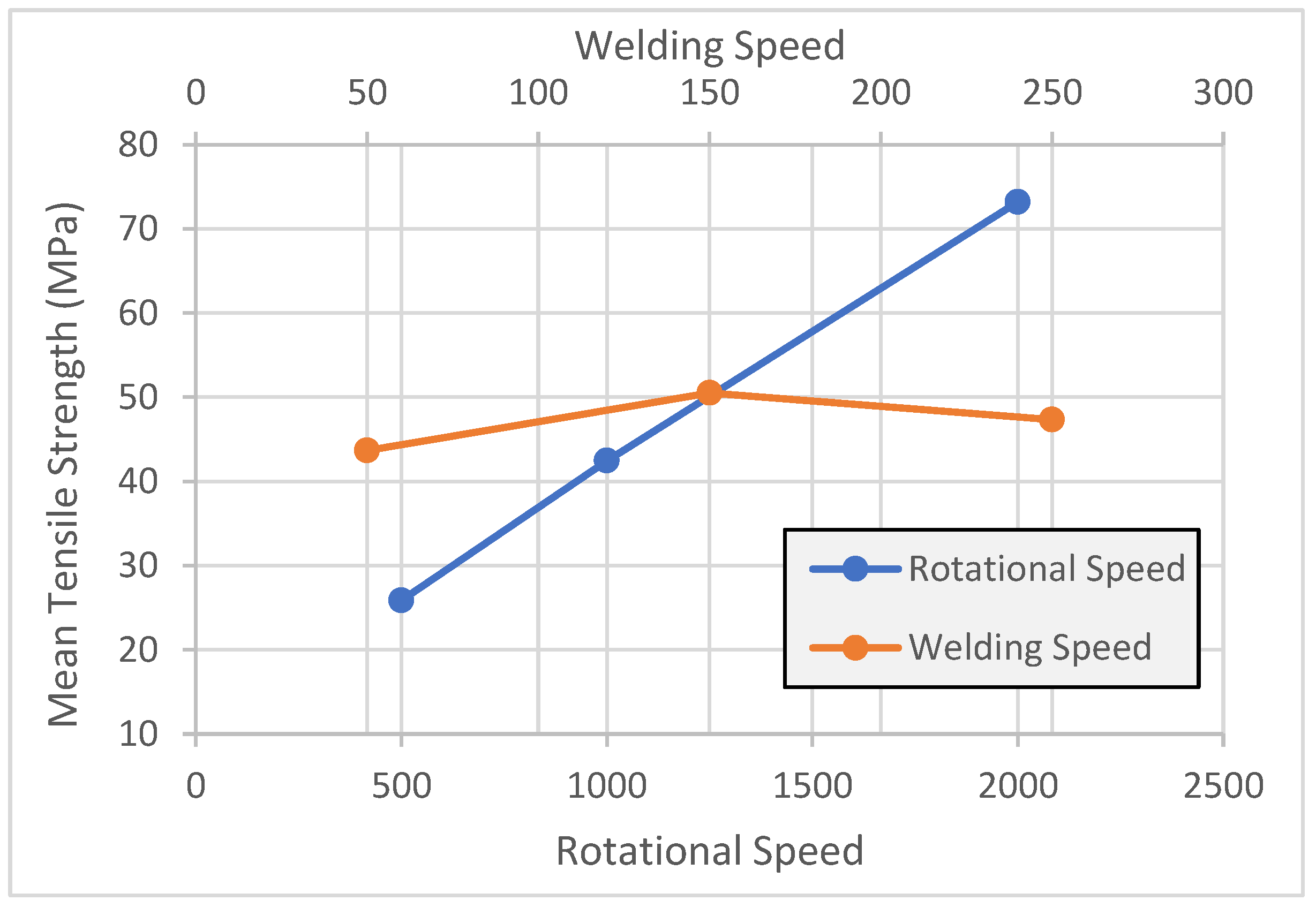
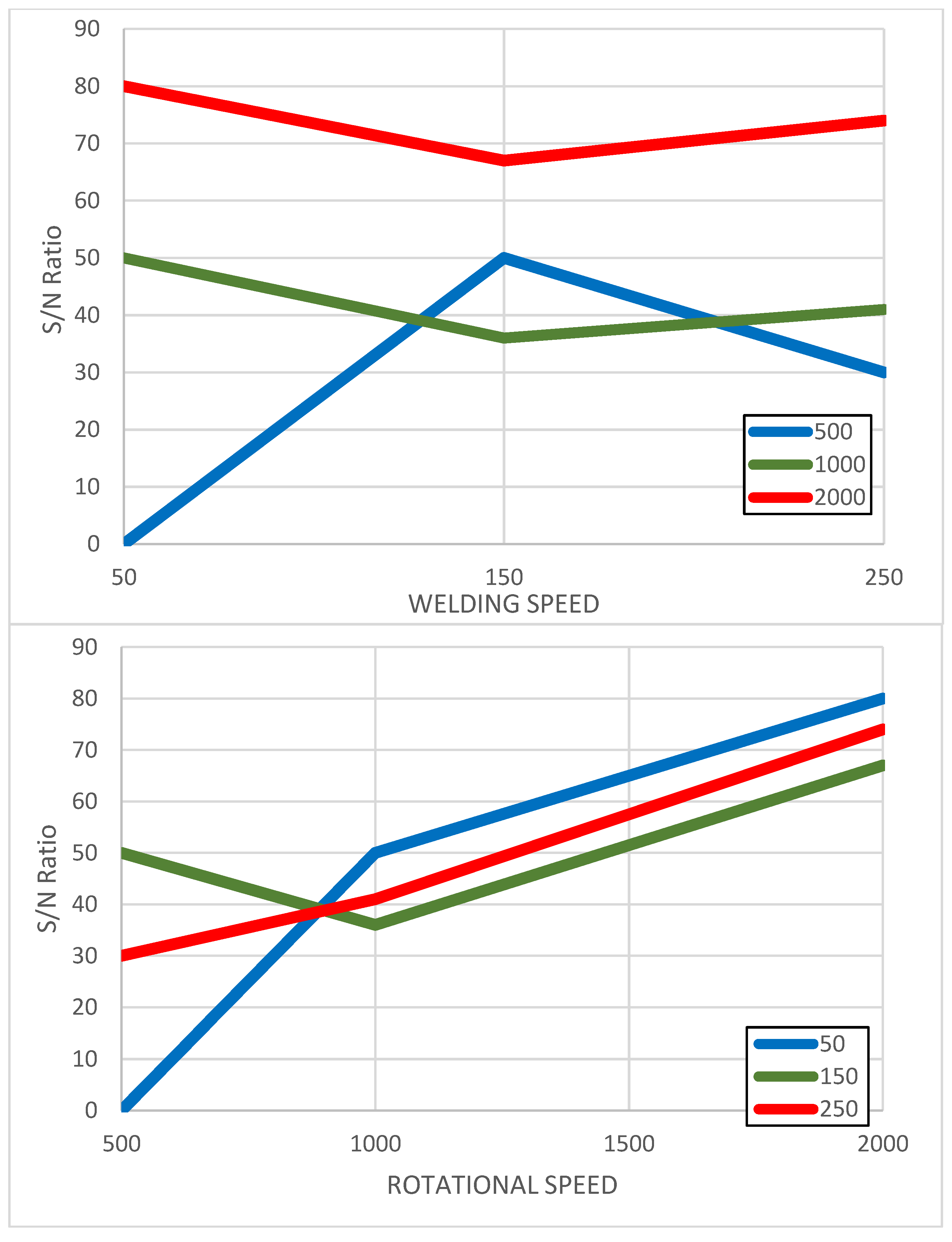
- There is a critical effect of rotational speed on the mechanical properties of the weld. For alloy AA1050, the optimal rotational speed was approximately 1000 RPM, while for AA5754 it was around 2000 RPM. At lower rotational speeds, insufficient heat was generated, leading to poor material mixing and poor welds. Conversely, higher speeds often resulted in overheating, causing defects such as grain coarsening.
- Welding speed, although having a less pronounced effect, also played a significant role in tensile strength. For AA1050, a welding speed of 250 mm/min yielded the best results, whereas AA5754 performed optimally at a slower speed of 150 mm/min. Faster speeds facilitated improved material flow in the AA1050 series, while slower speeds helped maintain better heat control and joint formation in AA5754.
- The interaction between rotational and welding speeds was particularly evident. For instance, combining 1000 RPM with 250 mm/min for AAL1050 produced the highest tensile strength, whereas 2000 RPM paired with 150 mm/min resulted in the strongest welds for AA5754.
- There were variations in mechanical properties for specimens 10506-1, 10506-2, and 10506-3, despite identical welding parameters. These are related to the inherent characteristics of the solid-state welding process. Even slight differences in temperature, microstructure, and residual stress can lead to variations in the mechanical properties of the weld, despite the use of identical welding parameters. Variations in heat distribution and solidification conditions create zones with differing mechanical properties, thereby explaining the discrepancies observed in the stress–strain curves.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dawes, C.; Heedham, J.; Thomas, W.; Temple-Smith, P.; Nicholas, E.; Kallee, S. Friction Stir Welding Tool and Method. International Patent Application No: GB2306366, 7 May 1997. [Google Scholar]
- Schmidt, H.; Hattel, J. A Local Model for the Thermomechanical Conditions in Friction Stir Welding. Model. Simul. Mater. Sci. Eng. 2005, 13, 77–93. [Google Scholar] [CrossRef]
- Singh, R.; Rizvi, S.A.; Tewari, S.P. Effect of Friction Stir Welding on the Tensile Properties of AA6063 under Different Conditions. Int. J. Eng. 2017, 30, 597–603. [Google Scholar]
- Zhang, Z.; Li, W.; Li, J.; Chao, Y.J.; Vairis, A. Microstructure and Anisotropic Mechanical Behavior of Friction Stir Welded AA2024 Alloy Sheets. Mater. Charact. 2015, 107, 112–118. [Google Scholar] [CrossRef]
- Su, Y.; Li, W.; Shen, J.; Fu, B.; dos Santos, J.F.; Klusemann, B.; Vairis, A. Comparing the Local-Global Deformation Mechanism in Different Friction Stir Welding Sequences of Ti-4Al-0.005B Titanium Alloy T-Joints. Mater. Sci. Eng. A 2021, 823, 141698. [Google Scholar] [CrossRef]
- Patel, V.; Li, W.; Vairis, A.; Badheka, V. Recent Development in Friction Stir Processing as a Solid-State Grain Refinement Technique: Microstructural Evolution and Property Enhancement. Crit. Rev. Solid State Mater. Sci. 2019, 44, 378–426. [Google Scholar] [CrossRef]
- Gibson, B.T. Friction Stir Welding: Process, Automation, and Control. J. Manuf. Process. 2014, 16, 56–73. [Google Scholar] [CrossRef]
- Badheka, V.J.; Kulkarni, D.; Amirthalingam, M. Editorial. Weld. Int. 2025, 39, 163. [Google Scholar] [CrossRef]
- Gahlot, P. Mechanical Behavior of Friction Stir Welded Al-Alloy AA6063 + 5%SiCp. In Advances in Engineering Materials; Tyagi, R.K., Ed.; Springer Nature: Singapore, 2024; pp. 327–335. [Google Scholar]
- Rudrapati, R. Effects of Welding Process Conditions on Friction Stir Welding of Polymer Composites: A Review. Compos. Part C Open Access 2022, 8, 100269. [Google Scholar] [CrossRef]
- Baffari, D.; Buffa, G.; Campanella, D.; Fratini, L.; Micari, F. Friction Based Solid State Welding Techniques for Transportation Industry Applications. Procedia CIRP 2014, 18, 162–167. [Google Scholar] [CrossRef]
- Bharti, S. A Review of Recent Developments in Friction Stir Welding for Various Industrial Applications. J. Mar. Sci. Eng. 2023, 12, 71. [Google Scholar] [CrossRef]
- Haghshenas, M.; Gerlich, A.P. Joining of Automotive Sheet Materials by Friction-Based Welding Methods: A Review. Eng. Sci. Technol. Int. J. 2018, 21, 130–148. [Google Scholar] [CrossRef]
- Vairis, A.; Papazafeiropoulos, G.; Tsainis, A.-M. A Comparison between Friction Stir Welding, Linear Friction Welding and Rotary Friction Welding. Adv. Manuf. 2016, 4, 296–304. [Google Scholar] [CrossRef]
- Padmanaban, G.; Balasubramanian, V. Selection of FSW Tool Pin Profile, Shoulder Diameter and Material for Joining AZ31B Magnesium Alloy—An Experimental Approach. Mater. Des. 2009, 30, 2647–2656. [Google Scholar] [CrossRef]
- Quintana, K.J.; Silveira, J.L.L. Threaded Pin Effects Analysis on Forces in FSW. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 491. [Google Scholar] [CrossRef]
- Rana, H.; Patel, V.; Buffa, G.; Fratini, L.; Di Lorenzo, R. Influence of Distinct Tool Pin Geometries on Aluminum 8090 FSW Joint Properties. Sheet Metal 2023, 25, 195–202. [Google Scholar]
- Celik, S.; Cakir, R. Effect of Friction Stir Welding Parameters on the Mechanical and Microstructure Properties of the Al-Cu Butt Joint. Metals 2016, 6, 133. [Google Scholar] [CrossRef]
- Ahmed, W.H.; Kadhum, A.H. Optimization of Tool Pin Geometry Parameters to Improve the Performance of Friction Stir Welding of AA1050. In Studies in Systems, Decision and Control; Springer: Cham, Switzerland, 2024; Volume 564, pp. 117–136. [Google Scholar]
- Kayode, O.; Akinlabi, E.T. Microstructural and Mechanical Properties of Friction Stir Welding of AA1050. In Proceedings of the Advances in Material Science and Engineering; Awang, M., Emamian, S.S., Eds.; Springer: Singapore, 2021; pp. 72–78. [Google Scholar]
- Akbari, M.; Asadi, P.; Sadowski, T. A Review on Friction Stir Welding/Processing: Numerical Modeling. Materials 2023, 16, 5890. [Google Scholar] [CrossRef]
- Kwon, Y.-J.; Shim, S.-B.; Park, D.-H. Friction Stir Welding of 5052 Aluminum Alloy Plates. Trans. Nonferrous Met. Soc. China 2009, 19, 23–27. [Google Scholar] [CrossRef]
- Adamowski, J.; Szkodo, M. Friction Stir Welds (FSW) of Aluminium Alloy AW6082-T6. J. Achiev. Mater. Manuf. Eng. 2007, 20, 403–406. [Google Scholar]
- Patel, V.; Li, W.; Wang, G.; Wang, F.; Vairis, A.; Niu, P. Friction Stir Welding of Dissimilar Aluminum Alloy Combinations: State-of-the-Art. Metals 2019, 9, 270. [Google Scholar] [CrossRef]
- Wan, L.; Huang, Y. Friction Stir Welding of Dissimilar Aluminum Alloys and Steels: A Review. Int. J. Adv. Manuf. Technol. 2018, 99, 1781–1811. [Google Scholar] [CrossRef]
- Huang, Y.; Meng, X.; Xie, Y.; Wan, L.; Lv, Z.; Cao, J.; Feng, J. Friction Stir Welding/Processing of Polymers and Polymer Matrix Composites. Compos. Part A Appl. Sci. Manuf. 2018, 105, 235–257. [Google Scholar] [CrossRef]
- Haribalaji, V. Investigation on Corrosion and Tensile Characteristics: Friction Stir Welding of AA7075 and AA2014. Mater. Today Proc. 2022, 66, 743–748. [Google Scholar] [CrossRef]
- Balasubramanian, V. Relationship between Base Metal Properties and Friction Stir Welding Process Parameters. Mater. Sci. Eng. A 2008, 480, 397–403. [Google Scholar] [CrossRef]
- Sabry, I.; Mourad, A.-H.I.; Alkhedher, M.; Qazani, M.R.C.; El-Araby, A. A Comparative Study of Multiple-Criteria Decision-Making Methods for Selecting the Best Process Parameters for Friction Stir Welded Al 6061 Alloy. Weld. Int. 2023, 37, 626–642. [Google Scholar] [CrossRef]
- Shinde, V.R.; Sapre, M.; Jatti, S.V.K. Optimization of Friction Stir Welding Process Parameters Using Taguchi’s Method. Glob. J. Pure Appl. Math. 2015, 11, 777–787. [Google Scholar] [CrossRef]
- Ugrasen, G. Optimization of Process Parameters for Al6061-Al7075 Alloys in Friction Stir Welding Using Taguchi’s Technique. Mater. Today Proc. 2018, 5, 3027–3035. [Google Scholar] [CrossRef]
- Abdelhady, S.S.; Elbadawi, R.E.; Zoalfakar, S.H. Multi-Objective Optimization of FSW Variables on Joint Properties of AA5754 Aluminum Alloy Using Taguchi Approach and Grey Relational Analysis. Int. J. Adv. Manuf. Technol. 2024, 130, 4235–4250. [Google Scholar] [CrossRef]
- Alam, M.P.; Sinha, A.N. Optimization of Process Parameters of Friction Stir Welding Using Desirability Function Analysis. Weld. Int. 2022, 36, 129–143. [Google Scholar] [CrossRef]
- Brahami, A.; Kaid, M.; Zemri, M. Thermo-Mechanical Characterization of Pinless Friction Stir Welding in AA6060-T4 Thin Sheets. Weld. Int. 2024, 38, 650–659. [Google Scholar] [CrossRef]
- Liu, H.; Fujii, H.; Maeda, M.; Nogi, K. Friction Stir Weldabilities of AA1050-H24 and AA6061-T6 Aluminum Alloys. J. Mater. Sci. Technol. 2005, 21, 415–418. [Google Scholar]
- Baumeister, T.I.; Avalone, E. Marks’ Standard Handbook for Mechanical Engineers, 8th ed.; McGraw Hill: New York, NY, USA, 1978; ISBN 978-0-07-004123-3. [Google Scholar]
- Dimopoulos, A. On the Friction Stir Welding of Al 7075 Thin Sheets. Metals 2020, 11, 57. [Google Scholar] [CrossRef]
- Muzamil, M.; Wu, J.; Akhtar, M.; Azher, K.; Majeed, A.; Zhang, Z.; Shazad, A. Nanoparticle-Induced Control (MWCNTs–TiO2) on Grain Size and Tensile Strength Response and Multi-Response Optimization on TIG Welded Joints. Trans. Can. Soc. Mech. Eng. 2022, 46, 626–638. [Google Scholar] [CrossRef]
- Muzamil, M.; Siddiqui, N.A.; Kumar, K.; Hussain, G.; Alkahtani, M.; Sattar, M. Impact of Machining Parameters on Wire Arc Additively Manufactured Mild Steel Specimens of E6013 and E7018 Using an Electric Arc Heat Source. Crystals 2025, 15, 222. [Google Scholar] [CrossRef]
- Vidakis, N. Effect of the Tool Rotational Speed on the Mechanical Properties of Thin AA1050 Friction Stir Welded Sheets. J. Eng. Sci. Technol. Rev. 2016, 2016, 123–129. [Google Scholar] [CrossRef]
- Vural, M.; Ogur, A.; Cam, G.; Ozarpa, C. On the Friction Stir Welding of Aluminium Alloys EN AW 2024-0 and EN AW 5754-H22. Arch. Mater. Sci. Eng. 2007, 28, 49–54. [Google Scholar]
- Patsalias, G. Georgios Study of Friction Stir Welding for Thin Aluminum Sheets. Master’s Thesis, University of West Attica, Athens, Greece, 2024. [Google Scholar]






| Aluminum Alloy | AA1050 | AA5754 |
|---|---|---|
| Composition (wt.%) | ||
| Cu | 0.05 | 0.10 |
| Fe | 0.40 | 0.40 |
| Mg | 0.05 | 2.60 |
| Mn | 0.05 | 0.10 |
| Si | 0.25 | 0.40 |
| Zn | 0.05 | 0.20 |
| Ti | 0.03 | 0.15 |
| Al | 99.5 | 94.2 |
| Cr | - | 0.30 |
| Mechanical properties | ||
| Ultimate Tensile Strength (MPa) | 70–100 | 190–240 |
| Yield Strength (MPa) | 25–35 | 80–150 |
| Elongation (%) | 25–35 | 20–28 |
| Hardness (HB) | 25–35 | 40–80 |
| Level | Rotational Speed (RPM) | Welding Speed (mm/min) |
|---|---|---|
| 1 | 500 | 50 |
| 2 | 1000 | 150 |
| 3 | 2000 | 250 |
| ID | Rotational Speed (RPM) | Welding Speed (mm/min) | |
|---|---|---|---|
| 10501 | 57541 | 500 | 50 |
| 10502 | 57542 | 500 | 150 |
| 10503 | 57543 | 500 | 250 |
| 10504 | 57544 | 1000 | 50 |
| 10505 | 57545 | 1000 | 150 |
| 10506 | 57546 | 1000 | 250 |
| 10507 | 57547 | 2000 | 50 |
| 10508 | 57548 | 2000 | 150 |
| 10509 | 57549 | 2000 | 250 |
| DWELL TIME (S) | 4 |
| OUT FEED RATE (mm/min) | 50 |
| PLUNGE FEED RATE (mm/min) | 10 |
| TILT ANGLE (DEG) | 0 |
| ID | UTS (MPa) | ε% |
|---|---|---|
| 10501 | 50 | 1.6 |
| 10502 | 22 | 1.1 |
| 10503 | 18 | 1.4 |
| 10504 | 84 | 6.1 |
| 10505 | 90 | 5.6 |
| 10506 | 95 | 2.0 |
| 10507 | 79 | 3.8 |
| 10508 | 78 | 3.2 |
| 10509 | 65 | 3.1 |
| 1050 BM | 118 | 8.5 |
| ID | Rotational Speed (RPM) | Welding Speed (mm/min) |
|---|---|---|
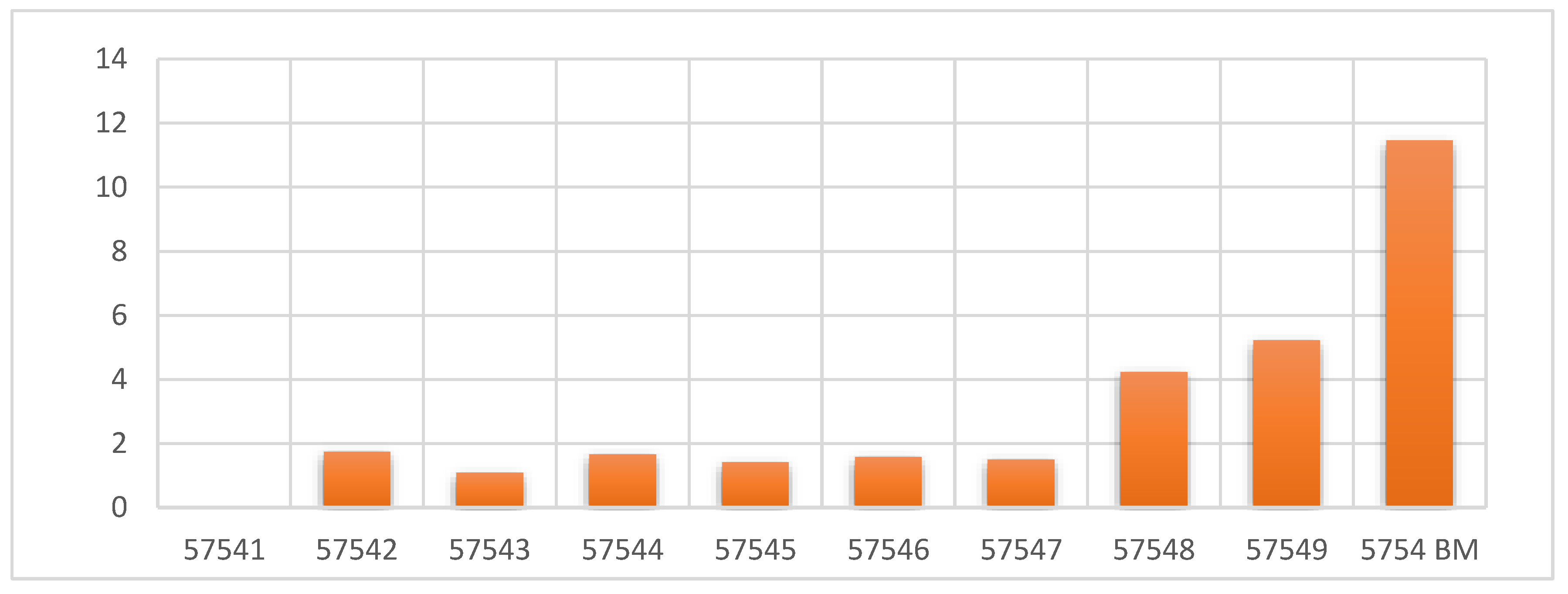
| 57541 | 0 | 0.0 |
| 57542 | 49 | 1.7 |
| 57543 | 28 | 1.1 |
| 57544 | 51 | 1.7 |
| 57545 | 35 | 1.4 |
| 57546 | 41 | 1.6 |
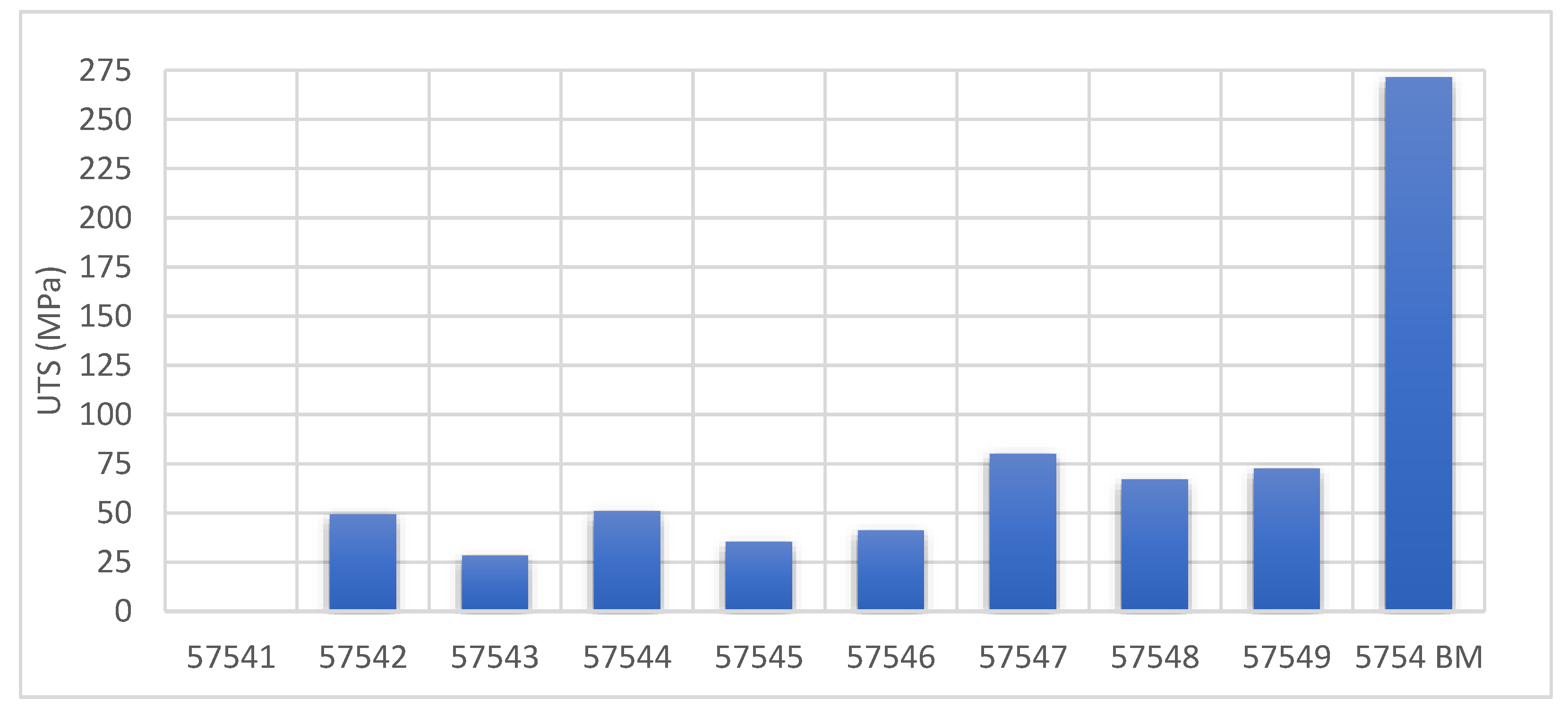
| 57547 | 80 | 1.5 |
| 57548 | 67 | 4.2 |
| 57549 | 73 | 5.2 |
| 5754 BM | 271 | 11.5 |
| Level | Signal-to-Noise Ratio: “Larger is Better” | Mean Tensile Strength (MPa) | ||
|---|---|---|---|---|
| Rotational Speed | Welding Speed | Rotational Speed | Welding Speed | |
| 1 | 28.69 | 36.89 | 30 | 72 |
| 2 | 40.73 | 34.65 | 114 | 64 |
| 3 | 37.42 | 35.31 | 75 | 84 |
| Delta | 12.04 | 2.24 | 84.06 | 20 |
| Rank | 1 | 2 | 1 | 2 |
| Level | Signal-to-Noise Ratio: “Larger is Better” | Mean Tensile Strength (MPa) | ||
|---|---|---|---|---|
| Rotational Speed | Welding Speed | Rotational Speed | Welding Speed | |
| 1 | 0.96 | 4.07 | 26 | 44 |
| 2 | 32.46 | 33.77 | 42 | 51 |
| 3 | 37.27 | 32.85 | 73 | 47 |
| Delta | 36.30 | 29.70 | 47.33 | 6.83 |
| Rank | 1 | 2 | 1 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patsalias, G.; Sofias, K.; Vairis, A. Solid-State Welding of Thin Aluminum Sheets: A Case Study of Friction Stir Welding Alloys 1050 and 5754. Metals 2025, 15, 463. https://doi.org/10.3390/met15040463
Patsalias G, Sofias K, Vairis A. Solid-State Welding of Thin Aluminum Sheets: A Case Study of Friction Stir Welding Alloys 1050 and 5754. Metals. 2025; 15(4):463. https://doi.org/10.3390/met15040463
Chicago/Turabian StylePatsalias, Georgios, Konstantinos Sofias, and Achilles Vairis. 2025. "Solid-State Welding of Thin Aluminum Sheets: A Case Study of Friction Stir Welding Alloys 1050 and 5754" Metals 15, no. 4: 463. https://doi.org/10.3390/met15040463
APA StylePatsalias, G., Sofias, K., & Vairis, A. (2025). Solid-State Welding of Thin Aluminum Sheets: A Case Study of Friction Stir Welding Alloys 1050 and 5754. Metals, 15(4), 463. https://doi.org/10.3390/met15040463







