Optimization and Finite Element Simulation of Wear Prediction Model for Hot Rolling Rolls
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Parameter Settings
2.2. Definition of Boundary Conditions and Related Parameters
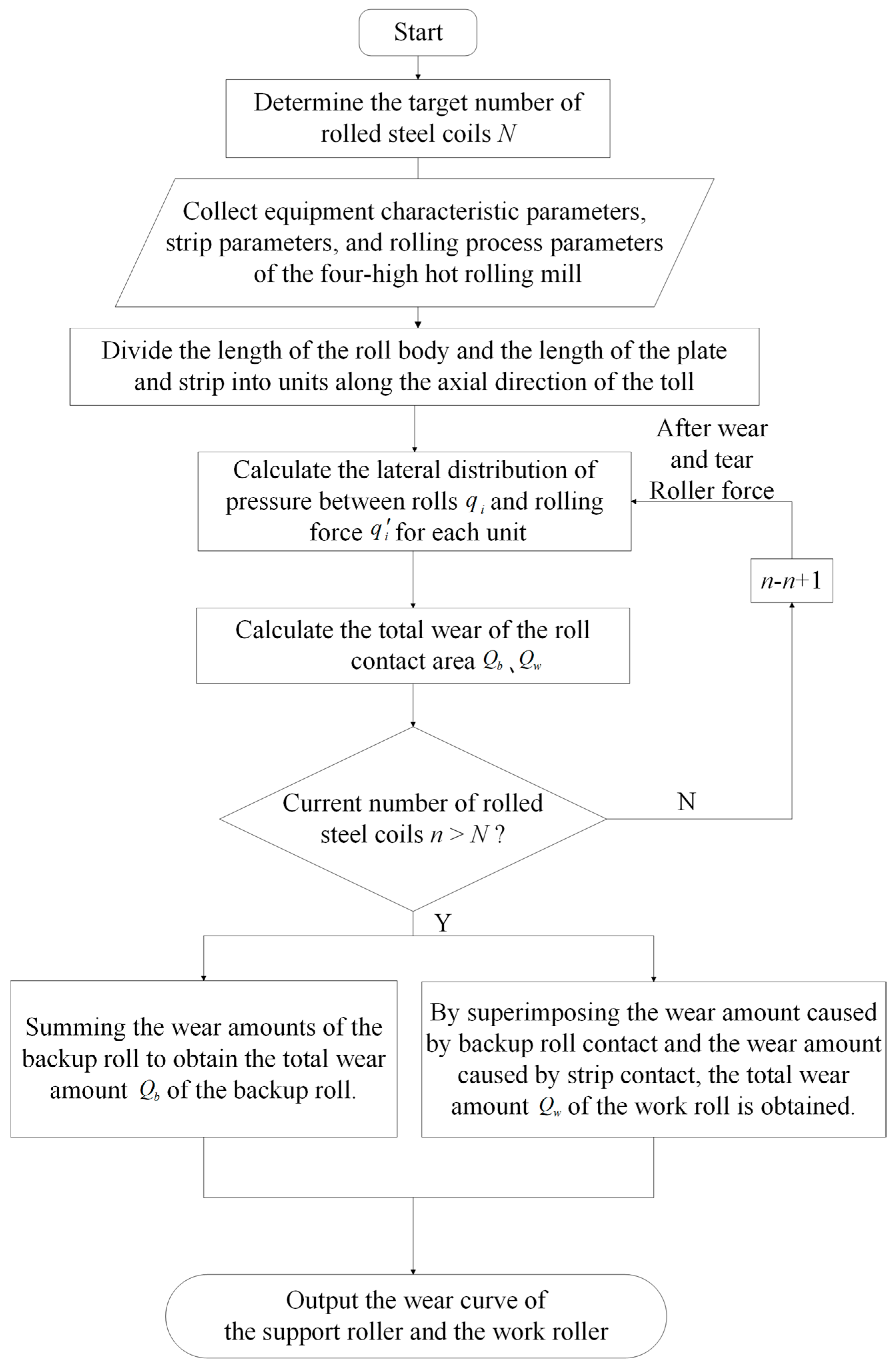
2.3. Dynamic Optimization Method for Roll Wear in Hot Tandem Rolling
3. Results and Discussion
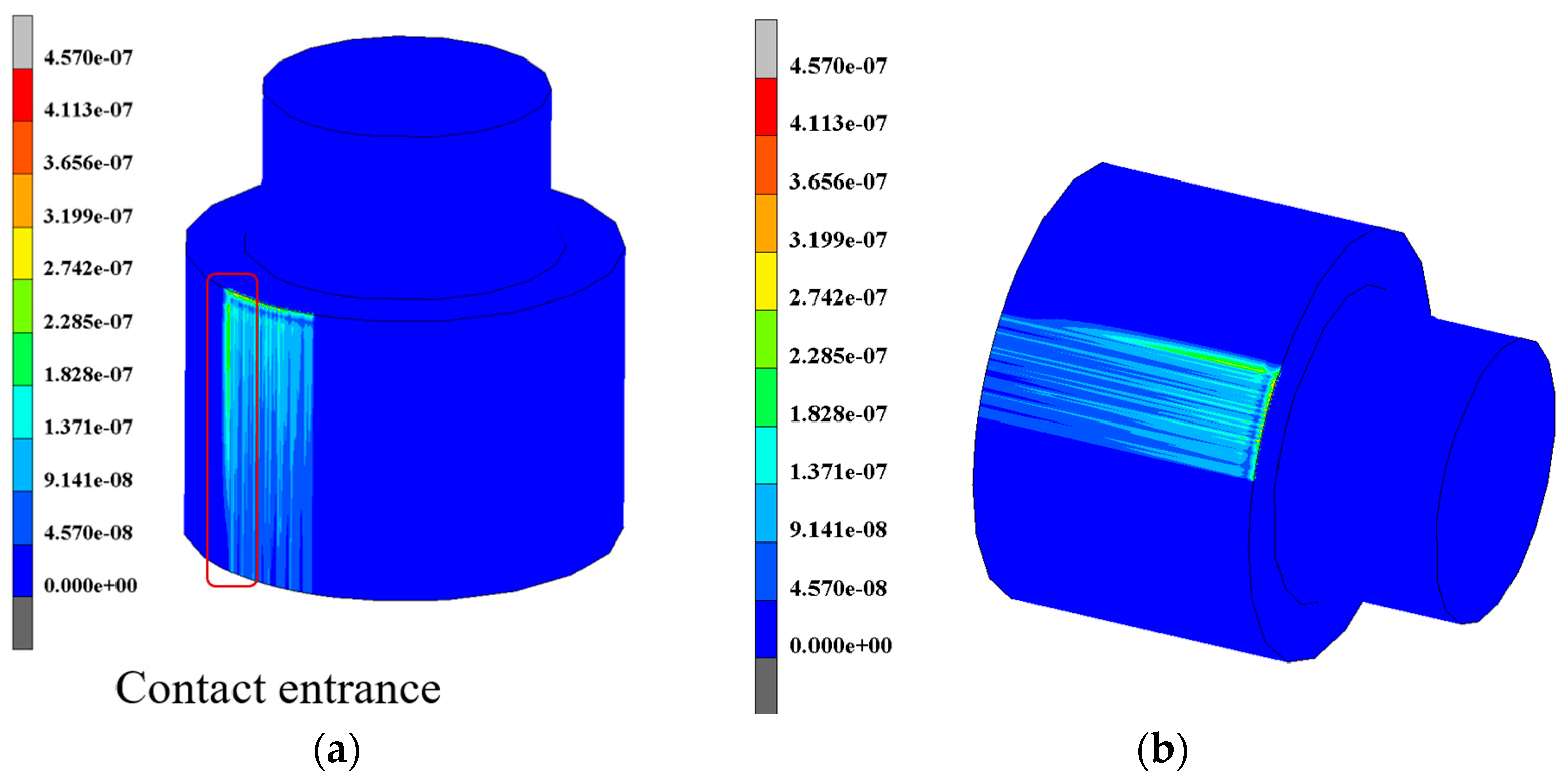
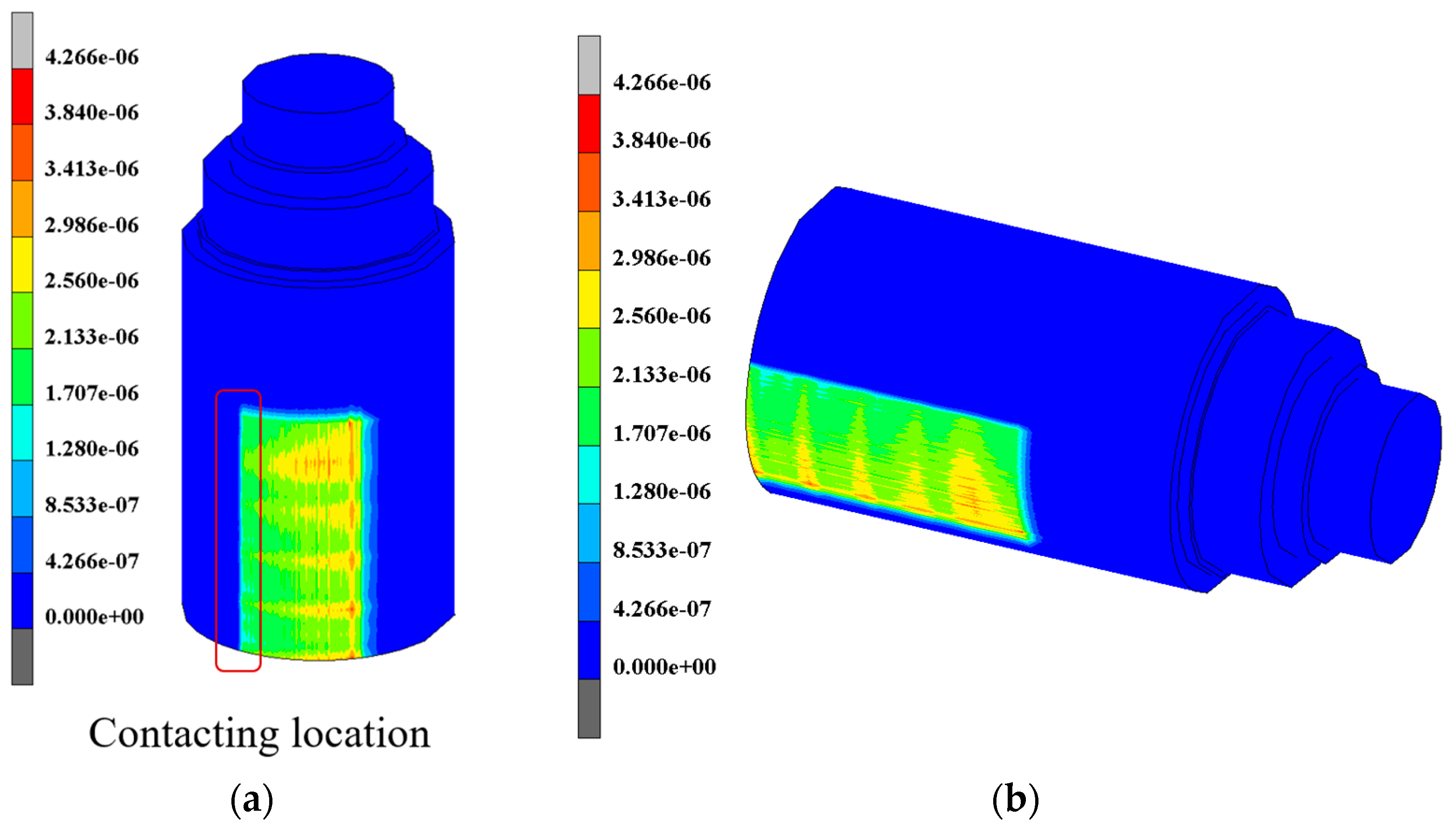
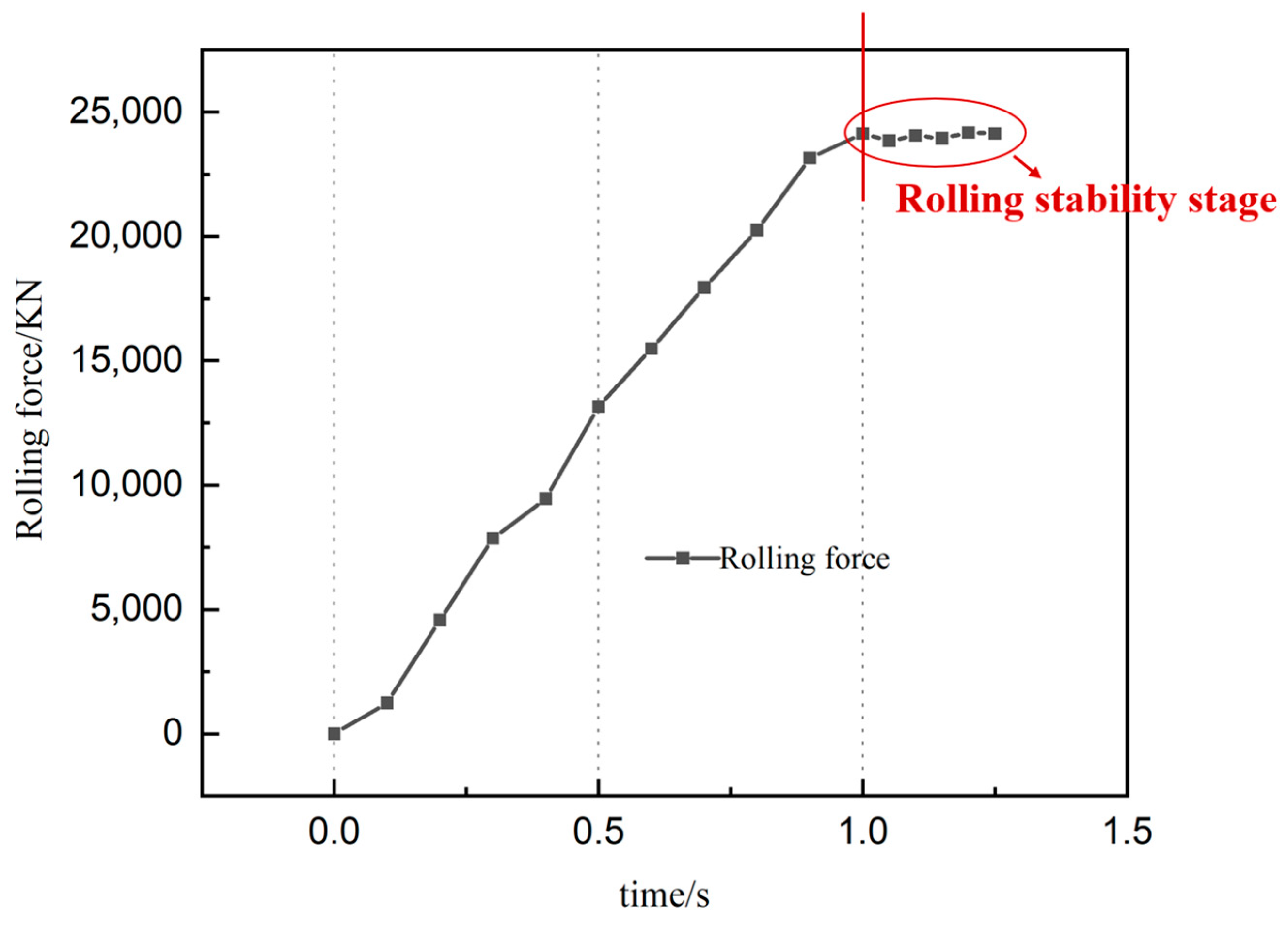
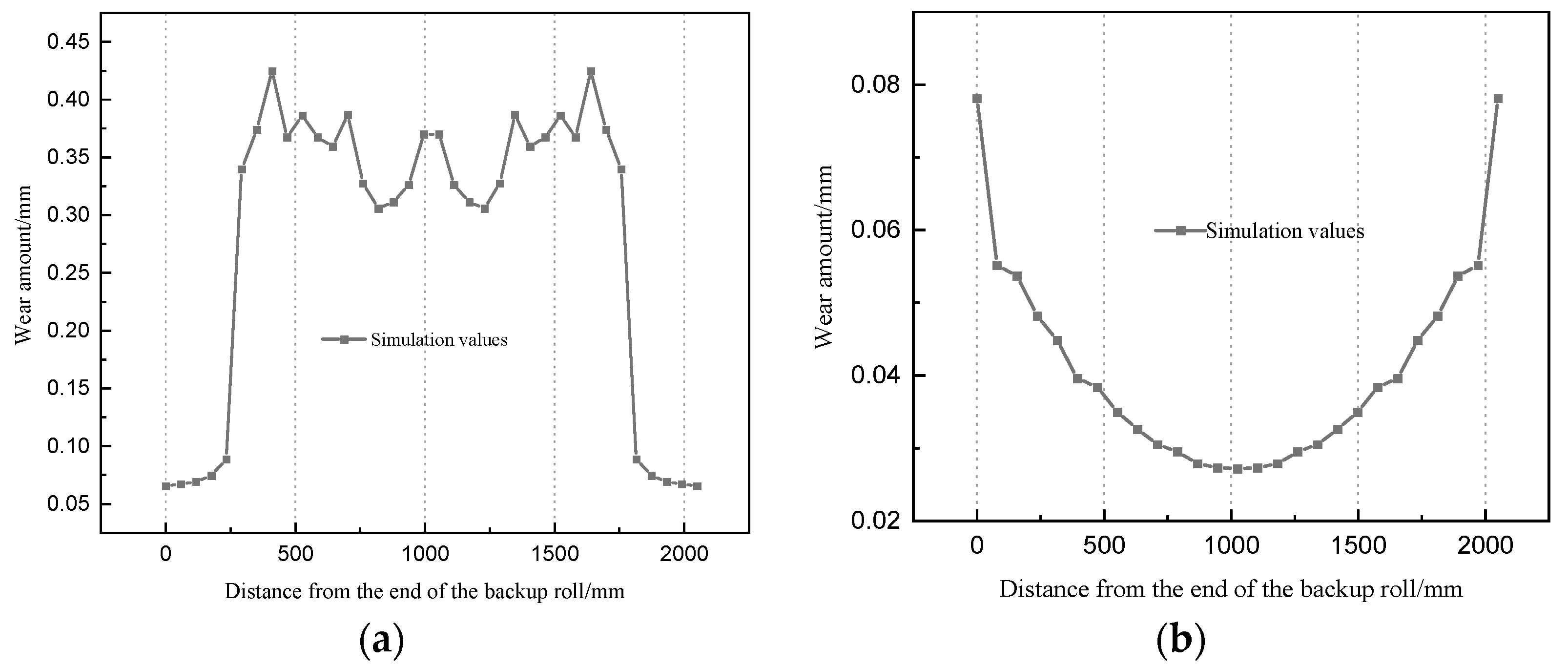
3.1. Finite Element Result Analysis
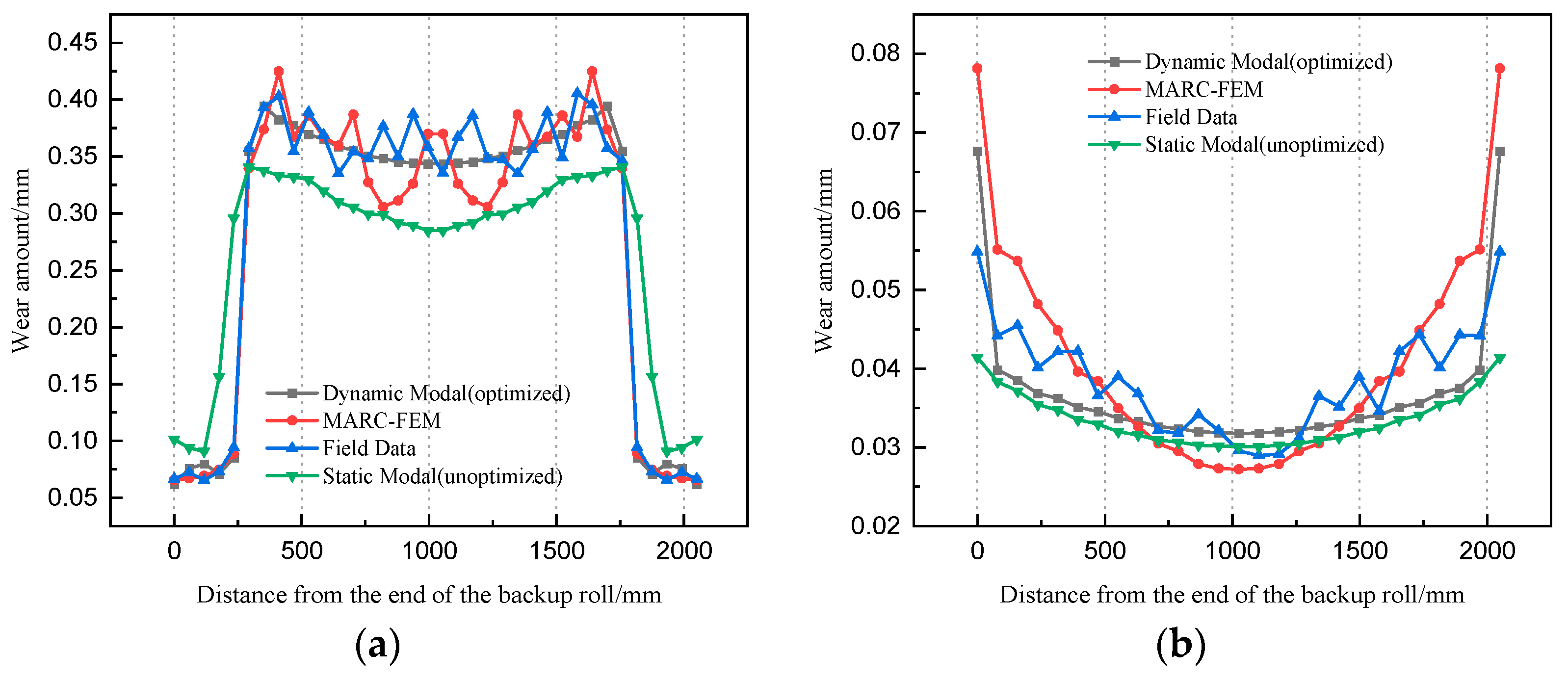
3.2. Field Application of the Model
4. Conclusions
- (1)
- The roll wear mechanism was analyzed, and a higher-precision roll wear optimization model was obtained by introducing the comprehensive influence coefficient of the steel type and the cyclic superposition processing of the pressure between the rolls, and a set of dynamic simulation software for the roll wear profile was developed to predict the wear amount.
- (2)
- Using the nonlinear finite element software MARC, a three-dimensional elastic-plastic thermosolid coupling finite element simulation model of the rolling process of the hot rolling four-high rolling mill was established on the basis of ensuring the accuracy of the model. An experimental analysis method was used to obtain the wear coefficient under a specific production environment. By setting the rolling process parameters for numerical simulation, the simulated distribution curve of roll wear was obtained.
- (3)
- By comparing the actual measured values of roll wear with simulated values, optimized values, and non-optimized values, it is proven that in the optimized wear model and the finite element wear model, the prediction accuracy of the work roll and backup roll wear is improved to a certain extent. After optimization, the dynamic simulation software indicates that the deviation value of the work roll wear amount is 0.012, and the deviation value of the backup roll is 0.004, both lower than the numerical deviation value of the wear before optimization and the numerical deviation value of the finite element simulation.
5. Discussion and Prospect
- (1)
- Adhesive wear and corrosive wear are important factors contributing to roll wear, but they account for a relatively low proportion under the working conditions of this study. Future research will focus on expanding the model to incorporate these mechanisms.
- (2)
- In order to explore and quantify the influence mechanisms of these key factors on roll wear more clearly, the model was appropriately simplified in this article by weakening the temperature factor. This approach helped us to focus on solving the main problems in the initial stage of the research, avoiding the interference of too many complex factors and making the model construction and optimization process clearer and more controllable. Subsequently, we will incorporate the impact of temperature on roll wear into the mathematical model to further improve the accuracy of the model.
- (3)
- From the above verification data, it can be found that the prediction accuracy of the model is improved more significantly when rolling strip steel of the same specification than when rolling strip steel of mixed specifications. Future research will further expand the verification under extreme working conditions (such as ultra-high-strength steel and ultra-thin strip steel) to improve the universality of the model.
- (4)
- Future research will focus on the dynamic calibration method of for multiple steel grades and wide temperature ranges (such as functional modeling based on material hardness and friction coefficient) to further enhance the universality of the model, thereby enabling the real-time correction of .
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, H.Q.; Yang, Q.; Wang, X.C.; Wang, L.S. Wear contour prediction model and application of the work roll in hot wide strip mill. Steel Roll. 2018, 35, 45–49. [Google Scholar]
- Ding, J.G.; Li, J.; Zhang, K.; Sun, J. Investigation on contact pressure of backup roll with parabolic chamfer curve and intelligent modeling of plate crown in plate rolling process. Int. J. Adv. Manuf. Technol. 2023, 127, 5633–5650. [Google Scholar] [CrossRef]
- Du, F.S.; Zhang, S.B.; Haung, H.G.; Wang, G.G.; Ren, X.Y. Finite element study of the rigidity characteristics of a six-high mill. J. Plast. Eng. 2010, 17, 148. [Google Scholar]
- Chen, B.G.; Chen, X.L.; Tieu, A.K. Prediction of work roll thermal deformarion with finite element method on hot strip mill. Iron Steel 1991, 8, 40–44. [Google Scholar]
- Sun, R.S.; Cui, X.Y.; Li, X.T.; Bai, X.S.; Wang, N.; Bai, Z.H. Finite element simulation of crushed wave defects during cold continuous rolling. J. Plast. Eng. 2023, 30, 58. [Google Scholar]
- Sonboli, A.; Serajzadeh, S. A model for evaluating thermal mechanical stresses within work-rolls in hot-strip rolling. J. Eng. Math. 2012, 72, 73–85. [Google Scholar] [CrossRef]
- Wang, J.; Cao, Y.; Hao, Z.Y.; Huang, Z.Y. Finite element analysis on tehperature field of work roll in hot rolling strip mill. Hot Work. Technol. 2013, 42, 102–104. [Google Scholar]
- Li, J.H.; Lian, J.C.; Yue, X.L. Prediction Model of Temperature Field and Crown of Work Roll for Hot Strip Mill. J. Iron Steel Res. 2003, 6, 25–28. [Google Scholar]
- Sun, Y.K. Model and Control of Hot Strip Rolling; Metallurgical Industry Press: Beijing, China, 2007; pp. 56–106. [Google Scholar]
- John, S.; Sikdar, S.; Mukhopadhyay, A.; Pandit, A. Roll wear prediction model for finishing stands of hot strip mill. Ironmak. Steelmak. 2006, 33, 169–175. [Google Scholar] [CrossRef]
- Wang, X.D.; Yang, Q.; He, A.R.; Wang, R.Z. Comprehensive contour prediction model of work roll used in online strip shape control model during hot rolling. Ironmak. Steelmak. 2023, 34, 303–311. [Google Scholar] [CrossRef]
- Zeng, S.W.; Li, J.G. Practical analysis of convexity control of hot rolled plate. Steel Roll. 2011, 28, 8–11. [Google Scholar]
- Liu, J.Y. Roll wear in rolling process and its effect on product properties. J. Metall. Mater. 2024, 44, 121–123. [Google Scholar]
- Zhang, C.L.; Wang, Q.N.; Zhu, H.M.; Wang, F.Q. Optimization of wear prediction model for 1580mm hot rolling mill rolls. Steel Roll. 2016, 33, 27–30. [Google Scholar]
- Wu, H.M.; Wu, B.S.; Zhao, L.X.; Liu, Z.M.; Wang, L.L.; Hao, W.; Pang, Z.F. Mathematical modeling of roll wear in strip mills. J. Steel Roll. 2010, 27, 13–17. [Google Scholar]
- Li, L.X.; Huang, Y.G.; Zhang, K.; Lv, X.Y.; Li, B.; Wu, X.D. Morphological image characteristics and fractals during roll wear. J. Iron Steel 2015, 50, 95–100. [Google Scholar]
- Zhang, Q.D.; Zhang, B.Y.; Li, R.; Ma, L. Research progress on the theory and technology of microscopic surface quality control of steel plates. J. Mech. Eng. 2016, 52, 32–45. [Google Scholar] [CrossRef]
- Liu, X.Q.; Lu, C.; Sun, T.L.; Chen, X.T. Analysis of the Evolution Law of Friction Block Wear Behavior of Train Brake Pads under Multiple Braking Conditions. J. Tribol. 2025, 1–20. [Google Scholar]
- Peng, W.; Sun, J.N.; Li, X.D.; Gong, D.Y.; Sun, Y.Z.; Sun, J.; Zhang, D.H. Wear prediction of work rolls in hot strip rolling process. J. Plast. Eng. 2023, 30, 214–225. [Google Scholar]
- Song, G.Y.; Yang, Q.; Wang, X.C.; Zhang, X.B.; Wang, F.M.; Wang, Q.N. Wear pattern of work rolls in hot strip mill leveler. J. Steel 2017, 52, 54–59. [Google Scholar]
- Pesin, A.; Pustovoytov, D.; Shveyova, T.; Sverdlik, M. Finite Element Modeling of Roll Wear during Cold Asymmetric Sheet Rolling of Aluminum Alloy 5083. J. MATEC Web Conf. 2015, 26, 01010. [Google Scholar] [CrossRef]
- Liu, G.F.; Cui, X.Y.; Li, Z.Z.; Wang, J.H.; Zhang, X.D.; Bai, Z.H. Shape change simulation analysis of wheel steel in a four-high hot rolling mill. Int. J. Simul. Model. 2022, 21, 603–614. [Google Scholar] [CrossRef]
- Li, L.J.; Xie, H.B.; Liu, T.W.; Huo, M.S.; Li, X.S.; Liu, X.; Wang, E.R.; Li, J.X.; Liu, H.Q.; Sun, L.; et al. Numerical analysis of the strip crown inheritance in tandem cold rolling by a novel 3D multi-stand FE model. Int. J. Adv. Manuf. Technol. 2022, 120, 3683–3704. [Google Scholar] [CrossRef]
- Cui, X.Y.; Li, Z.Z.; Yin, B.L.; Wang, W.Q.; Liu, Y.X.; Bai, Z.H. Modelling analysis of coupling deformation between strip steel and roller system. Int. J. Simul. Model. 2023, 22, 267–278. [Google Scholar] [CrossRef]
- Li, L.J.; Xie, H.B.; Zhang, T.; Huo, M.S.; Pan, D.; Wu, H.; Chen, F.H.; Liu, T.W.; Li, X.S.; Liu, X.; et al. Understanding the regulation ability of roll bending on strip shape in a CVC-6 tandem cold mill using a 3D multiple stand FE model. J. Manuf. Process. 2023, 101, 1013–1031. [Google Scholar] [CrossRef]
- Wang, D.G.; Zhang, J. Prediction of Fretting Fatigue Crack Propagation Life of Steel Wire Considering Fretting Wear. Tribology 2021, 41, 710–722. [Google Scholar]
- Wu, W.C.; Liu, S.H.; Chen, T. Research on the Friction and Wear Law of Continuous Pipe and Casing. J. Plast. Eng. 2024, 31, 240–249. [Google Scholar]
- Hu, Z. Study on Assessment of Fretting Damage and Fatigue Life of Mine Hoisting Wire Rope. Ph.D. Thesis, China University of Mining and Technology, Xuzhou, China, 2024. [Google Scholar]
- Chen, L.S.; Zhu, H.Y.; Ren, J. Hot Rolled Sheet Production Technology; Metallurgical Industry Press: Beijing, China, 2006; pp. 30–100. [Google Scholar]
- Lou, L. Research on the Thermal Crown and Wear for Work Roll of Medium and Heavy Plate Mill. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2013. [Google Scholar]
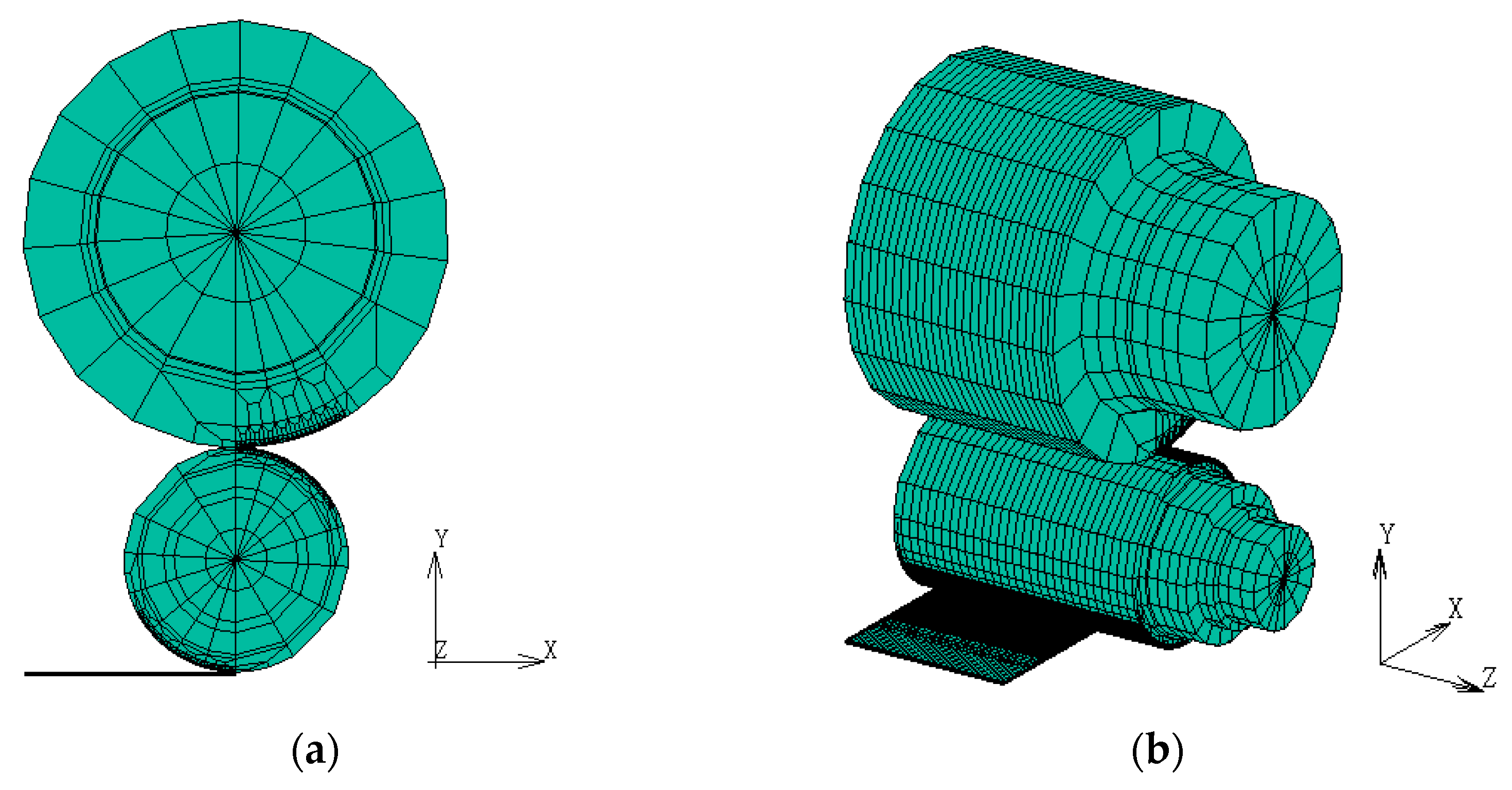
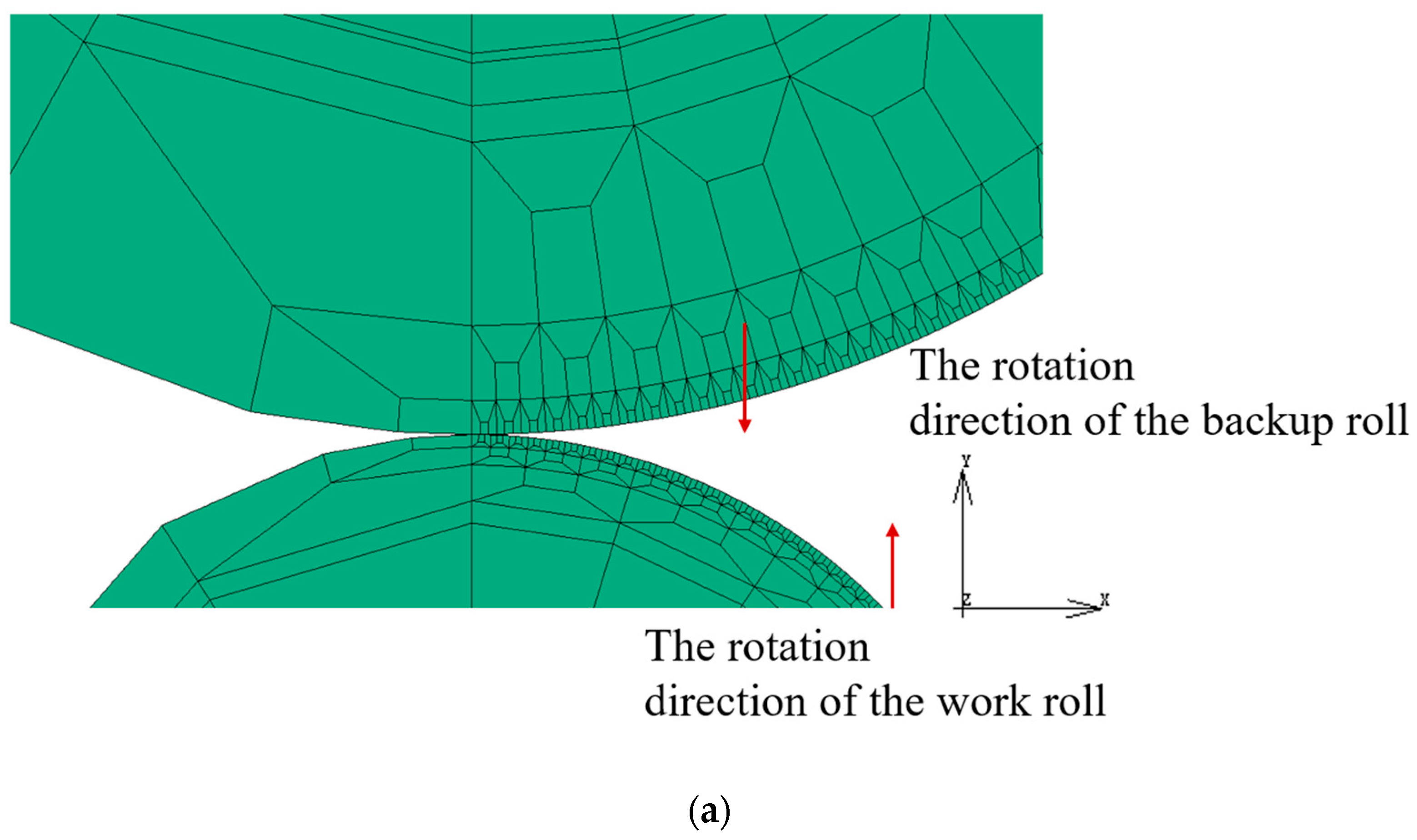

| Parameter Name | Value | Parameter Name | Value |
|---|---|---|---|
| Backup roll diameter/mm | Ø1520 | Backup roll length/mm | 2050 |
| Work roll diameter/mm | Ø800 | Work roll length/mm | 2350 |
| Strip entrance thickness/mm | 28 | Strip entrance width/mm | 1556 |
| Type | Material | Young Modulus Pa | Poisson Ratio | Yield Strength MPa |
|---|---|---|---|---|
| Roll | Elastic | 2.06 × 1011 | 0.3 | - |
| Products | Elastoplastic | 2.10 × 1011 | 0.3 | 189.6 |
| Strip Entrance Thickness/mm | Strip Entrance Width/mm | Strip Temperature/°C | Roll Bending Force/t | Front Tension/kg/mm2 | Rear Tension/kg/mm2 |
|---|---|---|---|---|---|
| 28 | 1556 | 905 | 50 | 20 | 18 |
| Wear Amount Value Group | Value Before Optimization | Finite Element Simulation Numerical Values | Dynamic Simulation Software Values |
|---|---|---|---|
| Deviation (Work roll) | 0.065 | 0.019 | 0.012 |
| Deviation (Backup roll) | 0.005 | 0.007 | 0.004 |
| Steel Grade | Stand | Strip Entrance Thickness/mm | Strip Entrance Width/mm | Strip Temperature/°C | Roll Bending Force/t | Front Tension/kg/mm2 | Rear Tension/kg/mm2 | Average Deviation/mm | |
|---|---|---|---|---|---|---|---|---|---|
| Test1 | Beam Steel 510L | 3 | 10.71 | 1276 | 978 | 0 | 6.15 | 7.43 | 0.008 |
| Test2 | Beam Steel 700L | 4 | 11.55 | 1533 | 982 | 800 | 0 | 0 | 0.0094 |
| Test3 | Wheel Steel 255PL | 5 | 18.16 | 1555 | 893 | 500 | 5.08 | 6.12 | 0.0064 |
| Test4 | Wheel Steel 380CL | 6 | 10.3 | 1612 | 880 | 650 | 6.1 | 6.99 | 0.0077 |
| Test5 | Wheel Steel 380CL | 1 | 30.22 | 1615 | 980 | 800 | / | 4.83 | 0.0051 |
| Test6 | Wheel Steel 380CL | 2 | 21.84 | 1614 | 959 | 800 | 4.83 | 4.91 | 0.0062 |
| Test7 | Wheel Steel 255PL | 2 | 28.01 | 1556 | 917 | 500 | 4.80 | 4.85 | 0.0071 |
| Test8 | Wheel Steel 255PL | 3 | 22.13 | 1555 | 905 | 500 | 4.85 | 4.91 | 0.0025 |
| Test9 | Beam Steel 700L | 6 | 3.90 | 1272 | 923 | 650 | 0 | 0 | 0.0038 |
| Test10 | Beam Steel 510L | 6 | 4.18 | 1272 | 912 | 0 | 9.23 | 10.69 | 0.0067 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Li, Z.; Zhang, B.; Wang, J.; Elmi, S.A.; Bai, Z. Optimization and Finite Element Simulation of Wear Prediction Model for Hot Rolling Rolls. Metals 2025, 15, 456. https://doi.org/10.3390/met15040456
Zhang X, Li Z, Zhang B, Wang J, Elmi SA, Bai Z. Optimization and Finite Element Simulation of Wear Prediction Model for Hot Rolling Rolls. Metals. 2025; 15(4):456. https://doi.org/10.3390/met15040456
Chicago/Turabian StyleZhang, Xiaodong, Zizheng Li, Boda Zhang, Jiayin Wang, Sahal Ahmed Elmi, and Zhenhua Bai. 2025. "Optimization and Finite Element Simulation of Wear Prediction Model for Hot Rolling Rolls" Metals 15, no. 4: 456. https://doi.org/10.3390/met15040456
APA StyleZhang, X., Li, Z., Zhang, B., Wang, J., Elmi, S. A., & Bai, Z. (2025). Optimization and Finite Element Simulation of Wear Prediction Model for Hot Rolling Rolls. Metals, 15(4), 456. https://doi.org/10.3390/met15040456






