Effect of Phase Structure on the Properties of Additively Manufactured NiTi Alloy Based on Molecular Dynamics Simulation
Abstract
1. Introduction
2. Experimental Materials and Methods
2.1. Test Equipment
2.2. Modeling and Methods
3. Results and Analysis
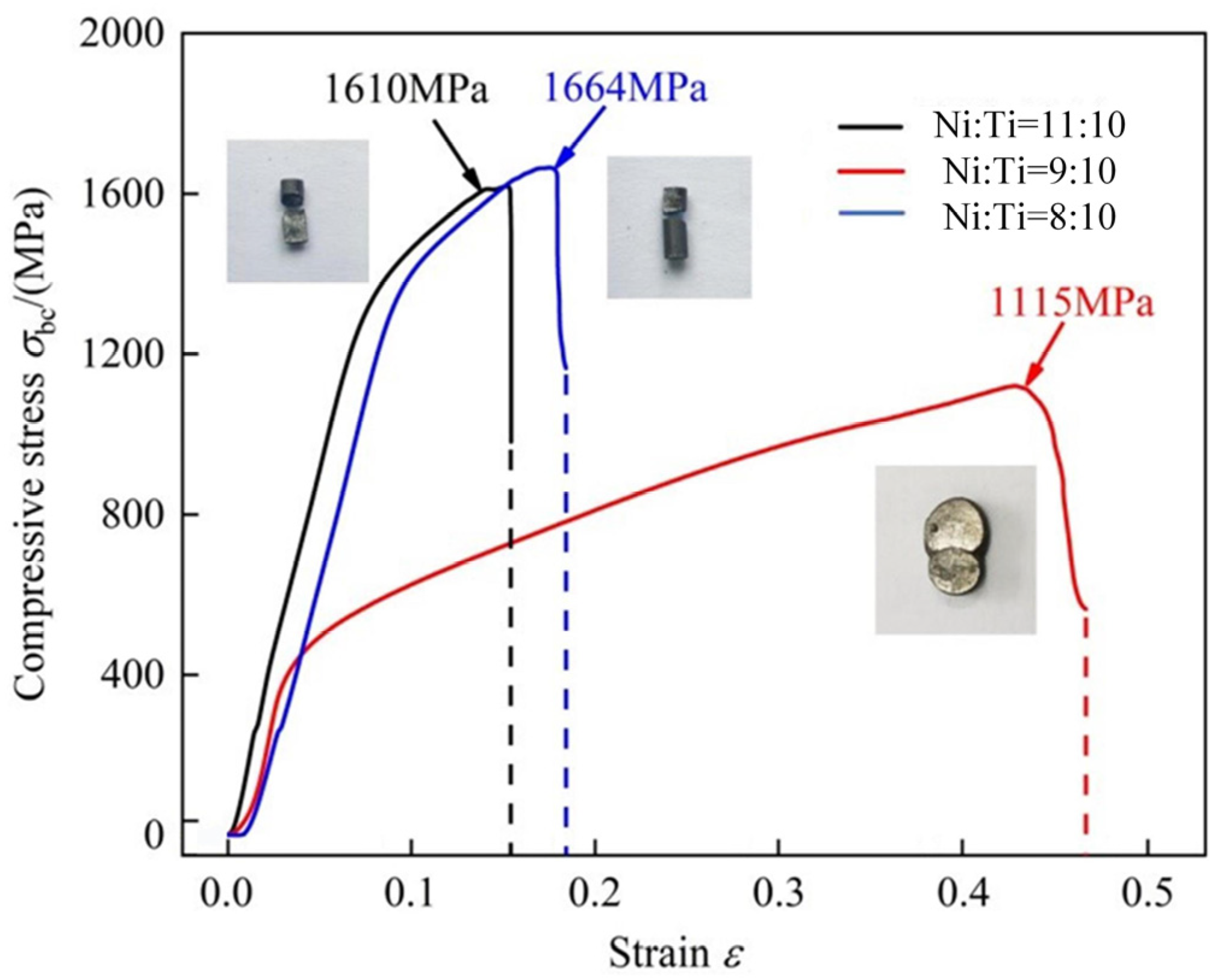
3.1. Test Results
3.2. Simulation Results
4. Discussion
5. Conclusions
- (1)
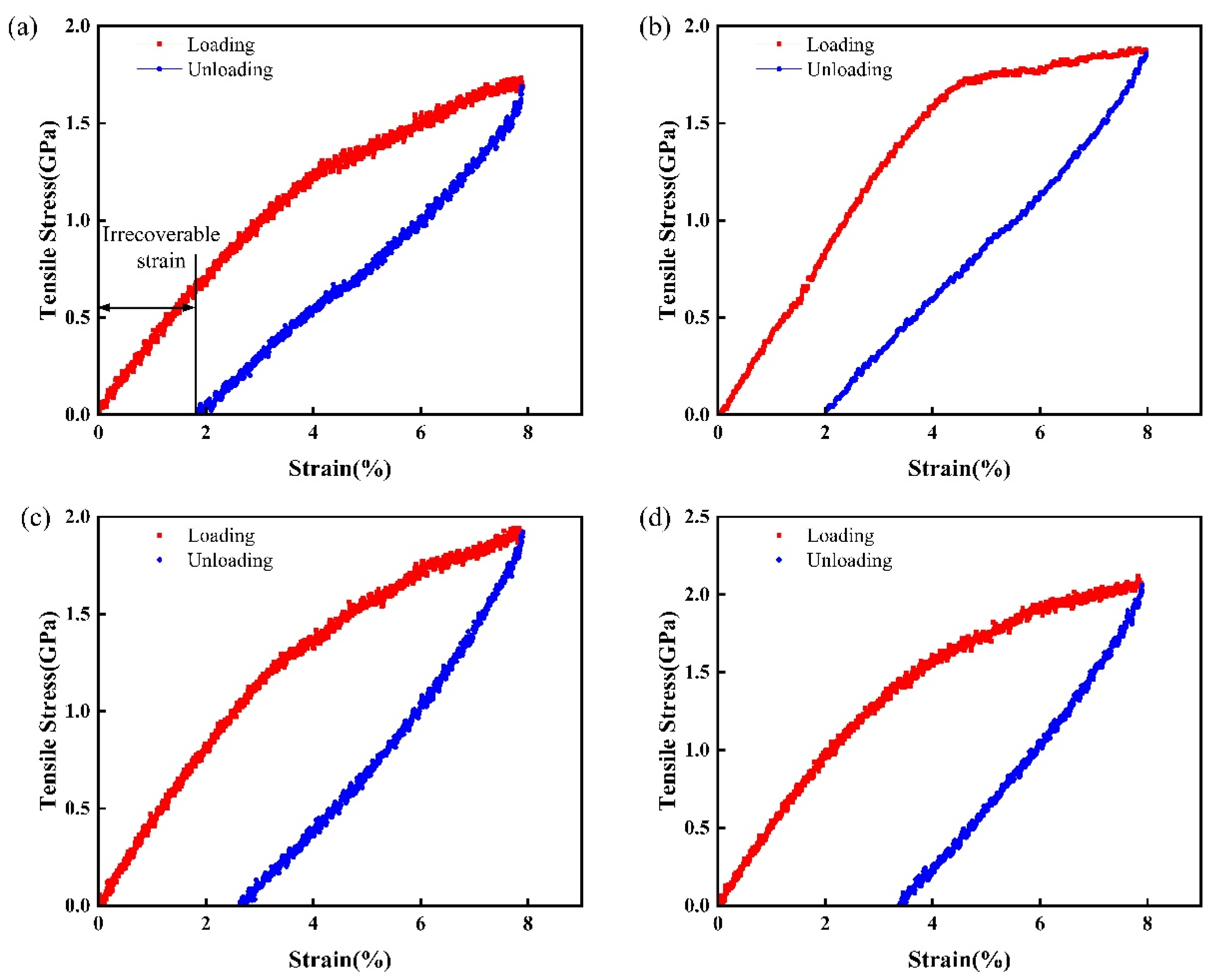
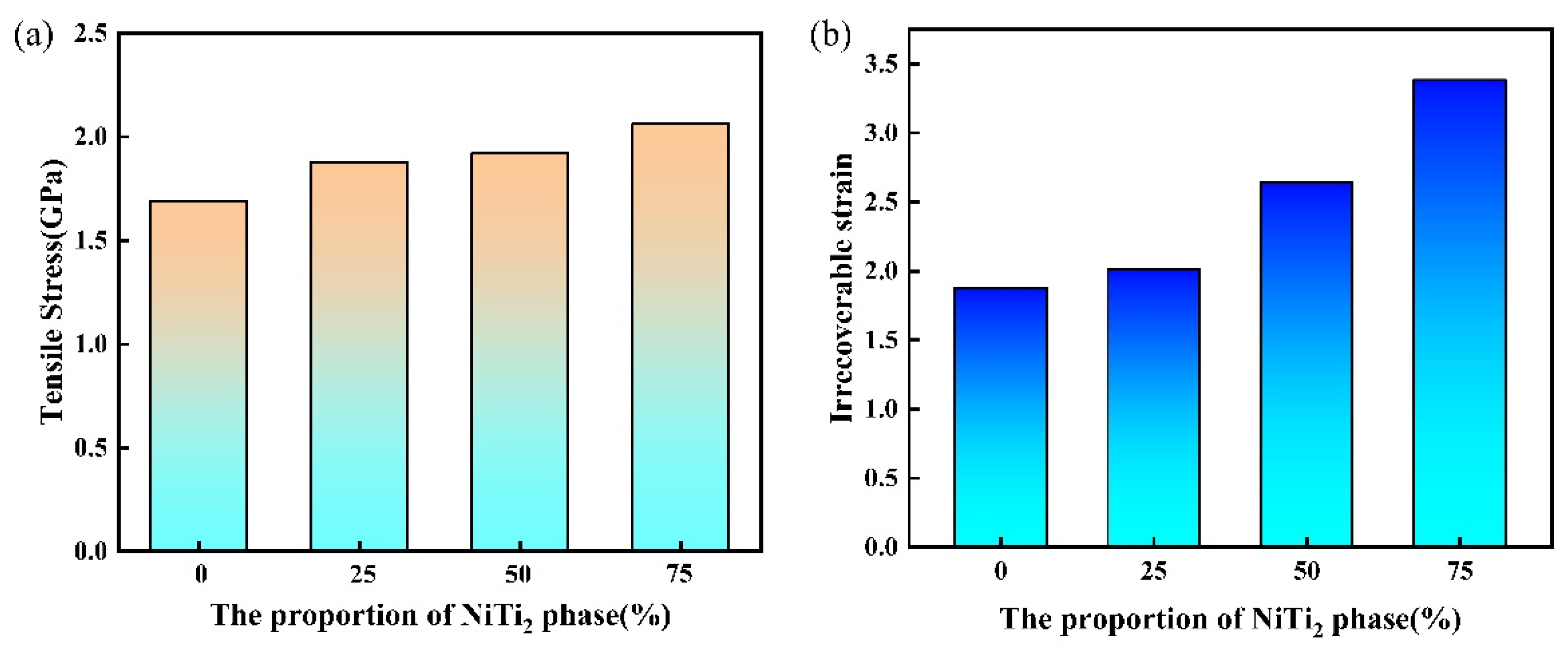
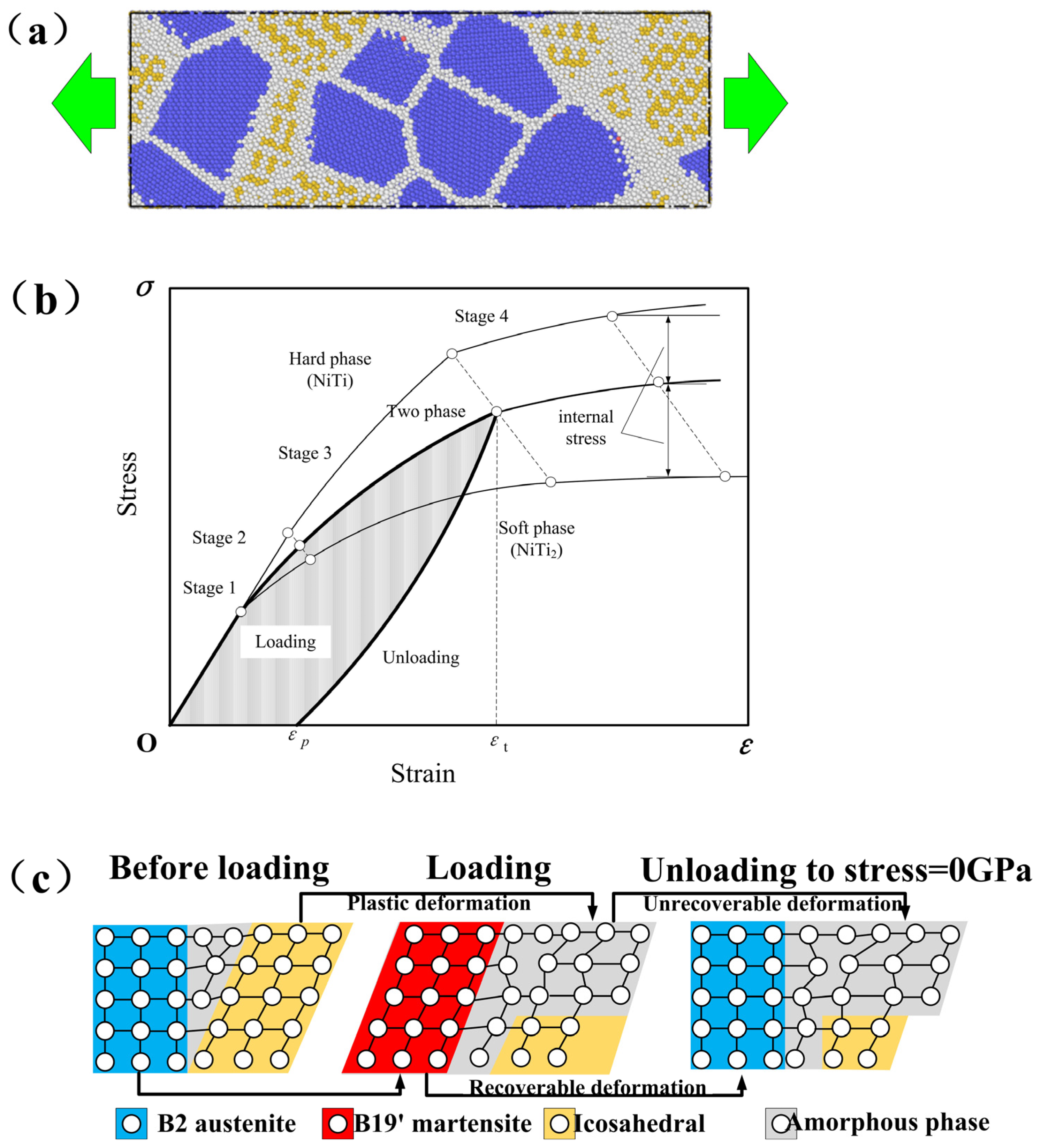
- Upon unloading external stress to zero, irrecoverable strain occurs in all models. The NiTi2 model exhibits the highest irrecoverable deformation, which increases as the proportion of the NiTi2 phase in the alloy model rises.
- (2)
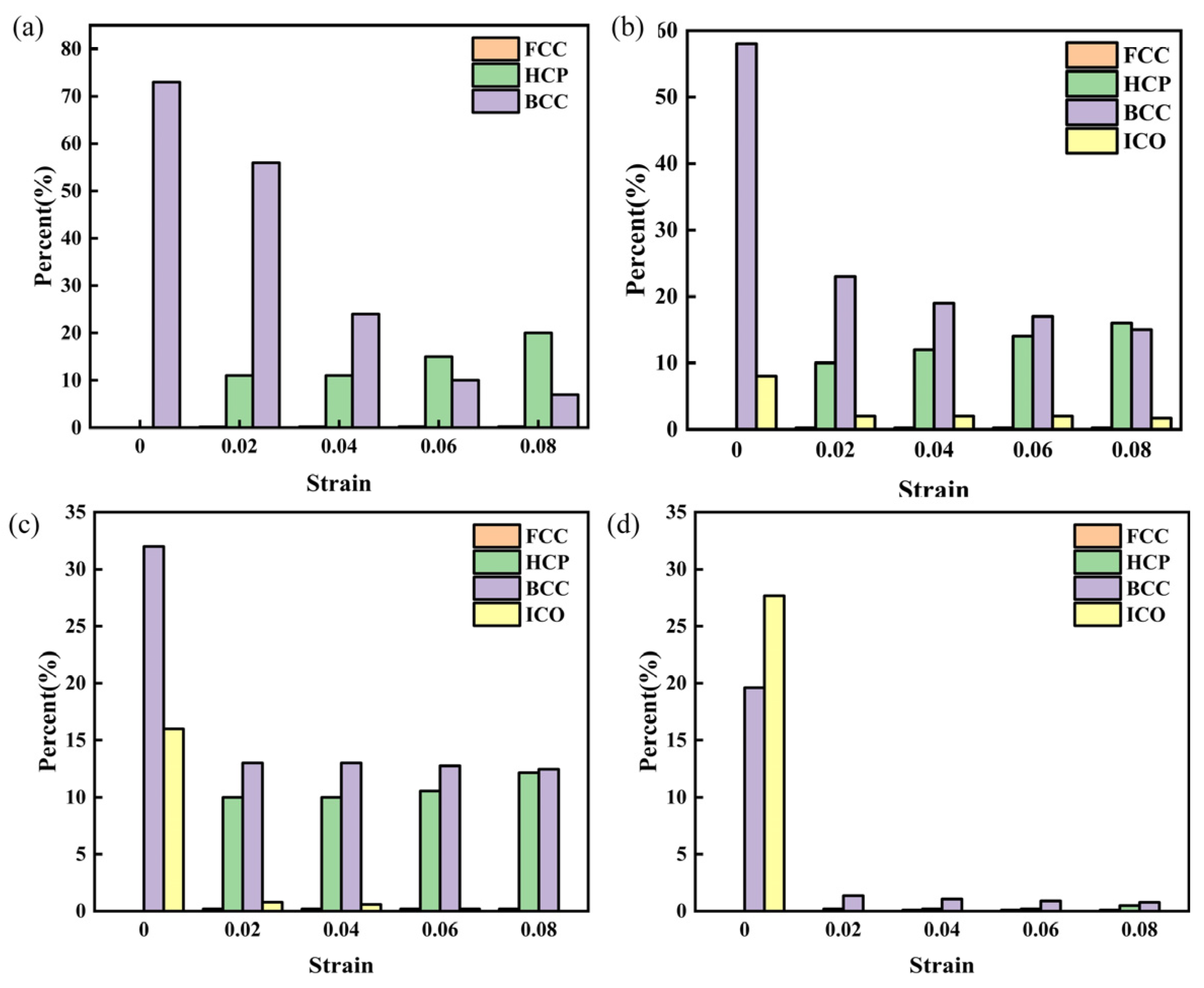
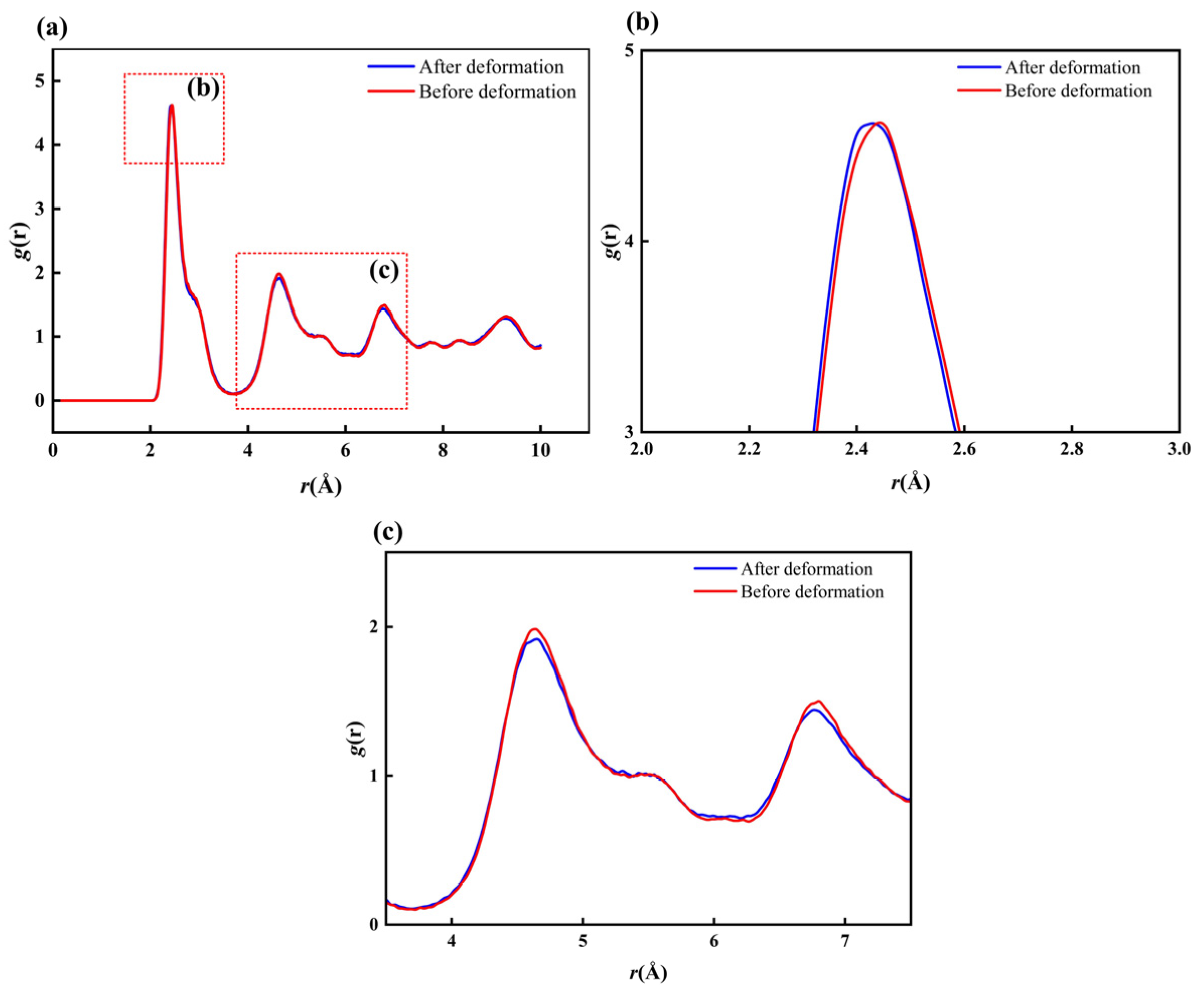
- The transformation from the NiTi2 phase to the amorphous phase plays a significant role in the formation of irrecoverable strain. An applied strain of 8% exceeds the elastic strain limit of NiTi2, leading to plastic deformation in the amorphous phase during the later stages of deformation.
- (3)
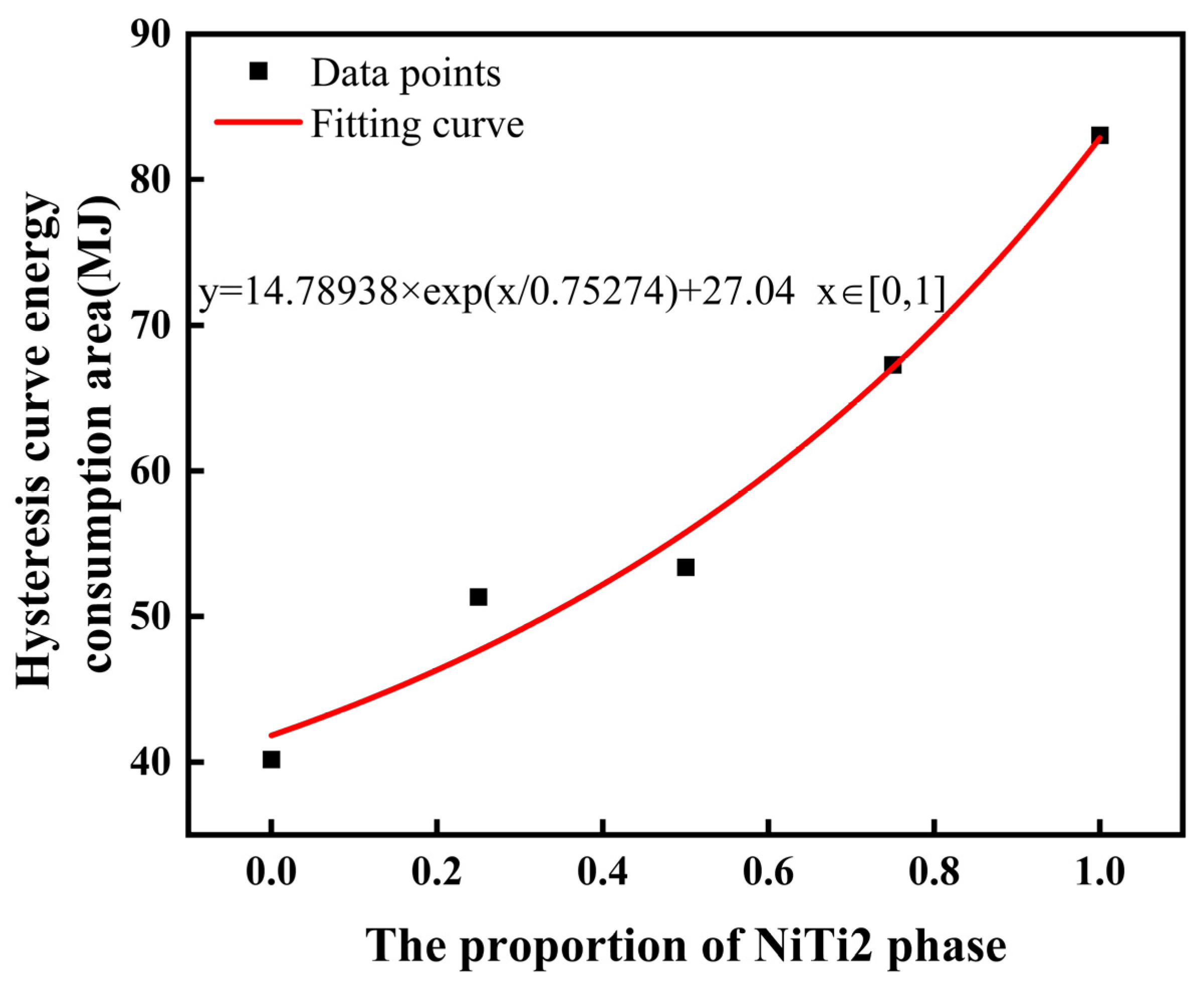
- Analysis of the hysteresis curve during tensile unloading reveals that a higher proportion of the NiTi2 phase results in a larger energy consumption area. Exponential fitting of the energy consumption data indicates that the area increases exponentially with the increasing proportion of the NiTi2 phase.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sevcikova, J.; Pavkova Goldbergova, M. Biocompatibility of NiTi alloys in the cell behaviour. Biometals 2017, 30, 163–169. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Lü, X.; Hong, Y.; Xi, T.; Zhang, D. The molecular mechanism for effects of TiN coating on NiTi alloy on endothelial cell function. Biomaterials 2014, 35, 6195–6205. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Lü, X.; Hong, Y.; Xi, T.; Zhang, D. The molecular mechanism of mediation of adsorbed serum proteins to endothelial cells adhesion and growth on biomaterials. Biomaterials 2013, 34, 5747–5758. [Google Scholar] [CrossRef] [PubMed]
- Naser, M.Z.; Chehab, A.I. Materials and design concepts for space-resilient structures. Prog. Aerosp. Sci. 2018, 98, 74–90. [Google Scholar] [CrossRef]
- Malik, V.; Srivastava, S.; Gupta, S.; Sharma, V.; Vishnoi, M.; Mamatha, T.G. A novel review on shape memory alloy and their applications in extraterrestrial roving missions. Mater. Today Proc. 2021, 44, 4961–4965. [Google Scholar] [CrossRef]
- Shreekrishna, S.; Nachimuthu, R.; Nair, V.S. A review on shape memory alloys and their prominence in automotive technology. J. Intell. Mater. Syst. Struct. 2023, 34, 499–524. [Google Scholar] [CrossRef]
- Riccio, A.; Sellitto, A.; Ameduri, S.; Concilio, A.; Arena, M. Shape memory alloys (SMA) for automotive applications and challenges. In Shape Memory Alloy Engineering; Elsevier: Amsterdam, The Netherlands, 2021; pp. 785–808. [Google Scholar] [CrossRef]
- Chaudhari, R.; Vora, J.J.; Parikh, D.M. A review on applications of nitinol shape memory alloy. In Recent Advances in Mechanical Infrastructure: Proceedings of ICRAM 2020; Springer: Berlin/Heidelberg, Germany, 2021; pp. 123–132. [Google Scholar] [CrossRef]
- Wen, S.; Liu, Y.; Zhou, Y.; Zhao, A.; Yan, C.; Shi, Y. Effect of Ni content on the transformation behavior and mechanical property of NiTi shape memory alloys fabricated by laser powder bed fusion. Opt. Laser Technol. 2021, 134, 106653. [Google Scholar] [CrossRef]
- Elahinia, M.; Moghaddam, N.S.; Andani, M.T.; Amerinatanzi, A.; Bimber, B.A.; Hamilton, R.F. Fabrication of NiTi through additive manufacturing: A review. Prog. Mater. Sci. 2016, 83, 630–663. [Google Scholar] [CrossRef]
- Jani, J.M.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Andani, M.T.; Saedi, S.; Turabi, A.S.; Karamooz, M.R.; Haberland, C.; Karaca, H.E.; Elahinia, M. Mechanical and shape memory properties of porous Ni50. 1Ti49. 9 alloys manufactured by selective laser melting. J. Mech. Behav. Biomed. Mater. 2017, 68, 224–231. [Google Scholar] [CrossRef]
- Zhou, Q.; Hayat, M.D.; Chen, G.; Cai, S.; Qu, X.; Tang, H.; Cao, P. Selective electron beam melting of NiTi: Microstructure, phase transformation and mechanical properties. Mater. Sci. Eng. A 2019, 744, 290–298. [Google Scholar] [CrossRef]
- Luo, M.; Li, R.; Zheng, D.; Kang, J.; Wu, H.; Deng, S.; Niu, P. Formation mechanism of inherent spatial heterogeneity of microstructure and mechanical properties of NiTi SMA prepared by laser directed energy deposition. Int. J. Extrem. Manuf. 2023, 5, 035005. [Google Scholar] [CrossRef]
- Bimber, B.A.; Hamilton, R.F.; Keist, J.; Palmer, T.A. Anisotropic microstructure and superelasticity of additive manufactured NiTi alloy bulk builds using laser directed energy deposition. Mater. Sci. Eng. A 2016, 674, 125–134. [Google Scholar] [CrossRef]
- Mosallanejad, M.H.; Niroumand, B.; Aversa, A.; Saboori, A. In-situ alloying in laser-based additive manufacturing processes: A critical review. J. Alloys Compd. 2021, 872, 159567. [Google Scholar] [CrossRef]
- Amadi, A.; Mohyaldinn, M.; Ridha, S.; Ola, V. Advancing engineering frontiers with NiTi shape memory alloys: A multifaceted review of properties, fabrication, and application potentials. J. Alloys Compd. 2024, 976, 173227. [Google Scholar] [CrossRef]
- Wang, J.; Pan, Z.; Wang, Y.; Wang, L.; Su, L.; Cuiuri, D.; Zhao, Y.; Li, H. Evolution of crystallographic orientation, precipitation, phase transformation and mechanical properties realized by enhancing deposition current for dual-wire arc additive manufactured Ni-rich NiTi alloy. Addit. Manuf. 2020, 34, 101240. [Google Scholar] [CrossRef]
- Zeng, Z.; Cong, B.; Oliveira, J.; Ke, W.; Schell, N.; Peng, B.; Qi, Z.; Ge, F.; Zhang, W.; Ao, S. Wire and arc additive manufacturing of a Ni-rich NiTi shape memory alloy: Microstructure and mechanical properties. Addit. Manuf. 2020, 32, 101051. [Google Scholar] [CrossRef]
- Resnina, N.; Palani, I.; Belyaev, S.; Prabu, S.M.; Liulchak, P.; Karaseva, U.; Manikandan, M.; Jayachandran, S.; Bryukhanova, V.; Sahu, A.; et al. Structure, martensitic transformations and mechanical behaviour of NiTi shape memory alloy produced by wire arc additive manufacturing. J. Alloys Compd. 2021, 851, 156851. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, D.; Wang, P.; Yan, M.; Yang, C.; Chen, Z.; Lu, J.; Lu, Z. Additive manufacturing of metals: Microstructure evolution and multistage control. J. Mater. Sci. Technol. 2022, 100, 224–236. [Google Scholar] [CrossRef]
- Rodrigues, T.A.; Duarte, V.; Avila, J.A.; Santos, T.G.; Miranda, R.; Oliveira, J. Wire and arc additive manufacturing of HSLA steel: Effect of thermal cycles on microstructure and mechanical properties. Addit. Manuf. 2019, 27, 440–450. [Google Scholar] [CrossRef]
- Wang, M.; Jiang, S.; Zhang, Y.; Sun, D.; Yan, B. Molecular dynamics investigation on mechanical behaviour and phase transition of nanocrystalline NiTi shape memory alloy containing amorphous surface. Appl. Surf. Sci. 2022, 587, 152871. [Google Scholar] [CrossRef]
- Li, G.; Yu, T.; Zhang, N.; Chen, M. The effect of Ni content on phase transformation behavior of NiTi alloys: An atomistic modeling study. Comput. Mater. Sci. 2022, 215, 111804. [Google Scholar] [CrossRef]
- Ataollahi, S.; Mahtabi, M.J. Effects of precipitate on the phase transformation of single-crystal NiTi alloy under thermal and mechanical loads: A molecular dynamics study. Mater. Today Commun. 2021, 29, 102859. [Google Scholar] [CrossRef]
- Ehrich, H.J.; Dollmann, A.; Grützmacher, P.G.; Gachot, C.; Eder, S.J. Automated identification and tracking of deformation twin structures in molecular dynamics simulations. Comput. Mater. Sci. 2024, 236, 112878. [Google Scholar] [CrossRef]
- Fadila, N.; Arkundato, A.; Rohman, L.; Syarifah, R.D.; Shafii, M.A. Effect of chromium concentration addition for stabilizing the crystal structure of iron in liquid bismuth. In AIP Conference Proceedings; AIP Publishing: New York, NY, USA, 2023; Volume 2818. [Google Scholar] [CrossRef]
- Chen, X.; Liu, T.; Li, R.; Liu, J.; Zhao, Y. Molecular dynamics simulation on the shape memory effect and superelasticity in NiTi shape memory alloy. Comput. Mater. Sci. 2018, 146, 61–69. [Google Scholar] [CrossRef]
- Plummer, G.; Mendelev, M.I.; Lawson, J.W. Molecular dynamics simulations of austenite-martensite interface migration in NiTi alloy. Phys. Rev. Mater. 2022, 6, 123601. [Google Scholar] [CrossRef]
- Wang, M.; Jiang, S.; Sun, D.; Zhang, Y.; Yan, B. Molecular dynamics simulation of mechanical behavior and phase transformation of nanocrystalline NiTi shape memory alloy with gradient structure. Comput. Mater. Sci. 2022, 204, 111186. [Google Scholar] [CrossRef]
- Chen, J.; Huo, D.; Yeddu, H.K. Molecular dynamics study of phase transformations in NiTi shape memory alloy embedded with precipitates. Mater. Res. Express 2021, 8, 106508. [Google Scholar] [CrossRef]
- Mirzaeifar, R.; Gall, K.; Zhu, T.; Yavari, A.; DesRoches, R. Structural transformations in NiTi shape memory alloy nanowires. J. Appl. Phys. 2014, 115, 194307. [Google Scholar] [CrossRef]
- Ko, W.S.; Maisel, S.B.; Grabowski, B.; Jeon, J.B.; Neugebauer, J. Atomic scale processes of phase transformations in nanocrystalline NiTi shape-memory alloys. Acta Mater. 2017, 123, 90–101. [Google Scholar] [CrossRef]
- Timonova, M.; Thijsse, B.J. Optimizing the MEAM potential for silicon. Model. Simul. Mater. Sci. Eng. 2010, 19, 015003. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, S.; Wang, M. Atomistic investigation on superelasticity of NiTi shape memory alloy with complex microstructures based on molecular dynamics simulation. Int. J. Plast. 2020, 125, 27–51. [Google Scholar] [CrossRef]
- Nargatti, K.; Ahankari, S. Advances in enhancing structural and functional fatigue resistance of superelastic NiTi shape memory alloy: A Review. J. Intell. Mater. Syst. Struct. 2022, 33, 503–531. [Google Scholar] [CrossRef]
- Srinivasan, P.; Nicola, L.; Simone, A. Modeling pseudo-elasticity in NiTi: Why the MEAM potential outperforms the EAM-FS potential. Comput. Mater. Sci. 2017, 134, 145–152. [Google Scholar] [CrossRef]
- Guo, Y.; Zeng, X.; Chen, H.; Han, T.; Tian, H.; Wang, F. Molecular Dynamics Modeling of the Effect of Nanotwins on the Superelasticity of Single-Crystalline NiTi Alloys. Adv. Mater. Sci. Eng. 2017, 2017, 7427039. [Google Scholar] [CrossRef]
- Li, F.; Lannin, J.S. Radial distribution function of amorphous carbon. Phys. Rev. Lett. 1990, 65, 1905. [Google Scholar] [CrossRef]
- Oliveira, J.P.; Miranda, R.M.; Fernandes, F.B. Welding and joining of NiTi shape memory alloys: A review. Prog. Mater. Sci. 2017, 88, 412–466. [Google Scholar] [CrossRef]
- Song, X.; Huang, J.; Yu, X.; Zhang, J.; Xu, J.; Fan, D. Microstructure transformation and mechanical behavior in NiTi alloys fabricated by dissimilar double wires arc additive manufacturing. J. Mater. Res. Technol. 2024, 33, 9603–9613. [Google Scholar] [CrossRef]
- Zhang, D.; Qiu, D.; Gibson, M.A.; Zheng, Y.; Fraser, H.L.; StJohn, D.H.; Easton, M.A. Additive manufacturing of ultrafine-grained high-strength titanium alloys. Nature 2019, 576, 91–95. [Google Scholar] [CrossRef] [PubMed]
- Manh, D.N.; Pasturel, A.; Paxton, A.T.; Van Schilfgaarde, M. Structural stability of NiTi2 intermetallic compounds. J. Phys. Condens. Matter 1993, 5, 9087. [Google Scholar] [CrossRef]
- Mercier, O.; Melton, K.N.; Gremaud, G.; Hägi, J. Single-crystal elastic constants of the equiatomic NiTi alloy near the martensitic transformation. J. Appl. Phys. 1980, 51, 1833–1834. [Google Scholar] [CrossRef]
- Toprek, D.; Belosevic-Cavor, J.; Koteski, V. Ab initio studies of the structural, elastic, electronic and thermal properties of NiTi2 intermetallic. J. Phys. Chem. Solids 2015, 85, 197–205. [Google Scholar] [CrossRef]
- Hatcher, N.; Kontsevoi, O.Y.; Freeman, A.J. Role of elastic and shear stabilities in the martensitic transformation path of NiTi. Phys. Rev. B 2009, 80, 144203. [Google Scholar] [CrossRef]
- Zhong, Y.; Gall, K.; Zhu, T. Atomistic study of nanotwins in NiTi shape memory alloys. J. Appl. Phys. 2011, 110, 033532. [Google Scholar] [CrossRef]
- Sun, Q.; Aslan, A.; Li, M.; Chen, M. Effects of grain size on phase transition behavior of nanocrystalline shape memory alloys. Sci. China Technol. Sci. 2014, 57, 671–679. [Google Scholar] [CrossRef]
- Tian, L.; Cheng, Y.-Q.; Shan, Z.-W.; Li, J.; Wang, C.-C.; Han, X.-D.; Sun, J.; Ma, E. Approaching the ideal elastic limit of metallic glasses. Nat. Commun. 2012, 3, 609. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Qi, L.; Wang, L.; Pan, S.; Ma, M.; Zhang, X.; Li, G.; Liu, R. Atomic structure of shear bands in Cu64Zr36 metallic glasses studied by molecular dynamics simulations. Acta Mater. 2015, 95, 236–243. [Google Scholar] [CrossRef]
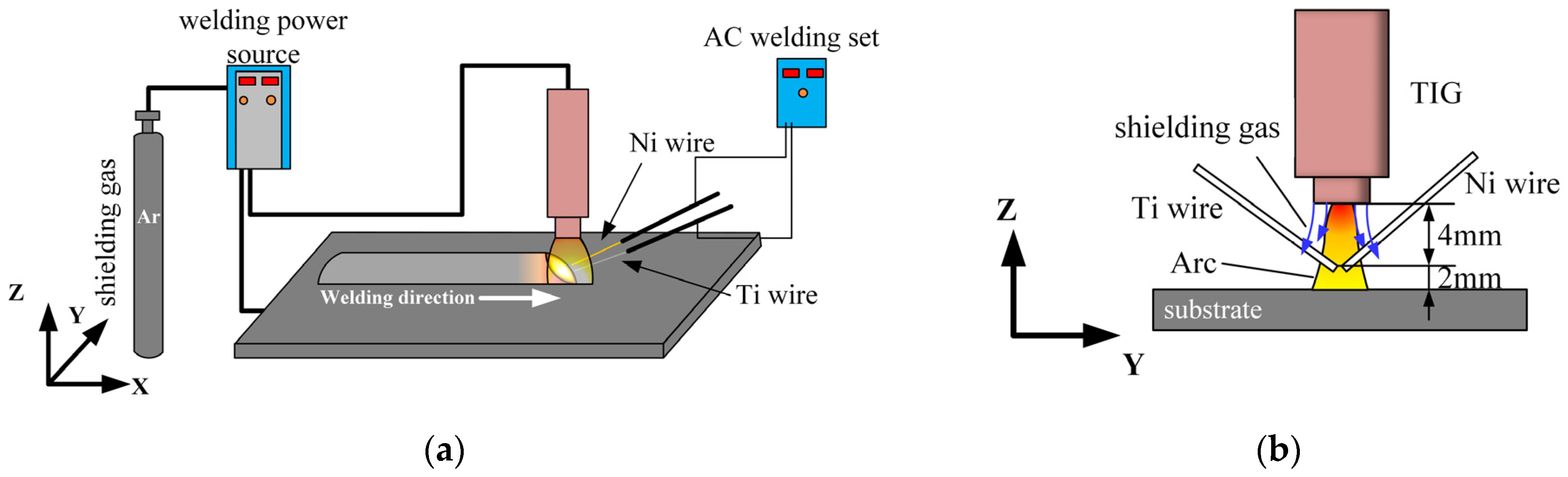
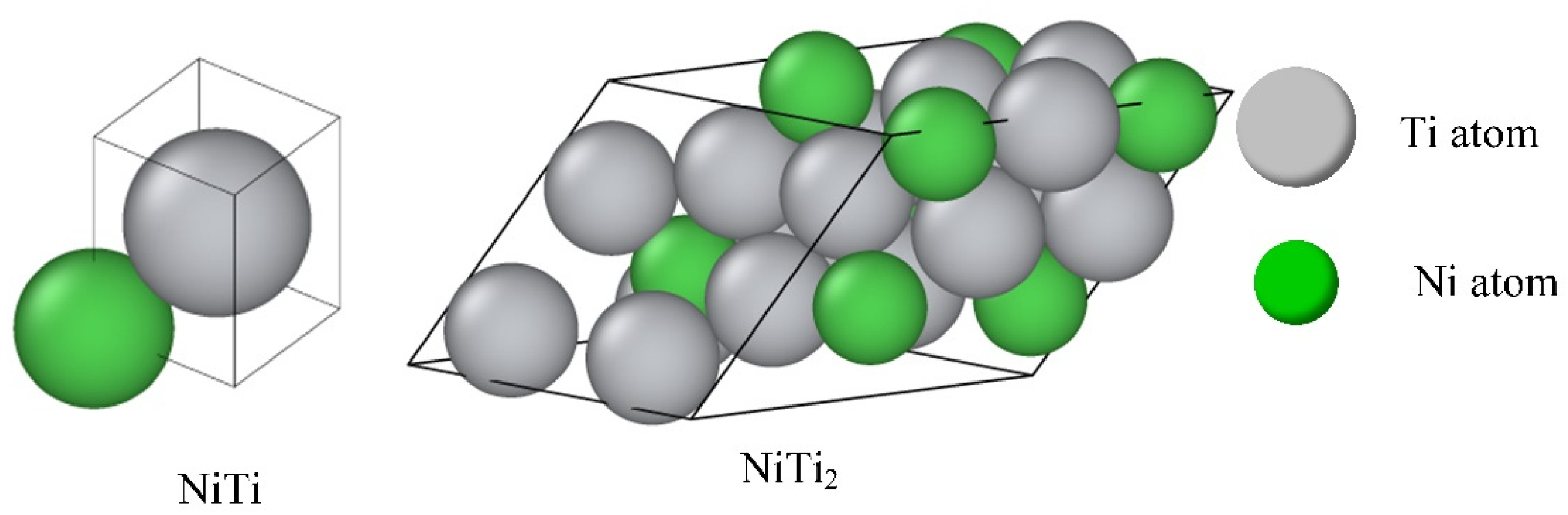

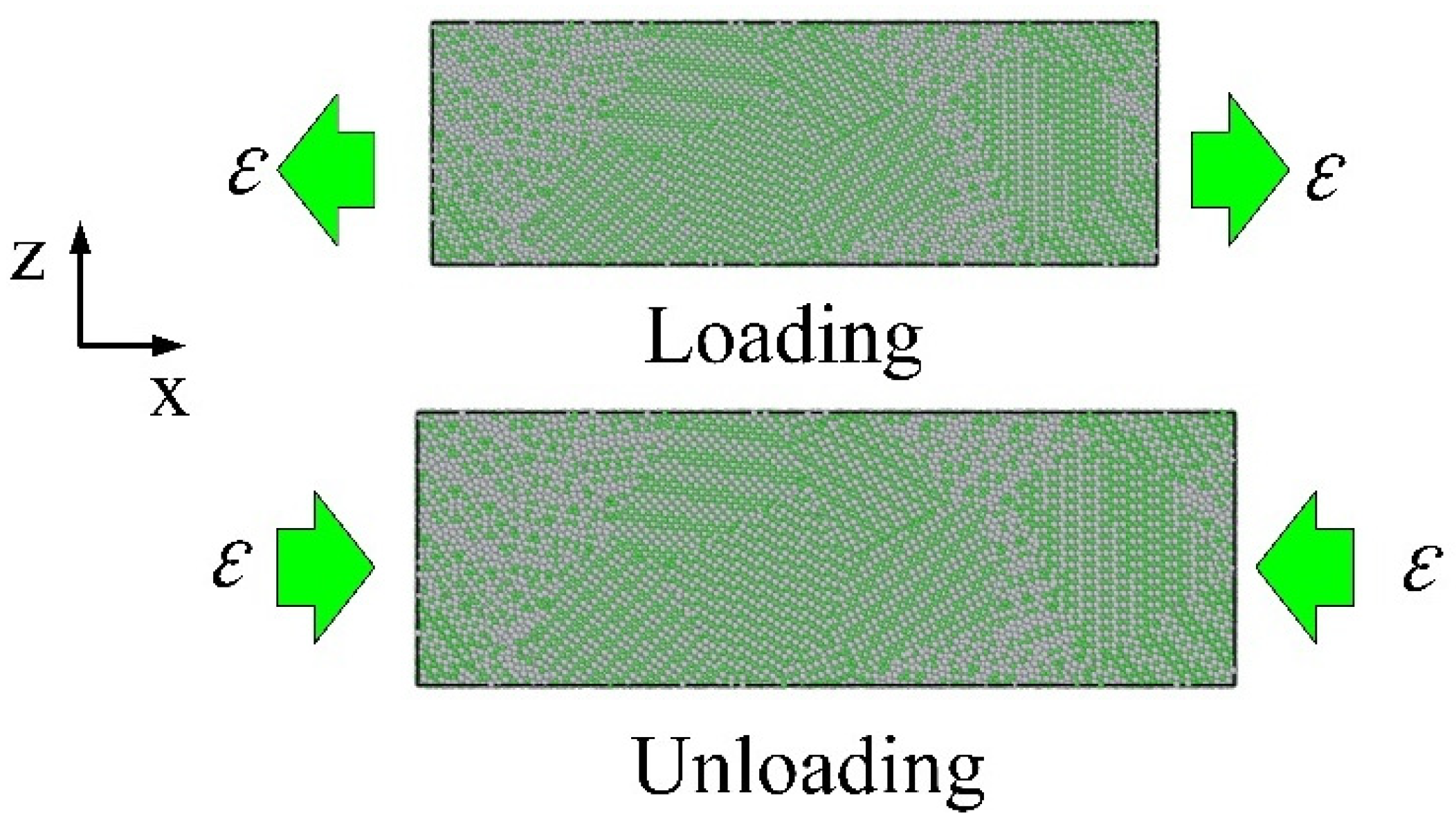







| Material | Mg | Al | V | Fe | Cu | Si | C | N | O | Ni | Ti |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ni wires | 0.01 | - | - | 0.015 | 0.005 | - | 0.093 | - | - | Bal. | - |
| Ti wires | - | - | - | 0.25 | - | 0.01 | 0.10 | 0.03 | 0.15 | - | Bal. |
| Substrate | - | 6.10 | 4.0 | 0.30 | - | - | 0.08 | 0.03 | 0.20 | - | Bal. |
| Parameters | Value |
|---|---|
| TIG arc current (A) | 110 |
| Movement speed (mm/min) | 80 |
| Shielding gas flow (L/min) | 15 |
| AC current size (A) | 40 |
| AC frequency (Hz) | 20 |
| Ti Atomic (%) | Ni Atomic (%) | ||
|---|---|---|---|
| Ni:Ti = 8:10 | #1 | 68.57 | 31.43 |
| #2 | 98.97 | 1.03 | |
| Ni:Ti = 9:10 | #1 | 53.47 | 46.53 |
| #2 | 63.29 | 36.41 | |
| Ni:Ti = 11:10 | #1 | 47.84 | 52.16 |
| #2 | 61.72 | 38.28 |
| Stress (MPa) | Strain | ||
|---|---|---|---|
| Ni:Ti = 8:10 | 1 | 1664 | 0.19 |
| 2 | 1500 | 0.15 | |
| 3 | 1550 | 0.12 | |
| Ni:Ti = 9:10 | 1 | 1080 | 0.41 |
| 2 | 1115 | 0.47 | |
| 3 | 1108 | 0.38 | |
| Ni:Ti = 11:10 | 1 | 1450 | 0.12 |
| 2 | 1400 | 0.09 | |
| 3 | 1610 | 0.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, T.; Huang, J.; Zhao, H.; Xiang, R.; Song, X.; Fan, D. Effect of Phase Structure on the Properties of Additively Manufactured NiTi Alloy Based on Molecular Dynamics Simulation. Metals 2025, 15, 411. https://doi.org/10.3390/met15040411
Zhao T, Huang J, Zhao H, Xiang R, Song X, Fan D. Effect of Phase Structure on the Properties of Additively Manufactured NiTi Alloy Based on Molecular Dynamics Simulation. Metals. 2025; 15(4):411. https://doi.org/10.3390/met15040411
Chicago/Turabian StyleZhao, Tianxiang, Jiankang Huang, Huayu Zhao, Rui Xiang, Xueping Song, and Ding Fan. 2025. "Effect of Phase Structure on the Properties of Additively Manufactured NiTi Alloy Based on Molecular Dynamics Simulation" Metals 15, no. 4: 411. https://doi.org/10.3390/met15040411
APA StyleZhao, T., Huang, J., Zhao, H., Xiang, R., Song, X., & Fan, D. (2025). Effect of Phase Structure on the Properties of Additively Manufactured NiTi Alloy Based on Molecular Dynamics Simulation. Metals, 15(4), 411. https://doi.org/10.3390/met15040411







