Upset Resistance Welding of a Microcomposite Cu-Nb Conductor for Pulsed Power Applications
Abstract
1. Introduction
2. The Peculiarities of Resistance Welding for Copper and Copper-Based Materials
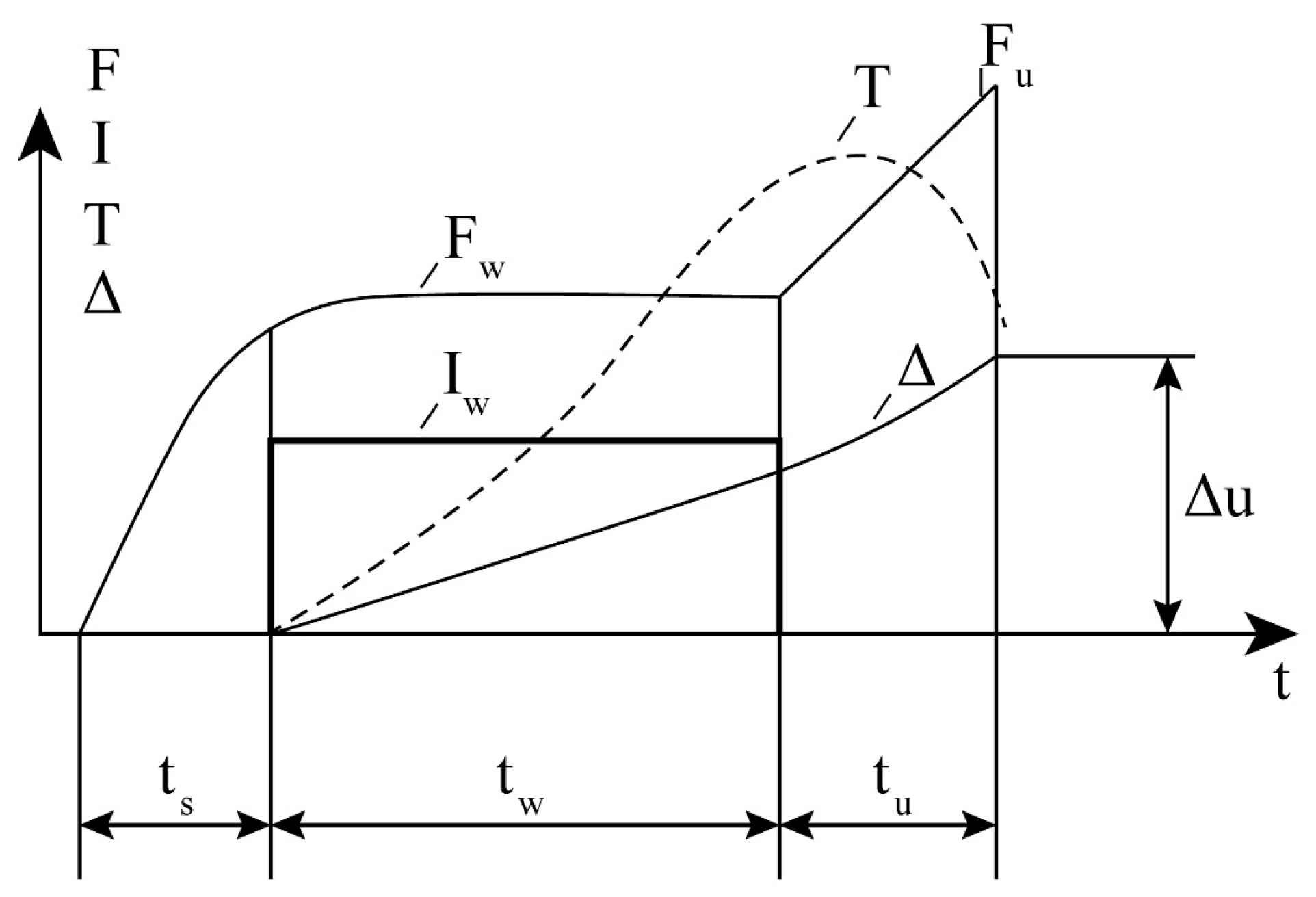
3. Calculation and Selection of Welding Parameters
4. Results of Calculating Upset Welding Parameters
5. Materials, Welding Equipment, Welding Procedures, and Joint Testing Methodology
| Specifications | CEA SQ/A121 |
|---|---|
| Welding wire diameter (Cu), mm | 1.5–20 |
| Supply voltage (AC industrial frequency 50 Hz), V | 380 |
| Number of phases used, pcs. | 3 |
| Maximum current of the secondary circuit, A | 30,000 ± 10% |
| Voltage of the secondary circuit of the welding transformer, V | Up to 5.1 |
| Secondary circuit voltage regulation | Electronic |
| Maximum power at short circuit, kW | 122 |
| Power at (Duty cycle = 50%), kW | 25 |
| Maximum welding force, N | 3500 |
| Maximum upsetting force, N | 9000 |
| Maximum base length, mm | 25 |
| Duration of heating (welding), s | 0.02–2 |
| Upset allowance, mm | Up to 5 |
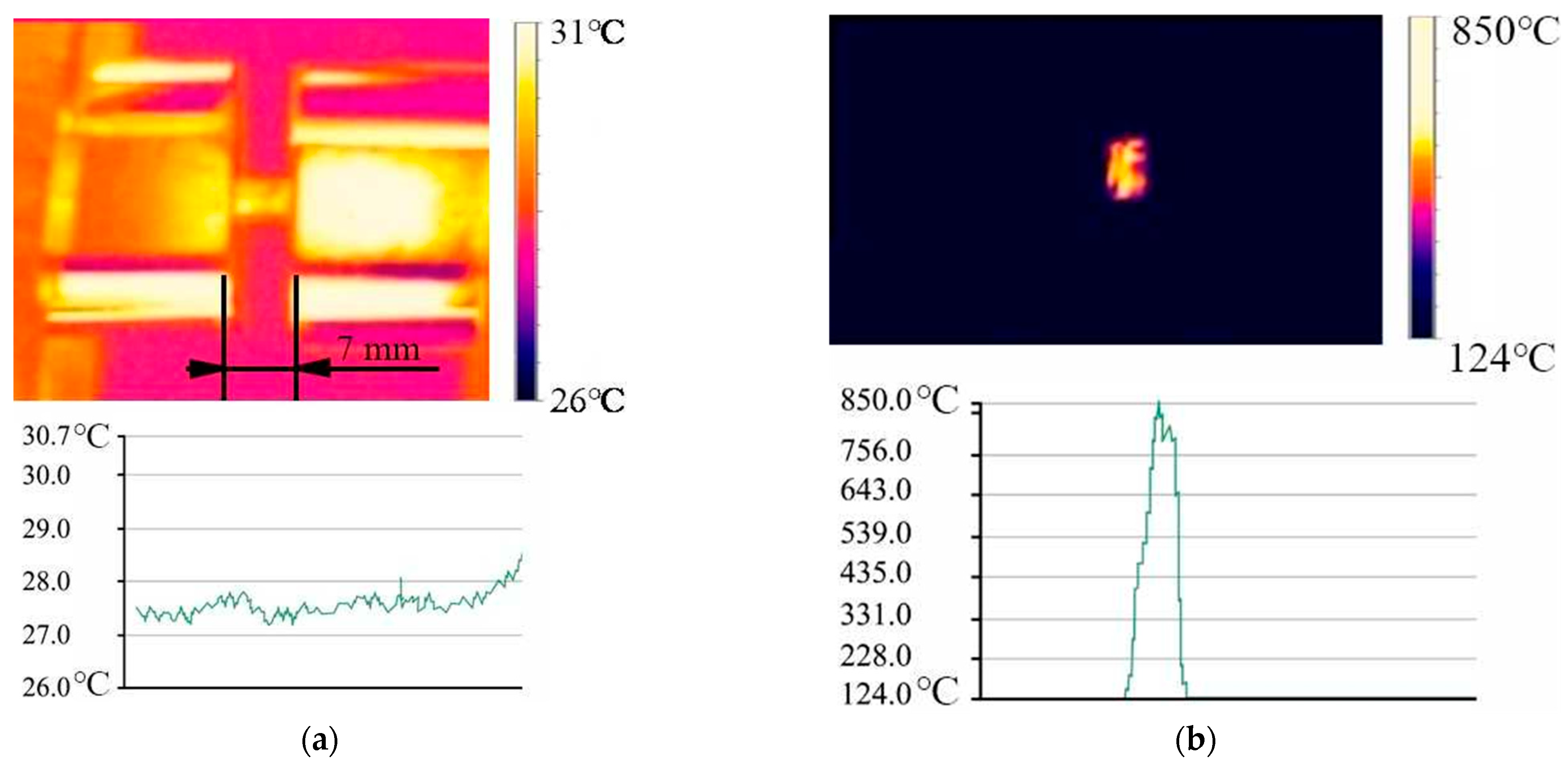
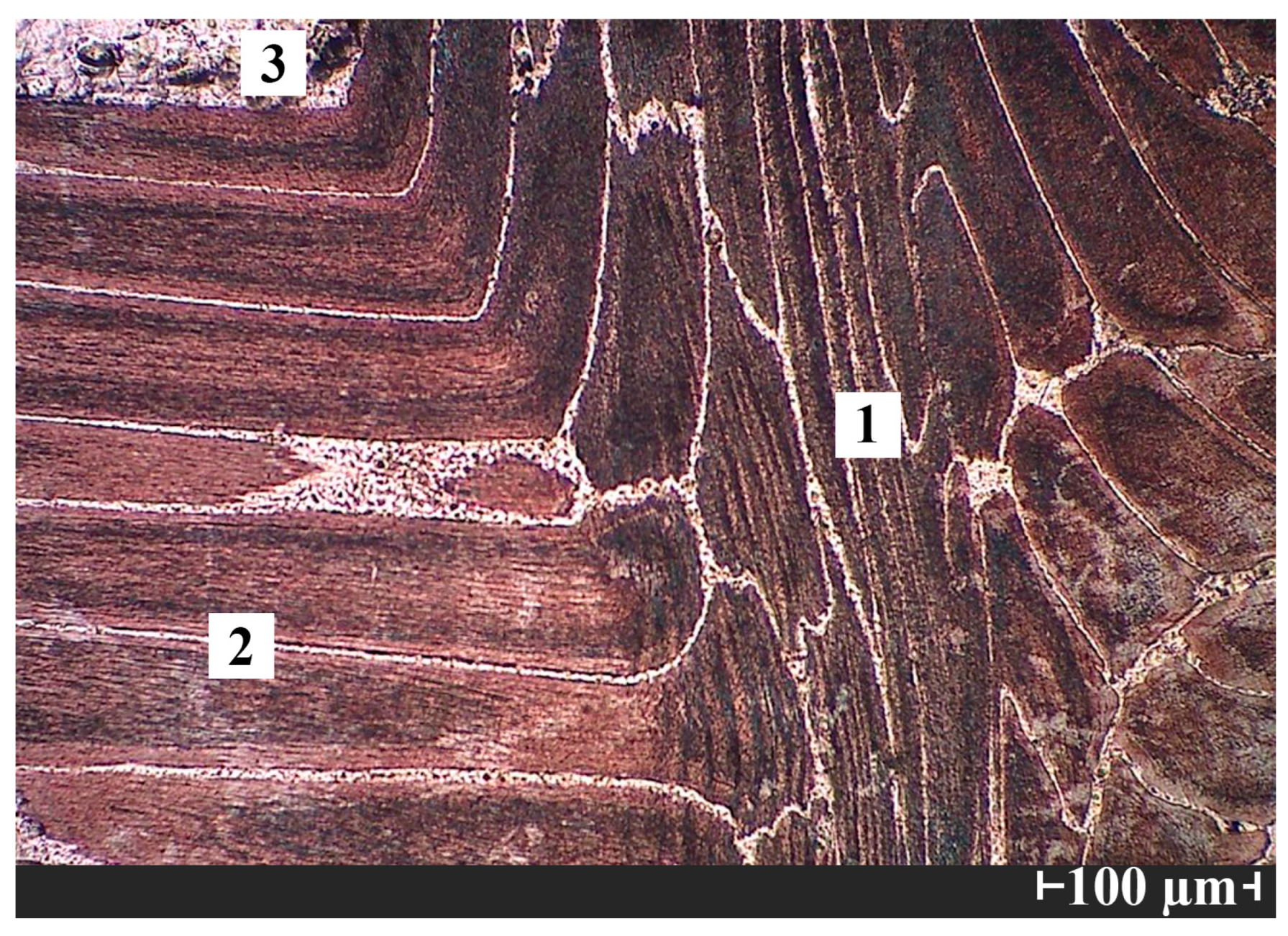
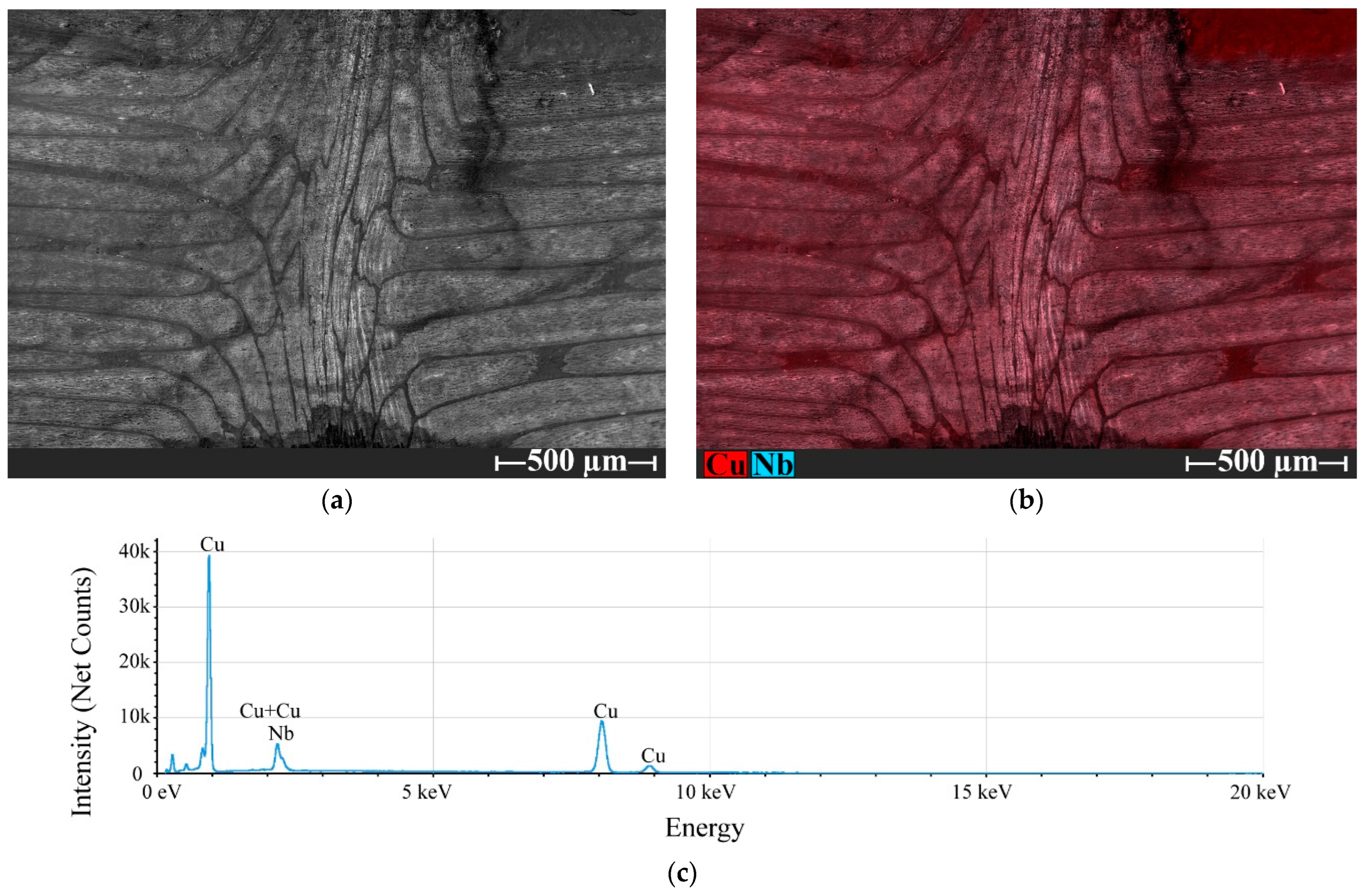
6. Experimental Results and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TW | Thermite welding |
| LW | Laser welding |
| EBW | Electron beam welding |
| ERW | Electric resistance welding |
References
- Shikov, A.K.; Pantsyrnyi, V.I.; Vorob’Eva, A.E.; Sud’Ev, S.V.; Khlebova, N.E.; Silaev, A.K.; Belyakov, N.A. Copper-Niobium High Strength and High Conductivity Winding Wires for Pulsed Magnets. Mater. Sci. Heat Treat. 2002, 44, 491–495. [Google Scholar]
- Głuchowski, W.; Rdzawski, Z.; Stobrawa, J.P.; Marszowski, K.J. Microstructure and Properties of Cu-Nb Wire Composites. Arch. Metall. Mater. 2014, 59, 35–40. [Google Scholar] [CrossRef]
- Višniakov, N.; Mikalauskas, G.; Černašėjus, O.; Škamat, J. Laser Welding of Copper-Niobium Microcomposite Wires for Pulsed Power Applications. Mater. Sci. Eng. Technol. 2019, 50, 646–662. [Google Scholar] [CrossRef]
- Višniakov, N.; Mikalauskas, G.; Černašėjienė, R.; Škamat, J.; Černašėjus, O.; Novickij, V. Feasibility Evaluation of Cu-Nb Microcomposite Joints Formed by Magnetic Field Pressing for Pulsed Power Applications. Teh. Vjesn. 2018, 25 (Suppl. S2), 326–329. [Google Scholar] [CrossRef]
- Višniakov, N.; Mikalauskas, G.; Černašėjienė, R.; Černašėjus, O.; Škamat, J. Electron beam welding of copper-niobium microcomposites for pulsed power applications. Mater. Sci. Eng. Technol. 2018, 49, 538–550. [Google Scholar] [CrossRef]
- Višniakov, N.; Mikalauskas, G.; Škamat, J.; Černašėjienė, R.; Černašėjus, O.; Rudzinskas, V.; Boris, R. Thermite welding of Cu–Nb microcomposite wires. Int. J. Mater. Res. 2017, 108, 832–839. [Google Scholar] [CrossRef]
- Mikalauskas, G. Investigation of Welded Joints and Weldability of Microcomposite Copper-Niobium Conductors for the Application in High Magnetic Field Systems. Ph.D. Dissertation, Vilnius Gediminas Technical University, Vilnius, Lithuania, 2020; p. 122. (In Lithuanian). Available online: http://dspace.vgtu.lt/handle/1/3838 (accessed on 11 February 2025).
- Višniakov, N.; Novickij, J.; Ščekaturovienė, D.; Petrauskas, A. Quality Analysis of Welded and Soldered Joints of Cu-Nb Microcomposite Wires. In Proceedings of the National Conference on Materials Engineering, Kaunas, Lithuania, 19 November 2010; Technologija: Kaunas, Lithuania, 2011; Volume 17, pp. 16–19. [Google Scholar] [CrossRef]
- Višniakov, N.; Škamat, J.; Černašėjus, O.; Kilikevičius, A. Flash welding of microcomposite wires for pulsed power applications. Metals 2020, 10, 1053. [Google Scholar] [CrossRef]
- ISO 17279-1:2018; Welding—Micro Joining of 2nd Generation High Temperature Superconductors—Part 1: General Requirements for the Procedure. International Organization for Standardization: Geneva, Switzerland, 2018.
- Paul, H.; Miszczyk, M.; Prażmowski, M.; Chulist, R.; Petrzak, P.; Schell, N.; Fatemi, M. Effect of Impact Loading on Structural Properties of Multi-Layered Ta/Cu, Nb/Cu and Fe/Cu Plates Fabricated by Single-Shot Explosive Welding. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1270, 012124. [Google Scholar] [CrossRef]
- Beinoras, P.; Mikalauskas, G.; Višniakov, N.; Kapustynskyi, P. Comparative Analysis of Cu-Nb Microcomposite Conductor Welding Techniques. In Proceedings of the International Conference on Metallurgy and Materials (METAL), Brno, Czech Republic, 22–24 May 2024; pp. 269–274. [Google Scholar] [CrossRef]
- Kanne, W.R., Jr. Solid-State Resistance Upset Welding: A Process with Unique Advantages for Advanced Materials; Westinghouse Savannah River Co.: Aiken, SC, USA, 1993. [Google Scholar]
- Messler, R.W. Joining of Advanced Materials; Butterworth-Heinemann: Oxford, UK, 2013; p. 560. [Google Scholar]
- O’Brien, A. Welding Handbook. Volume 3, Welding Processes, Part 2, 9th ed.; American Welding Society: Miami, FL, USA, 2007; p. 615. [Google Scholar]
- Campbell, F.C. Joining: Understanding the Basics; Resistance Welding; ASM International: Materials Park, OH, USA, 2011; Chapter 3; p. 322. [Google Scholar] [CrossRef]
- Kanne, W.R., Jr. Welding, Brazing, and Soldering; Upset Welding; ASM Handbook; ASM International: Materials Park, OH, USA, 1993; Volume 6, pp. 249–251. [Google Scholar] [CrossRef]
- Gelman, A.S. Fundamentals of Pressure Welding; Mashinostroenie: Moscow, Russia, 1970; p. 302. (In Russian) [Google Scholar]
- Weman, K. Welding Processes Handbook, 2nd ed.; Woodhead Publishing Limited: Cambridge, UK, 2012; pp. 119–132. [Google Scholar]
- Guo, J. Handbook of Manufacturing Engineering and Technology. Solid State Welding Processes in Manufacturing; Springer: London, UK, 2015; pp. 569–592. [Google Scholar] [CrossRef]
- Tierney, J.J.; Gillespie, J.W.; Bourban, P.E. Joining of Composites. In Comprehensive Composite Materials; Materials Science and Materials Engineering; Elsevier: Amsterdam, The Netherlands, 2000; Volume 2, pp. 1029–1047. [Google Scholar] [CrossRef]
- Pfeifer, M. Manufacturing Process Considerations. In Materials Enabled Designs, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2009; pp. 115–160. [Google Scholar] [CrossRef]
- Kerstens, N.F.H.; Richardson, I.M. Heat distribution in resistance upset butt welding. J. Mater. Process. Technol. 2009, 209, 2715–2722. [Google Scholar] [CrossRef]
- Lienert, T.; Siewert, T.; Babu, S.; Acoff, V. ASM Handbook, Welding Fundamentals and Processes; ASM International: Materials Park, OH, USA, 2011; Volume 6A. [Google Scholar] [CrossRef]
- Russell, J.D. The potential use of non-arc welding processes in energy-related fabrications. In Welding in Energy-Related Projects; Welding Institute of Canada: Windsor, ON, Canada; Pergamon Press: Toronto, ON, Canada, 1984; p. 491. [Google Scholar]
- Hook, I.T. The Welding of Copper and Its Alloys. Weld. J. 1955, 34, 177S–202S. [Google Scholar]
- Davis, J.R. ASM Specialty Handbook: Copper and Copper Alloys; ASM International: Materials Park, OH, USA, 2008; p. 621. [Google Scholar]
- Somers, B.R. Welding Handbook, 8th ed.; Welding of Copper and Copper Alloys; American Welding Society: Miami, FL, USA, 1997; Volume 3, p. 54. [Google Scholar]
- Kearns, W.H. Welding Handbook, 7th ed.; Metals and Their Weldability; American Welding Society: Miami, FL, USA, 1982; Volume 4, p. 561. [Google Scholar]
- Columbic Copper Reinforced Wires, Conductors & Wire Rod. Nanoelectro Superwires. Available online: https://www.monrf.ru/upload/iblock/31d/31dab85e9b572a77e4e70c0ae60ae892.pdf (accessed on 10 February 2025).
- Cu-Nb Phase Diagram. Springer Materials. Available online: https://link.springer.com/article/10.1007/s11669-012-0051-y (accessed on 10 February 2025).
- Hust, J.G.; Sparks, L.L. Lorenz Ratios of Technically Important Metals and Alloys; Technical Note 634; National Bureau of Standards: Washington, DC, USA, 1973; p. 276. Available online: https://nvlpubs.nist.gov/nistpubs/Legacy/TN/nbstechnicalnote634.pdf (accessed on 10 February 2025).
- ISO/TR 25901-3:2016; Welding and Allied Processes—Vocabulary—Part 3: Welding Processes. International Organization for Standardization: Geneva, Switzerland, 2016.
- Kochergin, K.A. Resistance Welding; Mashinostroenie: Moscow, Russia, 1987; p. 240. (In Russian) [Google Scholar]
- Katayev, R.F.; Milyutin, V.S.; Bliznik, M.G. Theory and Technology of Resistance Welding; Ural State University: Yekaterinburg, Russia, 2015; p. 144. (In Russian) [Google Scholar]
- ISO 4063:2009; Welding and Allied Processes—Nomenclature of Processes and Reference Numbers. International Organization for Standardization: Geneva, Switzerland, 2009.
- Ababkov, N.V.; Pimonov, M.V. Technology and Equipment of Resistance Welding; Kuzbass State Technical University: Kemerovo, Russia, 2011; p. 258. (In Russian) [Google Scholar]
- Glebov, L.V.; Filippov, J.I.; Chiuloshnikov, P.P. Design and Exploitation of Resistance Machines; Energoizdat: Leningrad, Russia, 1987; p. 312. (In Russian) [Google Scholar]
- AWS C1.1M/C1.1:2012; Recommended Practices for Resistance Welding. American Welding Society: Miami, FL, USA, 2012.
- American Welding Society. RWMA Resistance Welding Manual, 4th ed.; American Welding Society: Miami, FL, USA, 2003. [Google Scholar]
- Orlov, B.D. Technology and Equipment for Resistance Welding; Mashinostroenie: Moscow, Russia, 1986; p. 352. (In Russian) [Google Scholar]
- Banov, M.D. Technology and Equipment for Resistance Welding, 3rd ed.; Akademiya: Moscow, Russia, 2008; p. 224. (In Russian) [Google Scholar]
- Gelman, A.S. Technology of Electric Resistance Welding; Mashinostroenie: Moscow, Russia, 1952; p. 322. (In Russian) [Google Scholar]
- Sergeev, N.P. Handbook for Young Welders with Resistance Machines; Vishaya Shkola: Moscow, Russia, 1984; p. 157. (In Russian) [Google Scholar]
- Gulyaev, A.I. Technology and Equipment for Resistance Welding; Mashinostroenie: Moscow, Russia, 1985; p. 256. (In Russian) [Google Scholar]
- Vural, M. Comprehensive Materials Processing; Welding Processes and Technologies; Elsevier: Amsterdam, The Netherlands, 2014; Volume 6, pp. 3–48. [Google Scholar] [CrossRef]
- Ovchinnikov, V.; Gureeva, M. Technology and Equipment for Resistance Welding: Handbook; Infra-Inzhenerija: Moscow, Russia, 2020; p. 160. (In Russian) [Google Scholar]
- American Welding Society. RWPH:2011 Resistance Welding Pocket Handbook, 1st ed.; American Welding Society: Miami, FL, USA, 2011; p. 45. [Google Scholar]
- Zhang, H.; Senkara, J. Resistance Welding: Fundamentals and Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; p. 427. [Google Scholar]
- Fang, Y.; Jiang, X.; Mo, D.; Zhu, D.; Luo, Z. A Review on Dissimilar Metals’ Welding Methods and Mechanisms with Interlayer. Int. J. Adv. Manuf. Technol. 2019, 102, 2845–2863. [Google Scholar] [CrossRef]
- Martinsen, K.; Hu, S.J.; Carlson, B.E. Joining of Dissimilar Materials. CIRP Ann.—Manuf. Technol. 2015, 64, 679–699. [Google Scholar] [CrossRef]
- ISO/TR 23413:2019; Resistance Welding—Overview of Standards for Resistance Welding. International Organization for Standardization: Geneva, Switzerland; Beijing, China, 2019.
- Devanathan, V. The Wiedemann-Franz Law for Electrical and Thermal Conduction in Metals. J. Chennai Acad. Sci. 2021, 4, 1–26. [Google Scholar]
- Solovjev, G.I. Fundamentals of Technology of Pressure Vessel; Kurgan State University: Kurgan, Russia, 2014; p. 40. (In Russian) [Google Scholar]
- Gomez, M.R.; French, D.M.; Tang, W.; Zhang, P.; Lau, Y.Y.; Gilgenbach, R.M. Experimental Validation of a Higher Dimensional Theory of Electrical Contact Resistance. Appl. Phys. Lett. 2009, 95, 071501. [Google Scholar] [CrossRef]
- Hamedi, M.; Atashparva, M. A Review of Electrical Contact Resistance Modeling in Resistance Spot Welding. Weld. World 2017, 61, 269–290. [Google Scholar] [CrossRef]
- Qi, A.; Yang, W.; Liu, B.; Zheng, S. Interface Effects on the Properties of Cu–Nb Nanolayered Composites. J. Mater. Res. 2020, 35, 2684–2700. [Google Scholar] [CrossRef]
- Hashemi, N.; Vazir, H.; Ziemer, K. Wear Resistance of Cu–18vol.% Nb (P/M) Composites. Mater. Sci. Eng. A 2008, 478, 390–396. [Google Scholar] [CrossRef]
- Optris PI 450i Infrared Camera. Optris GmbH. Available online: https://optris.com/products/infrared-cameras/precision-line/pi-450i (accessed on 11 February 2025).
- XINTEST HT-6899 Non-Contact High Temperature Infrared Thermometer Datasheet. Santa Technology. Available online: https://santatechnology.com/products-datasheet/8341-1628154065.pdf (accessed on 11 February 2025).
- SQ-AS Welding Wire. CEA Welding. Available online: https://www.ceaweld.com/en/product/sq-as (accessed on 11 February 2025).
- ISO 14175:2008; Welding Consumables—Gases and Gas Mixtures for Fusion Welding and Allied Processes. International Organization for Standardization: Geneva, Switzerland, 2008.
- ISO 17279-3:2021; Welding—Micro Joining of Second Generation High Temperature Superconductors—Part 3: Test Methods for Joints. International Organization for Standardization: Geneva, Switzerland, 2021.
- Changzhou Eucol Electronic Technology Co., Ltd. Available online: http://www.en.eucol.com.cn (accessed on 11 February 2025).
- FLIR Exx-Series Advanced Thermal Imaging Cameras. FLIR Systems. Available online: https://www.flir.com/instruments/exx-series (accessed on 11 February 2025).
- VELGA VILNIUS. Available online: https://www.velga.lt (accessed on 11 February 2025).
- ERESCO 42 MF4 Portable X-Ray Unit Brochure. GE Sensing & Inspection Technologies. Available online: https://pratita.com/wp-content/uploads/2020/04/eresco_42_mf4_air-cooled_brochure_english-pdf.pdf (accessed on 11 February 2025).
- HD-CR 35 NDT. Dürr NDT GmbH. Available online: https://www.duerr-ndt.de/produkte/computer-radiographie/hd-cr-35-ndt.html (accessed on 11 February 2025).
- JSC Tochpribor. Available online: https://www.tochpribor-kb.ru (accessed on 11 February 2025).
- PXIe-1073. National Instruments. Available online: https://www.ni.com/en-us/shop/model/pxie-1073.html (accessed on 11 February 2025).
- EN 61788-6:2011; Superconductivity—Mechanical Properties Measurement. Room Temperature Tensile Test of Cu/Nb-Ti Composite Superconductors. European Committee for Electrotechnical Standardization: Brussels, Belgium, 2011.
- 10kN Load Cell. Torbal Scales. Available online: https://www.torbalscales.com/10kn-load-cell.html (accessed on 11 February 2025).
- Axial Extensometer—Model 3542. Epsilon Technology Corp. Available online: https://www.epsilontech.com/products/axial-extensometer-model-3542 (accessed on 11 February 2025).
- ISO 6892-1:2019; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. Lietuvos Standartizacijos Departamentas: Vilnius, Lithuania, 2020.
- PoliMat® 2 Electropolishing and Etching System. Buehler. Available online: https://www.buehler.com/products/grinding-and-polishing/electropolishing-and-etching/polimat-2-electropolishing-and-etching-system/ (accessed on 11 February 2025).
- Axia ChemiSEM. Thermo Fisher Scientific. Available online: https://www.thermofisher.com/lt/en/home/electron-microscopy/products/scanning-electron-microscopes/axia-chemisem (accessed on 11 February 2025).
- Inverted Eclipse MA200. Nikon Instruments Inc. Available online: https://industry.nikon.com/en-us/products/industrial-microscopy/industrial-microscopes/inverted-eclipse-ma200 (accessed on 11 February 2025).
- Moticam A16. Motic Europe. Available online: https://moticeurope.com/en/moticam-a16.html (accessed on 11 February 2025).
- Blaschke, D.N.; Miller, C.; Mier, R.; Osborn, C.; Thomas, S.M.; Tegtmeier, E.L.; Winter, W.P.; Carpenter, J.S.; Hunter, A. Predicting Electrical Conductivity in Cu/Nb Composites: A Combined Model-Experiment Study. J. Appl. Phys. 2022, 132, 045105. [Google Scholar] [CrossRef]
- Mao, Q.; Wang, L.; Nie, J.F.; Zhao, Y. Enhancing Strength and Electrical Conductivity of Cu–Cr Composite Wire by Two-Stage Rotary Swaging and Aging Treatments. Compos. Part B Eng. 2022, 231, 109567. [Google Scholar] [CrossRef]
- High Strength, High Conductivity Nanocomposite Cu-Nb Wires. Alphysica. Available online: https://alphysica.rhymedigital.com/cu-nb.html (accessed on 11 February 2025).
- Beinoras, P.; Višniakov, N. Measurement of Electrical Conductivity and Resistivity of Cu-Nb18% Microcomposite Conductor and Its Welded Joint. Sci. Future Lith. 2024, 16, 1–8. (In Lithuanian) [Google Scholar] [CrossRef]
- ISO 6520-1:2007; Welding and Allied Processes—Classification of Geometric Imperfections in Metallic Materials—Part 1: Fusion Welding. International Organization for Standardization: Geneva, Switzerland, 2007.
- De Almeida, R.; De Aguiar, J.; Passos, C. Investigating the “Cocoon Effect” in Niobium-Copper Alloy: Metallic Nano-Precipitate Distribution and Niobium Migration. arXiv 2024, arXiv:2309.06385. [Google Scholar] [CrossRef]
- Deng, L.; Han, K.; Wang, B.; Yang, X.; Liu, Q. Thermal Stability of Cu–Nb Microcomposite Wires. Acta Mater. 2015, 101, 181–188. [Google Scholar] [CrossRef]
- Yang, W.; Beyerlein, I.J.; Jin, Q.; Ge, H.; Xiong, T.; Yang, L.; Pang, J.; Zhou, Y.; Shao, X.; Zhang, B.; et al. Strength and Ductility of Bulk Cu/Nb Nanolaminates Exposed to Extremely High Temperatures. Scripta Mater. 2019, 166, 73–77. [Google Scholar] [CrossRef]
- Spitzig, W.; Krotz, P.; Chumbley, L.S.; Downing, H.; Verhoeven, J. Effect of Temperature on the Mechanical Properties and Microstructures of In Situ Formed Cu-Nb and Cu-Ta Composites. MRS Proc. 2011, 120, 45. [Google Scholar] [CrossRef]
- Popova, E.N.; Sudareva, S.V.; Popov, V.V.; Rodionova, L.A.; Romanov, E.P.; Vorob’eva, A.E.; Dergunova, E.A.; Malafeeva, O.V.; Khlebova, N.E.; Shikov, A.K. Plastic Deformation of Composites Cu/Nb, Cu/Nb(Ti) and Cu-Sn/Nb(NbTi). Fiz. Met. Metalloved. 2001, 90, 115–124. (In Russian) [Google Scholar]
- Popova, E.N.; Popov, V.; Romanov, E.P.; Pilyugin, V.P. Effect of the Degree of Deformation on the Structure and Thermal Stability of Nanocrystalline Niobium Produced by High-Pressure Torsion. Phys. Met. Metallogr. 2007, 103, 407–413. [Google Scholar] [CrossRef]
- Popova, E.N.; Deryagina, I.L.; Valova-Zaharevskaya, E.G.; Ruello, M.L.; Popov, V.V., Jr. Microstructural Features in Multicore Cu-Nb Composites. Materials 2021, 14, 7033. [Google Scholar] [CrossRef]
- Ananth, C.R.; Voleti, S.R.; Chandra, N. Effect of Fiber Fracture and Interfacial Debonding on the Evolution of Damage in Metal Matrix Composites. Compos. Part A Appl. Sci. Manuf. 1998, 29, 1203–1211. [Google Scholar] [CrossRef]
- King, J.E. Failure in Composite Materials. Met. Mater. 1989, 5, 720–726. [Google Scholar]
- Nickolas, T.; Ahmad, J. Modeling Fiber Breakage in a Metal-Matrix Composite. Compos. Sci. Technol. 1994, 52, 29–38. [Google Scholar] [CrossRef]
- Xia, Z.; Curtin, W.A.; Peters, P.W.M. Multiscale Modeling of Failure in Metal Matrix Composites. Acta Mater. 2001, 49, 273–284. [Google Scholar] [CrossRef]



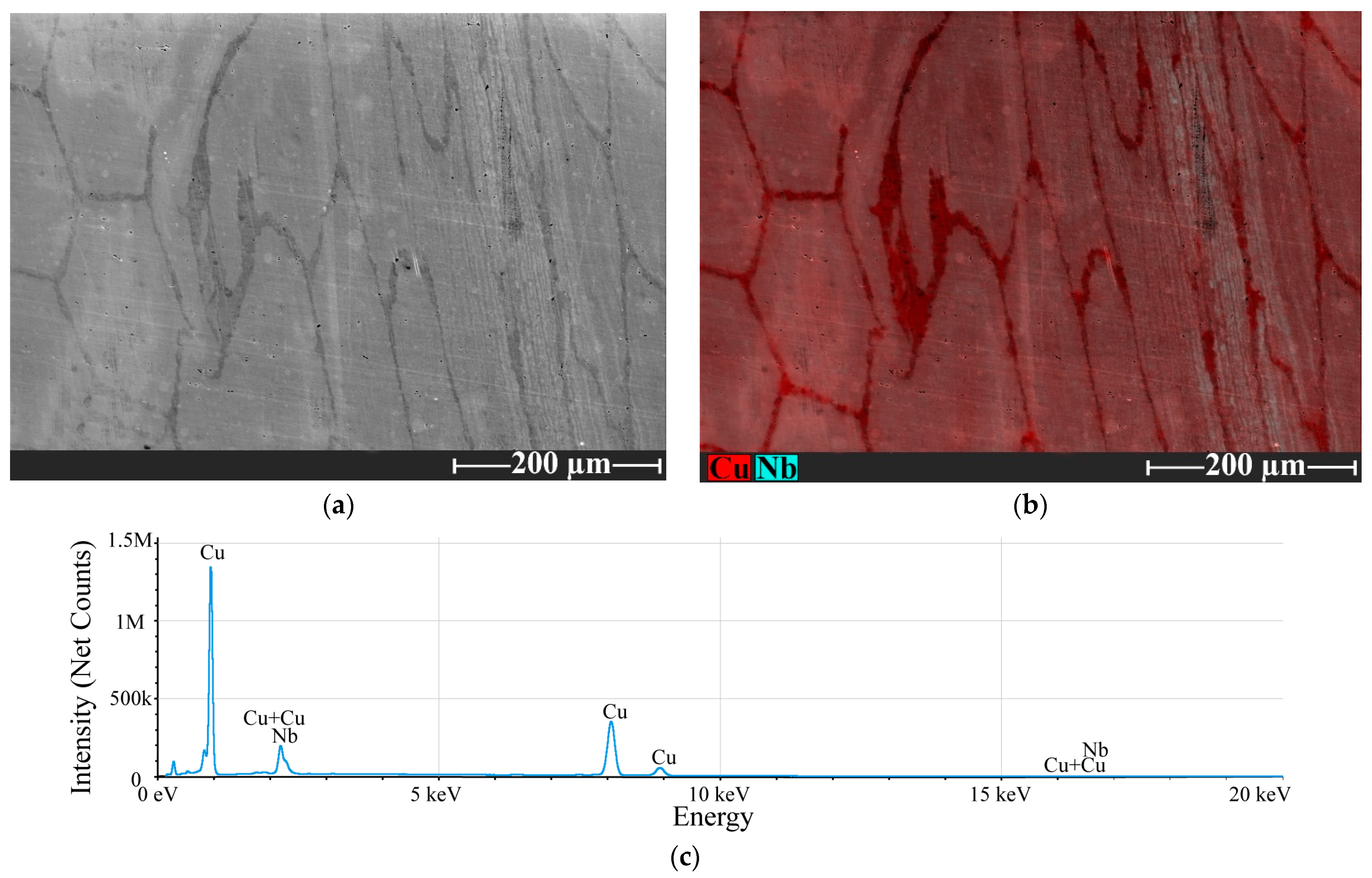

| Melting Temperature of Cu Matrix | Melting Temperature of Nb Reinforcement Phase | Melting Temperature of Cu-18 wt. % Nb Composite |
|---|---|---|
| Tm, (Cu) °C | Tm, (Nb) °C | Tm, (Cu-Nb) °C |
| 1085 | 2469 | 1675–1800 |
| Electrical Resistivity ρo at Room Temperature, µΩ cm | Electrical Resistivity ρt at Temperature Near Melting, µΩ cm | Relative Thermal Conductivity Kt | Electrical Conductivity IACS, % | Lorenz Number L, 10−8 · W · Ω/°K2 |
|---|---|---|---|---|
| 2.30–2.87 | 18.86–23.53 | 0.75 | 60–75 | 2.4–2.54 |
| Electrical conductivity, σ, Ω−1 cm−1 | Conductor Density γ, g/cm3 | Specific heat c, J/kg °C (cal/g °C) | Thermal conductivity coefficient λ, W/m °C (cal/ cm s °C) | Thermal diffusivity, a, mm2/s |
| 0.348–0.435 | 8.882 | 381 (0.09100033) | 401 (0.958413002) | 118.5 |
| Welding Pressure Pw, MPa | Upsetting Pressure Pu, MPa | Welding Force Fw, N | Upsetting Force Fd, N | Minimum Basic Length l0, mm | Upset Allowance Δu, mm | Heating Temperature T, °C |
|---|---|---|---|---|---|---|
| 350 | 430 | 3500 | 4300 | 7–10.7 | 0.7–1.1 | 868–1085 |
| Contact Resistance Between Connecting Surfaces Rc, µΩ | Specific Resistance of the Metal of the Parts That Are Being Welded at the Beginning of the Process 2Rd1, µΩ | Specific Resistance of the Metal of the Welded Parts at the End of the Process 2Rd2, µΩ | Total Resistance of the Welding Circuit at the Beginning of the Process R1, µΩ | Total Resistance of the Welding Circuit at the End of the Process R2, µΩ | Calculated Average Loop Resistance R, µΩ |
|---|---|---|---|---|---|
| 1.31 | 18.1 | 48.6 | 19.41 | 48.6 | 34 |
| Welding Current Density J, A/mm2 | Welding Time tw, s | Heating Up to T = 868 °C Requires a Welding Current Iw, A | Heating Up to T = 977 °C Requires a Welding Current Iw, A | Heating Up to T = 1085 °C Requires a Welding Current Iw, A |
|---|---|---|---|---|
| 335–3743 | 0.25 | 3348 | 3552 | 3743 |
| 307–342 | 0.3 | 3067 | 3253 | 3428 |
| 285–318 | 0.35 | 2846 | 3020 | 3182 |
| 267–298 | 0.4 | 2669 | 2831 | 2983 |
| 252–282 | 0.45 | 2520 | 2674 | 2817 |
| 240–268 | 0.5 | 2395 | 2540 | 2677 |
| 229–256 | 0.55 | 2286 | 2425 | 2556 |
| Rectangular Profile Size, mm × mm | Cross-Section S, cm2 | Yield Strength σγ, MPa | Ultimate Tensile Strength σu, MPa | Elongation After Fracture A, % | Electrical Conductivity IACS, % |
|---|---|---|---|---|---|
| 2.4 × 4.2 | 0.1 | 830 | 1120 | 4.2 | 60–70 |
| Set of Experiments | Welding Current I, A | Welding Current Density A/mm2 | Welding Force N | Upsetting Force N | Base Length mm | Upset Allowance mm | Welding Time s | Achieved Welding Temperature T, °C |
|---|---|---|---|---|---|---|---|---|
| A.1 | 2846 | 285 | 3500 | 4300 | 7 | 1 | 0.35 | 868 |
| A.2 | 3020 | 302 | 977 | |||||
| A.3 | 3182 | 318 | 1085 | |||||
| A.4 | 2669 | 267 | 0.4 | 868 | ||||
| A.5 | 2831 | 283 | 977 | |||||
| A.6 | 2983 | 298 | 1085 | |||||
| A.7 | 2520 | 252 | 0.45 | 868 | ||||
| A.8 | 2674 | 267 | 977 | |||||
| A.9 | 2817 | 282 | 1085 | |||||
| L.1 | 2846 | 285 | 3500 | 4300 | 6 | 1 | 0.35 | 868 |
| L.2 | 2846 | 285 | 8 | |||||
| L.3 | 2846 | 285 | 9 | |||||
| L.4 | 2846 | 285 | 10 | |||||
| L.5 | 2669 | 267 | 6 | 0.4 | ||||
| L.6 | 2669 | 267 | 8 | |||||
| L.7 | 2669 | 267 | 9 | |||||
| L.8 | 2669 | 267 | 10 | |||||
| L.9 | 2520 | 252 | 6 | 0.45 | ||||
| L.10 | 2520 | 252 | 8 | |||||
| L.11 | 2520 | 252 | 9 | |||||
| L.12 | 2520 | 252 | 10 | |||||
| Δ.1 | 2846 | 285 | 3500 | 4300 | 7 | 0.7 | 0.35 | 868 |
| Δ.2 | 2669 | 267 | 0.4 | |||||
| Δ.3 | 2520 | 252 | 0.45 | |||||
| Δ.4 | 2846 | 285 | 0.8 | 0.35 | ||||
| Δ.5 | 2669 | 267 | 0.4 | |||||
| Δ.6 | 2520 | 252 | 0.45 | |||||
| Δ.7 | 2846 | 285 | 0.9 | 0.35 | ||||
| Δ.8 | 2669 | 267 | 0.4 | |||||
| Δ.9 | 2520 | 252 | 0.45 | |||||
| Δ.10 | 2846 | 285 | 1.1 | 0.35 | ||||
| Δ.11 | 2669 | 267 | 0.4 | |||||
| Δ.12 | 2520 | 252 | 0.45 | |||||
| F.1 | 2846 | 285 | 4160 | 4300 | 7 | 1 | 0.35 | 868 |
| F.2 | 2669 | 267 | 0.4 | |||||
| F.3 | 2520 | 252 | 0.45 | |||||
| F.4 | 2846 | 285 | 4680 | 0.35 | ||||
| F.5 | 2669 | 267 | 0.4 | |||||
| F.6 | 2520 | 252 | 0.45 | |||||
| U.1 | 2846 | 285 | 3500 | 4160 | 0.35 | |||
| U.2 | 2669 | 267 | 0.4 | |||||
| U.3 | 2520 | 252 | 0.45 | |||||
| U.4 | 2846 | 285 | 4680 | 0.35 | ||||
| U.5 | 2669 | 267 | 0.4 | |||||
| U.6 | 2520 | 252 | 0.45 |
| Welding Current I, A | Welding Current Density A/mm2 | Welding Force Fw, N | Upsetting Force Fd, N | Base Length l0, mm | Upset Allowance Δu, mm | Welding Time, s | Achieved Welding Temperature T, °C |
|---|---|---|---|---|---|---|---|
| 2670 | 267 | 3500 | 4300 | 7 | 1 | 0.4 | 868 |
| Set of experiments | A.1 | A.2 | A.3 | A.4 | A.5 | A.6 | A.7 | A.8 | A.9 |
| Welding quality | poor | poor | poor | good | poor | poor | no * | poor | poor |
| Set of experiments | L.1 | L.2 | L.3 | L.4 | L.5 | L.6 | L.7 | L.8 | L.9 |
| Welding quality | poor | poor | poor | no * | good | poor | no * | no | no |
| Set of experiments | L.10 | L.11 | L.12 | Δ.1 | Δ.2 | Δ.3 | Δ.4 | Δ.5 | Δ.6 |
| Welding quality | no * | no * | no * | no * | no * | no * | poor | poor | no * |
| Set of experiments | Δ.7 | Δ.8 | Δ.9 | Δ.10 | Δ.11 | Δ.12 | F.1 | F.2 | F.3 |
| Welding quality | poor | good | no * | poor | poor | no * | poor | poor | no * |
| Set of experiments | F.4 | F.5 | F.6 | U.1 | U.2 | U.3 | U.4 | U.5 | U.6 |
| Welding quality | poor | poor | no * | poor | good | no * | poor | poor | no * |
| Measured Parameters | Base Material (Cu-Nb Wire) | Sample with Flash Welding Joint [7] | Sample with Upset Welding Joint |
|---|---|---|---|
| Length of material sample L, mm | 45 | 45 | 45 |
| Electrical resistance R, µΩ | 119.3 | 123.8 | 122.4 |
| Electrical resistivity of the metal at room temperature ρ0, µΩ cm | 2.65 | 2.75 | 2.72 |
| Electrical conductivity σ, MS/m | 37.76 | 36.33 | 36.75 |
| Electrical conductivity IACS, % | 65.10 | 62.63 | 63.37 |
| Element | Weight Percentage in Wt. % |
|---|---|
| Cu | 82.3 |
| Nb | 17.7 |
| N | 0.0 |
| O | 0.0 |
| Element | Weight Percentage in Wt. % |
|---|---|
| Cu | 80.7 |
| Nb | 19.3 |
| N | 0.0 |
| O | 0.0 |
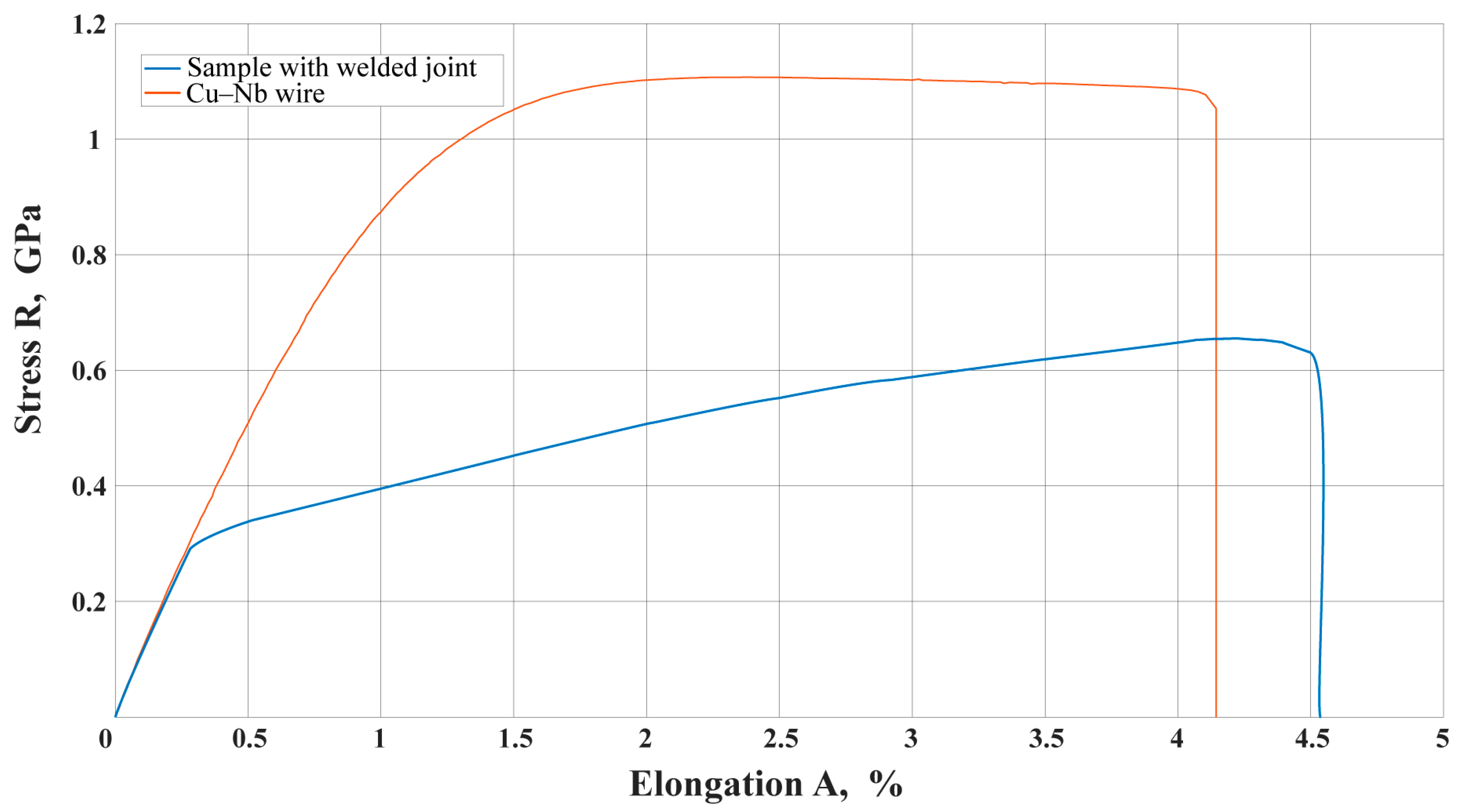
| Sample | Average Yield Strength σγ, GPa | Average Tensile Strength σu, GPa | Average Elongation at Break A, % | Deformation Speed, mm/mm | Testing Temperature T, °C |
|---|---|---|---|---|---|
| Cu-Nb wire | 0.83 | 1.12 | 4.2 | 1.5 | 20 |
| Sample with welded joint | 0.33 | 0.62 | 4.5 | 1.5 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Višniakov, N.; Beinoras, P.; Kapustynskyi, O. Upset Resistance Welding of a Microcomposite Cu-Nb Conductor for Pulsed Power Applications. Metals 2025, 15, 394. https://doi.org/10.3390/met15040394
Višniakov N, Beinoras P, Kapustynskyi O. Upset Resistance Welding of a Microcomposite Cu-Nb Conductor for Pulsed Power Applications. Metals. 2025; 15(4):394. https://doi.org/10.3390/met15040394
Chicago/Turabian StyleVišniakov, Nikolaj, Paulius Beinoras, and Oleksandr Kapustynskyi. 2025. "Upset Resistance Welding of a Microcomposite Cu-Nb Conductor for Pulsed Power Applications" Metals 15, no. 4: 394. https://doi.org/10.3390/met15040394
APA StyleVišniakov, N., Beinoras, P., & Kapustynskyi, O. (2025). Upset Resistance Welding of a Microcomposite Cu-Nb Conductor for Pulsed Power Applications. Metals, 15(4), 394. https://doi.org/10.3390/met15040394






