The Impact of Structural Units on Copper Grain Boundary–Dislocation Interactions
Abstract
1. Introduction
2. Methodology
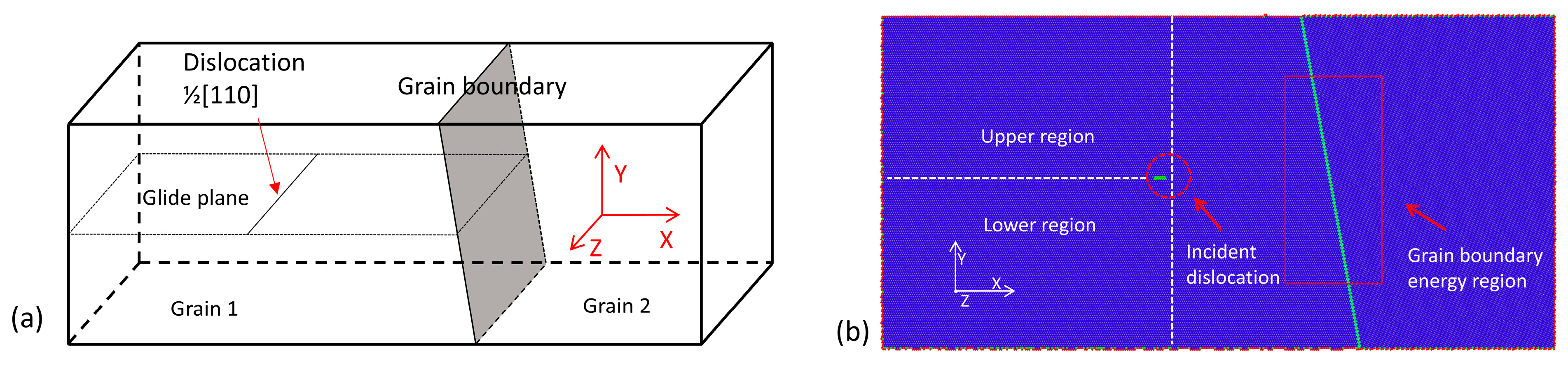
2.1. Model Construction
2.2. Simulation Process
3. Results and Discussion
3.1. Σ51(117)-22.84°
3.2. Σ27(115)-31.59°
3.3. Σ9(114)-38.94°
3.4. Σ11(113)-50.48°
3.5. Σ33(225)-58.99°
3.6. Σ3(112)-70.53°
4. Conclusions
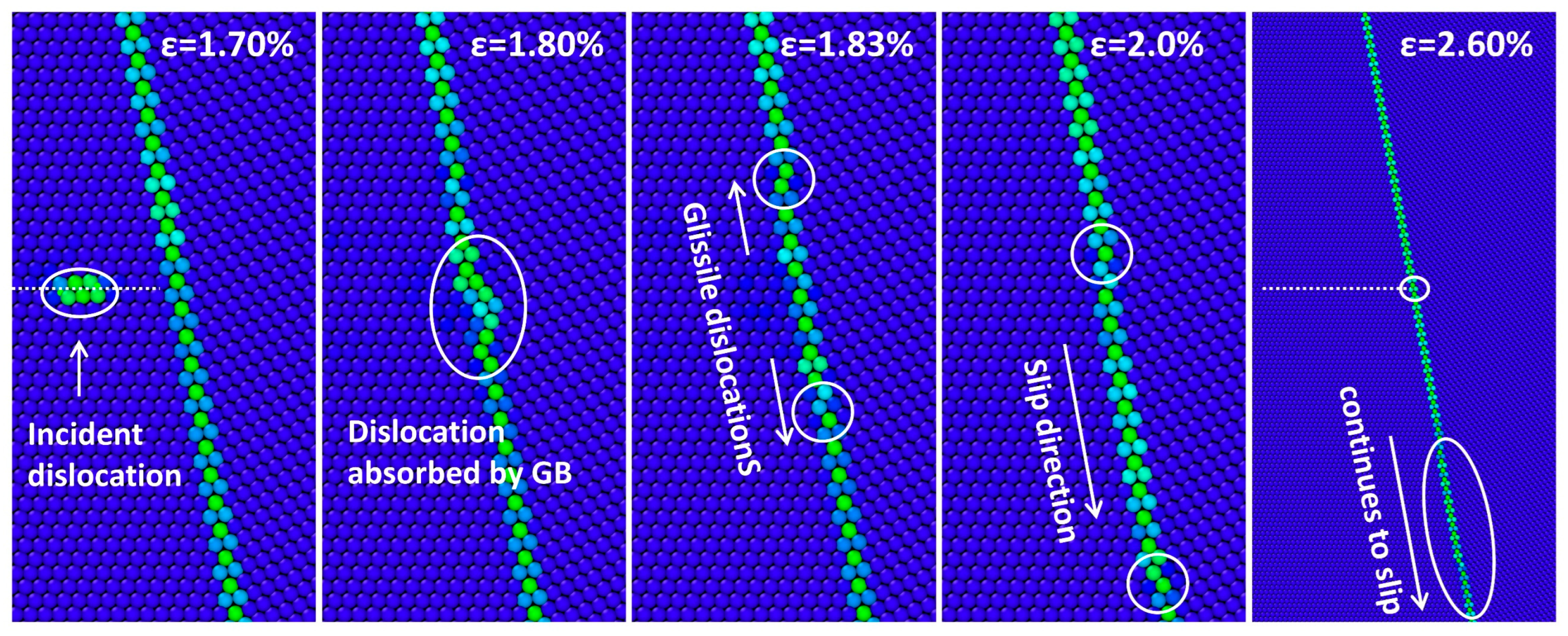
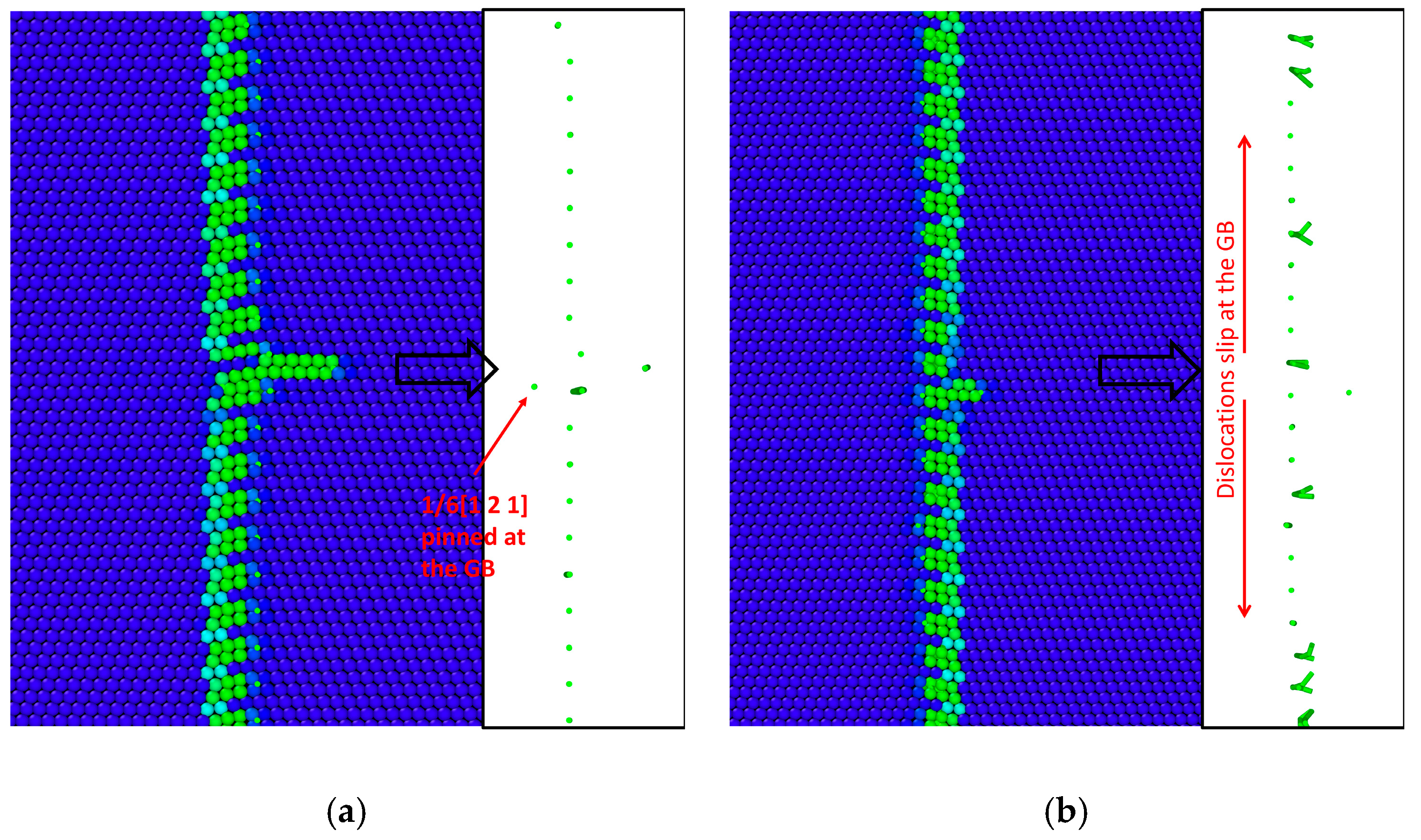
- GBs composed of a single type of SU exhibit pronounced dislocation absorption capability. For the Σ27(115)-31.59° with B-GB configuration, the dislocation becomes pinned at the impact site, inducing slight local atomic rearrangement. For the Σ11(113)-50.48° with C-GB configuration, the absorbed dislocation slips along the GB plane as glissile dislocations, leading to atomic-scale sliding behavior within the GB.
- In the Σ27(115)-31.59° GBs with CA-GB and B-GB configurations, dislocation impact induces SU transformation. Specifically, the SUs in the impact region reconstruct into a local BCA-GB configuration, effectively reducing the interfacial energy and promoting structural optimization of the GB.
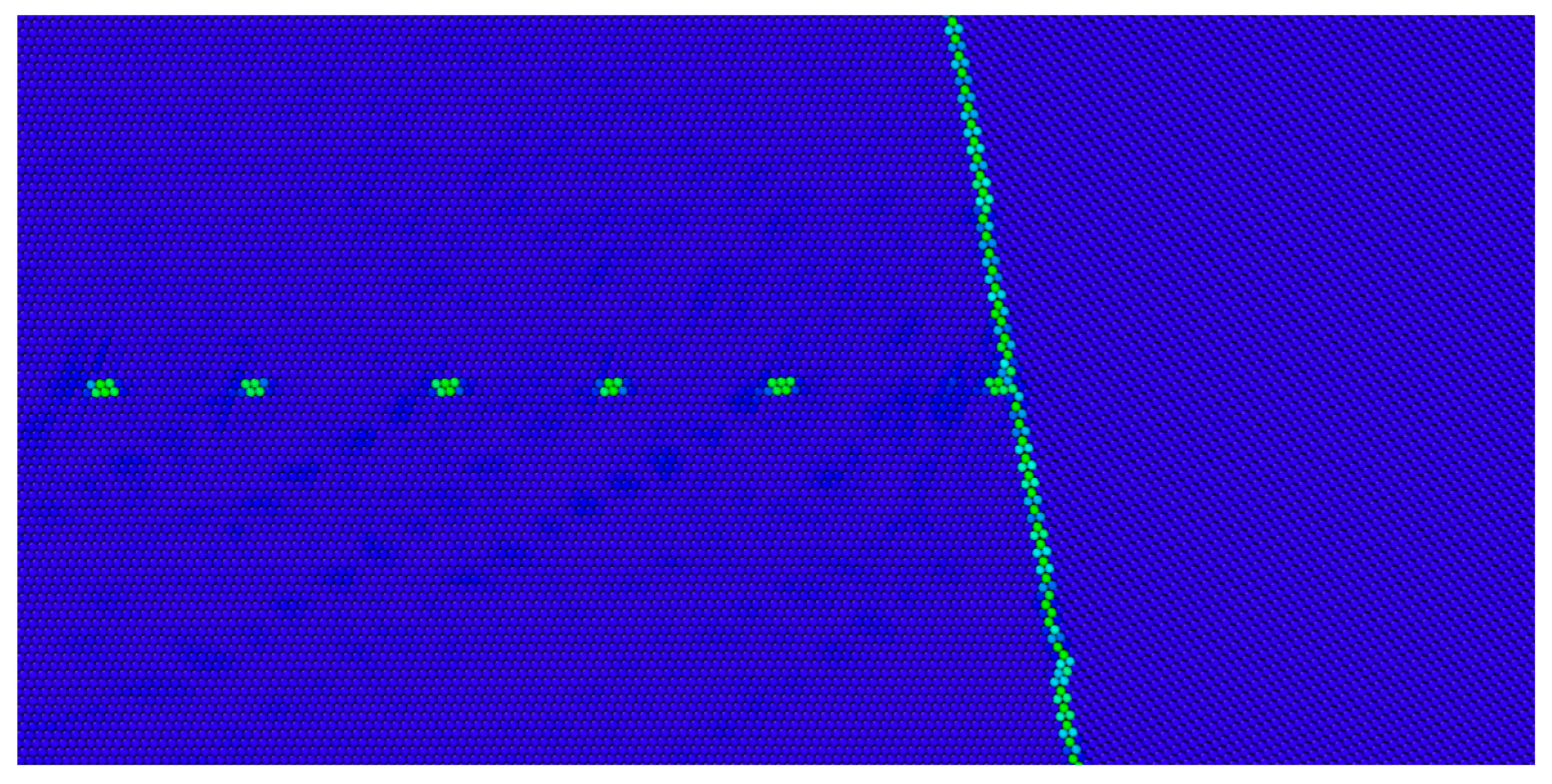
- For GB containing both C SUs and ISF facets, the accommodation of incident dislocations primarily occurs within the “island” regions of C SUs isolated by adjacent ISF facets. When multiple consecutive C SUs are present within such an “island”, cooperative coupling among SUs facilitates efficient dislocation absorption and energy dissipation, thereby suppressing dislocation transmission across the GB.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Read, W.T.; Shockley, W. Dislocation Models of Crystal Grain Boundaries. Phys. Rev. 1950, 78, 275–289. [Google Scholar] [CrossRef]
- Cottrell, A.H. Theory of dislocations. Prog. Met. Phys. 1953, 4, 205–264. [Google Scholar] [CrossRef]
- Bollmann, W. Crystal Defects and Crystalline Interfaces; Springer: Heidelberg, Berlin, 1970. [Google Scholar]
- Hirth, J.P. The influence of grain boundaries on mechanical properties. Metall. Trans. 1972, 3, 3047–3067. [Google Scholar] [CrossRef]
- de Koning, M.; Kurtz, R.J.; Bulatov, V.V.; Henager, C.H.; Hoagland, R.G.; Cai, W.; Nomura, M. Modeling of dislocation–grain boundary interactions in FCC metals. J. Nucl. Mater. 2003, 323, 281–289. [Google Scholar] [CrossRef]
- Spearot, D.E.; Sangid, M.D. Insights on slip transmission at grain boundaries from atomistic simulations. Curr. Opin. Solid State Mater. Sci. 2014, 18, 188–195. [Google Scholar] [CrossRef]
- Smith, D.A.; Vitek, V.; Pond, R.C. Computer simulation of symmetrical high angle boundaries in aluminium. Acta Metall. 1977, 25, 475–483. [Google Scholar] [CrossRef]
- Ashby, M.F.; Spaepen, F.; Williams, S. The structure of grain boundaries described as a packing of polyhedra. Acta Metall. 1978, 26, 1647–1663. [Google Scholar] [CrossRef]
- Pond, R.C.; Smith, D.A.; Vitek, V. A model for grain boundary structure based on random close packing. Scr. Metall. 1978, 12, 699–702. [Google Scholar] [CrossRef]
- Sutton, A.P.; Vitek, V. On the structure of tilt grain boundaries in cubic metals I. Symmetrical tilt boundaries. Philos. Trans. R. Soc. London Ser. A Math. Phys. Sci. 1983, 309, 1–36. [Google Scholar] [CrossRef]
- Sutton, A.P.; Vitek, V. On the structure of tilt grain boundaries in cubic metals. III. Generalizations of the structural study and implications for the properties of grain boundaries. Philos. Trans. R. Soc. London Ser. A Math. Phys. Sci. 1983, 309, 55–68. [Google Scholar]
- Rittner, J.; Seidman, D.N. <110> symmetric tilt grain-boundary structures in fcc metals with low stacking-fault energies. Phys. Rev. B 1996, 54, 6999–7015. [Google Scholar]
- Kronberg, M.L.; Wilson, F.H. Secondary Recrystallization in Copper. Trans. Metall. Soc. AIME 1949, 185, 501–514. [Google Scholar] [CrossRef]
- Tschopp, M.A.; Spearot, D.E.; McDowell, D.L. Influence of Grain Boundary Structure on Dislocation Nucleation in FCC Metals. In Dislocations in Solids; Hirth, J.P., Ed.; Elsevier: Amsterdam, The Netherlands, 2008; Volume 14, pp. 43–139. [Google Scholar]
- Tucker, G.J.; Tschopp, M.A.; McDowell, D.L. Evolution of structure and free volume in symmetric tilt grain boundaries during dislocation nucleation. Acta Mater. 2010, 58, 6464–6473. [Google Scholar] [CrossRef]
- Tucker, G.J.; McDowell, D.L. Non-equilibrium grain boundary structure and inelastic deformation using atomistic simulations. Int. J. Plast. 2011, 27, 841–857. [Google Scholar] [CrossRef]
- Koning, M.D.; Miller, R.; Bulatov, V.V.; Abraham, F.F. Modelling grain-boundary resistance in intergranular dislocation slip transmission. Philos. Mag. A 2002, 82, 2511–2527. [Google Scholar] [CrossRef]
- Lee, T.; Robertson, I.; Birnbaum, H. Prediction of slip transfer mechanisms across grain boundaries. Scr. Metall. 1989, 23, 799–803. [Google Scholar] [CrossRef]
- Lee, T.C.; Robertson, I.M.; Birnbaum, H.K. Anomalous slip in an FCC system. Ultramicroscopy 1989, 29, 212–216. [Google Scholar] [CrossRef]
- Lee, T.C.; Robertson, I.M.; Birnbaum, H.K. AnIn Situ transmission electron microscope deformation study of the slip transfer mechanisms in metals. Metall. Trans. A 1990, 21, 2437–2447. [Google Scholar] [CrossRef]
- Lee, T.C.; Robertson, I.M.; Birnbaum, H.K. TEM in situ deformation study of the interaction of lattice dislocations with grain boundaries in metals. Philos. Mag. A 1990, 62, 131–153. [Google Scholar] [CrossRef]
- Dewald, M.P.; Curtin, W.A. Multiscale modelling of dislocation/grain-boundary interactions: I. Edge dislocations impinging on Σ11 (1 1 3) tilt boundary in Al. Model. Simul. Mater. Sci. Eng. 2007, 15, S193–S215. [Google Scholar] [CrossRef]
- Dewald, M.P.; Curtin, W.A. Multiscale modelling of dislocation/grain boundary interactions. II. Screw dislocations impinging on tilt boundaries in Al. Philos. Mag. 2007, 87, 4615–4641. [Google Scholar] [CrossRef]
- Dewald, M.; Curtin, W.A. Multiscale modeling of dislocation/grain-boundary interactions: III. 60° dislocations impinging on Σ3, Σ9 and Σ11 tilt boundaries in Al. Model. Simul. Mater. Sci. Eng. 2011, 19, 055002. [Google Scholar] [CrossRef]
- Shimokawa, T. Asymmetric ability of grain boundaries to generate dislocations under tensile or compressive loadings. Phys. Rev. B 2010, 82, 174122. [Google Scholar] [CrossRef]
- Jin, Z.H.; Gumbsch, P.; Ma, E.; Albe, K.; Lu, K.; Hahn, H.; Gleiter, H. The interaction mechanism of screw dislocations with coherent twin boundaries in different face-centred cubic metals. Scr. Mater. 2006, 54, 1163–1168. [Google Scholar] [CrossRef]
- Jin, Z.H.; Gumbsch, P.; Albe, K.; Ma, E.; Lu, K.; Gleiter, H.; Hahn, H. Interactions between non-screw lattice dislocations and coherent twin boundaries in face-centered cubic metals. Acta Mater. 2008, 56, 1126–1135. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Mishin, Y.; Mehl, M.J.; Papaconstantopoulos, D.A.; Voter, A.F.; Kress, J.D. Structural stability and lattice defects in copper:Ab initio, tight-binding, and embedded-atom calculations. Phys. Rev. B 2001, 63, 224106. [Google Scholar] [CrossRef]
- Carter, C.B.; Ray, I.L.F. On the stacking-fault energies of copper alloys. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1977, 35, 189–200. [Google Scholar] [CrossRef]
- Hestenes, M.R.; Stiefel, E. Methods of conjugate gradients for solving linear systems. J. Res. Natl. Bur. Stand. 1952, 49, 409–435. [Google Scholar] [CrossRef]
- Tschopp, M.A.; Tucker, G.J.; McDowell, D.L. Structure and free volume of <110> symmetric tilt grain boundaries with the E structural unit. Acta Mater. 2007, 55, 3959–3969. [Google Scholar] [CrossRef]
- Tschopp, M.A.; Tucker, G.J.; McDowell, D.L. Atomistic simulations of tension–compression asymmetry in dislocation nucleation for copper grain boundaries. Comput. Mater. Sci. 2008, 44, 351–362. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Kelchner, C.L.; Plimpton, S.J.; Hamilton, J.C. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 1998, 58, 11085–11088. [Google Scholar] [CrossRef]
- Hirel, P. Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Gao, Y.; Jin, Z. Interactions between lattice dislocation and Lomer-type low-angle grain boundary in nickel. Comput. Mater. Sci. 2017, 138, 225–235. [Google Scholar] [CrossRef]
- Stukowski, A.; Albe, K. Extracting dislocations and non-dislocation crystal defects from atomistic simulation data. Model. Simul. Mater. Sci. Eng. 2010, 18, 085001. [Google Scholar] [CrossRef]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mater. Sci. Eng. 2012, 20, 085007. [Google Scholar] [CrossRef]
- Wang, K.; Xu, Y.; Zhang, W.; Xu, J. The impact of structural units on the dislocation nucleation of bi-crystal copper grain boundary. Comput. Mater. Sci. 2023, 218, 111900. [Google Scholar] [CrossRef]
- Wang, K.; Xu, L.; Zhang, W.; Xu, J.; Xu, Y. Atomistic simulation on the transformation behaviour of structural units at Σ27 tilt grain boundary. Mol. Simul. 2024, 50, 821–835. [Google Scholar] [CrossRef]
- Zhu, Q.; Cao, G.; Wang, J.; Deng, C.; Li, J.; Zhang, Z.; Mao, S.X. In situ atomistic observation of disconnection-mediated grain boundary migration. Nat. Commun. 2019, 10, 156. [Google Scholar] [CrossRef]
- Ishida, Y.; McLean, M. Burgers vectors of boundary dislocations in ordered grain boundaries of cubic metals. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1973, 27, 1125–1134. [Google Scholar] [CrossRef]
- Rae, C.M.F.; Smith, D.A. On the mechanisms of grain boundary migration. Philos. Mag. A 1980, 41, 477–492. [Google Scholar] [CrossRef]
- Wan, L.; Wang, S. Shear response of the Σ11, ⟨1 1 0⟩{1 3 1} symmetric tilt grain boundary studied by molecular dynamics. Model. Simul. Mater. Sci. Eng. 2009, 17, 045008. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, C.; Tieu, K.; Zhao, X.; Pei, L. The shear response of copper bicrystals with Sigma11 symmetric and asymmetric tilt grain boundaries by molecular dynamics simulation. Nanoscale 2015, 7, 7224–7233. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Z.; Huang, M. Atomistic modeling of the interaction between matrix dislocation and interfacial misfit dislocation networks in Ni-based single crystal superalloy. Comput. Mater. Sci. 2013, 70, 178–186. [Google Scholar] [CrossRef]
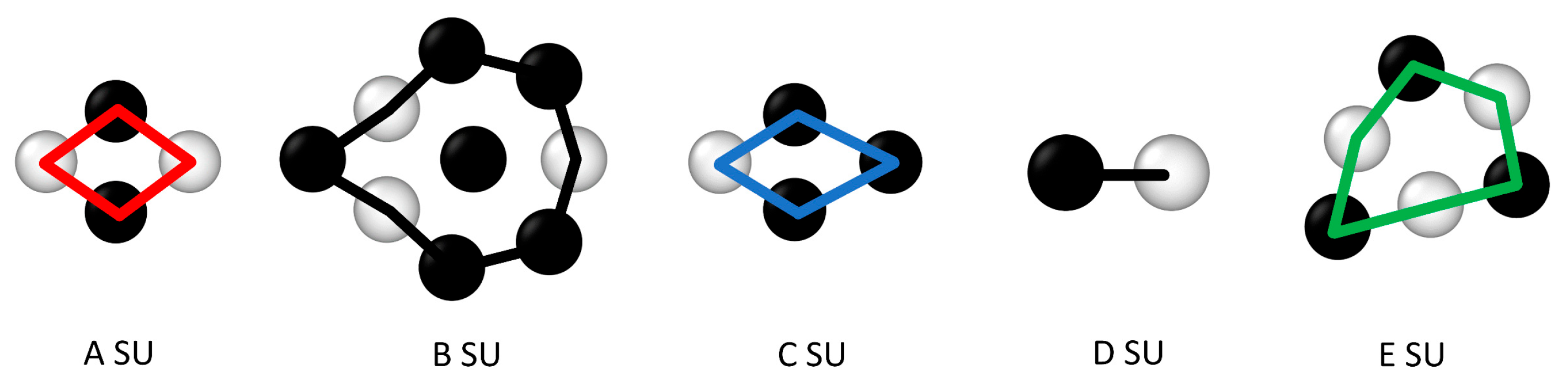
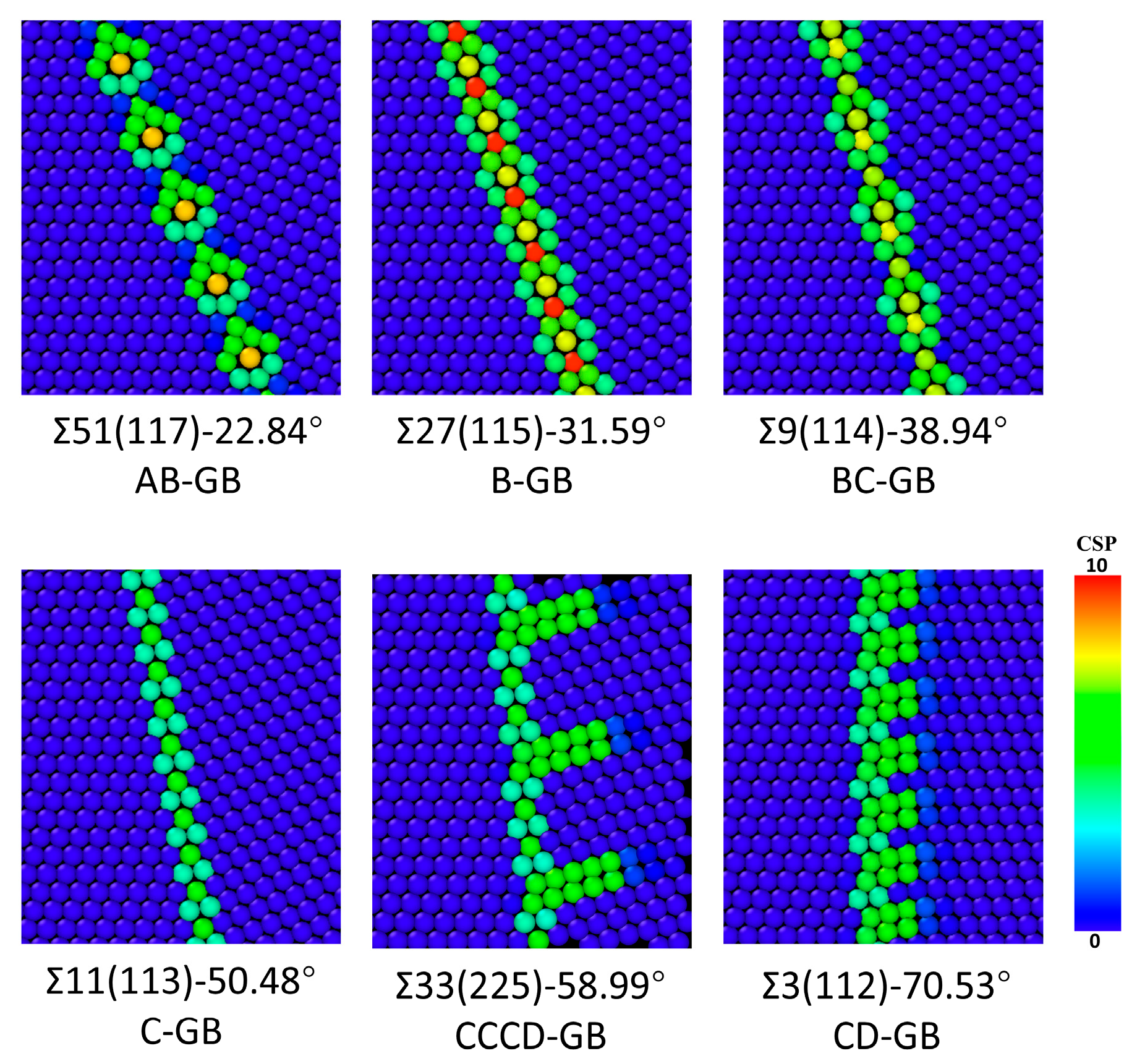

| Model | GB Configuration | GB Plane | GB Period | GB Energy () |
|---|---|---|---|---|
| Σ51(117)-22.84° | AB-GB | {1 1 7} | AB-AB | 718.62 |
| Σ27(115)-31.59° | B-GB | {1 1 5} | B-B | 720.92 |
| Σ9(114)-38.94° | BC-GB | {1 1 4} | BC-BC | 666.21 |
| Σ11(113)-50.48° | C-GB | {1 1 3} | C-C | 308.92 |
| Σ33(225)-58.99° | CCCD-GB | {2 2 5} | CCCD-CCCD | 516.21 |
| Σ3(112)-70.53° | CD-GB | {1 1 2} | CD-CD | 572.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Xu, Y.; Xu, L.; Zhang, W.; Xu, J. The Impact of Structural Units on Copper Grain Boundary–Dislocation Interactions. Metals 2025, 15, 1291. https://doi.org/10.3390/met15121291
Wang K, Xu Y, Xu L, Zhang W, Xu J. The Impact of Structural Units on Copper Grain Boundary–Dislocation Interactions. Metals. 2025; 15(12):1291. https://doi.org/10.3390/met15121291
Chicago/Turabian StyleWang, Ke, Yongsheng Xu, Lingchao Xu, Weigang Zhang, and Jinquan Xu. 2025. "The Impact of Structural Units on Copper Grain Boundary–Dislocation Interactions" Metals 15, no. 12: 1291. https://doi.org/10.3390/met15121291
APA StyleWang, K., Xu, Y., Xu, L., Zhang, W., & Xu, J. (2025). The Impact of Structural Units on Copper Grain Boundary–Dislocation Interactions. Metals, 15(12), 1291. https://doi.org/10.3390/met15121291








