First-Principles Study of Irradiation Defects in γ′-U₂Mo

Abstract

Understanding defect behavior and fission gas transport in uranium-molybdenum (U-Mo) fuels is key to explaining their swelling during reactor operation. In this study, we employed density functional theory (DFT) to systematically investigate the point defect structures and self-diffusion mechanisms in U₂Mo, with particular emphasis on the diffusion behavior of fission gas atoms Xe. Among intrinsic defects, vacancies and substitutional defects are the most stable, combining low formation energies with relatively small migration barriers; as a result, they largely control defect-mediated processes. Further analysis shows that self-diffusion in U₂Mo is strongly element-dependent, as U atoms migrate predominantly through vacancy-mediated mechanisms, while Mo atoms diffuse primarily via substitutional pathways. In addition, Xe atoms migrate through two distinct pathways: by combining with vacancies to form stable complexes and diffusing via vacancy-assisted migration, or by migrating as interstitial species along the Tetrahedral → Octahedral → Tetrahedral path between interstitial sites, eventually moving outward along defect channels and leading to gas release. Self-diffusion and fission gas transport in U-Mo fuels are governed by point defects, linking defect behavior to the swelling resistance of advanced nuclear materials.

1. Introduction

The U-Mo and U-Zr solid solutions have attracted sustained technological interest owing to their potential applications as advanced nuclear fuels, particularly in Generation IV (Gen-IV) power reactors [1]. Among them, U-Mo stands out as a particularly promising candidate for the development of high-density uranium fuels suitable for use in Material Testing Reactors (MTRs) [2]. U₂Mo is the only thermodynamically stable compound observed in the U-Mo binary phase diagram at finite temperatures [3].

U-Mo alloy fuel, as an advanced metallic nuclear fuel, exhibits high thermal conductivity and uranium density, along with good irradiation stability [4,5,6]. However, one notable drawback is the severe swelling of the fuel matrix [7]. During irradiation, the volume of U-Mo alloy fuel increases while its density decreases significantly. This swelling effect is primarily caused by the formation of voids and the accumulation and release of fission gas products in the fuel, constituting a key limiting factor for applying U-Mo alloy fuels [7,8,9].

Fuel swelling is the most prominent degradation issue for U-Mo alloys in service, typically manifested as the formation and growth of fission gas bubbles [7]. At the microscopic level, however, bubble nucleation and swelling are not solely determined by the production rate of fission gases or their low solubility in the matrix but are strongly influenced by the behavior of point defects and self-diffusion [10,11]. Point defects—including vacancies, interstitials, and substitutionals—constitute the most fundamental products of irradiation damage [12]. Their formation energies govern defect stability and equilibrium concentrations, while migration barriers define the mobility of both defects and host atoms. Self-diffusion, mediated by these defects, represents the primary atomic-scale mechanism driving microstructural rearrangements and defect redistribution. Under irradiation, large populations of vacancies and interstitials are continuously produced, recombined, and clustered, reshaping the spatial distribution of defects and directly altering the pathways and trapping efficiency for fission gases. Self-diffusion further accelerates defect redistribution and controls the nucleation and growth rates of irradiation-induced features such as voids, bubbles, and dislocation structures [13]. Consequently, fuel swelling is not simply a gas-driven process but rather a strongly coupled phenomenon arising from the interplay between defect generation, self-diffusion, and fission gas behavior.

Fission gases generated under irradiation initially occupy interstitial sites and migrate through interstitial networks or defect-assisted pathways [7,14,15]. They are subsequently trapped by vacancies, clusters, dislocations, and grain boundaries, forming gas-vacancy complexes that further evolve into bubbles [16]. This process is strongly coupled to self-diffusion, which governs the availability and mobility of defects. Conversely, bubble nucleation and growth modify local stress and chemical potentials, feeding back into defect production and annihilation. Due to the extremely low solubility of Xe and Kr in U-Mo alloys, bubble nucleation and growth become the primary cause of metallic fuel swelling. Understanding this coupled behavior is essential for developing swelling mitigation strategies and advancing high-power-density Low-Enriched Uranium (LEU) fuels.

This coupled perspective was already emphasized in the dynamic intragranular fission gas behavior model proposed by Griesmeyer et al. [11]. In their framework, fission gas transport is intrinsically linked to the creation, migration, and annihilation of defects. Vacancies and interstitials not only constitute the primary products of irradiation damage but also provide the essential pathways for gas atom migration, trapping, and release. Self-diffusion, mediated by these defects, governs the rate of lattice rearrangements and defect redistribution, thereby directly controlling the kinetics of gas-defect interactions. Therefore, a realistic description of swelling and fission gas release must explicitly incorporate defect energetics and self-diffusion mechanisms, which serve as the atomistic foundation for multiscale models that bridge irradiation-driven defect dynamics with the macroscopic performance of metallic fuels.

According to the equilibrium phase diagram, high-temperature γU-Mo decomposes upon cooling into orthorhombic α-U and tetragonal U₂Mo (the γ′ phase), the latter adopting a MoSi₂-type C11b structure [17] as shown in Figure 1, which space group is I4/mmm. The γ phase, stabilized when Mo ≥ 7–10 wt%, has been widely adopted as a baseline for low-enriched uranium research reactor fuels [8,18,19]. However, during thermal treatments, slow cooling, or irradiation-induced ordering, the γ′ phase may inevitably form [20]. Its layered ordering of U and Mo atoms significantly alters defect formation energies and diffusion pathways, thereby influencing the solubility, migration, and trapping of fission gases. The occurrence of γ′ domains introduces local instabilities within the γ matrix, accelerates bubble nucleation, and exacerbates swelling, ultimately affecting fuel reliability [11,21].

Current studies on the γ′ phase (U₂Mo, C11b structure) have mainly focused on its crystal structure and thermodynamic stability, whereas systematic investigations of defect energetics and fission gas diffusion mechanisms are still lacking. This knowledge gap hampers a comprehensive understanding of microstructural evolution and swelling in U–Mo fuels, particularly under high-flux irradiation. Neglecting the role of γ′ makes it difficult to fully elucidate local instabilities and their impact on bubble nucleation and growth.

Therefore, the present work aims to systematically investigate defect energetics and fission gas behavior in the γ′ phase. By calculating the formation energies of intrinsic defects, migration barriers, and the incorporation and diffusion characteristics of Xe atoms, this study elucidates the potential role of the γ′ phase in fuel swelling. The results not only complement the existing understanding of the γ phase but also provide critical parameters for predictive models of U-Mo fuel performance, thereby offering theoretical guidance for alloy design and processing optimization of advanced nuclear fuels.

The above analysis determined the configuration of U₂Mo. However, the effects of point defect diffusion, self-diffusion, and Xe on swelling behavior in U₂Mo under intrinsic or irradiation conditions remain unclear. In this work, we employ density functional theory (DFT) [22,23] combined with the climbing image nudged elastic band (CI-NEB) [24] method to systematically investigate the diffusion behavior of U, Mo, and Xe atoms in U₂Mo. We analyze the diffusion pathways of U and Mo atoms mediated by vacancies, substitutional defects, and vacancy-complex mechanisms, and evaluate the corresponding formation energies and dominant diffusion channels. In contrast, we examine the interstitial diffusion mechanism and the substitutional vacancy-coupled diffusion mechanism for Xe atoms. We also provide a detailed analysis of the associated defect formation energies and kinetic characteristics. This study not only elucidates the primary diffusion mechanisms and defect-related properties of each species within the U₂Mo matrix but also offers valuable theoretical insights into the migration behavior of extrinsic species, especially fission gas atoms like Xe. In this work, irradiation refers to the self-irradiation effects caused by the α-decay of uranium, rather than external beam exposure.

2. Computational Details

All calculations in this paper are performed using the Vienna ab initio simulation package (VASP) [25,26] based on Density Functional Theory (DFT) [22,23]. The electronic wave function is described by the projected augmented wave method (PAW) [27,28] and the exchange-correlation functional is represented by the Perdew-Burke-Ernzerhof (PBE) form within the generalized gradient approximation (GGA) [28,29]. For uranium (U), the PAW pseudopotentials (Xe, 5d, 4f) contain 14 valence electrons. For molybdenum (Mo), the PAW pseudopotential (4p5s4d) contains 14 valence electrons. The Methfessel-Paxton [30] method with a spread width of 0.1 eV was used for geometry relaxation and total energy calculations. Regarding the plane-wave basis, these calculations are converged at a 400 eV energy cutoff. Brillouin-zone (BZ) integrals were calculated with a 9 × 9 × 4 k-point sampling mesh generated by the Monkhorst-Pack (MP) [31] scheme for primitive cells, and a 3 × 3 × 2 k-point mesh for supercells including 108 atoms. Using the conjugate gradient (CG) method [32], the structural parameters were optimized until the forces on the atoms were less than 0.01 eVÅ⁻¹.

The formation energies of vacancies ($E_v^f$) are given by

$$E_v^f=E_v-E_0+{\mu }_X.$$

(1)

Here, $E_v$ and $E_0$ are the total energies of vacancy defective and perfect supercells, respectively. The ${\mu }_X$ indicates the chemical potentials of host atom X (X = U or Mo) removed from the supercell. In this work, the study does not consider the charge state of the defect, since U₂Mo is metallic, and only neutral defects can occur in a metal [33].

The substitution formation energies ($E_s^f$) when Element B replaces Element A is described as

$$E_{s\left(A\to B\right)}^f=E_s^{A\to B}-E_0+{\mu }_A-{\mu }_B,$$

(2)

where $E_s^{A\to B}$ is the total energy of the bulk containing the substitution defect; and ${\mu }_A$ and ${\mu }_B$ are the chemical potentials of A and B, respectively, which can represent U, Mo and Xe. The interstitial formation energy ($E_i^f$) is calculated as follows:

$$E_i^f=E_i-E_0-{\mu }_X,$$

(3)

where $E_i$ is the total energy of a bulk with an interstitial defect. ${\mu }_X$ is the chemical potentials of U or Mo.

The defect complexes formation energies ($E_c^f$) are described as

$$E_c^f=E_{Dc}-E_0+M{\mu }_U+N{\mu }_{Mo},$$

(4)

where $E_c^f$ is the total energy of the bulk containing the defect complexes; and ${\mu }_U$ and ${\mu }_{Mo}$ are the chemical potentials of U and Mo, respectively. M and N are the number of defective U and Mo atoms compared with the perfect supercell U₂Mo.

The ordered γ′-U₂Mo phase is known to be metastable with respect to decomposition into α-U and bcc-Mo at 0 K. Therefore, it is thermodynamically impossible to define a closed stability window simultaneously satisfying $2{\mu }_U+{\mu }_{Mo}={\mu }_{U2Mo}$, ${\mu }_U\le {\mu }_U^{\alpha -U}$ and ${\mu }_{Mo}\le {\mu }_{Mo}^{bcc}$.

In this work, γ′-U₂Mo is treated as a kinetically trapped metastable phase. Accordingly, the chemical potentials of uranium and molybdenum are set to their most stable elemental references, ${\mu }_U={\mu }_U^{\alpha -U}$ and ${\mu }_{Mo}={\mu }_{Mo}^{bcc}$, without introducing artificial U-rich or Mo-rich limits. This convention represents a physically meaningful reference point near the U₂Mo tie-line, and any hypothetical variation in μ within a feasible range would only cause linear shifts in the defect formation energy E_f according to atom counts n_i, without altering relative defect stabilities or the mechanistic conclusions.

The binding energies of the defect complexes and doped Xe are calculated as follows, respectively [34]:

$$E_b=E_{D1}+E_{D2}-E_D-E_0,$$

(5)

$$E_{b\left(Xe\right)}=E_{defect}+E_{Xe}-E_{doped}-E_0,$$

(6)

where $E_D$, $E_{D1}$ and $E_{D2}$ are the total energy of the crystal containing the defect complexes $D_1+D_2$, the total energy of the crystal containing the defect $D_1$ and the total energy of the crystal containing the defect $D_2$ respectively. $E_{defect}$, $E_{doped}$ and $E_{Xe}$ are the total energy of the defective but undoped crystal, the total energy of the defective and Xe-doped crystal, and the total energy of the isolated Xe atoms, respectively.

The linear interpolation method sifted possible migration paths and was optimized by the climbing image nudged elastic band (CI-NEB) [24] method.

All calculations were performed within the non-spin-polarized GGA framework without explicit inclusion of spin-orbit coupling (SOC) or +U corrections. This choice follows previous ab initio studies on U-Mo alloys, which consistently reported that U₂Mo and related U-Mo compounds are Pauli paramagnetic and nonmagnetic [35,36,37]. These studies have also demonstrated that SOC has a negligible influence on total energies and phase stability, and that the U-5f electrons are itinerant and strongly hybridized with Mo-4d orbitals, exhibiting metallic behavior without strong correlation effects [35,36,37]. Therefore, omitting spin polarization, SOC, and +U corrections does not affect the accuracy of our results.

3. Results

3.1. Self-Defect Formation

We constructed a 3 × 3 × 2 supercell for investigating the formation and diffusion of defects. During the continuous reaction process of U-Mo alloy nuclear fuel, the constant consumption of uranium atoms inevitably generates many defects. The U₂Mo structure adopted in this study is a tetragonal crystal with the I4/mmm space group, which is widely used to describe experimentally observed phases in the U-Mo alloy system. Although this structure is not the thermodynamic ground state in first-principles calculations at 0 K, it exhibits good kinetic stability under high-temperature conditions. It frequently appears in experiments, making it widely used in theoretical studies. It should be noted that due to its metastable nature, the chemical potential construction process may not fully satisfy thermodynamic stability constraints. This study employs the standard states of elements as chemical potential references to calculate defect formation energies, as shown in Figure 2. There are four basic point defects in U₂Mo: uranium vacancy (V_U), molybdenum vacancy (V_Mo), U substitutional defect on Mo site (U_Mo), and Mo substitutional defect on U site (Mo_U). In addition to vacancy and substitutional defects, we calculated the formation energies of molybdenum and uranium interstitial defects, denoted as I_Mo and I_U, respectively, as shown in Figure 2. Since U₂Mo in this study is metastable, the following defect formation energies are analyzed based on its existence.

Figure 2 shows that among all considered point defect types, the two substitutional defects U_Mo (U atoms occupying Mo sites) and Mo_U (Mo atoms occupying U sites) exhibit the lowest formation energies, significantly lower than those of vacancies and interstitials. In U₂Mo structures, substitutional defects are the most readily formed point defect type. However, compared to substitutions and vacancies, interstitial-type defects display greater diversity, with their formation sites, lattice distortions, and energy distributions exhibiting more complex behaviors.

To comprehensively evaluate the evolution mechanisms of intrinsic defects, the subsequent analysis will investigate different configurations of interstitial defects and compare their thermodynamic feasibility with spatial distribution characteristics. This study primarily examines three possible interstitial occupation mechanisms for U and Mo: (a) U/Mo forming dumbbell-type interstitial defects; (b) U/Mo occupying octahedral interstitial sites; and (c) U/Mo occupying tetrahedral interstitial sites, as illustrated in Figure 3. Based on the interstitial formation energies listed in Figure 2 U/Mo tends to form dumbbell-type interstitial states in U₂Mo, making them one of the most probable defect types in the alloy. Among the intrinsic interstitial sites, the initially constructed defect was of the tet5 configuration. During geometric optimization, the interstitial atom spontaneously migrated and stabilized at a tet2 interstitial site, indicating that the tet5 site is not locally stable. In contrast, the tet2 site is thermodynamically more favorable in the current structure. Therefore, this study excludes tet5 interstitial sites from consideration in intrinsic interstitial defects. These results also show that for interstitial-type defects, the choice of initial configuration may significantly influence the final structure, necessitating special attention to their configurational reconstruction behavior.

As shown in Figure 2, the formation energy of interstitial point defects is higher than that of other point defects, making interstitial defects more difficult to form. Therefore, we initially consider defect complexes that do not include interstitial defects. Isolated point defects may participate in atomic diffusion by aggregating to form defect complexes. Among defect complexes composed of two adjacent lattice-site point defects, the structures typically consist of five defect complexes [38]. Thus, point defect aggregation in U₂Mo can form five defect complexes as diffusion media.

Table 1. Formation energies (E_f) and binding energies (E_b) of C11b type U₂Mo defect complexes.

Properties	Ef (eV)	Eb (eV)
VU + UMo	/	/
VU + VMo	1.322	2.411
VU + VU	3.276	0.685
VU + MoU	0.854	1.131
VMo + MoU	0.232	1.525

presents the formation and binding energies of defect complexes calculated by Equations (4) and (5). Among these defect complexes, the V_U + U_Mo defect complex undergoes structural relaxation, after which the U atom moves from the substitutional position to the U vacancy, altering the original structure of the defect complex. Consequently, V_U + U_Mo cannot exist as a stable defect complex. The reason is that U atoms prefer to occupy U sites rather than Mo sites. Upon relaxation, the U atom substituting for Mo moves to the U site, fills the U vacancy, and reduces the system energy by eliminating the high formation energy of V_U.

As shown in Table 1, the binding energies of all four defect complexes are positive values. These results show that point defects in U₂Mo exhibit attractive interactions and aggregate to form clusters. The binding energy of the V_Mo + Mo_U complex is higher than that of other defects, while its formation energy is lower than that of different defects. The results show that V_Mo + Mo_U is the predominant defect complex in U₂Mo, characterized by lower formation energy and higher binding energy, serving as potential mediators for the self-diffusion of Mo and U atoms in U₂Mo.

3.2. Self-Diffusion in U₂Mo

Due to the relatively low formation energies of vacancy and substitutional defects (as shown in Figure 2), this paper first considers the migration of U and Mo atoms via vacancies (Mo or U vacancies) and substitutional defects through intrasublattice or intersublattice hopping.

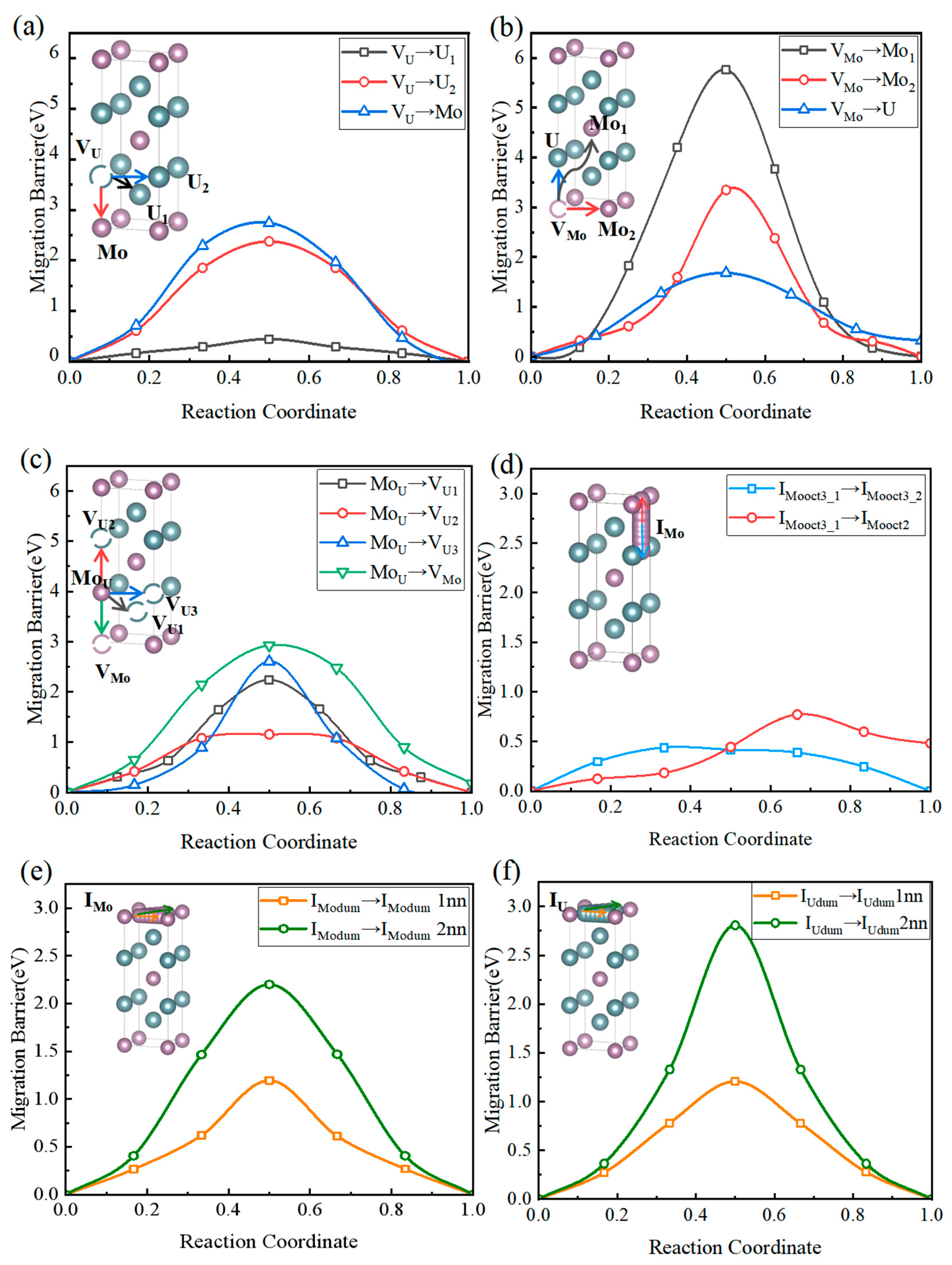
Figure 4a illustrates the diffusion pathways and minimum energy paths (MEP) of molybdenum (Mo) and uranium (U) atoms via uranium vacancies within intrasublattice and intersublattice migrations. As shown, uranium atoms exhibit the lowest migration barrier (approximately 0.44 eV) when moving along the nearest-neighbor direction within the uranium sublattice (path: V_U → U₁), indicating strong intrinsic diffusivity. The barrier increases significantly with migration distance, reaching 2.38 eV for the second-nearest-neighbor (U₂) path, revealing pronounced spatial anisotropy and localized constraints in uranium-vacancy-mediated diffusion. In contrast, intersublattice migration of molybdenum atoms mediated by uranium vacancies (path: V_U → Mo) requires overcoming a higher barrier of ~2.74 eV. Intersublattice hopping of uranium vacancies (V_U) leads to their transition into the molybdenum sublattice, forming molybdenum substitutional defects (Mo_U) and molybdenum vacancies (V_Mo), thereby providing pathways for Mo diffusion. This shows that Mo atoms substituting U sites (Mo_U defects) are thermodynamically stable, but high migration barriers hinder their formation. Therefore, effective diffusion of substitutional defects is unlikely under irradiation or field-free conditions. Overall, U-vacancy-driven diffusion is confined to the U sublattice and governed by nearest-neighbor vacancy connectivity, whereas intersublattice substitutional defect migration remains kinetically inaccessible under conventional thermal conditions.

Figure 4b shows the migration pathways and MEPs for intra-sublattice and inter-sublattice jumps of Mo vacancies. Three migration pathways are identified: V_Mo → Mo₁, V_Mo → Mo₂, and V_Mo → U. Judging from the migration energy barriers, the Mo self-diffusion pathway (V_Mo → Mo₁) exhibits the highest energy barrier of approximately 5.76 eV, indicating significant diffusion resistance and thermodynamic unfavorability. Although V_Mo → Mo₂ represents second-nearest-neighbor diffusion, its energy barrier remains as high as 3.1 eV, demonstrating strong localization of Mo atoms in this system. In contrast, the diffusion pathway of Mo vacancies toward U lattice sites shows significantly lower migration barriers. The V_Mo → U pathway has an energy barrier of 1.68 eV, with a smooth and continuous trajectory devoid of additional local minima, suggesting favorable feasibility for this diffusion route. Notably, the V_Mo → U pathway possesses the lowest migration barrier, indicating that under realistic defect-containing or thermally perturbed conditions, Mo is more likely to preferentially undergo substitutional diffusion via the Mo → U mechanism rather than traditional Mo-Mo self-diffusion. These results show that inter-sublattice substitutional migration may emerge as the dominant diffusion channel in Mo-vacancy-dominated diffusion mechanisms, providing critical insights into understanding Mo behavior in alloy phases, coatings, or ceramics. (Intra-sublattice jumps of molybdenum vacancies (V_Mo) do not constitute the dominant mechanism governing Mo atomic self-diffusion. In U₂Mo, other more active migration mechanisms dominate the self-diffusion behavior of Mo atoms.)

This section further investigates the migration mechanism mediated by the defect complex (V_U + Mo_U) formed by uranium vacancies (V_U) and molybdenum substitutional defects (Mo_U). Since U atoms spontaneously migrate back to the U vacancy sites during structural optimization, making it impossible to maintain the substitutional defect configuration, this study did not select the U_Mo + V_U configuration as a stable defect for analysis. Our calculations show these two complexes exhibit the lowest formation energies among all defect configurations. Although researchers have identified such substitutional defect-assisted migration mechanisms in other alloys and intermetallic compounds [39], these mechanisms remain unverified in U₂Mo.

Figure 4c illustrates the atomic migration mechanism of molybdenum substitutional defects (Mo_U) in γ′-U₂Mo by analyzing the minimum energy paths (MEPs) and migration barriers for Mo atoms occupying U sublattice sites and migrating toward adjacent U and Mo vacancies (V_U1, V_U2, V_U3, and V_Mo). Among these paths, the second-nearest-neighbor exchange Mo_U → V_U2 exhibits the lowest energy barrier of 1.16 eV, while diffusion toward a Mo vacancy (Mo_U → V_Mo) shows the highest barrier of 2.92 eV. Therefore, the substitution-assisted exchange (Mo_U + V_U) mechanism exhibits a diffusion-barrier range of 1.16–2.24 eV, and the Mo_U + V_Mo exchange path reaches up to 2.92 eV. These values are still markedly lower than the vacancy-mediated Mo migration barriers (3.34–5.76 eV, Figure 4b). Overall, as shown in Figure 4b,c, the substitution-assisted mechanism involves a lower energy cost and pronounced directional anisotropy, indicating that it dominates the Mo diffusion process in γ′-U₂Mo.

Although intrinsic metal atoms are generally considered not to diffuse via interstitial mechanisms in most metallic systems—primarily due to their large atomic radii and high interstitial formation energies, which render interstitial migration in bulk phases highly improbable—specific conditions such as high crystal defect density, loosely packed atomic structures near grain boundaries, or high-pressure/high-energy irradiation environments may enable Mo and U atoms to occupy interstitial sites locally, forming metastable states that induce interstitial diffusion behavior. To comprehensively evaluate potential diffusion pathways in this system, this study incorporates modeling of migration paths for Mo and U atoms in octahedral and tetrahedral interstitial sites and conventional substitutional diffusion mechanisms. The climbing image nudged elastic band (CI-NEB) method is employed to assess migration energy barriers and thermodynamic feasibility, providing a theoretical basis for understanding interstitial migration mechanisms that may be activated under non-equilibrium conditions.

To investigate the diffusion mechanisms of intrinsic interstitial atoms in the U-Mo system, initial configurations were constructed with U and Mo atoms occupying octahedral interstitial sites (oct3), followed by mapping their migration paths to the first-nearest-neighbor octahedral interstitial sites. This study performed CI-NEB calculations to determine the diffusion energy barriers. As shown in Figure 4d, Mo atoms exhibit a well-defined diffusion barrier along the octahedral-octahedral migration path, with stable transition-state structures and energy barriers below 0.8 eV, consistent with typical metallic interstitial diffusion mechanisms.

In contrast, U atoms display markedly different diffusion behavior under the same structural conditions. One migration path features a distinct local minimum at the midpoint of the migration coordinate, forming an intermediate energy well and suggesting a stable intermediate configuration and a multi-step migration mechanism.

Another path exhibits a monotonically increasing energy profile without local transition states or energy minima, indicating thermodynamic instability of the final configuration of this pathway and kinetic inaccessibility.

Although U atoms have lower interstitial formation energies than Mo, their diffusion is strongly constrained by kinetics due to the absence of favorable low-energy migration pathways. In contrast, Mo atoms, despite their relatively higher formation energy, exhibit continuous and smooth migration potential energy surfaces with well-defined transition states, thereby possessing superior diffusion capabilities. In multi-component metallic systems, interstitial diffusion is determined not only by defect formation energies but also by the morphology of the migration path’s potential energy surface and its kinetic accessibility.

As shown in Figure 4e,f, this study takes the dumbbell configuration, formed by U and Mo atoms occupying the 2a sites along the <110> direction, as the initial and final states. It constructs their migration paths to the first and second nearest neighbors. A diffusion energy barrier map was constructed for U and Mo, covering multiple octahedral and tetrahedral interstitial sites, to further elucidate the global migration pathways of interstitial atoms. We systematically calculated each path’s energy barriers and identified typical transition processes (O → T, T → O, T → T, etc.) and their barrier distributions. In Figure 5a,b, interstitial atoms achieve long-range diffusion through multistep hopping. At the same time, the differences in energy barriers among various pathways show the connection probabilities between sites and the relative advantages of migration directions. As shown in Figure 5a,b, the linear migration from tet2 → tet1 passes through a dumbbell interstitial site, where the formation energy of the dumbbell interstitial is lower than that of tetrahedral and octahedral interstitials, leading to a collapse of the energy barrier. Consequently, we insert an octahedral interstitial site midway.

By comparing the migration energy barriers of different diffusion paths, we find that the Mo atom most likely diffuses by jumping from one octahedral interstitial position to an adjacent equivalent octahedral interstitial position. In contrast, the most difficult diffusion occurs when jumping from one dumbbell interstitial position to the second nearest neighbor dumbbell interstitial position. The most difficult diffusion path for the U atom involves jumping from one dumbbell interstitial position to the second nearest neighbor dumbbell interstitial position.

3.3. Xe Diffusion in U₂Mo

To gain an in-depth understanding of the diffusion behavior of xenon (Xe) atoms in U₂Mo, we systematically calculated and compared their formation energies at different lattice sites, including substitutional sites, tetrahedral interstitial sites, octahedral interstitial sites, and dumbbell configurations.

Table 2. Solution energy of a single Xe atom in substitutional and interstitial sites of U₂Mo.

Properties	Ef (eV)
XeMo	7.13
XeU	6.59
IXeoct1	12.00
IXeoct2	11.37
IXeoct3	10.60
IXetet1	10.59
IXetet2	10.60

lists the formation energies of various defect configurations.

In U₂Mo, the calculated formation energies for Xe atoms substituting U and Mo atoms are shown in Table 2, with values of 6.59 eV and 7.13 eV, respectively. The formation energy of Xe substituting U atoms in the lattice is lower than that in α-U (6.69 eV [40]). This shows that the U-atom sites in U₂Mo exhibit a more substantial capacity to accommodate oversized impurity Xe atoms, primarily due to the weaker lattice distortion response and higher geometric compatibility introduced by Xe substitution.

In U₂Mo, the formation of interstitial Xe defects is relatively favorable, with an average formation energy of 10.89 eV, lower than that in α-U (11.43 eV [40]). Due to the complex atomic environment and diverse interstitial types in the U₂Mo crystal structure, it is challenging to precisely determine the most stable interstitial occupation site for Xe atoms.

This study focuses on analyzing three possible interstitial occupation mechanisms: (a) Xe forming dumbbell-type interstitial defects, (b) Xe occupying octahedral interstitial sites, and (c) Xe occupying tetrahedral interstitial sites. As an oversized impurity atom, Xe tends to form dumbbell-type interstitial states in U₂Mo, making it one of the most likely defect types in the alloy.

Starting from the substitution defects, interstitial defects, and diffusion behavior of Xe atoms, this study comprehensively investigates the behavior of Xe in γ’-U₂Mo. The substitution behavior of Xe atoms in the metal matrix reflects their ability to occupy vacancy defects. Since the energy required for direct hopping of Xe atoms through adjacent interstitial sites is relatively high, vacancies are introduced into the U₂Mo system to examine their influence on the hopping of substitutional Xe atoms. During the hopping process, U vacancies easily capture Xe atoms, forming substitutional atoms. Due to the larger atomic radius of U compared to Mo, U occupies more space in the U₂Mo system, making it more favorable to introduce Xe atoms.

Figure 6a,b, respectively, illustrate the migration of Xe atoms occupying U sites substitutionally (Xe_U) toward adjacent U vacancies (V_U) and the migration of Xe atoms occupying Mo sites substitutionally (Xe_Mo) toward adjacent Mo vacancies (V_Mo) in U₂Mo, both following a vacancy-assisted diffusion mechanism. A comparison between Figure 6a,b show that the energy barrier for fission gas Xe occupying Mo fission gas Xe occupying U vacancies to hop to U vacancies. Relatively, the hopping of fission gas Xe occupying U vacancies to U vacancies occurs more readily. This is because, compared to Mo atoms, the size difference between U and Xe atoms is minor, resulting in weaker induced lattice distortion.

The Xe atom is an inert gas, exhibiting weak chemical adsorption capabilities in most metals and semiconductor materials, with a tendency toward physical adsorption or occupying interstitial sites. Comparative analysis of formation energies obtained through structural relaxation shows that the atom is more stable in the dumbbell interstitial site, with its formation energy being lower than that of both tetrahedral and octahedral interstitial sites.

The diffusion of interstitial Xe is representative of Xe migration behavior and is a primary focus in studying impurity element migration in nuclear fuels. Long-range diffusion of impurity atoms often relies on interstitial pathways, making the study of interstitial Xe diffusion significant for understanding Xe nucleation and growth. Due to its relatively large atomic radius, Xe diffusion typically requires assistance from other atoms, as observed in α-U [40], which somewhat affects its diffusion rate.

In U₂Mo, the migration pathways of Xe atoms can be categorized into three main types, based on the 2a-<110> dumbbell, octahedral interstitial, and tetrahedral interstitial sites: (1) diffusion within the (001) crystal plane, and (2) diffusion along the <001> direction from one (001) plane to another. Since the tetrahedral interstitial, octahedral interstitial, and 2a-<110> dumbbell sites all lie on the (001) plane and are close to each other, we anticipate that the diffusion energy barrier for Xe on this plane is relatively low. However, assistance from other atoms is often required when Xe migrates to another (001) plane.

By connecting various octahedral and tetrahedral interstitial sites, possible diffusion pathways for Xe are illustrated, as shown in Figure 6e. Among the multiple migration paths tested, some exhibit distinct saddle-point structures in NEB simulations. In contrast, others flatten or revert after structural optimization, exhibit atomic rearrangements, or undergo local collapse or nonphysical distortion, thus failing to form practical migration barriers. Consequently, we calculated multiple diffusion paths for Xe atoms. As presented in

Table 3. Xe atom’s 8 diffusion pathways and diffusion energy barriers at interstitial sites in U₂Mo. E_m represents the migration barrier.

Xe Path	Xe Diffusion Path	Em (eV)
Path1	oct3 → oct3	1.11
Path2	oct3 → oct2	/
Path3	tet1 → tet1 2nn	1.41
Path4	tet2 → tet2 2nn	1.12
Path5	tet2 → oct3	1.12
Path6	tet2 → oct2 → tet1	0.77
Path7	dum → dum 1nn	1.49
Path8	dum → dum 2nn	2.10

and Figure 6c–e, Path 6 incorporates an octahedral interstitial site because the direct migration from tet2 to tet1 passes through a dumbbell interstitial site, where the formation energy is lower than that of the tetrahedral interstitial site, leading to a collapse of the energy barrier.

Through comparison of the migration energy barriers along different diffusion pathways, it was found that the Xe atom has the lowest migration barrier along Path 6 (tet2 → oct2 → tet1), making it the most favorable diffusion direction; whereas Path 8 (dum → dum 2nn) exhibits the highest migration barrier, representing the most difficult diffusion pathway.

4. Discussion

The present computational results substantiate the reliability of the proposed defect behavior and fission gas transport mechanism in U₂Mo. As illustrated in Figure 2, substitutional defects (U_Mo and Mo_U) exhibit the lowest formation energies, indicating that they are the most favorable intrinsic defects under irradiation and are expected to dominate the defect landscape. In contrast, interstitial configurations display strong site preference. Table 2 shows that U, Mo, and Xe atoms preferentially occupy the dumbbell configuration at the 2a site along the <110> direction (2a-<110> dumbbell) and the tet1 tetrahedral interstitial, both of which possess lower formation energies compared with other interstitial sites. The local chemical environment is decisive for the stability of specific interstitial configurations.

For defect complexes, V_U + Mo_U and V_Mo + Mo_U possess both lower formation energies and higher binding energies, identifying them as the most stable complexes in U₂Mo (Figure 4). This suggests that point defects interact attractively and tend to form clusters, while also providing effective channels for atomic diffusion. Further analysis shows that U self-diffusion primarily occurs via vacancy hopping, whereas Mo diffusion is dominated by a substitution-induced mechanism, which is more efficient than the conventional vacancy mechanism. These results show that local defect environments not only determine stability but also significantly modify diffusion kinetics.

The transport of fission gases is also strongly governed by defect environments. In the initial stage, Xe atoms are more likely to exist in interstitial configurations due to the lack of vacancy matching. As shown in Table 2, the formation energy of substitutional Xe in U₂Mo is much lower than that in α-U (11.43 eV [40]), suggesting that Xe is more easily trapped and transported via vacancy-assisted substitutional diffusion. Meanwhile, the dumbbell interstitial is found to be the most stable Xe configuration, with a formation energy lower than those of the tetrahedral and octahedral sites, explaining its preference as the initial trapping site. During subsequent evolution, Xe can further transform from the interstitial to the substitutional state, thereby lowering the migration barrier and facilitating diffusion. The diffusion and trapping of Xe are strongly governed by these defect environments. DFT calculations predict that Xe is initially stabilized in interstitial states, particularly dumbbell configurations, before being trapped at substitutional sites via vacancy-assisted mechanisms. This explains why experimental studies observe that Xe in shallow regions with few defects remains largely in a dissolved state, whereas in high-damage regions with abundant vacancies, Xe is efficiently captured, forming nanobubbles [8,9,41]. The stability of defect complexes is consistent with experimental evidence that bubbles preferentially nucleate at dislocations and grain boundaries, where defect clustering lowers the energetic barrier for gas accumulation.

A quantitative comparison of diffusion barriers further supports this interpretation. As shown in Table 3 and Figure 6, the migration barriers for interstitial Xe diffusion in U₂Mo fall within the range of 0.77–2.10 eV, among which path 6 (tet₂ → oct₂ → tet₁) exhibits the lowest value of 0.77 eV, and Xe migration between adjacent octahedral interstitial sites (oct → oct) has a barrier of 1.11 eV, both much lower than the interstitial migration barrier in UO₂ (5.29 eV [42] or 3.90 eV [43]).

In addition, the U-vacancy-mediated substitutional diffusion (Xe_U + V_U) in U₂Mo has a migration barrier of 0.93 eV, lower than that of α-U (1.14 eV sand 1.58 eV [40,44]) for the same mechanism (Figure 6a).

These results indicate that U₂Mo provides both a more open interstitial network and a lower-energy substitutional diffusion pathway for Xe migration.

Experimental activation energies Q obtained from post-irradiation annealing or implantation-anneal studies are often comparable to DFT migration barriers E_m, since under defect-rich conditions Q ≈ Em. The comparative results summarized in

Table 4. Comparison between experimentally measured diffusion activation energies Q and DFT calculated migration barriers E_m for Xe in different nuclear fuel systems. Experimental values are typically obtained from post-irradiation annealing (PIA) or implantation-anneal studies, where Q ≈ E_m due to externally introduced defects.

System/Phase	Diffusing Species	Mechanism/Regime	Experimental Q (eV)	Em (eV)	Reference
α-U	Xe	Vacancy	/	1.14–1.58	Gui-Yang Huang and B D Wirth [45]
α-U	Xe	Interstitial	/	1.01–1.24	Gui-Yang Huang and B D Wirth [45]
UO2	Xe	Vacancy	3.50–4.30	/	Miekeley and Felix [46]
UO2	Xe	Interstitial	/	3.78 or 5.29	Y. Yun and H. Kim [42]
UO2	Xe	Interstitial	/	3.90 (Exp.)	Hj. Matzke [43]
γ′-U2Mo	Xe	Vacancy	/	0.93–1.59	This study
γ′-U2Mo	Xe	Interstitial	/	0.77–2.10	This study

provide additional insight into the energetics of Xe diffusion across different nuclear fuel systems. In α-U, DFT predicts that Xe diffusion occurs via both vacancy-mediated and interstitial pathways, with relatively low migration barriers of 1.01–1.58 eV. In contrast, experiments on UO₂ show much higher activation energies (3.50–4.30 eV), reflecting the combined effects of intrinsic defect formation and migration in an oxide matrix.

For γ′-U₂Mo, the present calculations reveal that both vacancy-assisted and interstitial-mediated mechanisms are energetically accessible, with migration barriers ranging from 0.77 to 2.10 eV. These values are comparable to or even lower than those for α-U, suggesting that Xe transport in γ′-U₂Mo is more favorable. This helps rationalize experimental observations of high-density nanobubbles forming in defect-rich regions: the relatively low migration barriers facilitate Xe mobility once defects are available, while stable defect complexes provide efficient trapping sites for bubble nucleation and growth.

The present results highlight the fundamental role of point defects, self-diffusion, and fission gas diffusion in determining the microstructural stability and swelling behavior of U-Mo fuels. The γ′-U₂Mo phase, with its ordered C11b structure, exhibits distinct defect energetics and diffusion characteristics compared to the disordered γ phase, which significantly influence fission gas transport and trapping. These findings suggest that neglecting the contribution of the γ′ phase may lead to incomplete or inaccurate predictions of swelling and fuel performance, particularly under conditions where γ′ domains inevitably form during cooling or irradiation-induced ordering. Therefore, the atomistic insights obtained in this work provide critical input for multiscale models and constitute a valuable theoretical foundation for the design and optimization of advanced U-Mo fuels.

5. Conclusions

This study shows that in γ′-U₂Mo, substitutional defects (such as U_Mo and Mo_U) have the lowest formation energies and are the most favorable intrinsic defects, dominating the defect distribution in the material. From an energetic perspective, U, Mo, and Xe preferentially occupy the dumbbell configuration formed along the <110> direction at 2a sites (2a-<110> dumbbell) and tet1 tetrahedral interstitial sites. Due to their low formation energies and high binding energies, defect complexes (such as V_U + Mo_U and V_Mo + Mo_U) are the most stable complexes, indicating that point defects tend to aggregate and promote atomic diffusion. For Xe, it predominantly exists in interstitial configurations, with the dumbbell interstitial being the most stable configuration, having a lower formation energy than other interstitial sites, making it the primary capture site. Furthermore, Xe migrates most efficiently along path 6 (tet2 → oct2 → tet1) in γ′-U₂Mo, suggesting that both interstitial and vacancy-assisted mechanisms cooperatively facilitate efficient gas migration.