Research on the Application of the Taguchi-TOPSIS Method in the Multi-Objective Optimization of Punch Wear and Equivalent Stress in Cold Extrusion Forming of Thin-Walled Special-Shaped Holes
Abstract
1. Introduction
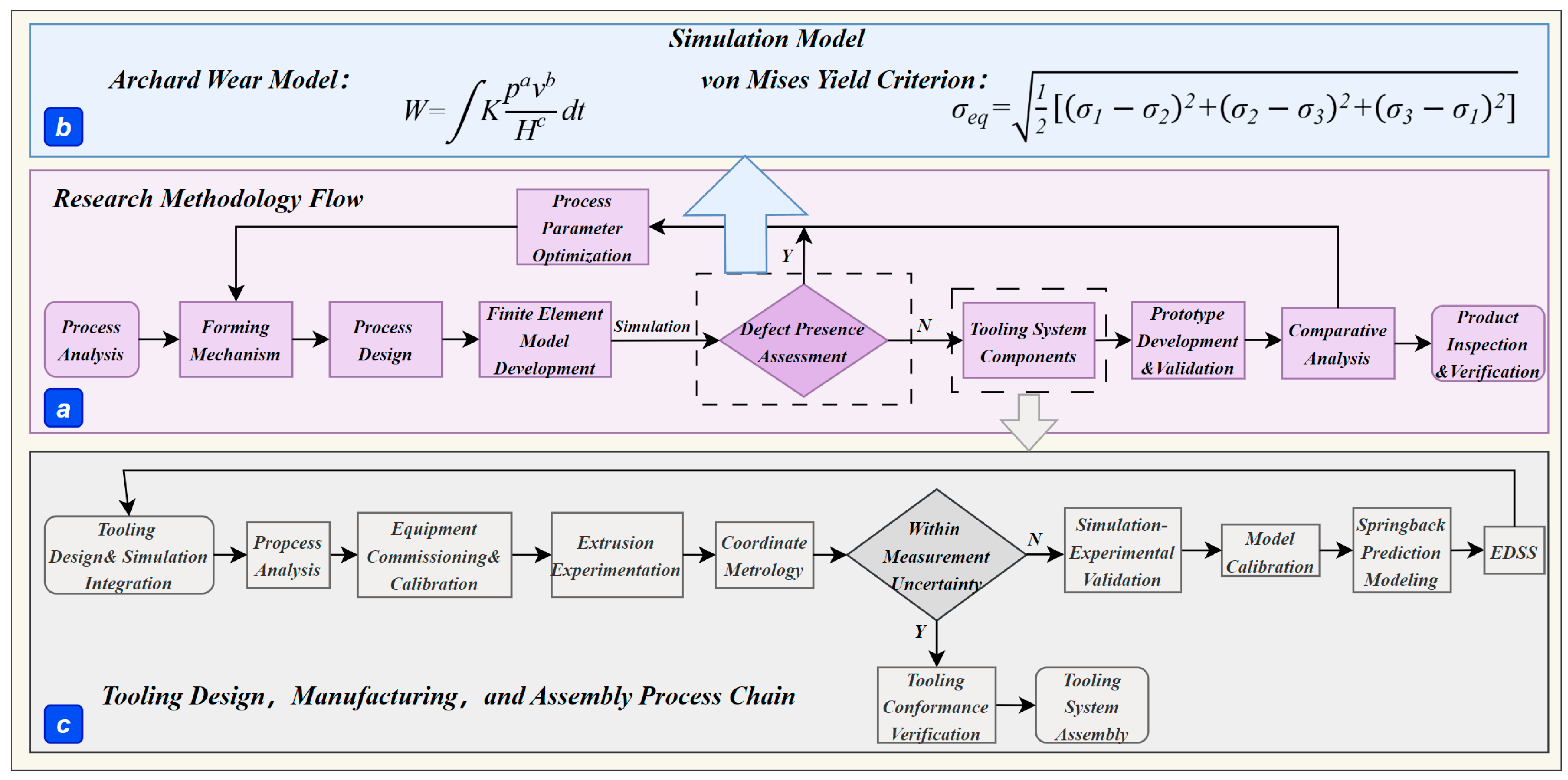
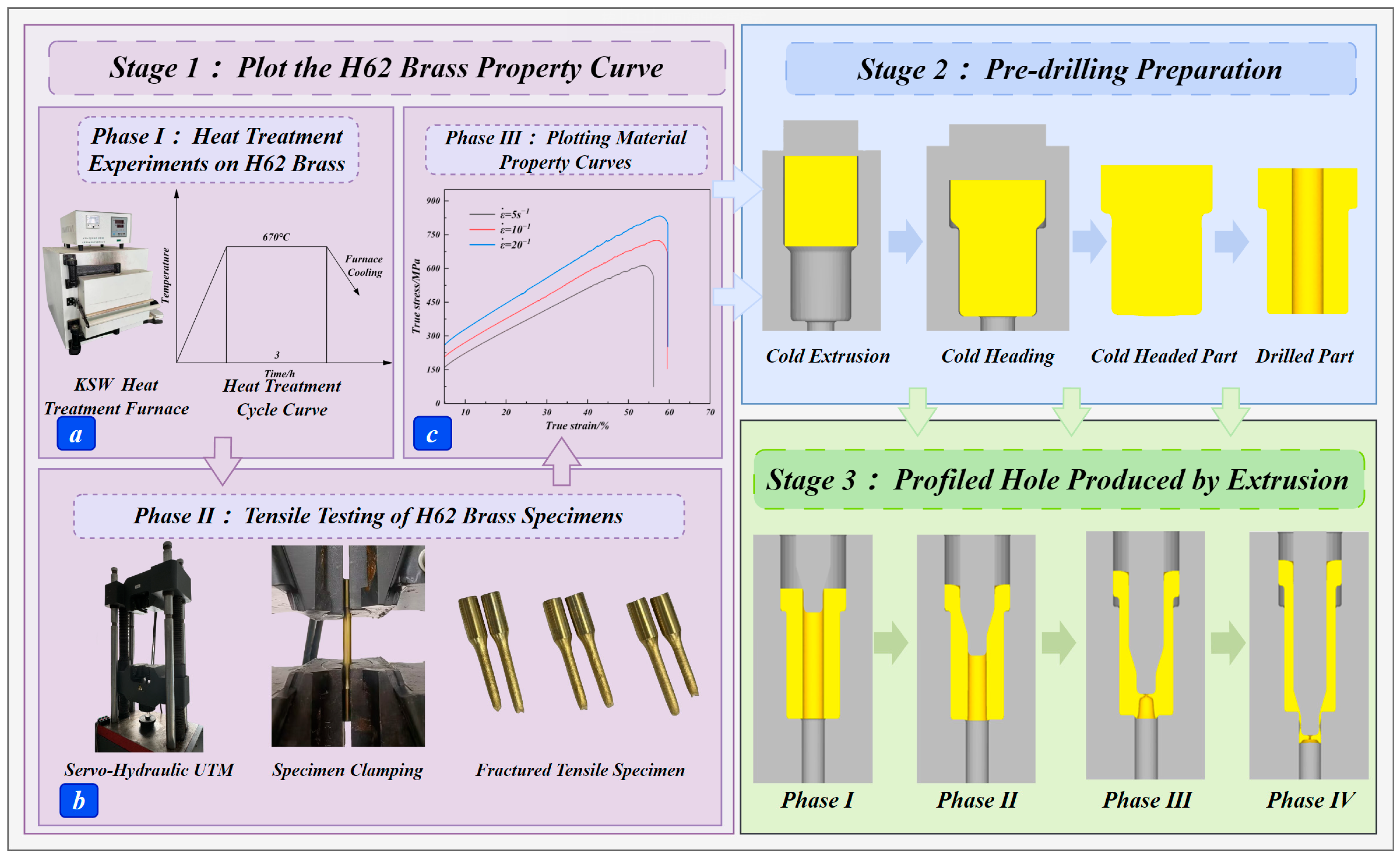
2. Experimental Procedure
2.1. Trial Protocol
2.2. Constitutive Equation of H62 Material
2.3. Simulation Experiment
3. Punch Simulation Analysis
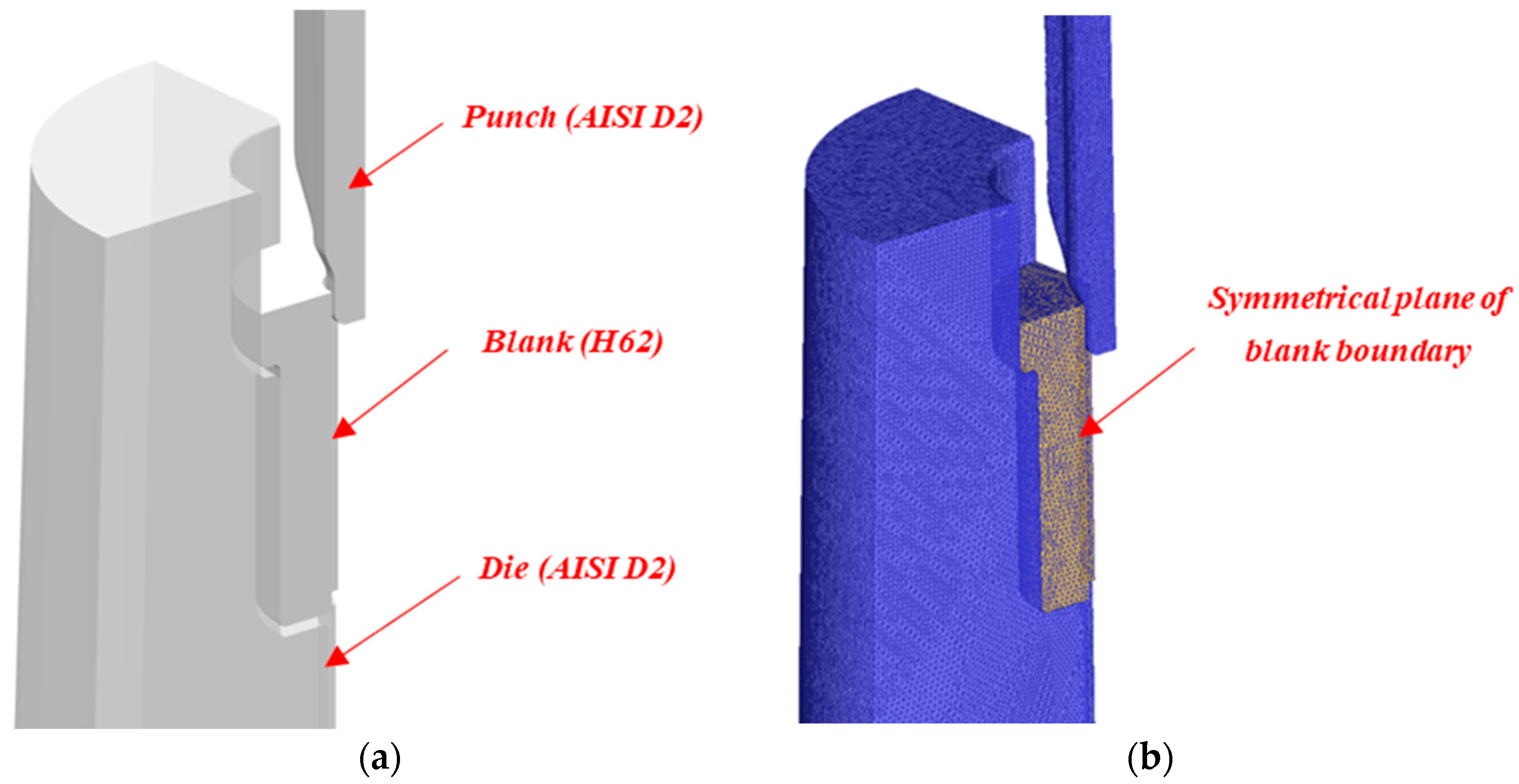
3.1. Finite Element Simulation Model
3.2. Development and Simulation
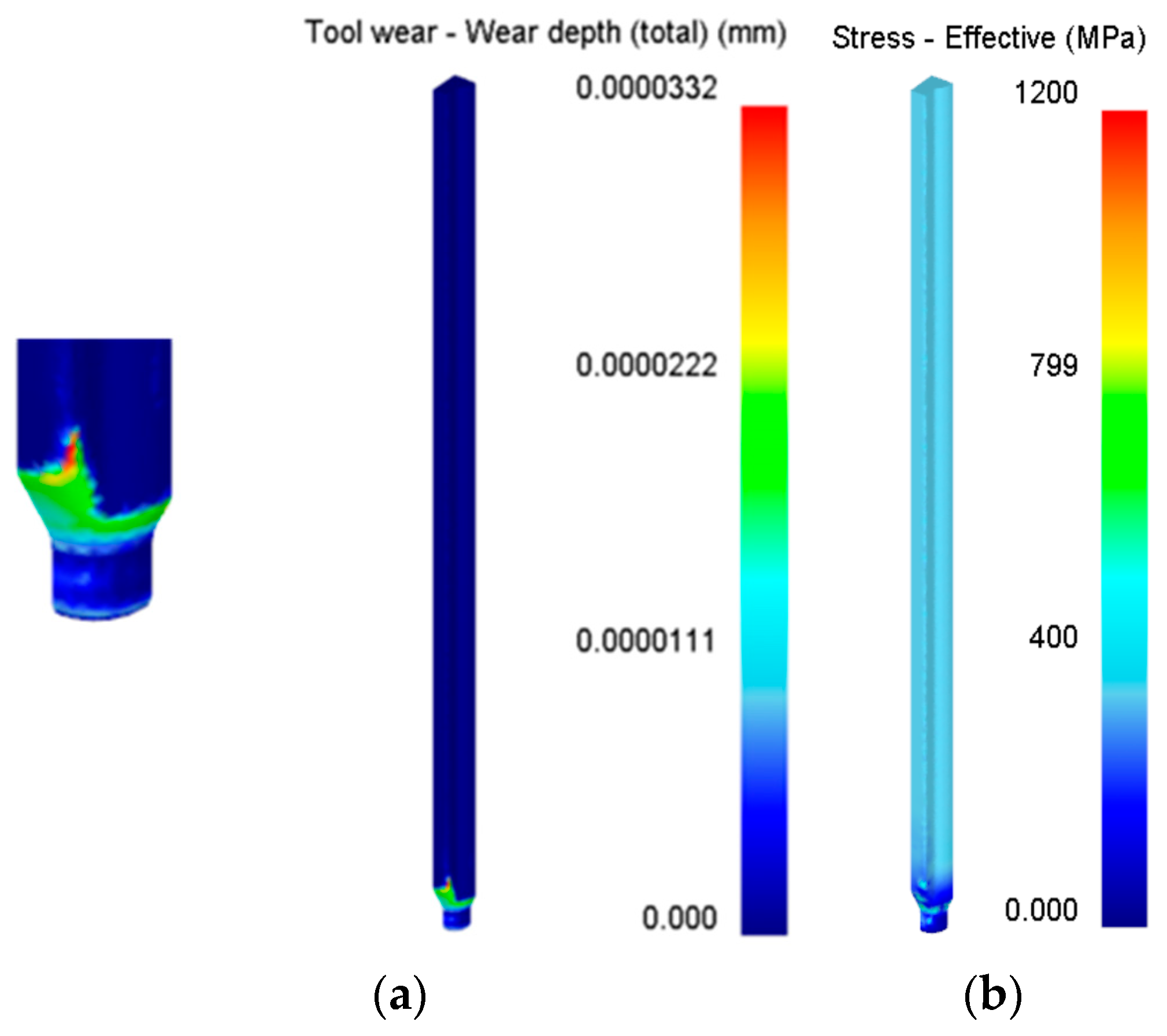
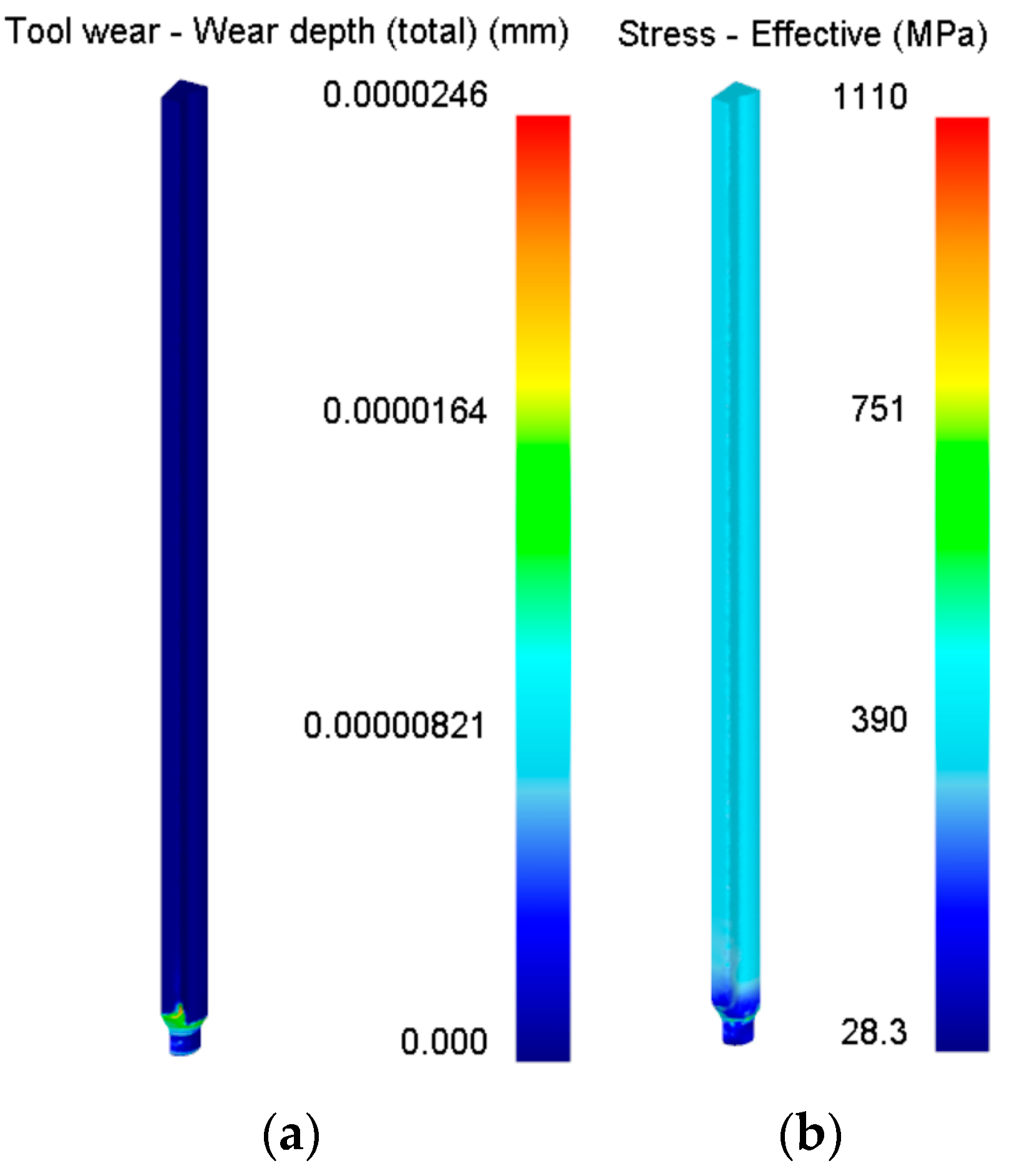
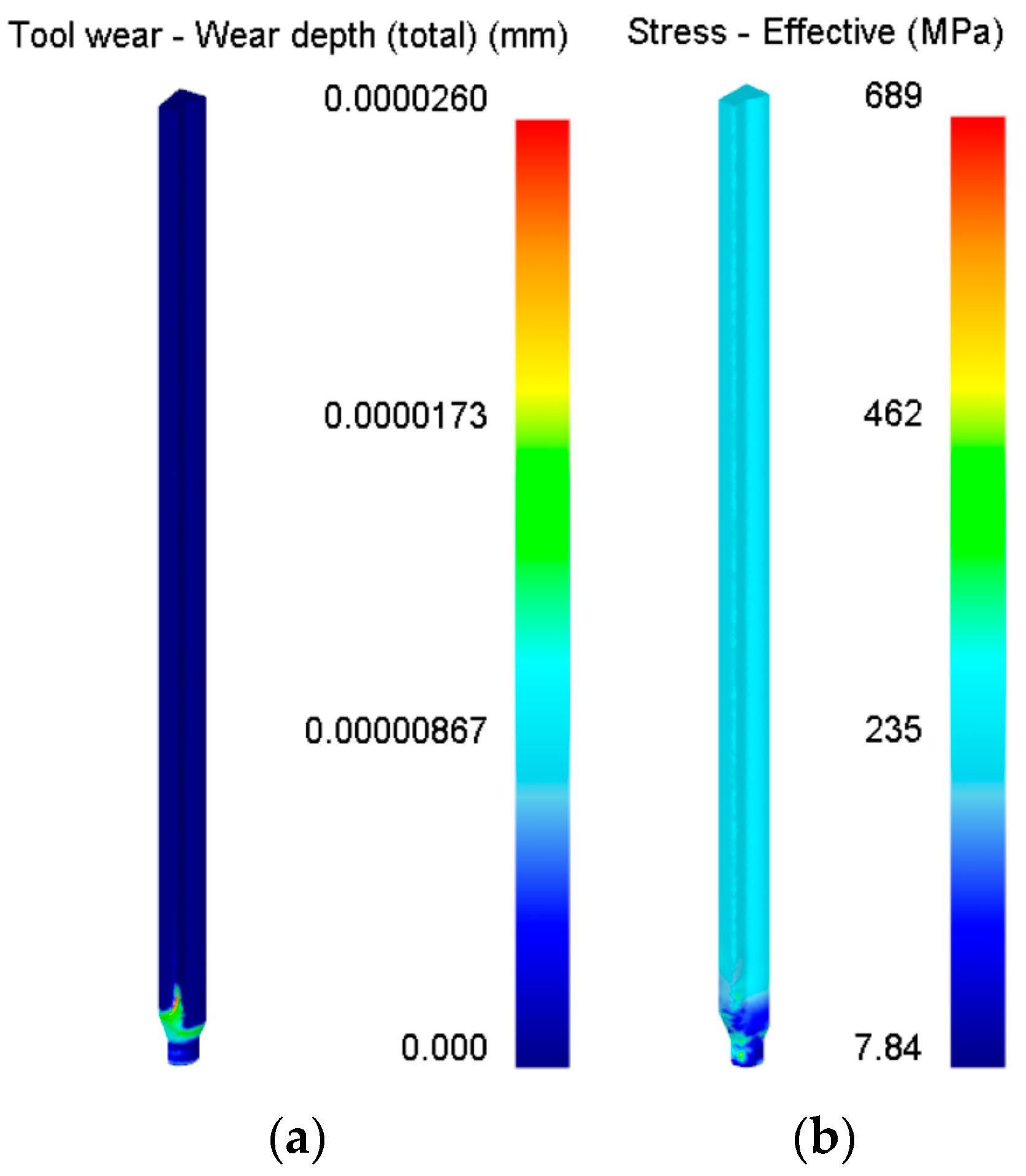
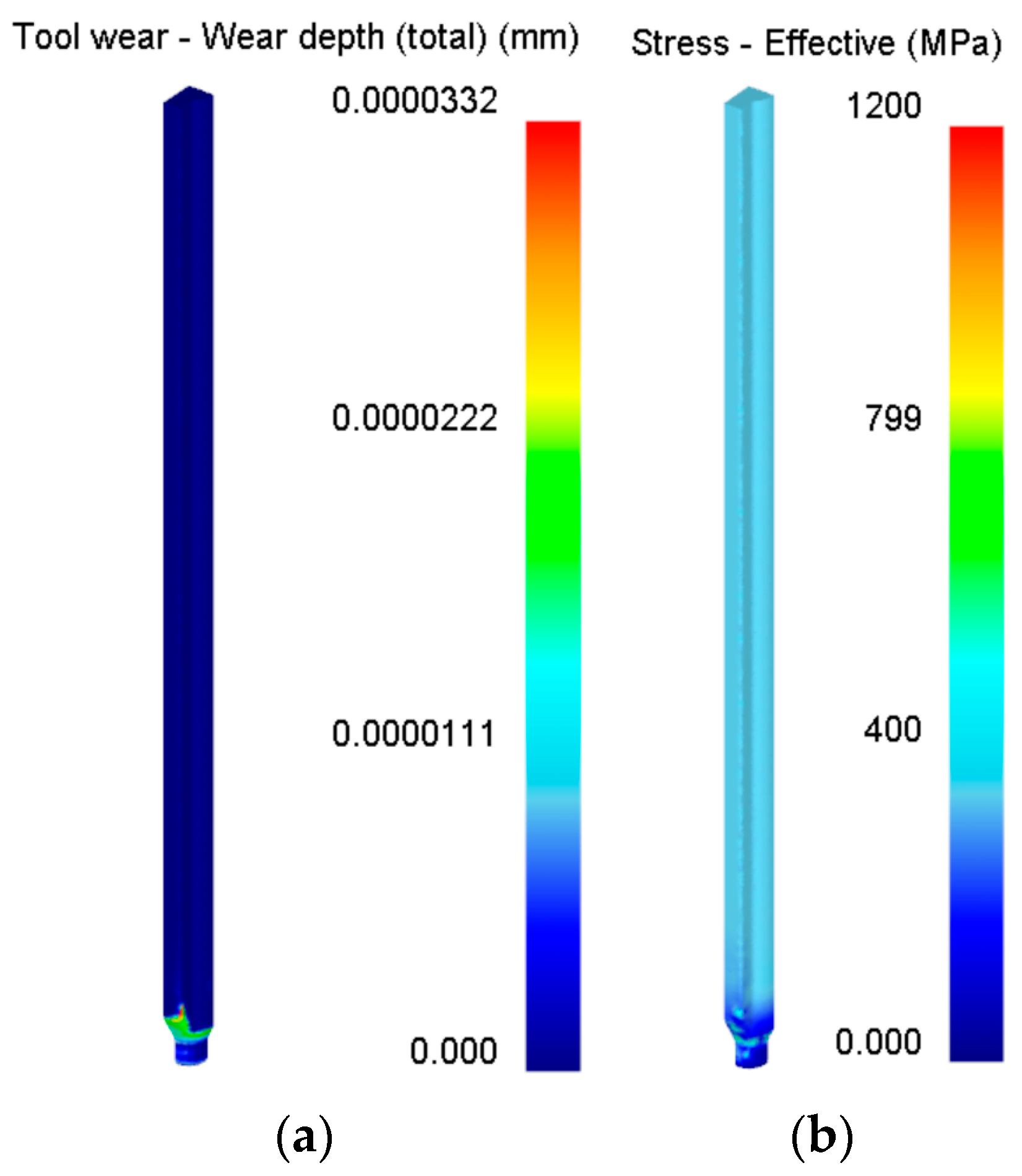
3.3. Analysis of Simulation Results
4. Integrated Application of Taguchi-TOPSIS Method
4.1. Experimental Design Process
4.2. Evaluation Indicators and Orthogonal Experiments
4.3. Taguchi Analysis
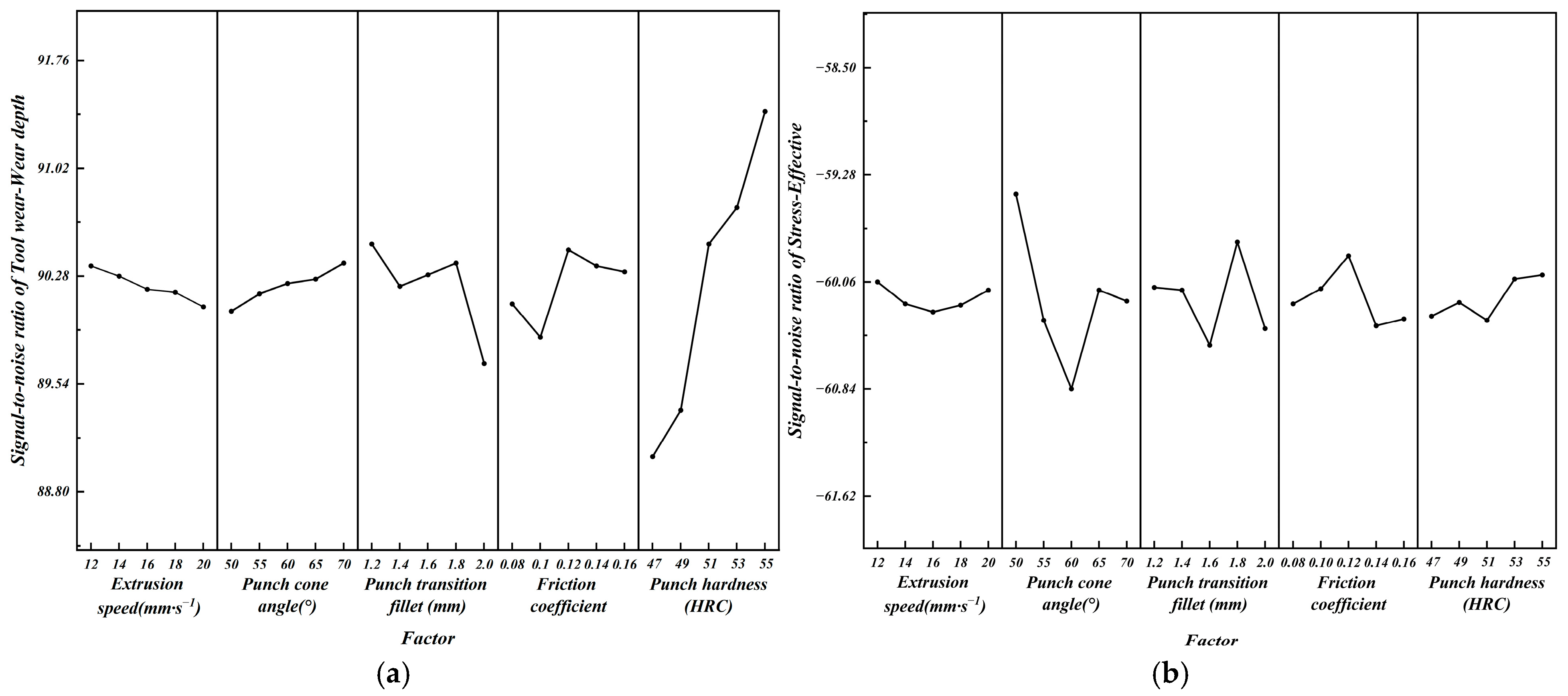
4.4. Range Analysis
4.5. Simulation Analysis
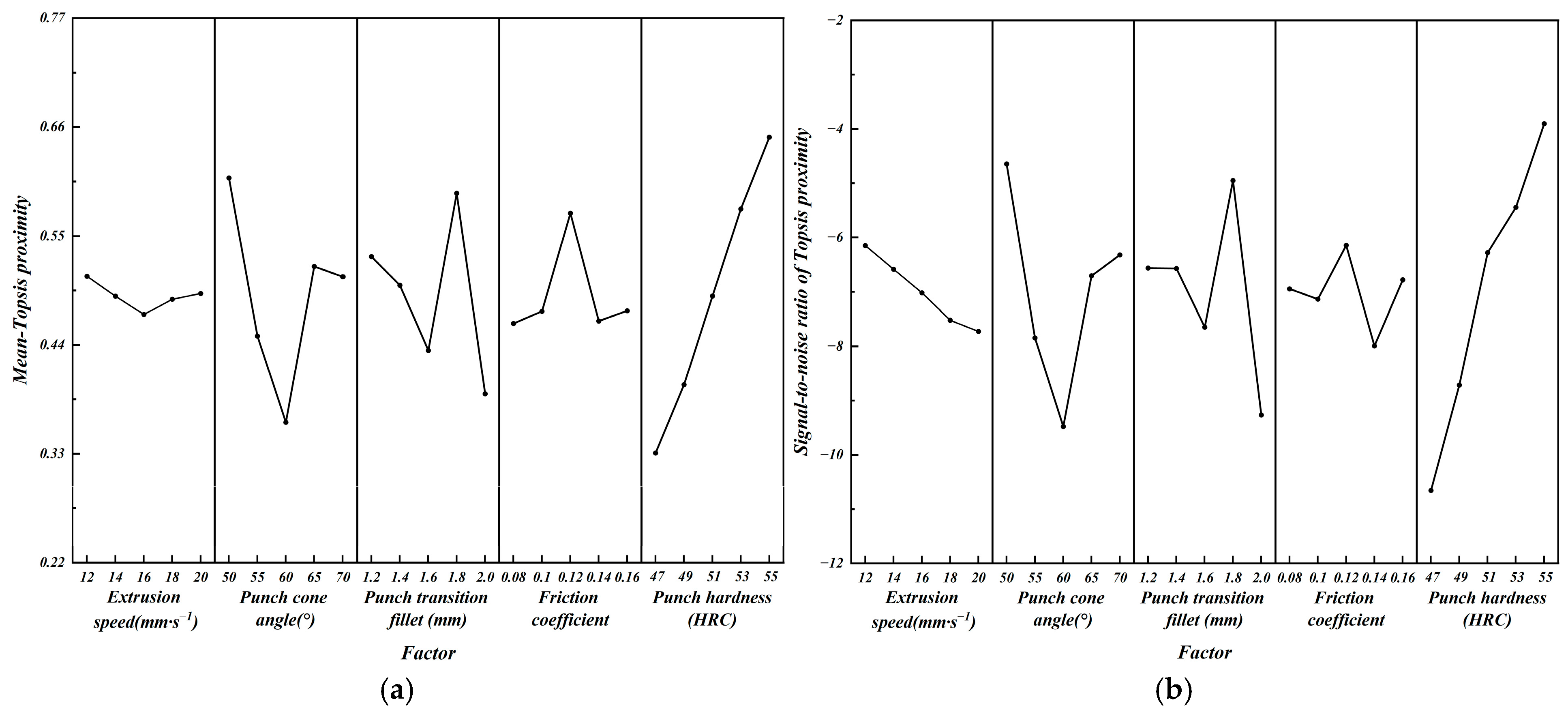
4.6. TOPSIS Analysis
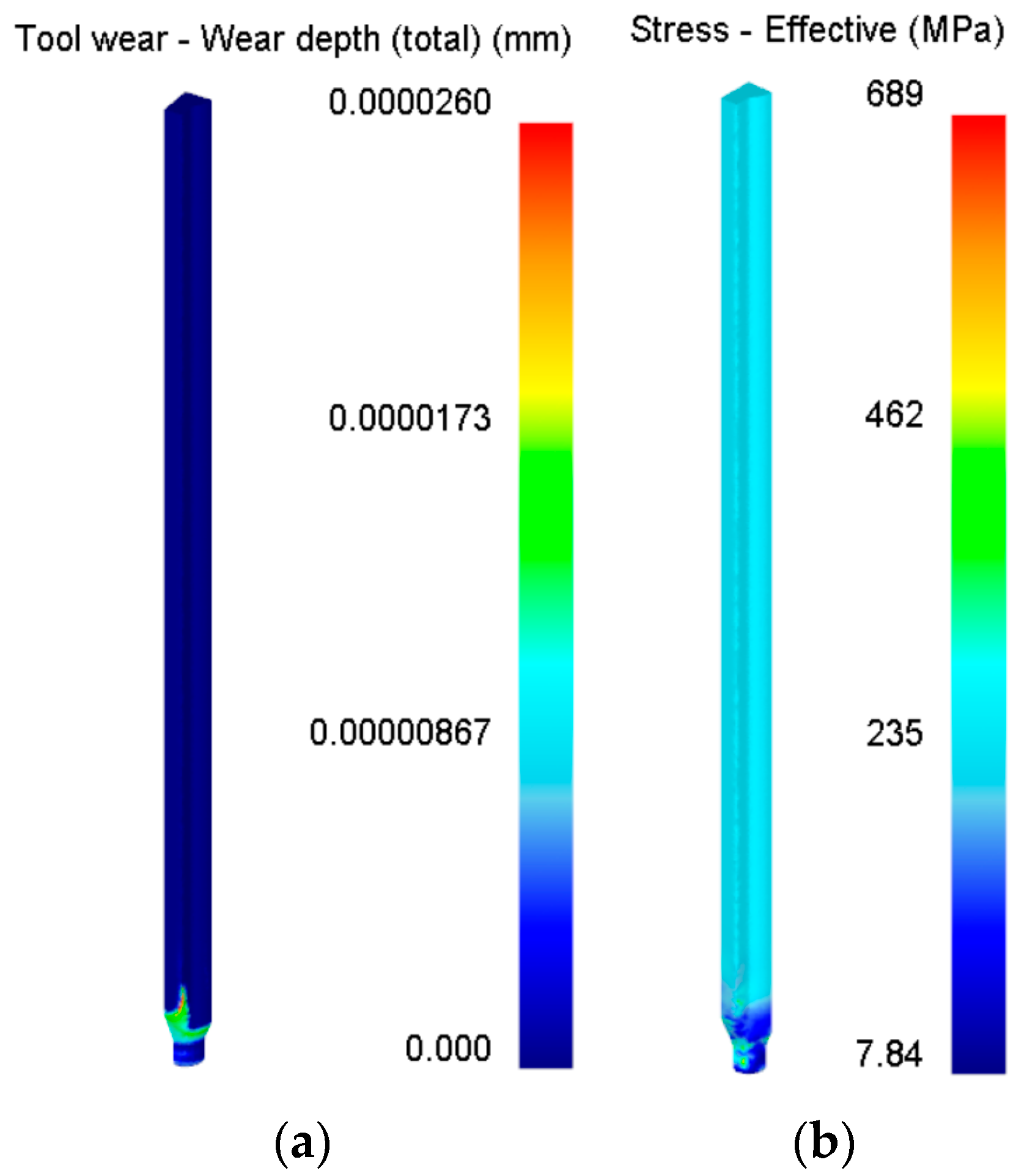
4.7. Validation of the Finite Element Model
5. Processing and Trial Production
5.1. Processing and Assembly
5.2. Trial Production and Testing
6. Conclusions
- For the optimization of the thin-walled special-shaped hole punch for the fine, elongated, and irregularly shaped cross-section of an aviation motor brush holder, this study designed an L25(56) orthogonal experimental table with five factors and five levels based on the Taguchi design method and using SPSSAU software. Signal-to-noise ratio and range analyses were conducted on the experimental results to quantify the significance of the influence of various process parameters on wear depth and equivalent stress. The analysis indicates that when the wear depth is taken as the optimization objective, the influencing weights in descending order are punch hardness > punch transition filet > friction coefficient > punch cone angle > extrusion speed. When the equivalent stress is taken as the optimization objective, the influencing weights in descending order are punch cone angle > punch transition filet > friction coefficient > punch hardness > extrusion speed.
- The Taguchi-TOPSIS integrated application method was employed, using the collaborative proximity of each target response value as the basis for weight determination and combining it with range analysis to derive the optimal process parameter combination. The optimal process parameter combination is as follows: extrusion speed of 12 mm·s−1, punch cone angle of 50°, punch transition filet radius of 1.8 mm, friction coefficient of 0.12, and punch hardness of 55 HRC. Compared with the initial process parameter combination, this optimized combination reduced the wear depth by 21.68% and the equivalent stress by 42.58%, significantly improving the part forming quality and the service life of the punch.
- This study validates the Taguchi-TOPSIS integrated framework through coupled numerical and physical experiments. The results demonstrate that this method significantly reduces the required experimental effort while efficiently identifying a robust parameter set. This leads to substantial savings in manufacturing costs, alongside improved qualification rates and productivity for thin-walled special-shaped parts in cold extrusion. Consequently, it provides a reliable and cost-effective multi-objective optimization strategy for addressing complex process parameter challenges.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Callister, W.D., Jr.; Rethwisch, D.G. Materials Science and Engineering: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Parida, S.-P.; Jena, P.-C.; Das, S.-R.; Basem, A.; Khatua, A.-K.; Elsheikg, A.-H. Transverse vibration of laminated-composite-plates with fillers under moving mass rested on elastic foundation using higher order shear deformation theory. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 9878–9888. [Google Scholar] [CrossRef]
- Pradhan, S.; Dhupal, D.; Das, S.-R.; Jena, P.-C. Experimental investigation and optimization on machined surface of Si3N4 ceramic using hot SiC abrasive in HAJM. Mater. Today Proc. 2021, 44, 1877–1887. [Google Scholar] [CrossRef]
- Farzad, H.; Ramin, E. An investigation of die profile effect on die wear of plane strain extrusion using incremental slab method and finite element analysis. Int. J. Adv. Manuf. Technol. 2020, 111, 627–644. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Yan, S.; Zou, L. Transformation of material removal behavior and its mechanism modeling with the wear evolution of pyramidal structured abrasive belts. J. Manuf. Process. 2025, 137, 125–134. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, R.; Hu, J. High-temperature wear mechanism of roller cone bit spiral seal. Wear 2023, 532, 205112. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, H.; Wang, H.; Tang, S.; Hao, H.; Huang, J. A novel wear prediction method and wear characteristic analysis of piston/cylinder pair in axial piston pump. Wear 2024, 550, 205402. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, B.; Liang, X.; Chen, J.; Gao, L.; Chen, J.; Zhang, Z.; Wang, Q.; Zhang, X.; Ren, X.; et al. Effects of “free flow” coupled with severe shear strain on the volume of the refined microstructure in a 7075 aluminum alloy under rotary extrusion. J. Mater. Process. Technol. 2025, 338, 118772. [Google Scholar] [CrossRef]
- Xia, Y.; Shu, X.; Zhu, D.; Pater, Z.; Bartnicki, J. Effect of process parameters on microscopic uniformity of cross wedge rolling of GH4169 alloy shaft. J. Manuf. Process. 2021, 66, 145–152. [Google Scholar] [CrossRef]
- Chen, M.; Zhu, C.; Yu, Z.; Ma, C. A novel process for manufacturing large-diameter thin-walled metal ring: Double-roll pendulum hot rotary forging technology. J. Manuf. Process. 2022, 76, 379–396. [Google Scholar] [CrossRef]
- Çakıroğlu, R.; Mustafa, G. Comprehensive analysis of material removal rate, tool wear and surface roughness in electrical discharge turning of L2 tool steel. J. Mater. Res. Technol. 2020, 9, 7305–7317. [Google Scholar] [CrossRef]
- Rajiev, R.; Sadagopan, P.; Prakash, R.-S. Study on investigation of hot forging die wear analysis—An industrial case study. Mater. Today Proc. 2020, 27, 2752–2757. [Google Scholar] [CrossRef]
- Behrens, B.-A.; Brunotte, K.; Hübner, S.; Wester, H.; Müller, F.; Müller, P.; Wälder, J.; Matthias, T. Further development of wear calculation and wear reduction in cold forging processes. J. Manuf. Mater. Process. 2021, 5, 36. [Google Scholar] [CrossRef]
- Ma, C.; Li, T.; Xue, C.; Jin, R.; Chu, Z.; Shuai, M.; Tuo, L. Optimization of Roll Configuration and Investigation of Forming Process in Three-Roll Planetary Rolling of Stainless Steel Seamless Tubes. Metals 2025, 15, 540. [Google Scholar] [CrossRef]
- Yang, J.; Heogh, W.; Ju, H.; Kang, S.; Jang, T.S.; Jung, H.D.; Jahazi, M.; Han, C.S.; Park, J.S.; Kim, S.H.; et al. Functionally graded structure of a nitride-strengthened Mg2Si-based hybrid composite. J. Magnes. Alloys 2024, 12, 1239–1256. [Google Scholar] [CrossRef]
- Davoudi, M.; Nejad, A.-F.; Koloor, S.-S.-R.; Petru, M. Investigation of effective geometrical parameters on wear of hot forging die. J. Mater. Res. Technol. 2021, 15, 5221–5231. [Google Scholar] [CrossRef]
- Ogbezode, J.-E.; Ajide, O.-O. Tool wear analysis of C-shaped equal channel reciprocating extrusion process of AISI-H13 steel die using finite element method. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 568. [Google Scholar] [CrossRef]
- Fernández, D.; Rodriguez-Prieto, A.; Camacho, A.-M. Optimal Parameters Selection in Advanced Multi-Metallic Co-Extrusion Based on Independent MCDM Analytical Approaches and Numerical Simulation. Mathematics 2022, 10, 4489. [Google Scholar] [CrossRef]
- Jeyakumar, M.; Hari Prasath, R.; Giridharan, S.; Prabhu, C.; Domnic, D. Deform 3D and Taguchi Techniques for Investigating Cutting Force for AISI 1030 Steel. In Recent Advances in Materials and Modern Manufacturing: Select Proceedings of ICAMMM 2021, Tamil Nadu, India, 26–28 March 2021; Springer Nature: Singapore, 2022; pp. 771–788. [Google Scholar]
- Jantepa, N.; Nattarawee, S.; Surasak, S. Predictive modeling and optimization of hot forging parameters for AISI 1045 ball joints using Taguchi methodology and finite element analysis. Metals 2024, 14, 1198. [Google Scholar] [CrossRef]
- Elplacy, F.; Samuel, M.; Mostafa, R. Modelling and simulation of hot direct extrusion process for optimal product characteristics: Single and multi-response optimization approach. Adv. Prod. Eng. Manag. 2022, 17, 33–44. [Google Scholar] [CrossRef]
- de Bruijn, A.-C.; Gómez-Gras, G.; Pérez, M.-A. On the effect upon the surface finish and mechanical performance of ball burnishing process on fused filament fabricated parts. Addit. Manuf. 2021, 46, 102133. [Google Scholar] [CrossRef]
- Bakhtiarian, M.; Omidvar, H.; Mashhuriazar, A.; Sajuri, Z.; Gur, H. The effects of SLM process parameters on the relative density and hardness of austenitic stainless steel 316L. J. Mater. Res. Technol. 2024, 29, 1616–1629. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, S.; Bilga, P.-S.; Jatin; Singh, J.; Singh, S.; Scutaru, M.-L.; Pruncu, C.-I. Revealing the benefits of entropy weights method for multi-objective optimization in machining operations: A critical review. J. Mater. Res. Technol. 2021, 10, 1471–1492. [Google Scholar] [CrossRef]
- Singh, S.; Agrawal, V.; Saxena, K.-K.; Mohammed, K.-A. Optimization on manufacturing processes at Indian industries using TOPSIS. Indian J. Eng. Mater. Sci. 2023, 30, 32–44. [Google Scholar] [CrossRef]
- Shih, H.-S.; Olson, D.-L. TOPSIS and Its Extensions: A Distance-Based MCDM Approach; Springer Nature: Berlin/Heidelberg, Germany, 2022; Volume 447. [Google Scholar]
- Chatterjee, S.; Shankar, C. A study on the effects of objective weighting methods on TOPSIS-based parametric optimization of non-traditional machining processes. Decis. Anal. J. 2024, 11, 100451. [Google Scholar] [CrossRef]
- Wei, X.; Chen, T.; Shen, G.; Ding, F. Alkali-activated slag backfill grout materials optimization: Statistical RSM modelling and NSGA-II performance control. J. Mater. Res. Technol. 2023, 24, 5613–5627. [Google Scholar] [CrossRef]
- Kamalizadeh, S.; Niknam, S.-A.; Balazinski, M.; Turenne, S. The use of TOPSIS method for multi-objective optimization in milling Ti-MMC. Metals 2022, 12, 1796. [Google Scholar] [CrossRef]
- Faheem, A.; Hasan, F.; Khan, A.-A.; Singh, B.; Ayaz, M.; Shamim, F.; Saxena, K.-K.; Eldin, S.-M. Parametric optimization of electric discharge machining of Ni 55.65 Ti based shape memory alloy using NSGA II with TOPSIS. J. Mater. Res. Technol. 2023, 26, 1306–1324. [Google Scholar] [CrossRef]
- Chen, X.; Li, X.; Li, Z.; Cao, W.; Zhang, Y.; Ni, J.; Wu, D.; Wang, Y. Control parameter optimization of dry hobbing under user evaluation. J. Manuf. Process. 2025, 133, 46–54. [Google Scholar] [CrossRef]
- Yuan, J.; Geng, H.; Alfano, M. Multi-response optimization of M2 steel coatings deposited by co-axial laser cladding on A2 steel tool surfaces. J. Mater. Res. Technol. 2024, 29, 1102–1117. [Google Scholar] [CrossRef]
- Gajević, S.; Markovic, A.; Markovic, S.; Asonja, A.; Ivanovic, L.; Stojanovic, B. Multi-objective optimization of tribological characteristics for aluminum composite using Taguchi grey and TOPSIS approaches. Lubricants 2024, 12, 171. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, S.; Aggarwal, V.; Singh, S.; Pimenov, D.-Y.; Giasin, K.; Nadolny, K. Hand and abrasive flow polished tungsten carbide die: Optimization of surface roughness, polishing time and comparative analysis in wire drawing. Materials 2022, 15, 1287. [Google Scholar] [CrossRef]
- Imran, M.; Suo, S.; Bai, Y.; Wang, Y.; Raheel, N. Optimising subsurface integrity and surface quality in mild steel turning: A multi-objective approach to tool wear and machining parameters. J. Mater. Res. Technol. 2025, 35, 3440–3462. [Google Scholar] [CrossRef]
- Sur, G.; Motorcu, A.-R.; Nohutçu, S. Single and multi-objective optimization for cutting force and surface roughness in peripheral milling of Ti6Al4V using fixed and variable helix angle tools. J. Manuf. Process. 2022, 80, 529–545. [Google Scholar] [CrossRef]
- Ashby, M.-F.; Shercliff, H.; Cebon, D. Materials: Engineering, Science, Processing and Design; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Hu, J.; Song, H.; Sandfeld, S.; Liu, X.; Wei, Y. Breakdown of Archard law due to transition of wear mechanism from plasticity to fracture. Tribol. Int. 2022, 173, 107660. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, W.; Zhao, C.; Cai, Z.; Li, B.; Zhu, M. Numerical Simulation of Contact and Wear Between Deformed Mold and Solidified Shell Based on Archard Model. Metall. Mater. Trans. B 2025, 56, 3774–3792. [Google Scholar] [CrossRef]
- Wei, C.; He, C.; Tan, H.; Su, Y.; Chen, G.; Sun, Y.; Ren, C. A predictive model for tool wear behavior during ultra-precision lapping. Int. J. Adv. Manuf. Technol. 2025, 136, 875–895. [Google Scholar] [CrossRef]
- Pereira, L.-D.-S.; Donato, G.-H.-B.; Neto, M.-M. Assessment of the von Mises stresses and stress triaxiality in notches using modified tensile specimens. Mater. Res. 2023, 26, e20220572. [Google Scholar] [CrossRef]
- Manikandan, P.; Rao, G.-S.; Murty, S.-N.; Venugopal, A.; Narayanan, P.-R.; Mohan, M. Biaxial Tensile Behavior of Aluminum Alloy AA2219-T852 using Tension and Internal Pressure. J. Mater. Eng. Perform. 2023, 32, 6930–6941. [Google Scholar] [CrossRef]
- Bhandari, R.; Biswas, P.; Malliik, M.; Mondal, M.-K. Microstructure based numerical simulation of the micromechanics and fracture in hypereutectic Al–Mg2Si composites. Mater. Chem. Phys. 2023, 297, 127427. [Google Scholar] [CrossRef]
- Oda, S.; Tanaka, S.-I. Effect of local texture and residual stress on the bendability of extruded 6000-series Al alloy profiles. Mater. Sci. Eng. A 2022, 829, 142167. [Google Scholar] [CrossRef]
- Zhao, S.; Bao, J.; Zhang, Q.; Yin, Y.; Wang, X.; Ai, J. Preparation process optimization of hard magnetic brake friction material based on NdFeB additive. Ind. Lubr. Tribol. 2022, 74, 258–264. [Google Scholar] [CrossRef]
- Dorkhah, A.; Arab-Solghar, A.; Rezaeizadeh, M. Experimental Analysis of Semi-autogenous Grinding Mill Characteristics Under Different Working Conditions. Iran. J. Sci. Technol. Trans. Mech. Eng. 2020, 44, 1103–1114. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, C.; He, L.; Cao, Y. A Multifactor Combination Optimization Design Based on Orthogonality for a Two-Degree-of-Freedom Floating Machine Gun Vibration System. Shock. Vib. 2024, 1, 6686238. [Google Scholar] [CrossRef]








| Parameter | Tensile Strength/MPa | Yield Strength/MPa | Elongation/% | Reduction in Area/% | Hardness/HB |
|---|---|---|---|---|---|
| Numerical Value | ≥345 | ≥295 | ≥20 | ≥18 | ≤120 |
| Level | Factor | ||||
|---|---|---|---|---|---|
| Extrusion Speed (mm·s−1) | Punch Cone Angle (°) | Punch Transition Filet (mm) | Friction Coefficient | Punch Hardness (HRC) | |
| 1 | 12 | 50 | 1.2 | 0.08 | 47 |
| 2 | 14 | 55 | 1.4 | 0.10 | 49 |
| 3 | 16 | 60 | 1.6 | 0.12 | 51 |
| 4 | 18 | 65 | 1.8 | 0.14 | 53 |
| 5 | 20 | 70 | 2.0 | 0.16 | 55 |
| Exp. No | Input | Output Response | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Extrusion Speed (mm·s−1) | Punch Cone Angle (°) | Punch Transition Filet (mm) | Friction Coefficient | Punch Hardness (HRC) | Wd (×10−5 mm) | S/N(Wd) | Es (MPa) | S/N(Es) | |
| 01 | 12 | 50 | 1.2 | 0.08 | 47 | 3.35 | 89.49 | 859 | −58.67 |
| 02 | 12 | 55 | 1.6 | 0.14 | 55 | 2.53 | 91.93 | 1050 | −60.42 |
| 03 | 12 | 60 | 2.0 | 0.10 | 53 | 3.25 | 89.76 | 1090 | −60.74 |
| 04 | 12 | 65 | 1.4 | 0.16 | 51 | 2.92 | 90.69 | 1110 | −60.90 |
| 05 | 12 | 70 | 1.8 | 0.12 | 49 | 3.20 | 89.89 | 956 | −59.60 |
| 06 | 14 | 50 | 2.0 | 0.14 | 51 | 3.22 | 89.84 | 1030 | −60.25 |
| 07 | 14 | 55 | 1.4 | 0.10 | 49 | 3.41 | 89.34 | 951 | −59.56 |
| 08 | 14 | 60 | 1.8 | 0.16 | 47 | 3.31 | 89.60 | 1070 | −60.58 |
| 09 | 14 | 65 | 1.2 | 0.12 | 55 | 2.57 | 91.80 | 957 | −59.61 |
| 10 | 14 | 70 | 1.6 | 0.08 | 53 | 2.87 | 90.84 | 1140 | −61.13 |
| 11 | 16 | 50 | 1.8 | 0.10 | 55 | 2.84 | 90.93 | 947 | −59.52 |
| 12 | 16 | 55 | 1.2 | 0.16 | 53 | 2.85 | 90.90 | 1070 | −60.58 |
| 13 | 16 | 60 | 1.6 | 0.12 | 51 | 2.77 | 91.15 | 1050 | −60.42 |
| 14 | 16 | 65 | 2.0 | 0.08 | 49 | 3.57 | 88.94 | 1040 | −60.34 |
| 15 | 16 | 70 | 1.4 | 0.14 | 47 | 3.53 | 89.04 | 1070 | −60.58 |
| 16 | 18 | 50 | 1.6 | 0.16 | 49 | 3.52 | 89.06 | 952 | −60.00 |
| 17 | 18 | 55 | 2.0 | 0.12 | 47 | 3.73 | 88.56 | 1130 | −61.06 |
| 18 | 18 | 60 | 1.4 | 0.08 | 55 | 2.78 | 91.11 | 1110 | −60.90 |
| 19 | 18 | 65 | 1.8 | 0.14 | 53 | 2.70 | 91.37 | 903 | −59.11 |
| 20 | 18 | 70 | 1.2 | 0.10 | 51 | 2.89 | 90.78 | 1010 | −60.08 |
| 21 | 20 | 50 | 1.4 | 0.12 | 53 | 2.85 | 90.90 | 858 | −58.66 |
| 22 | 20 | 55 | 1.8 | 0.08 | 51 | 3.13 | 90.08 | 1010 | −60.08 |
| 23 | 20 | 60 | 1.2 | 0.14 | 49 | 3.32 | 89.57 | 1200 | −61.58 |
| 24 | 20 | 65 | 1.6 | 0.10 | 47 | 3.75 | 88.51 | 1080 | −60.66 |
| 25 | 20 | 70 | 2.0 | 0.16 | 55 | 2.72 | 91.30 | 958 | −59.62 |
| Maximum Wear Depth | Maximum Equivalent Stress | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Level | A | B | C | D | E | Level | A | B | C | D | E |
| 1 | 90.35 | 90.04 | 90.50 | 90.09 | 89.04 | 1 | −60.06 | −59.42 | −60.10 | −60.22 | −60.31 |
| 2 | 90.28 | 90.16 | 90.21 | 89.86 | 89.36 | 2 | −60.22 | −60.34 | −60.12 | −60.11 | −60.21 |
| 3 | 90.19 | 90.23 | 90.29 | 90.46 | 90.50 | 3 | −60.28 | −60.84 | −60.52 | −59.87 | −60.34 |
| 4 | 90.17 | 90.26 | 90.37 | 90.35 | 90.75 | 4 | −60.23 | −60.12 | −59.77 | −60.38 | −60.04 |
| 5 | 90.07 | 90.37 | 89.68 | 90.31 | 91.41 | 5 | −60.12 | −60.20 | −60.40 | −60.33 | −60.01 |
| Delta | 0.28 | 0.33 | 0.82 | 0.60 | 2.37 | Delta | 0.22 | 1.42 | 0.75 | 0.51 | 0.33 |
| Rank | 5 | 4 | 2 | 3 | 1 | Rank | 5 | 1 | 2 | 3 | 4 |
| Opt | A1B5C1D3E5 | Opt | A1B1C4D3E5 | ||||||||
| Exp. No | Maximum Wear Depth | Maximum Stress | S/N(Ci) | |||||
|---|---|---|---|---|---|---|---|---|
| 01 | 89.49 | 0.1983 | −58.67 | −0.1949 | 0.0038 | 0.0070 | 0.6481 | −3.7671 |
| 02 | 91.93 | 0.2037 | −60.42 | −0.2007 | 0.0041 | 0.0060 | 0.5940 | −4.5242 |
| 03 | 89.76 | 0.1989 | −60.74 | −0.2018 | 0.0059 | 0.0028 | 0.3218 | −9.8482 |
| 04 | 90.69 | 0.2010 | −60.90 | −0.2023 | 0.0055 | 0.0038 | 0.4086 | −7.7740 |
| 05 | 89.89 | 0.1992 | −59.60 | −0.1980 | 0.0038 | 0.0051 | 0.5730 | −4.8369 |
| 06 | 89.84 | 0.1991 | −60.25 | −0.2002 | 0.0049 | 0.0037 | 0.4302 | −7.3265 |
| 07 | 89.34 | 0.1980 | −59.56 | −0.1979 | 0.0045 | 0.0049 | 0.5212 | −5.6599 |
| 08 | 89.60 | 0.1986 | −60.58 | −0.2012 | 0.0057 | 0.0029 | 0.3372 | −9.4422 |
| 09 | 91.80 | 0.2035 | −59.61 | −0.1980 | 0.0021 | 0.0070 | 0.7692 | −2.2792 |
| 10 | 90.84 | 0.2013 | −61.13 | −0.2031 | 0.0060 | 0.0038 | 0.3877 | −8.2300 |
| 11 | 90.93 | 0.2015 | −59.52 | −0.1977 | 0.0025 | 0.0062 | 0.7126 | −2.9430 |
| 12 | 90.90 | 0.2015 | −60.58 | −0.2012 | 0.0047 | 0.0045 | 0.4891 | −6.2120 |
| 13 | 91.15 | 0.2020 | −60.42 | −0.2007 | 0.0042 | 0.0049 | 0.5384 | −5.3778 |
| 14 | 88.94 | 0.1971 | −60.34 | −0.2005 | 0.0061 | 0.0030 | 0.3296 | −9.6402 |
| 15 | 89.04 | 0.1973 | −60.58 | −0.2012 | 0.0063 | 0.0025 | 0.2840 | −10.9336 |
| 16 | 89.06 | 0.1974 | −60.00 | −0.1993 | 0.0054 | 0.0038 | 0.4130 | −7.6809 |
| 17 | 88.56 | 0.1963 | −61.06 | −0.2028 | 0.0076 | 0.0013 | 0.1460 | −16.7129 |
| 18 | 91.11 | 0.2019 | −60.90 | −0.2023 | 0.0053 | 0.0043 | 0.4479 | −6.9763 |
| 19 | 91.37 | 0.2025 | −59.11 | −0.1964 | 0.0013 | 0.0073 | 0.8488 | −1.4238 |
| 20 | 90.78 | 0.2012 | −60.08 | −0.1996 | 0.0037 | 0.0050 | 0.5747 | −4.8111 |
| 21 | 90.90 | 0.2015 | −58.66 | −0.1949 | 0.0015 | 0.0078 | 0.8387 | −1.5278 |
| 22 | 90.08 | 0.1996 | −60.08 | −0.1996 | 0.0044 | 0.0043 | 0.4942 | −6.1219 |
| 23 | 89.57 | 0.1985 | −61.58 | −0.2046 | 0.0077 | 0.0015 | 0.1630 | −15.7562 |
| 24 | 88.51 | 0.1962 | −60.66 | −0.2015 | 0.0070 | 0.0022 | 0.2391 | −12.4284 |
| 25 | 91.30 | 0.2023 | −59.62 | −0.1981 | 0.0024 | 0.0063 | 0.7241 | −2.8040 |
| Level | A | B | C | D | E | Level | A | B | C | D | E |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.5091 | 0.6085 | 0.5288 | 0.4615 | 0.3308 | 1 | −6.1501 | −4.6491 | −6.5651 | −6.9471 | −10.6569 |
| 2 | 0.4891 | 0.4489 | 0.5000 | 0.4738 | 0.3996 | 2 | −6.5876 | −7.8462 | −6.5743 | −7.1381 | −8.7148 |
| 3 | 0.4707 | 0.3616 | 0.4344 | 0.5730 | 0.4892 | 3 | −7.0213 | −9.4802 | −7.6483 | −6.1469 | −6.2823 |
| 4 | 0.4860 | 0.5190 | 0.5931 | 0.4640 | 0.5772 | 4 | −7.5210 | −6.7091 | −4.9536 | −7.9929 | −5.4484 |
| 5 | 0.4918 | 0.5087 | 0.3903 | 0.4744 | 0.6495 | 5 | −7.7277 | −6.3231 | −9.2664 | −6.7826 | −3.9054 |
| Delta | 0.0384 | 0.2469 | 0.2028 | 0.1115 | 0.3187 | Delta | 1.5776 | 4.8311 | 4.3128 | 1.8460 | 6.7515 |
| Rank | 5 | 2 | 3 | 4 | 1 | Rank | 5 | 2 | 3 | 4 | 1 |
| Opt | A1B1C4D3E5 | Opt | A1B1C4D3E5 | ||||||||
| No. | Inspection Item | Unit | Inspection Method & Technical Requirement | Specification | |||
|---|---|---|---|---|---|---|---|
| 1# | 2# | 3# | |||||
| 1 | Length of upper rectangular cavity | mm | Universal Measuring Microscope | 9.014 | 9.016 | 9.016 | |
| 2 | Width of upper rectangular cavity | mm | Universal Measuring Microscope | 4.52 | 4.51 | 4.52 | |
| 3 | Diameter of upper cylindrical cavity | mm | Universal Measuring Microscope | 6.64 | 6.63 | 6.64 | |
| 4 | Length of lower rectangular cavity | mm | Universal Measuring Microscope | 9.012 | 9.013 | 9.021 | |
| 5 | Width of lower rectangular cavity | mm | Universal Measuring Microscope | 4.51 | 4.51 | 4.51 | |
| 6 | Diameter of lower cylindrical cavity | mm | Universal Measuring Microscope | 6.64 | 6.62 | 6.63 | |
| 7 | Surface roughness (Ra) of profiled thin-wall bore | μm | Surface roughness tester | ≤1.6 | 1.4 | 1.4 | 1.4 |
| 8 | Overall length | mm | Digital caliper | 25.0 | 25.0 | 25.0 | |
| 9 | Flange height | mm | Digital caliper | 7.5 | 7.4 | 7.5 | |
| 10 | Diameter of flange cylindrical surface | mm | Digital caliper | 17.06 | 17.04 | 17.06 | |
| 11 | Diameter of minor cylindrical surface | mm | Digital caliper | 13.9 | 13.9 | 13.9 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Yuan, Y.; Wu, Q. Research on the Application of the Taguchi-TOPSIS Method in the Multi-Objective Optimization of Punch Wear and Equivalent Stress in Cold Extrusion Forming of Thin-Walled Special-Shaped Holes. Metals 2025, 15, 1192. https://doi.org/10.3390/met15111192
Liu Z, Yuan Y, Wu Q. Research on the Application of the Taguchi-TOPSIS Method in the Multi-Objective Optimization of Punch Wear and Equivalent Stress in Cold Extrusion Forming of Thin-Walled Special-Shaped Holes. Metals. 2025; 15(11):1192. https://doi.org/10.3390/met15111192
Chicago/Turabian StyleLiu, Zhan, Yuhong Yuan, and Quan Wu. 2025. "Research on the Application of the Taguchi-TOPSIS Method in the Multi-Objective Optimization of Punch Wear and Equivalent Stress in Cold Extrusion Forming of Thin-Walled Special-Shaped Holes" Metals 15, no. 11: 1192. https://doi.org/10.3390/met15111192
APA StyleLiu, Z., Yuan, Y., & Wu, Q. (2025). Research on the Application of the Taguchi-TOPSIS Method in the Multi-Objective Optimization of Punch Wear and Equivalent Stress in Cold Extrusion Forming of Thin-Walled Special-Shaped Holes. Metals, 15(11), 1192. https://doi.org/10.3390/met15111192





