The Issues of the Radiation Hardening Determination of Steels After Ion Irradiation Using Instrumented Indentation
Abstract
1. Introduction
2. Investigation Methods
2.1. Methodology for Microhardness Determination with a Berkovich Indenter
2.2. Microhardness Determination Methods Using the Direct Measurement of the Indent Projection Area
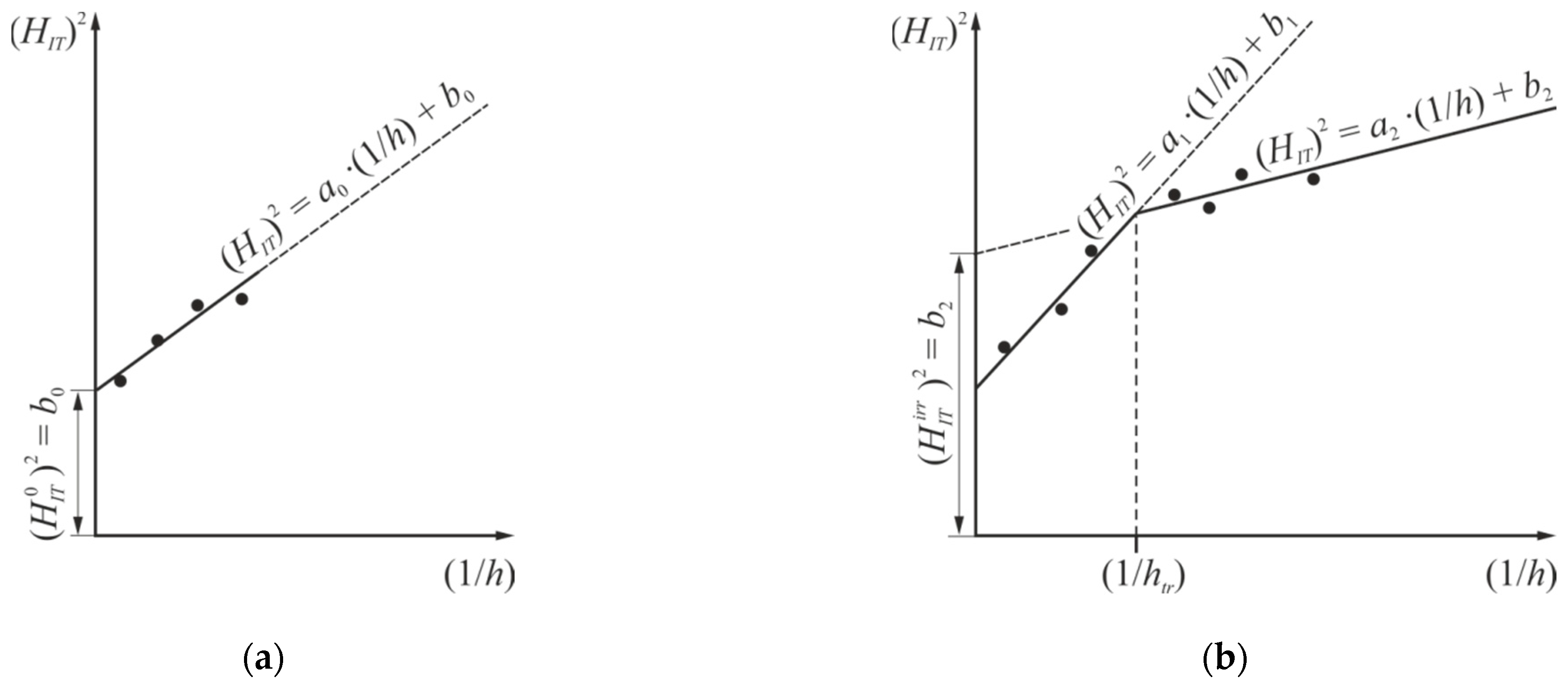
2.3. Microhardness Determination Method with a Berkovich Indenter Using the Indentation Diagram
3. Equipment, Samples and Materials
4. Experimental Results
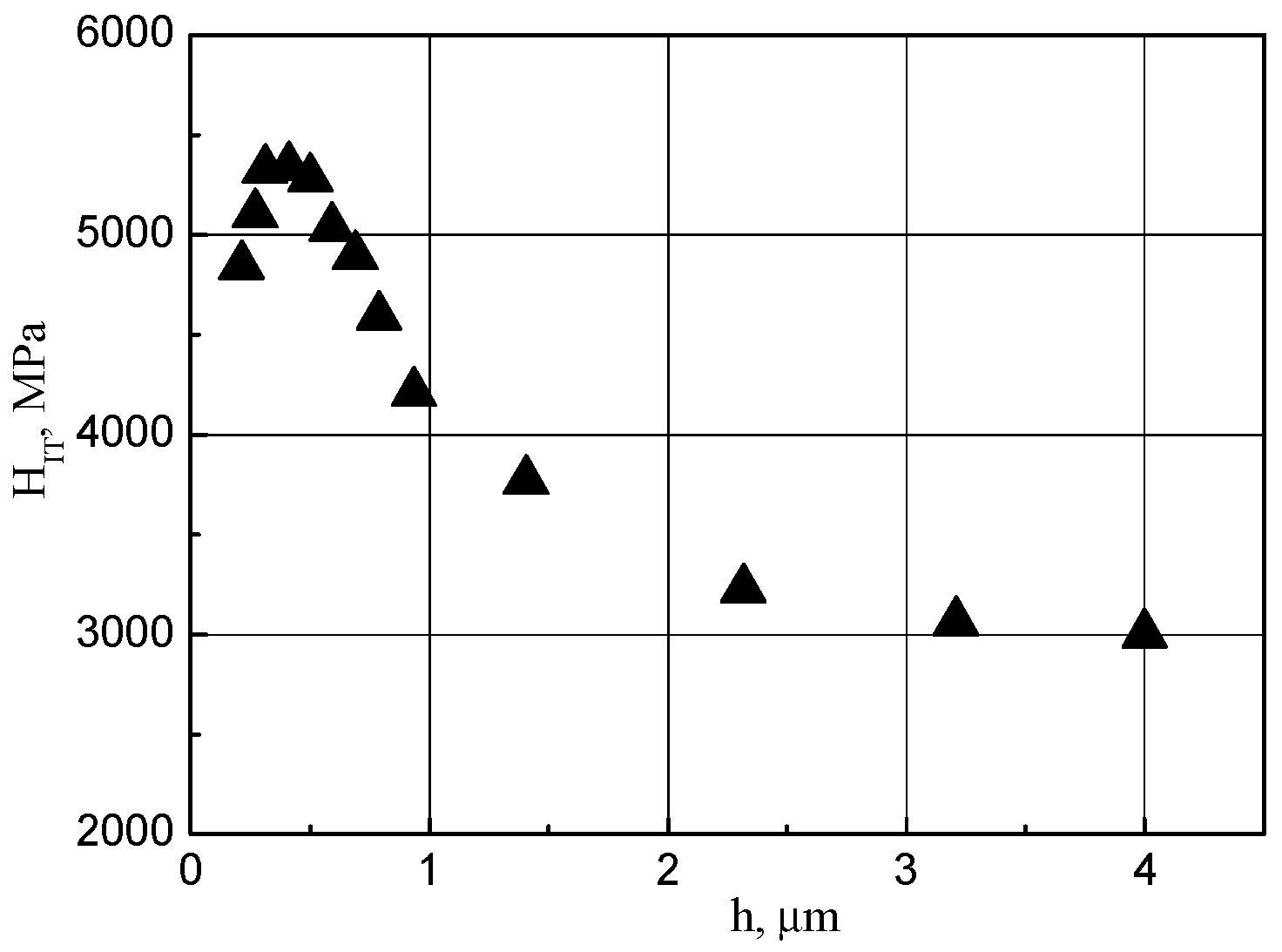
4.1. Microhardness Determination Using the Direct Measurement of the Indent Projection Area
4.2. Microhardness Determination with a Berkovich Indenter Using the Indentation Diagram
5. Determination of Radiation Hardening Under Ion Irradiation by Microhardness Measurement with Berkovich Pyramid Indentation
6. Discussion
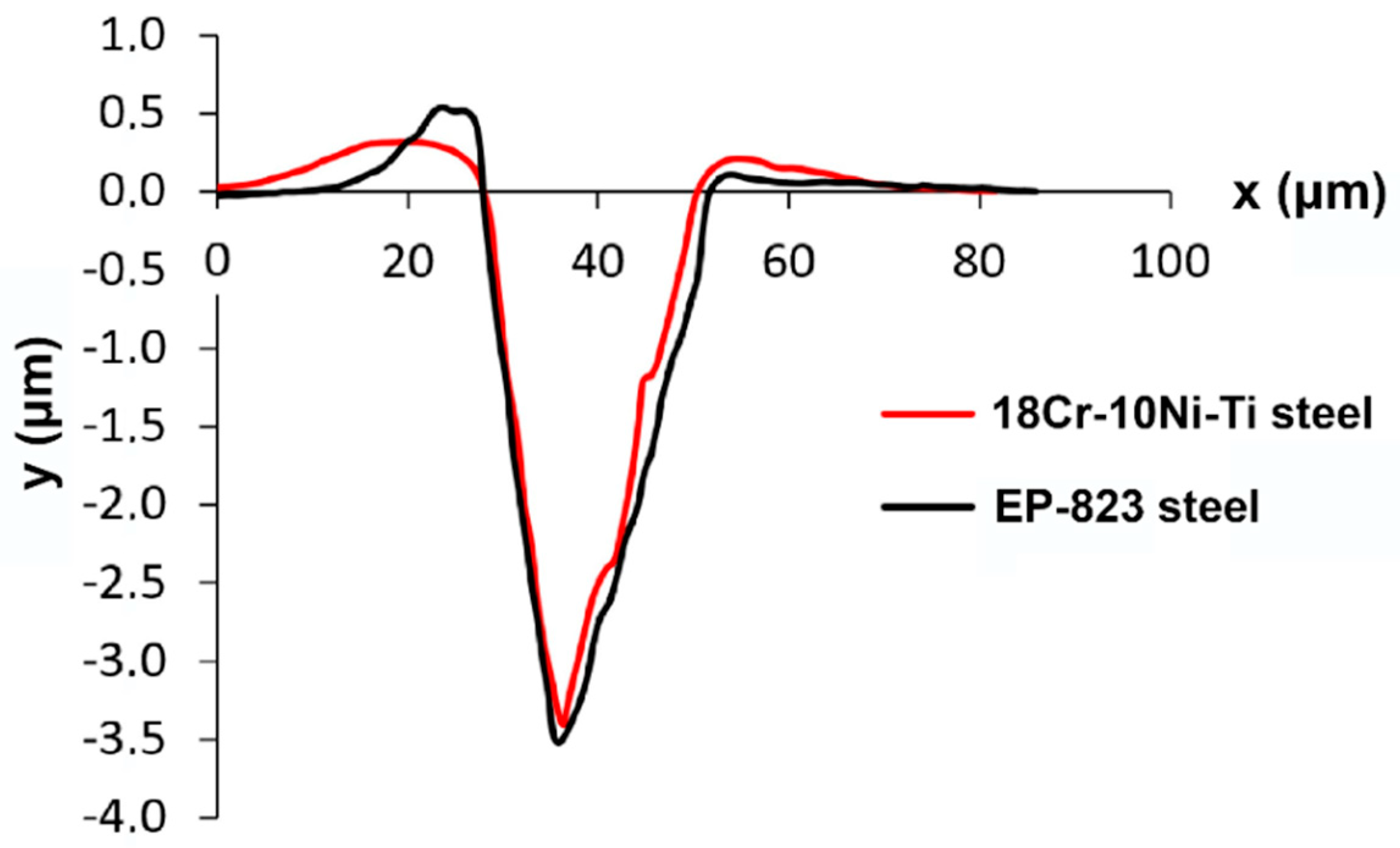
6.1. On Pile-Up Formation
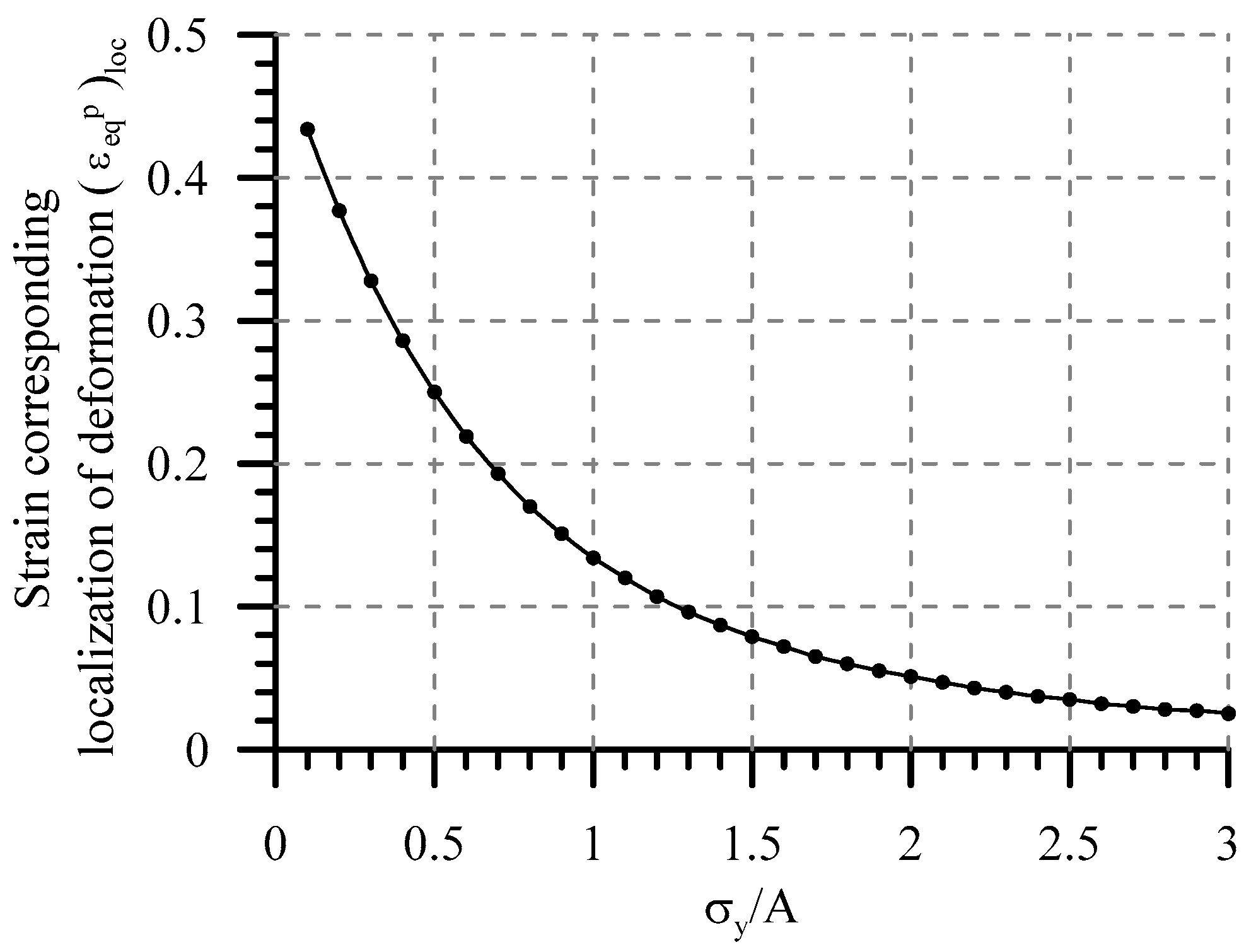
6.2. On the Physical Basis of the Nix–Gao Model
7. Conclusions
- It is shown that for a homogeneous material, the microhardness under Berkovich indenter indentation does not depend on the indentation depth if the indent projection area is determined directly by measurement of the indent geometric characteristics. When the microhardness is determined from the indentation diagram using the generally accepted Oliver–Pharr method, dependence of microhardness on the indentation depth is observed even for a homogeneous material.
- The main reason leading to the dependence of microhardness on the indentation depth is the formation of plastic pile-ups near the facets of the Berkovich indenter indent that is not taken into account in the microhardness determination from the indentation diagram.
- The proposed method allows one practically to exclude the influence of the indentation depth on microhardness of homogeneous material at least over the depth range from 0.2 to 4 μm and to obtain adequate assessment of the radiation hardening for a thin irradiated layer with depth about 2 μm.
- The microhardness values determined with Berkovich and Vickers indenters indentations coincide almost completely if the same geometric characteristic of the indent is used (either the indent projection area or the contact indent area) and this characteristic is determined by direct measurements.
- Formula (12) is proposed for taking into account the influence of pile-ups on the microhardness determined from the indentation diagram using the Oliver–Pharr method. The use of this formula makes it possible to practically eliminate the dependence of microhardness on the indentation depth for materials with a high susceptibility to deformation localization, including the studied ferritic-martensitic steels. At the same time, for materials with high strain hardening resulting in small localization of plastic deformation (for example, for austenitic steels), Formula (12) does not allow one to take into account the pile-ups adequately. The difference in applicability of Formula (12) is connected with different profiles of the pile-ups for ferritic-martensitic and austenitic steels.
- It is shown that the radiation hardening of a material may be adequately determined with Berkovich indenter indentation of a thin ion-irradiated layer if the microhardness is calculated on the results of direct measurement of the indent projection area. The use of the Nix–Gao model can lead to incorrect results and significant errors in the estimation of radiation hardening.
- Some assumptions have been analyzed that were taken in the Nix–Gao model [20] for derivation of Formula (1). It is shown that these assumptions are not sufficiently physically substantiated; that raises doubts in the correctness of the proposed dependence of microhardness on indentation depth.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Was, G.S.; Jiao, Z.; Getto, E.; Sun, K.; Monterrosa, A.M.; Maloy, S.A.; Anderoglu, O.; Sencer, B.H.; Hackett, M. Emulation of reactor irradiation damage using ion beams. Scr. Mater. 2014, 88, 33–36. [Google Scholar] [CrossRef]
- Was, G.S. Challenges to the use of ion irradiation for emulating reactor irradiation. J. Mater. Res. 2015, 30, 1158–1182. [Google Scholar] [CrossRef]
- Gupta, J.; Hure, J.; Laffont, L.; Lafont, M.-C.; Andreu, E. Characterisation of ion irradiation effects on the microstructure, hardness, deformation and crack initiation behavior of austenitic stainless steel: Heavy ions vs protons. J. Nucl. Mater. 2018, 501, 45–58. [Google Scholar] [CrossRef]
- Rogozhkin, S.V.; Aleev, A.A.; Zaluzhnyi, A.G.; Kuibida, R.P.; Kulevoi, T.V.; Nikitin, A.A.; Orlov, N.N.; Chalykh, B.B.; Shishmarev, V.B. Effect of irradiation by heavy ions on the nanostructure of perspective materials for nuclear power plants. Phys. Metals Metallogr. 2012, 113, 200–211. [Google Scholar] [CrossRef]
- Margolin, B.; Sorokin, A.; Belyaeva, L. Link between neutron and ion irradiation hardening for stainless austenitic and ferritic-martensitic steels. Metals 2024, 14, 99. [Google Scholar] [CrossRef]
- Jiao, Z.; Michalicka, J.; Was, G.S. Self-ion emulation of high dose neutron irradiated microstructure in stainless steels. J. Nucl. Mater. 2018, 501, 312–318. [Google Scholar] [CrossRef]
- Ayanoglu, M.; Motta, A.T. Emulation of neutron-irradiated microstructure of austenitic 21Cr32Ni model alloy using dual-ion irradiation. J. Nucl. Mater. 2022, 570, 153944. [Google Scholar] [CrossRef]
- Lee, S.; Chang, D.-S.; Lee, K.; Huh, S.-R.; Lee, S. Implementation of Fe ion irradiation and high-temperature target design at KAHIF for neutron damage simulation in fusion structural materials. Nucl. Eng. Technol. 2025, 57, 103815. [Google Scholar] [CrossRef]
- Skuratov, V.A.; Uglov, V.V.; O’Connell, J.; Sohatsky, A.S.; Neethling, J.H.; Rogozhkin, S.V. Radiation stability of the ODS alloys against swift heavy ion impact. J. Nucl. Mater. 2013, 442, 449–457. [Google Scholar] [CrossRef]
- Bückle, H. Progress in micro-indentation hardness testing. Met. Rev. 1959, 4, 49–100. [Google Scholar] [CrossRef]
- Voort, G.V.; Fowler, R. Low-load Vickers microindentation. Adv. Mater. Process. 2012, 170, 28–33. [Google Scholar]
- Broitman, E. Indentation Hardness Measurements at Macro-, Micro-, and Nanoscale: A Critical Overview. Tribol. Lett. 2017, 65, 23. [Google Scholar] [CrossRef]
- Zhu, P.; Zhao, Y.; Shrdha, A.; Zean, H.; Zinkle, S.J. Toward accurate evaluation of bulk hardness from nanoindentation testing at low indent depths. Mater. Des. 2022, 213, 110317. [Google Scholar] [CrossRef]
- Xiazi, X.; Long, Y. Nano-indentation of ion-irradiated nuclear structural materials: A review. Nucl. Mater. Energy 2022, 22, 100721. [Google Scholar] [CrossRef]
- Linmao, Q.; Ming, L.; Zhongrong, Z.; Hui, Y.; Xinyu, S. Comparison of nano-indentation hardness to microhardness. Surf. Coat. Technol. 2005, 195, 264–271. [Google Scholar] [CrossRef]
- Kapoor, G.; Chekhonin, P.; Kaden, C.; Vogel, K.; Bergner, F. Microstructure-informed prediction and measurement of nanoindentation hardness of an Fe-9Cr alloy irradiated with Fe-ions of 1 and 5 MeV energy. Nucl. Mater. Energy 2022, 30, 101105. [Google Scholar] [CrossRef]
- Pham, V.-T.; Kim, J.-S.; Eom, H.J.; Jang, C. Mechanical characterization of austenitic stainless steel under high-level ion-irradiation using nanoindentation experiment and simulation. J. Mater. Res. Technol. 2025, 34, 1777–1790. [Google Scholar] [CrossRef]
- Chudoba, T.; Schwaller, P.; Rabe, R.; Breguet, J.M.; Michler, J. Comparison of nanoindentation results obtained with Berkovich and cube-corner indenters. Philos. Mag. 2006, 86, 5265–5283. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Nix, W.D.; Gao, H. Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Yabuuchi, K.; Kuribayash, Y.; Nogami, S.; Kasad, R.; Hasegawa, A. Evaluation of irradiation hardening of proton irradiated stainless steels by nanoindentation. J. Nucl. Mater. 2014, 446, 142–147. [Google Scholar] [CrossRef]
- Bergler, F.; Cornelia, K.; Das, A.; Merino, S.; Diego, G.; Hahler, P. Nanoindentation applied to ion-irradiated and neutron-irradiated Fe-9Cr and Fe-9Cr-NiSiP model alloys. J. Appl. Phys. 2022, 132, 045101. [Google Scholar] [CrossRef]
- Das, A.; Altstadt, E.; Kaden, C.; Kapoor, G.; Akhmadaliev, S.; Bergner, F. Nanoindentation Response of Ion- Irradiated Fe, Fe-Cr Alloys and Ferritic—Martensitic Steels Eurofer 97: The Effect of Ion Energy. Front. Mater. 2021, 8, 811851. [Google Scholar] [CrossRef]
- Hausild, P. Methodological comment on the nanoindentation of ion-irradiation hardened materials. J. Nucl. Mater. 2021, 551, 152987. [Google Scholar] [CrossRef]
- Reza, A.M.; Srivastava, A.K. Effect of Pile-up on Nanoindentation Measurements of Polycrystalline Bulk Metals. Adv. Mater. Res. 2014, 853, 143–150. [Google Scholar] [CrossRef]
- Miyake, K.; Fujisawa, S.; Korenaga, A.; Ishida, T.; Sasaki, S. The Effect of Pile-up and Contact Area on Hardness Test by Nanoindentation. Jpn. J. Appl. Phys. 2004, 43, 4602–4605. [Google Scholar] [CrossRef]
- Moharrami, N.; Bull, S.J. A Comparison of nanoindentation pile-up in bulk materials and thin films. Thin Solid Film. 2014, 572, 189–199. [Google Scholar] [CrossRef]
- George, F. Vander Voort, Metallographic Specimen Preparation for Electron Backscattered Diffraction. Pract. Metallogr. 2011, 48, 9. [Google Scholar] [CrossRef]
- Voort, G.V.; Van Geertruyden, W.; Dillon, S.; Metallographic, E.M. Specimen Preparation for Electron Backscattered Diffraction. Microsc. Microanal. 2006, 12, S02. [Google Scholar] [CrossRef]
- Ziegler, J. The Transport of Ions in Matter (TRIM). Available online: http://www.srim.org/ (accessed on 18 October 2025).
- Sorokin, A.A.; Margolin, B.Z.; Kursevich, I.P.; Minkin, A.J.; Neustroev, V.S. Effect of neutron irradiation on tensile properties of materials for pressure vessel internals of WWER type reactors. J. Nucl. Mater. 2014, 444, 373–384. [Google Scholar] [CrossRef]
- Yasnikov, I.S.; Vinogradov, A.; Estrin, Y. Revisiting the Considere criterion from the viewpoint of dislocation theory fundamentals. Scr. Mater. 2014, 76, 37–40. [Google Scholar] [CrossRef]
- Hill, R.; Storakers, B.; Zdunek, A.B. A Theoretical Study of the Brinell Hardness Test. Proc. R. Soc. Lond. A 1989, 423, 301–330. [Google Scholar] [CrossRef]
- Goto, K.; Watanabe, I.; Ohmura, T. Determining suitable parameters for inverse estimation of plastic properties based on indentation marks. Int. J. Plast. 2019, 116, 81–90. [Google Scholar] [CrossRef]
- Iost, A.; Bigot, R. Indentation size effect: Reality or artefact? J. Mater. Sci. 1996, 31, 3573–3577. [Google Scholar] [CrossRef]
- Hardie, C.D.; Roberts, S.G.; Bushby, A.J. Understanding the effects of ion irradiation using nanoindentation techniques. J. Nucl. Mater. 2015, 462, 391–401. [Google Scholar] [CrossRef]
- Mulewska, K.; Kalita, D.; Wilczopolovska, M.; Chrominski, W.; Ferreiros, P.A.; Kurpasks, L. Microstructural evolution and mechanical response of ion-irradiated Fe-9Cr alloys: Insights from nanoindentation. J. Nucl. Mater. 2025, 616, 156109. [Google Scholar] [CrossRef]



 ) and with a Vickers indenter (
) and with a Vickers indenter ( ) taking into account the pile-ups, depending on the indentation depth, h, for samples made of austenitic steels 18Cr-10Ni-Ti (a,b), 16Cr-20Ni-2Mo-Ti (c), 16Cr-25Ni-2Mo-Ti (d) and from FMS EP-823 (e) and EP-450 (f).
) taking into account the pile-ups, depending on the indentation depth, h, for samples made of austenitic steels 18Cr-10Ni-Ti (a,b), 16Cr-20Ni-2Mo-Ti (c), 16Cr-25Ni-2Mo-Ti (d) and from FMS EP-823 (e) and EP-450 (f).
 ) and with a Vickers indenter (
) and with a Vickers indenter ( ) taking into account the pile-ups, depending on the indentation depth, h, for samples made of austenitic steels 18Cr-10Ni-Ti (a,b), 16Cr-20Ni-2Mo-Ti (c), 16Cr-25Ni-2Mo-Ti (d) and from FMS EP-823 (e) and EP-450 (f).
) taking into account the pile-ups, depending on the indentation depth, h, for samples made of austenitic steels 18Cr-10Ni-Ti (a,b), 16Cr-20Ni-2Mo-Ti (c), 16Cr-25Ni-2Mo-Ti (d) and from FMS EP-823 (e) and EP-450 (f).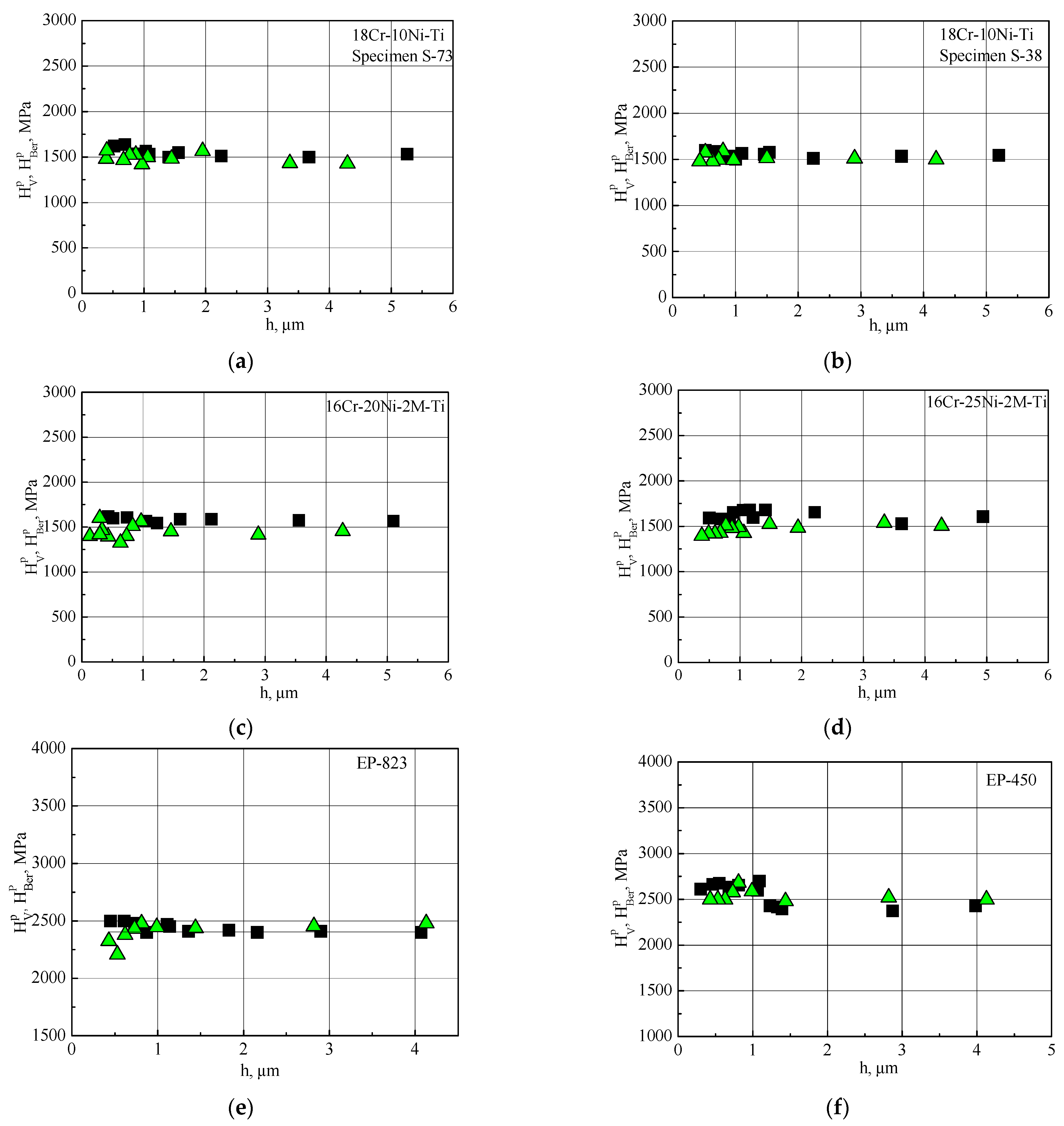
 )—determined from the indent projection area, ; (
)—determined from the indent projection area, ; ( )—determined from the indentation diagram without taking account of the pile-ups, (
)—determined from the indentation diagram without taking account of the pile-ups, ( )—determined from the indentation diagram taking account of the pile-ups with Formula (12), .
)—determined from the indentation diagram taking account of the pile-ups with Formula (12), .
 )—determined from the indent projection area, ; (
)—determined from the indent projection area, ; ( )—determined from the indentation diagram without taking account of the pile-ups, (
)—determined from the indentation diagram without taking account of the pile-ups, ( )—determined from the indentation diagram taking account of the pile-ups with Formula (12), .
)—determined from the indentation diagram taking account of the pile-ups with Formula (12), .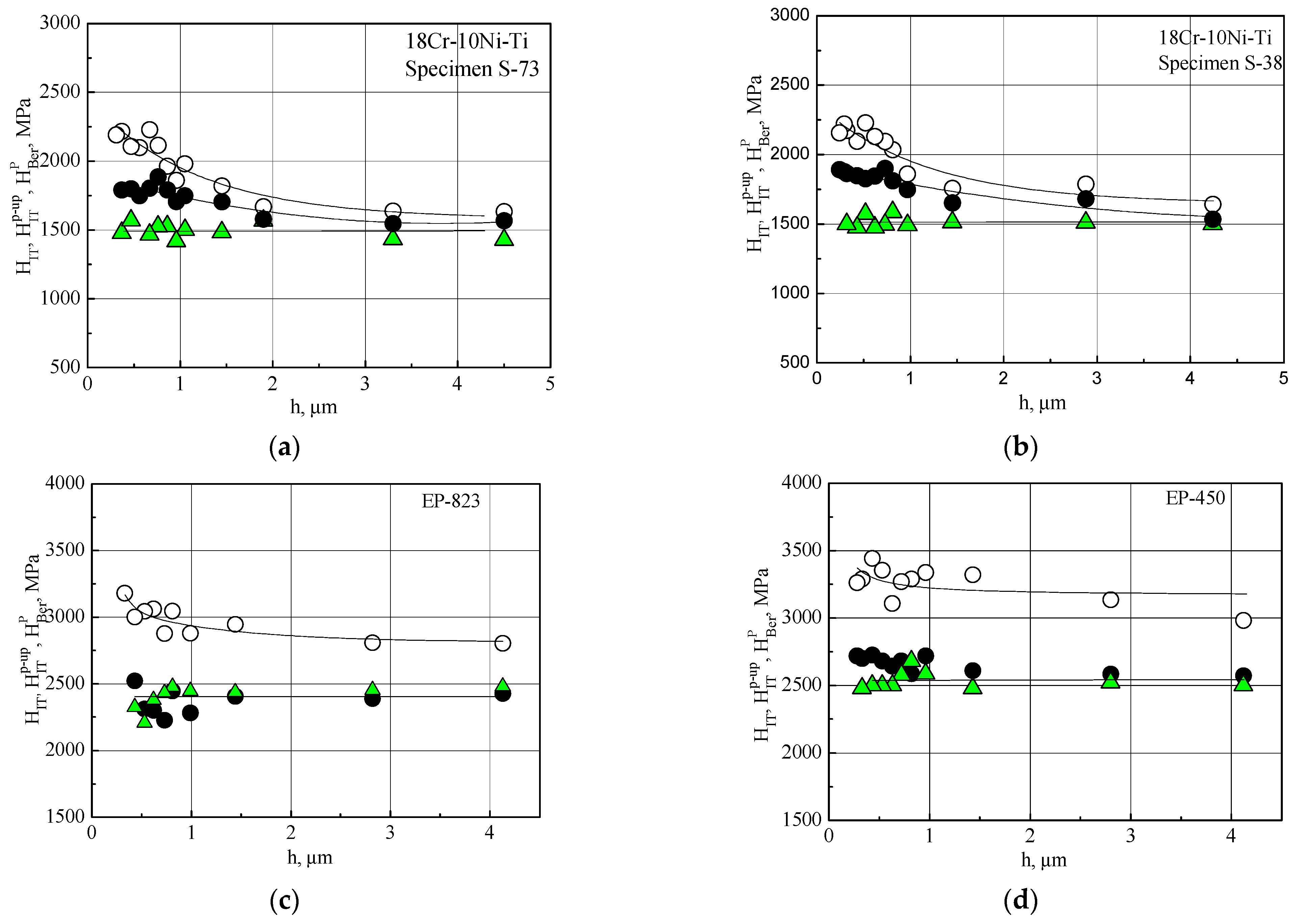
 ) and Vickers indenter (
) and Vickers indenter ( ); (b)—EP-823 (
); (b)—EP-823 ( ) and EP-450 (
) and EP-450 ( ) steels, Berkovich indenter.
) steels, Berkovich indenter.
 ) and Vickers indenter (
) and Vickers indenter ( ); (b)—EP-823 (
); (b)—EP-823 ( ) and EP-450 (
) and EP-450 ( ) steels, Berkovich indenter.
) steels, Berkovich indenter.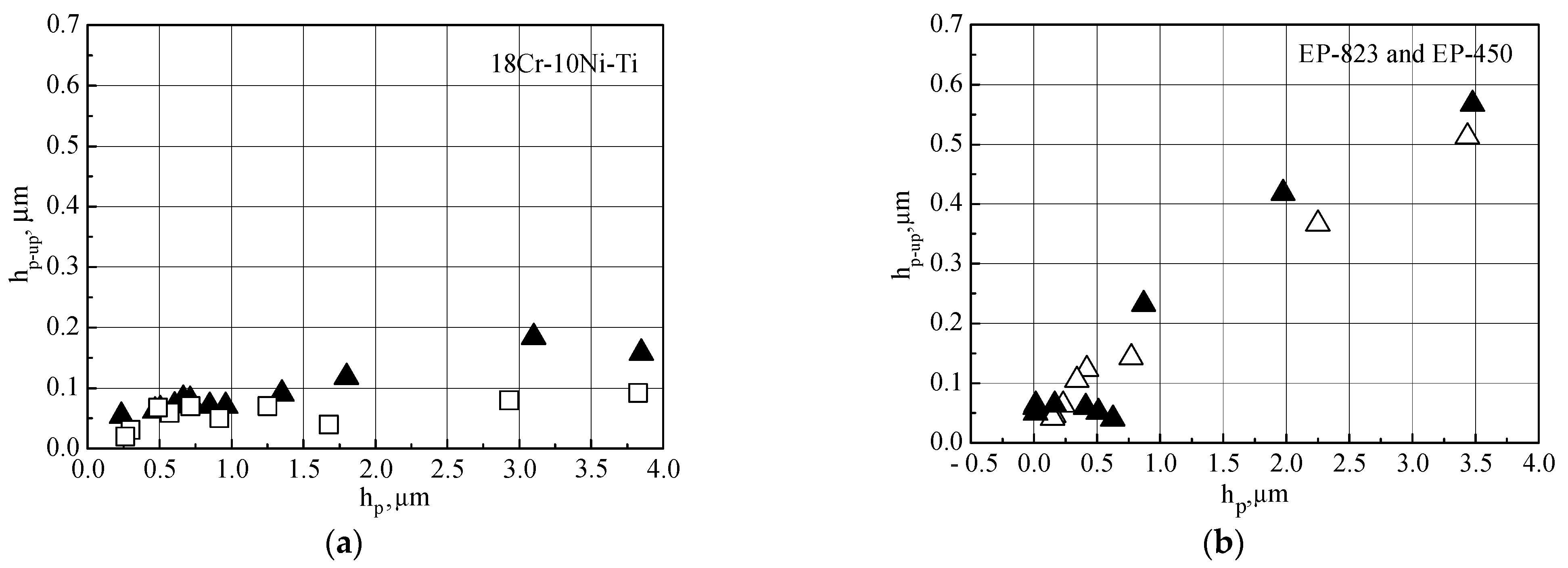
 ;—, irradiated material;
;—, irradiated material;  —, unirradiated material;
—, unirradiated material;  —, irradiated material;
—, irradiated material;  —, unirradiated material;
—, unirradiated material;  —, irradiated material;
—, irradiated material;  — unirradiated material.
— unirradiated material.
 ;—, irradiated material;
;—, irradiated material;  —, unirradiated material;
—, unirradiated material;  —, irradiated material;
—, irradiated material;  —, unirradiated material;
—, unirradiated material;  —, irradiated material;
—, irradiated material;  — unirradiated material.
— unirradiated material.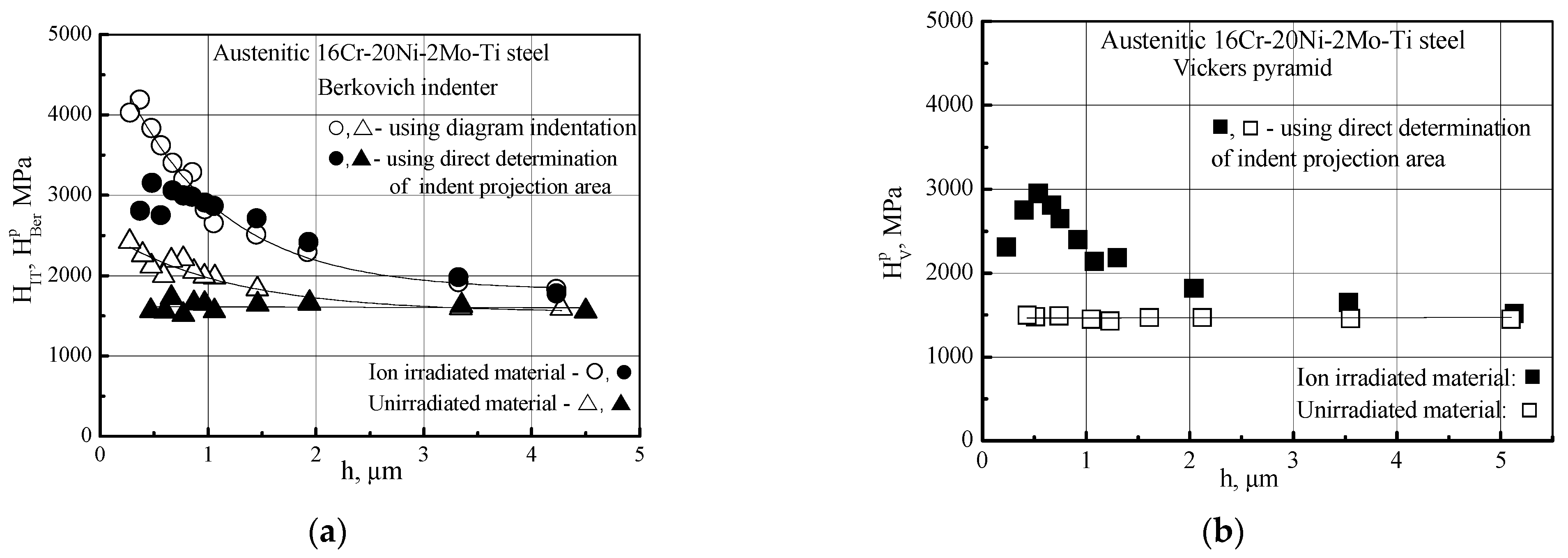
| Material | Mass Fraction of Chemical Elements, % | |||||||
|---|---|---|---|---|---|---|---|---|
| C | Si | Mn | Cr | Ni | Mo | S | P | |
| EP-823 | 0.14–0.18 | 1.0–1.3 | 0.5–0.8 | 10.0–12.0 | 0.5–0.8 | 0.6–0.9 | <0.01 | <0.015 |
| EP-450 | 0.10–0.15 | ≤0.50 | ≤0.8 | 11.0–13.5 | 0.05–0.3 | 1.2–1.8 | ≤0.015 | ≤0.025 |
| Nb | V | W | Ti | Al | B | N | ||
| EP-823 | 0.2–0.4 | 0.2–0.4 | 0.5–0.8 | <0.05 | <0.05 | <0.006 | <0.05 | |
| EP-450 | 0.25–0.55 | 0.1–0.3 | - | - | - | ≤0.08 | - | |
| Material | Mass Fraction of Chemical Elements, % | |||||||
|---|---|---|---|---|---|---|---|---|
| C | Si | Mn | Cr | Ni | Mo | S | P | |
| 18Cr-10Ni-Ti | 0.06–0.08 | 0.4–0.6 | 1.5–2.0 | 17.0–19.0 | 9.0–11.0 | ≤0.50 | ≤0.008 | 0.025–0.030 |
| 16Cr-20Ni-2Mo-Ti | 0.06–0.08 | 0.4–0.6 | 1.5–2.0 | 15.0–16.5 | 19.0–21.0 | 2.0–3.0 | ≤0.008 | 0.025–0.030 |
| 16Cr-25Ni-2Mo-Ti | 0.08–0.10 | 0.4–0.6 | 1.5–2.0 | 15.0–16.0 | 24.0–25.0 | 2.0–3.0 | ≤0.008 | 0.020–0.040 |
| Ti | Al | V | Cu | N | ||||
| 18Cr-10Ni-Ti | 5C-0.7 | ≤0.12 | ≤0.20 | ≤0.10 | ≤0.030 | |||
| 16Cr-20Ni-2Mo-Ti | 0.6–0.8 | ≤0.12 | ≤0.10 | ≤0.025 | ||||
| 16Cr-25Ni-2Mo-Ti | 0.6–0.8 | ≤0.12 | ≤0.10 | ≤0.025 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Margolin, B.; Belyaeva, L.; Sorokin, A. The Issues of the Radiation Hardening Determination of Steels After Ion Irradiation Using Instrumented Indentation. Metals 2025, 15, 1181. https://doi.org/10.3390/met15111181
Margolin B, Belyaeva L, Sorokin A. The Issues of the Radiation Hardening Determination of Steels After Ion Irradiation Using Instrumented Indentation. Metals. 2025; 15(11):1181. https://doi.org/10.3390/met15111181
Chicago/Turabian StyleMargolin, Boris, Lyubov Belyaeva, and Alexander Sorokin. 2025. "The Issues of the Radiation Hardening Determination of Steels After Ion Irradiation Using Instrumented Indentation" Metals 15, no. 11: 1181. https://doi.org/10.3390/met15111181
APA StyleMargolin, B., Belyaeva, L., & Sorokin, A. (2025). The Issues of the Radiation Hardening Determination of Steels After Ion Irradiation Using Instrumented Indentation. Metals, 15(11), 1181. https://doi.org/10.3390/met15111181






