Quantification of Austenite in Medium Manganese Steels Using the Magnetic Permeameter
Abstract
1. Introduction
2. Theoretical Basis
2.1. Physical Principle of Magnetic Measurement Methods of Austenite Content
2.2. The Law of Approach to Saturation Magnetization
2.3. Magnetization Measurements Methods and Selection
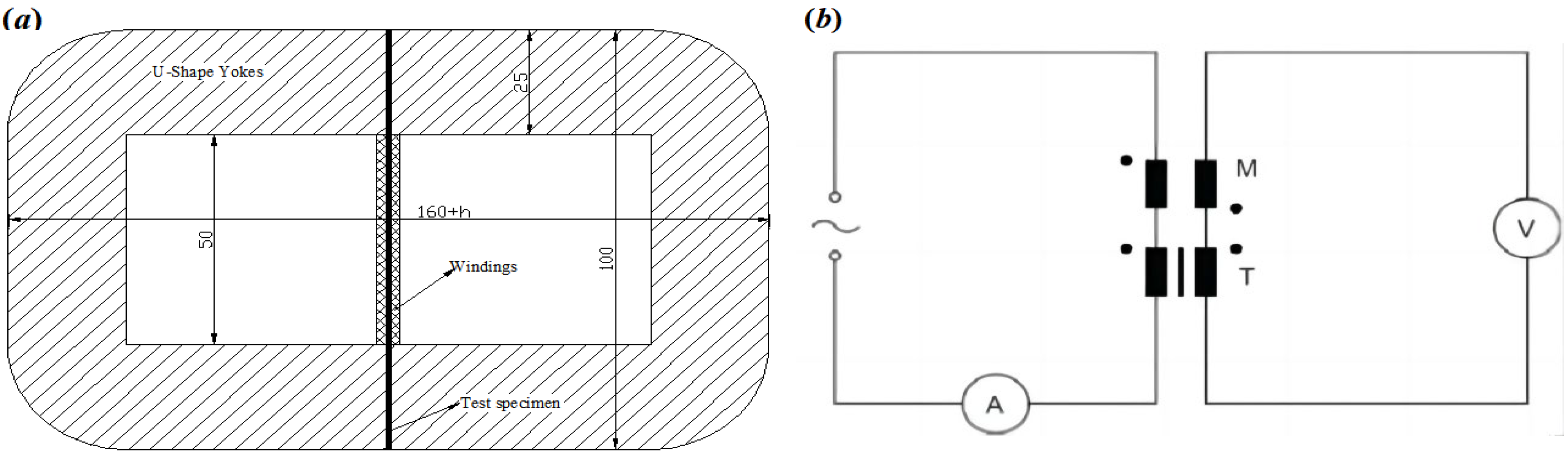
3. Materials and Experimental Procedures
4. Source of Measurement Errors in the Permeameter
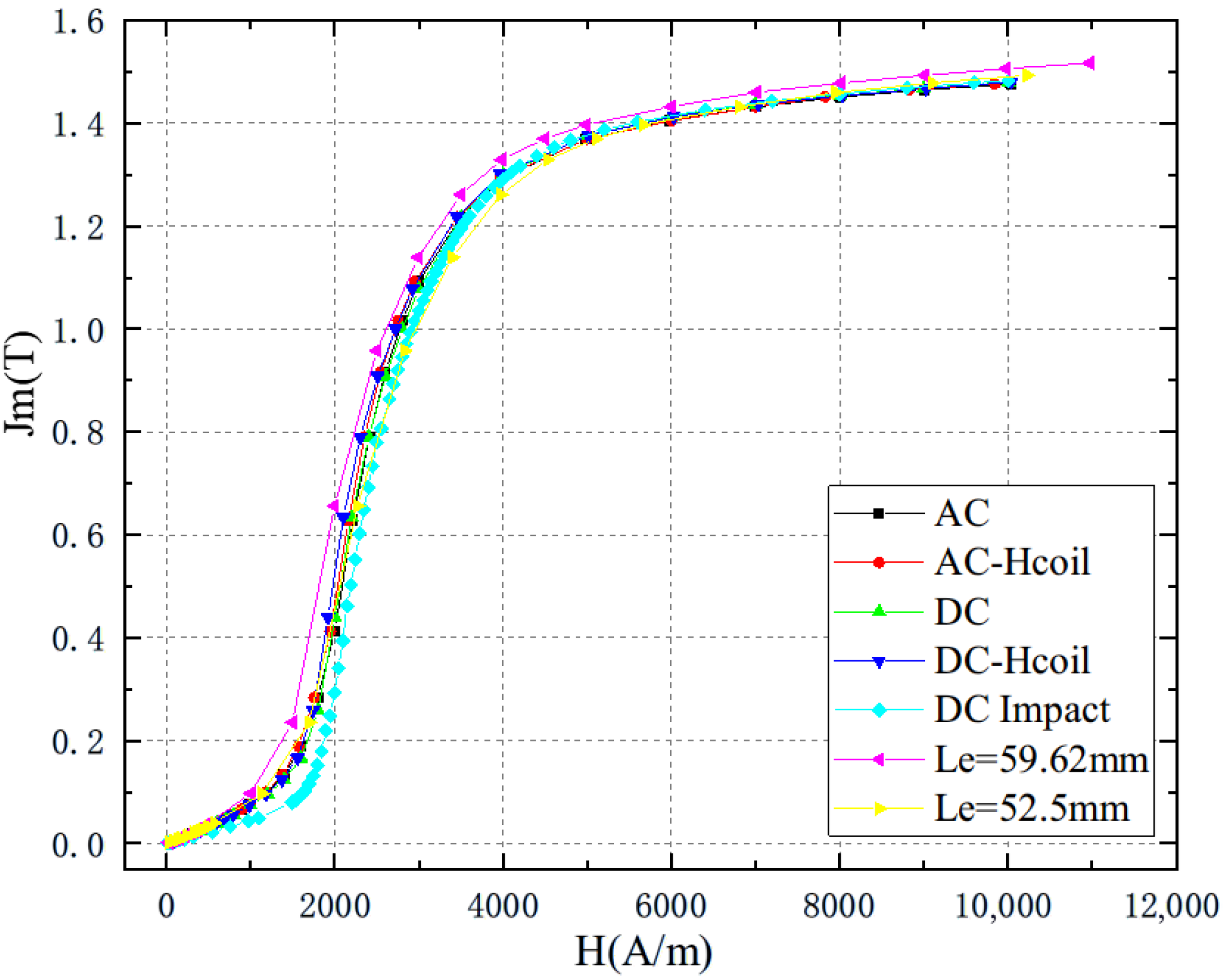
4.1. Magnetization Curve Measurement Method
4.2. Air Flux Compensation Efect Correction
5. Results
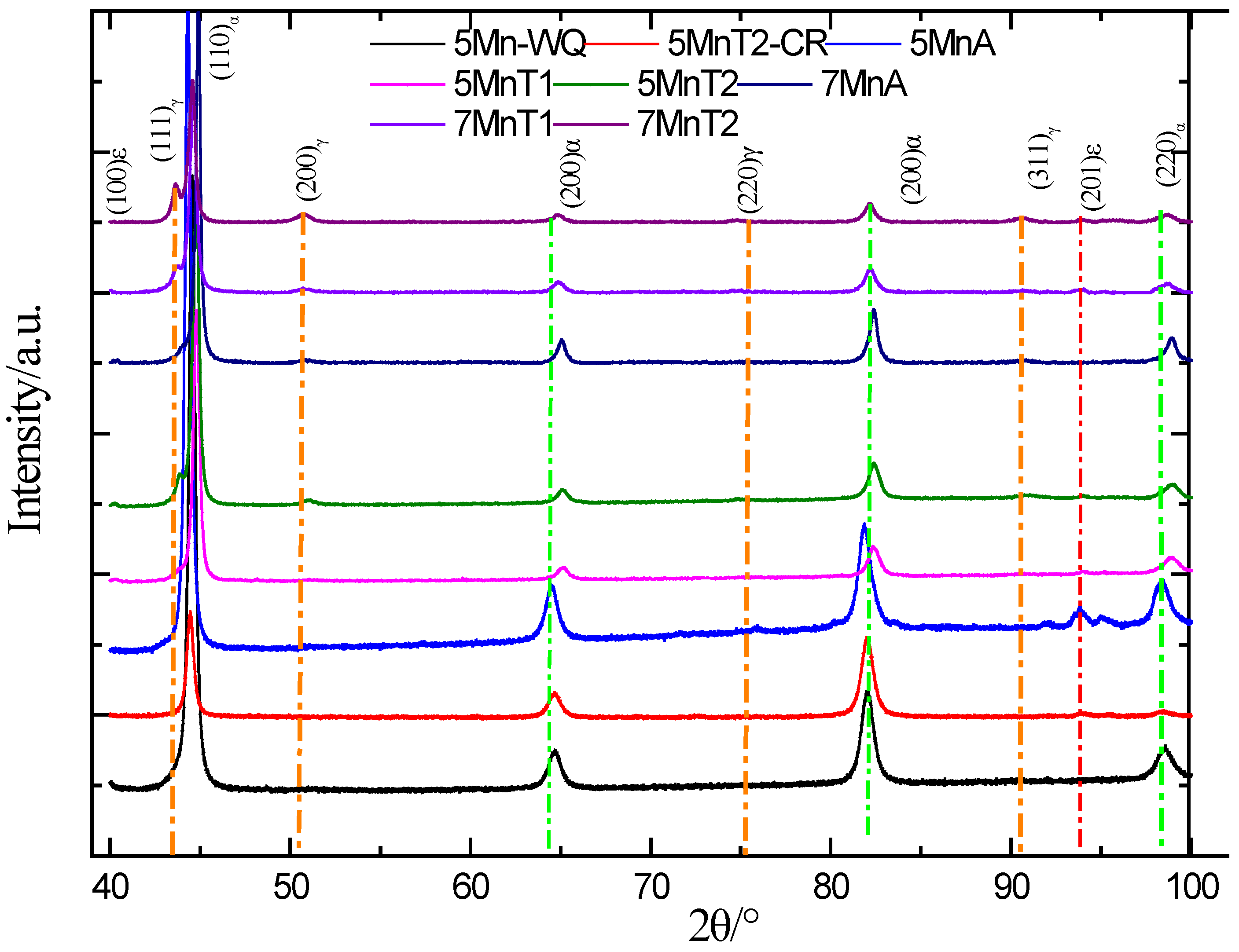
5.1. The Microstructure Characteristics of Medium Manganese Steels
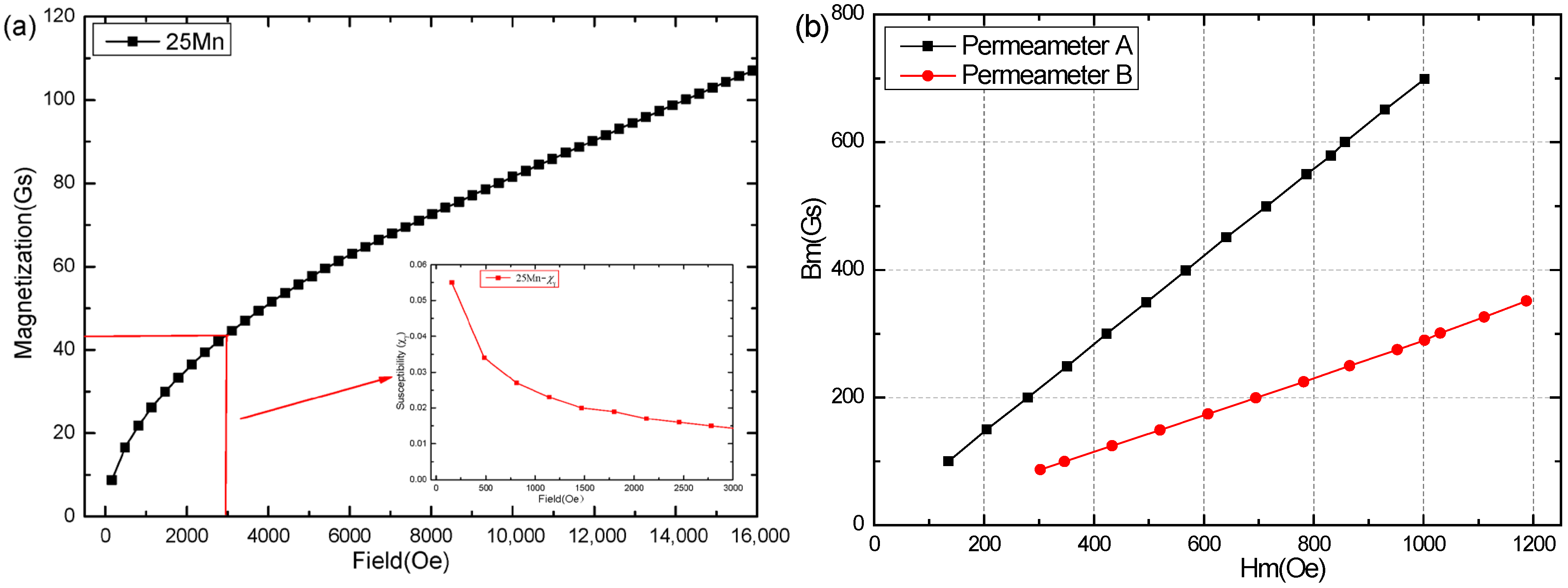
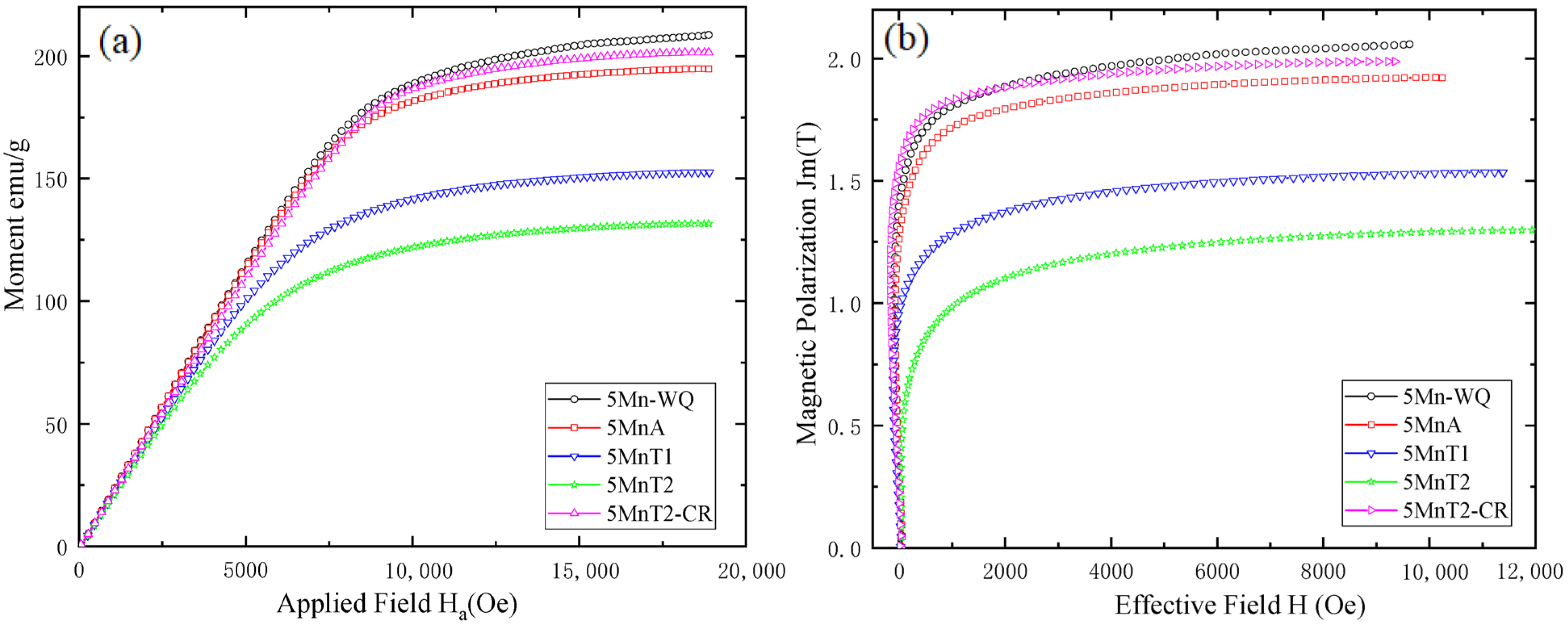
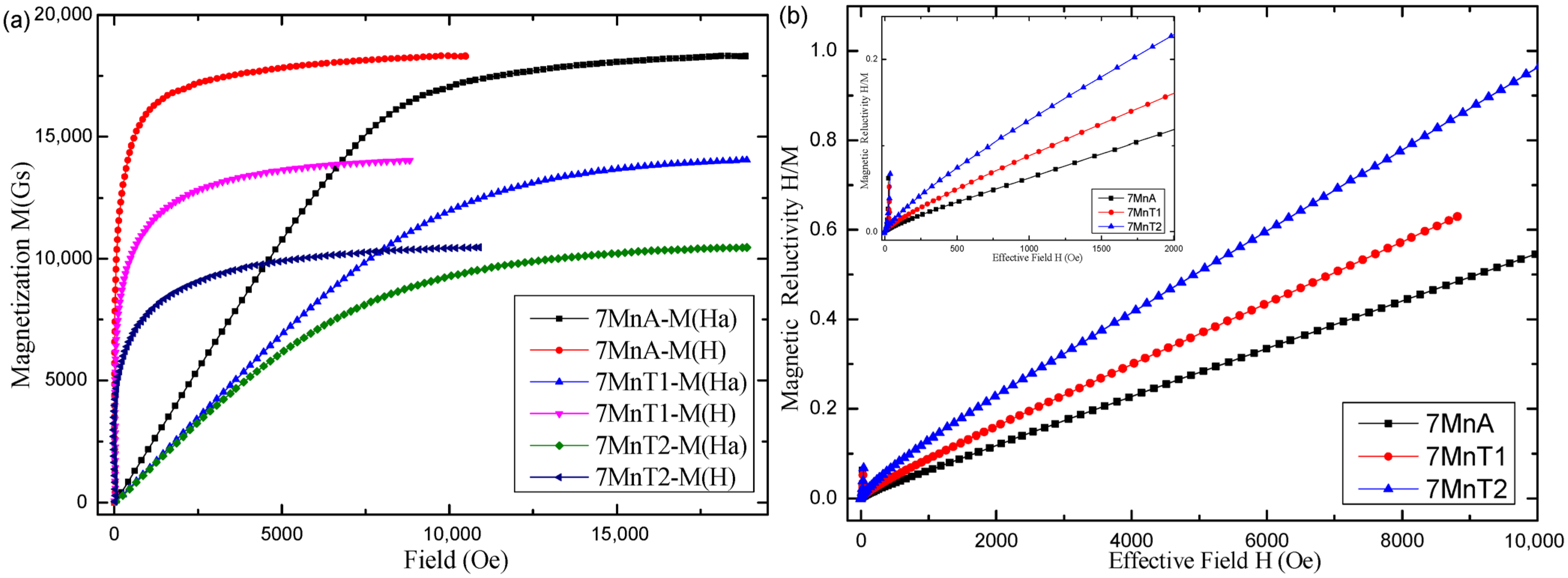
5.2. Determination of the Js Values of 5Mn and 7Mn Steels by the VSM
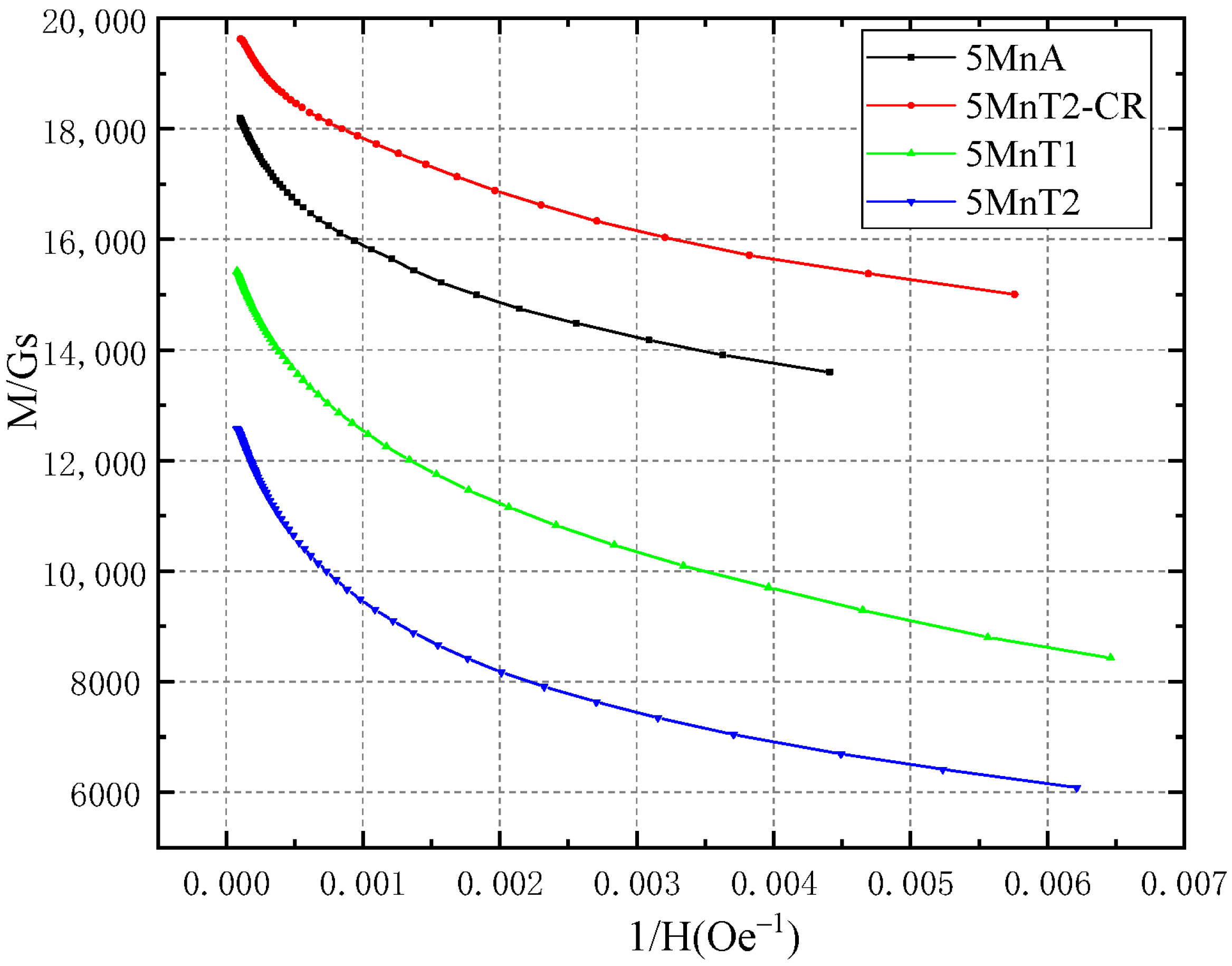
5.3. Determination of the Js Values of 5Mn and 7Mn Steels by the Permeameter
5.4. Comparison of Austenite Content of 5Mn and 7Mn Steels Measured by Different Methods
6. Discussion
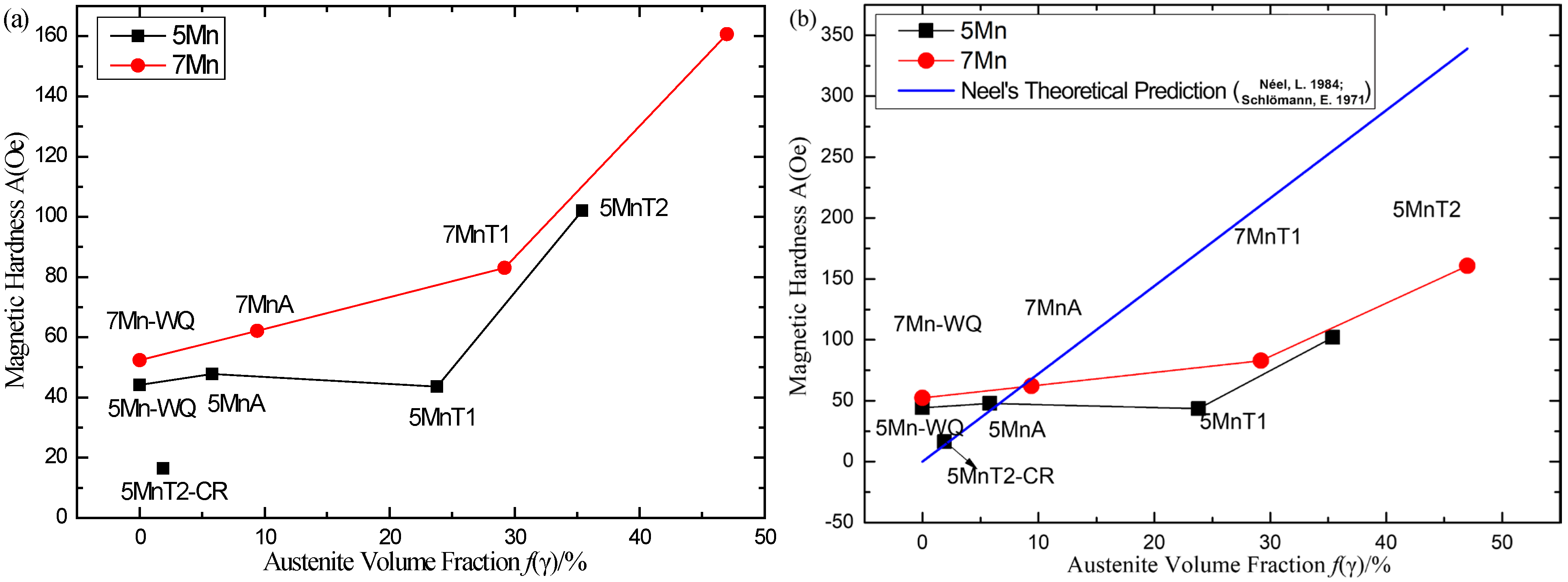
6.1. Theoretical Explanation of the Experimental Results
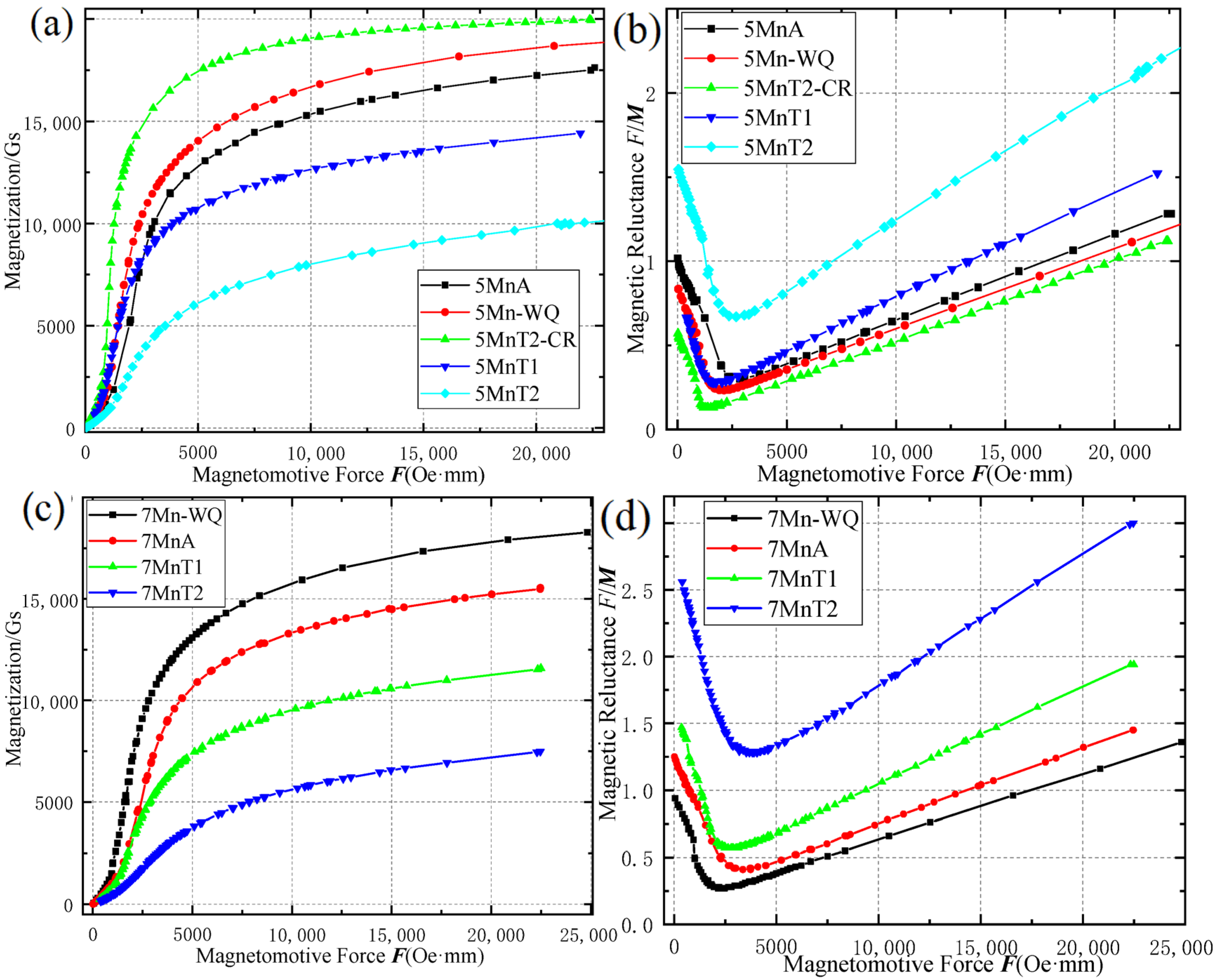
6.2. A General Theoretical Explanation for the Linear F-K Relation
6.3. The Limitations of Permeameter Method for Measuring Austenitic Content
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Bleck, W.; Brühl, F.; Ma, Y.; Sasse, C. Materials and processes for the third-generation advanced high-strength steels. Berg Huettenmaen. Monats. 2019, 164, 466–474. [Google Scholar] [CrossRef]
- Raabe, D.; Sun, B.; Da Silva, A.K.; Gault, B.; Yen, H.-W.; Sedighiani, K.; Sukumar, P.T.; Filho, I.R.S.; Katnagallu, S.; Jägle, E.; et al. Current challenges and opportunities in microstructure-related properties of advanced high-strength steels. Metall. Mater. Trans. A 2020, 51, 5517–5586. [Google Scholar] [CrossRef]
- Long, X.Y.; Kang, J.; Lv, B.; Zhang, F.C. Carbide-free bainite in medium carbon steel. Mater. Des. 2014, 64, 237–245. [Google Scholar] [CrossRef]
- Soleimani, M.; Kalhor, A.; Mirzadeh, H. Transformation-induced plasticity (trip) in advanced steels: A review. Mater. Sci. Eng. A 2020, 795, 140023. [Google Scholar] [CrossRef]
- Ariza, E.A.; Poplawsky, J.; Guo, W.; Unocic, K.; Ramirez, A.J.; Tschiptschin, A.P.; Babu, S.S. Evaluation of carbon partitioning in new generation of quench and partitioning (Q&P) steels. Metall. Mater. Trans. A 2018, 49, 4809–4823. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, J.-M.; Sun, G.-S.; Du, L.-X.; Liu, Y.; Dong, Y.; Misra, R.D.K. High strength and ductility combination in nano-/ultrafine-grained medium-mn steel by tuning the stability of reverted austenite involving intercritical annealing. J. Mater. Sci. 2019, 54, 6565–6578. [Google Scholar] [CrossRef]
- Li, Y.; Yuan, G.; Li, L.; Kang, J.; Yan, F.; Du, P.; Raabe, D.; Wang, G. Ductile 2-gpa steels with hierarchical substructure. Science 2023, 379, 168–173. [Google Scholar] [CrossRef]
- Hu, J.; Du, L.-X.; Sun, G.-S.; Xie, H.; Misra, R.D.K. The determining role of reversed austenite in enhancing toughness of a novel ultra-low carbon medium manganese high strength steel. Scr. Mater. 2015, 104, 87–90. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, M.X. The role of retained austenite stability on low-temperature mechanical behaviors of a quenching and partitioning steel. Metall. Mater. Trans. A 2019, 50, 5650–5655. [Google Scholar] [CrossRef]
- Qi, X.; Du, L.; Hu, J.; Misra, R.D.K. Effect of austenite stability on toughness, ductility, and work-hardening of medium-mn steel. Mater. Sci. Technol. 2019, 35, 2134–2142. [Google Scholar] [CrossRef]
- Xiong, X.C.; Chen, B.; Huang, M.X.; Wang, J.F.; Wang, L. The effect of morphology on the stability of retained austenite in a quenched and partitioned steel. Scr. Mater. 2013, 68, 321–324. [Google Scholar] [CrossRef]
- Solheim, K.G.; Solberg, J.K.; Walmsley, J.; Rosenqvist, F.; Bjørnå, T.H. The role of retained austenite in hydrogen embrittlement of supermartensitic stainless steel. Eng. Fail. Anal. 2013, 34, 140–149. [Google Scholar] [CrossRef]
- Sun, B.; Wang, D.; Lu, X.; Wan, D.; Ponge, D.; Zhang, X. Current challenges and opportunities toward understanding hydrogen embrittlement mechanisms in advanced high-strength steels: A review. Acta Metall. Sin. (Engl. Lett.) 2021, 34, 741–754. [Google Scholar] [CrossRef]
- Sidoroff, C.; Perez, M.; Dierickx, P.; Girodin, D. Advantages and shortcomings of retained austenite in bearing steels: A review. In Bearing Steel Technologies: 10th Volume, Advances in Steel Technologies for Rolling Bearings; ASTM International: West Conshohocken, PA, USA, 2014; pp. 1–37. [Google Scholar]
- Wang, M.; Liu, Z.-Y.; Li, C.-G. Correlations of ni contents, formation of reversed austenite and toughness for ni-containing cryogenic steels. Acta Metall. Sin. (Engl. Lett.) 2016, 30, 238–249. [Google Scholar] [CrossRef]
- Zheng, S.-Q.; Jiang, W.; Bai, X.; Li, S.-H.; Zhao, K.-Y.; Zhu, X.-K. Effect of deep cryogenic treatment on formation of reversed austenite in super martensitic stainless steel. J. Iron Steel Res. Int. 2015, 22, 451–456. [Google Scholar] [CrossRef]
- Trudel, A.; Lévesque, M.; Brochu, M. Microstructural effects on the fatigue crack growth resistance of a stainless steel ca6nm weld. Eng. Fract. Mech. 2014, 115, 60–72. [Google Scholar] [CrossRef]
- Jacques, P.J.; Allain, S.; Bouaziz, O.; De, A.; Gourgues, A.F.; Hance, B.M.; Houbaert, Y.; Huang, J.; Iza-Mendia, A.; Kruger, S.E.; et al. On measurement of retained austenite in multiphase trip steels—Results of blind round robin test involving six different techniques. Mater. Sci. Technol. 2009, 25, 567–574. [Google Scholar] [CrossRef]
- Talonen, J.; Aspegren, P.; Hänninen, H. Comparison of different methods for measuring strain induced α-martensite content in austenitic steels. Mater. Sci. Technol. 2004, 20, 1506–1512. [Google Scholar] [CrossRef]
- Jatczak, C.F. Retained austenite and its measurement by x-ray diffraction. In SAE Transactions; SAE International: Warrendale, PA, USA, 1980; pp. 1657–1676. [Google Scholar]
- Epp, J. X-ray diffraction (xrd) techniques for materials characterization. In Materials Characterization Using Nondestructive Evaluation (Nde) Methods; Woodhead Publishing: Amsterdam, The Netherlands, 2016; pp. 81–124. [Google Scholar]
- Blondé, R.; Jimenez-Melero, E.; Zhao, L.; Wright, J.P.; Brück, E.; van der Zwaag, S.; van Dijk, N.H. High-energy x-ray diffraction study on the temperature-dependent mechanical stability of retained austenite in low-alloyed trip steels. Acta Mater. 2012, 60, 565–577. [Google Scholar] [CrossRef]
- Vandijk, N.; Butt, A.; Zhao, L.; Sietsma, J.; Offerman, S.; Wright, J.; Vanderzwaag, S. Thermal stability of retained austenite in trip steels studied by synchrotron x-ray diffraction during cooling. Acta Mater. 2005, 53, 5439–5447. [Google Scholar] [CrossRef]
- Witte, M.; Lesch, C. On the improvement of measurement accuracy of retained austenite in steel with x-ray diffraction. Mater. Charact. 2018, 139, 111–115. [Google Scholar] [CrossRef]
- Zhao, L.; van Dijk, N.H.; Brück, E.; Sietsma, J.; van der Zwaag, S. Magnetic and x-ray diffraction measurements for the determination of retained austenite in trip steels. Mater. Sci. Eng. A 2001, 313, 145–152. [Google Scholar] [CrossRef]
- Mumtaz, K.; Takahashi, S.; Echigoya, J.; Kamada, Y.; Zhang, L.F.; Kikuchi, H.; Ara, K.; Sato, M. Magnetic measurements of martensitic transformation in austenitic stainless steel after room temperature rolling. J. Mater. Sci. 2004, 39, 85–97. [Google Scholar] [CrossRef]
- Tavares, S.S.M.; Mello, S.R.; Gomes, A.M.; Neto, J.M.; da Silva, M.R.; Pardal, J.M. X-ray diffraction and magnetic characterization of the retained austenite in a chromium alloyed high carbon steel. J. Mater. Sci. 2006, 41, 4732–4736. [Google Scholar] [CrossRef]
- Sicupira, F.L.; Sandim, M.J.R.; Sandim, H.R.Z.; Santos, D.B.; Renzetti, R.A. Quantification of retained austenite by x-ray diffraction and saturation magnetization in a supermartensitic stainless steel. Mater. Charact. 2016, 115, 90–96. [Google Scholar] [CrossRef]
- Arguelles, A.; Barbes, F.; Espeso, J.I.; Garcia-Mateo, C. Cryogenic study of the magnetic and thermal stability of retained austenite in nanostructured bainite. Sci. Technol. Adv. Mater. 2019, 20, 673–687. [Google Scholar] [CrossRef]
- Ahmadzade-Beiraki, E.; Kahrobaee, S.; Kashefi, M.; Akhlaghi, I.A.; Mazinani, M. Quantitative evaluation of deformation induced martensite in austenitic stainless steel using magnetic nde techniques. J. Nondestruct. Eval. 2020, 39, 28. [Google Scholar] [CrossRef]
- Radu, M.; Valy, J.; Gourgues, A.-F.; Le Strat, F.; Pineau, A. Continuous magnetic method for quantitative monitoring of martensitic transformation in steels containing metastable austenite. Scr. Mater. 2005, 52, 525–530. [Google Scholar] [CrossRef]
- Becker, R.; Döring, W. Ferromagnetismus; Springer: Berlin/Heidelberg, Germany, 2013; p. 167. [Google Scholar]
- Kittel, C. Physical theory of ferromagnetic domains. Rev. Mod. Phys. 1949, 21, 541–583. [Google Scholar] [CrossRef]
- Slater, J.C. The ferromagnetism of nickel. Phys. Rev. 1936, 49, 537–545. [Google Scholar] [CrossRef]
- McHenry, M.E.; Laughlin, D.E. Magnetic properties of metals and alloys. In Physical Metallurgy; Elsevier: Amsterdam, The Netherlands, 2014; pp. 1881–2008. [Google Scholar]
- Cina, B. A transitional h.C.P. Phase in the γ → α transformation in certain fe-base alloys. Acta Metall. 1958, 6, 748–762. [Google Scholar] [CrossRef]
- Kittel, C.; Galt, J. Ferromagnetic domain theory. In Solid State Physics; Elsevier: Amsterdam, The Netherlands, 1956; Volume 3, pp. 437–564. [Google Scholar]
- Cullity, B.D.; Graham, C.D. Introduction to Magnetic Materials, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; p. 360. [Google Scholar]
- Fiorillo, F. (Ed.) Chapter 9-measurement of intrinsic magnetic properties of ferromagnets. In Characterization and Measurement of Magnetic Materials; Academic Press: San Diego, CA, USA, 2004; pp. 549–579. [Google Scholar]
- Néel, L. La loi d’approche en a: H et une nouvelle théorie de la dureté magnétique. J. Phys. Radium 1984, 9, 184–192. [Google Scholar] [CrossRef]
- Grössinger, R. A critical examination of the law of approach to saturation. I. Fit procedure. Phys. Status Solidi (A) 1981, 66, 665–674. [Google Scholar] [CrossRef]
- Bozorth, R.M. Ferromagnetism; Wiley-IEEE Press: Piscataway, NJ, USA, 1993; p. 484. [Google Scholar]
- Fiorillo, F. Measurements of magnetic materials. Metrologia 2020, 47, S114–S142. [Google Scholar] [CrossRef]
- Fiorillo, F. (Ed.) Chapter 7-characterization of soft magnetic materials. In Characterization and Measurement of Magnetic Materials; Academic Press: San Diego, CA, USA, 2004; pp. 307–474. [Google Scholar]
- Fiorillo, F. Dc and ac magnetization processes in soft magnetic materials. J. Magn. Magn. Mater. 2002, 242–245, 77–83. [Google Scholar] [CrossRef]
- IEC 60404-4; Magnetic Materials-Part 4: Methods of Measurement of Dc Magnetic Properties of Magnetically Soft Materials. IEC Standard Publication: Geneva, Switzerland, 2008.
- Gokhale, S. Saturation permeameter. J. AIEE 1928, 47, 196–200. [Google Scholar]
- Bowler, N. Frequency-dependence of relative permeability in steel. AIP Conf. Proc. 2006, 820, 1269–1276. [Google Scholar] [CrossRef]
- IEC 60404-3; Magnetic Materials-Part 3: Methods of Measurement of the Magnetic Properties of Electrical Steel Strip and Sheet by Means of a Single Sheet Tester. IEC Standard Publication: Geneva, Switzerland, 2022.
- Hofmann, M.; Kahraman, D.; Herzog, H.-G.; Hoffmann, M.J. Numerical determination of the effective magnetic path length of a single-sheet tester. IEEE Trans. Magn. 2014, 50, 929–932. [Google Scholar] [CrossRef]
- Pfutzner, H.; Shilyashki, G.; Huber, E. Physical assessment of the magnetic path length of energy loss testers. IEEE Trans. Magn. 2020, 56, 1–7. [Google Scholar] [CrossRef]
- Gmyrek, Z. Single sheet tester with variable dimensions. IEEE Trans. Instrum. Meas. 2016, 65, 1661–1668. [Google Scholar] [CrossRef]
- Chen, D.X.; Zhu, Y.H. Permeameter and solenoid measurements of epstein strips of electrical steels. Rev. Sci. Instrum. 2023, 94, 093904. [Google Scholar] [CrossRef] [PubMed]
- Arpaia, P.; Liccardo, A.; Buzio, M.; Parrella, A. On the use of fluxmetric methods for characterizing feebly magnetic materials. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 22–25 May 2017; pp. 1404–1409. [Google Scholar] [CrossRef]
- Aharoni, A. Demagnetizing factors for rectangular ferromagnetic prisms. J. Appl. Phys. 1998, 83, 3432–3434. [Google Scholar] [CrossRef]
- Luo, H.W.; Shi, J.; Wang, C.; Cao, W.Q.; Sun, X.J.; Dong, H. Experimental and numerical analysis on formation of stable austenite during the intercritical annealing of 5mn steel. Acta Mater. 2011, 59, 4002–4014. [Google Scholar] [CrossRef]
- Gramlich, A.; Schmiedl, T.; Schönborn, S.; Melz, T.; Bleck, W. Development of air-hardening martensitic forging steels. Mater. Sci. Eng. A 2020, 784, 139321. [Google Scholar] [CrossRef]
- Han, J.; Lee, Y.-K. The effects of the heating rate on the reverse transformation mechanism and the phase stability of reverted austenite in medium mn steels. Acta Mater. 2014, 67, 354–361. [Google Scholar] [CrossRef]
- Jin, X.J.; Hsu, T.Y. Thermodynamic consideration of antiferromagnetic transition on fcc(γ)→hcp(ε) martensitic transformation in fe–mn–si shape memory alloys. Mater. Chem. Phys. 1999, 61, 135–138. [Google Scholar] [CrossRef]
- Sahu, P.; Hamada, A.; Ghosh, R.; Karjalainen, L. X-ray diffraction study on cooling-rate-induced γ fcc→ ε hcp martensitic transformation in cast-homogenized fe-26mn-0.14 c austenitic steel. Metall. Mater. Trans. A 2007, 38, 1991–2000. [Google Scholar] [CrossRef]
- Tsuzaki, K.; Fukasaku, S.-I.; Tomota, Y.; Maki, T. Effect of prior deformation of austenite on the γ→ε martensitic transformation in fe-mn alloys. Mater. Trans. JIM 1991, 32, 222–228. [Google Scholar] [CrossRef]
- Brown, W.F. Theory of the approach to magnetic saturation. Phys. Rev. 1940, 58, 736–743. [Google Scholar] [CrossRef]
- Brown, W.F. The effect of dislocations on magnetization near saturation. Phys. Rev. 1941, 60, 139–147. [Google Scholar] [CrossRef]
- Schlömann, E. Approach to saturation in inhomogeneous magnetic materials. J. Appl. Phys. 1971, 42, 5798–5807. [Google Scholar] [CrossRef]
- Steinmetz, C.P. On the law of hysteresis. Trans. Am. Inst. Electr. Eng. 1892, 9, 1–64. [Google Scholar] [CrossRef]
- Steinmetz, C.P. On the law of hysteresis (part ii.) and other phenomena of the magnetic circuit. Trans. Am. Inst. Electr. Eng. 1892, 9, 619–758. [Google Scholar] [CrossRef]
- Hauser, H.; Jiles, D.C.; Melikhov, Y.; Li, L.; Grössinger, R. An approach to modeling the dependence of magnetization on magnetic field in the high field regime. J. Magn. Magn. Mater. 2006, 300, 273–283. [Google Scholar] [CrossRef]
- Steinhaus, W.; Gumlich, E. Experimentelle untersuchungen zur theorie des ferromagnetismus. Arch. Für Elektrotechnik 1915, 4, 89–98. [Google Scholar] [CrossRef]
- Steinhaus, W.; Gumlich, E. Experimentelle untersuchungen zur theorie des ferromagnetismus: Ii. Ideale, dh hysteresefreie magnetisierung. Arch. Elektrotechnik 1915, 4, 149–158. [Google Scholar] [CrossRef]
- Weiss, P. L’hypothèse du champ moléculaire et la propriété ferromagnétique. J. Phys. Theor. Appl. 1907, 6, 661–690. [Google Scholar] [CrossRef]
- Jiles, D.C.; Atherton, D.L. Theory of ferromagnetic hysteresis (invited). J. Appl. Phys. 1984, 55, 2115–2120. [Google Scholar] [CrossRef]
- Stoner, E.C.; Wohlfarth, E.P. A mechanism of magnetic hysteresis in heterogeneous alloys. IEEE Trans. Magn. 1991, 27, 3475–3518. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H. Cementite. Int. Mater. Rev. 2019, 65, 1–27. [Google Scholar] [CrossRef]
- Yamamoto, S.; Terai, T.; Fukuda, T.; Sato, K.; Kakeshita, T.; Horii, S.; Ito, M.; Yonemura, M. Magnetocrystalline anisotropy of cementite pseudo single crystal fabricated under a rotating magnetic field. J. Magn. Magn. Mater. 2018, 451, 1–4. [Google Scholar] [CrossRef]




| Steel No. | C | Si | Mn | Al | P | S | Cr | Ni | Mo | Cu | Ti | V |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5Mn | 0.06 | 0.17 | 5.50 | 0.028 | 0.015 | 0.005 | 0.45 | 0.27 | 0.22 | 0.22 | 0.015 | <0.004 |
| 7Mn | 0.17 | 0.16 | 6.80 | 0.010 | 0.014 | 0.004 | 0.43 | 0.27 | 0.22 | 0.22 | 0.006 | 0.194 |
| 25Mn | 0.58 | 0.61 | 25.2 | 1.86 | 0.023 | 0.011 | / | / | / | / | / | / |
| Steel No. | Frölich–Kennelly Method | Magnetomotive Force Method | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Intercept a | Slope b | R Square | Js/T | A/Oe | Intercept aLe | Slope b | R Square | Js/T | ALe/Oe | A/Oe | |
| 5Mn-WQ | 0.00213 | 4.82 × 10−5 | 0.99997 | 2.07 ± 0.02 | 44.2 | 0.1182 | 4.82 × 10−5 | 0.99998 | 2.07 ± 0.02 | 2452.8 | 46.7 |
| 5MnT2-CR | 7.92 × 10−4 | 4.86 × 10−5 | 1 | 2.04 ± 0.02 | 16.4 | 0.0443 | 4.84 × 10−5 | 0.99993 | 2.05 ± 0.02 | 918.4 | 17.5 |
| 5MnA | 0.00247 | 5.17 × 10−5 | 0.99995 | 1.94 ± 0.02 | 47.8 | 0.1348 | 5.16 × 10−5 | 0.99997 | 1.94 ± 0.02 | 2615.8 | 49.8 |
| 5MnT1 | 0.00279 | 6.39 × 10−5 | 0.99984 | 1.56 ± 0.02 | 43.6 | 0.1586 | 6.35 × 10−5 | 0.99974 | 1.57 ± 0.02 | 2498.9 | 47.6 |
| 5MnT2 | 0.00821 | 8.06 × 10−5 | 0.99952 | 1.25 ± 0.02 | 102 | 0.4353 | 8.02 × 10−5 | 0.99961 | 1.26 ± 0.02 | 5426.4 | 103.3 |
| 7Mn-WQ | / | / | / | / | / | 0.13588 | 4.94 × 10−5 | 0.9999 | 2.02 ± 0.02 | 2750.6 | 52.4 |
| 7MnA | / | / | / | / | / | 0.18444 | 5.66 × 10−5 | 0.9998 | 1.78 ± 0.02 | 3258.6 | 62.1 |
| 7MnT1 | / | / | / | / | / | 0.31785 | 7.30 × 10−5 | 0.9997 | 1.37 ± 0.02 | 4354.1 | 83.0 |
| 7MnT2 | / | / | / | / | / | 0.82047 | 9.73 × 10−5 | 0.9996 | 1.02 ± 0.02 | 8432.3 | 160.6 |
| Steel No. | VSM Results | Permeameter Results | XRD Results | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Jm/T | Js/T | f(γ)/% | Jm/T | Js/T | f(γ)/% | A/Oe | f(γ)/% | f(ε)/% | f(ε) + f(γ)/% | a(bcc-Fe)/Å | |
| 5Mn-WQ | 2.04 | 2.06 ± 0.01 | 0 | 1.96 | 2.07 ± 0.02 | 0 | 44.2 | 0 | 0 | 0 | 2.892 |
| 5MnT2-CR | 1.98 | 2.02 ± 0.01 | 1.9 ± 0.5 | 1.98 | 2.04 ± 0.02 | 0.5 ± 1 | 16.4 | 0 | 0 | 0 | 2.876 |
| 5MnA | 1.90 | 1.94 ± 0.01 | 5.8 ± 0.5 | 1.75 | 1.94 ± 0.02 | 5.8 ± 1 | 47.8 | 0 | 4.8 (a) | 4.8 ±5 | 2.881 |
| 5MnT1 | 1.52 | 1.57 ± 0.01 | 23.8 ± 0.5 | 1.44 | 1.56 ± 0.02 | 24.3 ± 1 | 43.6 | 16.2 | 6.4 (a) | 22.6 ± 5 | 2.865 |
| 5MnT2 | 1.30 | 1.33 ± 0.01 | 35.4 ± 0.5 | 1.06 | 1.24 ± 0.02 | 39.8 ± 1 | 102 | 29.6 | 6.9 (a) | 36.5 ± 5 | 2.864 |
| 7Mn-WQ | / | / | 0 | 1.90 | 2.02 ± 0.02 | 0 | 52.4 | / | / | / | / |
| 7MnA | 1.81 | 1.83 ± 0.01 | 9.4 ± 0.5 | 1.56 | 1.78 ± 0.02 | 11.8 ± 1 | 62.1 | 1.9 | 4.1 (a) | 6 ± 5 | 2.877 |
| 7MnT1 | 1.42 | 1.43 ± 0.01 | 29.2 ± 0.5 | 1.16 | 1.37 ± 0.02 | 32.1 ± 1 | 83.0 | 18.3 | 7.9 (a) | 26.2 ± 5 | 2.870 |
| 7MnT2 | 1.04 | 1.07 ± 0.01 | 47.0 ± 0.5 | 0.87 | 1.02 ± 0.02 | 49.5 ± 1 | 160.6 | 43.7 | 4.5 (a) | 48.2 ± 5 | 2.869 |
| He/a ((H + αM)/a) | 2 | 3 | 4 | 5 | 7 | 8 | 10 | 15 | 20 |
|---|---|---|---|---|---|---|---|---|---|
| coth (He/a) | 1.037 | 1.0050 | 1.0007 | 1.0001 | 1.0000 | 1.0000 | 1.000 | 1.000 | 1.000 |
| Error (coth (He/a)-1) (%) | 3.73% | 0.50% | 0.07% | 0.01% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| M/Ms | 0.5373 | 0.6716 | 0.750 | 0.80 | 0.857 | 0.875 | 0.90 | 0.93 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Du, L.; Wu, H.; Gao, X. Quantification of Austenite in Medium Manganese Steels Using the Magnetic Permeameter. Metals 2025, 15, 1151. https://doi.org/10.3390/met15101151
Huang H, Du L, Wu H, Gao X. Quantification of Austenite in Medium Manganese Steels Using the Magnetic Permeameter. Metals. 2025; 15(10):1151. https://doi.org/10.3390/met15101151
Chicago/Turabian StyleHuang, Hongqian, Linxiu Du, Hongyan Wu, and Xiuhua Gao. 2025. "Quantification of Austenite in Medium Manganese Steels Using the Magnetic Permeameter" Metals 15, no. 10: 1151. https://doi.org/10.3390/met15101151
APA StyleHuang, H., Du, L., Wu, H., & Gao, X. (2025). Quantification of Austenite in Medium Manganese Steels Using the Magnetic Permeameter. Metals, 15(10), 1151. https://doi.org/10.3390/met15101151







