On the Problem of the Distillation Separation of Secondary Alloys of Magnesium with Zinc and Magnesium with Cadmium
Abstract
1. Introduction
2. Materials and Methods
2.1. Method of Calculating the Boundaries of the Liquid–Vapor Phase Transition
2.2. Method for Determining the Values of Saturated Metal Vapor Pressure
2.3. Preparation of Magnesium Alloys with Zinc and Cadmium
3. Results and Discussion
3.1. Results of Determining the Partial Pressures of Components for Magnesium Alloys with Zinc and Cadmium
3.2. Boundaries of the Fields of Liquid and Vapor Coexistence in Mg–Zn and Mg–Cd Systems
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Prasad, S.V.S.; Prasad, S.B.; Verma, K.; Mishra, R.K.; Kumar, V.; Singh, S. The role and significance of Magnesium in modern day research—A review. J. Magnes. Alloy 2021, 10, 1–61. [Google Scholar] [CrossRef]
- Yang, Y.; Xiong, X.; Chen, J.; Peng, X.; Chen, D.; Pan, F. Research advances of magnesium and magnesium alloys worldwide in 2022. J. Magnes. Alloy 2023, 11, 2611–2654. [Google Scholar] [CrossRef]
- Miryuk, O.A. Magnesia composite materials for layered products. Kompleks. Ispolz. Miner. Syra Complex Use Miner. Resour. 2024, 328, 5–12. [Google Scholar] [CrossRef]
- Kiselevsky, M.V.; Anisimova, N.Y.; Polotsky, B.E.; Martynenko, N.S.; Lukyanova, E.A.; Sitdikova, S.M.; Dobatkin, S.V.; Estrin, Y.Z. Biodegradable magnesium alloys as promising for medical applications (review). Sovrem. Tehnol. Med. 2019, 11, 146–157. [Google Scholar] [CrossRef]
- Juraimi, N.; Shah, A.; Hassan, M.A.; Mohamed, M.; Kenzhaliyev, B.; Khairudin, M.; Daud, R.; Abdelkarim, H.A. Performance Enhancement of Energy Saving and Machining Characteristic in Electrical Discharge Machining on Magnesium Alloy: A Review. J. Advan. Res. Fluid Mechan. Ther. Sci. 2020, 73, 29–45. [Google Scholar] [CrossRef]
- Li, L.; Bao, J.; Qiao, M.; Tian, J.; Yang, Y.; Sha, J.; Zhang, Z. Improvement of strength—Ductility balance and corrosion resistance in as—Extruded Mg–Gd–Zn–Zr alloys by Zn/Gd ratio. Mater. Sci. Eng. 2023, 872, 144979. [Google Scholar] [CrossRef]
- Zhao, X.; Kong, G.; Zhang, S.; Che, C.; Lai, D. Effect of Mg on the fluidity of zinc alloys. Mater. Lett. 2022, 320, 1322664. [Google Scholar] [CrossRef]
- Babenko, A.; Ghasali, E.; Raza, S.; Baghchesaraee, K.; Cheng, Y.; Hayat, A.; Liu, P.; Zhao, S.; Orooji, Y. Comprehensive insights into recent innovations: Magnesium-inclusive high-entropy alloys. J. Magnes. Alloys 2024, 12, 1311–1345. [Google Scholar] [CrossRef]
- Pavlov, A.V.; Naimanbaev, M.A.; Onaev, M.I.; Ulasyuk, S.M.; Zhenisov, B.Z.; Ultarakova, A.A. Development of technological processes for thermal vacuum production of high purity magnesium from industrial products and waste of magnesium production. Kompleks. Ispolz. Miner. Syra Complex Use Miner. Resour. 2010, 271, 70–83. [Google Scholar]
- Volodin, V.N.; Аbdulvaliyev, R.A.; Trebukhov, S.T.; Nitsenko, A.V.; Linnik, X.A. Recycling of beryllium, manganese, and zirconium from secondary alloys by magnesium distillation in vacuum. Kompleks. Ispolz. Miner. Syra Complex Use Miner. Resour. 2024, 331, 90–100. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Song, J.; Pan, F.; Willumeit-Römer, R.; Kainer, K.U.; Hort, N. Development and prospects of degradable magnesium alloys for structural and functional applications in the fields of environment and energy. J. Magnes. Alloys 2023, 11, 3926–3947. [Google Scholar] [CrossRef]
- Kainer, K.U. (Ed.) Magnesium Alloys and Technology; DGM; Wiley-VCH: Weinheim, Germany, 2003; p. 273. [Google Scholar]
- Xu, S.; Ikpi, M.E.; Dong, J.; Wei, J.; Ke, W.; Chen, N. Effect of Cadmium alloying on the Corrosion and Mechanical Properties of Magnesium. Int. J. Electrochem. Sci. 2012, 7, 4735–4755. [Google Scholar] [CrossRef]
- Shan, G.; Shujie, R.; Cuirong, L.; Zhisheng, W.; Hongzhan, L. Effect of Cd Addition on Microstructure and Properties of Mg–Cd Binary Magnesium Alloy. Rare Metal Mat. Eng. 2015, 44, 2401–2404. [Google Scholar] [CrossRef]
- Li, C.; Huang, T.; Liu, Z. Effects of thermomechanical processing on microstructures, mechanical properties, and biodegradation behavior of dilute Zn–Mg alloys. J. Mater. Res. Technol. 2023, 23, 2940–2955. [Google Scholar] [CrossRef]
- Zhong, L.; Wang, L.; Dou, Y.; Wang, Y. Critical role of dynamic precipitation on enhanced creep resistance in Mg–Zn alloy by Mn substitution for Zr. J. Mater. Res. Technol. 2023, 24, 9082–9095. [Google Scholar] [CrossRef]
- Hashemi, M.; Alizadeh, R.; Langdon, T.G. Recent advances using equal—Channel angular pressing to improve the properties of biodegradable Mg Zn alloys. J. Magnes. Alloys 2023, 11, 2260–2284. [Google Scholar] [CrossRef]
- Recycling and Use of Magnesium Scrap. Available online: http://fccland.ru/magnievye-splavy/6228-pererabotka-I-ispolzovanie-magnievogo-loma.html (accessed on 19 January 2024).
- Kubashevskiy, O.; Olkokk, S.B. Metallurgical Thermochemistry; Metallurgy: Moskow, Russia, 1982; p. 390. [Google Scholar]
- Dai, Y.N.; Yang, B. Vacuum Metallurgy of Non—Ferrous Metals; Metallurgicаl Ind. Press: Beijing, China, 2000; p. 547. [Google Scholar]
- Sommer, F. Bildungsbedingungen glasartiger Legierungen. Z. Met. 1981, 72, 219–224. [Google Scholar] [CrossRef]
- Khanna, K.N.; Sing, P. Entropy of mixing of liquid metal alloys. Physica B+C 1982, 114, 174–180. [Google Scholar] [CrossRef]
- Luo, Z.; Zhang, S.; Tang, Y.; Zhao, D. Thermodynamics of Mg–Zn–RE systemsolutions forming stable quasicrystals. Scr. Metall. Mater. 1994, 30, 393–398. [Google Scholar] [CrossRef]
- Morishita, M.; Yamamoto, H.; Shikada, S.; Kusumoto, M.; Matsumoto, Y. Thermodynamics of the formation of magnesium—Zinc intermetallic compounds in the temperature range from absolute zero to high temperature. Acta Mater. 2006, 54, 3151–3159. [Google Scholar] [CrossRef]
- Berche, A.; Drescher, C.; Rogez, J.; Record, M.-C.; Brühne, S.; Assmus, W. Thermodynamic measurement in the Mg–Zn system. J. Alloys Compd. 2010, 503, 44–49. [Google Scholar] [CrossRef]
- Plevachuk, Y.; Sklyarchuk, V.; Pottlachtr, G.; Yakymovych, A. Thermophysical properties of some liquid binary Mg—Based alloys. J. Min. Met. B 2017, 53, 279–284. [Google Scholar] [CrossRef]
- Ghosh, P.; Mezbahul-Islam, M.; Medraj, M. Critical assessment, and thermodynamic modeling of Mg–Zn, Mg–Sn, Sn–Zn and Mg–Sn–Zn systems. Calphad 2012, 36, 28–43. [Google Scholar] [CrossRef]
- Trumbore, F.A.; Wallace, W.E.; Craig, R.S. Magnesium—Cadmium Alloys. II. The Use of the Electrochemical Cell to Determine the Heats, Free Energies and Entropies of the Solid Alloys in the temperature Range Above the Order—Disorder Curie Points. J. Am. Chem. Soc. 1952, 74, 132–136. [Google Scholar] [CrossRef]
- Buck, T.M.; Wallace, W.E.; Rulon, R.M. Magnesium—Cadmium Alloys. III. Some Calorimetrically Determined Heats of Formation at 25°. J. Am. Chem. Soc. 1952, 74, 136–139. [Google Scholar] [CrossRef]
- Johnston, W.V.; Sterrett, K.F.; Wallace, W.E. Magnesium—Cadmium Alloys. VIII. Heat Capacities of Mg3Cd and MgCd2 between 20 and 290°. The Standard Heats, Free Energies and Entropies of Formation and the Residual Entropies. J. Am. Chem. Soc. 1957, 79, 3633–3637. [Google Scholar] [CrossRef]
- Saba, W.G.; Sterret, K.F.; Craig, R.S.; Wallace, W.E. The Heat Capacities of Magnesium and Cadmium between 20 and 270°. J. Am. Chem. Soc. 1957, 79, 3637–3638. [Google Scholar] [CrossRef]
- Kubaschewski, O.; Chart, T.G. Calculation of Metallurgical Equilibrium Diagrams from Thermochemical Data. J. Inst. Met. 1964, 93, 329–338. [Google Scholar]
- Palatnik, L.S.; Fedorov, G.V.; Bogatov, P.N. The study of the laws of evaporation of alloys. Phys. Met. Met. Sci. 1966, 21, 409–413. [Google Scholar]
- Malyshev, V.P.; Turdukozhayeva, A.M.; Ospanov, Y.A.; Sarkenov, B. Evaporation and Boiling of Simple Substances; Nauchnyi Mir: Moscow, Russia, 2010; p. 304. [Google Scholar]
- Boos, A.; Steeb, S.; Godel, D. Struktur geschmolzener Magnesium—Cadmium-Legierungen. Z. Naturforschung A 1972, 27, 271–276. [Google Scholar] [CrossRef]
- Zhang, J.; Oates, W.A.; Zhang, F.; Chen, S.-L.; Chou, K.-C.; Chang, Y.A. Cluster/site approximation calculation of the ordering phase diagram for Cd–Mg alloys. Intermetallics 2001, 9, 5–8. [Google Scholar] [CrossRef]
- Ahmad, S.; Chaudhary, R.P.; Mandal, J.; Jha, I.S. Thermodynamics of compound forming Cd–Mg liquid alloys: A theoretical approach. Mater. Today Proc. 2023, in press. [Google Scholar] [CrossRef]
- Clark, J.B.; Richter, P.W. The Determination of Composition Temperature—Pressure Phase Diagrams of Binary Aloe Systems. In Proceedings of the 7th International AIRAPT Conference High Pressure Science and Technology, Le Creusot, France, 30 July–3 August 1979; pp. 363–371. [Google Scholar]
- Nitsenko, A.; Volodin, V.; Linnik, X.; Burabaeva, N.; Trebukhov, S.A. Melt—Vapor Phase Transition in the Aluminum—Selenium System in Vacuum. Metals 2023, 13, 1297. [Google Scholar] [CrossRef]
- Darken, L.S.; Gurry, R.W. Physical Chemistry of Metals; Hill Book Company, Inc.: McGraw-Hill Book: New York, NY, USA, 1953; p. 570. [Google Scholar]
- Morachevsky, A.G. Thermodynamics of Molten Metal and Salt Systems; Metallurgy: Moscow, Russia, 1987; p. 240. [Google Scholar]
- Volodin, V.N. Physical Chemistry and Technology of Cadmium Refining; Institute of Metallurgy and Beneficiation: Almaty, Kazakstan, 2011; p. 238. Available online: https://www. twirpx.com/file/2543691/ (accessed on 10 January 2024).
- Lyakishev, N.P. Diagrams of the State of Binary Metal Systems: Handbook; Mechanical Engineering, Ltd.: Moscow, Russia, 2001; Volume 3, p. 872. [Google Scholar]
- Lyakishev, N.P. Diagrams of the State of Binary Metal Systems: Handbook; Mechanical Engineering, Ltd.: Moscow, Russia, 1996; Volume 1, p. 992. [Google Scholar]
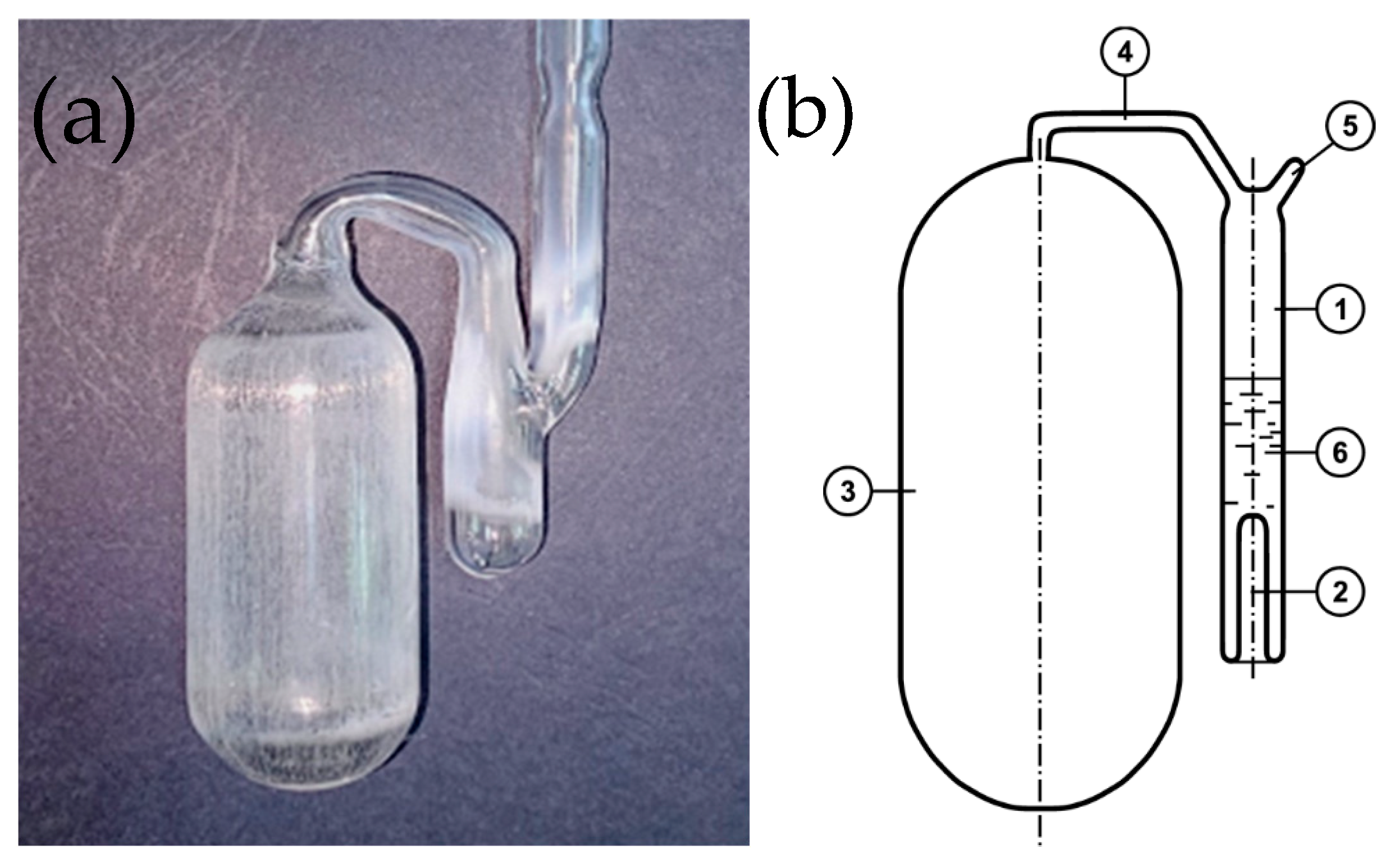
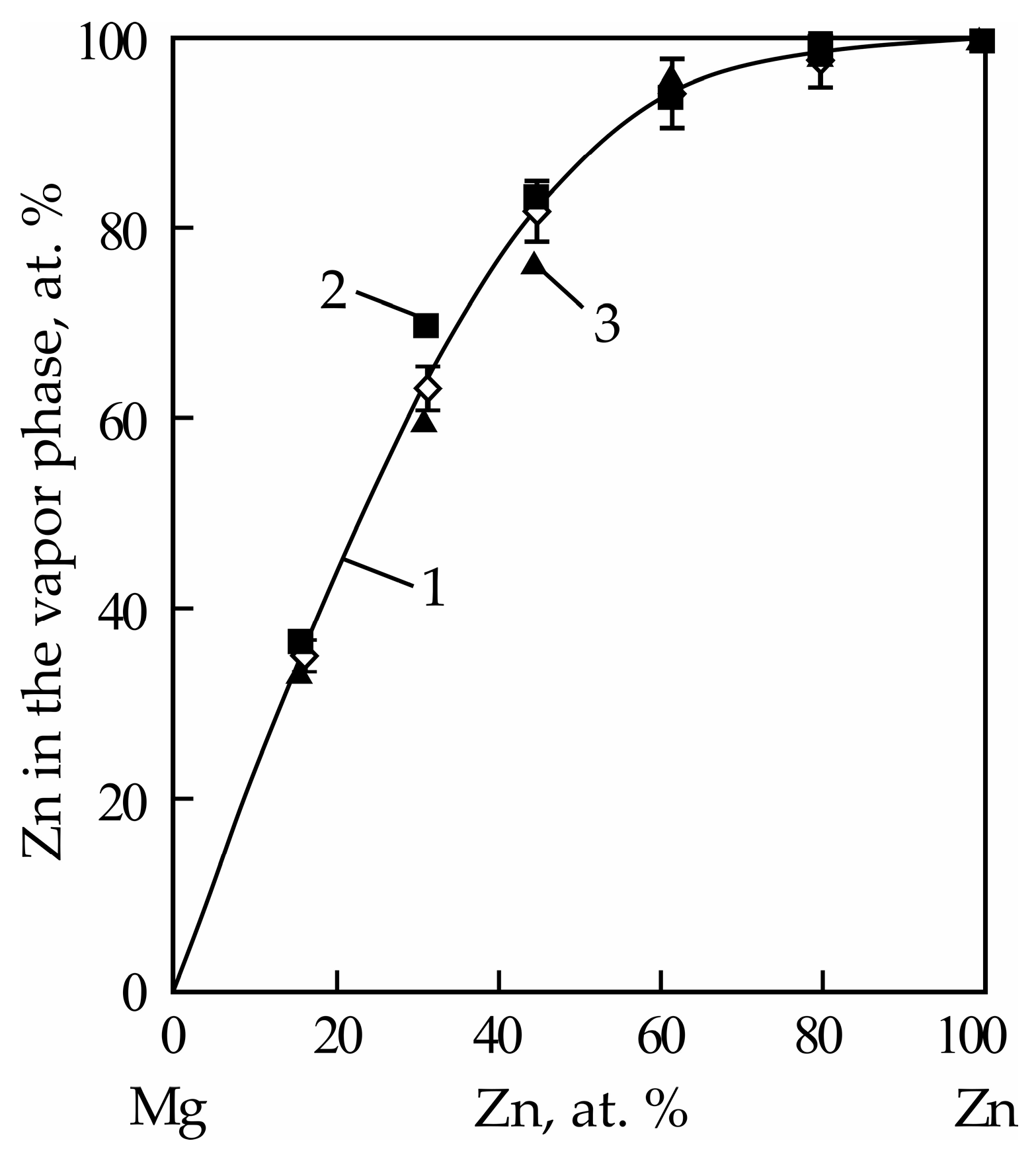

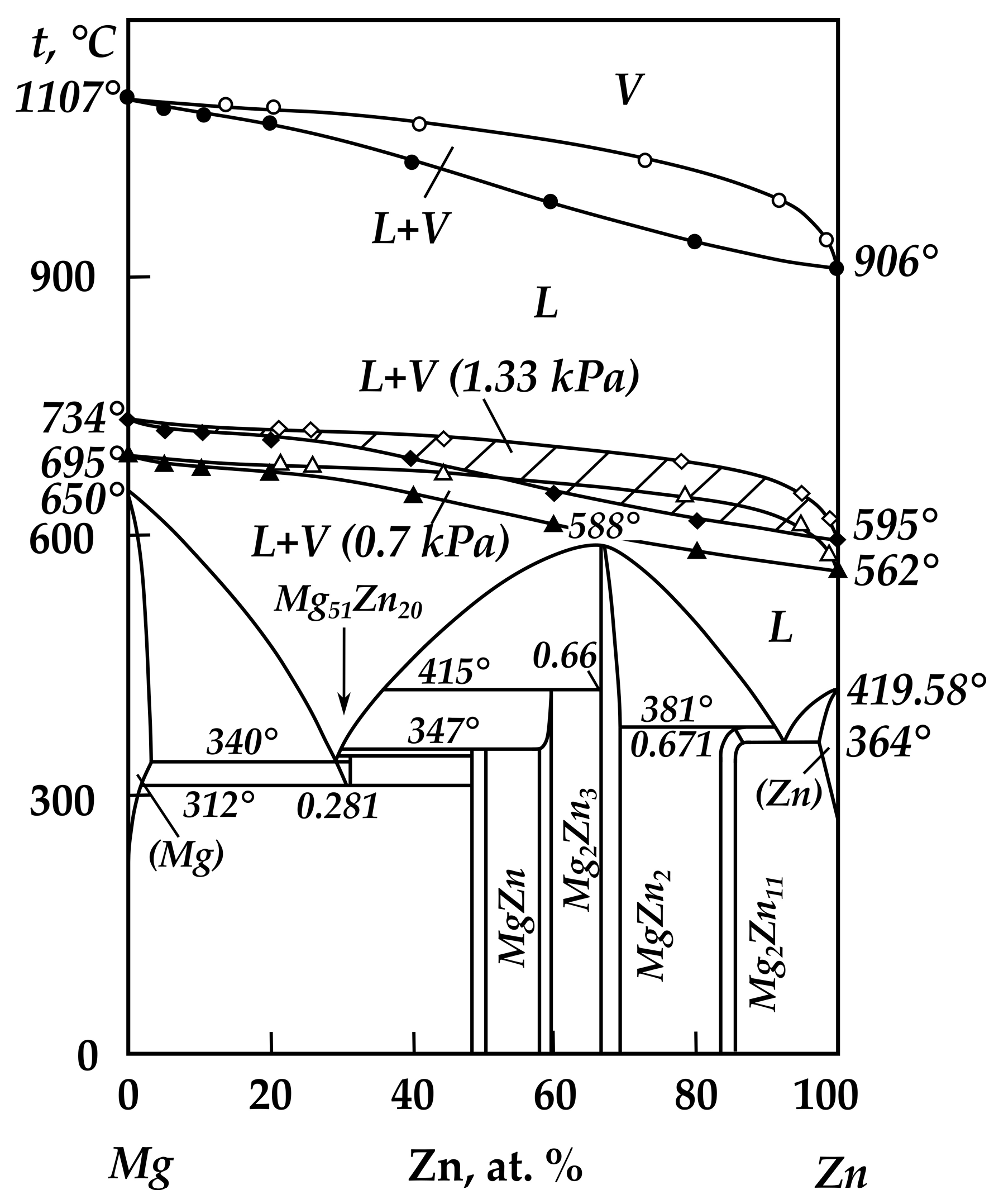
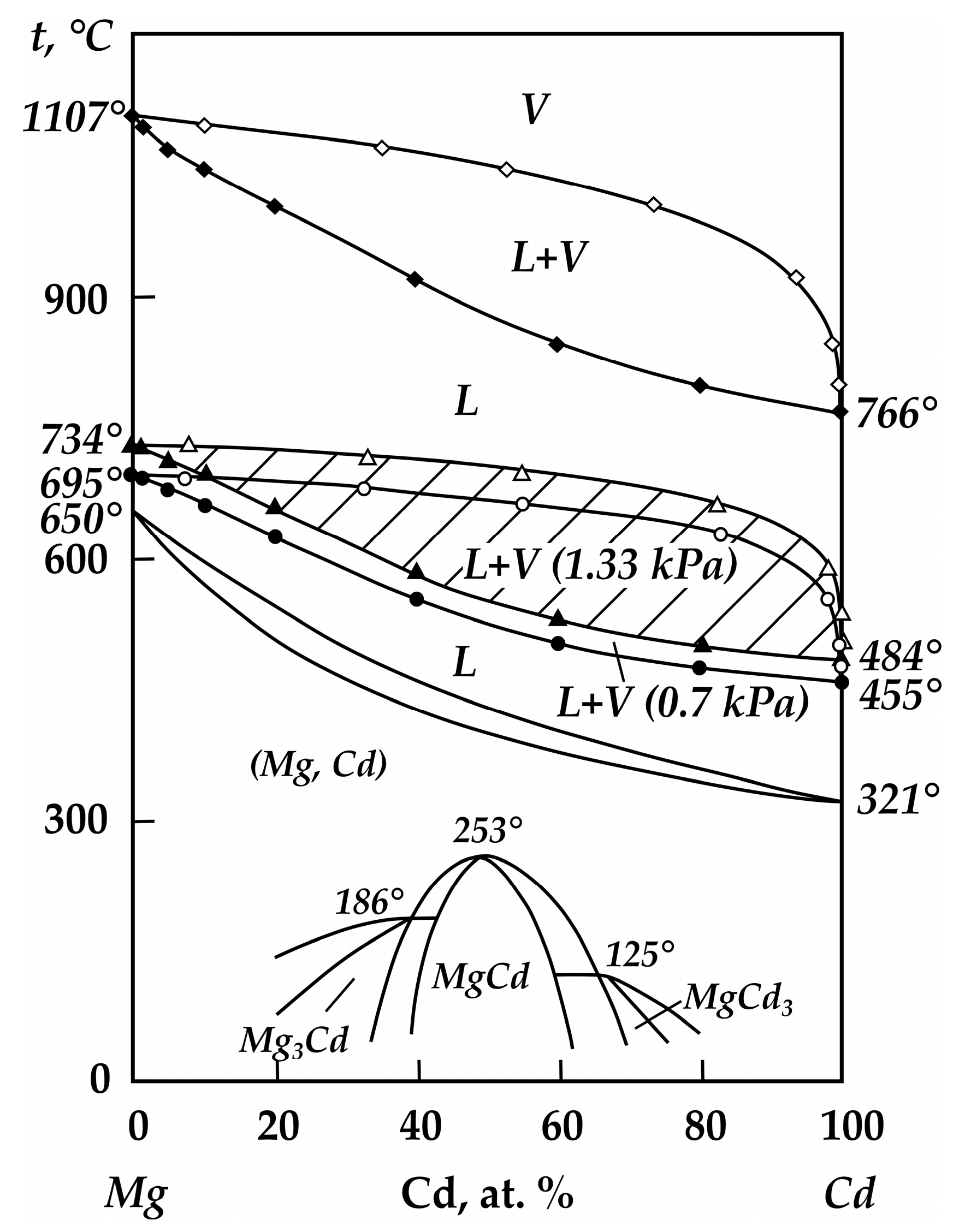
| Alloy No. | Mg | Zn | ||
|---|---|---|---|---|
| Atomic Fraction | mass. % | Atomic Fraction | mass. % | |
| 1 | 0.841 | 66.29 | 0.159 | 33.71 |
| 2 | 0.694 | 45.74 | 0.306 | 54.26 |
| 3 | 0.553 | 31.50 | 0.447 | 68.50 |
| 4 | 0.388 | 19.07 | 0.612 | 80.93 |
| 5 | 0.205 | 8.75 | 0.795 | 91.25 |
| Alloy No. | Mg | Cd | ||
|---|---|---|---|---|
| Atomic Fraction | mass. % | Atomic Fraction | mass. % | |
| 1 | 0.853 | 55.59 | 0.147 | 44.41 |
| 2 | 0.733 | 37.25 | 0.267 | 62.75 |
| 3 | 0.558 | 21.48 | 0.442 | 78.52 |
| 4 | 0.386 | 11.96 | 0.614 | 88.04 |
| 5 | 0.243 | 6.48 | 0.757 | 93.52 |
| Alloy Composition, Atomic Fraction | Т, К | , kPa | Estimated , kPa | , fraction | , kPa | , kPa | Relative Δ, % | |
|---|---|---|---|---|---|---|---|---|
| Zn | Mg | |||||||
| 1.0 | 0 | 873 | 1.47 | 1.46 | 1.0 | 1.46 | — | +0.55 |
| 1.33 | −7.95 | |||||||
| 1.60 | +9.44 | |||||||
| 1073 | 30.80 | 30.66 | 1.0 | 30.66 | — | +0.46 | ||
| 29.33 | −4.34 | |||||||
| 32.00 | +4.37 | |||||||
| 0.795 | 0.205 | 973 | 5.33 | 5.38 | 0.985 | 5.36 | 0.05 | −0.98 |
| 5.73 | +6.45 | |||||||
| 4.80 | −10.83 | |||||||
| 1173 | 68.79 | 67.46 | 0.985 | 67.16 | 0.99 | +1.98 | ||
| 67.33 | −0.19 | |||||||
| 66.26 | −1.77 | |||||||
| 0.612 | 0.388 | 973 | 3.33 | 3.43 | 0.951 | 3.19 | 0.16 | −2.92 |
| 3.33 | −2.92 | |||||||
| 3.73 | +8.75 | |||||||
| 1173 | 49.93 | 45.27 | 0.951 | 42.14 | 3.06 | −0.75 | ||
| 46.00 | +1.62 | |||||||
| 45.06 | −0.46 | |||||||
| 0.447 | 0.553 | 973 | 1.87 | 2.04 | 0.884 | 1.68 | 0.34 | −8.47 |
| 2.27 | +11.11 | |||||||
| 2.00 | −2.10 | |||||||
| 1173 | 29.06 | 29.04 | 0.884 | 23.93 | 5.81 | +0.06 | ||
| 28.80 | −0.83 | |||||||
| 29.33 | +0.99 | |||||||
| 0.306 | 0.694 | 973 | 1.47 | 1.37 | 0.753 | 0.87 | 0.46 | +7.69 |
| 1.33 | −2.56 | |||||||
| 1.33 | −2.56 | |||||||
| 1173 | 20.53 | 20.47 | 0.753 | 13.05 | 7.71 | +0.31 | ||
| 20.00 | −2.28 | |||||||
| 21.33 | +4.22 | |||||||
| 0.159 | 0.841 | 973 | 1.07 | 1.08 | 0.345 | 0.38 | 0.65 | −0.56 |
| 1.07 | −0.56 | |||||||
| 1.20 | +11.52 | |||||||
| 1173 | 16.00 | 15.98 | 0.345 | 5.61 | 10.77 | +0.13 | ||
| 15.20 | −4.88 | |||||||
| 16.93 | +5.94 | |||||||
| 0 | 1.0 | 1023 | 1.73 | 1.72 | 0 | — | 1.72 | +0.52 |
| 2.00 | +16.12 | |||||||
| 1.47 | −14.58 | |||||||
| 1273 | 38.00 | 38.01 | 0 | — | 38.01 | −0.03 | ||
| 37.20 | −2.13 | |||||||
| 38.80 | +2.08 | |||||||
| |Δ|av. = 4.02 | ||||||||
| Alloy Composition, Atomic Fraction | Т, К | , kPa | Estimated , kPa | , fraction | , kPa | , kPa | Relative Δ, % | |
|---|---|---|---|---|---|---|---|---|
| Zn | Mg | |||||||
| 0.757 | 0.243 | 773 | 1.20 | 1.18 | 0.985 | 1.16 | 3.51 × 10−4 | +1.87 |
| 1.33 | +12.90 | |||||||
| 1.07 | −9.17 | |||||||
| 923 | 15.20 | 15.49 | 0.985 | 15.25 | 1.69 × 10−2 | −1.85 | ||
| 14.93 | −3.59 | |||||||
| 15.60 | +0.74 | |||||||
| 0.614 | 0.386 | 823 | 2.00 | 2.95 | 0.983 | 2.90 | 3.51 × 10−3 | −2.63 |
| 1.73 | −15.77 | |||||||
| 2.13 | +3.70 | |||||||
| 973 | 20.53 | 21.01 | 0.983 | 20.65 | 9.76 × 10−2 | −2.28 | ||
| 21.46 | +2.15 | |||||||
| 19.73 | −6.08 | |||||||
| 0.442 | 0.558 | 873 | 2.13 | 2.17 | 0.977 | 2.12 | 2.86 × 10−2 | −1.62 |
| 2.67 | +24.46 | |||||||
| 1.73 | −20.09 | |||||||
| 1023 | 19.20 | 19.15 | 0.977 | 18.72 | 0.51 | +0.27 | ||
| 19.73 | +3.03 | |||||||
| 18.66 | −2.55 | |||||||
| 0.267 | 0.733 | 923 | 1.60 | 1.67 | 0.865 | 1.44 | 0.16 | −4.19 |
| 1.73 | +3.59 | |||||||
| 1.60 | −4.19 | |||||||
| 1073 | 13.87 | 14.08 | 0.865 | 12.18 | 1.97 | −1.49 | ||
| 13.47 | −4.33 | |||||||
| 14.13 | +0.36 | |||||||
| 0.147 | 0.853 | 973 | 1.60 | 1.54 | 0.626 | 0.97 | 0.56 | +3.76 |
| 1.73 | +12.12 | |||||||
| 1.33 | −13.80 | |||||||
| 1123 | 12.67 | 12.54 | 0.626 | 7.85 | 5.21 | +1.04 | ||
| 11.73 | −6.46 | |||||||
| 13.47 | +7.42 | |||||||
| 0 | 1.0 | 1023 | 1.73 | 1.72 | — | — | 1.72 | +0.52 |
| 2.00 | +16.12 | |||||||
| 1.47 | −14.58 | |||||||
| 1273 | 38.00 | 38.01 | — | — | 38.01 | −0.03 | ||
| 37.20 | −2.13 | |||||||
| 38.80 | +2.08 | |||||||
| |Δ|av. = 5.92 | ||||||||
| Distillation Process: | Zinc and Magnesium Content in Condensate: | |||
|---|---|---|---|---|
| Zn, at. % | Mg, at. % | Zn, mass. % | Mg, mass. % | |
| 1. Initial alloy | 2.46 | 97.54 | 6.00 | 94.00 |
| 2. Operation 1 condensate | 7.89 | 92.11 | 18.73 | 81.27 |
| 3. Operation 2 condensate | 21.35 | 78.65 | 42.20 | 57.80 |
| 4. Operation 3 condensate | 47.39 | 52.61 | 70.79 | 29.21 |
| 5. Operation 4 condensate | 87.13 | 12.87 | 94.79 | 5.21 |
| 6. Operation 5 condensate | 99.80 | 0.20 | 99.93 | 0.07 |
| Distillation Process: | Cadmium and Magnesium Content in Condensate: | |||
|---|---|---|---|---|
| Cd, at. % | Mg, at. % | Cd, mass. % | Mg, mass. % | |
| 1. Initial alloy | 0.44 | 99.56 | 2.00 | 98.00 |
| 2. Operation 1 condensate | 3.39 | 96.61 | 13.96 | 86.04 |
| 3. Operation 2 condensate | 23.24 | 76.76 | 58.34 | 41.66 |
| 4. Operation 3 condensate | 88.15 | 11.85 | 97.18 | 2.82 |
| 5. Operation 4 condensate | 99.99 | 0.01 | 99.998 | 0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volodin, V.; Kenzhaliyev, B.; Trebukhov, S.; Nitsenko, A.; Linnik, X.; Trebukhov, A. On the Problem of the Distillation Separation of Secondary Alloys of Magnesium with Zinc and Magnesium with Cadmium. Metals 2024, 14, 671. https://doi.org/10.3390/met14060671
Volodin V, Kenzhaliyev B, Trebukhov S, Nitsenko A, Linnik X, Trebukhov A. On the Problem of the Distillation Separation of Secondary Alloys of Magnesium with Zinc and Magnesium with Cadmium. Metals. 2024; 14(6):671. https://doi.org/10.3390/met14060671
Chicago/Turabian StyleVolodin, Valeriy, Bagdaulet Kenzhaliyev, Sergey Trebukhov, Alina Nitsenko, Xeniya Linnik, and Alexey Trebukhov. 2024. "On the Problem of the Distillation Separation of Secondary Alloys of Magnesium with Zinc and Magnesium with Cadmium" Metals 14, no. 6: 671. https://doi.org/10.3390/met14060671
APA StyleVolodin, V., Kenzhaliyev, B., Trebukhov, S., Nitsenko, A., Linnik, X., & Trebukhov, A. (2024). On the Problem of the Distillation Separation of Secondary Alloys of Magnesium with Zinc and Magnesium with Cadmium. Metals, 14(6), 671. https://doi.org/10.3390/met14060671






