Abstract
The mechanical properties of a fine-grained (FG) Ti-6Al-4V extra-low interstitial (ELI) alloy were investigated by tensile tests at 298 K and 77 K. The experimental results indicated that, at 77 K, the alloy exhibits a small uniform elongation of 2.65%, but has a fracture elongation of 19.2%, showing superior post-necking elongation. At 298 K, the alloy displays a single dislocation slipping, β→α″ phase transformation occurred, and 6.35% uniform elongation was obtained, whereas the coupling of dislocation slipping and twinning deformation behaviors dominated at 77 K. The limited uniform elongation is attributed to the absence of martensite phase transformation at 77 K, whereas the decent fracture elongation is ascribed to the resistance offered by twinning against plastic instability.
1. Introduction
At 77 K, Ti-6Al-4V ELI, a two-phase titanium alloy containing a certain amount of body-centered cubic (BCC) β phases showcases remarkable specific strength and toughness; therefore, it is widely employed in aerospace cryogenic temperature engineering [1,2,3,4]. FG Ti-6Al-4V ELI typically demonstrates a significantly elevated strength compared to materials with conventional grain sizes larger than several tens of micrometers [5]. Nevertheless, the occurrence of the yield-drop phenomenon and restricted uniform elongation are observable in the tensile stress–strain curves of FG materials, presenting a stark contrast to those observed in coarse-grained (CG) materials [6,7,8,9]. Due to the refined grain size and hindered dislocation mobility, the high strength of FG Ti-6Al-4V ELI at 77 K is typically accompanied by a reduced ductility, with the uniform elongation in FG materials (<3%) notably inferior to that seen in CG materials [10]. In the case of CG titanium alloys, deformation twins can enhance the tensile elongation through twinning-induced plasticity, fostering homogeneous deformation at 77 K [11,12,13]. According to the published investigations, FG metals exhibit the potential to maintain their ductility without compromising their strength to a considerable extent [14,15,16,17]. The discovery of the superplastic phenomenon for titanium at elevated or even cryogenic deformation temperatures underscores the conditional nature of these novel properties, which is contingent upon factors such as temperature [15,16,18]. Therefore, temperature stands as a pivotal factor influencing the properties of FG materials, as the plastic deformation of most metals can be regarded as a thermally activated process [19,20,21]. Consequently, the temperature sensitivity (TS) of flow stress can be defined as . Severe deformations such as rolling or drawing typically result in the formation of equiaxed sub-grains with low-angle misorientations [22,23]. Experiments conducted by Lu et al. on electrodeposited nanocrystalline copper samples showcased substantial elongations of up to 30%, with one important characteristic being the abundance of low-angle grain boundaries (LAGBs) [24]. The mechanical response of these samples is expected to be influenced by the nature of their grain boundaries [25,26]. While the majority of the published research has focused on the fracture elongation of materials, paying limited attention to the post-necking elongation, the establishment of a well-defined mechanism for achieving a significant amount of plastic strain post-necking remains inconclusive. It is crucial to acknowledge that titanium alloys exhibit reduced uniform elongation at a temperature of 77 K; however, they demonstrate the capability for substantial plastic deformation post-necking. Ductility is typically defined as the total elongation of a specimen in a tensile test, encompassing both uniform elongation and post-necking elongation. It is well recognized that the microstructure of fine-crystalline titanium materials usually shows excellent tensile strength and tensile ductility at cryogenic temperatures, along with a highly promising forming ability, while the post-necking elongation significantly influences the formability of the material. Therefore, understanding which deformation mechanisms (slip, twinning, or phase transformation) exist during cryogenic temperature tensile deformation that can impact the post-necking elongation is imperative.
2. Materials and Experimental Methods
The as-received FG Ti-6Al-4V ELI comprised a cold-rolled plate with a thickness of 2 mm and an average grain size of 5.8 μm. The chemical composition of the plate was determined and is presented in Table 1. Subsequently, the prepared samples underwent a microscopic morphology and physical phase analysis using scanning electron microscopy. The initial microstructures in the transverse direction–rolling direction (TD-RD) plane were characterized using electron backscattered diffraction (EBSD) technology. The EBSD samples were prepared through a standard metallographic procedure, followed by final electrochemical polishing utilizing a solution of 5% perchloric acid, 35% butanol, and 60% methanol at −25 °C and 50 V for 50 s. For the deformed samples, characterization was carried out using a scanning transmission microscopy (STEM) probe on a TESCAN MIRA 4 field emission scanning electron microscope manufactured in the Brno, Czech Republic. However, since the orientation information of the samples could not be determined by the STEM technique, the samples’ orientation information was further analyzed with higher accuracy using the transmission kikuchi diffraction (TKD) technique. Rectangular tensile specimens, measuring 10 mm in length and 4 mm in width, were machined in the direction of rolling. Tensile strains were measured at both 298 K and 77 K by attaching mechanical extensometers to both ends of the scalar section of the specimen. A freezer filled with liquid nitrogen was utilized to maintain the 77 K environment, with the specimen being immersed in liquid nitrogen throughout the test. Once the temperature stabilized, which typically took 30 min, the tensile test was performed. The strain rate was 10−3 s−1. The strain rate was automatically controlled by the tensile tester and computer. To ensure the reliability of the test results, three specimens from each case were tested, and the yield strength, ultimate tensile strength, and elongation were obtained by averaging the results of the three specimens. The tensile tests were carried out on a MTS C45.105 testing machine manufactured by MTS Corporation, Eden Prairie, MN, USA, with evaluations performed at both 298 K and 77 K to examine the impact of deformation temperature on the tensile properties.

Table 1.
Chemical composition of the as-received FG Ti-6Al-4V titanium alloy.
Figure 1 displays the typical X-ray diffraction (XRD) patterns of the as-received FG Ti-6Al-4V ELI titanium alloy. It is evident that the characteristic diffraction peaks of the α phase with a hexagonal close-packed (HCP) crystalline structure are detected, owing to the presence of very few β stabilizing elements.
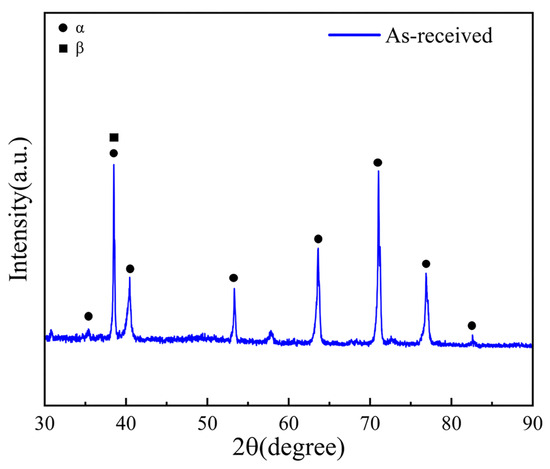
Figure 1.
XRD patterns of the as-received FG Ti-6Al-4V ELI titanium alloy.
3. Results and Discussions
3.1. The Initial Microstructures and Mechanical Property
In Figure 2, captured through scanning electron microscopy (SEM), the initial as-received FG Ti-6Al-4V ELI alloy is depicted. From Figure 2a,b, it is discernible that the alloy showcases a homogeneous FG equiaxed microstructure predominantly comprising α-Ti, interspersed with some retained β-Ti grains. Figure 2a presents the SEM image, while Figure 2b displays the backscattered electron (BSE) image. In the images, the bright regions denote the β-phase, contrasting with the dark regions representing the α-phase. A quantitative analysis using Image Pro-plus (6.0) software revealed that the β-phase possesses a grain size of approximately 1.3 μm, constituting 2.4% of the total composition. Notably, the β-phase predominantly surrounds the α-phase in a stripe-like distribution.

Figure 2.
Microstructure characterization of the as-received FG Ti-6Al-4V ELI titanium alloy: (a) SEM map; (b) BSE map.
The initial microstructure, as depicted in Figure 3a, showcases approximately equiaxed α-grains, interspersed with β phases exhibiting a typical basal texture. In Figure 3b, the grain boundary map contains blue lines representing low-angle grain boundaries (2–15°) (LAGBs), while black lines denote high-angle grain boundaries (15–90°) (HAGBs). Notably, the average size of the sub-grains is approximately 500 nm, as highlighted in Figure 3c. Figure 3d presents the correlated boundary misorientation angle distribution, revealing that LAGBs constitute 45% of the total boundary content. The EBSD-derived grain boundary distribution shows that the volume fractions of LAGBs and HAGBs in the FG Ti-6Al-4V ELI titanium alloy are 45% and 55%, respectively. This observation suggests that the strain hardening induced during the rolling process was largely retained, leading to a high density of LAGBs within the FG Ti-6Al-4V ELI titanium alloy. Furthermore, the EBSD inverse pole figure (IPF) map in Figure 3a indicates that the average grain size of the alloy is 5.8 μm. Intriguingly, LAGBs predominantly inhabit small-sized α-Ti grains (<1 μm), whereas HAGBs are prevalent in larger grains (>3 μm).
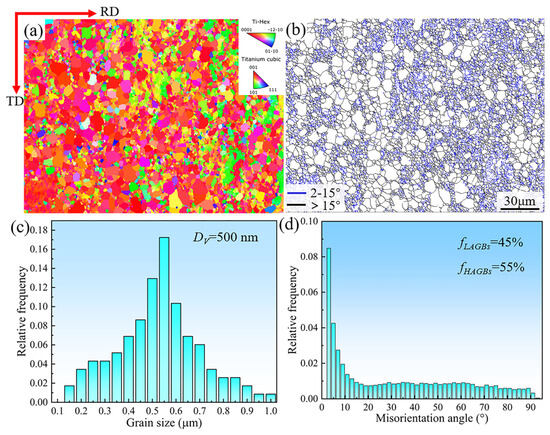
Figure 3.
Microstructures of the as-received material: (a) IPF map; (b) grain boundaries map; (c) average size of sub-grains; (d) misorientation angle.
Figure 4 presents the tensile properties of the FG Ti-6Al-4V ELI titanium alloy at both 298 K and 77 K. In Figure 4a, it is evident that the yield strength of the alloy increases from 971 MPa at 298 K to 1495 MPa at 77 K. Remarkably, the elongation remains relatively consistent, with values of 19.7% and 19.2% recorded at 298 K and 77 K, respectively. Despite there being no discernible penalty for ductility, a notable difference in uniform elongation is observed. Figure 4b illustrates the work-hardening curve of tensile deformation at both temperatures. At 77 K, the alloy exhibits a uniform elongation of 6.35% (red point), contrasting with 2.65% (black point) at 298 K. The work-hardening curves at both temperatures are characterized by three stages: the descending stage (Ⅰ), ascending stage (Ⅱ), and rapid descent stage (Ⅲ). At 77 K, stage Ⅱ commences at a true strain of 3.59%, followed by stage Ⅲ at a true strain of 9.21%. Conversely, at 298 K, stage Ⅱ begins at a true strain of 1.45%, with stage Ⅲ initiating at a true strain of 2.82%. Notably, at 77 K, the processing hardening curve displays an elongated ascending stage, with necking commencing at a true strain of 2.65%, indicative of excellent post-necking elongation. At 298 K, necking commences at a true strain of 6.35%. Interestingly, the work-hardening rate at 77 K surpasses that at 298 K until the true strain reaches 1.45%. However, within the true strain range of 1.45% to 2.82%, the work-hardening rate at 298 K begins to rise, eventually exceeding that at 77 K. This shift may imply a transition in the mechanism of tensile deformation (likely involving slip and phase transformation) at 298 K during this stage. Moreover, the gradual escalation in the work-hardening rate at 77 K within the true strain range of 3.59% to 9.21% suggests a change in the tensile deformation mechanism (involving slip and twinning) at this stage as the temperature drops to 77 K, surpassing the work-hardening rate at 298 K at a true strain of approximately 6%.
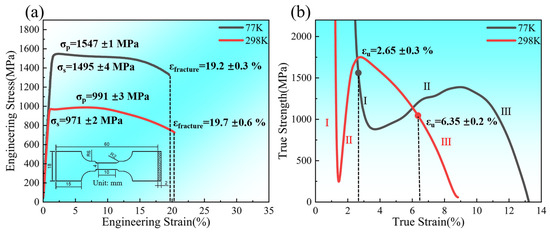
Figure 4.
Tensile properties at 298 K and 77 K: (a) tensile engineering stress–strain curves; (b) strain-hardening rate curves with three stages.
3.2. Tensile Deformation Microstructures and Fracture
Figure 5 illustrates the EBSD outcomes for various tensile strains of the alloy at test temperatures of 298 K and 77 K. Figure 5a–f corresponds to a temperature of 298 K, while Figure 5g–l corresponds to 77 K. Figure 5a–c,g–i depicts the IPF maps of different strains at distinct deformation temperatures, while Figure 5d–f,j–l showcases the kernel average misorientation (KAM) maps of varying strains at different deformation temperatures. The data in Figure 5 reveal that the deformed samples exhibit a higher average KAM value at 77 K compared to 298 K under the same strain. Moreover, the average KAM value escalates with the strain at the same deformation temperature. Notably, the KAM maps indicate that areas with larger orientation disparity angles and higher densities of geometrically necessary dislocations (GNDs) are concentrated near the LAGBs, suggesting a concentration of strain in these regions. Additionally, Figure 5 underscores that HAGBs with high levels of deformation energy are primarily distributed at the recrystallized matrix grain boundaries, facilitating grain rotation to an optimal orientation through boundary rotation and sliding during the deformation process [27,28,29]. During the cryogenic temperature deformation of the FG Ti-6Al-4V ELI titanium alloy, the accumulation of geometrically necessary dislocations (GNDs) occurs concurrently at both matrix grain boundaries and low-angle grain boundaries (LAGBs). This orchestrated ductility process is facilitated by the presence of GNDs. The buildup of the ductility strain in the deformed specimens notably escalates with increasing strain. Figure 5l vividly portrays the distinct plastic strain distribution between soft- and hard-orientation grains following tensile deformation at 298 K. Conversely, Figure 5f illustrates that the accumulated plastic strain distribution at 77 K is more uniform compared to that at 298 K. Moreover, upon comparing Figure 5b,c,h, and Figure 5i, it becomes evident that certain α-Ti grains undergo noticeable elongation along the stretching direction at 298 K. In contrast, at 77 K, the majority of α-Ti grains remain equiaxed, with no discernible distortion or elongation observed, indicating the suppression of dislocation motion within the α-Ti grains during the tensile deformation process at 77 K [27].
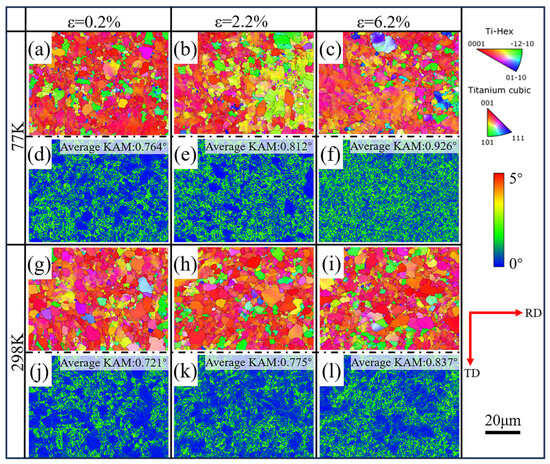
Figure 5.
EBSD results of tensile deformation microstructures at 77 Kand 298 K: (a–f) the test temperature is 77 K; (g–l) the test temperature is 298 K; (a–c) IPF maps of 77 K; (g–i) IPF maps of 298 K; (d–f) KAM maps of 77 K; (j–l) KAM maps of 298 K.
Figure 6 depicts the fracture morphology of the tensile specimens at deformation temperatures of 77 K and 298 K. At 298 K (Figure 6a), clear necking of the tensile specimen fracture is evident, characterized by a typical large shear lip displaying distinct and deep toughness dimples (Figure 6b,c). Conversely, necking is not apparent at 77 K deformation (Figure 6d). Instead, a high density of toughness nests is observed on the fracture surface, with these nests progressively becoming smaller and shallower (Figure 6e,f), accompanied by reduced fibrous zones. Within the fibrous zones, crack cores are formed. The surface of the shear lip appears smoother, with an angle of approximately 45° with respect to the tensile stress axis, indicative of the enhanced ductility of the specimens at 77 K. This smoother surface and the characteristic angle further underscore the heightened ductility observed at 77 K [13].

Figure 6.
Fracture morphologies of tensile specimens tested at (a–c) 298 K; (d–f) 77 K.
3.3. Deformation Mechanism of the FG Ti-6Al-4V ELI at 77 K and 298 K
The occurrence of elevated work-hardening curves at 298 K has been attributed to the martensitic phase transformation, as suggested by several reports [30,31,32]. An examination of the XRD patterns of the specimens reveals duplex α + β microstructures. Figure 7a displays the XRD map of the initial, 77 K-deformed, and 298 K-deformed samples. Further magnification in Figure 7b reveals distinct features: the α (102) diffraction peak of the 298 K-deformed sample exhibits cleavage, accompanied by the appearance of α″ (112) and α″ (022) diffraction peaks. Conversely, no cleavage phenomenon is observed in the 77 K-deformed sample. The deformation process at 298 K induces a β→α″ phase transformation. The presence of α″ martensite notably enhances the work-hardening rate and uniform elongation. This heightened work-hardening during tensile loading mitigates the premature onset of plastic instability, aligning with the Considère criterion:
where σ and ε are true stress and true strain, respectively. Considering the aforementioned factors and following the approach outlined by Liu [33], the relationship for the free energy change that occurs during stress induced martensitic (SIM) transformation can be modified to give the following:
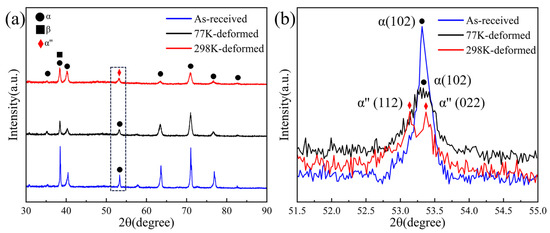
Figure 7.
XRD map of as-received and deformed samples: (a) as-received and 77 K-deformed and 298 K-deformed samples; (b) local magnification map of black rectangle in (a).
The above expression shows that the deformation temperature is one important factor influencing the free energy change. When the temperature drops from room temperature to cryogenic temperature, the free energy of the phase transformation becomes too hard to produce a phase transformation. Thus, the uniform elongation of the 298 K specimen (6.53%) was nearly triple that of its 77 K counterpart.
The observation of an upward phase in the work-hardening curve of the FG Ti-6Al-4V ELI titanium alloy at a deformation temperature of 77 K implies the involvement of deformation mechanisms beyond the dislocation slip. Given the 0.2 μm scan step of the EBSD, it is plausible that nanoscale deformation twins were generated during the ductile deformation process at 77 K. To investigate this further, STEM images of the samples were acquired at the 77 K deformation temperature.
Figure 8 illustrates the various stages of deformation at both 298 K and 77 K. At the onset of plastic deformation at 298 K, characterized by relatively low stress levels, plasticity is dominated by dislocations, and the work-hardening curves display a gradual decrease. At this stage, the mobile dislocations provided by the low-angle grain boundaries are smaller than the dislocation annihilation rate, leading to a decrease in flow stress post-yielding. The corresponding microstructure (Figure 8a) reveals the presence of a few dislocations within the grains. As the flow stress increases, strain-induced martensite (SIM) transformation becomes predominant, leading to the phenomenon of β→α″. The formation of α″ martensite introduces numerous new phase interfaces within the original β phase, which further impedes dislocation movement and shortens the mean free path of dislocations. This effectively enhances the work-hardening rate during this stage, explaining the monotonic increase in the work-hardening rate curve in the second stage (Figure 8b). In the final stage of plastic deformation, extensive dislocation pile-up occurs within the grains, resulting in significant stress concentration. This ultimately leads to the initiation of cracks and subsequent fracture damage (Figure 8c).

Figure 8.
Different stages of deformation at 298 K and 77 K: (a) descending stage of 77 K; (b) ascending stage of 77 K; (c) necking stage of 77 K; (d) descending stage of 298 K; (e) ascending stage of 298 K; (f) necking stage of 298 K.
At the onset of plastic deformation at 77 K (Figure 8d), stage Ⅰ reveals the occurrence of the yield-drop phenomenon. Within this stage, higher dislocation densities become entangled within sub-grain boundaries. The notable entanglement of dislocations and the retention of a high-density dislocation population within the grain interior are attributed to the hindered slipping, annihilation, and dynamic response processes of dislocations at cryogenic temperatures. Moreover, it is worth noting the higher efficiency of LAGBs compared to HAGBs as sites for dislocation nucleation. Consequently, the higher fraction of LAGBs can furnish more mobile dislocations to sustain the applied strain rate during tensile deformation at 77 K. This, in turn, leads to a gradual decrease in flow stress after the yield peak (Figure 4a). In stage Ⅱ, twinning-induced plasticity becomes predominant. At this juncture, the nucleation and expansion of the twins evolve into a complex twin network (Figure 8e). The formation of twinning boundaries drastically reduces the grain size to the nanometer scale, thereby enhancing the dynamic Hall–Petch effect. The augmented dislocation density and refinement in spacing within the twin network result in elevated activation stresses for subsequent twin generation, consequently escalating flow stresses [34]. Macroscopically, this is evidenced by an extension of the plateau and an elevation in the work-hardening rate. Despite the constrained uniform elongation in 77 K-deformed samples, a noteworthy amount of plastic strain is attained post-necking. In the final stage of plastic deformation, the work-hardening rate undergoes a rapid decline, and grain refinement becomes pronounced. STEM micrographs in the vicinity of the necking zone reveal a high density of equiaxed sub-grains (Figure 8f). Despite the generation of high flow stresses, the presence of ultrafine grains impedes dislocation activity and twinning, resulting in a swift reduction in work-hardening capacity [35].
In Figure 8, deformation twin crystals are observed in the FG Ti-6Al-4V ELI titanium alloy at a deformation temperature of 77 K. However, since the STEM images cannot determine the orientation information, the deformed specimen is analyzed using the TKD characterization method, as depicted in Figure 9. The results reveal that the c-axis orientation perpendicular to the tensile direction facilitates the formation of deformation twin crystals at a 77 K deformation temperature. Furthermore, the twin type was calibrated, and it was determined that grain A in Figure 9a exhibits a tensile twin, which is a common twin type in titanium alloys. Figure 9c illustrates the orientation difference information along the black line in Figure 9a, indicating an angle of orientation difference of 85° between the twin and the matrix. Additionally, Figure 9d provides the crystal structure information of the grain A twin and the matrix. Twinning is favored in alloys with low stacking fault energy, and a decrease in temperature reduces the stacking fault energy, promoting the generation of stacking faults and thus lowering the critical resolved shear stress (CRSS) value of the twinned crystals. It is also observed that twins generally do not propagate through grain boundaries; however, occasionally, they traverse grain boundaries if neighboring grains possess similar orientations. The occurrence of type twins facilitates the coordination of slip deformation in parent grains.
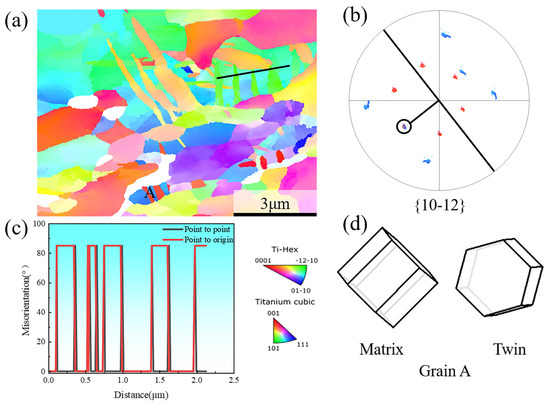
Figure 9.
TKD results of tensile deformation microstructures at 77K: (a) IPF map; (b) pole figure of grain A area; (c) misorientation angle profile plotted along route marked in (a); (d) schematic of grain A twinning to the matrix.
The activation of slips and twins is intricately linked to the critical resolved shear stress (CRSS), which is influenced by the Schmid Factor (SF) of individual grains, determined by their crystal orientations. The SF averages for the TKD map for each slip system, as well as for the twins, are summarized and plotted in Table 2. Analyzing the data in the table, it can be observed that the pyramidal slip has a high SF value (>0.46), indicating its potential for slip activation. However, the CRSS value associated with pyramidal slip is considerably larger than that of the basal slip and the Prismatic slip, rendering the activation of pyramidal slip challenging at a 77 K temperature. Previous research has indicated that the Prismatic slip has the lowest CRSS [11,13]. Although the SF of the prismatic slip, at 77 K deformation temperature, is slightly lower than the average value of pyramidal slip, prismatic slip is still significantly activated. Comparatively, the CRSS of the basal slip is slightly larger than or similar to that of the prismatic slip at 77 K. Consequently, the basal slip is more readily activated than the pyramidal slip at 77 K temperature. The higher average SF value of the twinned crystals in the table indicates that the twins facilitate the coordination of the parent crystals for the slip, which would otherwise be difficult to deform. Moreover, the twins provide an additional <0001> orientation for grain A, aiding in the deformation process.

Table 2.
Average SF values for each slip system and {102}<10> twins at 77 K temperature.
The FG Ti-6Al-4V ELI titanium alloy comprises an equiaxed α phase and a small fraction of β phase, enveloped by the α phase. Figure 10a illustrates that in the α phase, the {0001} orientation is prevalent, while the and orientations are scarcely observed. At a deformation temperature of 77 K, the deformation mechanism shifts from unit-dislocation slip to a coupled deformation involving both a dislocation slip and twinning. This transition occurs due to the more rapid increase in the critical fractional stress of the dislocation slip compared to twinning. Within the α phase, deformation twins are generated to coordinate plastic deformation. These twins transform the hard orientations into soft ones, facilitating subsequent plastic deformation. Conversely, no phase transformation occurs in the β phase at 77 K due to the substantially higher activation energy required for the martensitic phase transformation at low cryogenic temperatures compared to room temperature (Figure 10b). The formation of twins effectively delays plastic instability, enabling significant plastic deformation post-necking at 77 K, thereby resisting premature plastic instability. At a deformation temperature of 298 K, the predominant deformation mechanism is dislocation slip. In the β phase, stress-induced martensitic phase transformation occurs with increasing stress levels, promoting the homogeneity of ductile flow (Figure 10c,d).
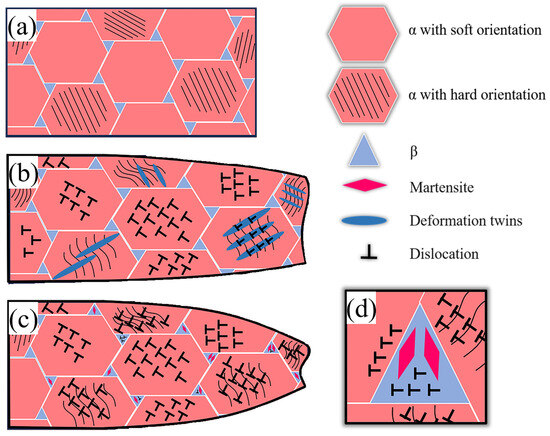
Figure 10.
Schematic diagram of the fracture’s cross-section and corresponding deformation mechanism before and after tensile at 298 K and 77 K: (a) before tensile; (b)77 K; (c) 298 K; (d) the enlarged view in (c).
4. Conclusions
The FG Ti-6Al-4V demonstrates the behavior of a single dislocation slipping deformation at 298 K, whereas, at 77 K, the prevailing mechanism involves the coupling of dislocation slipping and twinning deformation behaviors.
Significant dislocation entanglement and the retention of a high-density dislocation population at LAGBs and within the twin interior were observed due to the inhibition of the slipping, annihilation, and dynamic response processes of dislocations at cryogenic temperatures. The newly formed dislocations tend to entangle and accumulate at LAGBs and inside the twin crystals during 77 K deformation. LAGBs are the more efficient sites for dislocation nucleation compared with HAGBs. LAGBs can provide more mobile dislocations to maintain the applied strain rate during 77 K tensile deformation.
There is a clear sequence of the activation of the deformation mechanism at 77 K during the different stages of plastic deformation. This evolution establishes a stable and continuous source of hardening, which both increases strength and effectively delays necking, thereby improving ductility at 77 K and leading to superior post-necking elongation.
Author Contributions
Conceptualization, X.L., R.L. and H.W. (Hao Wu); methodology, K.M., X.L. and R.L.; resources, K.M. and H.W. (He Wu); data curation, H.W. (He Wu), Q.G. and C.L.; writing—original draft preparation, Q.G., X.L. and H.W. (Hao Wu); supervision, K.M., X.L. and H.W. (He Wu); project administration, C.L., X.L. and R.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Key R&D Program of China (No. 2022YFB3705500), and the National Natural Science Foundation of China (No. 52271104).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lu, Z.; Zhang, X.; Ji, W.; Wei, S.; Yao, C.; Han, D. Investigation on the deformation mechanism of Ti-5Al-2.5Sn ELI titanium alloy at cryogenic and room temperatures. Mater. Sci. Eng. A 2021, 818, 141380. [Google Scholar] [CrossRef]
- Wei, K.; Wang, Z.; Li, F.; Zhang, H.; Zeng, X. Densification behavior, microstructure evolution, and mechanical performances of selective laser melted Ti-5Al-2.5Sn α titanium alloy: Effect of laser energy input. J. Alloys Compd. 2019, 774, 1024–1035. [Google Scholar] [CrossRef]
- Di Iorio, S.; Briottet, L.; Rauch, E.F.; Guichard, D. Plastic deformation, damage and rupture of PM Ti-6Al-4V at 20K under monotonic loading. Acta Mater. 2007, 55, 105–118. [Google Scholar] [CrossRef]
- Wu, H.; Huang, M.; Xia, Y.; Li, X.; Li, R.; Liu, C.; Gan, W.; Xiao, T.; Geng, L.; Liu, Q.; et al. The importance of interfacial stress-affected zone in evading the strength-ductility trade-off of heterogeneous multi-layered composites. Int. J. Plast. 2023, 160, 103485. [Google Scholar] [CrossRef]
- Tsuji, N.; Ito, Y.; Saito, Y.; Minamino, Y. Strength and ductility of ultrafine grained aluminum and iron produced by ARB and annealing. Scr. Mater. 2002, 47, 893–899. [Google Scholar] [CrossRef]
- Wang, Y.M.; Cheng, S.; Wei, Q.M.; Ma, E.; Nieh, T.G.; Hamza, A. Effects of annealing and impurities on tensile properties of electrodeposited nanocrystalline Ni. Scr. Mater. 2004, 51, 1023–1028. [Google Scholar] [CrossRef]
- Valiev, R. Nanostructuring of metals by severe plastic deformation for advanced properties. Nat. Mater. 2004, 3, 511–516. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.-H.; Bingert, J.F.; Liao, X.-Z.; Cui, B.-Z.; Han, K.; Sergueeva, A.V.; Mukherjee, A.K.; Valiev, R.Z.; Langdon, T.G.; Zhu, Y.T. Simultaneously Increasing the Ductility and Strength of Ultra-Fine-Grained Pure Copper. Adv. Mater. 2006, 18, 2949–2953. [Google Scholar] [CrossRef]
- Tabachnikova, E.D.; Podolskiy, A.V.; Bengus, V.Z.; Smirnov, S.N.; Bidylo, M.I.; Csach, K.; Miskuf, J.; Saitova, L.R.; Semenova, I.P.; Valiev, R.Z. Mechanical characteristics, failure regularities, and dimple structures on failure surfaces of Ti-6Al-4V ‘ELI’ ultrafine-grained alloy at temperatures from 300 to 4.2K. Mater. Sci. Eng. A 2009, 503, 106–109. [Google Scholar] [CrossRef]
- Zhang, Y.; Figueiredo, R.B.; Alhajeri, S.N.; Wang, J.T.; Gao, N.; Langdon, T.G. Structure and mechanical properties of commercial purity titanium processed by ECAP at room temperature. Mater. Sci. Eng. A 2011, 528, 7708–7714. [Google Scholar] [CrossRef]
- Anne, B.R.; Okuyama, Y.; Morikawa, T.; Tanaka, M. Activated slip systems in bimodal Ti-6Al-4V plastically deformed at low and moderately high temperatures. Mater. Sci. Eng. A 2020, 798, 140211. [Google Scholar] [CrossRef]
- Anne, B.R.; Tanaka, M.; Morikawa, T. Temperature Dependence of Activation Enthalpy for Yielding in Bimodal Ti-6Al-4V. Mater. Trans. 2019, 60, 1828–1832. [Google Scholar] [CrossRef]
- Zhang, R.; Zhao, Q.; Guo, D.; Du, Y.; Zou, L.; Ying, Y.; Zhang, B.; Zhao, Y. Simultaneous improvement in strength and ductility of CT20 titanium alloy at cryogenic temperature. Mater. Des. 2023, 235, 112416. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, H.; Zhu, J.; Ding, M.; An, X.; Wu, D.; Hu, W.; Yang, T. High strength-ductility synergy of Inconel 625 alloy with a layered bimodal grain-structure. Mater. Charact. 2024, 207, 113510. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Islamgaliev, R.K.; Semenova, I.P. Superplasticity in nanostructured materials: New challenges. Mater. Sci. Eng. A 2007, 463, 2–7. [Google Scholar] [CrossRef]
- Prasad, M.J.N.V.; Chokshi, A.H. Superplasticity in electrodeposited nanocrystalline nickel. Acta Mater. 2010, 58, 5724–5736. [Google Scholar] [CrossRef]
- Li, G.; Jiang, J.; Ma, H.; Zheng, R.; Gao, S.; Zhao, S.; Ma, C.; Ameyama, K.; Ding, B.; Li, X. Superior strength-ductility synergy in three-dimensional heterogeneous-nanostructured metals. Acta Mater. 2023, 256, 119143. [Google Scholar] [CrossRef]
- Wang, Y.M.; Ma, E.; Valiev, R.Z.; Zhu, Y.T. Tough Nanostructured Metals at Cryogenic Temperatures. Adv. Mater. 2004, 16, 328–331. [Google Scholar] [CrossRef]
- Suo, T.; Li, Y.; Zhao, F.; Fan, X.; Guo, W. Compressive behavior and rate-controlling mechanisms of ultrafine grained copper over wide temperature and strain rate ranges. Mech. Mater. 2013, 61, 1–10. [Google Scholar] [CrossRef]
- Wei, Q.; Cheng, S.; Ramesh, K.T.; Ma, E. Effect of nanocrystalline and ultrafine grain sizes on the strain rate sensitivity and activation volume: fcc versus bcc metals. Mater. Sci. Eng. A 2004, 381, 71–79. [Google Scholar] [CrossRef]
- Meyers, M.A.; Mishra, A.; Benson, D.J. Mechanical properties of nanocrystalline materials. Prog. Mater Sci. 2006, 51, 427–556. [Google Scholar] [CrossRef]
- Gunderov, D.V.; Polyakov, A.V.; Semenova, I.P.; Raab, G.I.; Churakova, A.A.; Gimaltdinova, E.I.; Sabirov, I.; Segurado, J.; Sitdikov, V.D.; Alexandrov, I.V.; et al. Evolution of microstructure, macrotexture and mechanical properties of commercially pure Ti during ECAP-conform processing and drawing. Mater. Sci. Eng. A 2013, 562, 128–136. [Google Scholar] [CrossRef]
- Sajadifar, S.V.; Yapici, G.G. Elevated Temperature Mechanical Behavior of Severely Deformed Titanium. J. Mater. Eng. Perform. 2014, 23, 1834–1844. [Google Scholar] [CrossRef]
- Lu, L.; Wang, L.B.; Ding, B.Z.; Lu, K. High-tensile ductility in nanocrystalline copper. J. Mater. Res. 2000, 15, 270–273. [Google Scholar] [CrossRef]
- Majchrowicz, K.; Sotniczuk, A.; Adamczyk-Cieślak, B.; Chromiński, W.; Jóźwik, P.; Pakieła, Z.; Garbacz, H. The influence of microstructure and texture on the hardening by annealing effect in cold-rolled titanium. J. Alloys Compd. 2023, 948, 169791. [Google Scholar] [CrossRef]
- Tang, Z.C.; Xu, W.; Zhao, D.Y.; Zhang, B. Improving the strength and SCC resistance of an Al-5Mg-3Zn alloy with low-angle grain boundary structure. J. Mater. Sci. Technol. 2023, 161, 63–73. [Google Scholar] [CrossRef]
- Zang, M.C.; Niu, H.Z.; Yu, J.S.; Zhang, H.R.; Zhang, T.B.; Zhang, D.L. Cryogenic tensile properties and deformation behavior of a fine-grained near alpha titanium alloy with an equiaxed microstructure. Mater. Sci. Eng. A 2022, 840, 142952. [Google Scholar] [CrossRef]
- Liu, Z.; Li, P.; Geng, L.; Liu, T.; Gao, H. Microstructure and texture evolution of TA32 titanium alloy during superplastic deformation. Mater. Sci. Eng. A 2017, 699, 71–80. [Google Scholar] [CrossRef]
- Liu, Z.; Li, P.; Xiong, L.; Liu, T.; He, L. High-temperature tensile deformation behavior and microstructure evolution of Ti55 titanium alloy. Mater. Sci. Eng. A 2017, 680, 259–269. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, K.; Alexandrov, I.V.; Zhang, H.; Feng, L.; Ding, J.; Dong, Y.; Chang, H.; Zhou, L. Cyclic deformation response and strain-induced martensitic transformation of β single phase Ti-35421 alloy. Int. J. Fatigue 2023, 169, 107497. [Google Scholar] [CrossRef]
- Wang, H.; Fu, G.; Sheng, L.; Sun, W.; Yang, Q.; Zhang, S.; Gao, Z.; Chen, J.; Yi, X. Microstructure, martensitic transformation, mechanical properties and shape memory effect of (TiBw+TiCp)/Ti-V-Al shape memory alloy composites. Mater. Res. Bull. 2022, 152, 111868. [Google Scholar] [CrossRef]
- Kazantseva, N.; Krakhmalev, P.; Thuvander, M.; Yadroitsev, I.; Vinogradova, N.; Ezhov, I. Martensitic transformations in Ti-6Al-4V (ELI) alloy manufactured by 3D Printing. Mater. Charact. 2018, 146, 101–112. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, H. The concern of elasticity in stress-induced martensitic transformation in NiTi. Mater. Sci. Eng. A 1999, 260, 240–245. [Google Scholar] [CrossRef]
- Zhu, Y.T.; Liao, X.Z.; Wu, X.L. Deformation twinning in nanocrystalline materials. Prog. Mater. Sci. 2012, 57, 1–62. [Google Scholar] [CrossRef]
- Sun, J.L.; Trimby, P.W.; Yan, F.K.; Liao, X.Z.; Tao, N.R.; Wang, J.T. Grain size effect on deformation twinning propensity in ultrafine-grained hexagonal close-packed titanium. Scr. Mater. 2013, 69, 428–431. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).