Abstract
In this paper, the partially crystallized Zr70Cu13.5Ni8.5Al8 bulk metallic glasses (BMGs) were prepared, and their superplastic deformation ability in the supercooled liquid region was studied via compression over a wide range of strain rates from 5 × 10−4 s−1 to 1 × 10−2 s−1. It has been found that the superplastic deformation behavior of the BMGs is strongly dependent on the strain rate and temperature. The flow behavior of the BMGs transformed from Newtonian fluid to non-Newtonian fluid with the increase in the strain rate and the decrease in temperature. Based on the high-temperature compression results, a thermalplastic forming map was constructed, and the optimal superplastic forming parameters were obtained. Then, gears were successfully extruded using part of the optimal thermal processing parameters. Further studies showed that high-temperature extrusion induced the crystallization of the BMGs, which increased the microhardness of the gears.
1. Introduction
Compared with the traditional alloys, bulk metallic glasses (BMGs) have been paid attention by researchers worldwide due to their prominent mechanical properties, for instance, superior strength (compression strength up to 6 GPa and tensile strength up to 2 GPa) [1], high hardness [2] and excellent wear resistance [3], especially the low-cost Zr-based BMGs with critical dimension up to dozens of centimeters [4,5,6]. However, it is precisely because of its excellent mechanical properties that it cannot be cold processed, preventing its application in engineering. Fortunately, the superplastic deformation ability of most BMGs makes it possible for them to be shaped using near-net-shape technology [7] in their supercooled liquid region (SLR). Considering that the BMGs without the limitation of grains can accurately duplicate the mold shape and have great advantage in shaping tiny parts such as the spy fly, a variety of micro-parts for micro-electromechanical systems were formed by taking advantage of the superplastic deformation ability of BMGs [8]. But the forming of parts larger than millimeters has been neglected in recent years. For example, high-temperature compression experiments showed that most of the BMGs, including Zr-Cu-Ni-Al [9,10,11,12], Zr-Cu-Ag-Al [13], Zr-Cu-Ti-Al [14] and Zr-Co-Cu-Ti [15], were deformed in a Newtonian fluid at high temperatures and low strain rates in the supercooled liquid region. But few experts check these parameters in the real forming process, keeping in mind that the flow conditions of an alloy in mold are much different from the simple compression experiments.
In this paper, the uniaxial compression behaviors of Zr70Cu13.5Ni8.5Al8 BMGs under various temperatures and strain rates in the supercooled liquid region were studied. And based on the experiment results, a thermoplastic forming (TPF) map [16] of the BMGs was constructed. Then, gears were extruded using the optimal parameters obtained using the TPF map. The microstructure and microhardness of the gears were eventually detected.
2. Materials and Methods
Master ingots of Zr70Cu13.5Ni8.5Al8 (in atomic ratios) BMGs were fabricated using arc melting high-purity (>99.9%) metals in a high-purity argon atmosphere 3 times. Then, the ingots were remelted and suction cast into a water-cooled Cu mold to identify rods with diameters of 4 mm and lengths of 50 mm under the power of 8 kW. The thermal characteristic parameters were examined via differential scanning calorimetry (DSC, NETZSCH STA 449C Instruments, NETZSCH, Bayern, Germany) at a heating rate of 20 K/min. The glass transition temperature Tg was determined to be 629.12 K, and the crystallization temperature Tx was 705.98 K. Hence, the supercooled liquid region ∆Tx was up to 76.9 K.
Compression samples with an aspect ratio of 1:2 were cut from the as-cast rods using the diamond slicing machine. Both the bottom and top of the compression sample were polished to keep them parallel. High-temperature compression tests were carried out on these samples at various temperatures and strain rates using a Gleeble 3500 thermal simulator (Gleeble, Poestenkill, NY, USA). To avoid crystallization, temperatures of 643 K, 653 K and 663 K in the supercooled liquid region and strain rates of 1 × 10−2 s−1, 5 × 10−3 s−1, 1 × 10−3 s−1 and 5 × 10−4 s−1 were chosen for the deformation test. Then, the TPF map was drawn through analysis of the high-temperature compression results. The samples with an aspect ratio of 1:2 were also used for superplastic extrusion. Standard spur gears with moduli of 0.25 and 10 teeth were hot-extruded using a heating-cell equipped Instron 5500 machine (Instron, Kawasaki, Japan) [7] under the optimal parameters obtained from the TPF map. The heating-cell, as shown in Figure 1, is a resistance furnace with a temperature accuracy of ±1 K. The upper of the resistance furnace has an opening that is used both to put the sample in and to enable the extrusion punch to pass through it. The resistance furnace was first heated to the target temperature with the extrusion die in it. Then, the sample was put into the die, and the extrusion punch was driven down using the universal material testing machine to complete the extrusion operation.

Figure 1.
The heating-cell-equipped Instron 5500 machine.
The microstructures of the samples were observed using a X-ray diffractometer (XRD, Nikkaku D/max-2400, Tokyo, Japan) with momochromatic Cu Ka radiation, a transmission electron microscope (TEM, JEM-2010) and scanning electron microscopy (SEM, JSM-6700F). Samples were etched by 1% hydrofluoric acid aqueous solution for SEM observation. And 10% perchloric acid in ethanol was used as a chemically jet thinning solution for TEM observation. The microhardness of the samples was tested using the HV-1000 Vickers hardness tester (Vickers, London, UK), with a loading force of 300 g and a pressure holding time of 15 s.
3. Results and Discussion
Figure 2 shows the high-resolution TEM image and the corresponding selected area electron diffraction (SAED) pattern of the as-cast Zr70Cu13.5Ni8.5Al8 rods with a 4 mm diameter. The maze-like pattern in the high-resolution TEM image and the corresponding halo ring in the SAED pattern confirms the amorphous structure of the sample. Furthermore, a few nanocrystals smaller than 10 nm were embedded in the amorphous matrix. As the volume fraction of the crystalline is too small to be detected using the XRD, the XRD pattern of the sample only presents a broad halo peak in the 2θ range of 30–45°, indicating that the rods are basically amorphous structures.
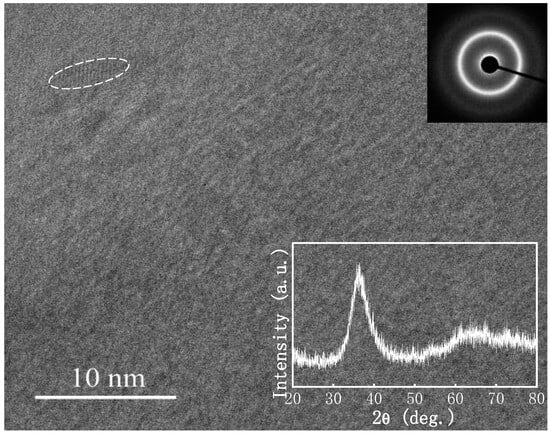
Figure 2.
TEM image and the corresponding SAED pattern (top right corner) of the as-cast Zr70Cu13.5Ni8.5Al8 rods, with the XRD pattern shown in the lower right corner.
3.1. Deformation Behavior
Figure 3 shows the true stress–true strain curves of the specimens deformed under different strain rates and at 643 K, 653 K and 663 K, respectively. Typically, the stress–strain curves of the samples deformed at high strain rates show an obvious yield peak, and then the stress reduced rapidly with strain. This phenomenon was usually called strain softening or stress overshoot, which has been widely discussed and interpreted in terms of stress-induced excess free volume [17,18,19]. According to the free volume theory, the generation and annihilation of the free volume changed dynamically during the deformation process. Lots of free volume of the sample annihilated at high temperatures, but the amount of free volume generated in the early stage of deformation is limited, resulting in the increase in the stress. With the increase in deformation, the generation of free volume increases, so the stress decreases gradually and a peak-yield stress is presented on the stress–strain curves. At last, the generation and annihilation of the free volume will reach a dynamic balance, and the stress will become constant, showing a steady-state stress on the stress–strain curve of the sample. But when the samples deformed at low strain rates, the stress overshoot phenomenon disappeared, and the samples deformed under an almost constant flow stress. Furthermore, the peak-yield stress on the stress–strain curves with stress overshoot and the steady-state stress decrease with the decrease in the strain rates.
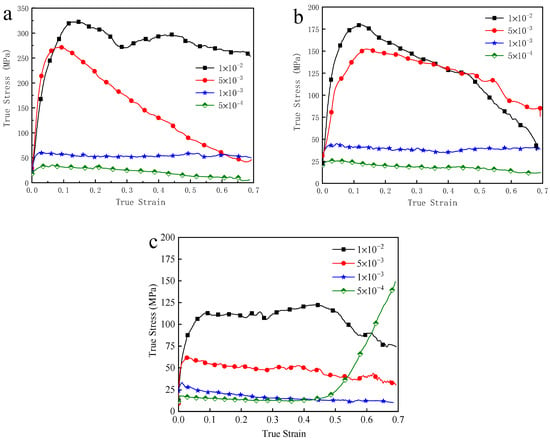
Figure 3.
True stress−true strain curves for different strain rates at different temperatures: (a) 643 K; (b) 653 K; (c) 663 K.
To understand the dependence of the true stress–true strain curves on temperature, the true stress–true strain curves deformed at the different temperatures shown in Figure 3 are replotted for different strain rates and shown in Figure 4. The rheological behavior of the BMGs in the supercooled liquid region depends strongly not only on strain rates but also on temperatures. Under the conditions of high temperatures and low strain rates, the samples deformed at a constant stress after reaching their peak-yield stress. In contrast, under low temperatures and high strain rates, the strain-softening phenomenon occurred after the stress reached its peak-yield stress, and then the flow stress gradually declined into a smooth state. Furthermore, the peak-yield stress and the steady-state stress also decrease with the increase in temperature. In particular, the flow stress of the sample deformed at 663 K, and the strain rate of 5 × 10−4 s−1 increased drastically after the true strain reached 0.5. Similar phenomenon was also observed in Fe-based [20] and Cu-based [21] BMGs. This strain-hardening phenomenon was usually related to the crystallization of the amorphous phase resulting from keeping it at high temperature for a long time. It is worth mentioning that the strain-hardening phenomenon was not observed, even though the samples were deformed at 643 K and 653 K for 1150 s. In addition, the ultimate strengths of the specimens show a trend that decreases upon decreasing the strain rate and increasing the temperature. Although the strength of the BMGs is as high as 2 Gpa at ambient temperature, the highest peak-yield stress is only 326.5 Mpa when the sample is deformed in the supercooled liquid region. In particular, the sample can be deformed at a constant stress as low as 1860 Mpa, when the sample deformed at a high temperature and low strain rate, which is very suitable for superplastic forming.
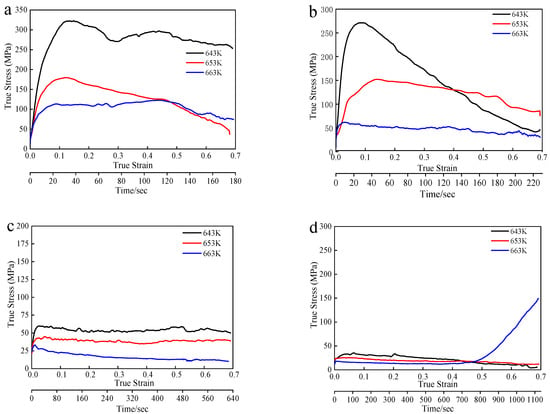
Figure 4.
True stress–true strain curves for different temperatures at different strain rates: (a) 1 × 10−2 s−1; (b) 5 × 10−3 s−1; (c) 1 × 10−3 s−1; (d) 5 × 10−4 s−1.
The strain rate sensitivity m is a key parameter used to characterize the rheological behavior of BMGs in the supercooled liquid region [22,23,24]. m reflects sensitivity of the flow stress to the strain rate during plastic deformation. Generally speaking, the m of common metal materials is between 0.02 and 0.2. The material undergoes a homogeneous Newtonian flow when m is close to 1, and the flow behavior transforms to non-Newtonian flow when m is no more than 0.5 [25]. According to the Backofen function [26], i.e., s = Km, the strain rate sensitivity m can be determined by the slope of lgsflow verses lg, where sflow is defined as the peak-yield stress and K is a constant. Figure 5 compares the double logarithmic plots of stress as a function of the strain rate for the samples deformed at different temperatures. The value of m can be calculated by fitting the double logarithmic plots of stress as a function of the strain rate. The value of m and variance were also marked in Figure 5. It can be seen that the average m is about 0.55 when the sample is deformed at 663 K, indicating a Newtonian fluid. When the sample was deformed at low strain rates at 653 K and 643 K, the m was close to unity. But m decreased to less than 0.3 when the samples were deformed at strain rates higher than 5 × 10−3 s−1, indicating that the deformation behavior of the BMGs transformed from a Newtonian fluid to a non-Newtonian fluid, which is not suitable for superplastic forming.
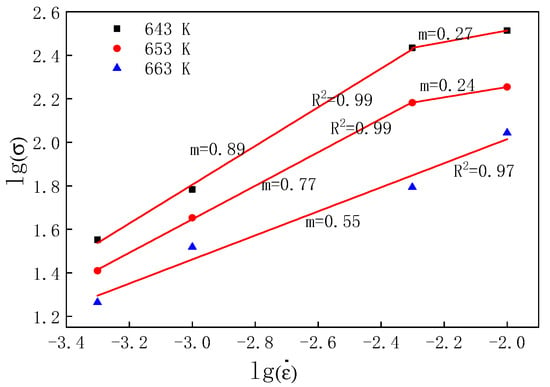
Figure 5.
Logarithm stress versus logarithm strain rate for the BMGs.
Figure 6 shows the macroscopic morphology of the specimens deformed at 653 K. The cylindrical specimens were uniformly compressed at a strain rate of 5 × 10−4 s−1. Nevertheless, the morphology of the compressed samples changed to an inverted letter “N” (strain rate of 1 × 10−3 s−1) and then to the drum shape (strain rate of 5 × 10−3 s−1 and 1 × 10−2 s−1) when the strain rate increased, indicating that the flow behavior in the hot deformation process changed from homogeneous to inhomogeneous [17]. The results are consistent with the changes in the value of m.

Figure 6.
Macroscopic morphology of the specimens after high-temperature compression.
Figure 7 shows the XRD patterns of the samples deformed under different conditions. Except for the sample deformed at 663 K and 5 × 10−4 s−1, the XRD patterns of the samples show broad halo peaks in the 2θ range of 30–45°, indicating that these samples basically keep their amorphous structures after high-temperature deformation. However, the diffraction peaks of the AlZr2 and Zr6NiAl2 phases were detected in the XRD patterns of the sample deformed at 663 K and 5 × 10−4 s−1. The XRD results further confirmed that the strain-hardening phenomenon in the stress–strain curve of the sample deformed at 663 K and 5 × 10−4 s−1 were caused by the crystallization of the amorphous phase. The results are consistent with the stress–strain curves of the samples deformed at various temperatures and strain rates shown in Figure 3. Therefore, an too low strain rate is unfavorable to the forming of amorphous parts due to the crystallization of the amorphous phase stemming from long-term heating at a high temperature.
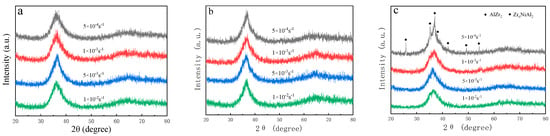
Figure 7.
XRD patterns of the samples deformed under different conditions: (a) 643 K; (b) 653 K; (c) 663 K.
3.2. Thermoplastic Forming Map
Based on the experimental results, a TPF map can be constructed to determine the hot processing parameters of BMGs. As the thermoplastic forming process is also an energy-dissipating system, the TPF map is usually constructed by superimposing the energy dissipation map and the instability map together in the form of contour lines on the two-dimensional plane of temperature and strain rate [27].
According to the dynamic material model (DMM), the total energy(P) dissipated in the deformation process consists of the energy absorbed via plastic deformation (G) and structural transformation (J), where J can be evaluated by the strain rate sensitivity exponent m as J = m/(m + 1) s. And J reaches its maximum value when the value of m reaches 1. Therefore, Jmax = s/2 [28]. Thus, the efficiency of power dissipation ηp, i.e., ηp = J/Jmax = 2m/(m + 1), represents the ratio of the energy dissipated via structural transformation. Typically, the alloy has good processing properties when ηp is higher than 0.6. The larger the ηp, the less the energy is consumed by plastic deformation. Figure 8 shows two-dimensional and three-dimensional energy dissipation maps of the BMGs calculated using the m at different strain rates and temperatures. Except for the shaded region corresponding to the sample deformed under a strain rate of 1 × 10−2 s−1 at 643 K and 653 K, the ηp of the other region is higher than 0.6, indicating good processing properties.
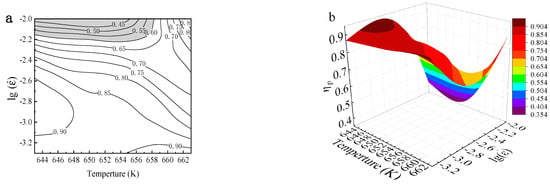
Figure 8.
(a) Two-dimensional and (b) three-dimensional energy dissipation maps of the BMGs under different deformation conditions.
Although the value of ηp is high, rheological instability may still occur. Therefore, it is necessary to introduce the rheological instability map to supplement the TPF map. According to the Prasad criterion [29], the rheological instability criterion can be expressed as follows:
where A, B and C are constant. When < 0, the rate of entropy applied to the system from outside does not coincide with the rate of entropy generated by the alloy itself; thus, the alloy presents rheological instability in this region. Figure 9 shows the two-dimensional and three-dimensional rheological instability map calculated using Equation (1). Coincidentally, the value of the is negative in the shaded region in the rheological instability map corresponding to the sample deformed under the strain rate of 1 × 10−2 s−1 at 643 K and 653 K, which is consistent with the energy dissipation map. Therefore, the energy dissipation map can be used as a TPF map to select suitable thermal processing parameters.
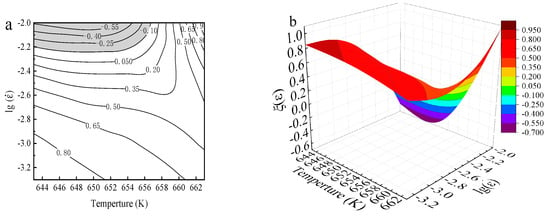
Figure 9.
(a) Two-dimensional and (b) three-dimensional rheological instability map of the BMGs.
Figure 10 illustrates the peak-yield stress of the samples deformed under different conditions. According to the TPF map, the value of ηp was less than 0.6 and not suitable for thermoplastic deformation when the sample was deformed under a strain rate of 1 × 10−2 s−1 at 643 K and 653 K (marked with red symbol in Figure 10). Furthermore, it is worth mentioning that although the specimen has good processing properties, it is not suitable for thermoplastic deformation under a strain rate of 5 × 10−4 s−1 at 663 K due to the crystallization of the sample (marked with blue symbol in Figure 10). In addition, the flow stress is higher than 150 MPa when the sample was deformed under a strain rate of 5 × 10−3 s−1 at 643 K and 653 K, which was not the optimal parameter for thermoplastic deformation (marked with black symbol in Figure 10). In contrast, the sample can be deformed under very low flow stress and high-efficiency power dissipation using the rest of the parameters shown in Figure 10 (marked with a cyan symbol in Figure 10). And it can be observed from Figure 5 that the flow behavior is Newtonian fluid when the samples deformed under these parameters. Therefore, these parameters are the optimal thermoplastic deformation parameters for the BMGs. Considering that under a strain rate of 1 × 10−3 s−1, the whole temperature region from 643 K to 663 K was suitable for thermoplastic deformation, a strain rate of 1 × 10−3 s−1 was chosen for the thermal forming of gears.
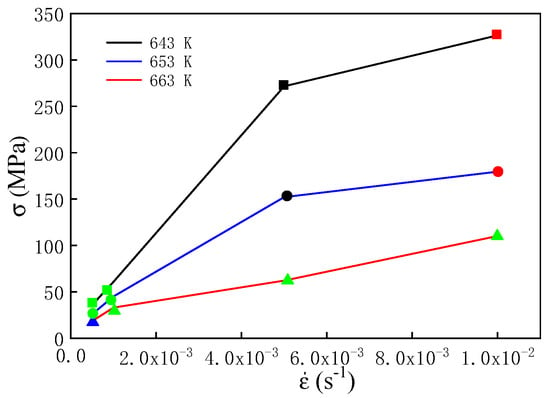
Figure 10.
Peak-yield stress as a function of strain rate for the Zr-based BMG.
3.3. Superplastic Forming of Gears
Figure 11 shows the macroscopic morphology of the gear end face obtained via superplastic extrusion under a constant strain rate of 1 × 10−3 s−1 and at different temperatures. It can be seen that although gears can be forming under a constant strain rate of 1 × 10−3 s−1 throughout the temperature range from 643 K to 663 K, the shape of the gear teeth was incomplete when it was extruded at a temperature of 643 K. In contrast, the gear teeth are relatively perfect when formed at 653 K and 663 K, indicating that the BMGs has excellent forming ability at 653 K and 663 K in the supercooled liquid region. Figure 12a shows the actual load–time curves when the three gears were formed. The curves can mainly be divided into two regions. At the beginning, because of the gap between the rod and the extrusion die, the deformation state is the same as that of the uniaxial compression, and the load is very low, as shown in region I. It is found by calculating the stress in this stage that is basically the same as that in the high-temperature compression shown in Figure 4c. Then, the load climbs rapidly when the rods contacted the inner wall of the die and the rods deformed in three-dimensional stress state, as shown in region II. In this stage, the load can rise as high as 20 kN, and the calculated stress can reach to 1.7 GPa. Therefore, a more reasonable structural design for the die and lubrication are necessary and essential for the superplastic forming of BMGs. Figure 12b shows the XRD patterns of the gears. The XRD patterns of the gears formed at 643 K show broad halo peaks in the 2θ range of 30–45°, indicating that the gear basically kept its amorphous structures during the hot extrusion process. However, unlike for the compressed rods in Figure 7, although the extrusion time is only 300 s, which is much shorter than the compression time at 653 K and 663 K, the diffraction peaks of the AlZr2 and Zr6NiAl2 phases were observed for the XRD patterns of the gears. It has been reported that high-temperature deformation promotes the isothermal crystallization process of BMGs [30,31], so it is possible that such high extrusion stress further accelerated the crystallization process.

Figure 11.
Morphology gears obtained via superplastic extrusion under a strain rate of 1 × 10−3 s−1 and at different temperatures: (a) 643 K; (b) 653 K; (c) 663 K.
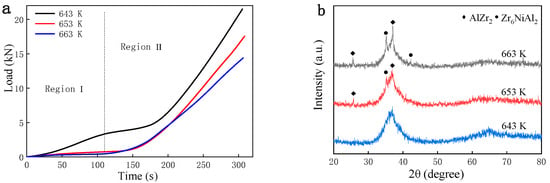
Figure 12.
(a) Load–time curves for the superplastic forming of amorphous gears at different forming temperatures under a strain rate of 1 × 10−3 s−1 and (b) corresponding XRD pattens.
Figure 13 shows SEM images of the center of the gears formed at different temperatures under a strain rate of 1 × 10−3 s−1. Grains were etched off by a hydrofluoric acid aqueous solution due to their poor corrosion resistance, and only an amorphous matrix was left behind. Compared with the as-cast alloy for a few nanoparticles smaller than 10 nm, grains in the gears increased and grew. The crystallization volume fractions of the gears formed at 643 K, 653 K and 663 K are approximately 0.2%, 16.2% and 22.9%, as calculated using the XRD patterns, respectively. Although the amount of the grains in the gear extruded at 643 K is still very low, the size of grains has grown to larger than 50 nm (marked with black arrows), as shown in Figure 13a. Figure 13b were taken from the gear extruded at 653 K. It can be observed that the grains increased and grew to a size larger than 100 nm. Figure 13c was taken from the center of the gear extruded at 663 K. The number and size of the grains increased, and they began to be aggregated with each other. The results are basically consistent with the XRD results.

Figure 13.
SEM images of the gears formed under the strain rate of 1 × 10−3 s−1 at different temperatures: (a) 643 K; (b) 653 K; (c) 663 K.
Figure 14 compares the average microhardness of the as-cast alloy and the gears extruded at different temperatures under the strain rate of 1 × 10−3 s−1. High-temperature extrusion increased the microhardness of the BMGs, and the microhardness of the gears increased gradually with the increase in the extrusion temperature. Obviously, the increase in microhardness must be related to the crystallization of the BMGs. The increase in microhardness, which was widely found in the annealing and high-temperature deformation process, is considered to be caused by the crystallization and annihilation of the free volume [24,32]. Generally, the greater the hardness of the metal, the better the abrasion resistance and fatigue strength. So, high hardness is essential to increase the service lives of gears.
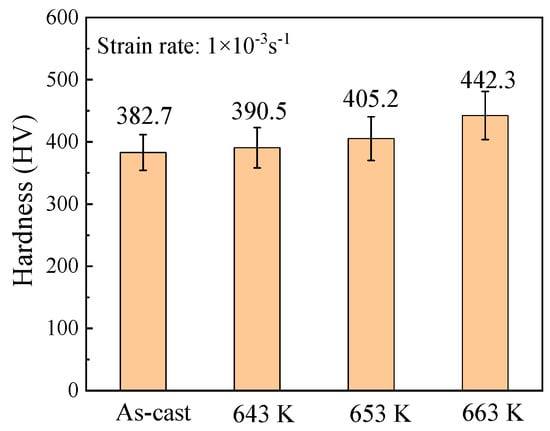
Figure 14.
Average microhardness of the gear end faces extruded at different temperatures under the strain rate of 1 × 10−3 s−1.
4. Conclusions
The research method of the hot forming of common metal materials is applied to the hot extrusion of BMGs. The superplastic flow behavior of Zr70Cu13.5Ni8.5Al8 BMGs in the supercooled liquid region was first studied using hot compression. Based on the experimental compression results, a TPF map was constructed. The TPF map, combined with the factors of amorphous structure and low stress, reach a conclusion for the optimal superplastic-forming parameters. Then, gears were successfully extruded using part of the optimal thermal processing parameters. The results are listed as follows:
- (1)
- The flow behavior of the BMGs compressed in the supercooled liquid region seriously depended on the strain rate and temperature. The flow stress of the BMGs increased with the increase in the strain rate and decrease in temperature. Furthermore, the flow behavior of the BMGs transformed from Newtonian fluid to non-Newtonian fluid with the increase in the strain rate and the decrease in temperature.
- (2)
- The optimal parameters can be divided into two parts: one part is the region with a temperature of 643 K~653 K and a strain rate of 5 × 10−4 s−1~1 × 10−3 s−1; the processing efficiency of this region ranges from 0.870 to 0.919, and the stress ranges from 25.68 MPa~60.77 MPa. The other part is the region with a temperature of 663 K and a strain rate of 1 × 10−3 s−1~1 × 10−2 s−1; the processing efficiency in this region ranges from 0.771 to 0.906, and the stress ranges from 33.36 MPa to 110.23 MPa.
- (3)
- Gears were extruded under a constant strain rate of 1 × 10−3 s−1 and at different temperatures. In particular, the gear extruded under the strain rate of 1 × 10−3 s−1 at 653 K exhibits the perfect shape. Microstructure investigation showed that crystallization happened in the superplastic-forming process for all three samples extruded under different parameters, and the number and size of the crystals increased with the increase in forming temperature. Furthermore, the microhardness of the gears increased compared to the as-cast sample due to crystallization and the annihilation of the free volume.
Overall, the research method of the hot forming of common metal materials can be used for the hot extrusion of BMGs. But, the high stress during the extrusion process accelerated the crystallization process, which made crystallization inevitable. A great number of experiments are still needed before the application of thermoforming to BMGs.
Author Contributions
Investigation, C.X.; writing—original draft preparation, C.Z.; writing—review and editing, J.H.; project administration, X.Z. and Z.Y.; funding acquisition, X.Z. and Z.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (NSFC) [No. 52061024 and No. 52161027], the Natural Science Foundation of Gansu Province (No. 21JR7RA260) and the Hongliu Research Funds of Lanzhou University of Technology for Distinguished Young Scholars.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lai, L.M.; Ding, K.L.; Liu, T.H.; Chen, Y.X.; Guo, S.F. Ternary Co-W-B bulk metallic glasses with ultrahigh strength. J. Non-Cryst. Solids 2020, 544, 120194. [Google Scholar] [CrossRef]
- Jiang, X.F.; Song, J.J.; Fan, H.Z.; Su, Y.F.; Zhang, Y.S. Sliding friction and wear mechanisms of Cu36Zr48Ag8Al8 bulk metallic glass under different sliding conditions: Dry sliding, deionized water, and NaOH corrosive solutions. Tribol. Int. 2020, 146, 106211. [Google Scholar] [CrossRef]
- Lin, B.Z.; Yang, K.H.; Bao, X.G.; Liu, J.L.; Guo, Q.H.; Zhang, L.; Wang, Q.T.; Hua, N.B. Enhanced wear, corrosion, and corrosive-wear resistance of the biocompatible Ti-based bulk metallic glass by oxidation treatment. J. Non-Cryst. Solids 2022, 576, 121231. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Yuan, Z.Z.; Feng, X.L.; Cui, L.Z.; Li, D.X. Homogeneous viscous flow behavior of a Cu-Zr based bulk metallic glass composites. Mater. Sci. Eng. A 2015, 620, 352–358. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Yuan, Z.Z.; Feng, X.L.; Cui, L.Z.; Li, D.X. Isothermal nanocrystallization behavior of bulk metallic glass composites in supercooled liquid region. Rare Met. 2017, 36, 919–924. [Google Scholar] [CrossRef]
- Wen, S.; Dai, C.Y.; Mao, W.G.; Zhao, Y.; Han, G.F.; Wang, X.M. Effects of Ag and Co microalloying on glass-forming abilities and plasticity of Cu-Zr-Al based bulk metallic glasses. Mater. Des. 2022, 220, 110896. [Google Scholar] [CrossRef]
- Ryu, W.H.; Kim, K.J.; Yoo, G.H.; Park, E.S. Alloy design strategy to improve fluidity of Zr-based bulk metallic glass for near-net-shape manufacturing. J. Alloys Compd. 2022, 896, 162680. [Google Scholar] [CrossRef]
- Gong, P.; Wang, S.; Liu, Z.; Chen, W.; Li, N.; Wang, X.Y.; Yao, K.F. Lightweight Ti-based bulk metallic glasses with superior thermoplastic formability. Intermetallics 2018, 98, 54–59. [Google Scholar] [CrossRef]
- Zhang, W.J.; Tao, P.J.; Chen, Y.G.; Si, J.F.; Huang, Z.H.; Zhu, K.S.; Yang, Y.Z. Study on isothermal crystallization kinetics of Zr55.7Cu22.4Ni7.2Al14.7 bulk amorphous alloy. Sci. Rep. 2022, 12, 5060. [Google Scholar] [CrossRef]
- Cheng, S.R.; Zhu, J.H.; Shen, J.; Wei, X.S. Effects of yttrium addition on thermoplastic formability of Zr-Cu-Ni-Al amorphous alloy under non-isothermal condition. J. Alloys Compd. 2021, 872, 159684. [Google Scholar] [CrossRef]
- Lyubenova, L.; Rangelova, V.; Spassova, M.; Spassov, T. Glass forming ability of Zr-based Zr-Cu-Ni-Al-(Ag) alloys. J. Therm. Anal. Calorim. 2023, 148, 3975–3980. [Google Scholar] [CrossRef]
- Zhou, Y.Z.; Zhao, L.; Qu, Y.W.; Hu, L.W.; Qi, L.; Qu, F.S.; He, S.X.; Liu, X. Effect of Yttrium Doping on Glass-Forming Ability, Thermal Stability, and Corrosion Resistance of Zr50.7Cu28Ni9Al12.3 Bulk Metallic Glass. Metals 2023, 13, 521. [Google Scholar] [CrossRef]
- Ding, Z.Y.; Song, Y.X.; Ma, Y.; Huang, X.W.; Zhang, T.H. Nanoindentation Investigation on the Size-Dependent Creep Behavior in a Zr-Cu-Ag-Al Bulk Metallic Glass. Metals 2019, 9, 613. [Google Scholar] [CrossRef]
- Prabhu, Y.; Vincent, S.; Manulal, S.; Nair, A.; Bhatt, J. Cu-Zr-Ti-Al metallic glass: Thermodynamic prediction, synthesis, and biocorrosion studies. Phys. B Condens. Matter 2021, 609, 412918. [Google Scholar] [CrossRef]
- Prabhu, Y.; Jain, A.; Vincent, S.; Ryu, W.H.; Park, E.S.; Kumar, R.; Bagde, A.D.; Bhatt, J. Compositional design and in vitro investigation on novel Zr-Co-Cu-Ti metallic glass for biomedical applications. Intermetallics 2022, 150, 107692. [Google Scholar] [CrossRef]
- Li, J.L.; Li, C.Y.; Wang, S.P.; Wang, H.B.; Kou, S.Z. Thermal processing map and thermoplastic forming map of Zr-based bulk metallic glass in the supercooled liquid region. J. Non-Cryst. Solids 2021, 570, 121008. [Google Scholar] [CrossRef]
- Tao, P.J.; Zhu, K.S.; Long, Z.Y.; Zhang, C.H.; Zhang, W.J.; Yang, Y.Z. Strain rate response and rheological characteristics of ZrCuNiAl bulk metallic glass in supercooled liquid region. J. Non-Cryst. Solids 2023, 607, 122216. [Google Scholar] [CrossRef]
- Mei, J.N.; Soubeyroux, J.L.; Blandin, J.J.; Li, J.S.; Kou, H.C.; Fu, H.Z.; Zhou, L. Homogeneous deformation of Ti41.5Cu37.5Ni7.5Zr2.5Hf5Sn5Si1 bulk metallic glass in the supercooled liquid region. Intermetallics 2011, 19, 48–53. [Google Scholar] [CrossRef]
- Wang, C.J.; Cheng, S.R.; Ma, M.Z.; Shan, D.B.; Guo, B. A Maxwell-extreme constitutive model of Zr-based bulk metallic glass in supercooled liquid region. Mater. Des. 2016, 103, 75–83. [Google Scholar] [CrossRef]
- Song, S.M.; Liao, Y.C.; Li, T.H.; Lee, C.K.; Tsai, P.H.; Jang, J.S.C.; Huang, J.C. Thermoplastic deformation behavior of a Fe-based bulk metallic glass within the supercooled liquid region. J. Mater. Res. Technol. 2019, 8, 1907–1914. [Google Scholar] [CrossRef]
- Bae, D.H.; Lim, H.K.; Kim, S.H.; Kim, D.H.; Kim, W.T. Mechanical behavior of a bulk Cu–Ti–Zr–Ni–Si–Sn metallic glass forming nano-crystal aggregate bands during deformation in the supercooled liquid region. Acta Mater. 2002, 50, 1749–1759. [Google Scholar] [CrossRef]
- Li, M.C. Effect of Annealing on Strain Rate Sensitivity of Metallic Glass under Nanoindentation. Metals 2020, 10, 1063. [Google Scholar] [CrossRef]
- Savaedi, Z.; Motallebi, R.; Mirzadeh, H.; Malekan, M. Superplasticity of bulk metallic glasses (BMGs): A review. J. Non-Cryst. Solids 2022, 583, 121503. [Google Scholar] [CrossRef]
- Zhu, S.L.; Wang, X.M.; Qin, F.X.; Inoue, A. Influence of temperature on viscous flow deformation of Zr55Cu30Al10Ni5 bulk glassy alloy in supercooled liquid region. Intermetallics 2007, 15, 885–890. [Google Scholar] [CrossRef]
- Liu, S.S.; Hou, C.N.; Wang, E.G.; Jia, P. Plastic Rheological Behaviors of Zr61Cu25Al12Ti2 and Zr52.5Cu17.9Ni14.6Al10Ti5 Amorphous Alloys in the Supercooled Liquid Region. Acta Metall Sin. 2022, 58, 807–815. [Google Scholar]
- Seshacharyulu, K.; Mahalle, G.; Kotkunde, N.; Singh, S.K.; Naik, B.B. High temperatures deformation and formability behavior of DP590 steel: Mechanical characterization and modeling. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 472. [Google Scholar] [CrossRef]
- Ha Ryu, W.; Kim, K.J.; Kwak, M.K.; Ryu, C.W.; Park, E.S. Development of Zr-based metallic glasses to utilize thermoplastic forming processes of engineering plastics. Mater. Des. 2023, 232, 112100. [Google Scholar] [CrossRef]
- Li, C.Y.; Yin, J.F.; Ding, J.Q.; Zhu, F.P.; Xu, F.; Zhao, Y.C.; Kou, S.Z. A thermal processing map of a ZrCuNiAlEr bulk metallic glass in the supercooled liquid region. J. Mater. Sci. 2019, 54, 7246–7255. [Google Scholar] [CrossRef]
- Chen, Q.; Hu, L.; Li, M.G.; Chen, Y.; Shi, L.X.; Zhou, T.; Yang, M.B. Optimizing Process Parameters of As-Homogenized Mg-Gd-Y-Zn-Zr Alloy in Isothermal Uniaxial Compression on the Basis of Processing Maps via Prasad Criterion and Murty Criterion. J. Mater. Eng. Perform. 2022, 31, 2257–2266. [Google Scholar] [CrossRef]
- Wu, X.L.; Lan, S.; Li, X.Y.; Yang, M.; Wu, Z.D.; Wei, X.Y.; He, H.Y.; Naeem, M.; Zhou, J.; Lu, Z.P.; et al. Continuous chemical redistribution following amorphous-to-crystalline structural ordering in a Zr-Cu-Al bulk metallic glass. J. Mater. Sci. Technol. 2022, 101, 285–293. [Google Scholar] [CrossRef]
- Rezaei-Shahreza, P.; Hasani, S.; Seifoddini, A.; Nabialek, M.; Czaja, P. The crystallization process in a new multicomponent Fe-based bulk amorphous alloy: A kinetic study approach. Mater. Charact. 2023, 196, 112602. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Zhang, M.; Chen, W.B.; Yuan, Z.Z. Effect of Friction Stir Welding on Bulk Metallic Glasses. J. Wuhan Univ. Technol. Sci. Ed. 2012, 36, 624–628. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).