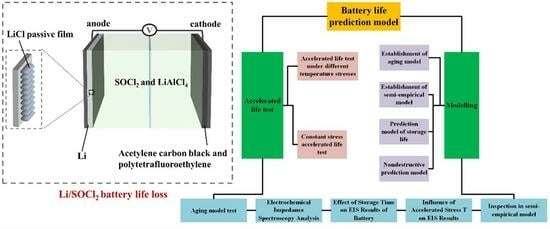
Design and Validation of Lifetime Prediction Model for Lithium-Thiocarbonyl Chloride Batteries Based on Accelerated Aging Experiments
Abstract
:1. Introduction
2. Experimental and Modeling
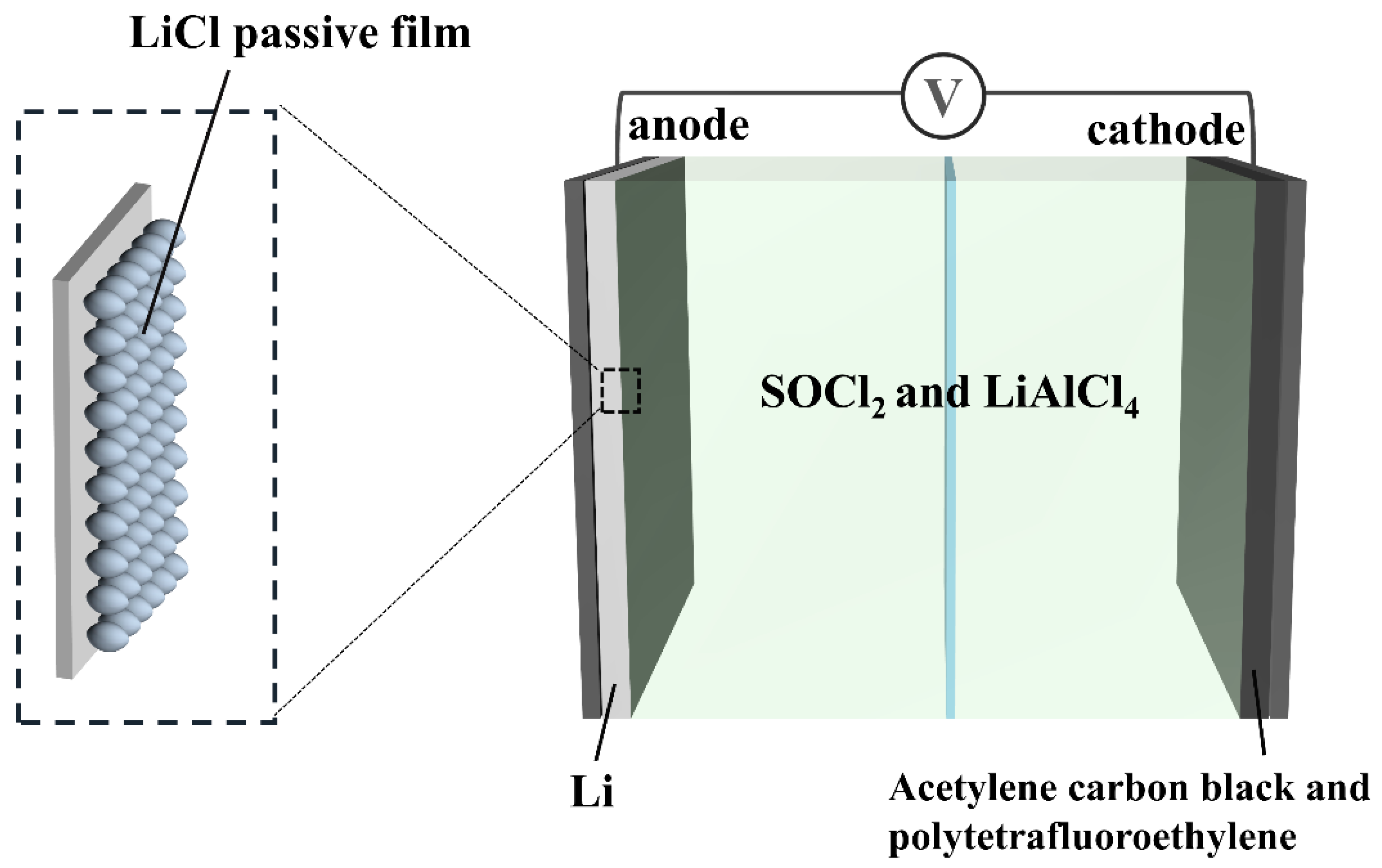
2.1. Materials
2.2. Accelerated Life Test
2.2.1. Accelerated Life Test under Different Temperature Stresses
2.2.2. Constant-Stress Accelerated Life Test
2.3. Modelling
2.3.1. Establishment of Aging Model
2.3.2. Establishment of Semi-Empirical Model
2.3.3. Prediction Model of Storage Life of Lithium-Thionyl Chloride Battery
2.3.4. Nondestructive Prediction Model of Residual Capacity of Lithium-Thionyl Chloride Battery
2.4. Electrochemical Impedance Spectroscopy Analysis
3. Results and Discussion
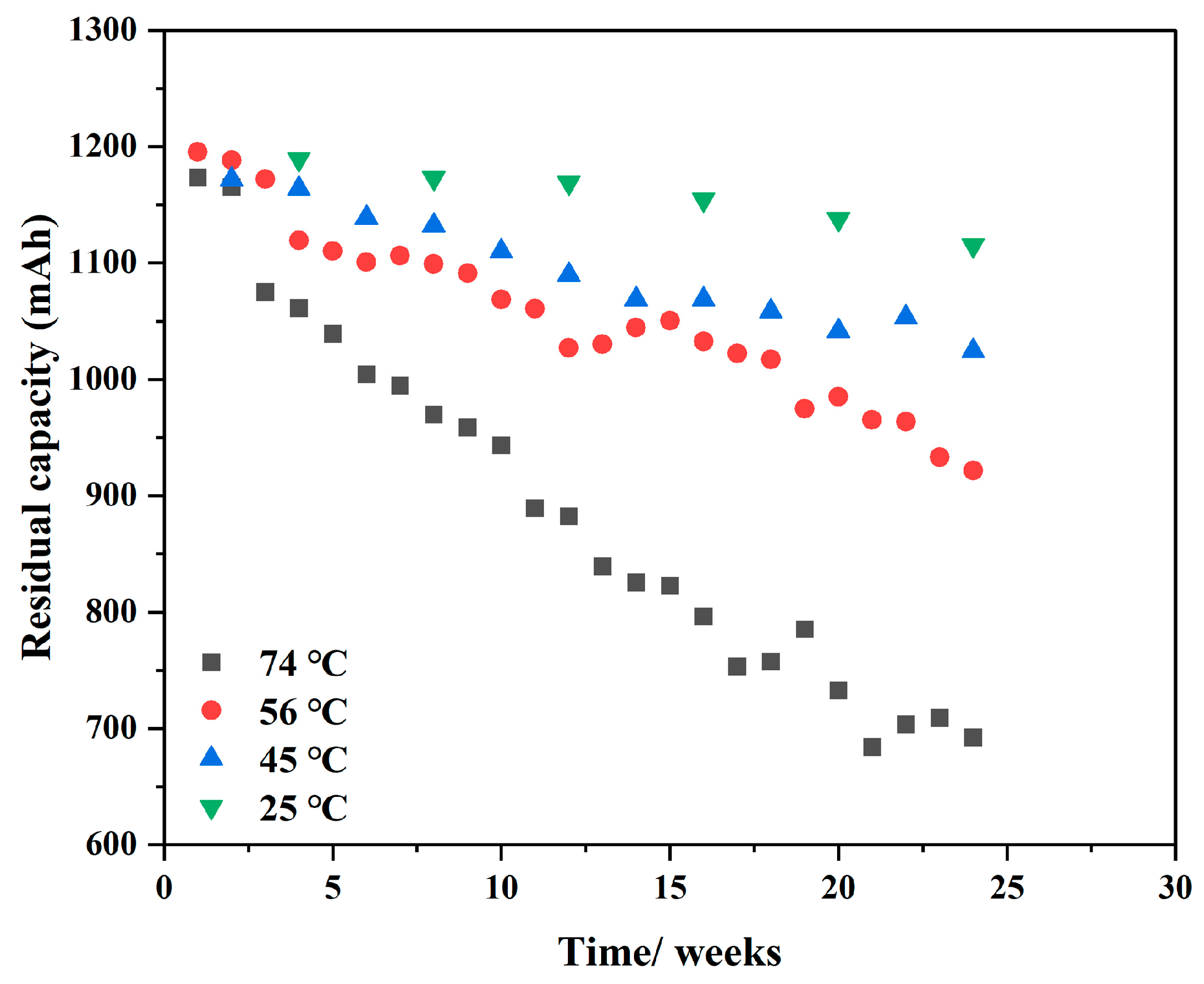
3.1. Analysis of Accelerated Life Test Data
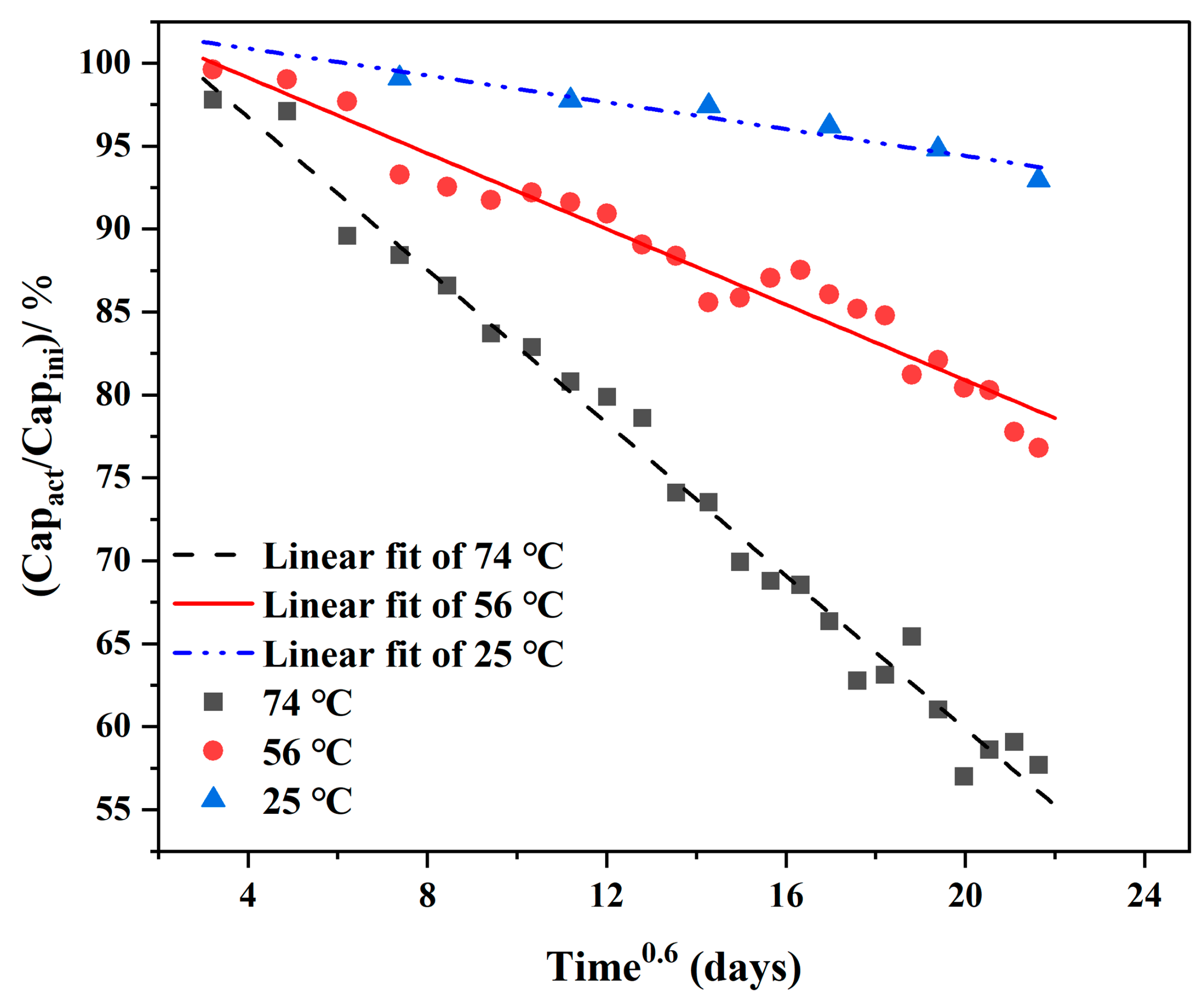
3.1.1. Aging Model Test
3.1.2. Aging Mechanism of Lithium-Thionyl Chloride Battery
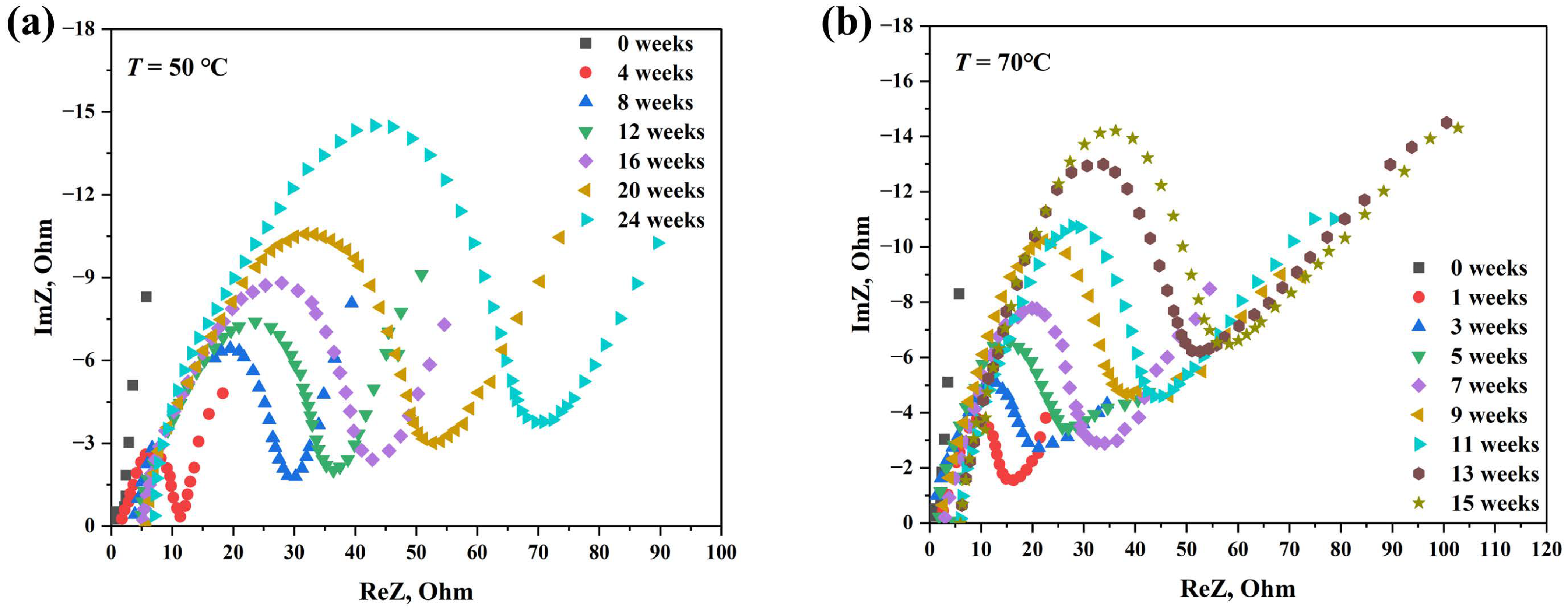
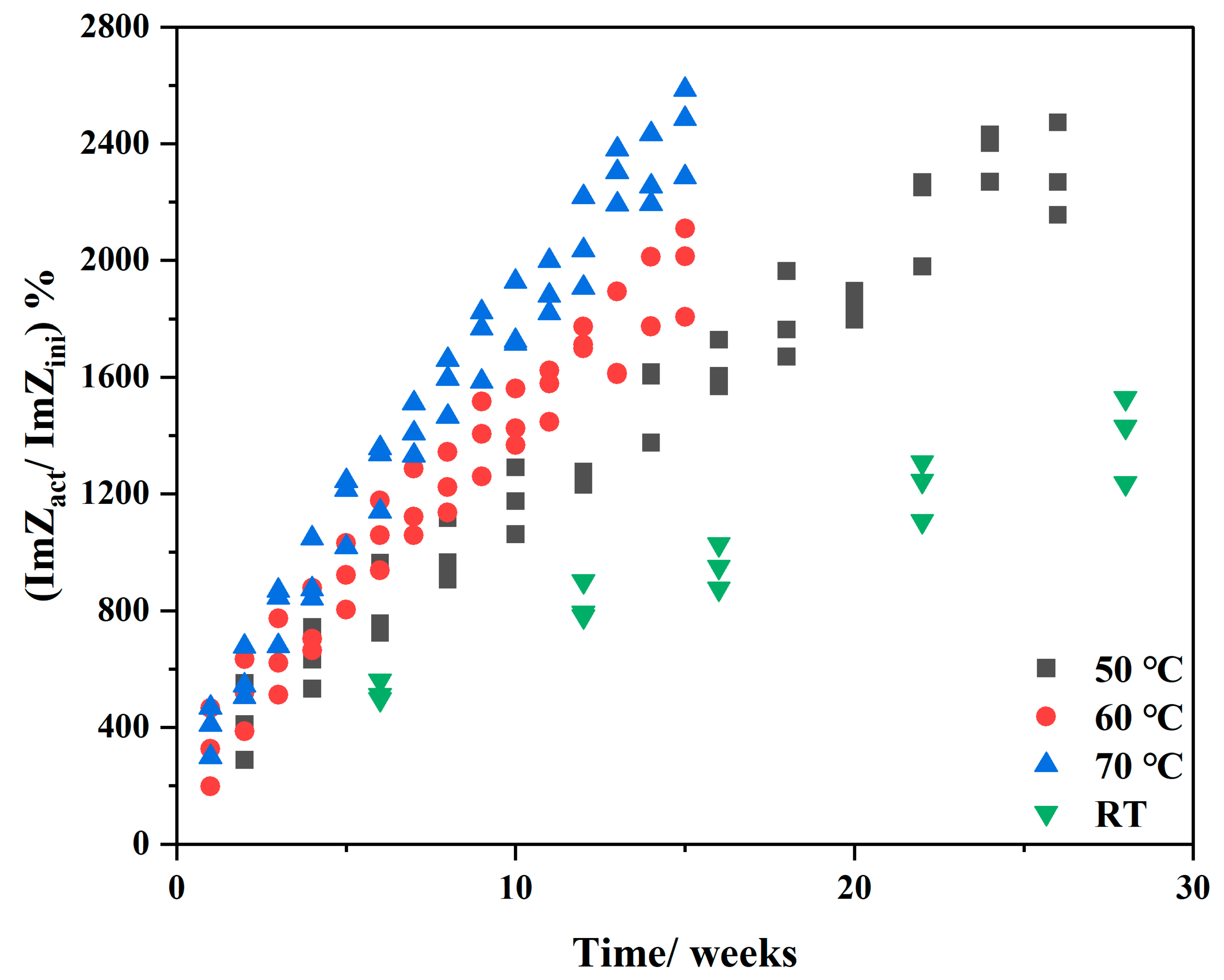
3.2. Effect of Storage Time on EIS Results of Battery after Accelerated Life Test
3.3. Influence of Accelerated Stress T on EIS Results of Battery
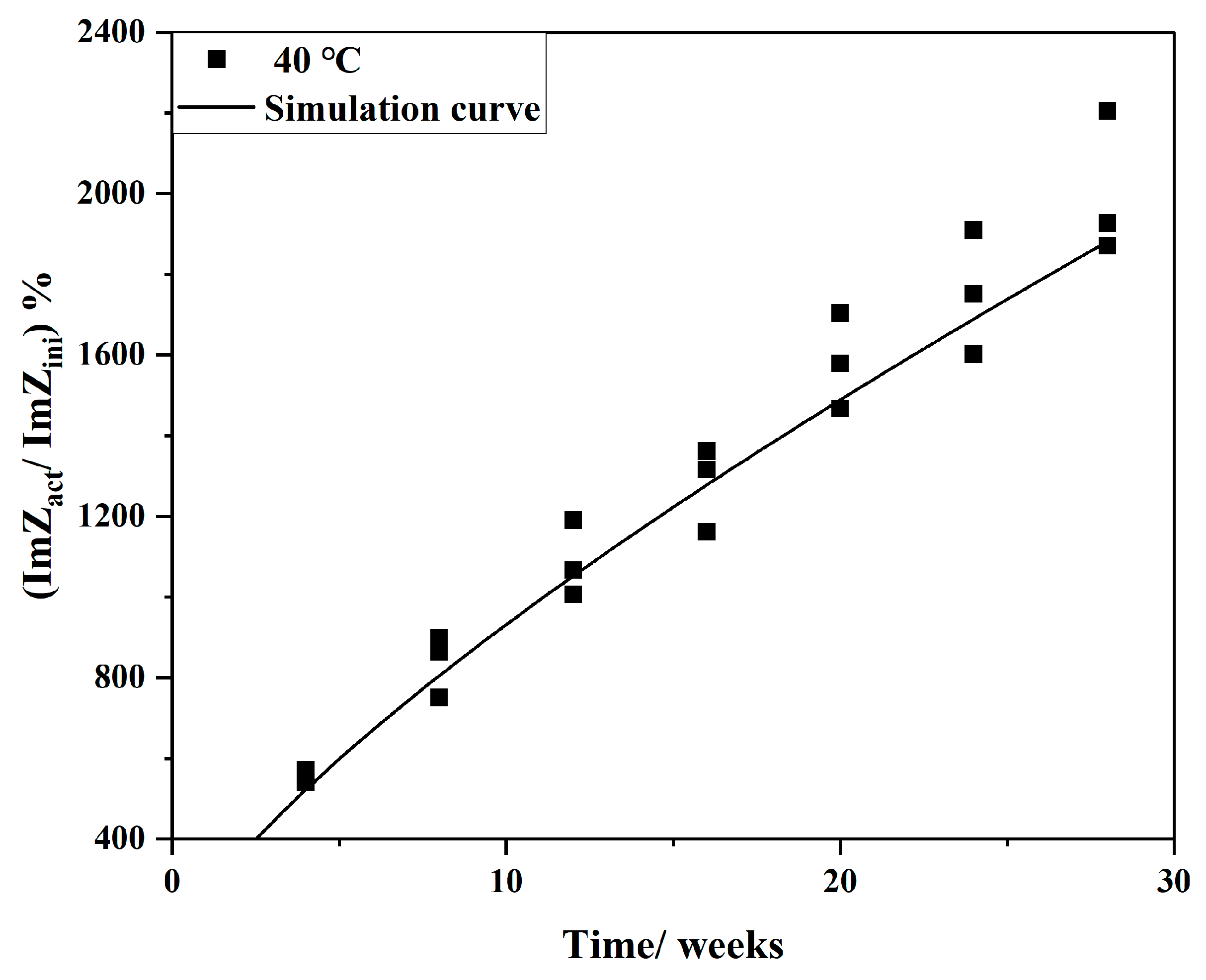
3.4. Inspection in Semi-Empirical Model
4. Conclusions
- By analyzing the accelerated life test data of a 1/2AA carbon-coated ER14250 battery at different temperatures (25 °C, 45 °C, 56 °C, and 74 °C), the aging law was obtained, and the aging model of the battery was established based on data driving. The accuracy of the model has been tested and the maximum deviation is 4.1036%.
- The accelerated life test results of an AA winding Li-SOCl2 battery at different temperatures were analyzed. Combined with the AC impedance spectrum, aging mechanism, and experimental data, a semi-empirical non-destructive prediction model of storage life was established. Combined with the previous capacity prediction semi-empirical model, a non-destructive prediction model of the remaining capacity of lithium-thionyl chloride battery was established. The prediction results show that it will take 378.83 days for the battery capacity to decay to 85% at room temperature. Compared with the experimental data, the error of 365 days is 3.7896%.
- The accelerated life test, semi-empirical life prediction model, and impedance spectrum used in this study can predict the capacity-degradation law of a lithium primary battery with very small error from experimental data and can infer the capacity-degradation mechanism of a battery under the same temperature stress through the similar impedance shape in a Nyquist diagram of a battery AC impedance test.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, C.; Xu, D.; Weng, J.; Zhou, S.; Li, W.; Wan, Y.; Jiang, S.; Zhou, D.; Wang, J.; Huang, Q. Phase Change Materials Application in Battery Thermal Management System: A Review. Materials 2020, 13, 4622. [Google Scholar] [CrossRef]
- Zabara, M.A.; Göçmez, H.; Karabatak, A.; Ulgut, B. Characterization of Different Electrolyte Composition Lithium Thionyl Chloride Reserve Battery by Electrochemical Impedance Spectroscopy. J. Electrochem. Soc. 2021, 168, 050529. [Google Scholar] [CrossRef]
- Ziesche, R.F.; Robinson, J.B.; Markötter, H.; Bradbury, R.; Tengattini, A.; Lenoir, N.; Helfen, L.; Kockelmann, W.; Kardjilov, N.; Manke, I.; et al. Editors’ Choice—4D Neutron and X-ray Tomography Studies of High Energy Density Primary Batteries: Part II. Multi-Modal Microscopy of LiSOCl2 Cells. J. Electrochem. Soc. 2020, 167, 140509. [Google Scholar] [CrossRef]
- Takata, K.; Osaka, R.; Matsushita, Y.; Nakanishi, T. In-situ imaging of Li-ion migration at interfaces in an all solid Li-ion battery. Surf. Interface Anal. 2020, 52, 1029–1033. [Google Scholar] [CrossRef]
- Xu, D.; Huang, G.; Guo, L.; Chen, Y.; Ding, C.; Liu, C. Enhancement of catalytic combustion and thermolysis for treating polyethylene plastic waste. Adv. Compos. Hybrid Mater. 2022, 5, 113–129. [Google Scholar] [CrossRef]
- Wang, D.; Jiang, J.; Pan, Z.; Li, Q.; Zhu, J.; Tian, L.; Shen, P.K. The Effects of Pore Size on Electrical Performance in Lithium-Thionyl Chloride Batteries. Front. Mater. 2019, 6, 245. [Google Scholar] [CrossRef]
- Ko, Y.-O.; Lee, C.-T. Effects of the structural characteristics of carbon cathode on the initial voltage delay in Li/SOCl2 battery. J. Ind. Eng. Chem. 2012, 18, 726–730. [Google Scholar] [CrossRef]
- Ui, K.; Yamamoto, K.; Ishikawa, K.; Minami, T.; Takeuchi, K.; Itagaki, M.; Watanabe, K.; Koura, N. Development of non-flammable lithium secondary battery with room-temperature ionic liquid electrolyte: Performance of electroplated Al film negative electrode. J. Power Source 2008, 183, 347–350. [Google Scholar] [CrossRef]
- Zabara, M.A.; Ulgut, B. Electrochemical Impedance Spectroscopy based voltage modeling of lithium Thionyl Chloride (Li\SOCl2) primary battery at arbitrary discharge. Electrochim. Acta 2019, 334, 135584. [Google Scholar] [CrossRef]
- Almessiere, M.; Slimani, Y.; Güngüneş, H.; Korkmaz, A.D.; Trukhanov, S.; Guner, S.; Alahmari, F.; Trukhanov, A.; Baykal, A. Correlation between chemical composition, electrical, magnetic and microwave properties in Dy-substituted Ni-Cu-Zn ferrites. Mater. Sci. Eng. B 2021, 270, 115202. [Google Scholar] [CrossRef]
- Zdorovets, M.V.; Kozlovskiy, A.L.; Shlimas, D.I.; Borgekov, D.B. Phase transformations in FeCo–Fe2CoO4/Co3O4-spinel nanostructures as a result of thermal annealing and their practical application. J. Mater. Sci. Mater. Electron. 2021, 32, 16694–16705. [Google Scholar] [CrossRef]
- Kozlovskiy, A.; Zdorovets, M. Effect of doping of Ce4+/3+ on optical, strength and shielding properties of (0.5−x)TeO2−0.25MoO-0.25Bi2O3−xCeO2 glasses. Mater. Chem. Phys. 2021, 263, 124444. [Google Scholar] [CrossRef]
- Almessiere, M.A.; Slimani, Y.; Algarou, N.A.; Vakhitov, M.G.; Klygach, D.S.; Baykal, A.; Zubar, T.I.; Trukhanov, S.V.; Trukhanov, A.V.; Attia, H.; et al. Tuning the Structure, Magnetic, and High Frequency Properties of Sc-Doped Sr0.5Ba0.5ScxFe12−xO19/NiFe2O4 Hard/Soft Nanocomposites. Adv. Electron. Mater. 2021, 8, 2101124. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, C.-Y. Cycle-Life Characterization of Automotive Lithium-Ion Batteries with LiNiO2 Cathode. J. Electrochem. Soc. 2009, 156, A527–A535. [Google Scholar] [CrossRef]
- Abraham, D.; Knuth, J.; Dees, D.; Bloom, I.; Christophersen, J. Performance degradation of high-power lithium-ion cells—Electrochemistry of harvested electrodes. J. Power Source 2007, 170, 465–475. [Google Scholar] [CrossRef]
- Kassem, M.; Bernard, J.; Revel, R.; Pélissier, S.; Duclaud, F.; Delacourt, C. Calendar aging of a graphite/LiFePO4 cell. J. Power Source 2012, 208, 296–305. [Google Scholar] [CrossRef]
- Choi, H.-S.; Seo, W.-S.; Choi, D.-K. Prediction of reliability on thermoelectric module through accelerated life test and Physics-of-failure. Electron. Mater. Lett. 2011, 7, 271–275. [Google Scholar] [CrossRef]
- Liu, C.; Huang, Q.; Zheng, K.; Qin, J.; Zhou, D.; Wang, J. Impact of Lithium Salts on the Combustion Characteristics of Electrolyte under Diverse Pressures. Energies 2020, 13, 5373. [Google Scholar] [CrossRef]
- Gu, W.; Sun, Z.; Wei, X.; Dai, H. A new method of accelerated life testing based on the Grey System Theory for a model-based lithium-ion battery life evaluation system. J. Power Source 2014, 267, 366–379. [Google Scholar] [CrossRef]
- Diao, W.; Saxena, S.; Pecht, M. Accelerated cycle life testing and capacity degradation modeling of LiCoO2-graphite cells. J. Power Source 2019, 435, 226830. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Source 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Omar, N.; Monem, M.A.; Firouz, Y.; Salminen, J.; Smekens, J.; Hegazy, O.; Gaulous, H.; Mulder, G.; Van Den Bossche, P.; Coosemans, T.; et al. Lithium iron phosphate based battery—Assessment of the aging parameters and development of cycle life model. Appl. Energy 2014, 113, 1575–1585. [Google Scholar] [CrossRef]
- Chiodo, E.; Lauria, D.; Andrenacci, N.; Pede, G. Accelerated life tests of complete lithium-ion battery systems for battery life statistics assessment. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 22–24 June 2016; pp. 1073–1078. [Google Scholar] [CrossRef]
- Ecker, M.; Gerschler, J.B.; Vogel, J.; Käbitz, S.; Hust, F.; Dechent, P.; Sauer, D.U. Development of a lifetime prediction model for lithium-ion batteries based on extended accelerated aging test data. J. Power Source 2012, 215, 248–257. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Ma, Z.; Jiang, Y. Lithium-ion battery aging mechanisms and life model under different charging stresses. J. Power Source 2017, 356, 103–114. [Google Scholar] [CrossRef]
- Ma, J.; Shang, P.; Zou, X.; Ma, N.; Ding, Y.; Sun, J.; Cheng, Y.; Tao, L.; Lu, C.; Su, Y.; et al. A hybrid transfer learning scheme for remaining useful life prediction and cycle life test optimization of different formulation Li-ion power batteries. Appl. Energy 2021, 282, 116167. [Google Scholar] [CrossRef]
- Liu, J.; Yue, M.; Wang, S.; Zhao, Y.; Zhang, J. A Review of Performance Attenuation and Mitigation Strategies of Lithium-Ion Batteries. Adv. Funct. Mater. 2022, 32, 2107769. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Liaw, B.Y. Synthesize battery degradation modes via a diagnostic and prognostic model. J. Power Source 2012, 219, 204–216. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Foley, A.M.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; Van Mierlo, J.; Hoster, H.E. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Z.; Grosu, R.; Deng, Z.; Hou, J.; Rong, Y.; Wu, R. An end-to-end neural network framework for state-of-health estimation and remaining useful life prediction of electric vehicle lithium batteries. Renew. Sustain. Energy Rev. 2022, 156, 111843. [Google Scholar] [CrossRef]
- Ma, G.; Zhang, Y.; Cheng, C.; Zhou, B.; Hu, P.; Yuan, Y. Remaining useful life prediction of lithium-ion batteries based on false nearest neighbors and a hybrid neural network. Appl. Energy 2019, 253, 113626. [Google Scholar] [CrossRef]
- Gao, N.; Abboud, A.W.; Mattei, G.S.; Li, Z.; Corrao, A.A.; Fang, C.; Liaw, B.; Meng, Y.S.; Khalifah, P.G.; Dufek, E.J.; et al. Fast Diagnosis of Failure Mechanisms and Lifetime Prediction of Li Metal Batteries. Small Methods 2020, 5, e2000807. [Google Scholar] [CrossRef] [PubMed]
- Cheng, S.; Li, B.; Yuan, Z.; Zhang, F.; Liu, J. Development of a lifetime prediction model for lithium thionyl chloride batteries based on an accelerated degradation test. Microelectron. Reliab. 2016, 65, 274–279. [Google Scholar] [CrossRef]
- Sun, T.; Xu, B.; Cui, Y.; Feng, X.; Han, X.; Zheng, Y. A sequential capacity estimation for the lithium-ion batteries combining incremental capacity curve and discrete Arrhenius fading model. J. Power Source 2020, 484, 229248. [Google Scholar] [CrossRef]
- Sun, T.; Wu, R.; Cui, Y.; Zheng, Y. Sequent extended Kalman filter capacity estimation method for lithium-ion batteries based on discrete battery aging model and support vector machine. J. Energy Storage 2021, 39, 102594. [Google Scholar] [CrossRef]
- Yang, N.; Fu, Y.; Yue, H.; Zheng, J.; Zhang, X.; Yang, C.; Wang, J. An improved semi-empirical model for thermal analysis of lithium-ion batteries. Electrochim. Acta 2019, 311, 8–20. [Google Scholar] [CrossRef]
- Bohlen, O.; Kowal, J.; Sauer, D.U. Ageing behaviour of electrochemical double layer capacitors: Part I. Experimental study and ageing model. J. Power Source 2007, 172, 468–475. [Google Scholar] [CrossRef]
- Qin, J.; Liu, C.; Huang, Q. Simulation on fire emergency evacuation in special subway station based on Pathfinder. Case Stud. Therm. Eng. 2020, 21, 100677. [Google Scholar] [CrossRef]
- Cheng, S.; Yuan, Z.; Ye, X.; Zhang, F.; Liu, J. Empirical prediction model for Li/SOCl2 cells based on the accelerated degradation test. Microelectron. Reliab. 2015, 55, 101–106. [Google Scholar] [CrossRef]
- Kozlovskiy, A.L.; Zdorovets, M.V. Synthesis, structural, strength and corrosion properties of thin films of the type CuX (X = Bi, Mg, Ni). J. Mater. Sci. Mater. Electron. 2019, 30, 11819–11832. [Google Scholar] [CrossRef]
- Zubar, T.I.; Usovich, T.I.; Tishkevich, D.I.; Kanafyev, O.D.; Fedkin, V.A.; Kotelnikova, A.N.; Panasyuk, M.I.; Kurochka, A.S.; Nuriev, A.V.; Idris, A.M.; et al. Features of Galvanostatic Electrodeposition of NiFe Films with Composition Gradient: Influence of Substrate Characteristics. Nanomaterials 2022, 12, 2926. [Google Scholar] [CrossRef]
- Adams, B.D.; Black, R.; Radtke, C.; Williams, Z.; Mehdi, B.L.; Browning, N.D.; Nazar, L.F. The Importance of Nanometric Passivating Films on Cathodes for Li–Air Batteries. ACS Nano 2014, 8, 12483–12493. [Google Scholar] [CrossRef]
- Mingant, R.; Bernard, J.; Moynot, V.S.; Delaille, A.; Mailley, S.; Hognon, J.-L.; Huet, F. EIS Measurements for Determining the SoC and SoH of Li-Ion Batteries. ECS Trans. 2011, 33, 41–53. [Google Scholar] [CrossRef]
- Zou, L.; He, Y.; Liu, Z.; Jia, H.; Zhu, J.; Zheng, J.; Wang, G.; Li, X.; Xiao, J.; Liu, J.; et al. Unlocking the passivation nature of the cathode–air interfacial reactions in lithium ion batteries. Nat. Commun. 2020, 11, 3204. [Google Scholar] [CrossRef] [PubMed]
- Ahad, S.A.; Bhattacharya, S.; Kilian, S.; Ottaviani, M.; Ryan, K.M.; Kennedy, T.; Thompson, D.; Geaney, H. Lithiophilic Nanowire Guided Li Deposition in Li Metal Batteries. Small 2022, 19, e2205142. [Google Scholar] [CrossRef] [PubMed]
- Li, N.-W.; Yin, Y.-X.; Li, J.-Y.; Zhang, C.-H.; Guo, Y.-G. Passivation of Lithium Metal Anode via Hybrid Ionic Liquid Electrolyte toward Stable Li Plating/Stripping. Adv. Sci. 2016, 4, 1600400. [Google Scholar] [CrossRef]
- Choi, S.; Jung, G.; Kim, J.E.; Kim, T.; Suh, K.S. Lithium Intercalated Graphite with Preformed Passivation Layer as Superior Anode for Lithium-Ion Batteries. Appl. Surf. Sci. 2018, 455, 367–372. [Google Scholar] [CrossRef]



| Battery Category | Analytical Test Method | Mathematical Model | Calculation and Experimental Error | Ref. |
|---|---|---|---|---|
| Li/SOCl2 and Li/MnO2 | Electrochemical impedance spectroscopy | Zero-free parameter method | 3% | [9] |
| Li/CoO2 | Accelerated cycle life test | Capacity-degradation model based on cycle number and environmental temperature stress factor | 2.6% | [20] |
| Li/SOCl2 | Accelerated cycle life test | Semi-empirical prediction model of residual capacity based on cycle number and environmental temperature stress factor | 5% | [40] |
| LiFePO4 | Non-destructive electrochemical test and electrochemical impedance spectroscopy | / | / | [19] |
| Li/SOCl2 | Accelerated cycle life test and electrochemical impedance spectroscopy | Semi-empirical prediction model of residual capacity based on cycle number and environmental temperature stress factor | 3.7896% | This work |
| Material. | Melting Point | Boiling Point |
|---|---|---|
| SOCl2 | −104.5 °C | 78.8 °C |
| Li | 180 °C | 1340 °C |
| LiAlCl4 | 143 °C | / |
| Acetylene black | 3550 °C | / |
| Polytetrafluoroethylene | 327 °C | 400 °C |
| Ethanol | −114° | 78 °C |
| Temperature/°C | Test Interval/Week |
|---|---|
| 25 | 4 |
| 45 | 2 |
| 56 | 1 |
| 74 | 1 |
| Temperature Stress/°C | Test Interval/Week |
|---|---|
| 25 (RT) | 6 |
| 40 | 4 |
| 50 60 | 2 1 |
| 70 | 1 |
| Parameter | R2 | Parameter | Fitted Value |
|---|---|---|---|
| ImZ | 0.9650 | CT | 1.27665 |
| Ca | 0.24885 | ||
| b | 0.73976 |
| Temperature Stress/°C | A | B | C |
|---|---|---|---|
| 74 °C | −2.30557 | 105.97761 | 0.6 |
| 56 °C | −1.14048 | 103.69369 | 0.6 |
| 25 °C | −0.40468 | 102.50312 | 0.6 |
| Parameter | Intercept b | Slope a |
|---|---|---|
| A(T) | 125.15992 | −6.82703 |
| B(T) | −12.94686 | 3.77341 |
| Accelerated Life Test Time/Week | Test Residual Capacity Percentage | Predicting Remaining Capacity Percentage | Deviation |
|---|---|---|---|
| 2 | 97.6599% | 98.8297% | 1.1979% |
| 4 | 96.9865% | 96.3173% | 0.6899% |
| 6 | 94.9131% | 94.9131% | 0.6632% |
| 8 | 94.3730% | 92.5093% | 1.9749% |
| 10 | 92.4995% | 90.9059% | 1.7229% |
| 12 | 90.8262% | 89.4267% | 1.5409% |
| 14 | 89.0860% | 88.0434% | 1.1703% |
| 16 | 89.0793% | 86.7373% | 2.6291% |
| 18 | 88.2059% | 85.4951% | 3.0733% |
| 20 | 86.7992% | 84.3070% | 2.8712% |
| 22 | 86.7244% | 83.1656% | 4.1036% |
| 24 | 85.3857% | 82.0650% | 3.8891% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Hou, X.; Wang, Y.; Chen, Y.; Xu, D.; Liu, C.; Huang, Q. Design and Validation of Lifetime Prediction Model for Lithium-Thiocarbonyl Chloride Batteries Based on Accelerated Aging Experiments. Metals 2023, 13, 1579. https://doi.org/10.3390/met13091579
Wang S, Hou X, Wang Y, Chen Y, Xu D, Liu C, Huang Q. Design and Validation of Lifetime Prediction Model for Lithium-Thiocarbonyl Chloride Batteries Based on Accelerated Aging Experiments. Metals. 2023; 13(9):1579. https://doi.org/10.3390/met13091579
Chicago/Turabian StyleWang, Silong, Xiaoyu Hou, Yuhao Wang, Yanjun Chen, Dengji Xu, Changcheng Liu, and Que Huang. 2023. "Design and Validation of Lifetime Prediction Model for Lithium-Thiocarbonyl Chloride Batteries Based on Accelerated Aging Experiments" Metals 13, no. 9: 1579. https://doi.org/10.3390/met13091579
APA StyleWang, S., Hou, X., Wang, Y., Chen, Y., Xu, D., Liu, C., & Huang, Q. (2023). Design and Validation of Lifetime Prediction Model for Lithium-Thiocarbonyl Chloride Batteries Based on Accelerated Aging Experiments. Metals, 13(9), 1579. https://doi.org/10.3390/met13091579