Study on the Tensile and Fatigue Properties of the FH36 Ship Steel Plates at Room and Low Temperatures
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
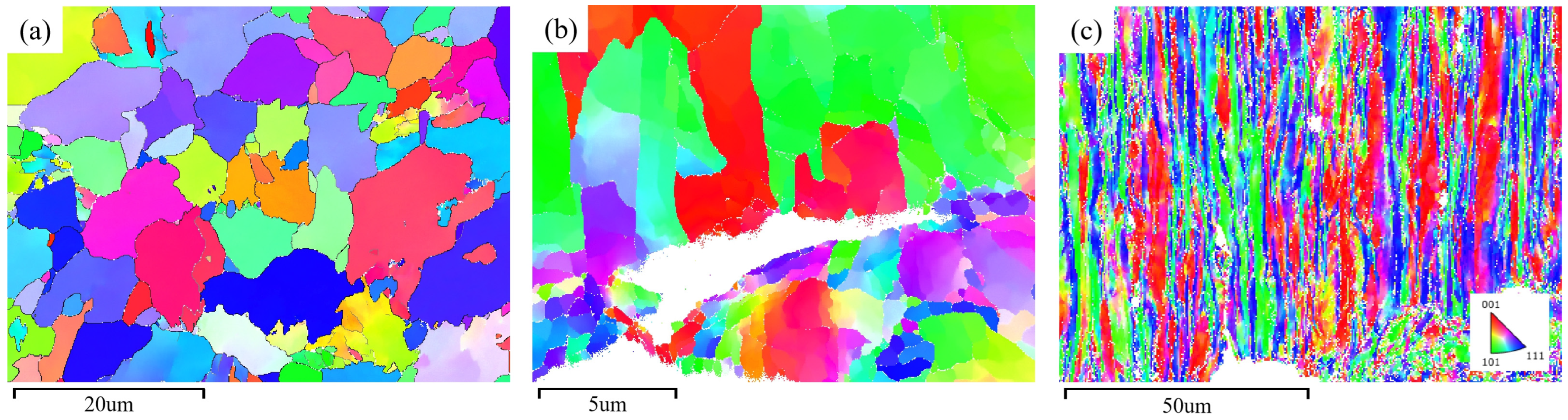
3.1. Observation of the Microstructure
3.2. Analysis of the Tensile Property Test Results and Morphological Observations
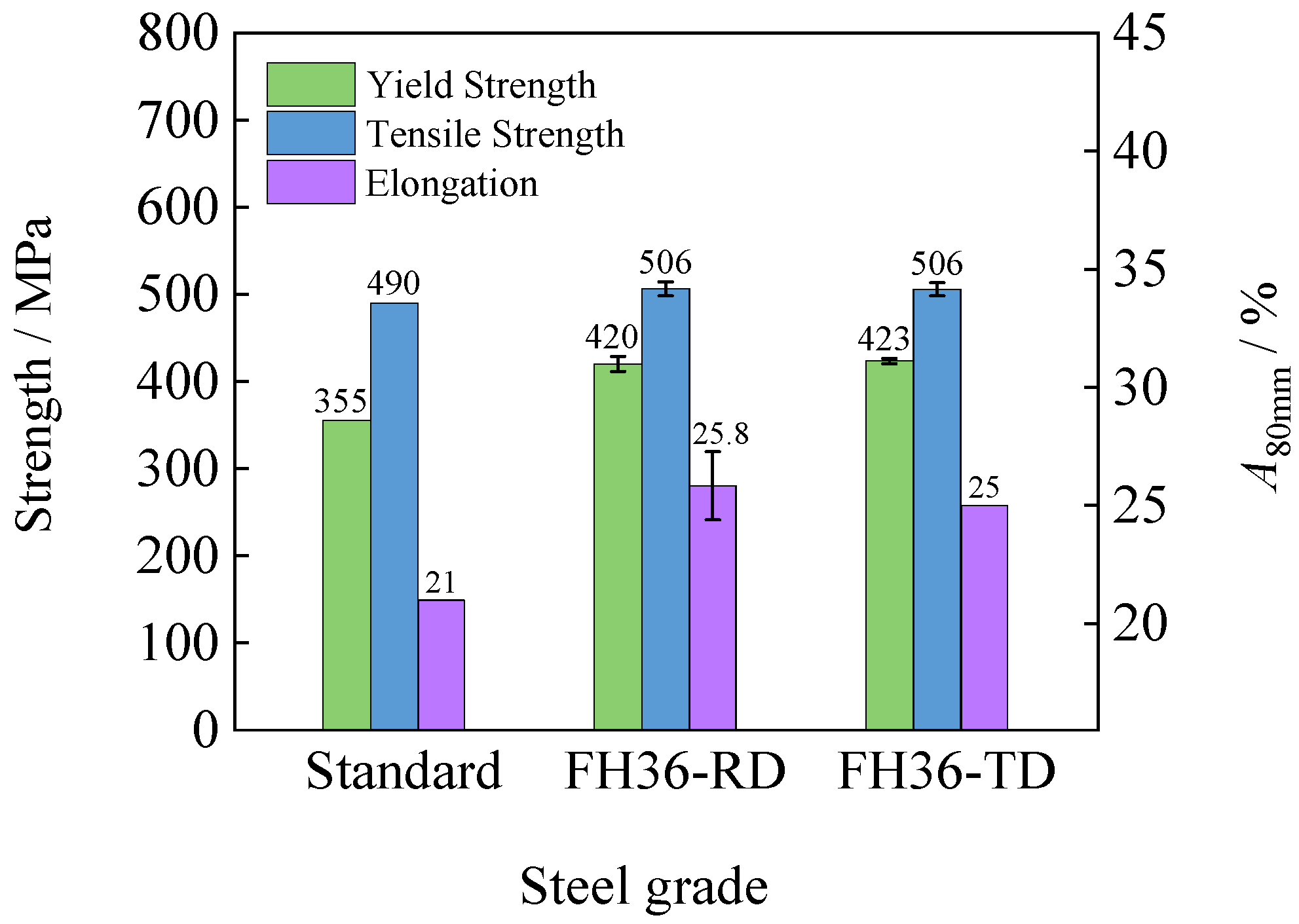
3.2.1. Analysis of the Tensile Property Test Results
3.2.2. Tensile Test Fracture Surface Observation
3.3. Fatigue Test Results and Analysis at Room Temperature
3.3.1. Fatigue Test Results at Room Temperature
3.3.2. Fatigue Test Fracture Morphology Observation and Analysis
3.3.3. Analysis of Grain Boundaries in Fatigue Fracture at Room Temperature
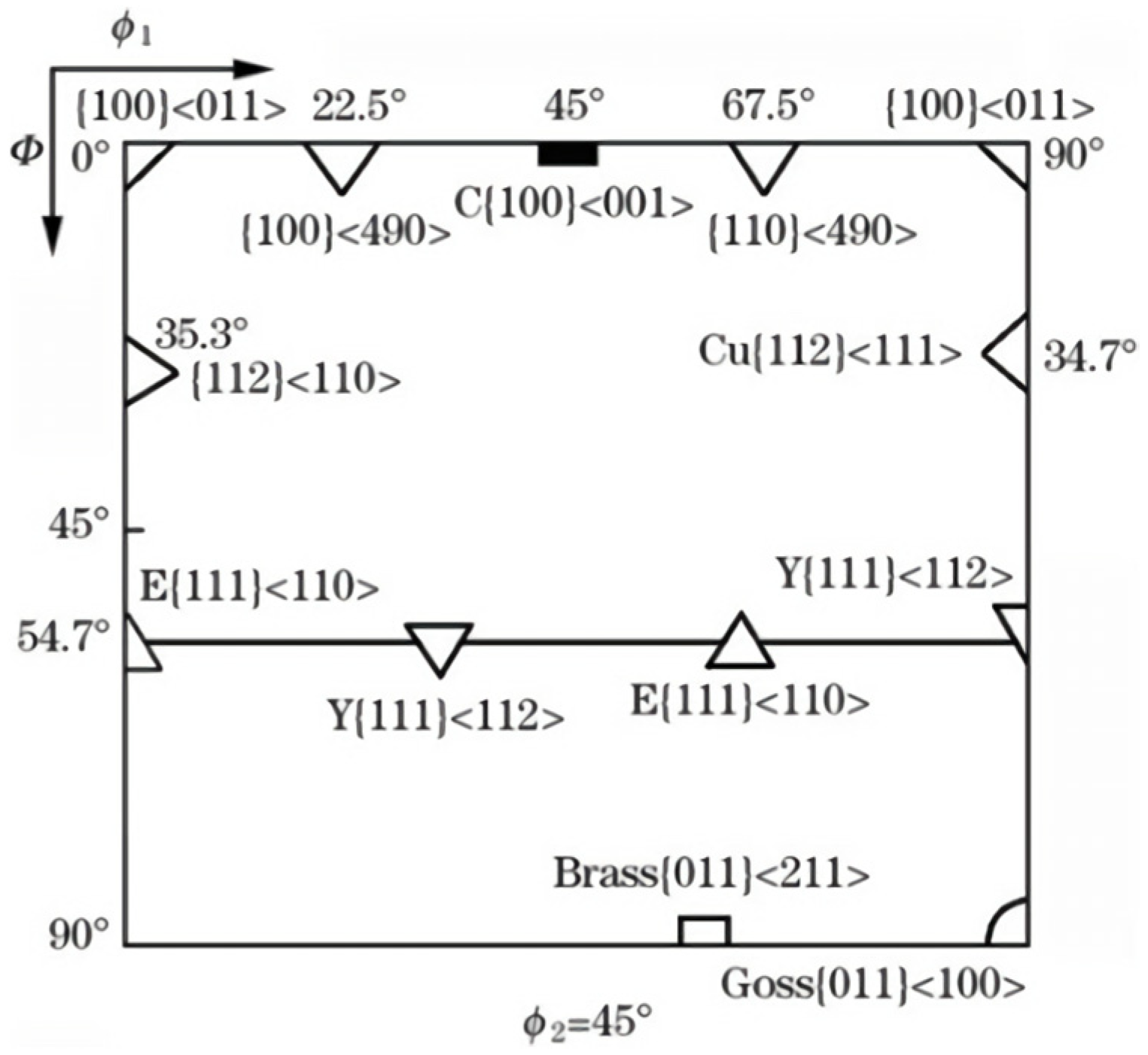
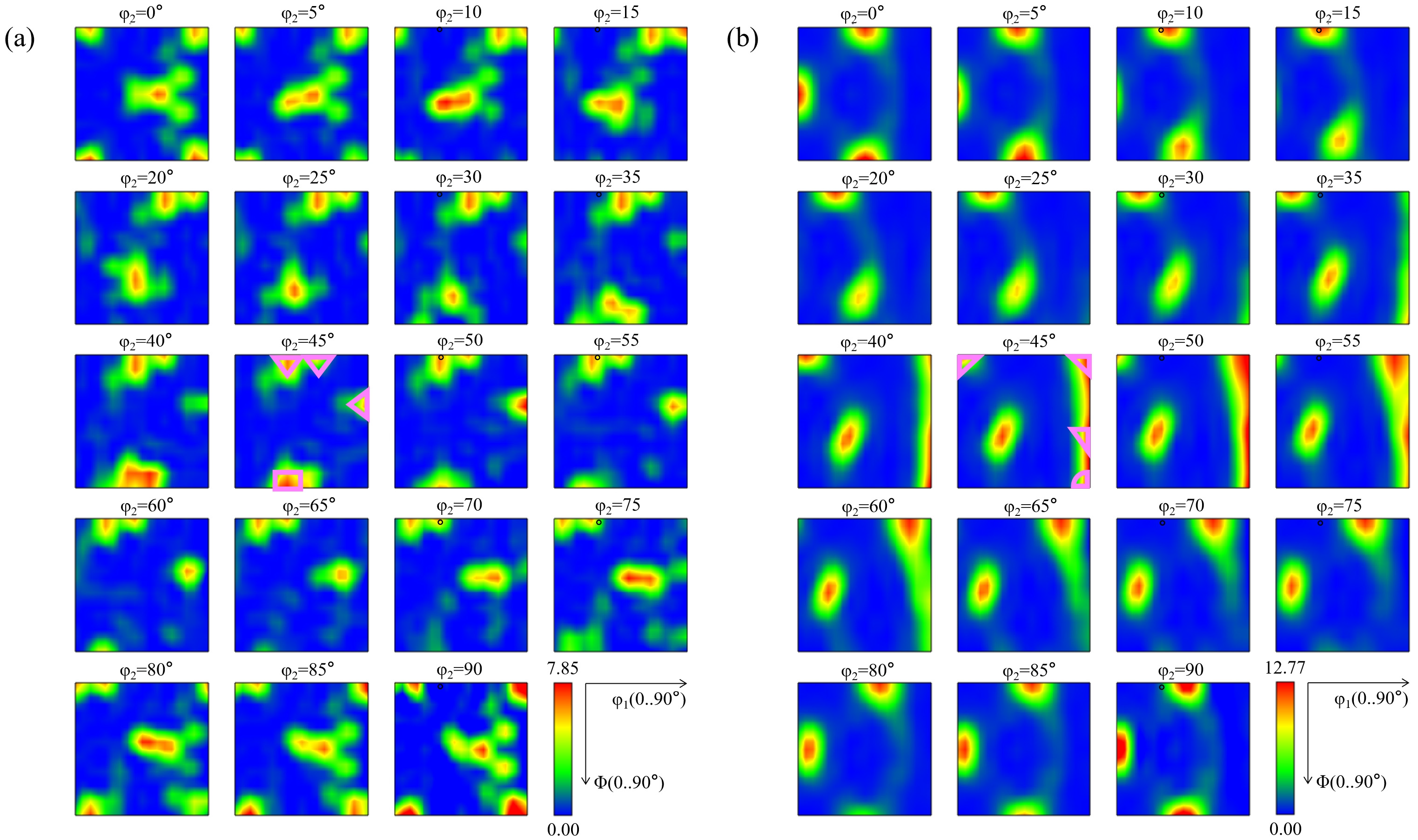
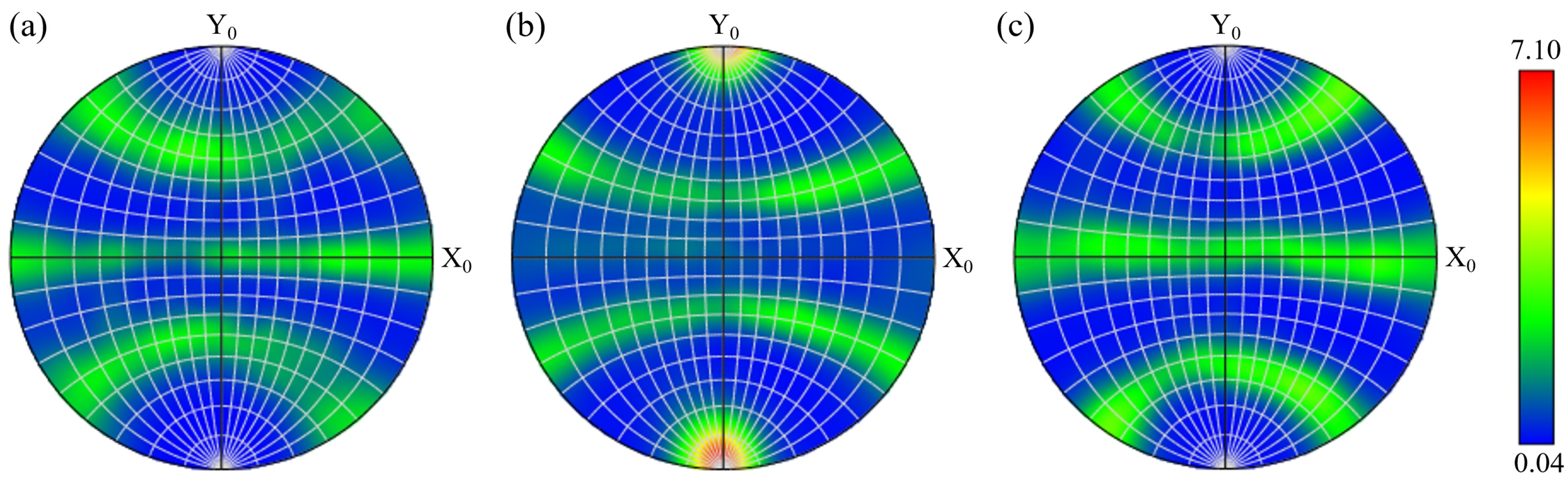
3.3.4. Texture and Orientation Difference Analysis of Fatigue Fracture at Room Temperature
3.4. Low-Temperature Fatigue Test Results and Analysis
3.4.1. Low-Temperature Fatigue Test Results
3.4.2. Observation of Fracture Surface in Low-Temperature Fatigue Tests
4. Conclusions
- By adopting the process of first rolling in the RD and then rolling in the TD, the differing properties of the steel plate in the RD and TD were effectively eliminated, resulting in almost identical tensile properties in the RD and TD at a thickness of 1/4 of the rolled plate. The yield and tensile strength of the steel plate were approximately 420 MPa and 506 MPa, respectively, and the elongation was approximately 25%.
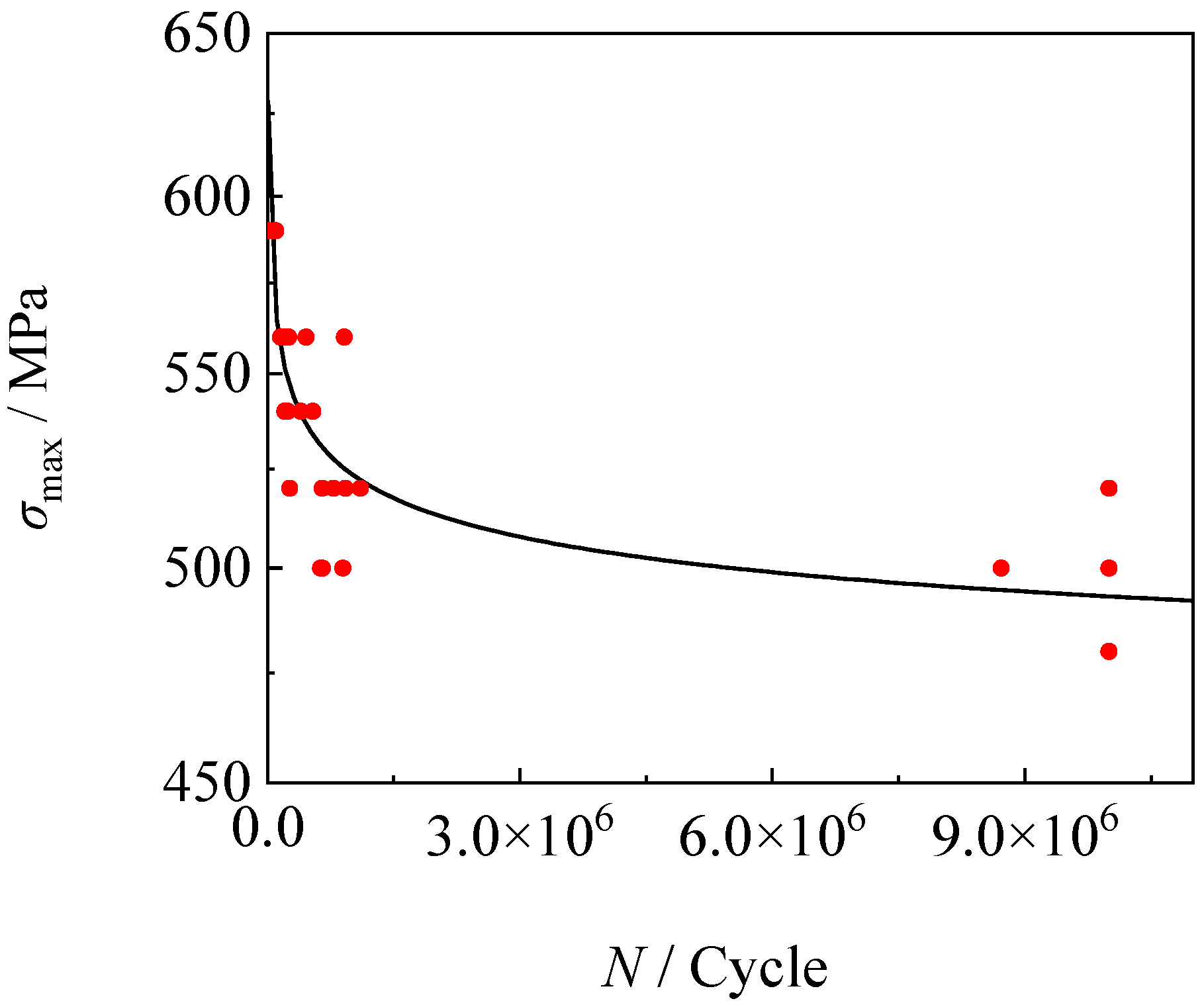
- The fatigue limit of the steel plate at room temperature was 488 MPa. When the maximum stress was below 500 MPa and above 520 MPa, the specimens failed under high-cycle and low-cycle fatigue, respectively. The high-cycle fatigue fracture exhibited an oblique shear fracture, while the low-cycle fatigue fracture was a cup-cone shape, and the CIZs were both on the surface of the specimens. As the maximum stress increased, the area of the CPZ for high-cycle fatigue decreased, while the area of the FFZ increased, and the number of dimples in the FFZ increased. The proportion of the LAGBs in the fracture surfaces of the high- and low-cycle fatigue specimens had significantly increased.
- The fatigue limit of the steel plate at −60 °C reached 500 MPa, which was higher than the fatigue limit at room temperature, indicating that its low temperature fatigue performance was better than that at room temperature. This was related to the increase in the yield strength as the temperature decreased, which subsequently led to an increase in the resistance to crack propagation. The specimens showed high-cycle and low-cycle fatigue failure when the maximum stress was below 560 MPa and above 590 MPa, respectively. The fatigue cracks were prone to initiate on the surface defects of the specimen, such as the machining scratches under high stress conditions. The surface of the high-cycle fatigue fracture was flat, and the CIZs were all located on the surface of the specimen. As the applied maximum stress increased, the boundary between the CPZ and the FFZ became less distinct, and the number of dimples in the FFZ increased. The low-cycle fatigue fracture surface exhibited significant plastic deformation and multiple CIZs.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Full Meaning |
| BOF | Basic oxygen furnace |
| CTOD | Crack tip opening isplacement |
| TMCP | Thermo-mechanical control process |
| SEM | Scanning electron microscope |
| RD | Rolling direction |
| TD | Transverse direction |
| ND | Normal direction |
| OM | Optical microscope |
| AF | Acicular ferrite |
| PF | Polygonal ferrite |
| GB | Granular bainite |
| CIZ | Crack initiation zone |
| CPZ | Crack propagation zone |
| FFZ | Fast fracture zone |
| IPF | Inverse pole figure |
| LAGBs | Low-angle grain boundaries |
| KAM | Kernel average misorientation |
| ODF | Orientation distribution function |
References
- Wang, K.; Wu, L.; Li, Y.; Qin, C. Experimental study on low temperature fatigue performance of polar icebreaking ship steel. Ocean Eng. 2020, 216, 107789. [Google Scholar] [CrossRef]
- Qin, C. Study on Low Temperature Fatigue Performance of Steel Used in Polar Icebreaker. Master’s Thesis, Jiangsu University of Science and Technology, Zhenjiang, China, 2020. [Google Scholar]
- Wang, D.; Zhang, P.; Peng, X.; Yan, L.; Li, G. Comparison of microstructure and mechanical properties of high strength and toughness ship plate steel Materials. Materials 2021, 14, 5886. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.; Yan, R.; Yao, G.; Dong, Q. Theoretical and Experimental Study on CTOD for Notch Plate Under Low Cycle Fatigue. J. Ship Mech. 2017, 21, 1128–1135. [Google Scholar]
- Wang, S.; Peng, X.; Zhang, P. Analysis of fatigue resistance of fh36 shipbuilding steel plate. Foundry Technol. 2022, 43, 531–536. [Google Scholar]
- Le, J.; Tu, W.; Xie, H.; Yang, K.; Tang, W. Simulation and experimental study on fatigue crack propagation of marine high-strength steel under variable amplitude loading. In Proceedings of the 2019 Conference on Ship Structural Mechanics, Wuhan, China, 22 August 2019. [Google Scholar]
- Jiang, F.; Liu, R. Low cycle fatigue behavior of marine steel 945. Appl. Sci. Technol. 1995, 3, 1–5. [Google Scholar]
- Li, Z.; Sun, J.; Hu, X.; Zheng, F.; Zhang, H. Gigacycle fatigue of high strength steel 65 Mn. Appl. Sci. Technol. 2007, 54–56. [Google Scholar]
- Wang, Y.; Feng, G.; Ren, H. Experiment of influence of specimen thickness on fatigue crack propagation rate of ship hull steel. Ship Eng. 2019, 41, 98–104. [Google Scholar]
- Wang, T. Modern Science of Rolling Steel; Metallurgical Industry Press: Beijing, China, 2014; p. 190. [Google Scholar]
- GB/T 228.1-2010; Metallic Materials-Tensile Testing-Part 1: Method of Test at Room Temperature. China Standard Press: Beijing, China, 2011.
- GB/T 3075-2008; Metallic Materials: Fatigue Testing: Axial-Force-Controlled Method. China Standard Press: Beijing, China, 2008.
- Gao, Z.; Xiong, J. Fatigue Reliability; Beihang University Press: Beijing, China, 2013; pp. 138–139. [Google Scholar]
- Yao, W. Fatigue Life Prediction of Structures; National Defense Industry Press: Beijing, China, 2003; pp. 50–54. [Google Scholar]
- Zhang, J. Effects of Aging Process on Microstructure and Fatigue Properties of 7N01 Aluminum Alloy. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2020. [Google Scholar]
- Li, W.; Lu, L. Research on Ultra-Long Life Duplex S-N Curve Model. China Railw. Sci. 2008, 3, 101–105. [Google Scholar]
- Little, R.E.; Jebe, E.H. Statistical Design of Fatigue Experiments; Applied Science Publishers LTD: London, UK, 1975; pp. 61–80. [Google Scholar]
- Ling, J.; Gao, Z. Maximum Likelihood Method for Measuring P-S-M curve. Acta Aeronaut. Astronaut. Sin. 1992, 5, 247–252. [Google Scholar]
- Zheng, R.; Qin, Z. Grey Method for Fitting S-N Curve. J. Natl. Univ. Def. Technol. 1989, 3, 84–88. [Google Scholar]
- Xie, J.; Yao, W. Double Weighted Least Square Method for Fatigue S-N Curve Fitting. J. Astronaut. 2010, 31, 1661–1665. [Google Scholar]
- Gao, Z.; Fu, H.; Liang, M. A Method For Fitting S-N Curve. J. Beijing Univ. Aeronaut. Astronaut. 1987, 115–119. [Google Scholar]
- Zhou, C.; Yan, L.; Zhang, P.; Zhu, L. Microstructure and Mechanical Properties of EH47 High Strength Brittle Crack Arrest Steel for Container Ship. Trans. Mater. Heat Treat. 2017, 38, 83–87. [Google Scholar]
- GB/T 712-2011; Ship and Ocean Engineering Structural Steel. China Standard Press: Beijing, China, 2011.
- Zhang, J.; Huo, F.; Gao, Y. Production Training of Medium Plates; Metallurgical Industry Press: Beijing, China, 2013; p. 48. [Google Scholar]
- Xu, B. Surface Engineering and Maintenance; China Machine Press: Beijing, China, 1996; p. 148. [Google Scholar]
- Wang, J. Principles and Experiments of Mechanical Properties of Materials; Tianjin University Press: Tianjin, China, 2018; p. 49. [Google Scholar]
- Li, J.; Wei, C.; Zhang, W.; Li, P. Analysis of Inclusions in Steel and Properties and Fracture of Steel; Metallurgical Industry Press: Beijing, China, 2012; p. 64. [Google Scholar]
- Luo, D. Study on Mechanism of Yttrium-Based Rare Earth on Inclusions Behavior and Microstructure and Properties of EH36 Shipbuilding Steel. Ph.D. Thesis, Jiangxi University of Science and Technology, Ganzhou, China, 30 May 2022. [Google Scholar]
- Ma, C. Chemical Analysis of Metallic Materials; Popular Science Press: Beijing, China, 2015; p. 244. [Google Scholar]
- Wang, D.; Li, G.; Yin, W.; Yan, L.; Wang, Z.; Zhang, P.; Hu, X.; Li, B.; Zhang, W. Studying on Alloying Elements, Phases, Microstructure and Texture in FH36 Ship Plate Steel. Materials 2023, 16, 4762. [Google Scholar] [CrossRef] [PubMed]
- Wu, R.; Wu, Z. Steel Quality and Failure Analysis of Its Components; Beihang University Press: Beijing, China, 2018; pp. 143–160. [Google Scholar]
- Wang, D. The Analysis of Breakage on 851 Blade of 300 MW Steam Turbine. Shandong Electric. Power 1996, 02, 68–70. [Google Scholar]
- Bai, R.; Cai, G.; Zhang, X.; Chen, W.; Jiang, Y. Numerical simulation analysis of asymmetric fatigue failure for iced electric power transmission line. Chin. J. Mater. Study 2016, 30, 149–155. [Google Scholar]
- Liu, X.; Tao, C.; Feng, Y.; Liang, J.; Wang, Y. Prediction of Damage Behavior and Life of Powder High-Temperature Alloys; Aviation Industry Press: Beijing, China, 2018; p. 26. [Google Scholar]
- Encyclopedia of China Publishing House Editorial Office. Encyclopedia of China Concise Edition; Encyclopedia of China Publishing House: Beijing, China, 1998; p. 3729. [Google Scholar]
- Yang, R.; Yang, F. Failure Analysis and Material Selection; Shanghai Jiaotong University Press: Shanghai, China, 2014; p. 46. [Google Scholar]
- Xu, P. Design Principles and Applications of Removable Partial Dentures and Complete Dentures; Peking University Health Science Center and Peking Union Medical College Associated Press: Beijing, China, 2000; p. 150. [Google Scholar]
- Xia, H. Automobile Mechanical Maintenance Skills Training Course; National Defense Industry Press: Beijing, China, 2006; p. 132. [Google Scholar]
- Sha, G. Mechanical Properties of Materials; Beijing Institute of Technology Press: Beijing, China, 2015; p. 103. [Google Scholar]
- Wu, Y. Fracture and Fatigue; China University of Geosciences Press: Wuhan, China, 2008; p. 120. [Google Scholar]
- Chen, L. Very High Cycle Fatigue and Fracture; National Defense Industry Press: Beijing, China, 2017; p. 79. [Google Scholar]
- Nishijima, S.; Kanazawa, K. Stepwise S-N curve and fish -eye failure in gigacycle fatigue. Fatigue Fract. Eng. Mater. 1999, 22, 601–607. [Google Scholar] [CrossRef]
- Sun, J.; Wang, S.; Liu, P.; Wang, J.; Xiao, C.; Sun, Z.; Yu, Z. Investigation of Fatigue S-N Curves On 400 MPa Fine-Grained high Strength Rebar. Ind. Constr. 2014, 44, 951–953. [Google Scholar]
- Yin, H.; Wu, Y.; Zhang, G.; Li, X.; Zhang, P.; Zhang, H.; Li, W. Effect of low temperature on fatigue properties of EA4T axle steel. China Railw. Sci. 2021, 42, 123–129. [Google Scholar]
- Zhao, S.; Wang, Z. Fatigue Design; China Machine Press: Beijing, China, 1992; p. 189. [Google Scholar]
- Li, D.; Yang, M.; Cao, J.; Zhou, X.; Jia, Y. Analysis of microstructure and fatigue performance of carburizing bearing steel. Trans. Mater. Heat Treat. 2014, 35, 137–141. [Google Scholar]
- Wang, S.; Han, J.; Zeng, W.; Zhang, X.; Zhao, J.; Dai, G. Effect of low temperature on mechanical properties of ER8 steel for wheel rim. Chin. J. Mater. Study 2018, 32, 401–408. [Google Scholar]
- Fu, C.; Dong, W.; Wu, J.; Zhu, L. Inspection Defect Analysis of Class B Ship Plate produced in TISC. Tianjin Metall. 2019, S1, 37–40. [Google Scholar]
- Liu, X. Study on Precipitation Behavior of MnS Inclusions in Steel. Master’s Thesis, Northeastern University, Shenyang, China, 25 June 2012. [Google Scholar]
- Yang, J.; Yu, H.; Gao, J. Effects of Ce on the Microstructure and Mechanical Properties of A36 Ship Plate Steel. Chin. Rare Earths 2015, 36, 43–48. [Google Scholar]
- Zhang, L. Non-Metallic Inclusions in Steel Industrial Practice; Metallurgical Industry Press: Beijing, China, 2019; p. 154. [Google Scholar]
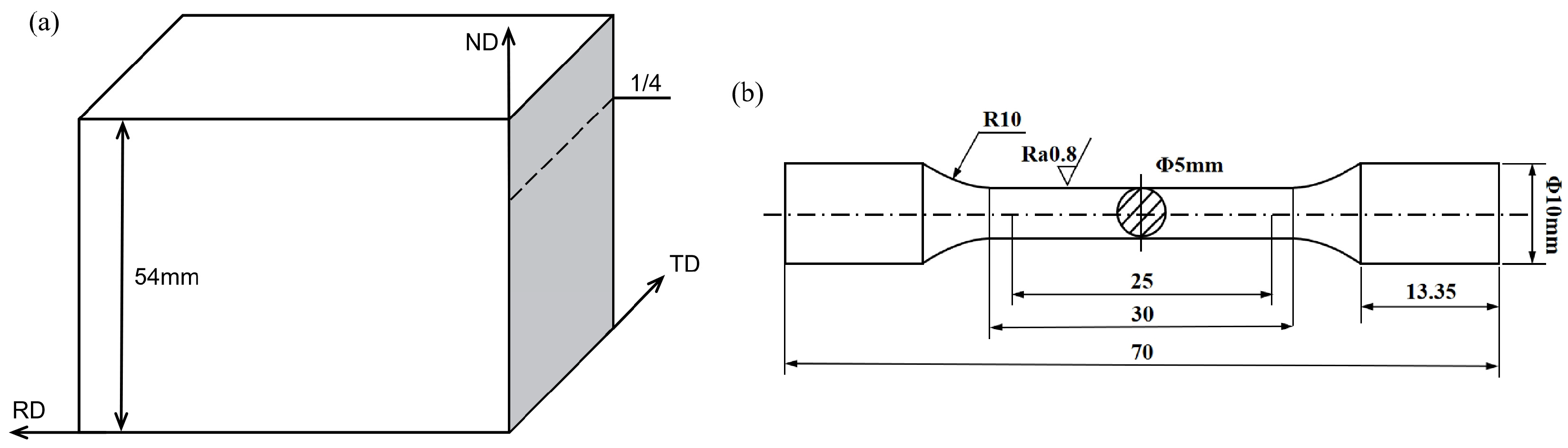
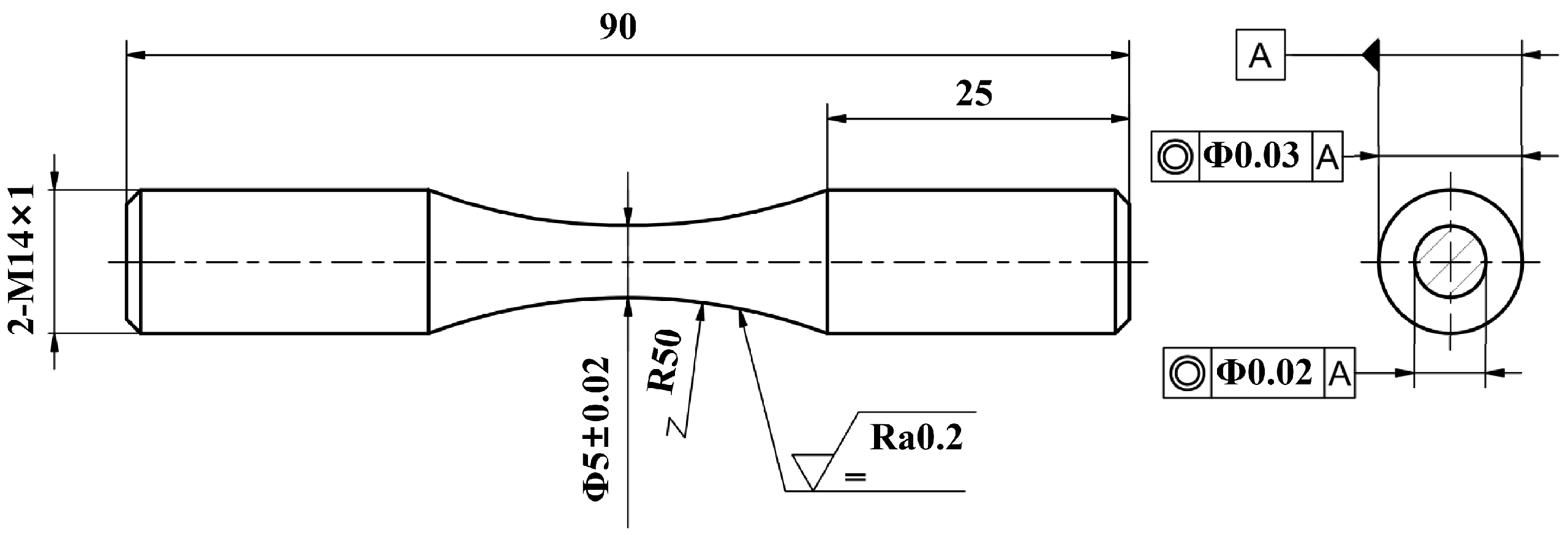















| Chemical Composition | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | Si | Mn | S | P | Nb | V | Ti | Als | Cu | Cr | Ni | Fe |
| 0.08 | 0.17 | 1.42 | 0.002 | 0.012 | 0.03 | 0.040 | 0.013 | 0.030 | 0.10 | 0.16 | 0.35 | Bal. |
| First-Stage Rolling Temperature | Second-Stage Rolling Temperature | Final Rolling Temperature | Water Inlet Temperature | Self-Tempering Temperature |
|---|---|---|---|---|
| 1050 | 820 | 790 | 760 | 500 |
| Chemical Composition | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| C | O | Al | Si | S | Ca | Ti | Mn | Fe | Nb | Ni | Cu |
| 5.30 | 28.35 | 23.04 | 0.83 | 2.40 | 21.77 | 1.96 | 0.33 | 15.53 | 0.45 | 0.02 | 0.03 |
| Specimen No. | Maximum Stress/MPa | Cycles/N | Result |
|---|---|---|---|
| RT1 | 500 | 10,000,000 | Pass |
| RT2 | 520 | 23,695 | Failure |
| RT3 | 500 | 10,000,000 | Pass |
| RT4 | 520 | 23,659 | Failure |
| RT5 | 500 | 292,586 | Failure |
| RT6 | 480 | 4,787,073 | Failure |
| RT7 | 460 | 10,000,000 | Pass |
| RT8 | 480 | 3,388,534 | Failure |
| RT9 | 460 | 10,000,000 | Pass |
| RT10 | 480 | 10,000,000 | Pass |
| RT11 | 500 | 167,802 | Failure |
| RT12 | 480 | 537,316 | Failure |
| RT13 | 460 | 10,000,000 | Pass |
| Temperature | Maximum Stress/MPa | |||
|---|---|---|---|---|
| 460 | 480 | 500 | 520 | |
| 20 °C | High-cycle fatigue | High-cycle fatigue | High-cycle fatigue | Low-cycle fatigue |
| Specimen No. | Maximum Stress/MPa | Cycles/N | Result |
|---|---|---|---|
| LT1 | 480 | 10,000,000 | Pass |
| LT2 | 480 | 10,000,000 | Pass |
| LT3 | 480 | 10,000,000 | Pass |
| LT4 | 500 | 8,718,127 | Failure |
| LT5 | 500 | 10,000,000 | Pass |
| LT6 | 500 | 10,000,000 | Pass |
| LT7 | 500 | 897,629 | Failure |
| LT8 | 500 | 634,092 | Failure |
| LT9 | 500 | 10,000,000 | Pass |
| LT10 | 500 | 654,200 | Failure |
| LT11 | 520 | 928,427 | Failure |
| LT12 | 520 | 10,000,000 | Pass |
| LT13 | 520 | 1,105,590 | Failure |
| LT14 | 520 | 785,297 | Failure |
| LT15 | 520 | 651,789 | Failure |
| LT16 | 520 | 266,784 | Failure |
| LT17 | 540 | 540,968 | Failure |
| LT18 | 540 | 227,497 | Failure |
| LT19 | 540 | 399,912 | Failure |
| LT20 | 540 | 242,145 | Failure |
| LT21 | 540 | 208,273 | Failure |
| LT22 | 560 | 914,834 | Failure |
| LT23 | 560 | 218,731 | Failure |
| LT24 | 560 | 460,801 | Failure |
| LT25 | 560 | 157,670 | Failure |
| LT26 | 560 | 254,022 | Failure |
| LT27 | 590 | 92,206 | Failure |
| LT28 | 590 | 21,273 | Failure |
| LT29 | 590 | 17,219 | Failure |
| LT30 | 590 | 99,197 | Failure |
| Temperature | Maximum Stress/MPa | |||||
|---|---|---|---|---|---|---|
| 480 | 500 | 520 | 540 | 560 | 590 | |
| −60 °C | High-cycle fatigue | High-cycle fatigue | High-cycle fatigue | High-cycle fatigue | High-cycle fatigue | Low-cycle fatigue |
| Position | Chemical Composition | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fe | C | O | Ti | S | Ca | Si | K | Cl | Al | Mg | Mn | |
| 1 | 4.18 | 70.57 | 21.13 | 0.29 | 1.15 | 0.35 | 0.88 | 0.45 | 0.72 | 0.27 | - | - |
| 2 | 1.32 | 64.44 | 29.88 | 0.33 | 0.78 | 0.72 | 0.56 | 0.28 | 1.70 | - | - | - |
| 3 | 5.74 | 72.68 | 16.52 | 0.24 | 1.24 | 0.39 | 0.80 | 0.73 | 1.66 | - | - | - |
| 4 | 4.51 | 16.24 | 53.16 | 0.11 | - | - | 22.02 | 1.17 | - | 2.79 | - | - |
| 5 | 3.71 | 18.41 | 38.61 | 0.58 | 0.33 | 10.02 | - | - | - | 27.27 | 0.77 | 0.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Yan, L.; Yin, W.; Zhang, P.; Wang, Z.; Li, G.; Hu, X.; Li, B.; Zhang, W.; Zhu, J. Study on the Tensile and Fatigue Properties of the FH36 Ship Steel Plates at Room and Low Temperatures. Metals 2023, 13, 1563. https://doi.org/10.3390/met13091563
Wang D, Yan L, Yin W, Zhang P, Wang Z, Li G, Hu X, Li B, Zhang W, Zhu J. Study on the Tensile and Fatigue Properties of the FH36 Ship Steel Plates at Room and Low Temperatures. Metals. 2023; 13(9):1563. https://doi.org/10.3390/met13091563
Chicago/Turabian StyleWang, Dong, Ling Yan, Wei Yin, Peng Zhang, Zhenmin Wang, Guanglong Li, Xiaodong Hu, Boyong Li, Wanshun Zhang, and Jing Zhu. 2023. "Study on the Tensile and Fatigue Properties of the FH36 Ship Steel Plates at Room and Low Temperatures" Metals 13, no. 9: 1563. https://doi.org/10.3390/met13091563
APA StyleWang, D., Yan, L., Yin, W., Zhang, P., Wang, Z., Li, G., Hu, X., Li, B., Zhang, W., & Zhu, J. (2023). Study on the Tensile and Fatigue Properties of the FH36 Ship Steel Plates at Room and Low Temperatures. Metals, 13(9), 1563. https://doi.org/10.3390/met13091563






