Ratcheting–Fatigue Damage Assessment of Additively Manufactured SS304L and AlSi10Mg Samples under Asymmetric Stress Cycles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fatigue Damage Assessment
2.2. Ratcheting Damage Assessment
2.2.1. Isotropic Hardening Description
2.2.2. Ahmadzadeh–Varvani (A–V) Kinematic Hardening Rule
2.2.3. Chaboche Hardening Rule
2.3. Fatigue–Ratcheting Interaction
3. Results and Discussion
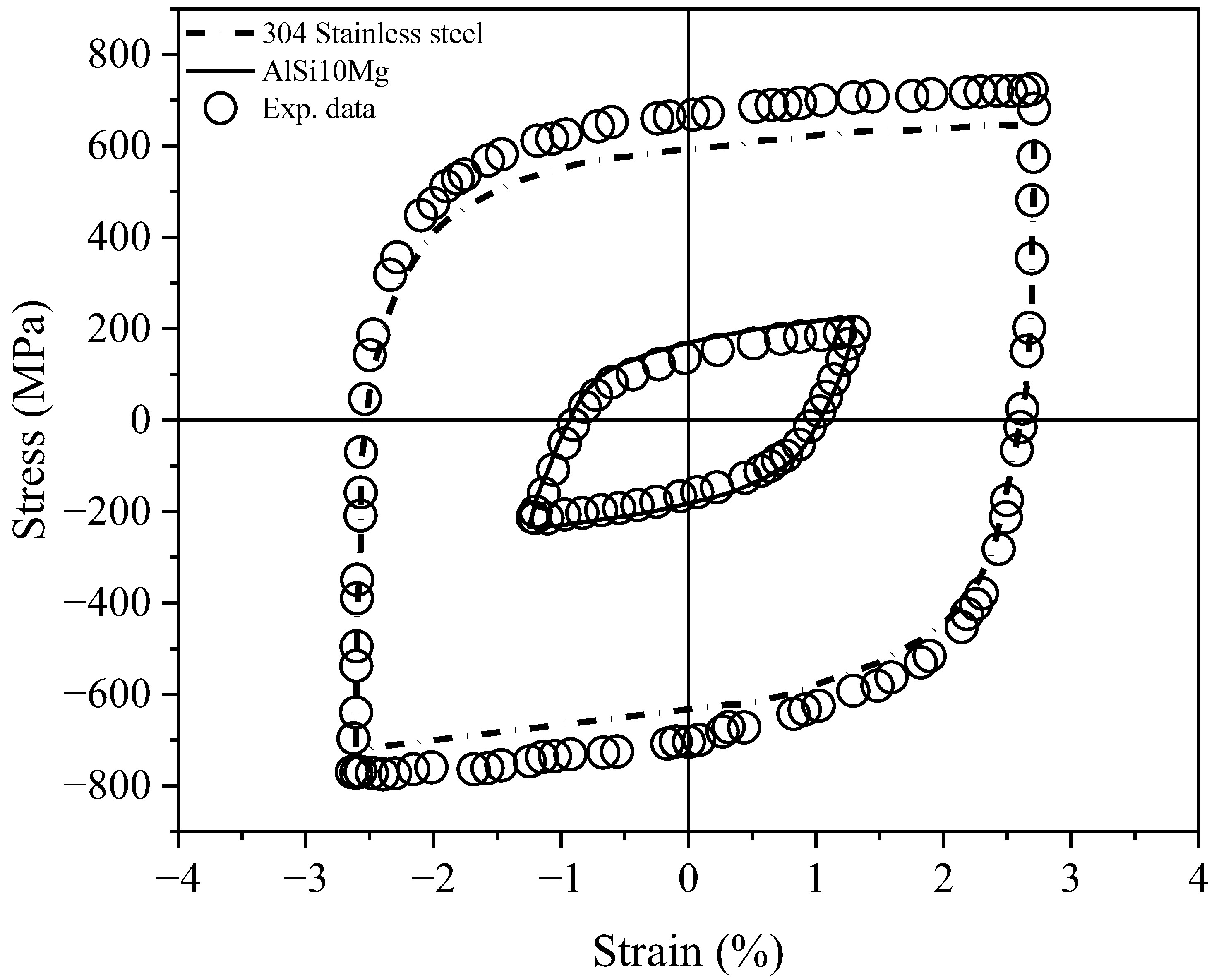
3.1. Materials, Tests, and Ratcheting Data
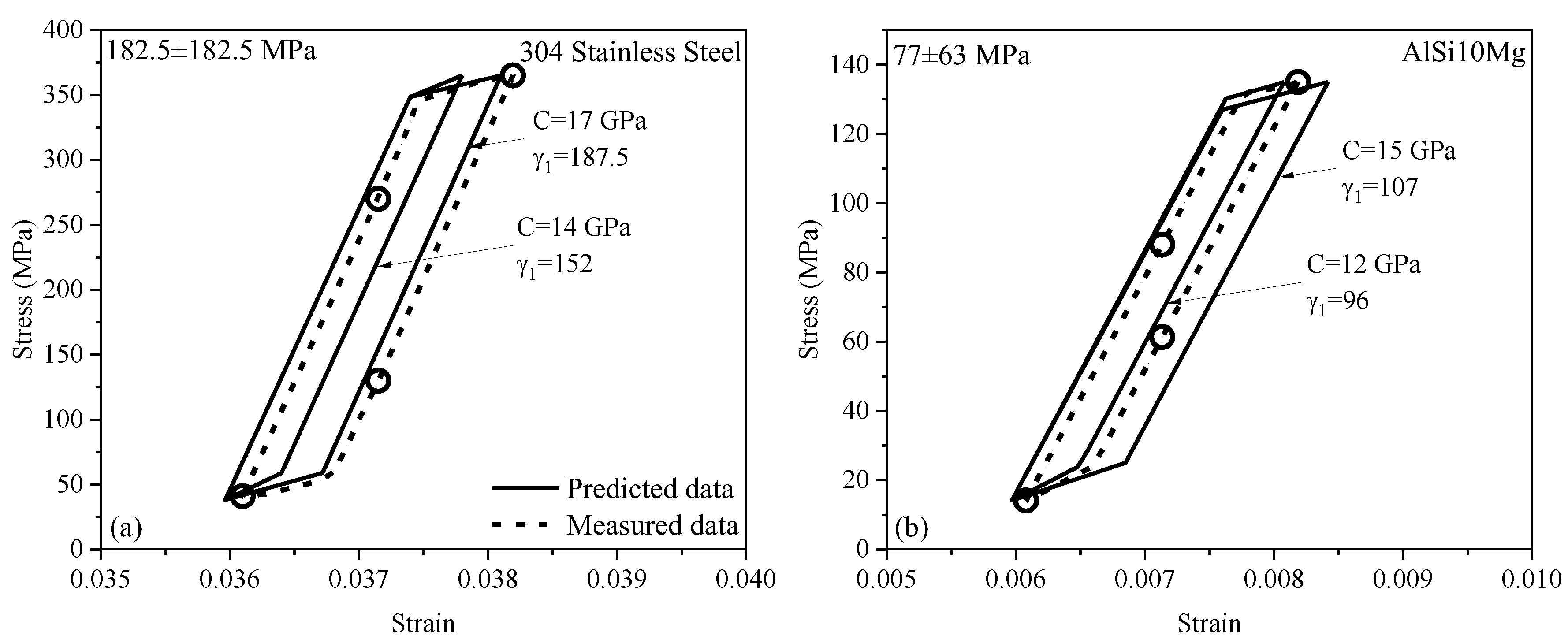
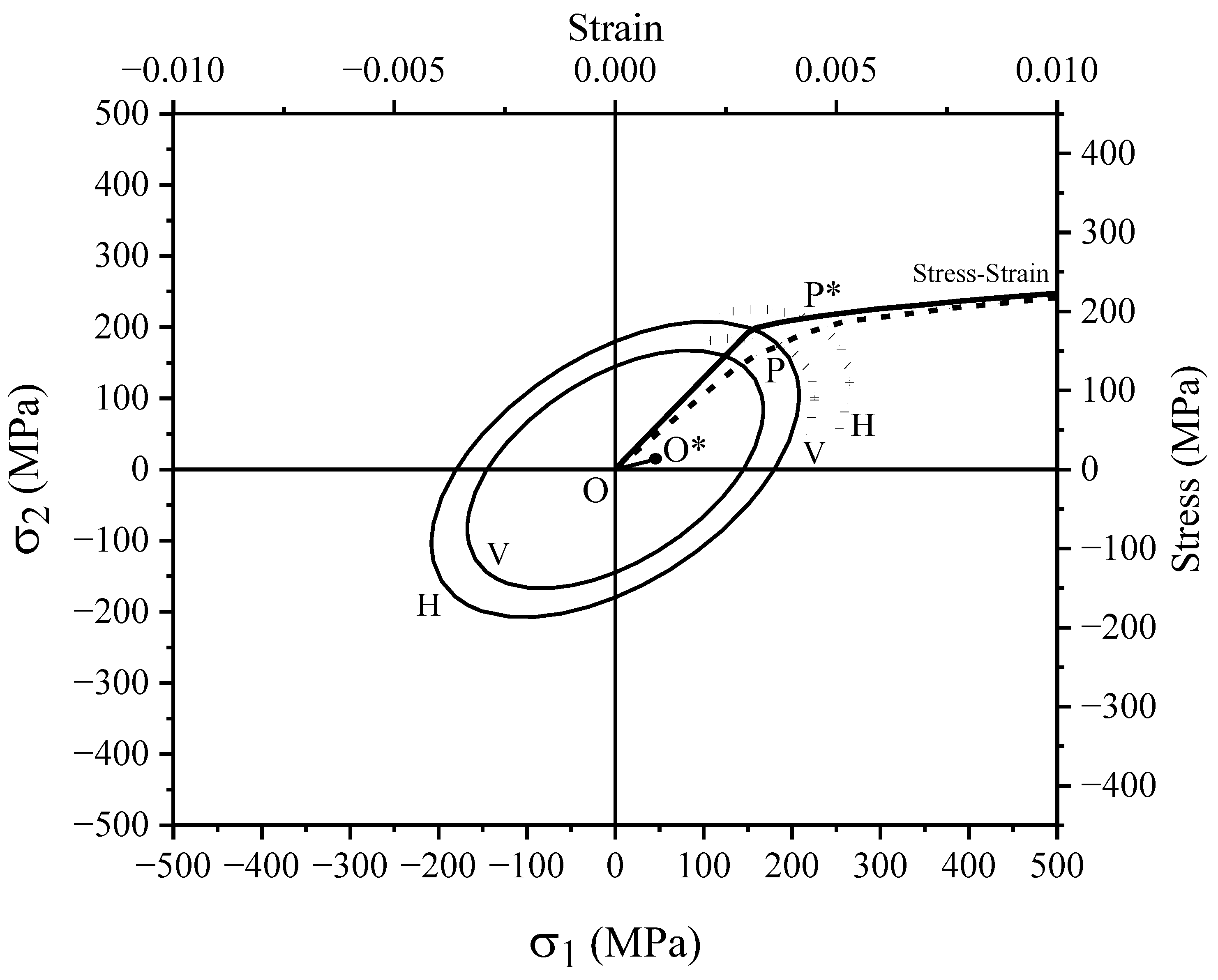
3.2. Backstress and Yield Surface Translation
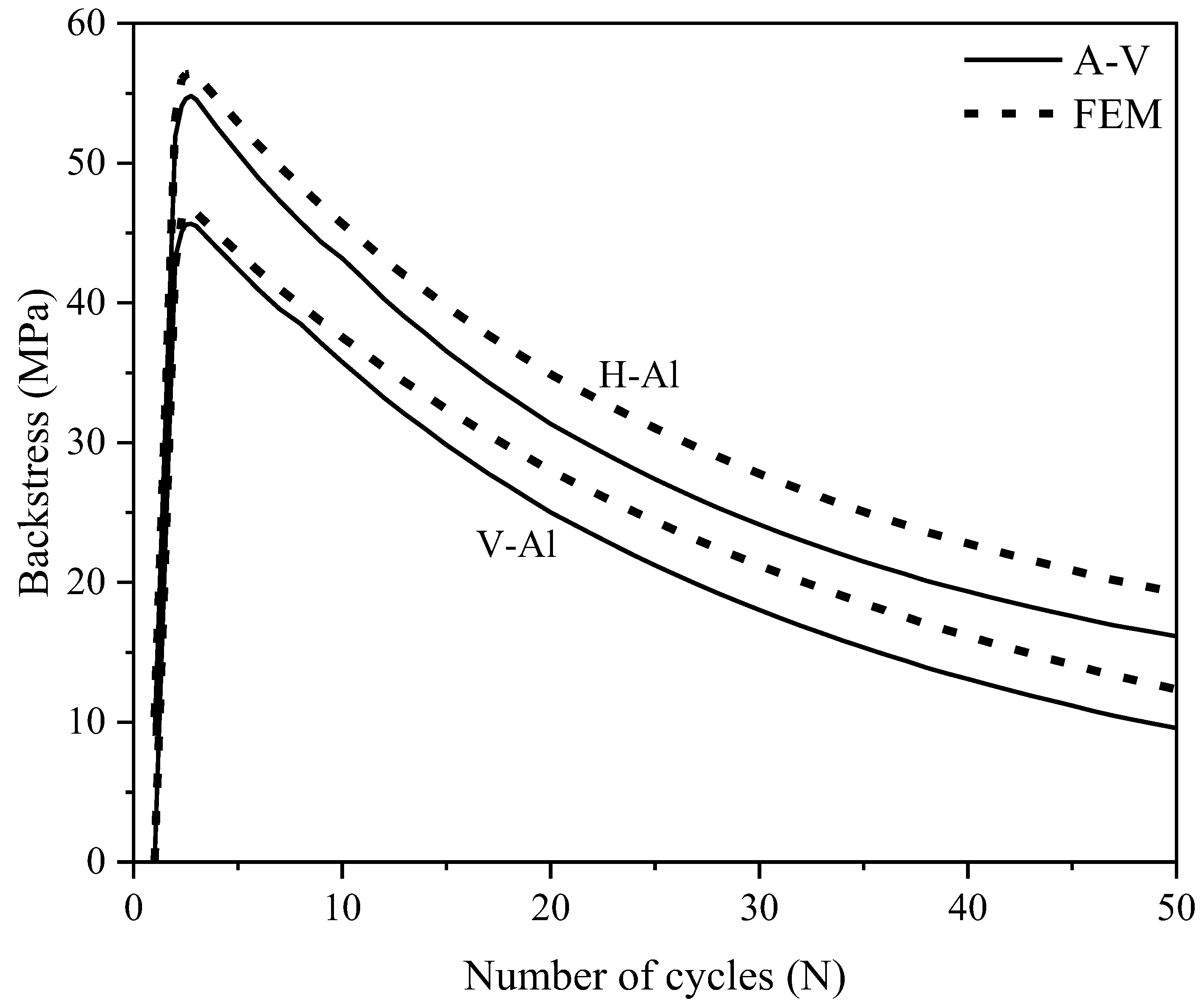
3.3. Finite Element Analysis
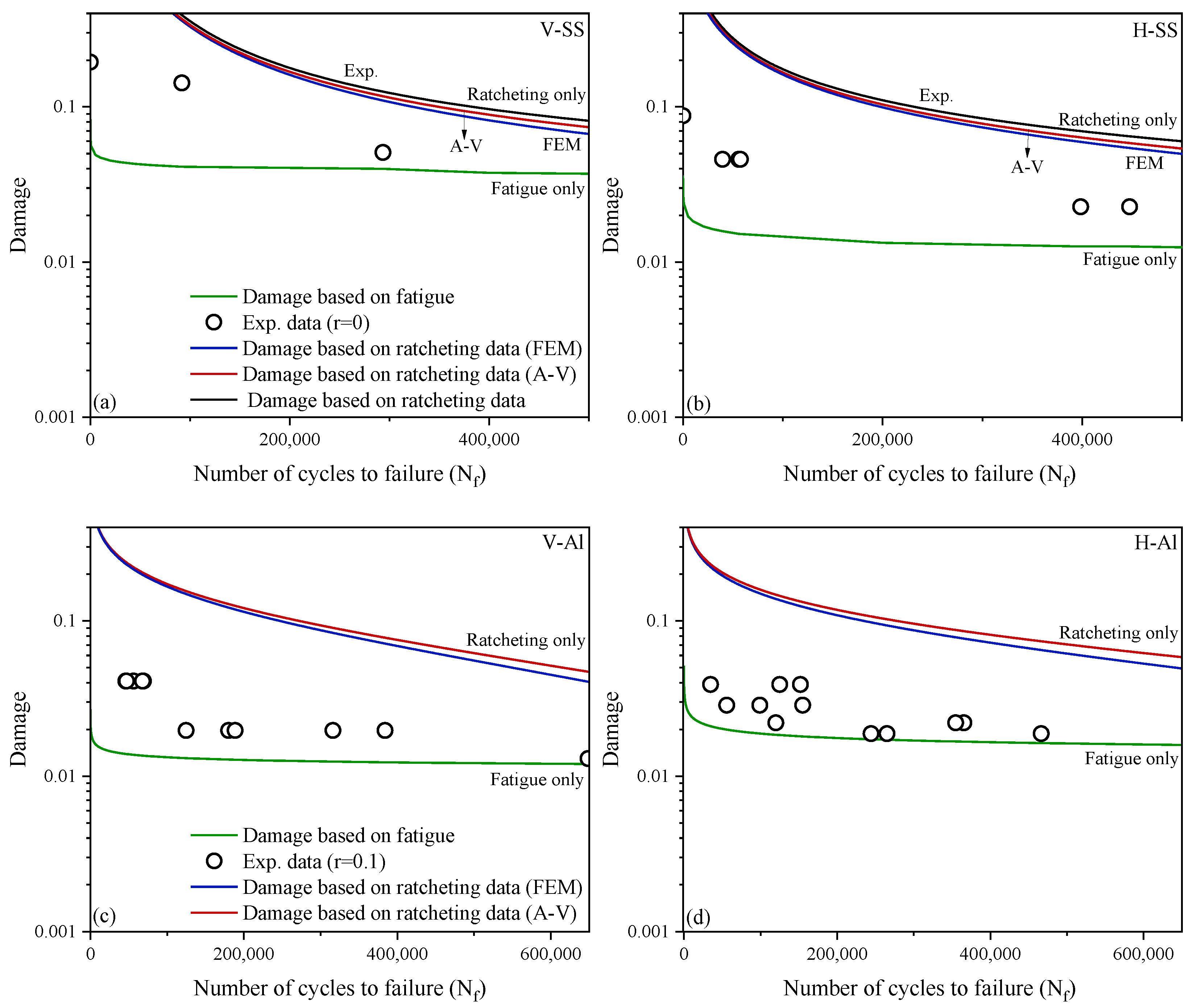
3.4. Ratcheting–Fatigue Damage Curves
Contribution of Fatigue and Ratcheting Damage
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blakey-Milner, B.; Gradl, P.; Snedden, G.; Brooks, M.; Pitot, J.; Lopez, E.; Leary, M.; Berto, F.; Du Plessis, A. Metal additive manufacturing in aerospace: A review. Mater. Des. 2021, 209, 110008. [Google Scholar] [CrossRef]
- Montanari, R.; Palombi, A.; Richetta, M.; Varone, A. Additive Manufacturing of Aluminum Alloys for Aeronautic Applications: Advantages and Problems. Metals 2023, 13, 716. [Google Scholar] [CrossRef]
- Gu, D.; Shi, X.; Poprawe, R.; Bourell, D.L.; Setchi, R.; Zhu, J. Material-structure-performance integrated laser-metal additive manufacturing. Science 2021, 372, eabg1487. [Google Scholar] [CrossRef] [PubMed]
- Molaei, R.; Fatemi, A.; Sanaei, N.; Pegues, J.; Shamsaei, N.; Shao, S.; Li, P.; Warner, D.H.; Phan, N. Fatigue of additive manufactured Ti-6Al-4V, Part II: The relationship between microstructure, material cyclic properties, and component performance. Int. J. Fatigue 2020, 132, 105363. [Google Scholar] [CrossRef]
- Mostafaei, A.; Zhao, C.; He, Y.; Ghiaasiaan, S.R.; Shi, B.; Shao, S.; Shamsaei, N.; Wu, Z.; Kouraytem, N.; Sun, T.; et al. Defects and anomalies in powder bed fusion metal additive manufacturing. Curr. Opin. Solid State Mater. Sci. 2022, 26, 100974. [Google Scholar]
- Sanaei, N.; Fatemi, A. Defects in additive manufactured metals and their effect on fatigue performance: A state-of-the-art review. Prog. Mater. Sci. 2021, 117, 100724. [Google Scholar] [CrossRef]
- Mower, T.M.; Long, M.J. Mechanical behavior of additive manufactured, powder-bed laser-fused materials. Mater. Sci. Eng. 2016, 651, 198–213. [Google Scholar] [CrossRef]
- Siddique, S.; Imran, M.; Rauer, M.; Kaloudis, M.; Wycisk, E.; Emmelmann, C.; Walther, F. Computed tomography for characterization of fatigue performance of selective laser melted parts. Mater. Des. 2015, 83, 661–669. [Google Scholar] [CrossRef]
- Avanzini, A.; Battini, D.; Gelfi, M.; Girelli, L.; Petrogalli, C.; Pola, A.; Tocci, M. Investigation on fatigue strength of sand-blasted DMLS-AlSi10Mg alloy. Procedia Struct. Integrity 2019, 18, 119–128. [Google Scholar] [CrossRef]
- Aboulkhair, N.T.; Everitt, N.M.; Ashcroft, I.; Tuck, C. Reducing porosity in AlSi10Mg parts processed by selective laser melting. Addit. Manuf. 2014, 1, 77–86. [Google Scholar] [CrossRef]
- Li, P.; Warner, D.H.; Fatemi, A.; Phan, N. Critical assessment of the fatigue performance of additively manufactured Ti–6Al–4V and perspective for future research. Int. J. Fatigue 2016, 85, 130–143. [Google Scholar] [CrossRef]
- Masuo, H.; Tanaka, Y.; Morokoshi, S.; Yagura, H.; Uchida, T.; Yamamoto, Y.; Murakami, Y. Effects of defects, surface roughness and HIP on fatigue strength of Ti-6Al-4V manufactured by additive manufacturing. Procedia Struct. 2017, 7, 19–26. [Google Scholar] [CrossRef]
- Jeyaprakash, N.; Yang, C.H.; Ramkumar, K.R. Correlation of microstructural evolution with mechanical and tribological behaviour of SS 304 specimens developed through SLM technique. Met. Mater. Int. 2021, 27, 5179–5190. [Google Scholar] [CrossRef]
- Shrestha, R.; Simsiriwong, J.; Shamsaei, N. Fatigue behavior of additive manufactured 316L stainless steel parts: Effects of layer orientation and surface roughness. Addit. Manuf. 2019, 28, 23–38. [Google Scholar] [CrossRef]
- Zhang, M.; Sun, C.N.; Zhang, X.; Goh, P.C.; Wei, J.; Hardacre, D.; Li, H. Fatigue and fracture behaviour of laser powder bed fusion stainless steel 316L: Influence of processing parameters. Mater. Sci. Eng. 2017, 703, 251–261. [Google Scholar] [CrossRef]
- Fatemi, A.; Molaei, R.; Simsiriwong, J.; Sanaei, N.; Pegues, J.; Torries, B.; Shamsaei, N. Fatigue behaviour of additive manufactured materials: An overview of some recent experimental studies on Ti-6Al-4V considering various processing and loading direction effects. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 991–1009. [Google Scholar] [CrossRef]
- Leuders, S.; Thöne, M.; Riemer, A.; Niendorf, T.; Tröster, T.; Richard, H.A.; Maier, H.J. On the mechanical behaviour of titanium alloy TiAl6V4 manufactured by selective laser melting: Fatigue resistance and crack growth performance. Int. J. Fatigue 2013, 48, 300–307. [Google Scholar] [CrossRef]
- Molaei, R.; Fatemi, A.; Phan, N. Significance of hot isostatic pressing (HIP) on multiaxial deformation and fatigue behaviors of additive manufactured Ti-6Al-4V including build orientation and surface roughness effects. Int. J. Fatigue 2018, 117, 352–370. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, S.L.; Gu, J.X.; Duan, C.F.; Xiong, Q. Effect of ratcheting strain on mechanical properties of additive manufactured 4043 aluminum alloy. Key Eng. Mater. 2019, 795, 43–48. [Google Scholar]
- Dong, B.; Cai, X.; Lin, S.; Li, X.; Fan, C.; Yang, C.; Sun, H. Wire arc additive manufacturing of Al-Zn-Mg-Cu alloy: Microstructures and mechanical properties. Addit. Manuf. 2020, 36, 101447. [Google Scholar] [CrossRef]
- Ghosh, A.; Sahu, V.K.; Gurao, N.P. Effect of heat treatment on the ratcheting behaviour of additively manufactured and thermo-mechanically treated Ti–6Al–4V alloy. Mater. Sci. Eng. 2022, 833, 142345. [Google Scholar] [CrossRef]
- Servatan, M.; Hashemi, S.M.; Varvani-Farahani, A. Ratcheting assessment of additively manufactured alloys through the hardening framework: Analysis and simulation. Mater. Today Commun. 2023, 35, 105916. [Google Scholar] [CrossRef]
- Zhang, M.; Sun, C.N.; Zhang, X.; Wei, J.; Hardacre, D.; Li, H. High cycle fatigue and ratcheting interaction of laser powder bed fusion stainless steel 316L: Fracture behaviour and stress-based modelling. Int. J. Fatigue 2019, 121, 252–264. [Google Scholar] [CrossRef]
- Servatan, M.; Hashemi, S.M.; Varvani-Farahani, A. Ratcheting evaluation of additively manufactured 4043 aluminum samples through a combined isotropic–kinematic hardening framework. Prog. Addit. Manuf. 2023, 8, 667–678. [Google Scholar] [CrossRef]
- Xia, Z.; Kujawski, D.; Ellyin, F. Effect of mean stress and ratcheting strain on fatigue life of steel. Int. J. Fatigue 1996, 18, 335–341. [Google Scholar] [CrossRef]
- Liu, Y.; Kang, G.; Gao, Q. Stress-based fatigue failure models for uniaxial ratchetting–fatigue interaction. Int. J. Fatigue 2008, 30, 1065–1073. [Google Scholar] [CrossRef]
- Kang, G.; Liu, Y.; Li, Z. Experimental study on ratchetting-fatigue interaction of SS304 stainless steel in uniaxial cyclic stressing. Mater. Sci. Eng. 2006, 435, 396–404. [Google Scholar] [CrossRef]
- Ahmadzadeh, G.R.; Varvani-Farahani, A. Concurrent ratcheting–fatigue damage analysis of uniaxially loaded A-516 Gr. 70 and 42CrMo Steels. Fatigue Fract. Eng. Mater. Struct. 2012, 35, 962–970. [Google Scholar] [CrossRef]
- Zhan, Z.; Li, H. A novel approach based on the elastoplastic fatigue damage and machine learning models for life prediction of aerospace alloy parts fabricated by additive manufacturing. Int. J. Fatigue 2021, 145, 106089. [Google Scholar] [CrossRef]
- Varvani-Farahani, A. A new energy-critical plane parameter for fatigue life assessment of various metallic materials subjected to in-phase and out-of-phase multiaxial fatigue loading conditions. Int. J. Fatigue 2000, 22, 295–305. [Google Scholar] [CrossRef]
- Karvan, P.; Varvani-Farahani, A. Isotropic-kinematic hardening framework to assess ratcheting response of steel samples undergoing asymmetric loading cycles. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 295–306. [Google Scholar] [CrossRef]
- Lee, D.; Zaverl, F., Jr. A generalized strain rate dependent constitutive equation for anisotropic metals. Acta Metall. 1978, 26, 1771–1780. [Google Scholar] [CrossRef]
- Ahmadzadeh, G.R.; Varvani-Farahani, A. Ratcheting assessment of materials based on the modified Armstrong–Frederick hardening rule at various uniaxial stress levels. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 1232–1245. [Google Scholar] [CrossRef]
- Varvani-Farahani, A. Nonlinear kinematic hardening cyclic plasticity. In Cyclic Plasticity of Metals; Elsevier: Amsterdam, The Netherlands, 2022; pp. 139–174. [Google Scholar]
- Chaboche, J.L. On some modifications of kinematic hardening to improve the description of ratchetting effects. Int. J. Plast. 1991, 7, 661–678. [Google Scholar] [CrossRef]
- Gordon, J.; Hochhalter, J.; Haden, C.; Harlow, D.G. Enhancement in fatigue performance of metastable austenitic stainless steel through directed energy deposition additive manufacturing. Mater. Des. 2019, 168, 107630. [Google Scholar] [CrossRef]
- Gordon, J.V.A. Fatigue Crack Growth Analysis of 3D Printed Type 304 Stainless Steel. Ph.D. Thesis, Lehigh University, Bethlehem, PA, USA, 2018. [Google Scholar]
- Wu, Z.; Wu, S.; Bao, J.; Qian, W.; Karabal, S.; Sun, W.; Withers, P.J. The effect of defect population on the anisotropic fatigue resistance of AlSi10Mg alloy fabricated by laser powder bed fusion. Int. J. Fatigue 2021, 151, 106317. [Google Scholar] [CrossRef]
- Yu, T.; Hyer, H.; Sohn, Y.; Bai, Y.; Wu, D. Structure-property relationship in high strength and lightweight AlSi10Mg microlattices fabricated by selective laser melting. Mater. Des. 2019, 182, 108062. [Google Scholar] [CrossRef]
- Vivekananthan, M.; Saravanakumar, M.; Ross, K.N.S.; Kumar, K.S.S.; Raj, F.S. Experimental investigation of Mechanical properties in friction welding parameters for dis-similar metals (SS-304 & SS-410). Manuf. Eng. 2020, 2214, 7853. [Google Scholar]
- Halama, R.; Fumfera, J.; Gál, P.; Kumar, T.; Markopoulos, A. Modeling the strain-range dependent cyclic hardening of SS304 and 08Ch18N10T stainless steel with a memory surface. Metals 2019, 9, 832. [Google Scholar] [CrossRef]
- Fernandes, R.; de Jesus, J.; Branco, R.; Borrego, L.P.; Ferreira, J.M. Cyclic deformation behaviour of AlSi10Mg aluminium alloy manufactured by laser-beam powder bed fusion. Procedia Struct. Integr. 2022, 37, 462–468. [Google Scholar] [CrossRef]
- Skelton, R.P.; Maier, H.J.; Christ, H.J. The Bauschinger effect, Masing model and the Ramberg–Osgood relation for cyclic deformation in metals. Mater. Sci. Eng. 1997, 238, 377–390. [Google Scholar] [CrossRef]
- Ansys® Workbench, Release 22.1. Help System, Static Structural Analysis Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2022. [Google Scholar]




| Material | Fatigue Coefficients | Models | Parameters and Coefficients |
|---|---|---|---|
| Isotropic | , | ||
| 304L Stainless Steel (Horizontal samples) | 0.016 | A–V | , , |
| −0.06 −0.3 | Chaboche | , | |
| 4200 | Isotropic | , | |
| 304L Stainless Steel (Vertical samples) | 0.026 | A–V | , , |
| −0.184 −0.2 | Chaboche | , | |
| 330 | Isotropic | , | |
| AlSi10Mg (Horizontal samples) | 0.024 | A–V | , , |
| −0.005 −0.2 | Chaboche | , | |
| 320 | Isotropic | , | |
| AlSi10Mg (Vertical samples) | 0.01 | A–V | , , |
| −0.005 −0.2 | Chaboche | , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Servatan, M.; Hashemi, S.M.; Varvani-Farahani, A. Ratcheting–Fatigue Damage Assessment of Additively Manufactured SS304L and AlSi10Mg Samples under Asymmetric Stress Cycles. Metals 2023, 13, 1534. https://doi.org/10.3390/met13091534
Servatan M, Hashemi SM, Varvani-Farahani A. Ratcheting–Fatigue Damage Assessment of Additively Manufactured SS304L and AlSi10Mg Samples under Asymmetric Stress Cycles. Metals. 2023; 13(9):1534. https://doi.org/10.3390/met13091534
Chicago/Turabian StyleServatan, M., S. M. Hashemi, and A. Varvani-Farahani. 2023. "Ratcheting–Fatigue Damage Assessment of Additively Manufactured SS304L and AlSi10Mg Samples under Asymmetric Stress Cycles" Metals 13, no. 9: 1534. https://doi.org/10.3390/met13091534
APA StyleServatan, M., Hashemi, S. M., & Varvani-Farahani, A. (2023). Ratcheting–Fatigue Damage Assessment of Additively Manufactured SS304L and AlSi10Mg Samples under Asymmetric Stress Cycles. Metals, 13(9), 1534. https://doi.org/10.3390/met13091534







