Dynamic Recrystallization Kinetics of As-Cast Fe-Cr-Al-La Stainless Steel during Hot Deformation
Abstract
1. Introduction
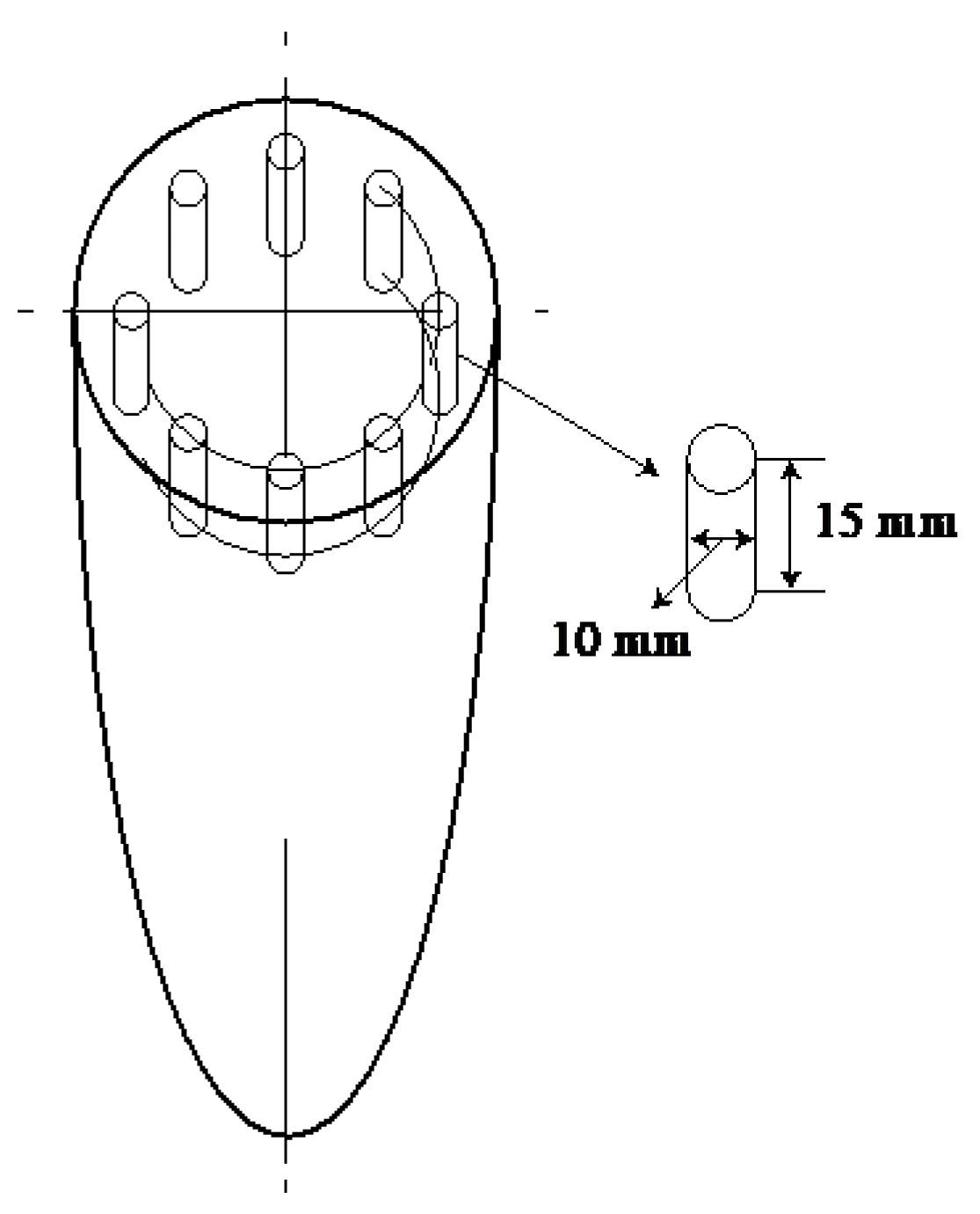
2. Materials and Methods
3. Results and Discussion
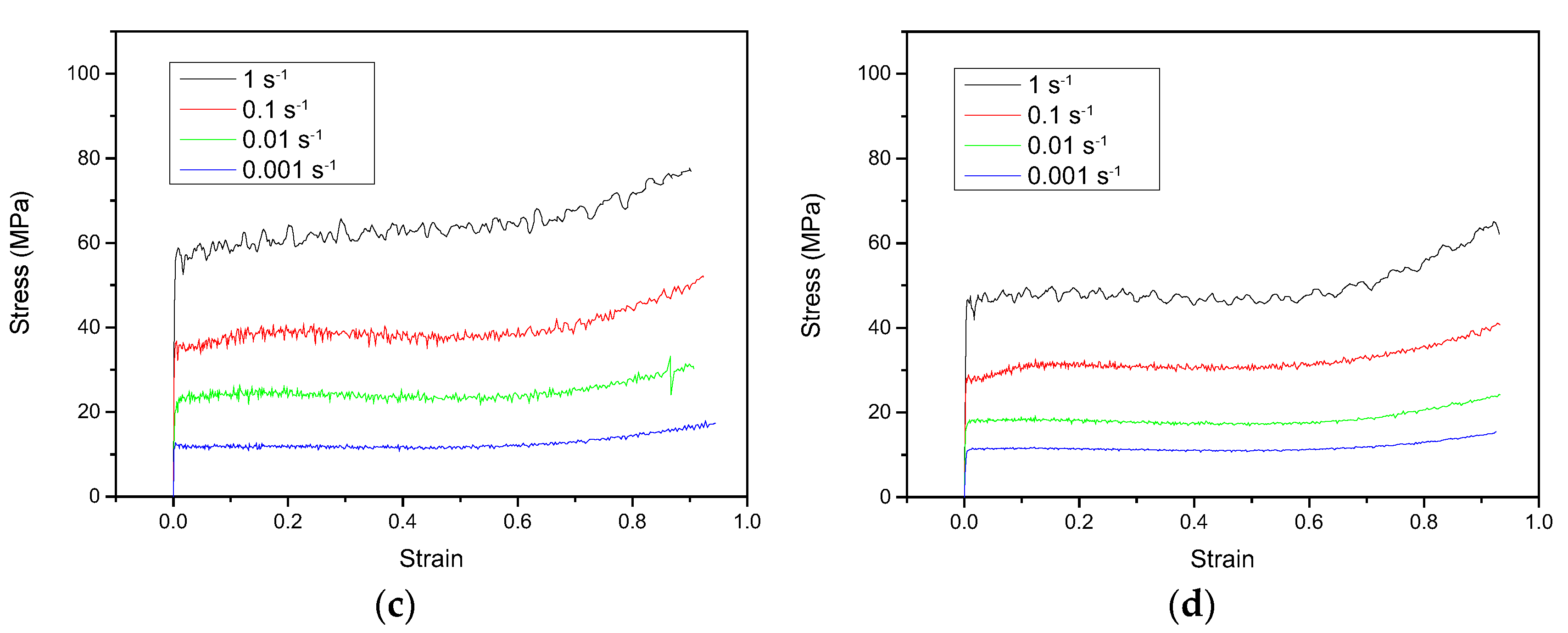
3.1. Flow Curves
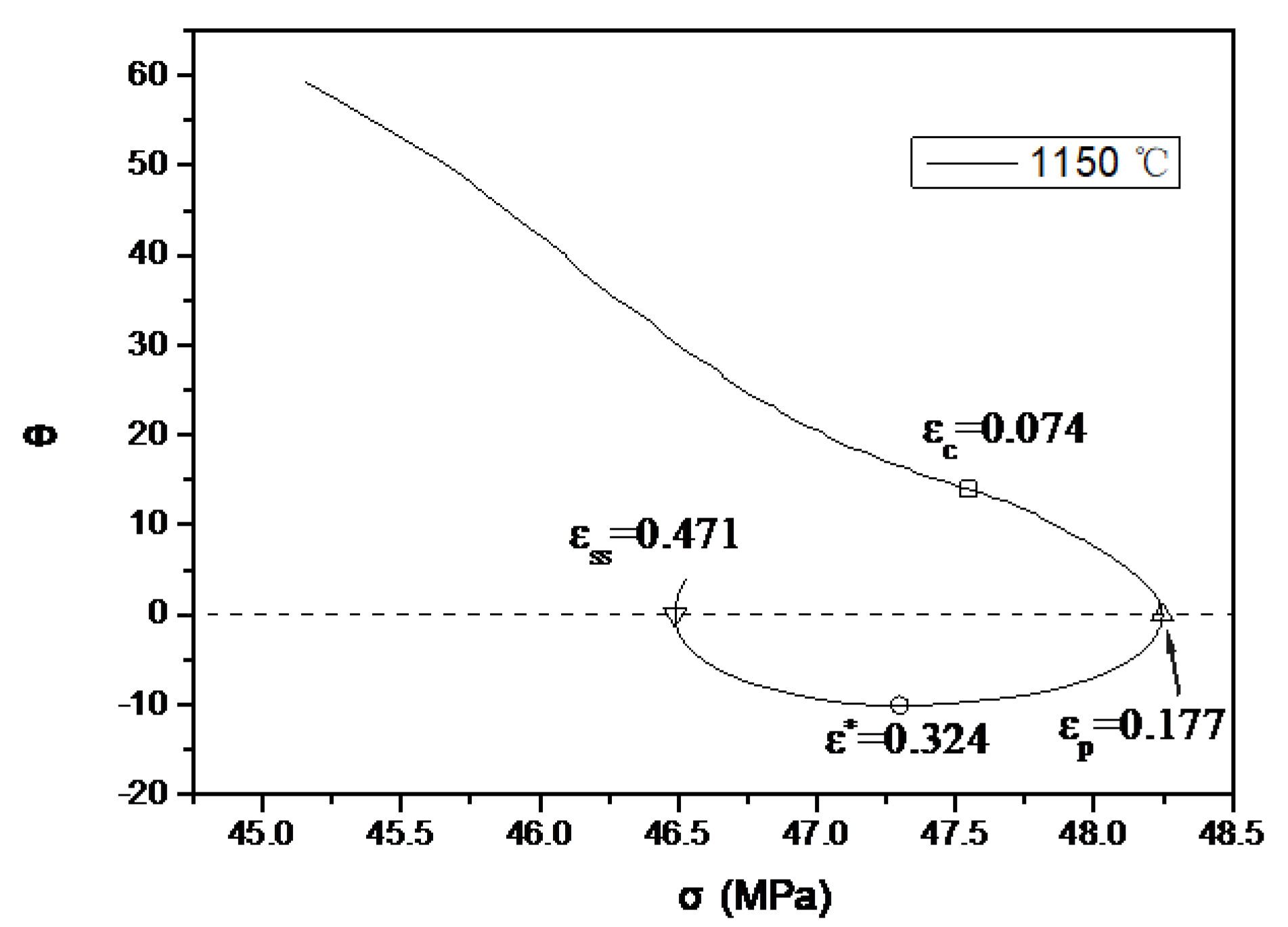
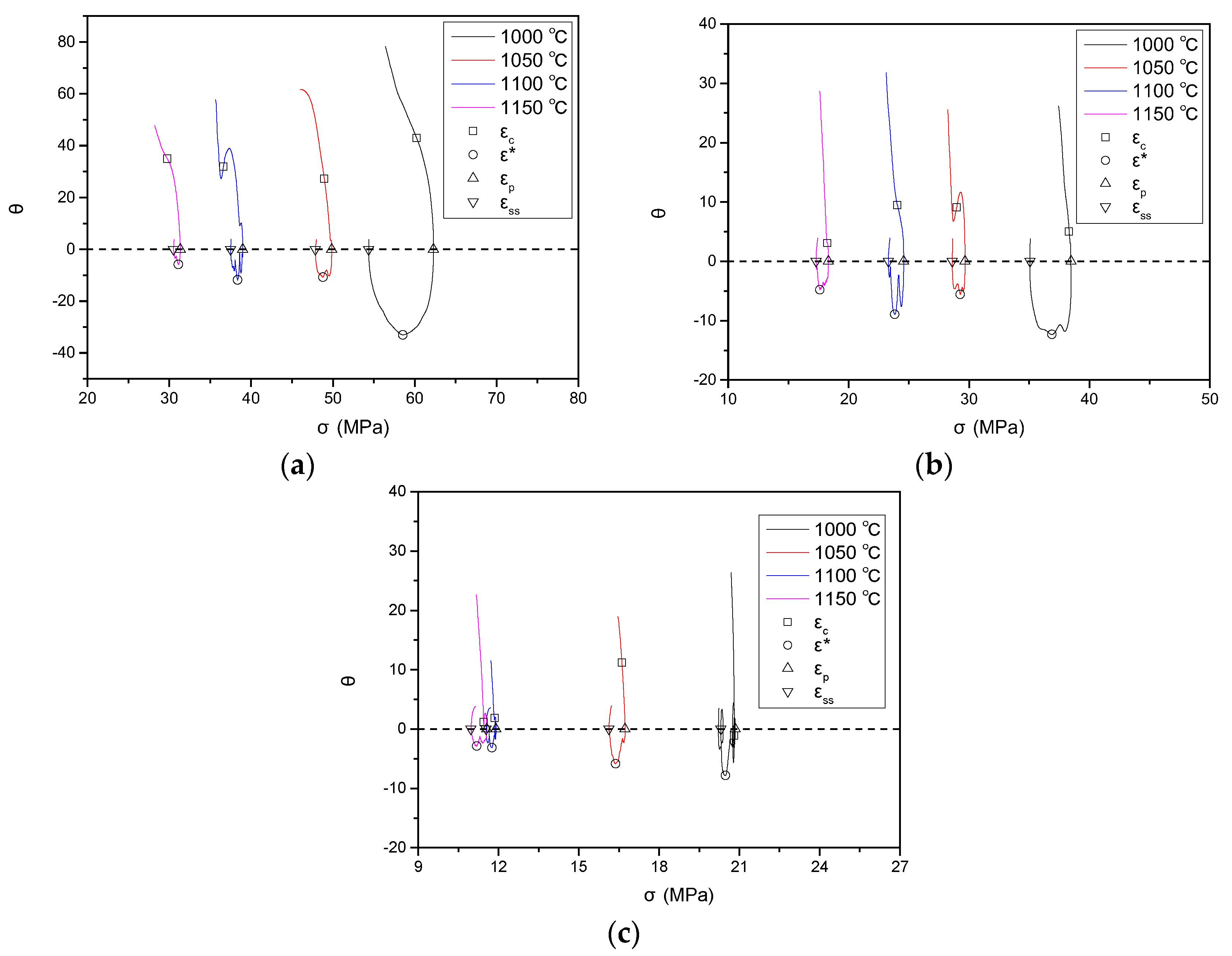
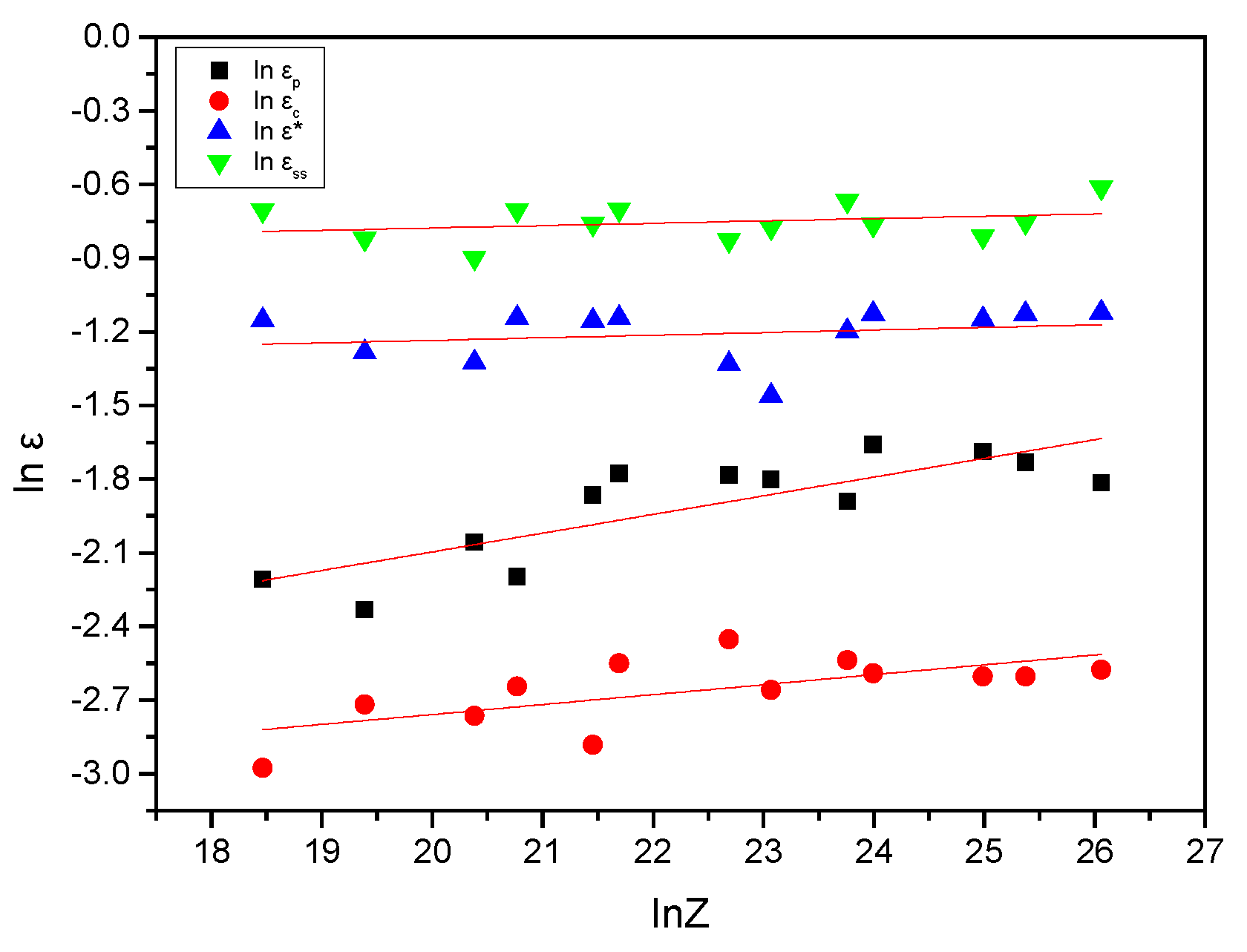
3.2. Determination of DRX Characteristic Parameters
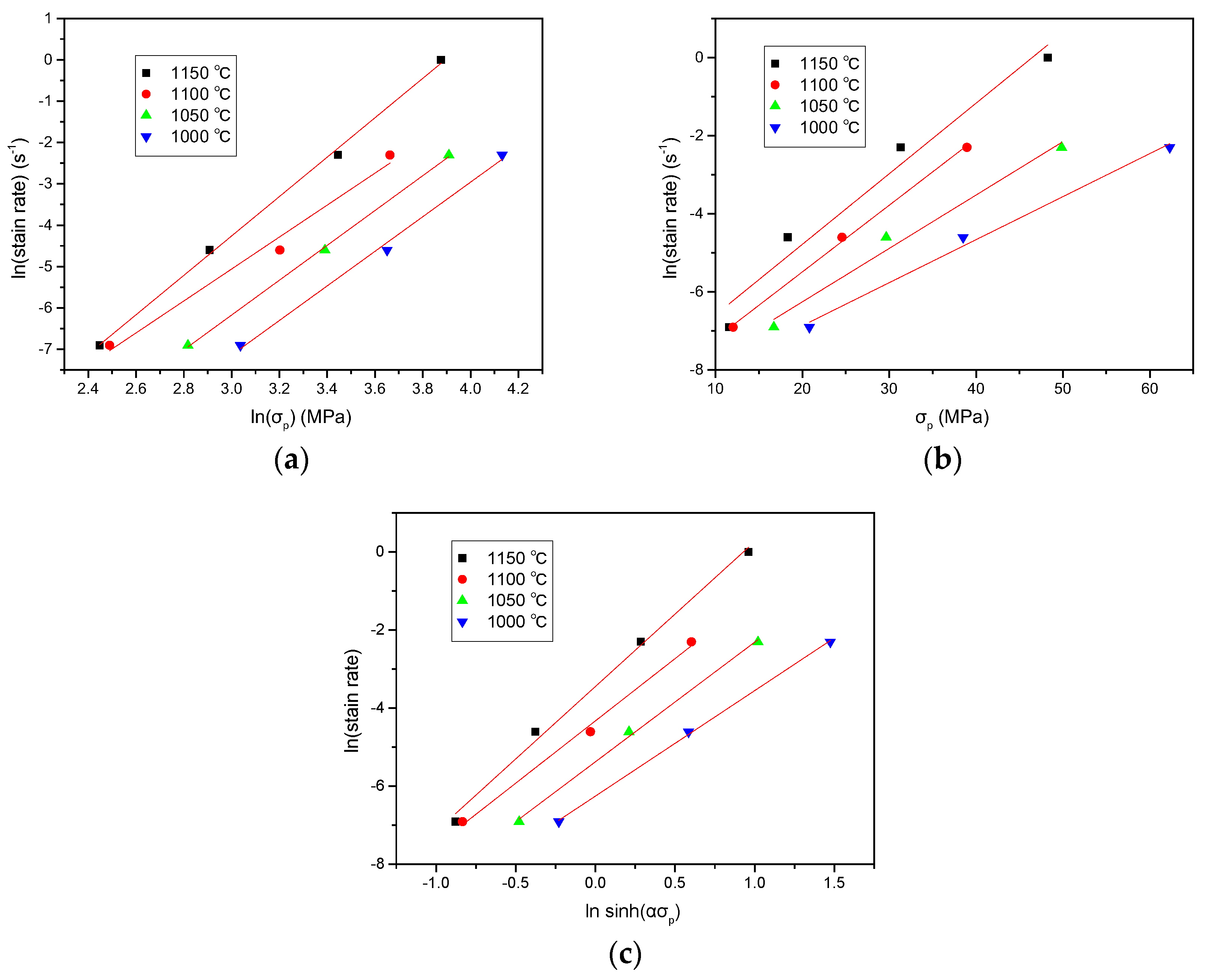
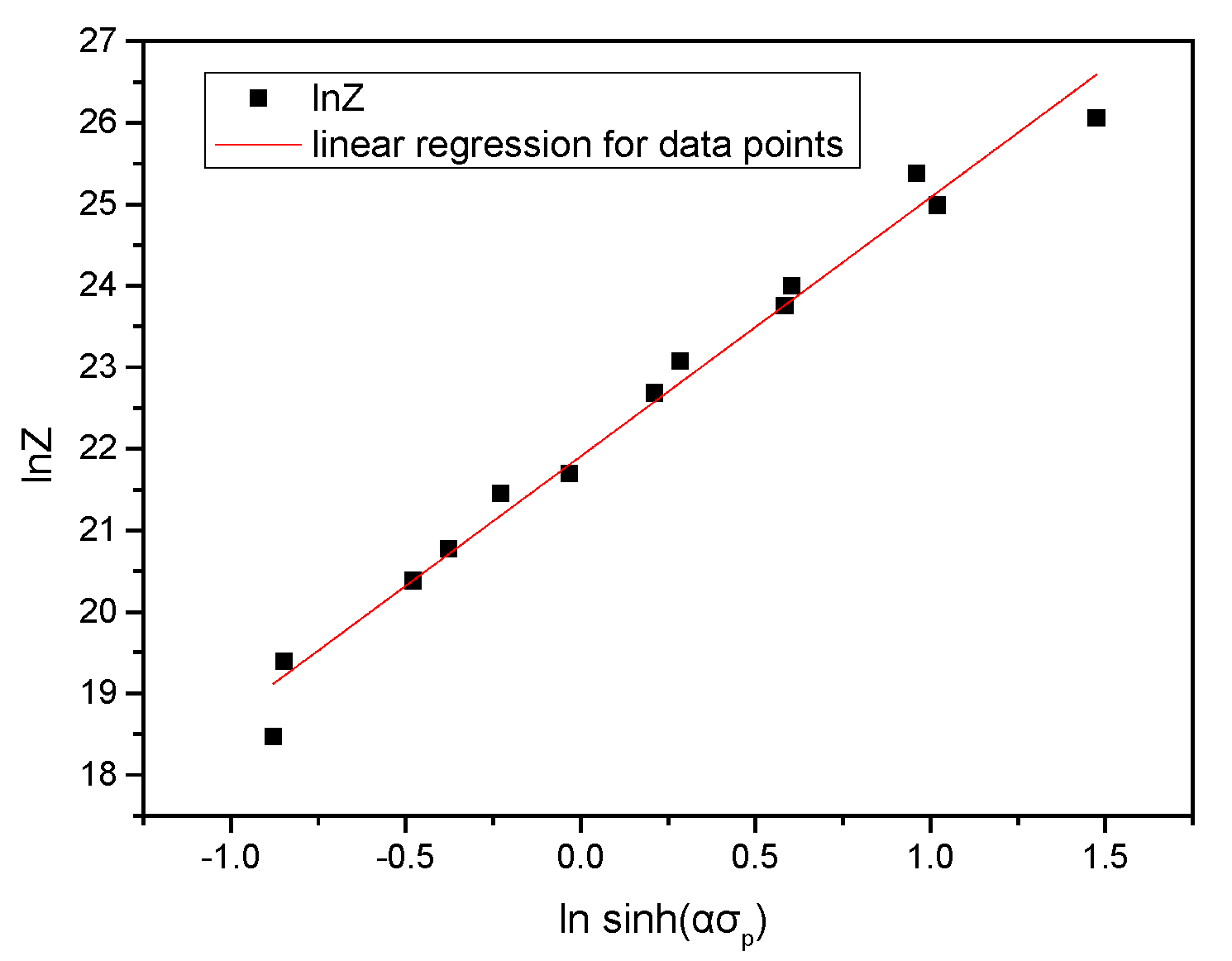
3.3. Constitutive Equations
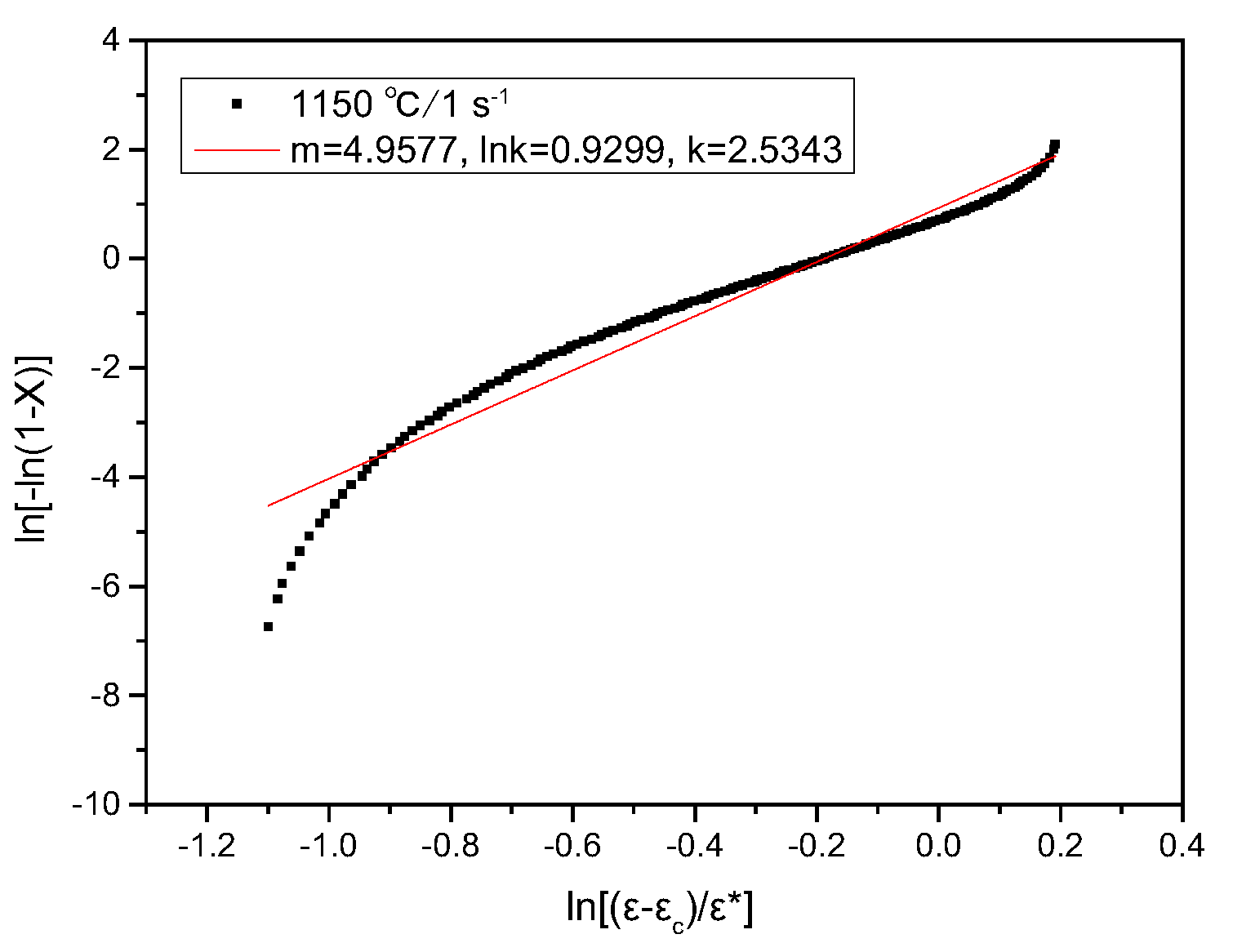
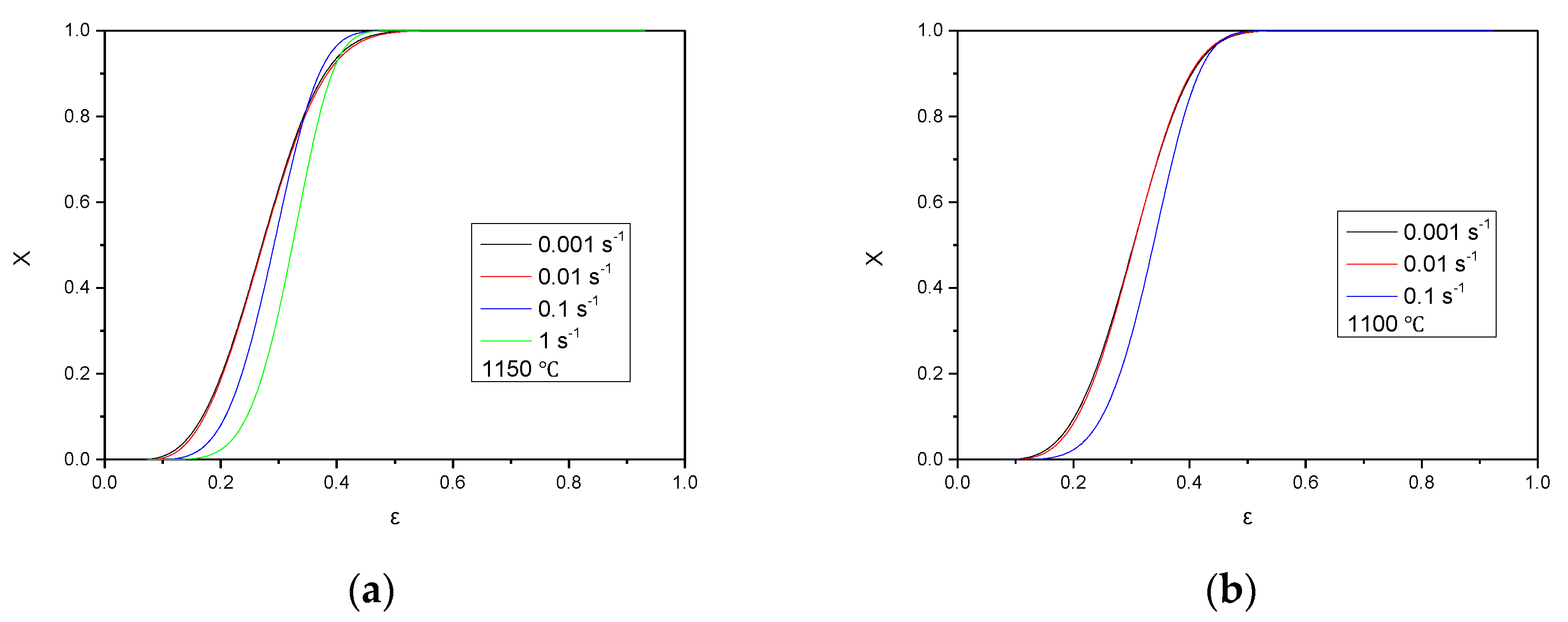
3.4. DRX Kinetic Model
3.5. Microstructure Evolution and DRX Mechanism
4. Conclusions
- The flow stress of the Fe-Cr-Al-La stainless steel increases with a decrease in deformation temperature and an increase in strain rate. Most of the flow curves exhibit a single peak, followed by a steady-state flow, which is a typical DRX softening characteristic. The low deformation temperature and high strain rate prevent the evolution of DRX.
- The apparent activation energy in the test conditions for the Fe-20Cr-5.5Al-0.64La stainless steel was calculated to be 300.19 kJ/mol. The constitutive equation was established with a hyperbolic sine equation by regression analysis and can be identified as: or expressed as a function of the Z parameter: . The correlations between the critical strain, the peak strain and the strain for maximum softening rate with the Z parameter were also obtained.
- Kinetics model of DRX was established to predict the microstructure evolution. The dynamic recrystallization kinetics at 1150 °C and 1 s−1 can be expressed as:
- Both the dynamic recrystallization kinetic model and microstructure observation show that the DRX volume fraction is larger at a lower strain rate for the same strain when the deformation temperature is fixed.
- The microstructure observation shows that fine DRX grains initially form at the original grain boundaries. The volume fraction of DRX grains increases with an increase in strain. The microstructure observation also validated the dynamic recrystallization kinetic model. The size of dynamic recrystallization grains increases with an increase in temperature or a decrease in strain rate.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Inoue, Y.; Kikuchi, M.; Tendo, M.; Tanoue, T.; Kajimura, H. Development of Heat Resistant Stainless Steel NSSC® 21M for Catalysis Substrate of Motorcycle Muffler. Nippon Steel Tech. Rep. 2010, 99, 45–50. [Google Scholar]
- Shen, L.; Lu, J. Overview of Researching of the Carrier Used for Automobile Gas Purfier. Shonghai Steel Iron Res. 2004, 1, 35–41. [Google Scholar]
- Ferguson, D.; Chen, W.; Bonesteel, T.; Vosburgh, J. A Look at Physical Simulation of Metallurgical Processes, Past, Present and Future. Mater. Sci. Eng. A 2009, 499, 329–332. [Google Scholar] [CrossRef]
- Song, R.; Ponge, D.; Raabe, D.; Speer, J.G.; Matlock, D.K. Overview of Processing, Microstructure and Mechanical Properties of Ultrafine Grained Bcc Steels. Mater. Sci. Eng. A 2006, 441, 1–17. [Google Scholar] [CrossRef]
- Liu, F.; Halvarsson, M.; Hellström, K.; Svensson, J.E.; Johansson, L.G. First Three-Dimensional Atomic Resolution Investigation of Thermally Grown Oxide on a FeCrAl Alloy. Oxid. Met. 2015, 83, 441–451. [Google Scholar] [CrossRef]
- He, Y.; Liu, J.; Han, Z.; Deng, Z.; Su, X.; Ji, Y. Phase Transformation and Precipitation during Solidification of FeCrAl Alloy for Automobile Exhaust Gas Purifying Systems. J. Alloys Compd. 2017, 714, 251–257. [Google Scholar] [CrossRef]
- Deng, Z.Q.; Liu, J.H.; He, Y.; Han, Z.B.; Su, X.F.; Ding, H. Phase Transformations and Precipitation Behavior in FeCrAl Stainless Steel during Equilibrium Solidification. Gongcheng Kexue Xuebao/Chin. J. Eng. 2017, 39, 710–720. [Google Scholar] [CrossRef]
- Deng, Z.; Liu, J.; He, Y.; Yang, Y.; McLean, A. Study on Phase Transition and Precipitation Behavior of Fecral Stainless Steel during Equilibrium Solidification. In AISTech-Iron and Steel Technology Conference Proceedings; AIST: Tokyo, Japan, 2019; Volume 2019, pp. 2311–2318. [Google Scholar] [CrossRef]
- Gao, F.; Yu, F.X.; Liu, F.T.; Liu, Z.Y. Hot Deformation Behavior and Flow Stress Prediction of Ultra Purified 17% Cr Ferritc Stainless Steel Stabilized with Nb and Ti. J. Iron Steel Res. Int. 2015, 22, 827–836. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M. A Critical Review of Experimental Results and Constitutive Descriptions for Metals and Alloys in Hot Working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Wang, Z.; Fu, W.; Sun, S.; Li, H.; Lv, Z.; Zhao, D. Mechanical Behavior and Microstructural Change of a High Nitrogen Crmn Austenitic Stainless Steel during Hot Deformation. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2010, 41, 1025–1032. [Google Scholar] [CrossRef]
- Mandal, S.; Bhaduri, A.K.; Sarma, V.S. Role of Twinning on Dynamic Recrystallization and Microstructure during Moderate to High Strain Rate Hot Deformation of a Ti-Modified Austenitic Stainless Steel. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2012, 43, 2056–2068. [Google Scholar] [CrossRef]
- Mataya, M.C.; Perkins, C.A.; Thompson, S.W.; Matlock, D.K. Flow Stress and Microstructural Evolution during Hot Working of Alloy 22Cr-13Ni-5Mn-0.3N Austenitic Stainless Steel. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 1996, 27, 1251–1266. [Google Scholar] [CrossRef]
- Mandal, S.; Bhaduri, A.K.; Subramanya Sarma, V. A Study on Microstructural Evolution and Dynamic Recrystallization during Isothermal Deformation of a Ti-Modified Austenitic Stainless Steel. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2011, 42, 1062–1072. [Google Scholar] [CrossRef]
- McQueen, H.J.; Bourell, D.L. Hot Workability of Metals and Alloys. Jom 1987, 39, 28–35. [Google Scholar] [CrossRef]
- Ryan, N.D.; McQueen, H.J. Effects of Alloying upon the Hot Workability of Carbon, Microalloyed, Tool, and Austenitic Stainless Steels. J. Mech. Work. Technol. 1986, 12, 279–296. [Google Scholar] [CrossRef]
- Glover, G.; Sellars, C.M. Recovery and Recrystallization during High Temperature Deformation of α-Iron. Metall. Trans. 1973, 4, 765–775. [Google Scholar] [CrossRef]
- Glover, G.; Sellars, C. Static Recrystallization after Hot Deformation of α Iron. Metall. Trans. 1972, 3, 2271–2280. [Google Scholar] [CrossRef]
- Najafi-Zadeh, A.; Jonas, J.J.; Yue, S. Effect of Dynamic Recrystallization on Grain Refinement of IF Steels. Mater. Sci. Forum 1993, 113–115, 441–446. [Google Scholar] [CrossRef]
- Gao, F.; Yourong, X.U.; Song, B.; Xia, K. Substructural Changes during Hot Deformation of an Fe-26Cr Ferritic Stainless Steel. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2000, 31, 21–27. [Google Scholar] [CrossRef]
- Yagi, H.; Tsuji, N.; Saito, Y. Dynamic Recrystallization in 18%Cr Ferritic Steel. Tetsu—Hagane/J. Iron Steel Inst. Japan 2000, 86, 349–356. [Google Scholar] [CrossRef]
- Zhu, Y.-Y.; Ning, L.-K.; Xin, T.-Z.; Liu, E.-Z.; Tong, J.; Tan, Z.; Zhou, Y.-T.; Zheng, Z. Hot Deformation Behavior and Microstructure Evolution of an Fe–30Cr–2Mo Ultra-Pure Super Ferritic Stainless Steel. J. Iron Steel Res. Int. 2021, 28, 1291–1304. [Google Scholar] [CrossRef]
- Cao, Y.; Di, H.; Zhang, J.; Ma, T.; Zhang, J. Research on Hot Deformation Behavior and Hot Workability of Alloy 800H. Jinshu Xuebao/Acta Metall. Sin. 2013, 49, 811–821. [Google Scholar] [CrossRef]
- Tsuji, N.; Matsubara, Y.; Saito, Y. Dynamic Recrystallization of Ferrite in Interstitial Free Steel. Scr. Mater. 1997, 37, 477–484. [Google Scholar] [CrossRef]
- Abedi, H.R.; Zarei Hanzaki, A.; Liu, Z.; Xin, R.; Haghdadi, N.; Hodgson, P.D. Continuous Dynamic Recrystallization in Low Density Steel. Mater. Des. 2017, 114, 55–64. [Google Scholar] [CrossRef]
- Han, Y.; Liu, G.; Zou, D.; Liu, R.; Qiao, G. Deformation Behavior and Microstructural Evolution of As-Cast 904L Austenitic Stainless Steel during Hot Compression. Mater. Sci. Eng. A 2013, 565, 342–350. [Google Scholar] [CrossRef]
- El Wahabi, M.; Cabrera, J.M.; Prado, J.M. Hot Working of Two AISI 304 Steels: A Comparative Study. Mater. Sci. Eng. A 2003, 343, 116–125. [Google Scholar] [CrossRef]
- Han, K.S.; Song, T.J.; De Cooman, B.C. Hot Deformation Behavior of Fe-2%Si. ISIJ Int. 2013, 53, 294–303. [Google Scholar] [CrossRef]
- Tsuji, N.; Shinmiya, T.; Saito, Y.; Muraki, M. Deformation Microstructure and Nucleation of Recrystallization in Hot-Deformed Single Crystals of 18% Cr Ferritic Steel. ISIJ Int. 1998, 38, 380–389. [Google Scholar] [CrossRef]
- Yue, C.-X.; Zhang, L.-W.; Liao, S.-L.; Pei, J.-B.; Gao, H.-J.; Jia, Y.-W.; Lian, X.-J. Research on the Dynamic Recrystallization Behavior of GCr15 Steel. Mater. Sci. Eng. A 2009, 499, 177–181. [Google Scholar] [CrossRef]
- Yang, X.; Ji, Z.; Miura, H.; Sakai, T. Dynamic Recrystallization and Texture Development during Hot Deformation of Magnesium Alloy AZ31. Trans. Nonferrous Met. Soc. China 2009, 19, 55–60. [Google Scholar] [CrossRef]
- Zheng, Q.G.; Ying, T.; Jie, Z. Dynamic Softening Behaviour of AZ80 Magnesium Alloy during Upsetting at Different Temperatures and Strain Rates. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2010, 224, 1707–1716. [Google Scholar] [CrossRef]
- Petkovic, R.A.; Luton, M.J.; Jonas, J.J. Recovery and Recrystallization of Polycrystalline Copper after Hot Working. Acta Metall. 1979, 27, 1633–1648. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Luo, H. Complicated Interaction of Dynamic Recrystallization and Precipitation During Hot Deformation of Ultrahigh-Strength Stainless Steel. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2016, 47, 6248–6258. [Google Scholar] [CrossRef]
- Kim, S.-I.; Lee, Y.; Lee, D.L.; Yoo, Y.C. Modeling of AGS and Recrystallized Fraction of Microalloyed Medium Carbon Steel during Hot Deformation. Mater. Sci. Eng. A 2003, 355, 384–393. [Google Scholar] [CrossRef]
- Kim, S.-I.; Yoo, Y.-C. Dynamic Recrystallization Behavior of AISI 304 Stainless Steel. Mater. Sci. Eng. A 2001, 311, 108–113. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Cabrera, J.M.; Najafizadeh, A. Modeling and Prediction of Hot Deformation Flow Curves. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2012, 43, 108–123. [Google Scholar] [CrossRef]
- Xu, Y.; Hua, L.; Sun, Y. Deformation Behaviour and Dynamic Recrystallization of AZ61 Magnesium Alloy. J. Alloys Compd. 2013, 580, 262–269. [Google Scholar] [CrossRef]
- McQueen, H.J.; Ryan, N.D. Constitutive Analysis in Hot Working. Mater. Sci. Eng. A 2002, 322, 43–63. [Google Scholar] [CrossRef]
- Samantaray, D.; Mandal, S.; Bhaduri, A.K.; Venugopal, S.; Sivaprasad, P.V. Analysis and Mathematical Modelling of Elevated Temperature Flow Behaviour of Austenitic Stainless Steels. Mater. Sci. Eng. A 2011, 528, 1937–1943. [Google Scholar] [CrossRef]
- Sellars, C.M.; Tegart, W.J.M. Hot Workability. Int. Metall. Rev. 1972, 17, 1–24. [Google Scholar] [CrossRef]
- Sellars, C.M.; McTegart, W.J. On the Mechanism of Hot Deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Quan, G.-Z.; Wu, D.-S.; Luo, G.-C.; Xia, Y.-F.; Zhou, J.; Liu, Q.; Gao, L. Dynamic Recrystallization Kinetics in α Phase of As-Cast Ti–6Al–2Zr–1Mo–1V Alloy during Compression at Different Temperatures and Strain Rates. Mater. Sci. Eng. A 2014, 589, 23–33. [Google Scholar] [CrossRef]
- Jia, J.; Zhang, K.; Lu, Z. Dynamic Recrystallization Kinetics of a Powder Metallurgy Ti-22Al-25Nb Alloy during Hot Compression. Mater. Sci. Eng. A 2014, 607, 630–639. [Google Scholar] [CrossRef]
- Yang, Z.; Guo, Y.C.; Li, J.P.; He, F.; Xia, F.; Liang, M.X. Plastic Deformation and Dynamic Recrystallization Behaviors of Mg-5Gd-4Y-0.5Zn-0.5Zr Alloy. Mater. Sci. Eng. A 2008, 485, 487–491. [Google Scholar] [CrossRef]
- Liu, J.; Cui, Z.; Ruan, L. A New Kinetics Model of Dynamic Recrystallization for Magnesium Alloy AZ31B. Mater. Sci. Eng. A 2011, 529, 300–310. [Google Scholar] [CrossRef]
- Ponge, D.; Gottstein, G. Necklace Formation during Dynamic Recrystallization: Mechanisms and Impact on Flow Behavior. Acta Mater. 1998, 46, 69–80. [Google Scholar] [CrossRef]
- Medina, S.F.; Hernandez, C.A. General Expression of the Zener-Hollomon Parameter as a Function of the Chemical Composition of Low Alloy and Microalloyed Steels. Acta Mater. 1996, 44, 137–148. [Google Scholar] [CrossRef]
- Rollett, A.; Humphreys, F.; Rohrer, G.S.; Hatherly, M. Recrystallization and Related Annealing Phenomena, 2nd ed.; Pergamon: Oxford, UK, 2004; ISBN 9780080441641. [Google Scholar]






| C | Si | Mn | P | S | Cr | Al | La | Fe + Others |
|---|---|---|---|---|---|---|---|---|
| 0.042 | 0.28 | 0.19 | 0.0076 | 0.0011 | 19.95 | 5.49 | 0.64 | balance |
| Temperature (°C) | (s−1) | (MPa) | (MPa) | (MPa) | (MPa) | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1150 | 1 | 48.25 | 0.177 | 47.3 | 0.324 | 46.49 | 0.471 | 47.55 | 0.074 |
| 0.1 | 31.34 | 0.165 | 31.11 | 0.232 | 30.52 | 0.461 | 29.75 | 0.070 | |
| 0.01 | 18.32 | 0.111 | 17.62 | 0.319 | 17.30 | 0.494 | 18.24 | 0.071 | |
| 0.001 | 11.56 | 0.11 | 11.12 | 0.316 | 10.97 | 0.494 | 11.46 | 0.051 | |
| 1100 | 0.1 | 38.97 | 0.19 | 38.34 | 0.324 | 37.51 | 0.466 | 36.62 | 0.075 |
| 0.01 | 24.57 | 0.169 | 23.84 | 0.319 | 23.31 | 0.496 | 24.05 | 0.078 | |
| 0.001 | 11.91 | 0.097 | 11.76 | 0.277 | 11.54 | 0.44 | 11.86 | 0.066 | |
| 1050 | 0.1 | 49.86 | 0.185 | 48.78 | 0.317 | 47.87 | 0.444 | 48.95 | 0.074 |
| 0.01 | 29.67 | 0.168 | 29.27 | 0.264 | 28.6 | 0.438 | 28.97 | 0.086 | |
| 0.001 | 16.73 | 0.128 | 16.37 | 0.266 | 16.13 | 0.407 | 16.61 | 0.063 | |
| 1000 | 0.1 | 62.3 | 0.163 | 58.56 | 0.326 | 54.37 | 0.542 | 60.23 | 0.076 |
| 0.01 | 38.48 | 0.151 | 36.88 | 0.302 | 35.06 | 0.514 | 38.3 | 0.079 | |
| 0.001 | 20.84 | 0.155 | 20.48 | 0.315 | 20.22 | 0.468 | 20.81 | 0.056 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Z.; Liu, J.; Shao, J.; McLean, A. Dynamic Recrystallization Kinetics of As-Cast Fe-Cr-Al-La Stainless Steel during Hot Deformation. Metals 2023, 13, 692. https://doi.org/10.3390/met13040692
Deng Z, Liu J, Shao J, McLean A. Dynamic Recrystallization Kinetics of As-Cast Fe-Cr-Al-La Stainless Steel during Hot Deformation. Metals. 2023; 13(4):692. https://doi.org/10.3390/met13040692
Chicago/Turabian StyleDeng, Zhenqiang, Jianhua Liu, Jian Shao, and Alexander McLean. 2023. "Dynamic Recrystallization Kinetics of As-Cast Fe-Cr-Al-La Stainless Steel during Hot Deformation" Metals 13, no. 4: 692. https://doi.org/10.3390/met13040692
APA StyleDeng, Z., Liu, J., Shao, J., & McLean, A. (2023). Dynamic Recrystallization Kinetics of As-Cast Fe-Cr-Al-La Stainless Steel during Hot Deformation. Metals, 13(4), 692. https://doi.org/10.3390/met13040692








