Hall–Petch Description of the Necking Point Stress
Abstract
1. Introduction
2. Dislocation Density Based Constitutive Modeling of the Hall–Petch Behavior
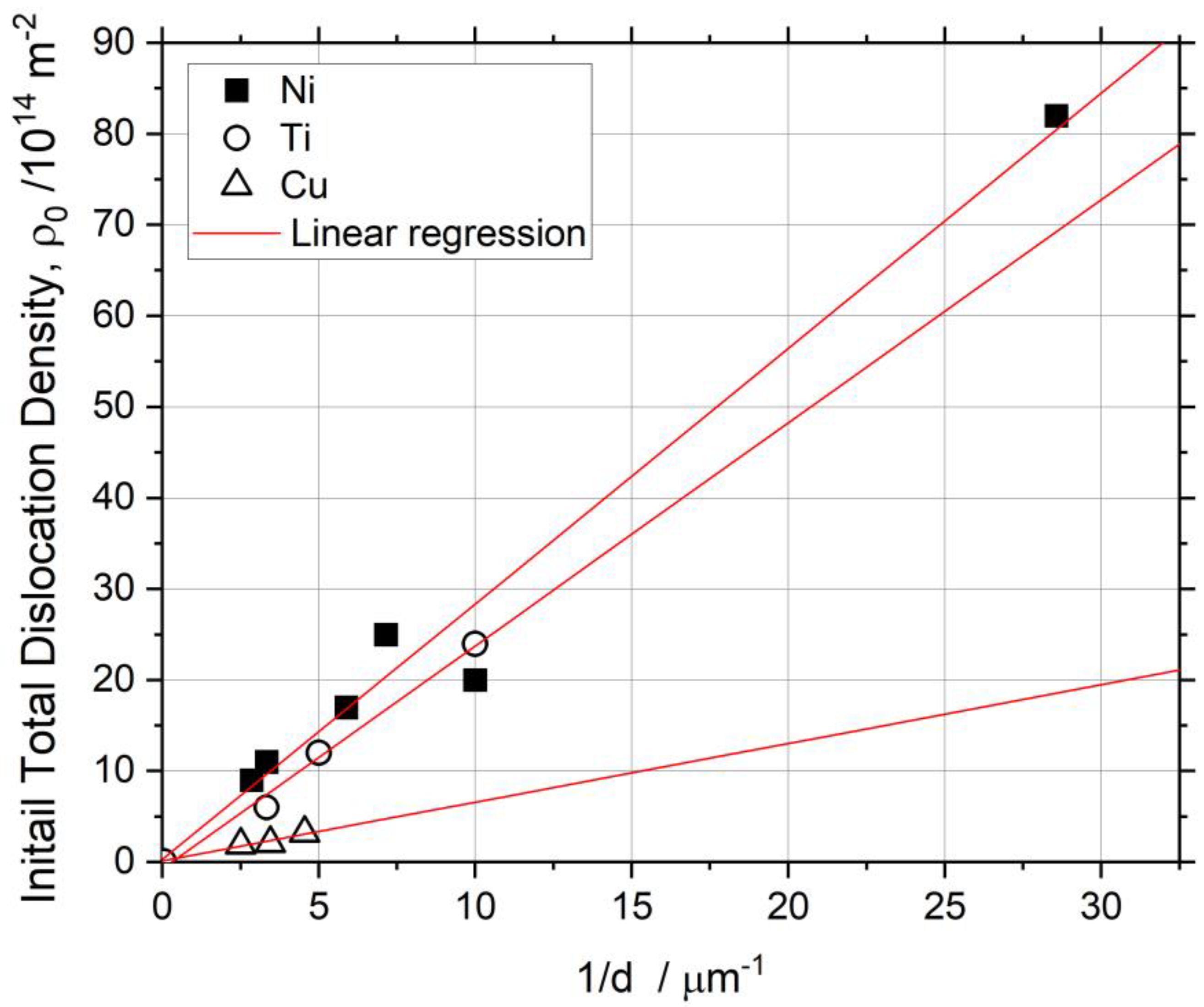
3. The Necking Stress Locus as a Basis for an H–P Analysis
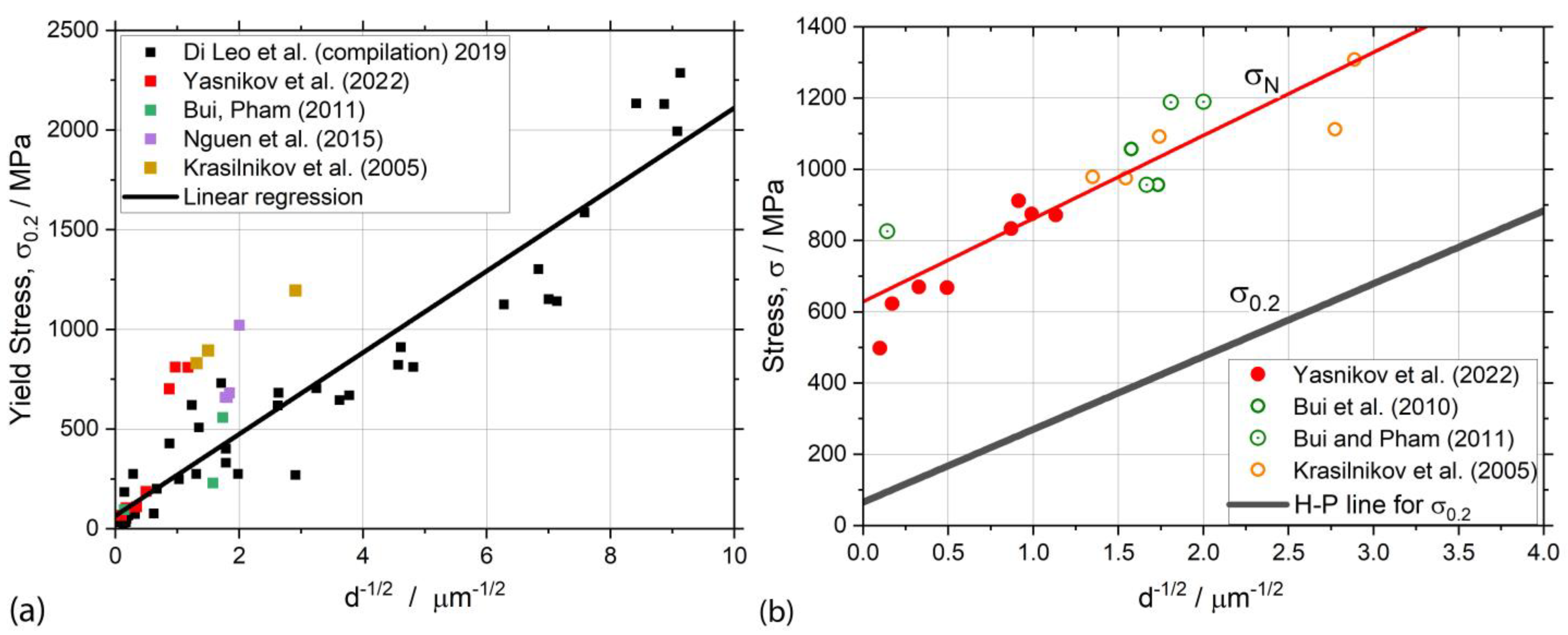
4. An H–P Dependence for of Nickel and Titanium—A Compilation of Experimental Results
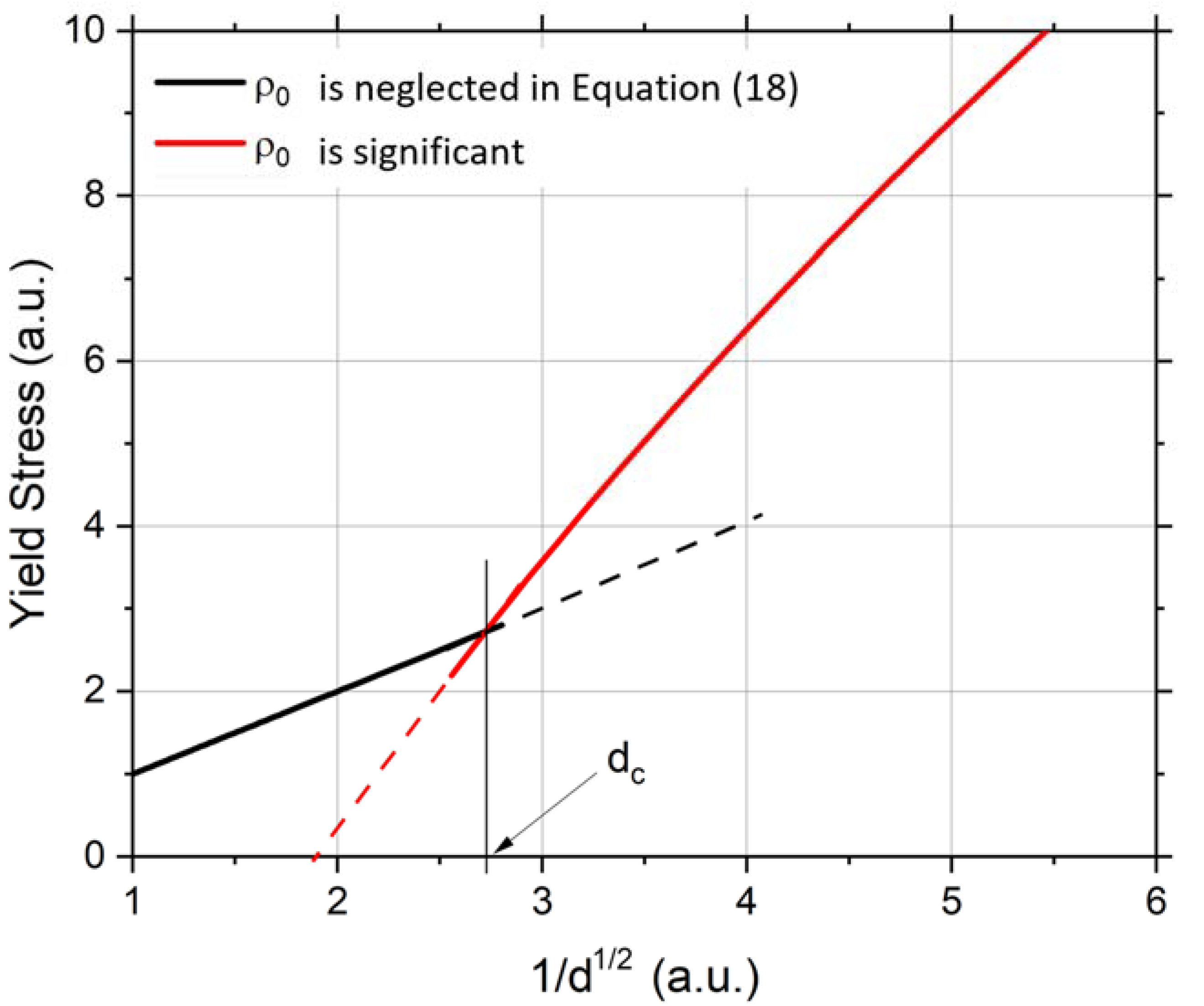
5. Discussion
6. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Armstrong, R.W. The influence of polycrystal grain size on several mechanical properties of materials. Metall. Mater. Trans. B 1970, 1, 1169–1176. [Google Scholar] [CrossRef]
- Armstrong, R.; Codd, I.; Douthwaite, R.M.; Petch, N.J. The plastic deformation of polycrystalline aggregates. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1962, 7, 45–58. [Google Scholar] [CrossRef]
- Armstrong, R.W. 60 years of Hall-Petch: Past to present nano-scale connections. Mater. Trans. 2014, 55, 2–12. [Google Scholar] [CrossRef]
- Armstrong, R.W.; Balasubramanian, N. Unified Hall-Petch description of nano-grain nickel hardness, flow stress and strain rate sensitivity measurements. AIP Adv. 2017, 7, 085010. [Google Scholar] [CrossRef]
- Zerilli, F.J.; Armstrong, R.W. Dislocation-mechanics-based constitutive relations for material dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef]
- Ludwik, P. Elemente der Technologischen Mechanik; Springer: Berlin/Heidelberg, Germany, 1909; p. 57S. [Google Scholar]
- Armstrong, R.W. Engineering science aspects of the Hall–Petch relation. Acta Mech. 2014, 225, 1013–1028. [Google Scholar] [CrossRef]
- Armstrong, R.W. The Dislocation Mechanics of Crystal/Polycrystal Plasticity. Crystals 2022, 12, 1199. [Google Scholar] [CrossRef]
- Kocks, U.F. Laws for work-hardening and low-temperature creep. J. Eng. Mater. Technol.-Trans. Asme 1976, 98, 76–85. [Google Scholar] [CrossRef]
- Estrin, Y.; Mecking, H. A unified phenomenological description of work hardening and creep based on one-parameter models. Acta Metall. 1984, 32, 57–70. [Google Scholar] [CrossRef]
- Estrin, Y. Unified Constitutive Laws of Plastic Deformation; Academic Press: San Diego, CA, USA; London, UK, 1996. [Google Scholar]
- Bergström, Y. A dislocation model for the stress-strain behaviour of polycrystalline α-Fe with special emphasis on the variation of the densities of mobile and immobile dislocations. Mater. Sci. Eng. 1970, 5, 193–200. [Google Scholar] [CrossRef]
- Klepaczko, J. Thermally activated flow and strain rate history effects for some polycrystalline f.c.c. metals. Mater. Sci. Eng. 1975, 18, 121–135. [Google Scholar] [CrossRef]
- Di Leo, C.V.; Rimoli, J.J. New perspectives on the grain-size dependent yield strength of polycrystalline metals. Scr. Mater. 2019, 166, 149–153. [Google Scholar] [CrossRef]
- Conrad, H.; Feuerstein, S.; Rice, L. Effects of grain size on the dislocation density and flow stress of niobium. Mater. Sci. Eng. 1967, 2, 157–168. [Google Scholar] [CrossRef]
- Ashby, M.F. The deformation of plastically non-homogeneous materials. Philos. Mag. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Cordero, Z.C.; Knight, B.E.; Schuh, C.A. Six decades of the Hall–Petch effect—A survey of grain-size strengthening studies on pure metals. Int. Mater. Rev. 2016, 61, 495–512. [Google Scholar] [CrossRef]
- Hazzledine, P.M. Direct versus indirect dispersion hardening. Scr. Metall. Mater. 1992, 26, 57–58. [Google Scholar] [CrossRef]
- Hazzledine, P.M.; Louat, N.P. Direct as against indirect dispersion work hardening. Philos. Mag. Lett. 1994, 70, 129–133. [Google Scholar] [CrossRef]
- Estrin, Y.; Mecking, H. A remark in connection with ‘direct versus indirect dispersion hardening’. Scr. Metall. Mater. 1992, 27, 647–648. [Google Scholar] [CrossRef]
- Godon, A.; Creus, J.; Cohendoz, S.; Conforto, E.; Feaugas, X.; Girault, P.; Savall, C. Effects of grain orientation on the Hall–Petch relationship in electrodeposited nickel with nanocrystalline grains. Scr. Mater. 2010, 62, 403–406. [Google Scholar] [CrossRef]
- Lefebvre, S.; Devincre, B.; Hoc, T. Yield stress strengthening in ultrafine-grained metals: A two-dimensional simulation of dislocation dynamics. J. Mech. Phys. Solids 2007, 55, 788–802. [Google Scholar] [CrossRef]
- Malygin, G.A. Plasticity and strength of micro- and nanocrystalline materials. Phys. Solid State 2007, 49, 1013–1033. [Google Scholar] [CrossRef]
- Lefebvre, S.; Devincre, B.; Hoc, T. Simulation of the Hall–Petch effect in ultra-fine grained copper. Mater. Sci. Eng. A 2005, 400–401, 150–153. [Google Scholar] [CrossRef]
- Tjerkstra, H.H. The effect of grain size on the stress-strain curve of α-iron and the connection with the plastic deformation of the grain boundaries. Acta Metall. 1961, 9, 259–263. [Google Scholar] [CrossRef]
- Ono, N.; Karashima, S. Grain size dependence of flow stress in copper polycrystals. Scr. Metall. 1982, 16, 381–384. [Google Scholar] [CrossRef]
- Thompson, A.W.; Baskes, M.I. The influence of grain size on the work hardening of face-center cubic polycrystals. Philos. Mag. A J. Theor. Exp. Appl. Phys. 1973, 28, 301–308. [Google Scholar] [CrossRef]
- Thompson, A.W.; Baskes, M.I.; Flanagan, W.F. The dependence of polycrystal work hardening on grain size. Acta Metall. 1973, 21, 1017–1028. [Google Scholar] [CrossRef]
- Hansen, N. The effect of grain size and strain on the tensile flow stress of aluminium at room temperature. Acta Metall. 1977, 25, 863–869. [Google Scholar] [CrossRef]
- Al-haidary, J.T.; Petch, N.J.; de los Rios, E.R. The plastic deformation of polycrystals I. Aluminium between room temperature and 400 °C. Philos. Mag. A 1983, 47, 869–890. [Google Scholar] [CrossRef]
- Sonon, D.; Smith, G. Effect of grain size and temperature on the strengthening of nickel and a nickel-cobalt alloy by carbon. Trans. Metall. Soc. AIME 1968, 242, 1527–1533. [Google Scholar]
- Feaugas, X.; Haddou, H. Grain-size effects on tensile behavior of nickel and AISI 316L stainless steel. Met. Mater. Trans. A 2003, 34, 2329–2340. [Google Scholar] [CrossRef]
- Jago, R.A.; Hansen, N. Grain size effects in the deformation of polycrystalline iron. Acta Metall. 1986, 34, 1711–1720. [Google Scholar] [CrossRef]
- Lederich, R.J.; Sastry, S.M.L.; O’Neal, J.E.; Rath, B.B. The effect of grain size on yield stress and work hardening of polycrystalline titanium at 295 K and 575 K. Mater. Sci. Eng. 1978, 33, 183–188. [Google Scholar] [CrossRef]
- Ramani, S.V.; Rodriguez, P. Grain size dependence of the deformation behaviour of alpha zirconium. Can. Met. Q 1972, 11, 61–67. [Google Scholar] [CrossRef]
- Cerreta, E.; Yablinsky, C.A.; Gray, G.T.; Vogel, S.C.; Brown, D.W. The influence of grain size and texture on the mechanical response of high purity hafnium. Mater. Sci. Eng. A 2007, 456, 243–251. [Google Scholar] [CrossRef]
- Lasalmonie, A.; Strudel, J.L. Influence of grain size on the mechanical behaviour of some high strength materials. J. Mater. Sci. 1986, 21, 1837–1852. [Google Scholar] [CrossRef]
- Kocks, U.F.; Mecking, H. Physics and phenomenology of strain hardening: The FCC case. Prog. Mater. Sci. 2003, 48, 171–273. [Google Scholar] [CrossRef]
- Considère, A. Mémoire sur l’emploi du fer et de l’acier dans les Constructions; Ch. Dunod, Editeur: Paris, France, 1885; Volume 9, pp. 574–775. [Google Scholar]
- Hart, E.W. Theory of the tensile test. Acta Metall. 1967, 15, 351–355. [Google Scholar] [CrossRef]
- Yasnikov, I.S.; Vinogradov, A.; Estrin, Y. Revisiting the Considère criterion from the viewpoint of dislocation theory fundamentals. Scr. Mater. 2014, 76, 37–40. [Google Scholar] [CrossRef]
- Yasnikov, I.S.; Estrin, Y.; Vinogradov, A. What governs ductility of ultrafine-grained metals? A microstructure based approach to necking instability. Acta Mater. 2017, 141, 18–28. [Google Scholar] [CrossRef]
- Dalla Torre, F.; Lapovok, R.; Sandlin, J.; Thomson, P.F.; Davies, C.H.J.; Pereloma, E.V. Microstructures and properties of copper processed by equal channel angular extrusion for 1–16 passes. Acta Mater. 2004, 52, 4819–4832. [Google Scholar] [CrossRef]
- Vinogradov, A.; Yasnikov, I.S.; Matsuyama, H.; Uchida, M.; Kaneko, Y.; Estrin, Y. Controlling strength and ductility: Dislocation-based model of necking instability and its verification for ultrafine grain 316L steel. Acta Mater. 2016, 106, 295–303. [Google Scholar] [CrossRef]
- Yasnikov, I.S.; Kaneko, Y.; Uchida, M.; Vinogradov, A. The grain size effect on strain hardening and necking instability revisited from the dislocation density evolution approach. Mater. Sci. Eng. A 2022, 831, 142330. [Google Scholar] [CrossRef]
- Bui, Q.H.; Dirras, G.; Ramtani, S.; Gubicza, J. On the strengthening behavior of ultrafine-grained nickel processed from nanopowders. Mater. Sci. Eng. A 2010, 527, 3227–3235. [Google Scholar] [CrossRef]
- Bui, Q.H.; Pham, X.T. Modeling of microstructure effects on the mechanical behavior of ultrafine-grained nickels processed by hot isostatic pressing. Int. J. Mech. Sci. 2011, 53, 812–826. [Google Scholar] [CrossRef]
- Nguyen, T.-D.; Phan, V.-T.; Bui, Q.-H. Modeling of Microstructure Effects on the Mechanical Behavior of Ultrafine-Grained Nickels Processed by Severe Plastic Deformation by Crystal Plasticity Finite Element Model. J. Eng. Mater. Technol. 2015, 137, 021010. [Google Scholar] [CrossRef]
- Krasilnikov, N.; Lojkowski, W.; Pakiela, Z.; Valiev, R. Tensile strength and ductility of ultra-fine-grained nickel processed by severe plastic deformation. Mater. Sci. Eng. A 2005, 397, 330–337. [Google Scholar] [CrossRef]
- Beygelzimer, Y.; Orlov, D. Metal plasticity during the twist extrusion. Defect Diffus. Forum 2002, 208–209, 311–314. [Google Scholar] [CrossRef]
- Pachla, W.; Kulczyk, M.; Sus-Ryszkowska, M.; Mazur, A.; Kurzydlowski, K.J. Nanocrystalline titanium produced by hydrostatic extrusion. J. Mater. Process. Technol. 2008, 205, 173–182. [Google Scholar] [CrossRef]
- Kim, W.-J.; Hyun, C.-Y.; Kim, H.-K. Fatigue strength of ultrafine-grained pure Ti after severe plastic deformation. Scr. Mater. 2006, 54, 1745–1750. [Google Scholar] [CrossRef]
- Stolyarov, V.V.; Zhu, Y.T.; Lowe, T.C.; Islamgaliev, R.K.; Valiev, R.Z. A two step SPD processing of ultrafine-grained titanium. Nanostruct. Mater. 1999, 11, 947–954. [Google Scholar] [CrossRef]
- Stolyarov, V.V.; Beigel’zimer, Y.E.; Orlov, D.V.; Valiev, R.Z. Refinement of microstructure and mechanical properties of titanium processed by twist extrusion and subsequent rolling. Phys. Met. Met. 2005, 99, 204–211. [Google Scholar]
- Yapici, G.G.; Karaman, I.; Maier, H.J. Mechanical flow anisotropy in severely deformed pure titanium. Mater. Sci. Eng. A 2006, 434, 294–302. [Google Scholar] [CrossRef]
- Anibal, M.; Andrea, M.K.; Maurizio, F.; Vitor, L.S. How severe plastic deformation at cryogenic temperature affects strength, fatigue, and impact behaviour of grade 2 titanium. IOP Conf. Ser. Mater. Sci. Eng. 2014, 63, 012161. [Google Scholar]
- Rao, M.S.; Chakkingal, U.; Raghu, T. Mechanical behavior of commercial purity titanium processed by equal channel angular pressing followed by cold rolling. Trans. Indian Inst. Met. 2013, 66, 357–362. [Google Scholar] [CrossRef]
- Salishchev, G.A.; Galeev, R.M.; Malysheva, S.P.; Zherebtsov, S.V.; Mironov, S.Y.; Valiakhmetov, O.R.; Ivanisenko, É.I. Formation of submicrocrystalline structure in titanium and titanium alloys and their mechanical properties. Met. Sci. Heat Treat. 2006, 48, 63–69. [Google Scholar] [CrossRef]
- Miura, H.; Kobayashi, M.; Aoba, T.; Aoyama, H.; Benjanarasuth, T. An approach for room-temperature multi-directional forging of pure titanium for strengthening. Mater. Sci. Eng. A 2018, 731, 603–608. [Google Scholar] [CrossRef]
- Kang, D.-H.; Kim, T.-W. Mechanical behavior and microstructural evolution of commercially pure titanium in enhanced multi-pass equal channel angular pressing and cold extrusion. Mater. Des. 2010, 31, S54–S60. [Google Scholar] [CrossRef]
- Terada, D.; Inoue, S.; Tsuji, N. Microstructure and mechanical properties of commercial purity titanium severely deformed by ARB process. J. Mater. Sci. 2007, 42, 1673–1681. [Google Scholar] [CrossRef]
- Milner, J.L.; Abu-Farha, F.; Bunget, C.; Kurfess, T.; Hammond, V.H. Grain refinement and mechanical properties of CP-Ti processed by warm accumulative roll bonding. Mater. Sci. Eng. A 2013, 561, 109–117. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, L. The ultrafine-grained titanium and biomedical titanium alloys processed by severe plastic deformation (SPD). SOJ Mater. Sci. Eng. 2013, 1, 1–5. [Google Scholar] [CrossRef]
- Luo, P.; McDonald, D.T.; Palanisamy, S.; Dargusch, M.S.; Xia, K. Ultrafine-grained pure Ti recycled by equal channel angular pressing with high strength and good ductility. J. Mater. Process. Technol. 2013, 213, 469–476. [Google Scholar] [CrossRef]
- Medvedev, A.; Ng, H.P.; Lapovok, R.; Estrin, Y.; Lowe, T.C.; Anumalasetty, V.N. Comparison of laboratory-scale and industrial-scale equal channel angular pressing of commercial purity titanium. Mater. Lett. 2015, 145, 308–311. [Google Scholar] [CrossRef]
- Petch, N.J.; Armstrong, R.W. The tensile test. Acta Metall. Mater. 1990, 38, 2695–2700. [Google Scholar] [CrossRef]
- Tsuji, N.; Ito, Y.; Saito, Y.; Minamino, Y. Strength and ductility of ultrafine grained aluminum and iron produced by ARB and annealing. Scr. Mater. 2002, 47, 893–899. [Google Scholar] [CrossRef]
- Takebe, H.; Ushioda, K. Effects of Grain Size, Thickness and Tensile Direction on Yield Behavior of Pure Titanium Sheet. J. Jpn. Inst. Met. Mater. 2022, 86, 53–61. [Google Scholar] [CrossRef]
- Figueiredo, R.B.; Langdon, T.G. Deformation mechanisms in ultrafine-grained metals with an emphasis on the Hall–Petch relationship and strain rate sensitivity. J. Mater. Res. Technol. 2021, 14, 137–159. [Google Scholar] [CrossRef]
- Dangwal, S.; Edalati, K.; Valiev, R.Z.; Langdon, T.G. Breaks in the Hall–Petch relationship after severe plastic deformation of magnesium, aluminum, copper, and iron. Crystals 2023, 13, 413. [Google Scholar] [CrossRef]
- Khamsuk, S.; Park, N.; Gao, S.; Terada, D.; Adachi, H.; Tsuji, N. Mechanical properties of bulk ultrafine grained aluminum fabricated by torsion deformation at various temperatures and strain rates. Mater. Trans. 2014, 55, 106–113. [Google Scholar] [CrossRef]
- Tian, Y.Z.; Ren, Y.P.; Gao, S.; Zheng, R.X.; Wang, J.H.; Pan, H.C.; Zhang, Z.F.; Tsuji, N.; Qin, G.W. Two-stage Hall-Petch relationship in Cu with recrystallized structure. J. Mater. Sci. Technol. 2020, 48, 31–35. [Google Scholar] [CrossRef]
- Bai, Y.; Kitamura, H.; Gao, S.; Tian, Y.; Park, N.; Park, M.-h.; Adachi, H.; Shibata, A.; Sato, M.; Murayama, M.; et al. Unique transition of yielding mechanism and unexpected activation of deformation twinning in ultrafine grained Fe-31Mn-3Al-3Si alloy. Sci. Rep. 2021, 11, 15870. [Google Scholar] [CrossRef]
- Fu, B.; Pei, C.; Pan, H.; Guo, Y.; Fu, L.; Shan, A. Hall-Petch relationship of interstitial-free steel with a wide grain size range processed by asymmetric rolling and subsequent annealing. Mater. Res. Express 2020, 7, 116516. [Google Scholar] [CrossRef]
- Kashyap, B.P.; Tangri, K. On the Hall-Petch relationship and substructural evolution in type 316L stainless steel. Acta Metall. Et Mater. 1995, 43, 3971–3981. [Google Scholar] [CrossRef]
- Thompson, A.W. Effect of grain size on work hardening in nickel. Acta Metall. 1977, 25, 83–86. [Google Scholar] [CrossRef]
- Bergström, Y.; Hallén, H. Hall–Petch relationships of iron and steel. Met. Sci. 1983, 17, 341–347. [Google Scholar] [CrossRef]
- Lloyd, D.J. Deformation of fine-grained aluminium alloys. Met. Sci. 1980, 14, 193–198. [Google Scholar] [CrossRef]
- Armstrong, R.W. The Yield and Flow Stress Dependence Polycrystal Grain Size. In Yield, Flow and Fracture of Polycrystals; Baker, T.N., Ed.; Applied Science Publishers, Ltd.: London, UK; New York, NY, USA, 1983. [Google Scholar]
- Holt, D.L. Dislocation Cell Formation in Metals. J. Appl. Phys. 1970, 41, 3197–3201. [Google Scholar] [CrossRef]
- Zhilyaev, A.P.; Gubicza, J.; Nurislamova, G.; Revesz, A.; Surinach, S.; Baro, M.D.; Ungar, T. Microstructural characterization of ultrafine-grained nickel. Phys. Status Solidi A 2003, 198, 263–271. [Google Scholar] [CrossRef]
- Gubicza, J.; Fogarassy, Z.; Krállics, G.; Lábár, J.; Törköly, T. Microstructure and mechanical behavior of ultrafine-grained titanium. Mater. Sci. Forum 2008, 589, 99–104. [Google Scholar] [CrossRef]
- Fattah-alhosseini, A.; Keshavarz, M.K.; Mazaheri, Y.; Reza Ansari, A.; Karimi, M. Strengthening mechanisms of nano-grained commercial pure titanium processed by accumulative roll bonding. Mater. Sci. Eng. A 2017, 693, 164–169. [Google Scholar] [CrossRef]
- Meyers, M.A.; Mishra, A.; Benson, D.J. Mechanical properties of nanocrystalline materials. Prog. Mater. Sci. 2006, 51, 427–556. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vinogradov, A.; Estrin, Y. Hall–Petch Description of the Necking Point Stress. Metals 2023, 13, 690. https://doi.org/10.3390/met13040690
Vinogradov A, Estrin Y. Hall–Petch Description of the Necking Point Stress. Metals. 2023; 13(4):690. https://doi.org/10.3390/met13040690
Chicago/Turabian StyleVinogradov, Alexey, and Yuri Estrin. 2023. "Hall–Petch Description of the Necking Point Stress" Metals 13, no. 4: 690. https://doi.org/10.3390/met13040690
APA StyleVinogradov, A., & Estrin, Y. (2023). Hall–Petch Description of the Necking Point Stress. Metals, 13(4), 690. https://doi.org/10.3390/met13040690