Development of a Non-Integral Form of Coordination Number Equation Based on Pair Distribution Function and Gaussian Function
Abstract
1. Introduction
2. The g(r) Data
3. Coordination Number Equation
3.1. Tao Coordination Number Model (Tao CN)
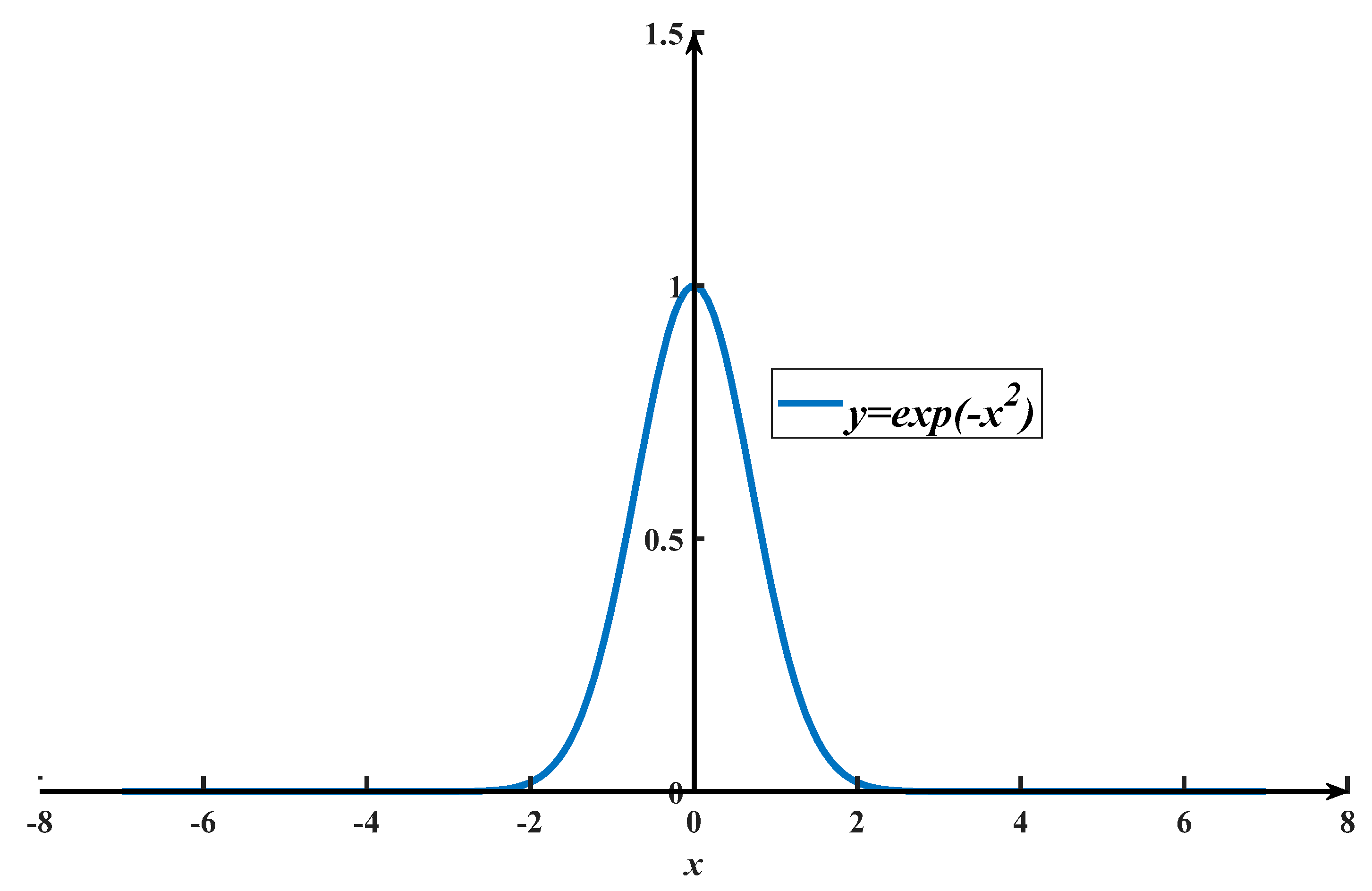
3.2. Gaussian Extrapolation Method
3.3. Classical Coordination Number Calculation Method
3.3.1. Symmetrical g(r)
3.3.2. Symmetrical r2g(r)
3.3.3. Symmetrical rg(r)
3.3.4. Integrate to the First Minimum Position in g(r)
4. Result and Discussion
4.1. The Parameter of First Coordination Shell
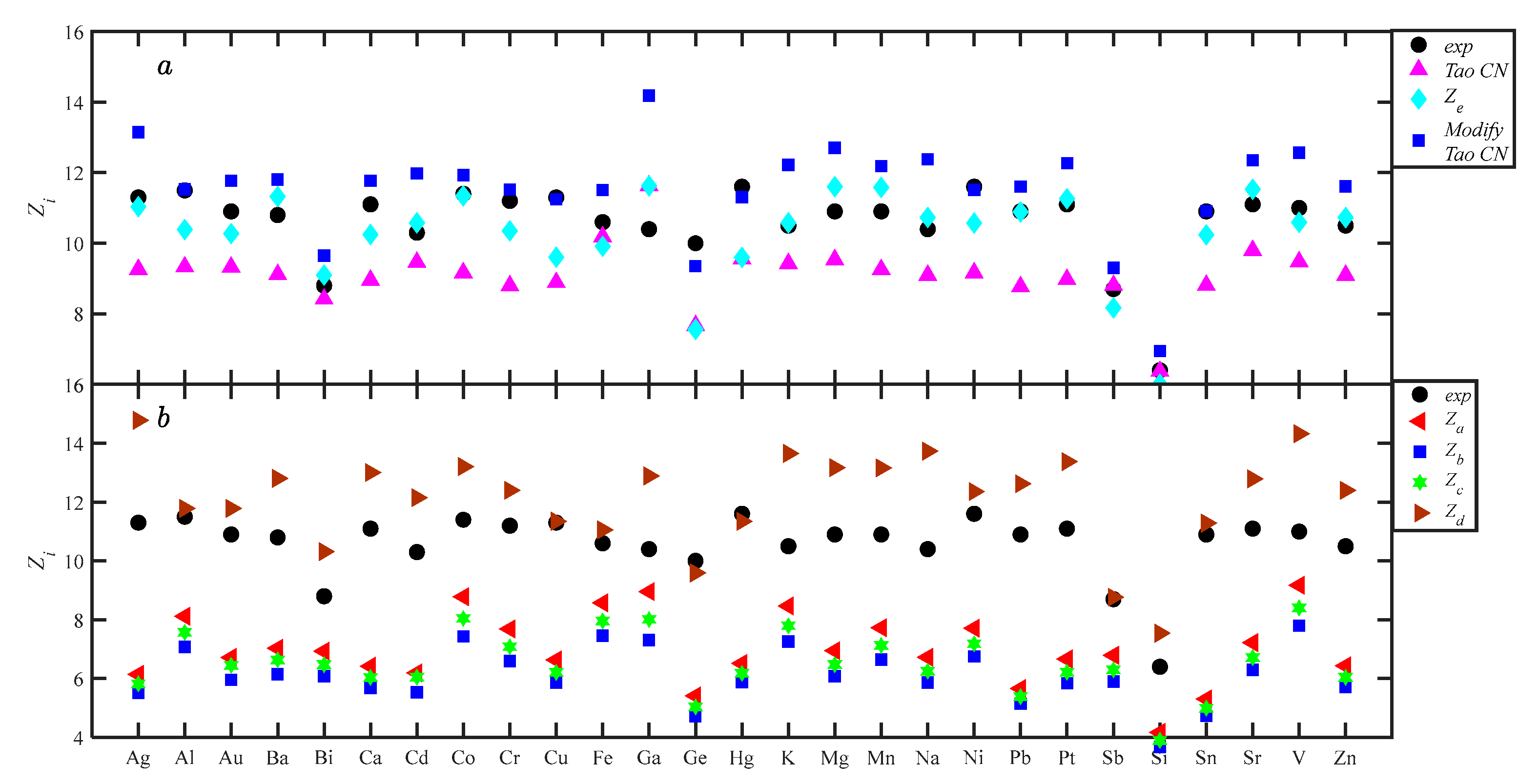
4.2. Verification of the Modified Tao Coordination Number Model (Tao CN)
4.3. Calculation of Coordination Number
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Equation Derivation
References
- Hines, A.L.; Walls, H.A. Determination of self diffusion coefficients using the radial distribution function. J. Metall. Trans. A 1979, 10, 1365–1370. [Google Scholar] [CrossRef]
- Kutzelnigg, W. Pair Correlation Theories. In Methods of Electronic Structure Theory; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Wilson, G.M. Vapor-Liquid Equilibrium. XI. A New Expression for the Excess Free Energy of Mixing. J. Am. Chem. Soc. 1963, 86, 127–130. [Google Scholar] [CrossRef]
- Tao, D.P. A new model of thermodynamics of liquid mixtures and its application to liquid alloys. Thermochim. Acta 2000, 363, 105–113. [Google Scholar] [CrossRef]
- Tao, D.-P. Correct Expressions of Enthalpy of Mixing and Excess Entropy from MIVM and Their Simplified Forms. Met. Mater. Trans. B 2016, 47, 1–9. [Google Scholar] [CrossRef]
- Belashchenko, D.K. Liquid Metals from Atomistic Potentials to Properties, Shock Compression, Earths Core and Nanoclusters Cited Pages; Nova Science Publishers: Hauppauge, NY, USA, 2018. [Google Scholar]
- Furukawa, K. The radial distribution curves of liquids by diffraction methods. Rep. Prog. Phys. 1962, 25, 332. [Google Scholar] [CrossRef]
- Eisenstein, A.; Gingrich, N.S. The Diffraction of X-rays by Argon in the Liquid, Vapor, and Critical Regions. Phys. Rev. 1942, 1, 261–270. [Google Scholar] [CrossRef]
- Coulson, C.A.; Rushbrooke, G.S. On the Interpretation of Atomic Distribution Curves for Liquids. Phys. Rev. 1939, 12, 1216–1223. [Google Scholar] [CrossRef]
- Hendus, V.H. Die Atomverteilung im flüssigen Quecksilber. Z. Nat. 1948, 7, 416–422. [Google Scholar] [CrossRef]
- Mikolaj, P.G.; Pings, C.J. The Use of the Coordination Number in the Interpretation of Fluid Structure. Phys. Chem. Liq. 1968, 1, 93–108. [Google Scholar] [CrossRef]
- Hong, X.; Masanori, I.; Matsusaka, T. X-ray diffraction measurements for expanded fluid mercury using synchrotron radiation: From the liquid to dense vapor. J. Non-Cryst. Solids 2002, 02, 284–289. [Google Scholar] [CrossRef]
- Vineyard, G.H. Neutron Diffraction Study of Liquid Mercury. J. Chem. Phys. 1954, 22, 1665–1667. [Google Scholar] [CrossRef]
- Higham, J.; Henchman, R.H. Overcoming the limitations of cutoffs for defining atomic coordination in multicomponent systems. J. Comput. Chem. 2018, 39, 705–710. [Google Scholar] [CrossRef] [PubMed]
- Caputi, R.W. Studies of liquid mercury and liquid mercury–gallium systems by X-ray diffraction. PhD Thesis, California Institute of Technology, Pasadena, CA, USA, 1965. [Google Scholar]
- Srirangam, P. Partial pair correlation functions and viscosity of liquid Al-Si hypoeutectic alloys via high-energy X-ray diffraction experiments. Philos. Mag. 2011, 91, 3867–3904. [Google Scholar] [CrossRef]
- Hines, A.L.; Walls, H.A.; Jethani, K.R. Determination of the Coordination Number of Liquid Metals near the Melting Point. Metall. Trans. A 1985, 1, 267–274. [Google Scholar] [CrossRef]
- Cahoon, J.R. The first coordination number for liquid metals. Can. J. Phys. 2004, 82, 291–301. [Google Scholar] [CrossRef]
- Tao, D.P. Prediction of the coordination numbers of liquid metals. Metall. Mater. Trans. A 2005, 36, 3495–3497. [Google Scholar] [CrossRef]
- Feller, W. An Introduction to Probability Theory and Its Applications; United States of America: Washington, DC, USA, 1950. [Google Scholar]
- Dorini, T.T.; Eleno, L. Liquid Bi–Pb and Bi–Li alloys: Mining thermodynamic properties from ab-initio molecular dynamics calculations using thermodynamic models. Calphad 2019, 67, 101687. [Google Scholar] [CrossRef]
- Haghtalab, A.; Yousefi, J.S. A new insight to validation of local composition models in binary mixtures using molecular dynamic simulation. AIChE J. 2015, 1, 275–286. [Google Scholar] [CrossRef]
- Waseda, Y. The Structure of Non-Crystalline Materials: Liquids and Amorphous Solids; United States of America: Washington, DC, USA, 1980. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: Oxford, UK, 1989. [Google Scholar]
- Coelho, A.A.; Chater, P.A.; Kern, A. Fast synthesis and refinement of the atomic pair distribution function. J. Appl. Crystallogr. 2015, 48, 869–875. [Google Scholar] [CrossRef]
- Gu, R.; Banerjee, S.; Du, Q.; Billinge, S.J.L. Algorithm for distance list extraction from pair distribution functions. Acta Crystallogr. Sect. A 2019, 75, 658–668. [Google Scholar] [CrossRef]
- Jakse, N.; Pasturel, A. Local order of liquid and supercooled zirconium by ab initio molecular dynamics. Phys. Rev. Lett. 2003, 91, 195501. [Google Scholar] [CrossRef] [PubMed]
- Iida, T.; Guthrie, R. The Physical Properties of Liquid Metals; Clarendon Press: Oxford, UK, 1988. [Google Scholar]
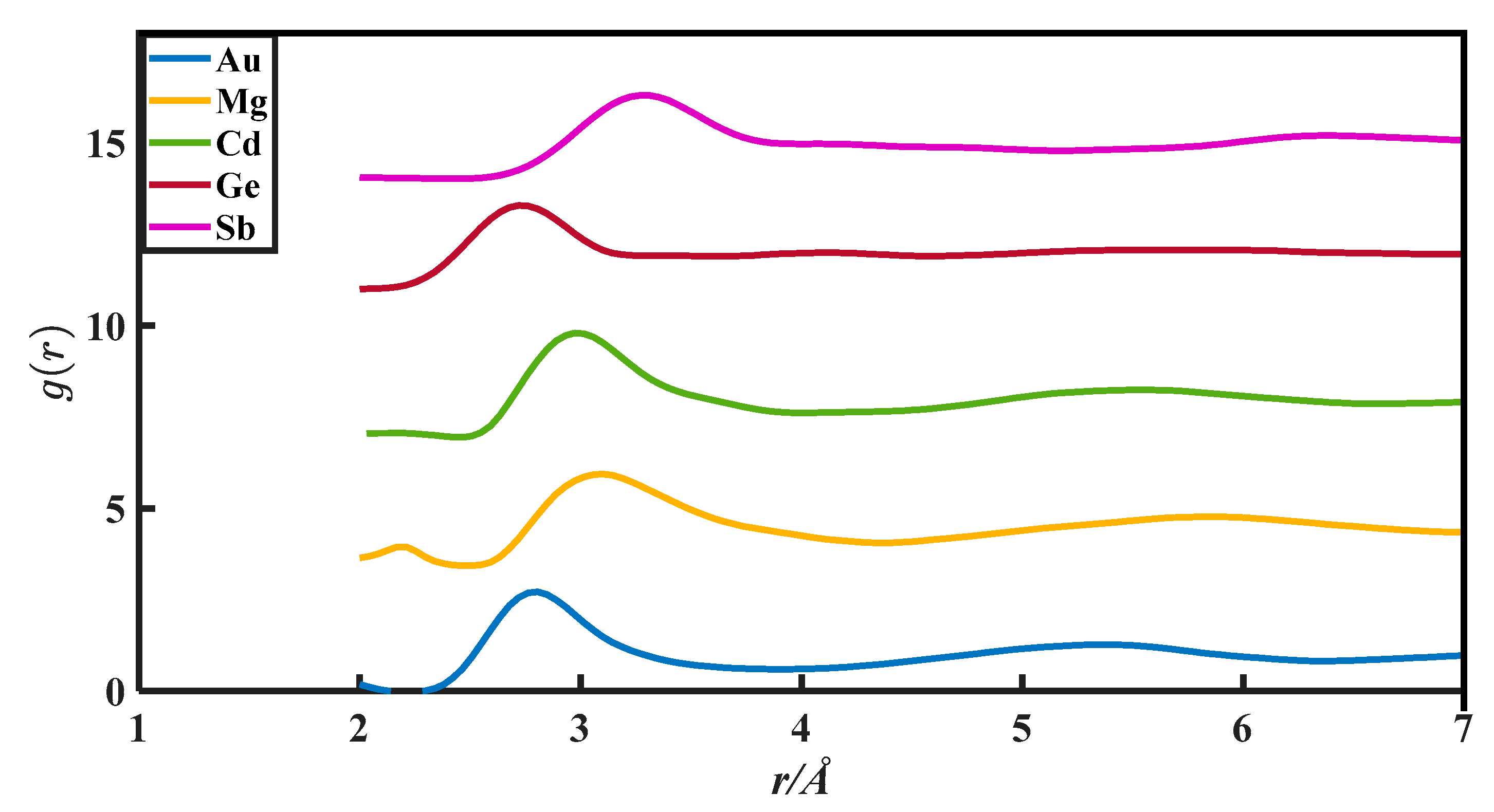
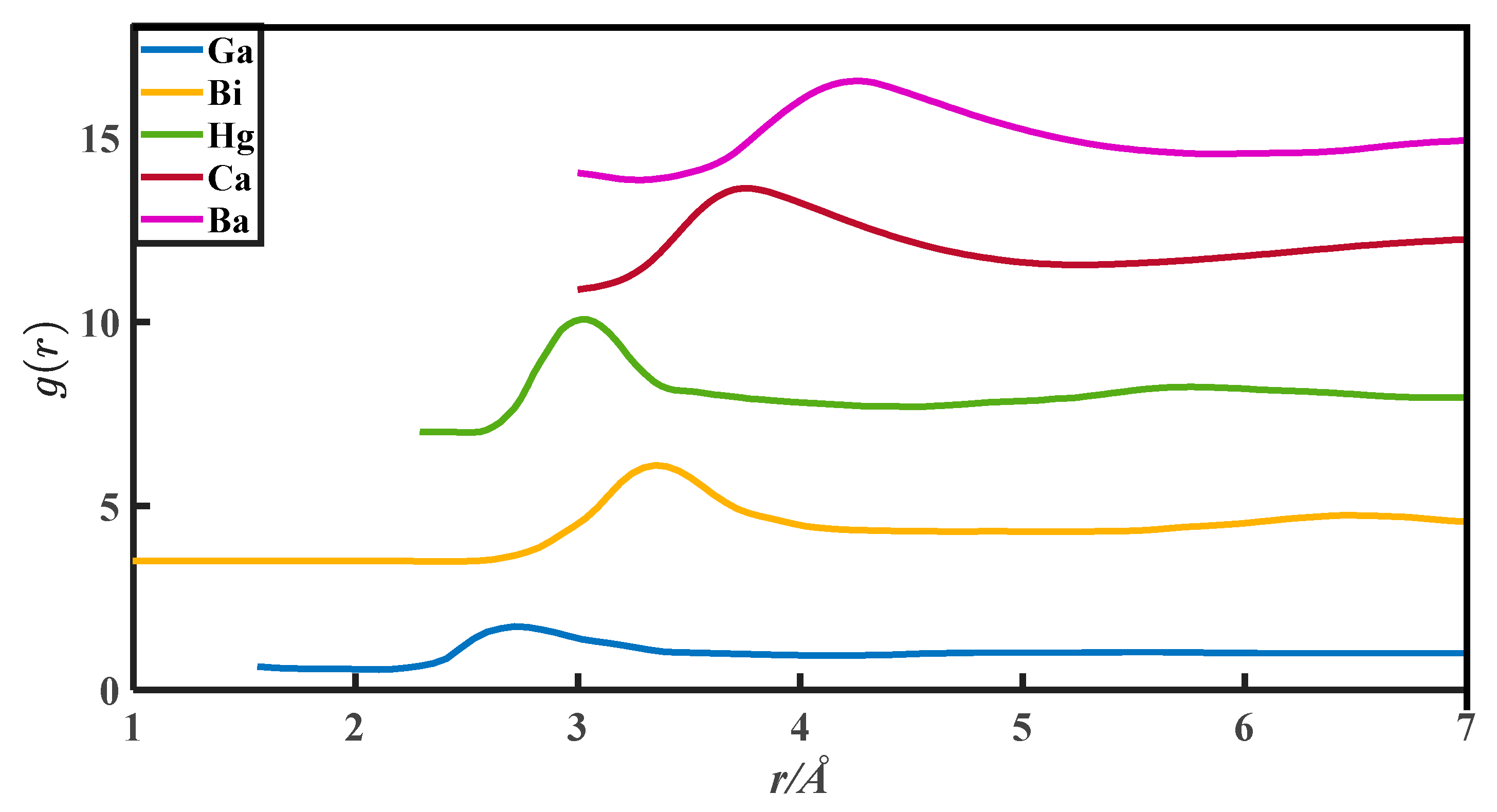
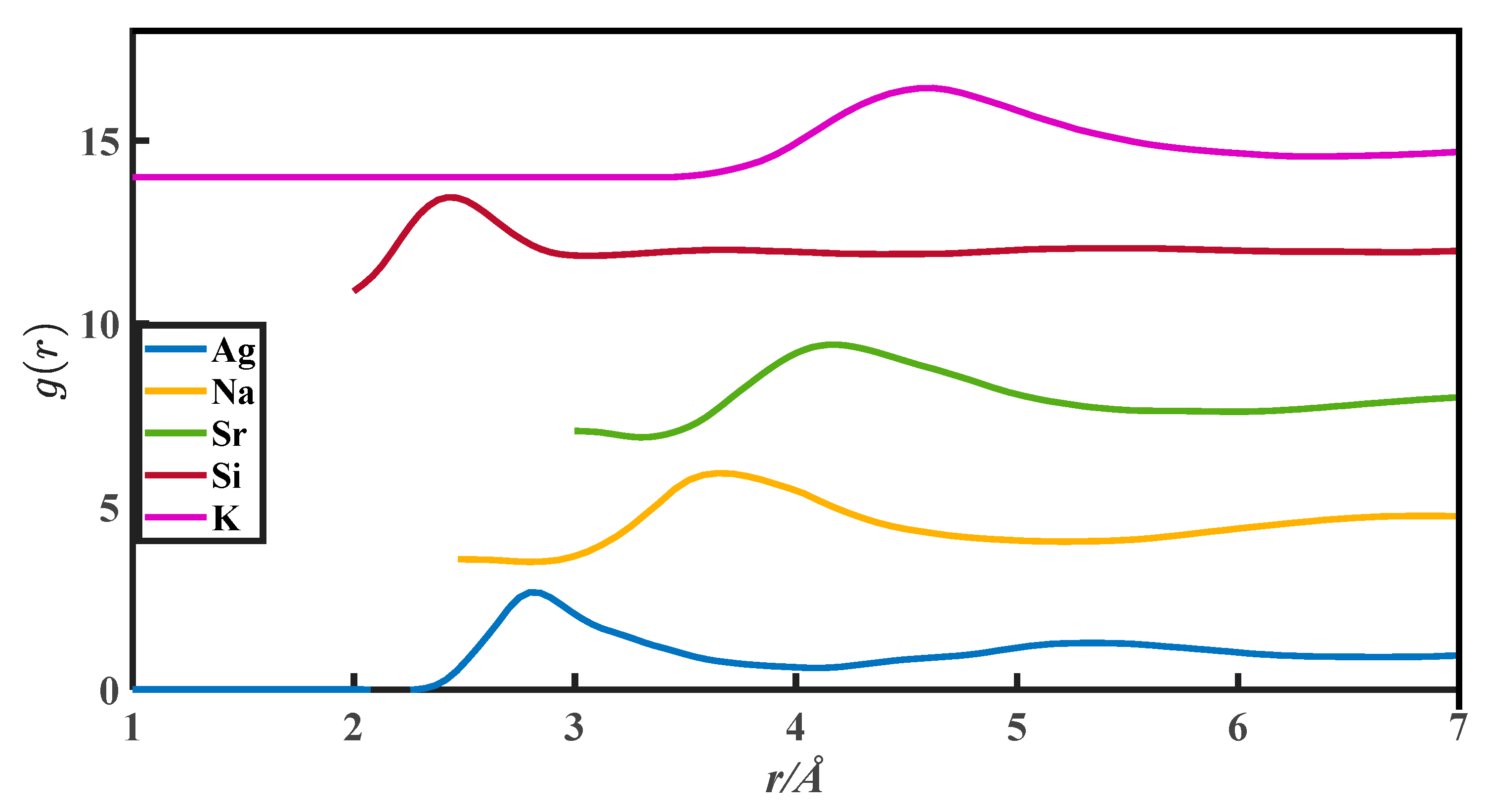
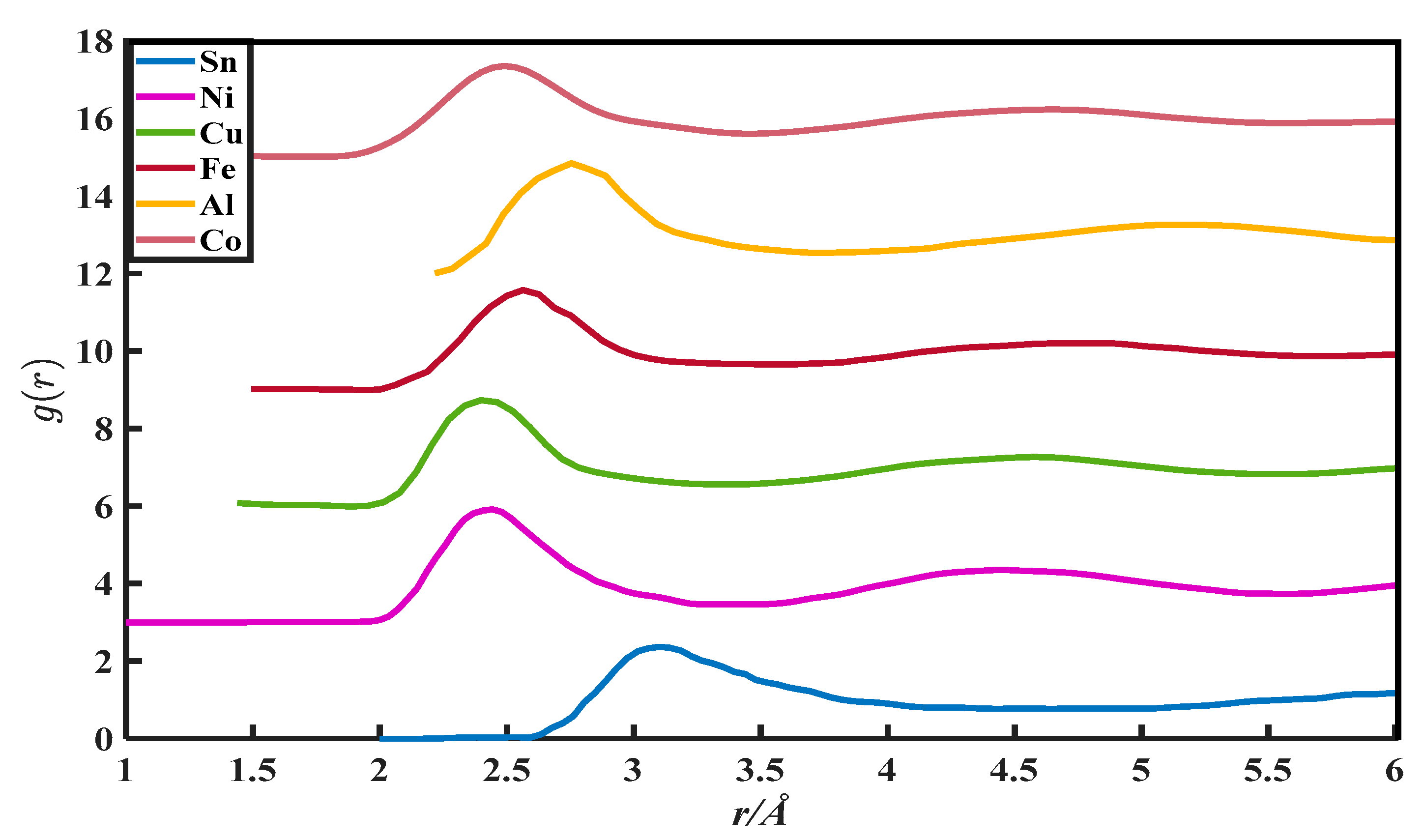
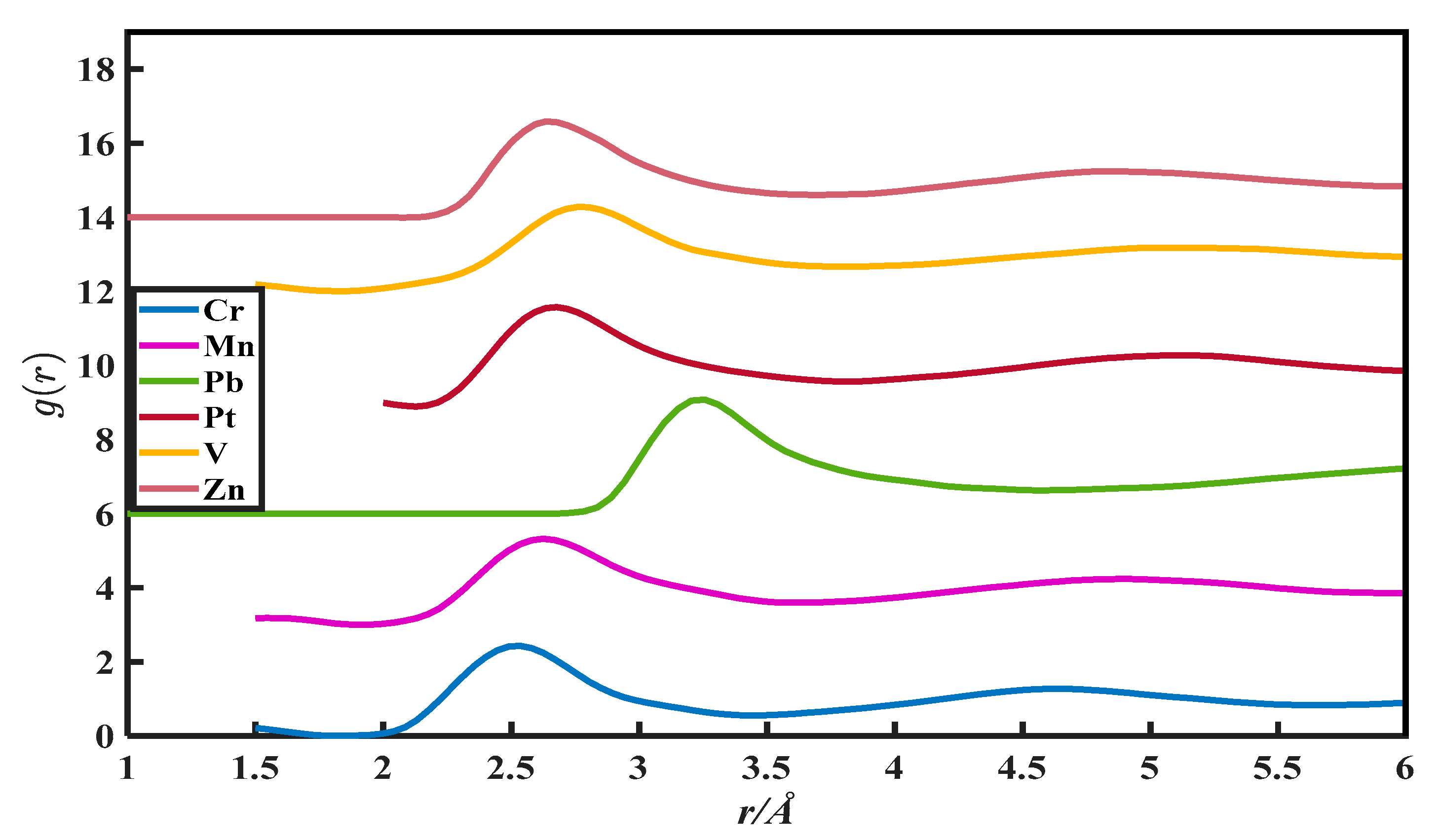
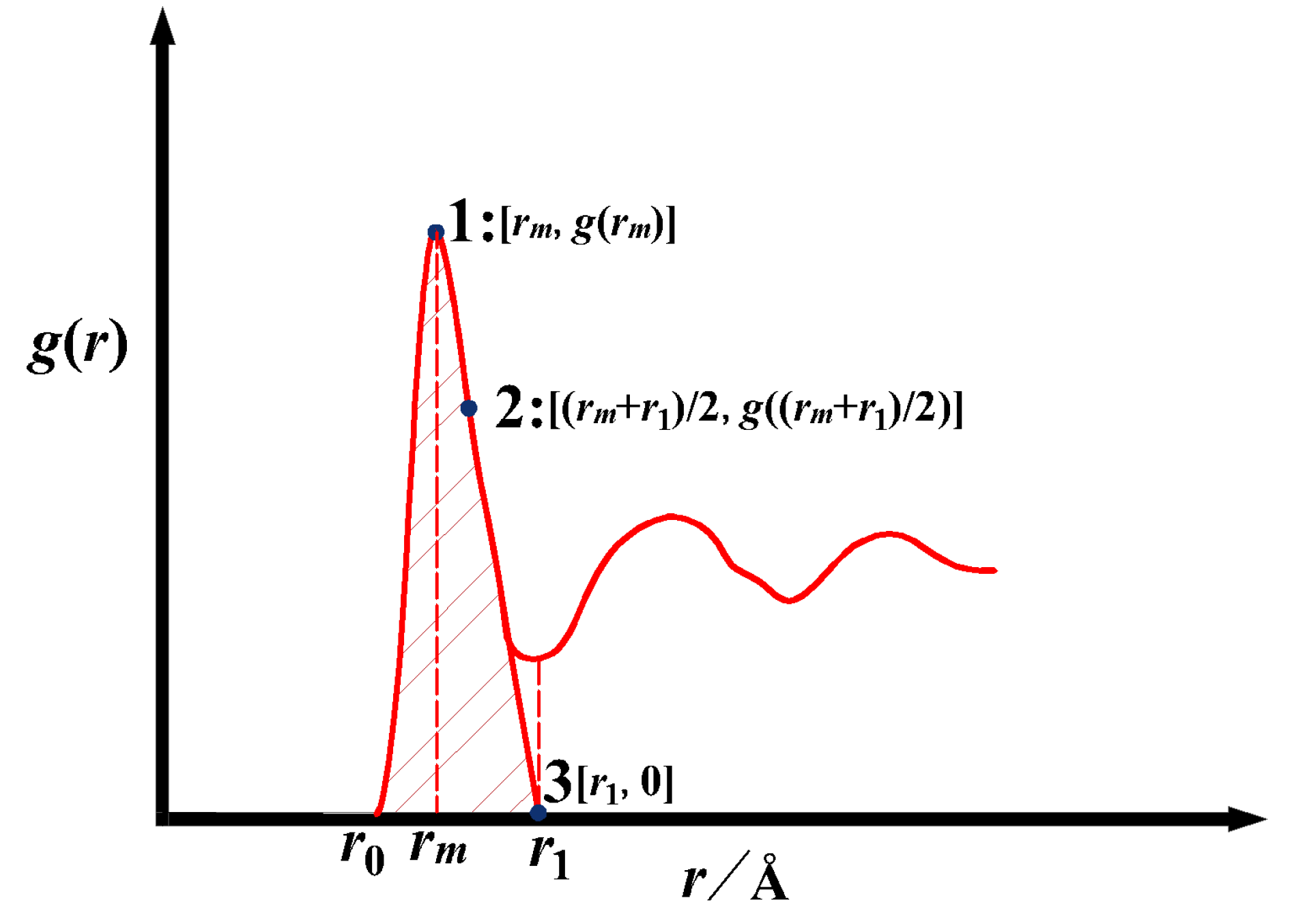
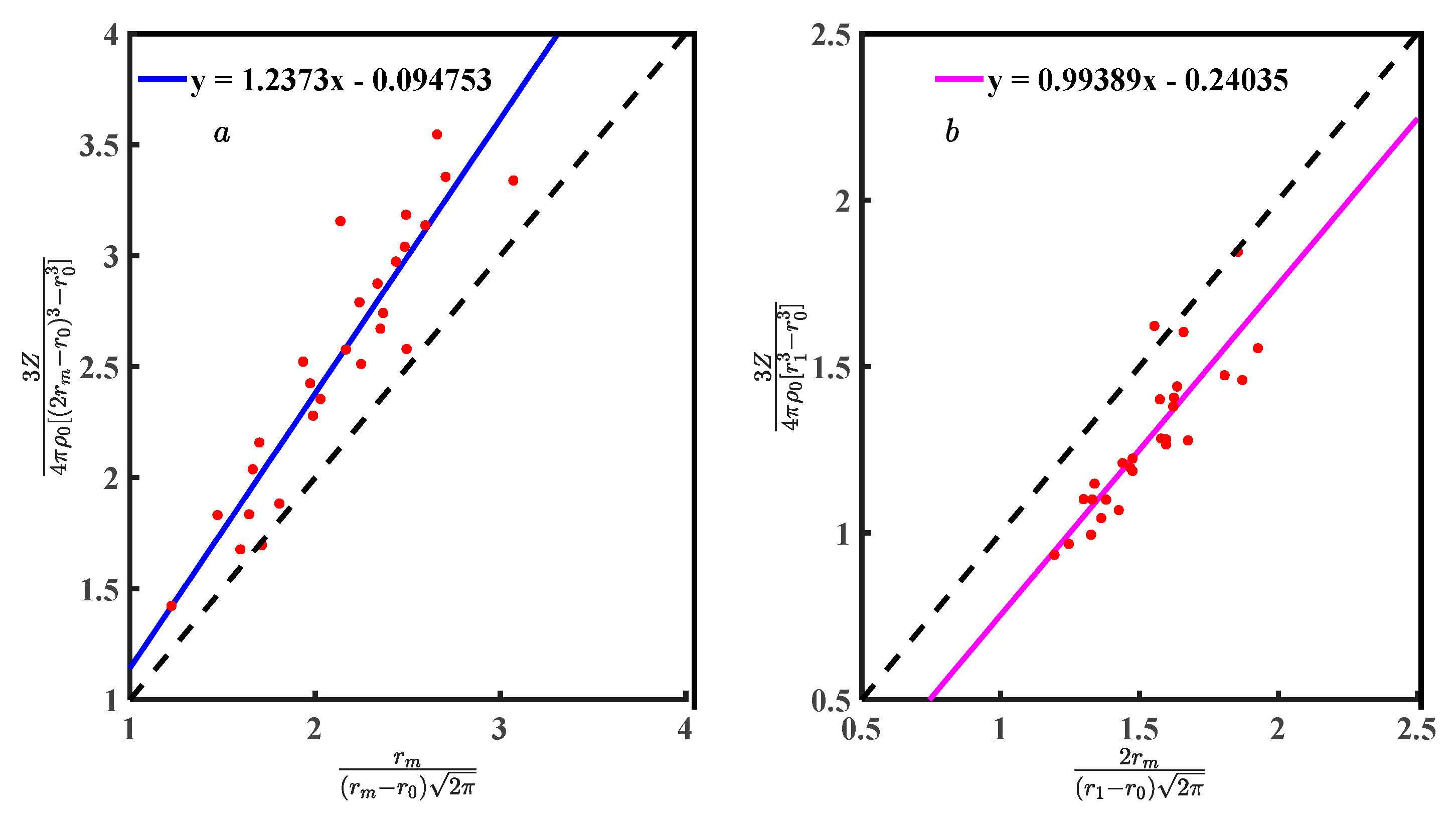
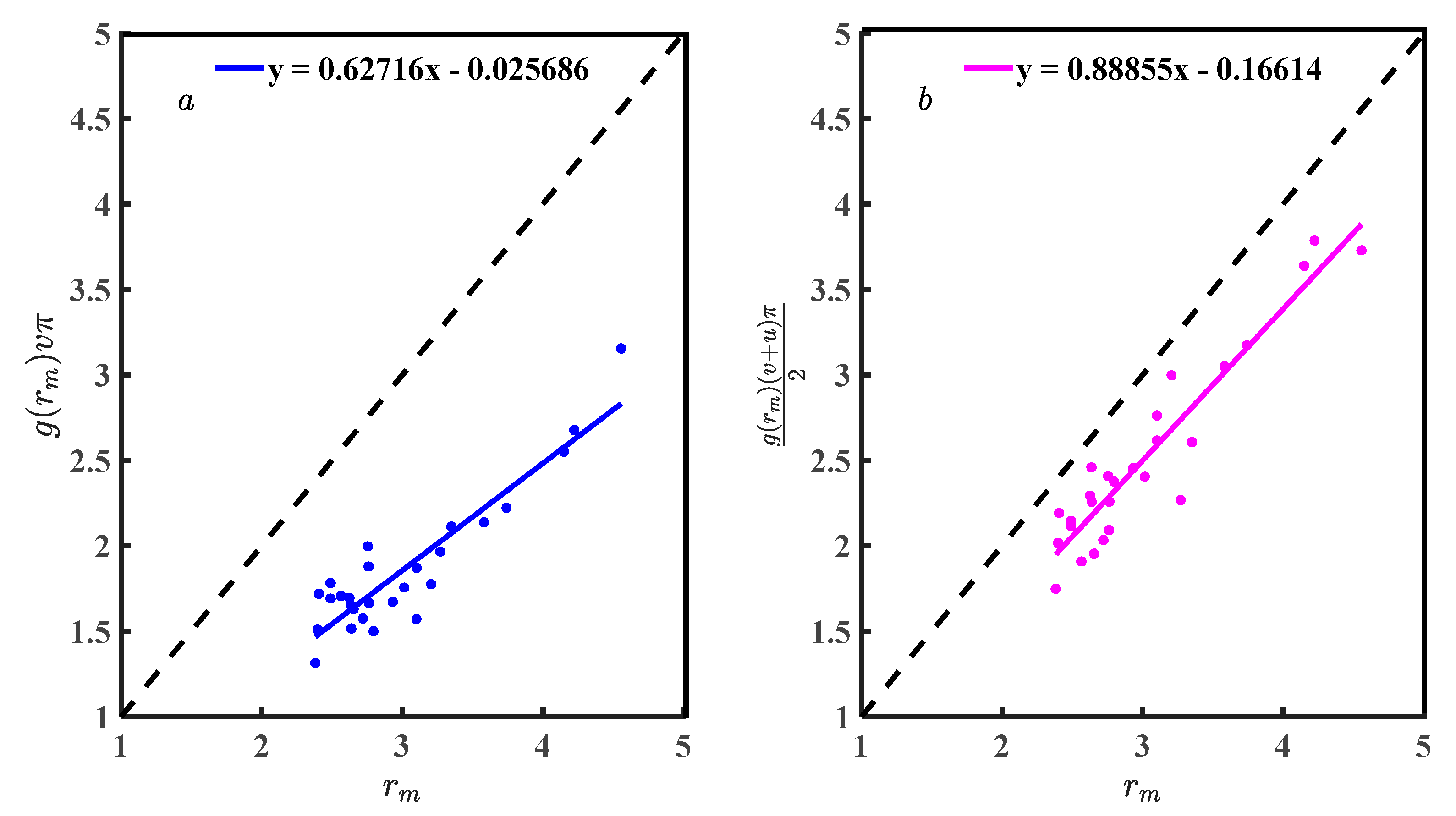
| Metals | (a), Zexp | (b), Vm/ | (c), r0/10−8 cm | (d), rm/10−8 cm | (e), r1/10−8 cm | (f), g(rm) | (g), u | (h), v |
|---|---|---|---|---|---|---|---|---|
| cm3/mol | ||||||||
| Ag | 11.3 | 11.64 | 2.23 | 2.80 | 4.02 | 2.66 | 0.18 | 0.39 |
| Al | 11.5 | 11.32 | 2.28 | 2.75 | 3.63 | 2.84 | 0.22 | 0.32 |
| Au | 10.9 | 11.37 | 2.30 | 2.76 | 3.69 | 2.69 | 0.20 | 0.34 |
| Ba | 10.8 | 41.42 | 3.44 | 4.22 | 5.74 | 2.54 | 0.34 | 0.61 |
| Bi | 8.8 | 20.87 | 2.51 | 3.35 | 4.19 | 2.60 | 0.26 | 0.38 |
| Ca | 11.1 | 29.54 | 3.07 | 3.74 | 5.15 | 2.63 | 0.27 | 0.50 |
| Cd | 10.3 | 14.06 | 2.55 | 2.93 | 3.95 | 2.73 | 0.19 | 0.38 |
| Co | 11.4 | 7.66 | 1.81 | 2.49 | 3.34 | 2.35 | 0.24 | 0.34 |
| Cr | 11.2 | 8.28 | 1.90 | 2.49 | 3.39 | 2.41 | 0.22 | 0.33 |
| Cu | 11.3 | 7.99 | 2.01 | 2.40 | 3.23 | 2.73 | 0.18 | 0.29 |
| Fe | 10.6 | 7.96 | 2.00 | 2.56 | 3.13 | 2.57 | 0.21 | 0.26 |
| Ga | 10.4 | 11.42 | 2.11 | 2.65 | 3.32 | 1.67 | 0.31 | 0.45 |
| Ge | 10 | 14.8 | 2.13 | 2.64 | 3.82 | 2.20 | 0.19 | 0.49 |
| Hg | 11.6 | 16.3 | 2.56 | 3.01 | 3.86 | 3.07 | 0.18 | 0.32 |
| K | 10.5 | 47.17 | 3.45 | 4.56 | 6.12 | 2.43 | 0.41 | 0.56 |
| Mg | 10.9 | 15.37 | 2.55 | 3.10 | 4.29 | 2.44 | 0.24 | 0.48 |
| Mn | 10.9 | 9.56 | 1.99 | 2.62 | 3.57 | 2.32 | 0.23 | 0.40 |
| Na | 10.4 | 24.84 | 2.86 | 3.58 | 5.02 | 2.37 | 0.29 | 0.53 |
| Ni | 11.6 | 7.48 | 2.04 | 2.41 | 3.22 | 2.88 | 0.19 | 0.29 |
| Pb | 10.9 | 19.45 | 2.73 | 3.20 | 4.47 | 3.05 | 0.19 | 0.44 |
| Pt | 11.1 | 10.33 | 2.21 | 2.63 | 3.74 | 2.55 | 0.21 | 0.41 |
| Sb | 8.7 | 18.87 | 2.51 | 3.27 | 3.86 | 2.30 | 0.27 | 0.36 |
| Si | 6.4 | 11.18 | 2.00 | 2.38 | 3.02 | 2.38 | 0.18 | 0.29 |
| Sn | 10.9 | 17.03 | 2.59 | 3.10 | 4.12 | 2.37 | 0.21 | 0.49 |
| Sr | 11.1 | 37.04 | 3.44 | 4.15 | 5.52 | 2.42 | 0.34 | 0.62 |
| V | 11 | 9.51 | 1.86 | 2.76 | 3.70 | 2.28 | 0.26 | 0.32 |
| Zn | 10.5 | 9.99 | 2.12 | 2.64 | 3.54 | 2.58 | 0.19 | 0.37 |
| Metals | Zexp | Tao’s | Tao’s | Ze | Za | Zb | Zc | Zd |
|---|---|---|---|---|---|---|---|---|
| Equation (8) | Equation (21) | Equation (14) | Equation (25) | Equation (28) | Equation (31) | Equation (32) | ||
| Ag | 11.3 | 9.26 | 14.15 | 6.15 | 5.52 | 5.82 | 14.78 | 11.04 |
| Al | 11.5 | 9.33 | 12.53 | 8.12 | 7.07 | 7.57 | 11.78 | 10.39 |
| Au | 10.9 | 9.33 | 12.77 | 6.72 | 5.96 | 6.45 | 11.79 | 10.27 |
| Ba | 10.8 | 9.11 | 12.81 | 7.03 | 6.14 | 6.63 | 12.81 | 11.32 |
| Bi | 8.8 | 8.42 | 10.65 | 6.93 | 6.08 | 6.47 | 10.31 | 9.10 |
| Ca | 11.1 | 8.96 | 12.77 | 6.42 | 5.69 | 6.04 | 13.00 | 10.25 |
| Cd | 10.3 | 9.46 | 12.98 | 6.19 | 5.54 | 6.05 | 12.15 | 10.58 |
| Co | 11.4 | 9.16 | 12.93 | 8.78 | 7.44 | 8.04 | 13.21 | 11.34 |
| Cr | 11.2 | 8.80 | 12.53 | 7.69 | 6.60 | 7.08 | 12.40 | 10.35 |
| Cu | 11.3 | 8.89 | 12.25 | 6.63 | 5.86 | 6.21 | 11.35 | 9.61 |
| Fe | 10.6 | 10.19 | 12.51 | 8.57 | 7.46 | 7.96 | 11.05 | 9.91 |
| Ga | 10.4 | 11.63 | 15.18 | 8.96 | 7.30 | 8.01 | 12.89 | 11.63 |
| Ge | 10 | 7.67 | 10.35 | 5.42 | 4.73 | 5.04 | 9.59 | 7.56 |
| Hg | 11.6 | 9.55 | 12.31 | 6.51 | 5.89 | 6.18 | 11.35 | 9.60 |
| K | 10.5 | 9.43 | 13.22 | 8.47 | 7.25 | 7.79 | 13.66 | 10.58 |
| Mg | 10.9 | 9.53 | 13.71 | 6.95 | 6.08 | 6.47 | 13.17 | 11.60 |
| Mn | 10.9 | 9.25 | 13.19 | 7.73 | 6.64 | 7.12 | 13.16 | 11.58 |
| Na | 10.4 | 9.09 | 13.39 | 6.72 | 5.87 | 6.25 | 13.73 | 10.73 |
| Ni | 11.6 | 9.16 | 12.52 | 7.71 | 6.75 | 7.18 | 12.36 | 10.57 |
| Pb | 10.9 | 8.77 | 12.61 | 5.67 | 5.14 | 5.39 | 12.62 | 10.89 |
| Pt | 11.1 | 8.97 | 13.27 | 6.67 | 5.84 | 6.21 | 13.37 | 11.26 |
| Sb | 8.7 | 8.81 | 10.30 | 6.79 | 5.90 | 6.30 | 8.77 | 8.17 |
| Si | 6.4 | 6.37 | 7.95 | 4.17 | 3.68 | 3.90 | 7.54 | 6.00 |
| Sn | 10.9 | 8.81 | 11.91 | 5.30 | 4.73 | 4.99 | 11.28 | 10.24 |
| Sr | 11.1 | 9.80 | 13.36 | 7.22 | 6.30 | 6.71 | 12.79 | 11.53 |
| V | 11 | 9.47 | 13.57 | 9.18 | 7.79 | 8.40 | 14.33 | 10.59 |
| Zn | 10.5 | 9.09 | 12.62 | 6.43 | 5.71 | 6.04 | 12.40 | 10.73 |
| ARD% | ±15.44 | ±18.51 | ±6.46 | ±34.12 | ±42.52 | ±38.57 | ±15.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Chen, X.; Tao, D. Development of a Non-Integral Form of Coordination Number Equation Based on Pair Distribution Function and Gaussian Function. Metals 2023, 13, 384. https://doi.org/10.3390/met13020384
Wang C, Chen X, Tao D. Development of a Non-Integral Form of Coordination Number Equation Based on Pair Distribution Function and Gaussian Function. Metals. 2023; 13(2):384. https://doi.org/10.3390/met13020384
Chicago/Turabian StyleWang, Chunlong, Xiumin Chen, and Dongping Tao. 2023. "Development of a Non-Integral Form of Coordination Number Equation Based on Pair Distribution Function and Gaussian Function" Metals 13, no. 2: 384. https://doi.org/10.3390/met13020384
APA StyleWang, C., Chen, X., & Tao, D. (2023). Development of a Non-Integral Form of Coordination Number Equation Based on Pair Distribution Function and Gaussian Function. Metals, 13(2), 384. https://doi.org/10.3390/met13020384





