Effectiveness of Design Procedures in Counteracting Second Order Effects in Steel Moment Resisting Frames
Abstract
:1. Introduction
2. P–Δ Effects in Seismic Codes
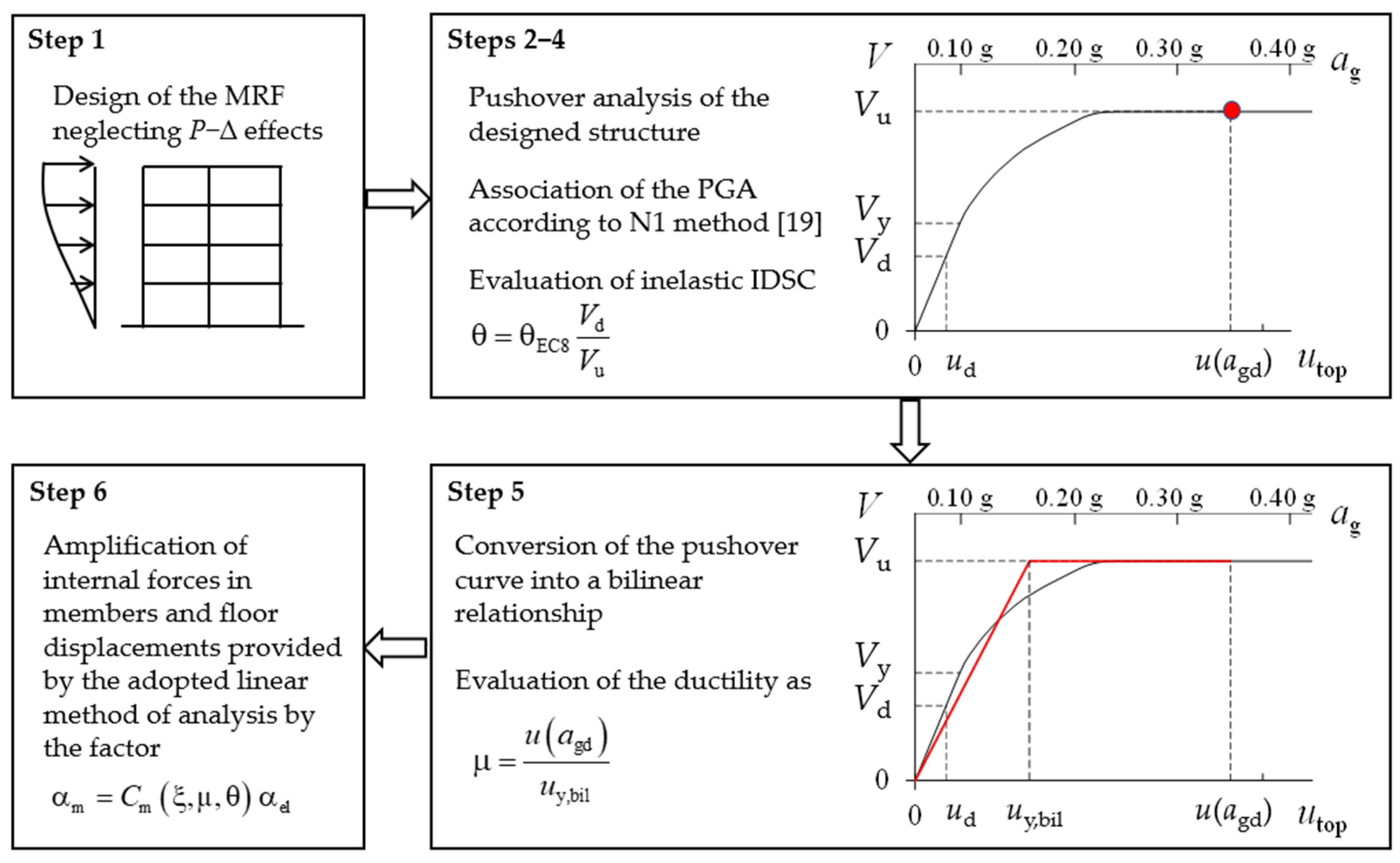
3. The Proposed Procedure
- MRFs are preliminarily designed based on internal forces derived by a first order analysis (with a design base shear equal to Vd);
- A pushover analysis of the designed structure is carried out assuming a distribution of equivalent horizontal seismic forces proportional to the first mode of vibration. The Peak Ground Acceleration (PGA) associated with the points of the pushover curve is determined according to the N1 method [19];
- The base shear corresponding to the top displacement u(agd) associated with the design value of the PGA, agd, is considered as the ultimate lateral strength Vu;
- The interstory drift sensitivity coefficient to be used in Equation (5) is
- 5.
- The pushover curve is transformed into a bilinear relationship in the relevant range of displacements and the ductility demand μ is determined as the ratio of the inelastic displacement demand to the top displacement at yield (uy,bil);
- 6.
- Internal forces in members and floor displacements provided by the linear method of analysis are increased by means of the amplification factor given in Equation (3).
4. Methodology
- Step #1a: Each structure is designed by modal response spectrum analysis without P–Δ effects;
- Step #1b: The seismic response of the structures above is determined by either nonlinear static or nonlinear incremental dynamic analysis without P–Δ effects. The response and the performance levels of these structures are assumed as the target in following analyses;
- Step #2a: Each structure is redesigned considering P–Δ effects in keeping with provisions of seismic codes or according to the formulation proposed by Bernal or that proposed by the authors;
- Step #2b: The nonlinear seismic response of the structures designed in Step 2a is determined with P–Δ effects.
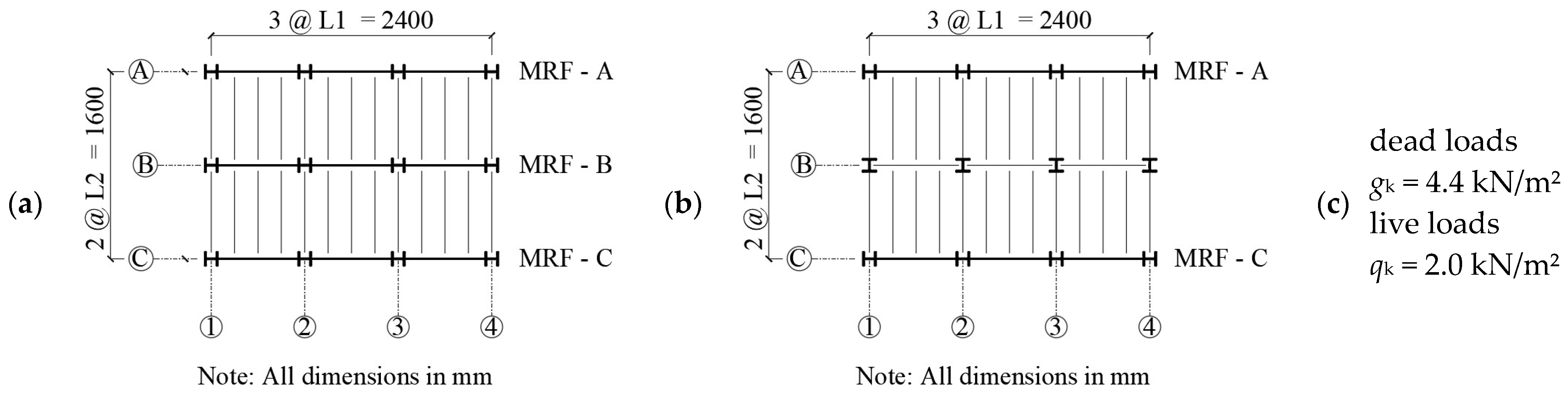
5. Case-Study
5.1. Buildings Designed without P−Δ Effects
5.2. Buildings Designed with P−Δ Effects
6. Numerical Analyses and Response Parameters
7. Response of the Considered Structures
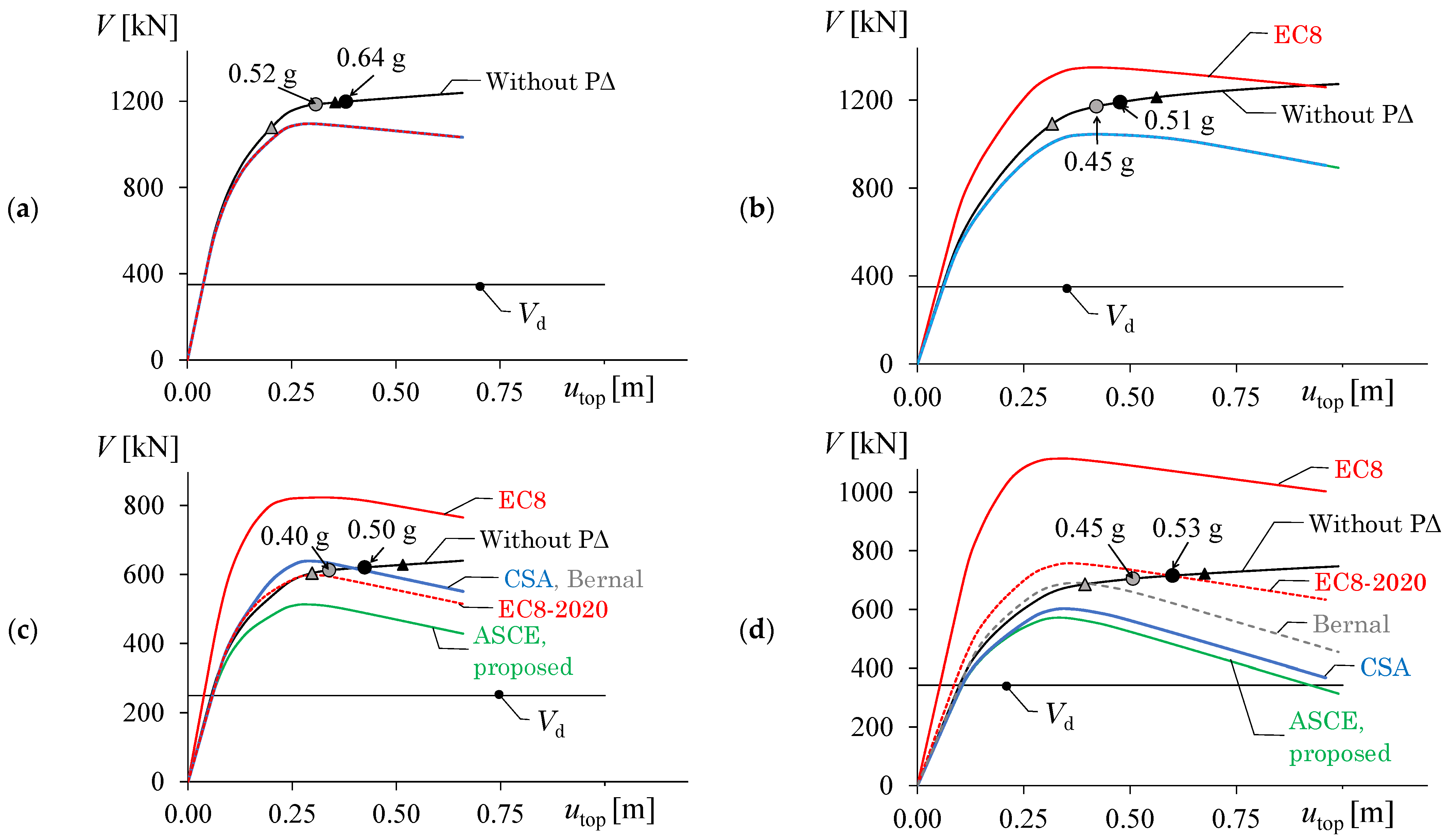
7.1. Capacity Curves
7.2. Response at the Design Level
7.3. Fragility Curves
7.4. Mean Annual Frequency of Exceedance of the Considered Limit States
8. Conclusions
- requires the highest increase of the lateral stiffness of the frame, especially in the case of perimeter frames;
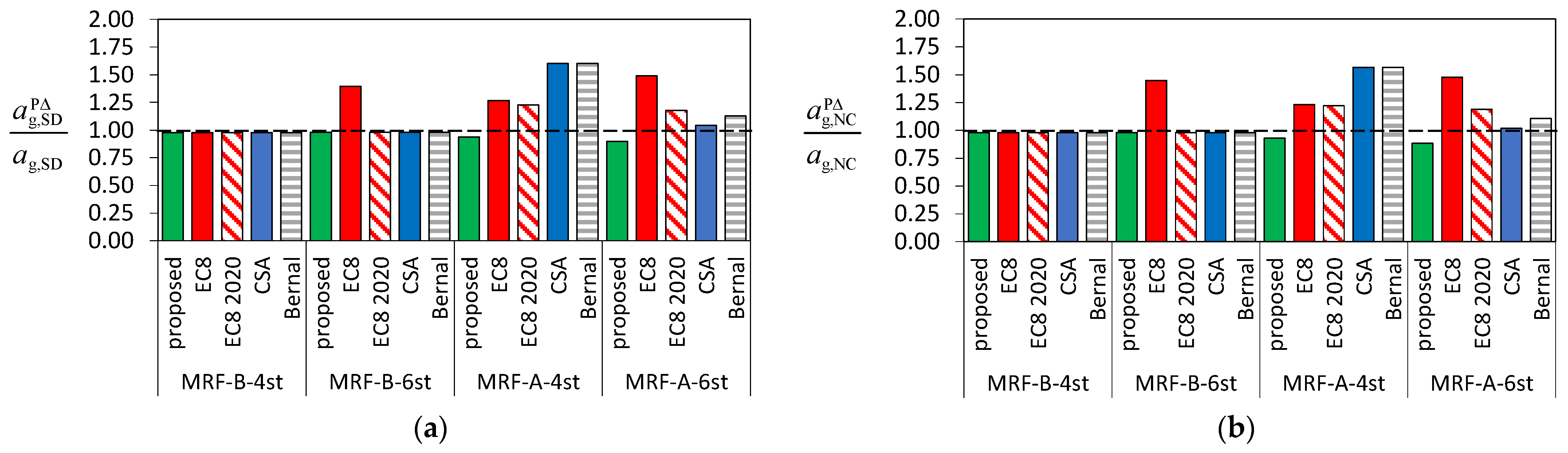
- leads to values of the PGA corresponding to the attainment of SD and NC limit states in Stage #2 that are about 30% higher than those determined in Stage #1 when nonlinear static analysis is used to assess the seismic performance;
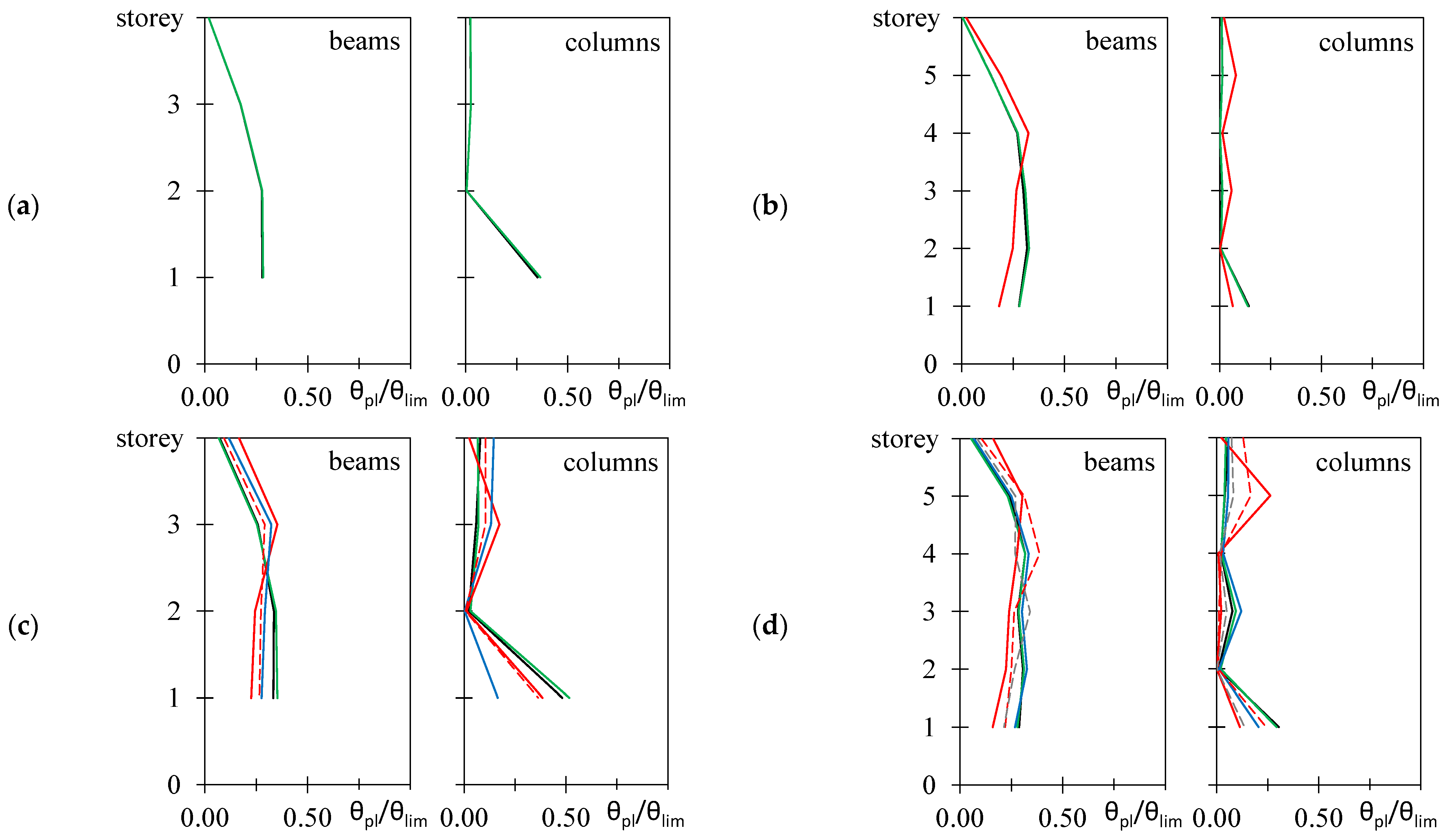
- significantly alters the heightwise distribution of the plastic rotation demand to capacity ratio. The above ratio is often increased at the top stories;
- despite the required significant increase of lateral stiffness and strength, leads to PGA corresponding to the attainment of SD and NC limit states in Stage #2 that are higher than those in Stage #1 for only two cases when IDA is considered to assess the seismic performance;
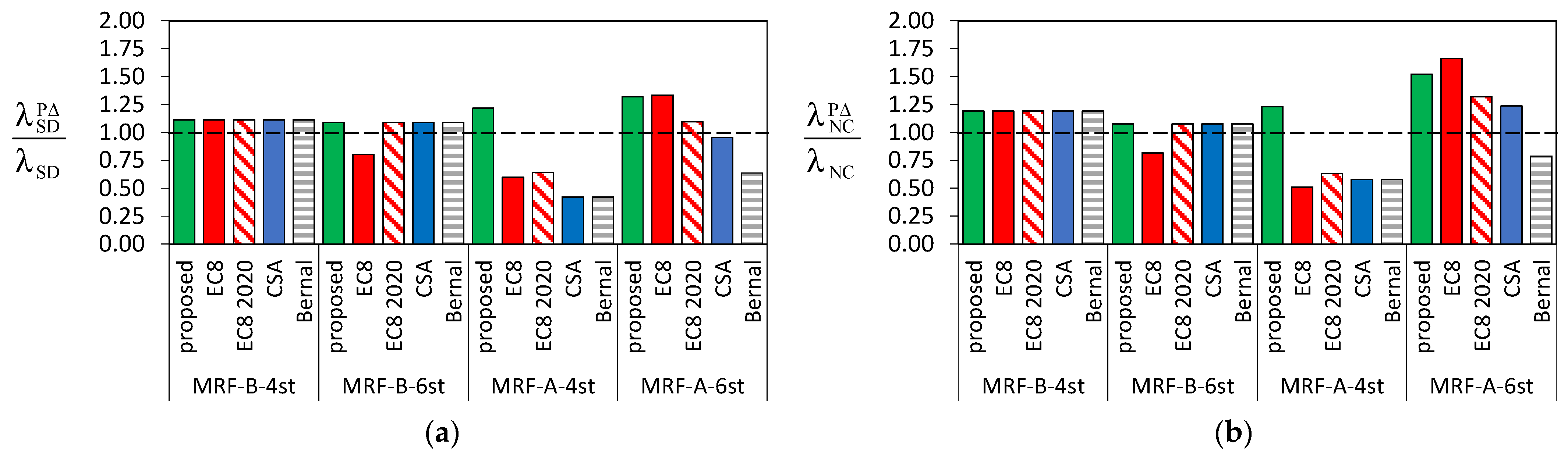
- leads to mean annual frequencies of exceedance of SD and NC limit states in Stage #2 that can be either smaller or higher than those in Stage #1.
- require only a moderate increase of the lateral stiffness and strength;
- lead to values of the PGA corresponding to the attainment of SD and NC limit states in Stage #2 that are about 12% higher than those determined in Stage #1 when nonlinear static analysis is used to assess the seismic performance;
- in the occurrence of the design value of the PGA, lead to ductility demand to capacity ratio at the single story of buildings that can be even significantly larger than that of the same buildings in Stage #1. However, the maximum ductility demand to capacity ratios along the height of the frame are similar in Stage #1 and #2;
- lead to PGA corresponding to the attainment of SD and NC limit states in Stage #2 that can be smaller (up to 10%) or higher (up to about 30%) than those in Stage #1 when IDA is considered to assess the seismic performance;
- lead to mean annual frequencies of exceedance of SD and NC limit states in Stage #2 that can be either smaller or higher than those in Stage #1.
- Both the proposed procedure and ASCE prescriptions:
- do not require any increase of the cross section of the members, thus these two procedures lead to the cheapest structural solution;
- lead to values of the PGA corresponding to the attainment of SD and NC limit states in Stage #2 that are about 6% lower than those determined in Stage #1 when nonlinear static analysis is used to assess the seismic performance. However, the PGAs are larger than the reference values given in the Italian seismic code for the SD and NC limit states (i.e., 0.35 g and 0.45 g, respectively);
- lead to values and heightwise distribution of the plastic rotation demand to capacity ratio that are similar in Stage #1 and in Stage #2 for a PGA equal to the design level;
- lead to values of the PGA corresponding to the attainment of SD and NC limit states in Stage #2 that are about 5% lower than those determined in Stage #1 when nonlinear incremental dynamic analysis is used to assess the seismic performance;
- lead to mean annual frequencies of exceedance of SD and NC limit states in Stage #2 that are higher than those in Stage #1, but lower than the limit values reported in CNR-DT-212/2013.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronym | Meaning |
| DL | Damage Limitation |
| IDA | Incremental Dynamic Analysis |
| IDSC | Interstory Drift Sensitivity Coefficient |
| LS | Limit State |
| MDOF | Multi Degree Of Freedom |
| MRF | Moment Resisting Frame |
| NC | Near Collapse |
| SAF | Scale Amplification Factor |
| SD | Significant Damage |
| SDOF | Single Degree Of Freedom |
References
- Bernal, D. Amplification factors for inelastic dynamic P-Δ effects in earthquake analysis. Earthq. Eng. Struct. Dyn. 1987, 15, 635–651. [Google Scholar] [CrossRef]
- Chung, B.T. Dynamic Behaviour of Multi-Story Buildings; School of Engineering Report No. 492; University of Auckland: Auckland, New Zealand, 1991. [Google Scholar]
- Fenwick, R.C.; Davidson, B.J.; Chung, B.T. P-delta actions in seismic resistant structures. Bull. N. Zeal. Soc. Earthq. 1992, 25, 56–72. [Google Scholar] [CrossRef]
- MacRae, G.A. P-Δ effects on single-degree-of-freedom structures in earthquakes. Earthq. Spectra 1994, 10, 539–568. [Google Scholar] [CrossRef]
- Tremblay, R.; Duval, C.; Léger, P. Effects of viscous damping models, hysteretic models and ground motion characteristics on seismic P-delta strength amplification factors. In Stability and Ductility of Steel Structures; Usami, T., Itoh, Y., Eds.; Elsevier: Oxford, UK, 1998; pp. 103–118. [Google Scholar]
- Williamson, E.B. Evaluation of damage and P-Δ effects for systems under earthquake excitation. J. Struct. 2003, 129, 1036–1046. [Google Scholar] [CrossRef]
- Humar, J.; Mahgoub, M.; Ghorbanie-Asl, M. Effect of second-order forces on seismic response. Can. J. Civ. Eng. 2006, 33, 692–706. [Google Scholar] [CrossRef]
- Amara, F.; Bosco, M.; Marino, E.M.; Rossi, P.P. An accurate strength amplification factor for the design of SDOF systems with P-Δ effects. Earthq. Eng. Struct. Dyn. 2014, 43, 589–611. [Google Scholar] [CrossRef]
- De Francesco, G.; Sullivan, T.J. P-delta effects on short-period systems subjected to earthquake excitation. Eng. Struct. 2022, 254, 113642. [Google Scholar] [CrossRef]
- Barbagallo, F.; Bosco, M.; Ghersi, A.; Rossi, P.P. A Strength Amplification Factor to Counterbalance P–Δ Effects in Steel Moment Resisting Frames. Lect. Notes Civ. Eng. 2022, 262, 1048–1055. [Google Scholar]
- Piluso, V. Parameters for measuring structural sensitivity to second-order effects: Seismic code critical issues. In Proceedings of the XXVIII Conference “the Italian Steel Days” (CTA), Francavilla a Mare, Italy, 29 September–1 October 2022. [Google Scholar]
- Dell’Aglio, G.; Montuori, R.; Nastri, E.; Piluso, V. Consideration of second-order effects on plastic design of steel moment resisting frames. Bull. Earthq. Eng. 2019, 17, 3041–3070. [Google Scholar] [CrossRef]
- CEN. EN 1998-1:2004; Eurocode 8. Design of Structures for Earthquake Resistance–Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2003.
- prEN 1998-1-2:2022; Eurocode 8:—Design of Structures for Earthquake Resistance—Part 1–2: Buildings. Version of prEN 1998-1-2:2022 Submitted to TC 250 for Preparation to ENQ Stage. European Committee for Standardization: Brussels, Belgium, 1998.
- ASCE/SEI. Minimum Design Loads for Buildings and Other Structures; ASCE 7-10; American Society of Civil Engineers/Structural Engineering Institute: Reston, VA, USA, 2010. [Google Scholar]
- Tartaglia, R.; D’Aniello, M.; Landolfo, R. Seismic performance of Eurocode-compliant ductile steel MRFs. Earthq. Eng. Struct. Dyn. 2022, 51, 2527–2552. [Google Scholar] [CrossRef]
- National Research Council of Canada (NRCC). National Building Code of Canada and Structural Commentaries Part 4 of Division B; National Research Council of Canada (NRCC): Ottawa, ON, Canada, 2015. [Google Scholar]
- Canadian Standards Association (CSA). Limit States Design of Steel Structures, S16-14; Canadian Standards Association (CSA): Mississauga ON, Canada, 2014. [Google Scholar]
- Bosco, M.; Ghersi, A.; Marino, E.M. On the evaluation of seismic response of structures by nonlinear static methods. Earthq. Eng. Struct. Dyn. 2009, 38, 1465–1482. [Google Scholar] [CrossRef]
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L.; Jeremic, B. Open System for Earthquake Engineering Simulation Command Language Manual, Pacific Earthquake Engineering Research Center; University of California: Berkeley, CA, USA, 2007. [Google Scholar]
- Menegotto, M.; Pinto, P.E. Method of analysis for cyclically loaded reinforced concrete plane frames including changes in geometry and non-elastic behaviour of elements under combined normal force and bending. In IABSE Symposium of Resistance and Ultimate Deformability of Structures Acted on by Well-Defined Repeated Loads; International Association of Bridge and Structural Engineering: Lisbon, Portugal, 1973; Volume 13, pp. 15–22. [Google Scholar]
- Barbagallo, F.; Bosco, M.; Marino, E.M.; Rossi, P.P. On the fibre modelling of beams in RC framed buildings with rigid diaphragm. Bull. Earthq. Eng. 2020, 18, 189–210. [Google Scholar] [CrossRef]
- CEN. EN 1998-3; EuroCode 8: Design of Structures for Earthquake Resistance. Part 3: Assessment and Retrofitting of Buildings. European Committee for Standardization: Brussels, Belgium, 2005.
- Backer, J.W. Efficient analytical fragility functions fitting using dynamic structural analysis. Earthq. Spectra 2015, 31, 579–599. [Google Scholar] [CrossRef]
- Barbagallo, F.; Bosco, M.; Marino, E.M.; Rossi, P.P. Seismic performance and cost comparative analysis of steel braced frames designed in the framework of EC8. Eng. Struct. 2021, 240, 112379. [Google Scholar] [CrossRef]
- CNR-DT 212/2013; Instruction for the Probabilistic Assessment of the Seismic Performance of Existing Buildings. Consiglio Nazionale delle Ricerche: Roma, Italy, 2014. (In Italian)
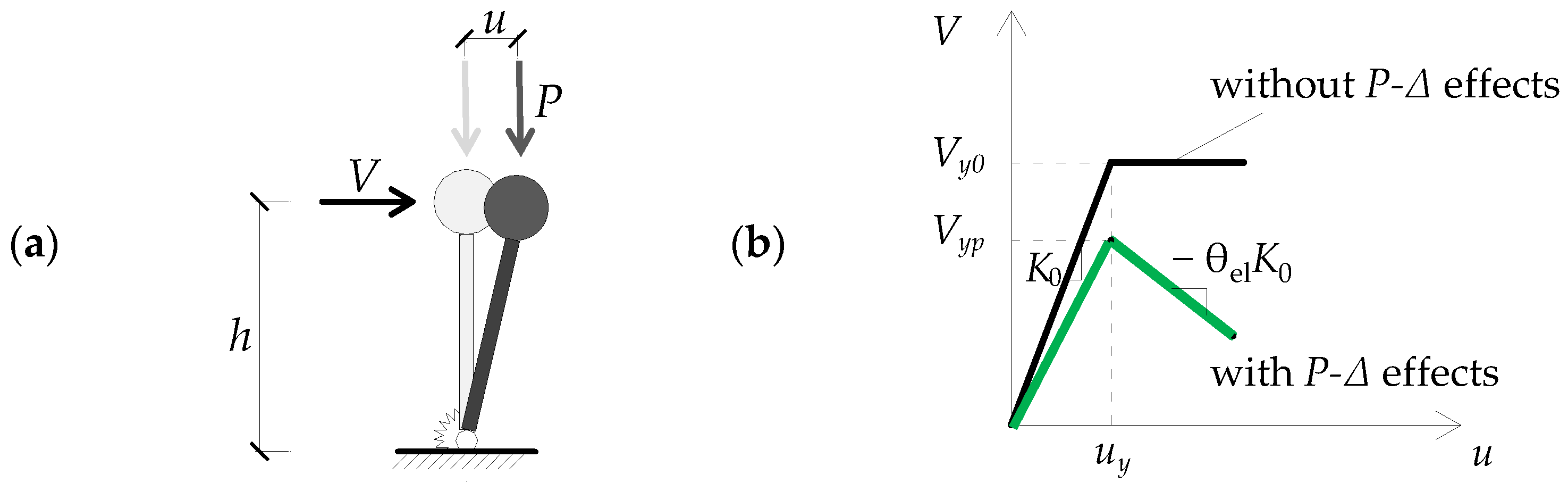

| Building | MRF-A-4st | MRF-A-6st | MRF-B-4st | MRF-B-6st |
|---|---|---|---|---|
| T1 [s] | 1.48 | 2.00 | 1.01 | 1.53 |
| Ws [kN] | 104.3 | 170.0 | 165.7 | 264.8 |
| Ωmin | 1.16 | 1.08 | 1.56 | 1.43 |
| θEC8 | 0.37 | 0.48 | 0.17 | 0.28 |
| θEC8,2020 | 0.19 | 0.24 | 0.09 | 0.14 |
| θASCE = θel | 0.07 | 0.09 | 0.03 | 0.05 |
| U2 | 1.19 | 1.24 | 1.09 | 1.14 |
| θpro | 0.17 | 0.27 | 0.05 | 0.08 |
| Building | MRF-A-4st | MRF-A-6st | MRF-B-4st | MRF-B-6st |
|---|---|---|---|---|
| EC8 | 18.3% | 32.4% | 0.0% | 5.6% |
| EC8,2020 | 8.7% | 10.6% | 0.0% | 0.0% |
| ASCE | 0.0% | 0.0% | 0.0% | 0.0% |
| CSA | 13.8% | 2.2% | 0.0% | 0.0% |
| BERNAL | 13.8% | 10.5% | 0.0% | 0.0% |
| PROPOSED | 0.0% | 0.0% | 0.0% | 0.0% |
| Building | MRF-A-4st | MRF-A-6st | MRF-B-4st | MRF-B-6st |
|---|---|---|---|---|
| ag,SD (g) | 0.487 | 0.688 | 0.564 | 0.804 |
| ag,NC (g) | 0.594 | 0.876 | 0.680 | 0.970 |
| Limit Value | MRF-A-4st | MRF-A-6st | MRF-B-4st | MRF-B-6st | |
|---|---|---|---|---|---|
| λSD (×10−3) | 4.7 | 0.938 | 0.319 | 0.575 | 0.220 |
| λNC (×10−3) | 2.3 | 0.521 | 0.148 | 0.325 | 0.124 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbagallo, F.; Bosco, M.; Floridia, A.; Marino, E.M.; Rossi, P.P. Effectiveness of Design Procedures in Counteracting Second Order Effects in Steel Moment Resisting Frames. Metals 2023, 13, 321. https://doi.org/10.3390/met13020321
Barbagallo F, Bosco M, Floridia A, Marino EM, Rossi PP. Effectiveness of Design Procedures in Counteracting Second Order Effects in Steel Moment Resisting Frames. Metals. 2023; 13(2):321. https://doi.org/10.3390/met13020321
Chicago/Turabian StyleBarbagallo, Francesca, Melina Bosco, Andrea Floridia, Edoardo M. Marino, and Pier Paolo Rossi. 2023. "Effectiveness of Design Procedures in Counteracting Second Order Effects in Steel Moment Resisting Frames" Metals 13, no. 2: 321. https://doi.org/10.3390/met13020321
APA StyleBarbagallo, F., Bosco, M., Floridia, A., Marino, E. M., & Rossi, P. P. (2023). Effectiveness of Design Procedures in Counteracting Second Order Effects in Steel Moment Resisting Frames. Metals, 13(2), 321. https://doi.org/10.3390/met13020321










