Research on the 2A11 Aluminum Alloy Sheet Cyclic Tension–Compression Test and Its Application in a Mixed Hardening Model
Abstract
1. Introduction
- designing a set of a reasonable thin-plate in-plane normal constraint device of thin sheets that can not only prevent the instability of the sample, but also minimize the increase in the axial compressive capacity caused by the friction force of the normal constraint;
- determining the best sample geometry that can minimize the effect of in-plane buckling and improve the accuracy of stress measurement;
- selecting a high-precision optical strain-measuring instrument in order to accurately measure the deformation of the thin sheet sample gauge.
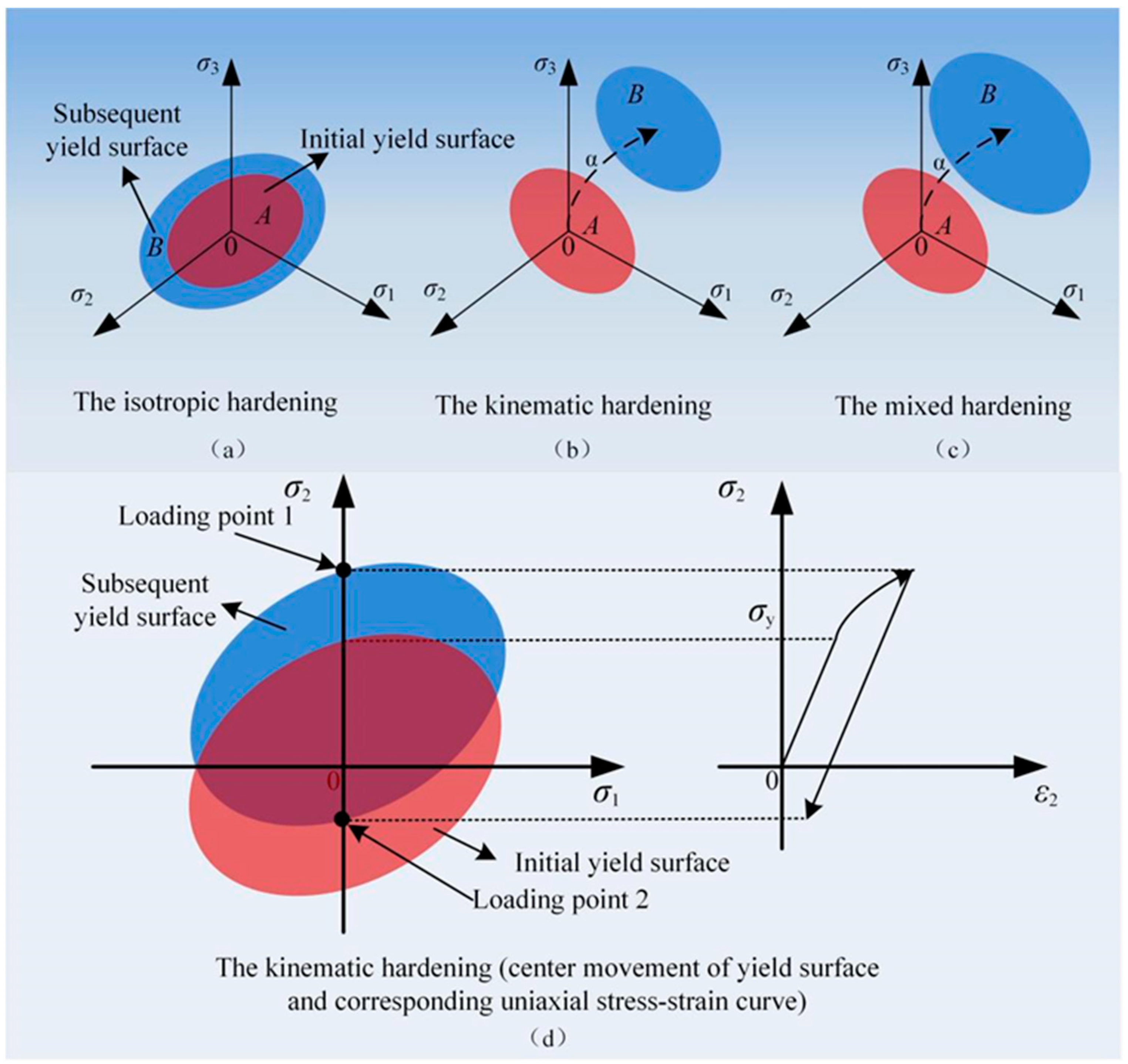
2. Description of the Constitutive Model
2.1. Establishment and Parameter Determination of the Nonlinear Kinematic Hardening Constitutive Model
2.2. Establishment of the Mixed Hardening Constitutive Model
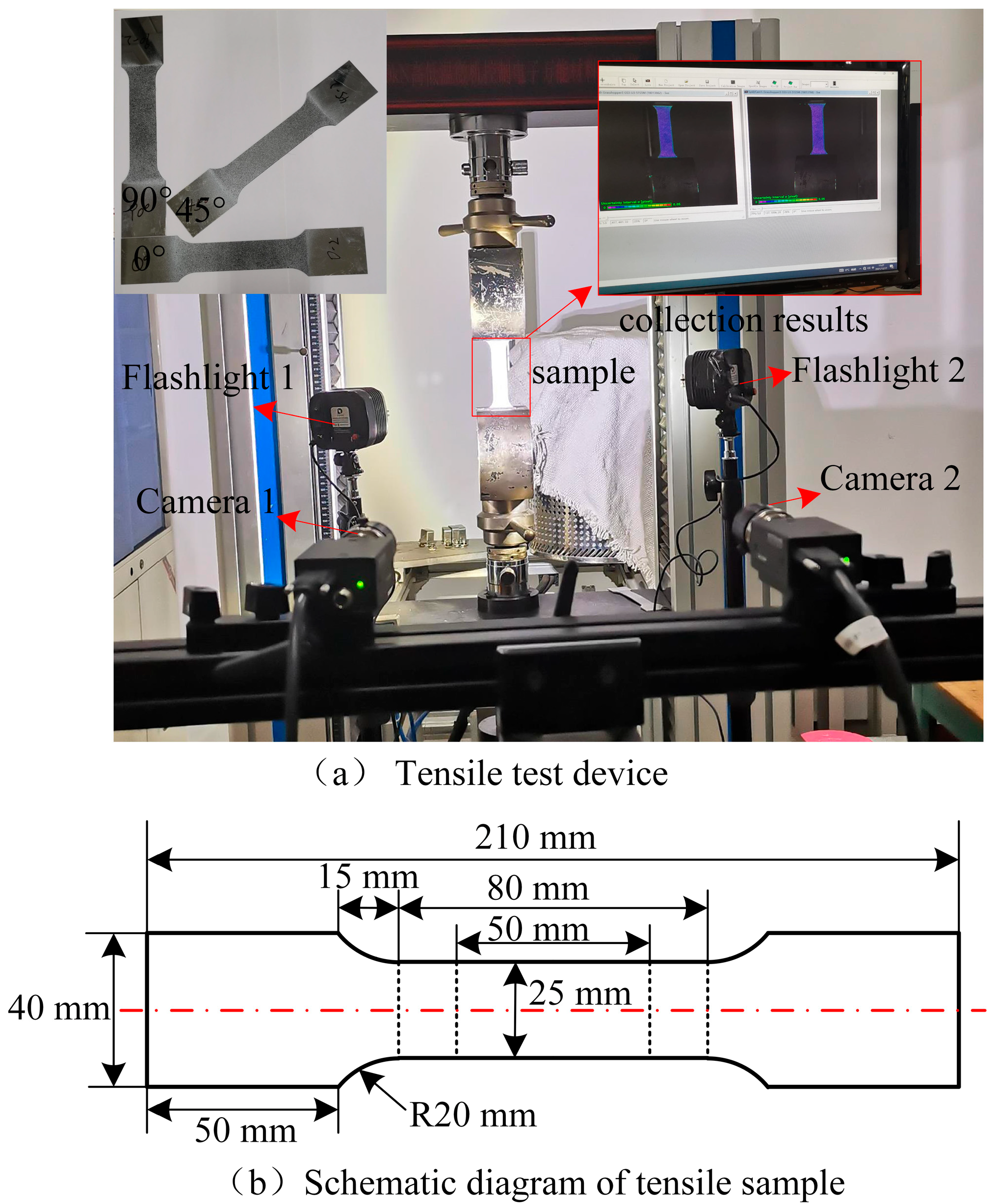
2.3. Material and Experimental Procedure
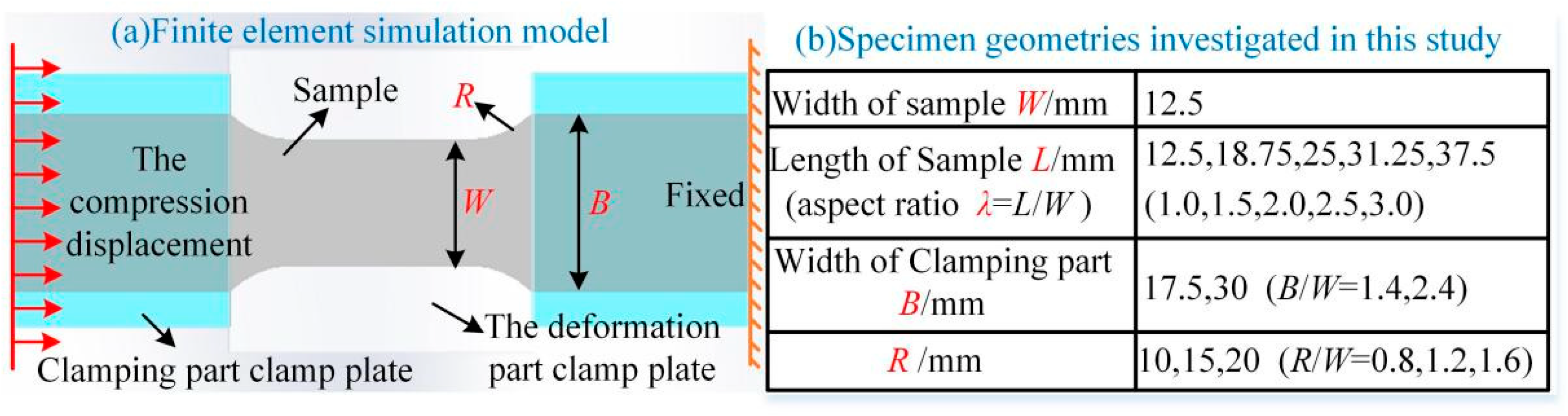
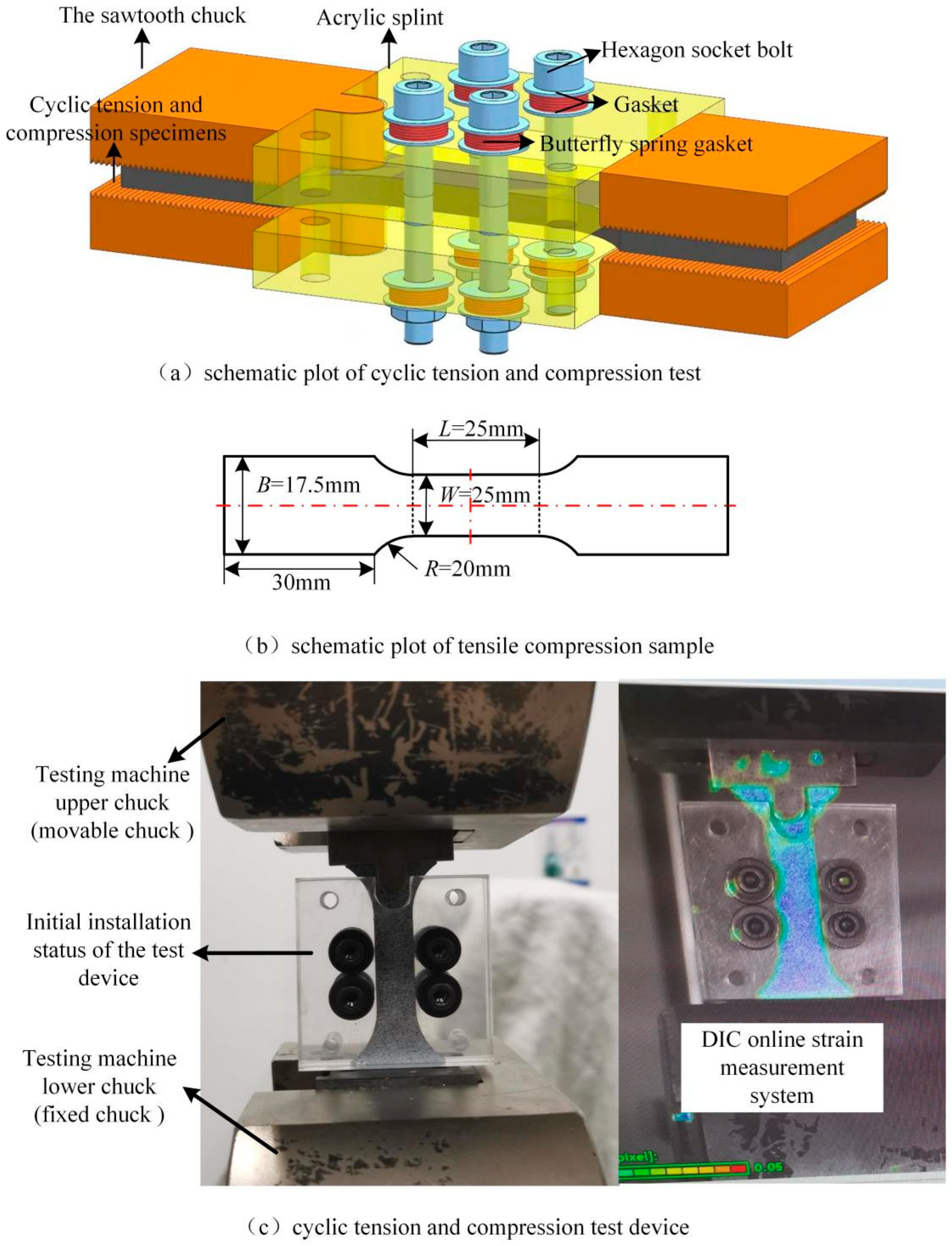
3. Cyclic Sheet Tension-Compression Test and Sample Shape Optimization
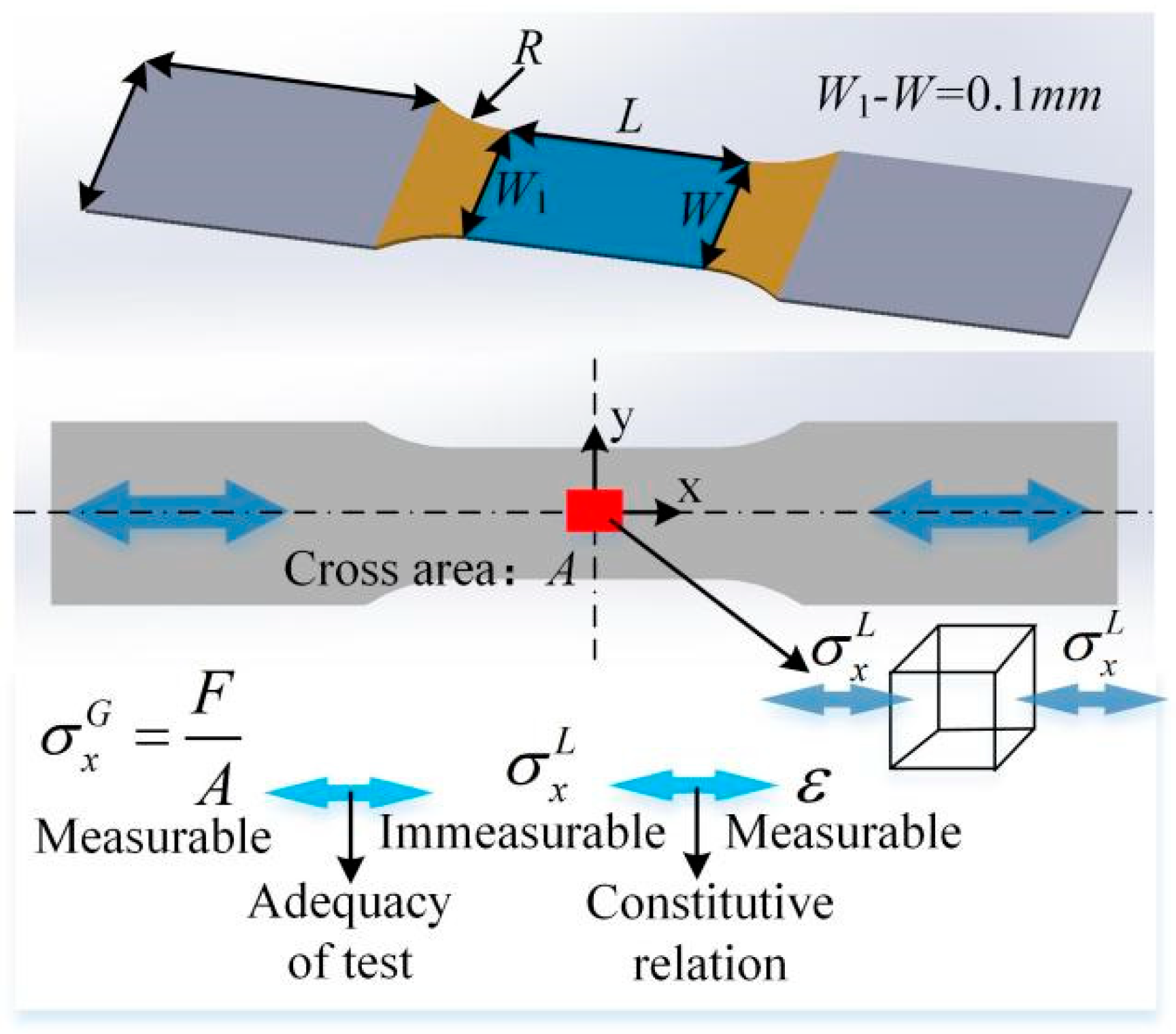
3.1. Shape Optimization of Cyclic Sheet Tension-Compression Sample
3.2. FEM Model for Sample Shape Optimization
3.3. Sample Shape Optimization Simulation Results
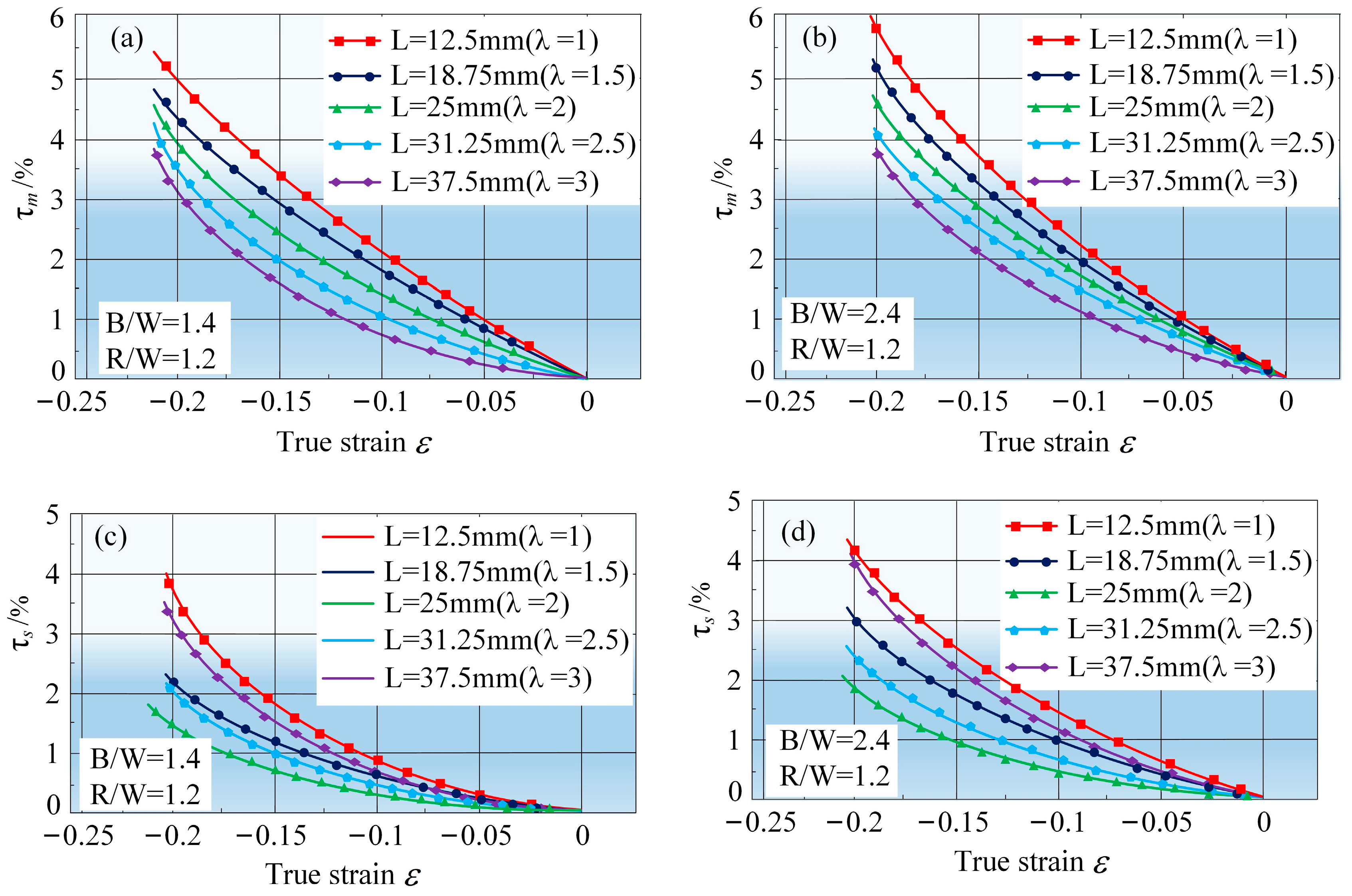
3.3.1. Effect of Sample Deformation Zone Aspect Ratio and Clamping End Width B
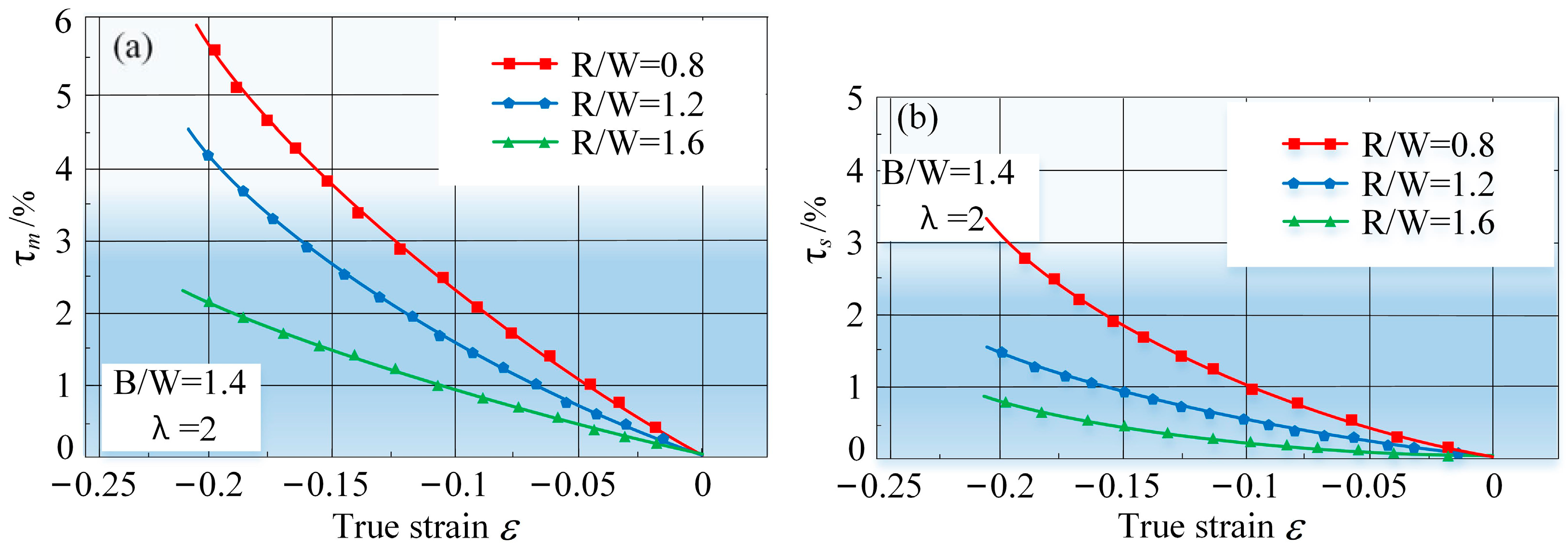
3.3.2. Effect of Fillet Radius R in the Fillet Area of the Sample
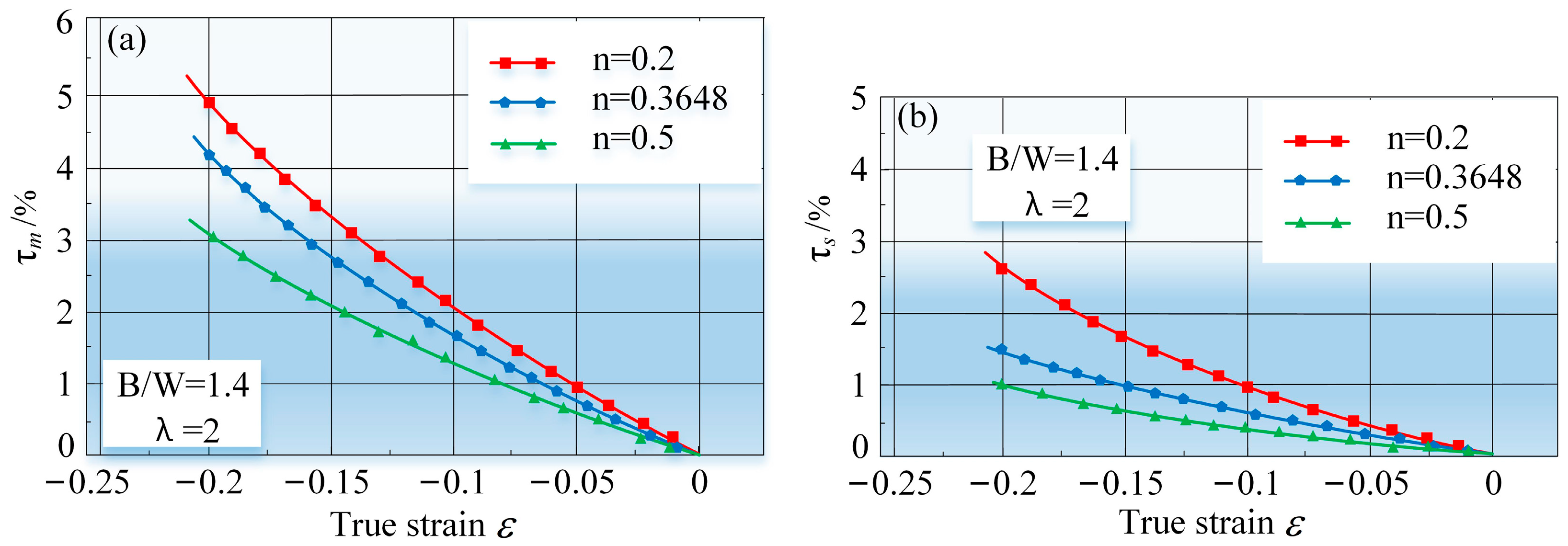
3.3.3. Influence of n-Values of the Sample
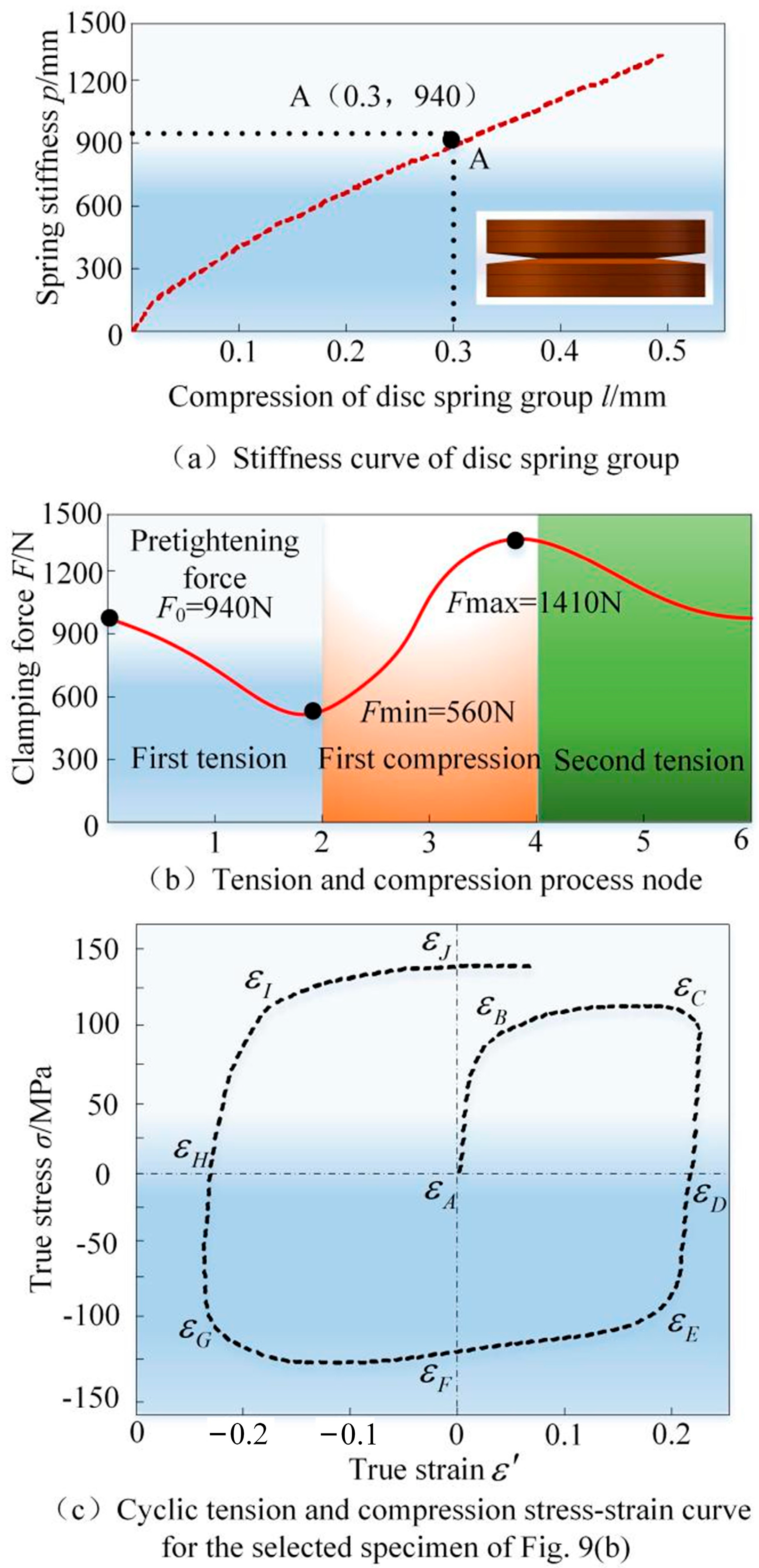
3.4. The Cyclic Sheet Tensile–Compression Test
3.5. Determination of the Mixed Hardening Constitutive Model Parameter
4. Reliability Analysis of the Constitutive Model
4.1. The Application of the Constitutive Model in the Cyclic Sheet Tensile–Compression Problem
4.2. The Application of the Constitutive Model in the Continuous Bending Problem
4.3. Application of Constitutive Model in the Springback Problem
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, H.; Hong, X.; Tian, Y.; Zhang, D. Az31 magnesium alloy tube manufactured by composite forming technology including extruded-shear and bending based on finite element numerical simulation and experiments. Int. J. Adv. Manuf. Tech. 2021, 115, 2395–2402. [Google Scholar] [CrossRef]
- He, B.; Huang, S.; He, X. Numerical simulation of gear surface hardening using the finite element method. Int. J. Adv. Manuf. Tech. 2014, 74, 665–672. [Google Scholar] [CrossRef]
- Xin, C. Establishment and Application of Elastic-Plastic Constitutive Model for Cyclic Loading. Doctoral Dissertation, Yanshan University, Yanshan, China.
- Li, Q.; Xin, C.; Jin, M.; Zhang, Q. Establishment and application of an anisotropic nonlinear kinematic hardening constitutive model. Chin. J. Mech. Eng. 2006, 42, 6. [Google Scholar] [CrossRef]
- Xiao, Y.Z.; Chen, J. A review of research in macroscopic hardening models in numerical simulation of sheet metal forming. Int. J. Plast. 2009, 16, 8. [Google Scholar]
- Ziegler, H. A modification of prager’s hardening rule. Q. Appl. Math. 1959, 17, 55–65. [Google Scholar] [CrossRef]
- Armstrong, P.J.; Frederick, C.O. A mathematical representation of the multiaxial bauschinger effect. Mater. High Temp. 2007, 24, 1–26. [Google Scholar]
- Yu, H.Y. Comparative study on strain hardening models of thin metal sheet. Forg. Stamp. Technol. 2012, 37, 6. [Google Scholar]
- Yu, H.Y.; Wang, Y. A combined hardening model based on chaboche theory and its application in the springback simulation. Chin. J. Mech. Eng. 2015, 51, 8. [Google Scholar] [CrossRef]
- Han, C.; Dong, X.H. An equivalent drawbead model considering Bauschinger effect. Forg. Stamp. Technol. 2017, 42, 7. [Google Scholar]
- Li, Q.; Jin, M.; Zou, Z.Y.; Guo, J.; Yang, C. Parameter determination and application research of mixed hardening model based on cyclic tension-compression test. Chin. J. Mech. Eng. 2020, 2, 6. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, C.C.; Yang, Z.Y.; Dong, G.J.; Cao, M.Y. Effects of Q235 Coated Tubes on Bulging Behavior of AA5052 Aluminum Alloy Base Tube with Granular Medium. Chin. J. Mech. Eng. 2021, 32, 10. [Google Scholar]
- Boger, R.K.; Wagoner, R.H.; Barlat, F.; Lee, M.G.; Chung, K. Continuous, large strain, tension/compression testing of sheet material. Int. J. Plast. 2005, 21, 2319–2343. [Google Scholar] [CrossRef]
- Kuwabara, T.; Kumano, Y.; Ziegelheim, J.; Kurosaki, I. Tension-compression asymmetry of phosphor bronze for electronic parts and its effect on bending behavior. Int. J. Plast. 2005, 25, 1759–1776. [Google Scholar] [CrossRef]
- Yoshida, F.; Uemori, T. Cyclic Plasticity Model for Accurate Simulation of Springback of Sheet Metals; Springer Vieweg: Berlin/Heidelberg, Germany, 2015; pp. 65–66. [Google Scholar]
- Jian, C.; Lee, W.; Hang, S.C.; Seniw, M.; Chung, K. Experimental and numerical investigation of combined isotropic-kinematic hardening behavior of sheet metals. Int. J. Plast. 2009, 25, 942–972. [Google Scholar]
- Hang, S.C.; Lee, W.; Jian, C.; Seniw, M.; Chung, K. Experimental and Numerical Investigation of Kinematic Hardening Behavior in Sheet Metals. In Proceedings of the 10th Esaform Conference on Material Forming, Zaragoza, Spain, 18–20 April 2007; Volume 907, pp. 337–342. [Google Scholar]
- Kurukuri, S.; Worswick, M.J.; Ghaffari Tari, D.; Mishra, R.K.; Carter, J.T. Rate sensitivity and tension-compression asymmetry in AZ31B magnesium alloy sheet. Philos. Trans. 2014, 372, 20130216. [Google Scholar] [CrossRef] [PubMed]
- Abedini, A.; Butcher, C.; Nemcko, M.J.; Kurukuri, S.; Worswick, M.J. Constitutive characterization of a rare-earth magnesium alloy sheet (ZEK100-O) in shear loading: Studies of anisotropy and rate sensitivity. Int. J. Mech. Sci. 2017, 128, 54–69. [Google Scholar] [CrossRef]
- Ma, M.T. A review of the Bauschinger effect in metals and alloys. Mater. Mech. Eng. 1986, 10, 15–21. [Google Scholar]
- Wang, Y.F.; Li, C.; Ling, X.Y.; Shen, B.L.; Gao, S.J.; Ying, S.H. An overview on the Bauschinger effect in metallic materials. China Nucl. Sci. Technol. Rep. 2002, 1, 14. [Google Scholar]
- Noma, N.; Kuwabara, T. Numerical investigation of specimen geometry for in-plane compression tests and its experimental validation. J. Jpn. Soc. Technol. Plast. 2012, 53, 574–579. [Google Scholar] [CrossRef]
- Dong, X.H. Principles of Metal Forming; China Machine Press: Beijing, China, 2011; pp. 154–196. [Google Scholar]
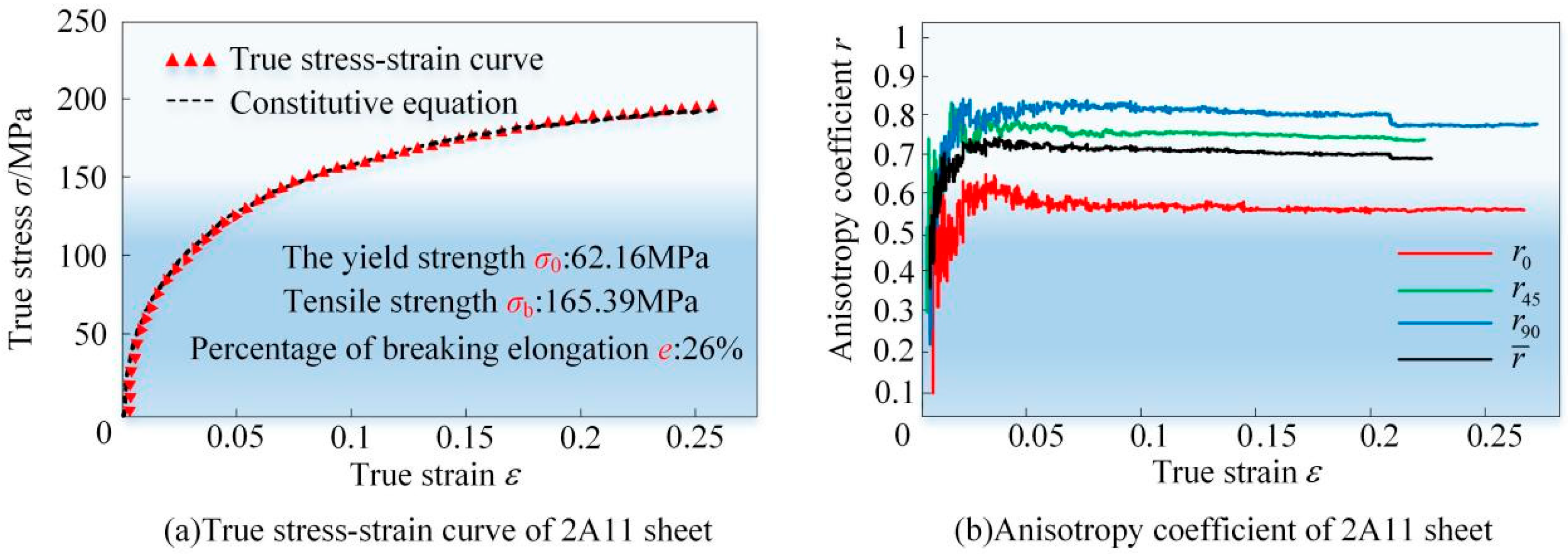





| Material | Yield Strength (MPa) | Poisson’s Ratio | Young’s Modulus (GPa) | C/MPa | γ |
|---|---|---|---|---|---|
| 2A11 | 62.16 | 0.31 | 68.016 | 1258 | 152 |
| Material | R11 | R22 | R33 | R12 | R13 | R23 |
|---|---|---|---|---|---|---|
| 2A11 | 1 | 1.09 | 0.96 | 1.05 | 1 | 1 |
| Material | Yield Strength (MPa) | Q/MPa | B | C/MPa | γ | R2 |
|---|---|---|---|---|---|---|
| 2A11 | 62.16 | 65.5 | 37 | 1453 | 168 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Zhao, C.; Shi, H.; Zhu, Q.; Shen, G.; Liu, Z.; Wang, C.; Chen, D. Research on the 2A11 Aluminum Alloy Sheet Cyclic Tension–Compression Test and Its Application in a Mixed Hardening Model. Metals 2023, 13, 229. https://doi.org/10.3390/met13020229
Chen G, Zhao C, Shi H, Zhu Q, Shen G, Liu Z, Wang C, Chen D. Research on the 2A11 Aluminum Alloy Sheet Cyclic Tension–Compression Test and Its Application in a Mixed Hardening Model. Metals. 2023; 13(2):229. https://doi.org/10.3390/met13020229
Chicago/Turabian StyleChen, Guang, Changcai Zhao, Haiwei Shi, Qingxing Zhu, Guoyi Shen, Zheng Liu, Chenyang Wang, and Duan Chen. 2023. "Research on the 2A11 Aluminum Alloy Sheet Cyclic Tension–Compression Test and Its Application in a Mixed Hardening Model" Metals 13, no. 2: 229. https://doi.org/10.3390/met13020229
APA StyleChen, G., Zhao, C., Shi, H., Zhu, Q., Shen, G., Liu, Z., Wang, C., & Chen, D. (2023). Research on the 2A11 Aluminum Alloy Sheet Cyclic Tension–Compression Test and Its Application in a Mixed Hardening Model. Metals, 13(2), 229. https://doi.org/10.3390/met13020229




