Numerical and Experimental Buckling and Post-Buckling Analyses of Sphere-Segmented Toroidal Shell Subject to External Pressure
Abstract
1. Introduction
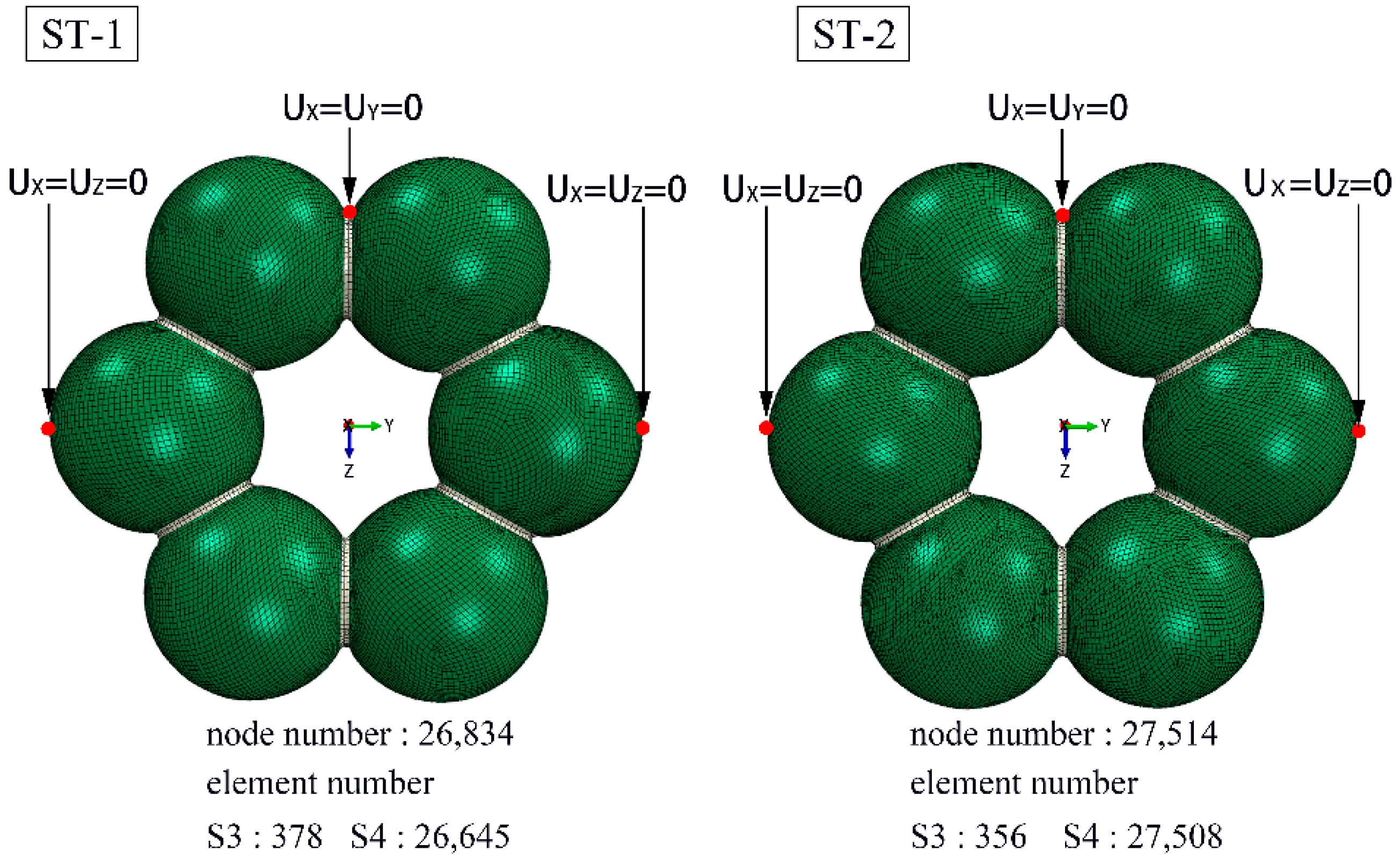
2. Materials and Methods
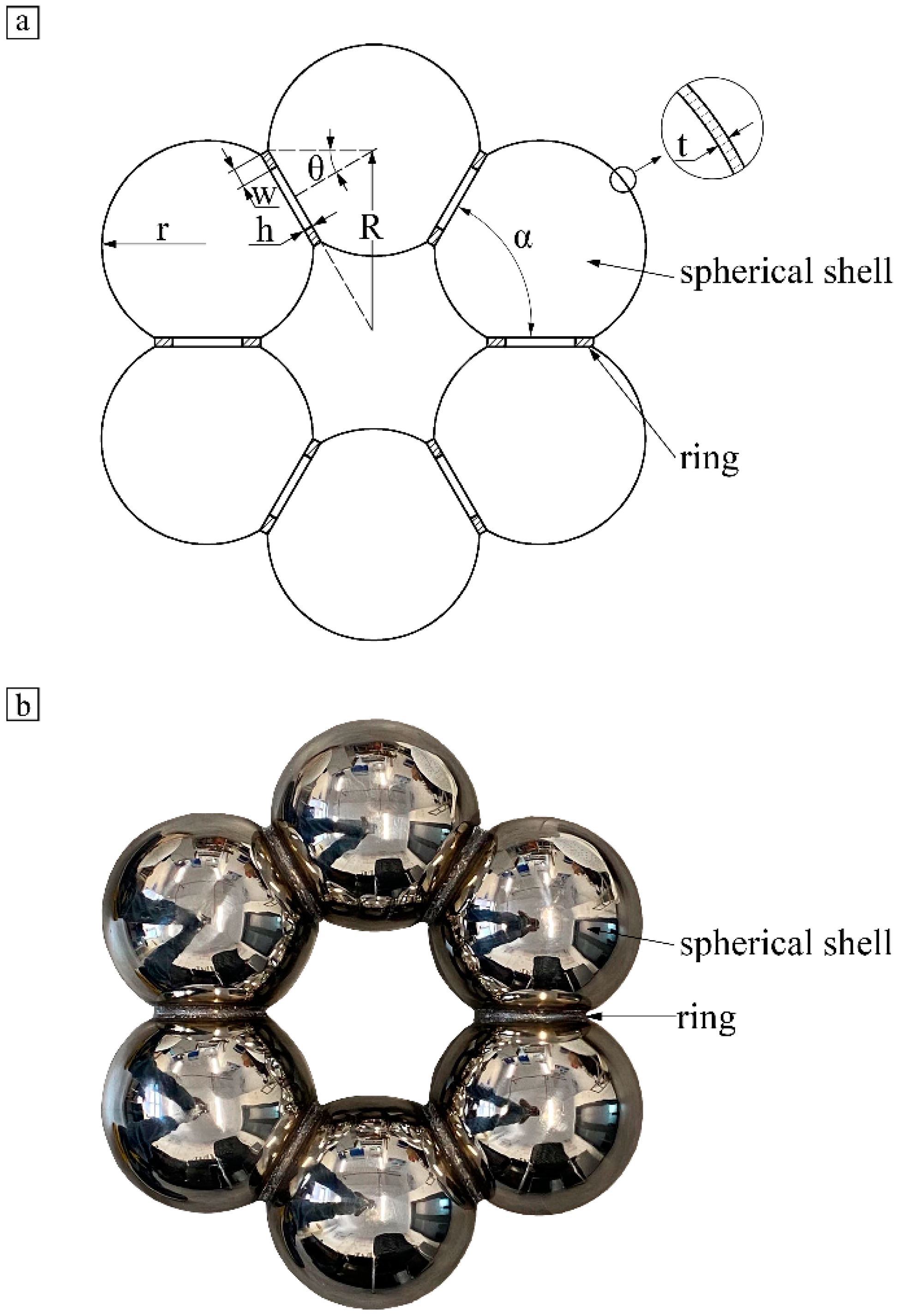
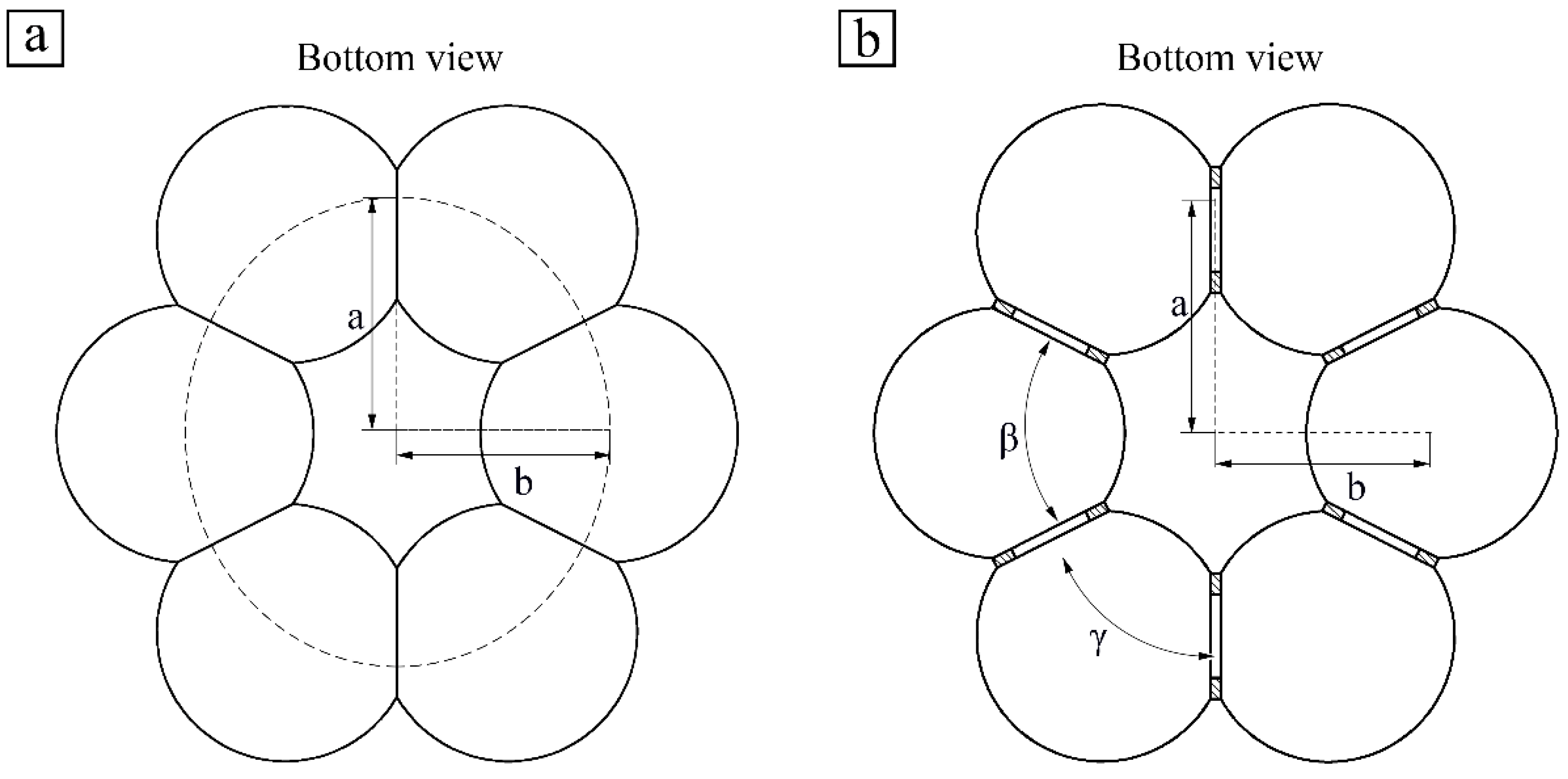
2.1. Geometry and Manufacture
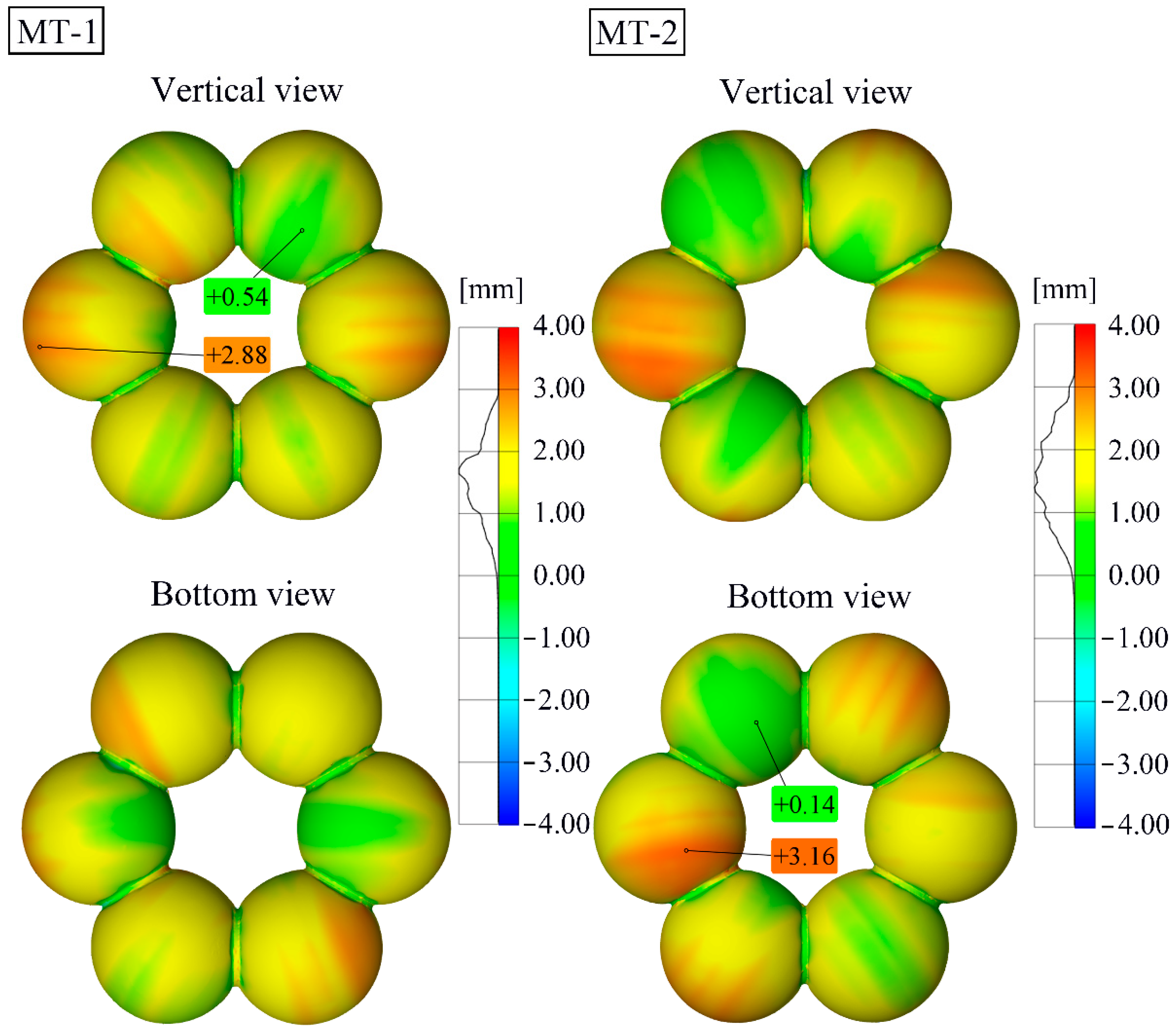
2.2. Geometric Measurement and Hydrostatic Testing
3. Results and Discussion
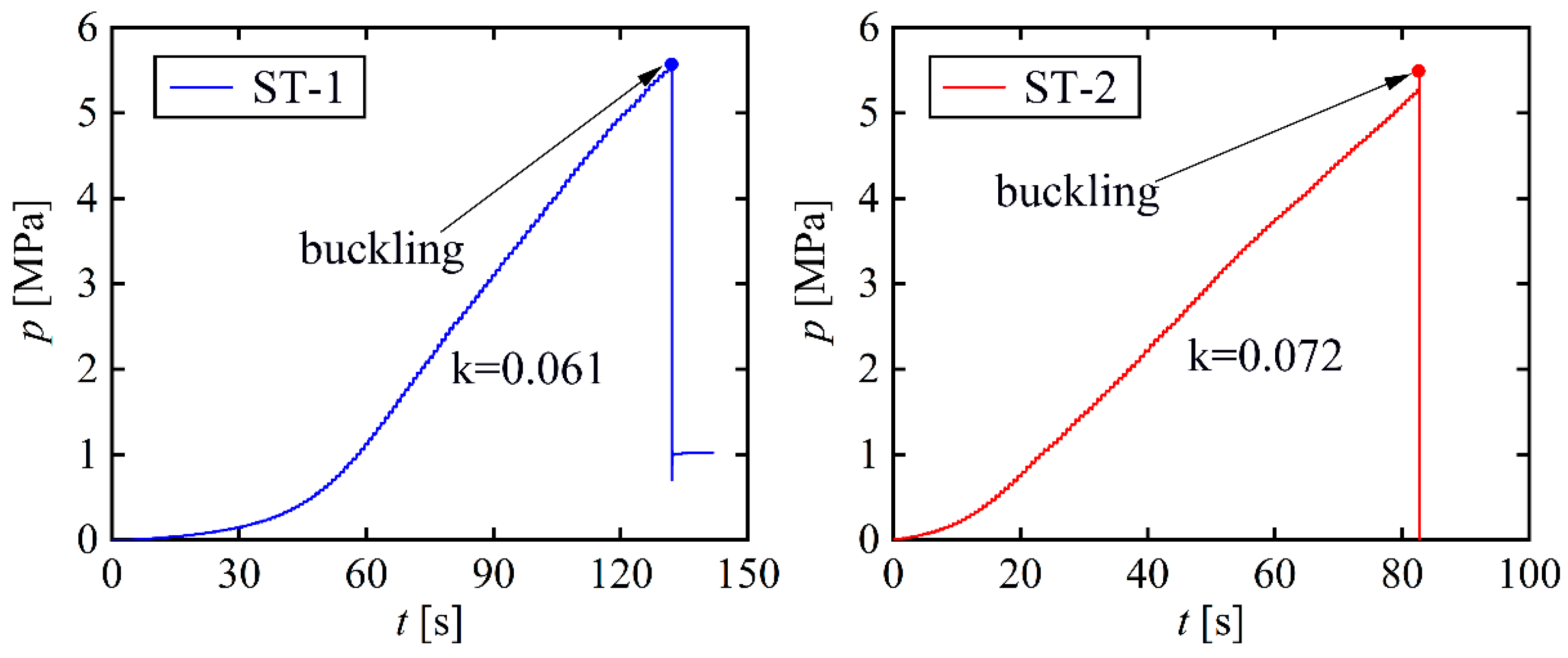
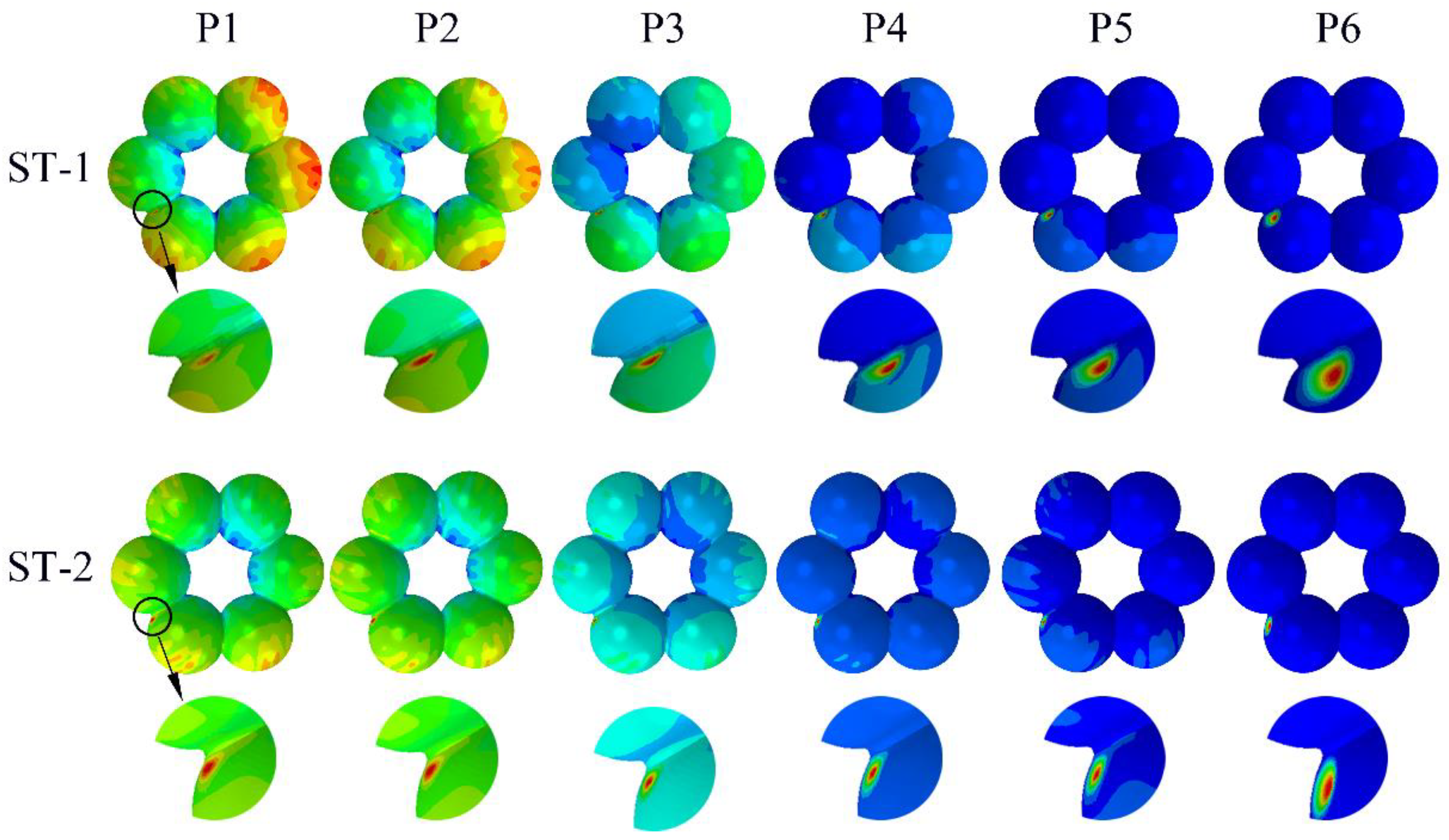
3.1. Experimental Analysis of the Two Sphere-Segmented Toroidal Shells
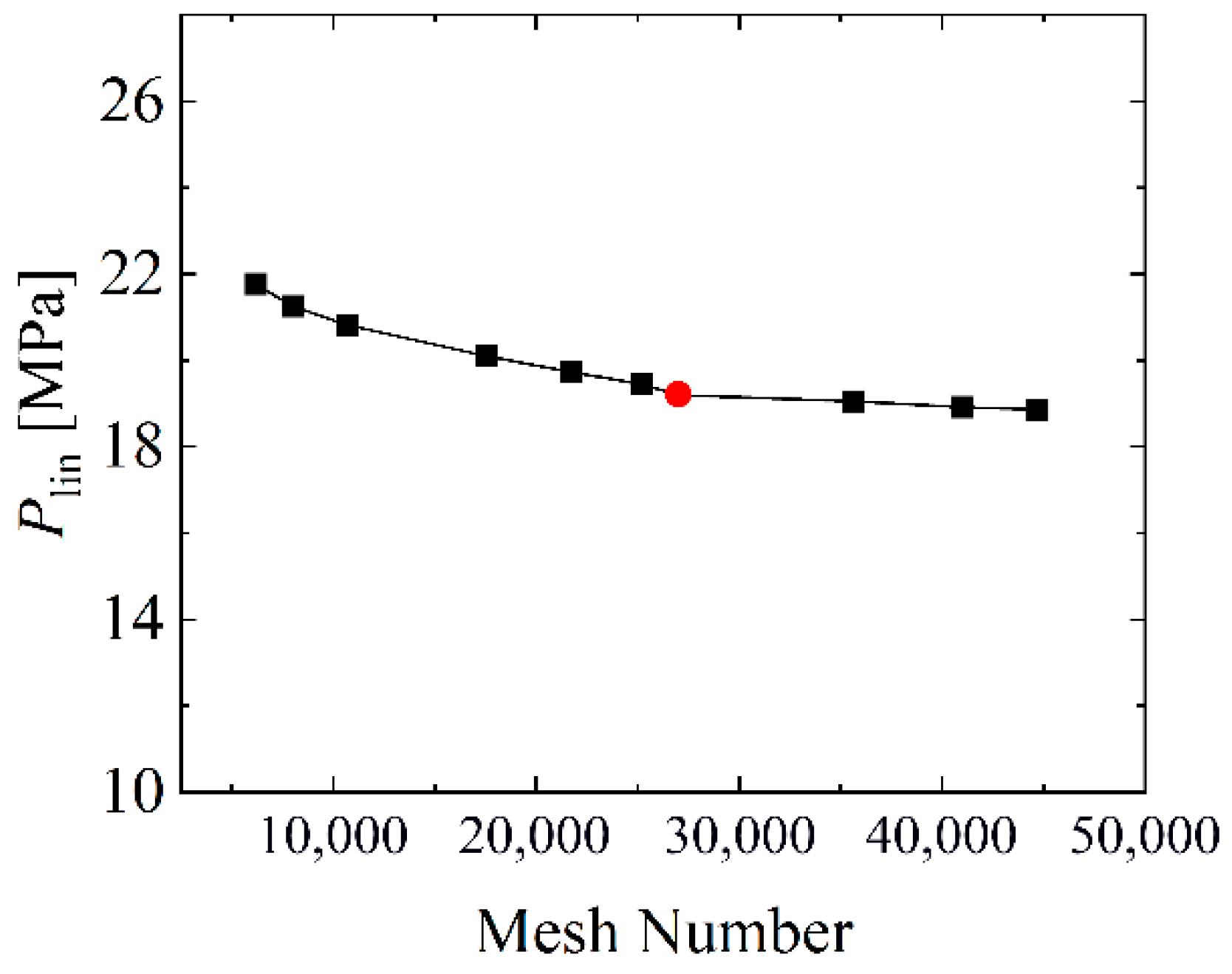
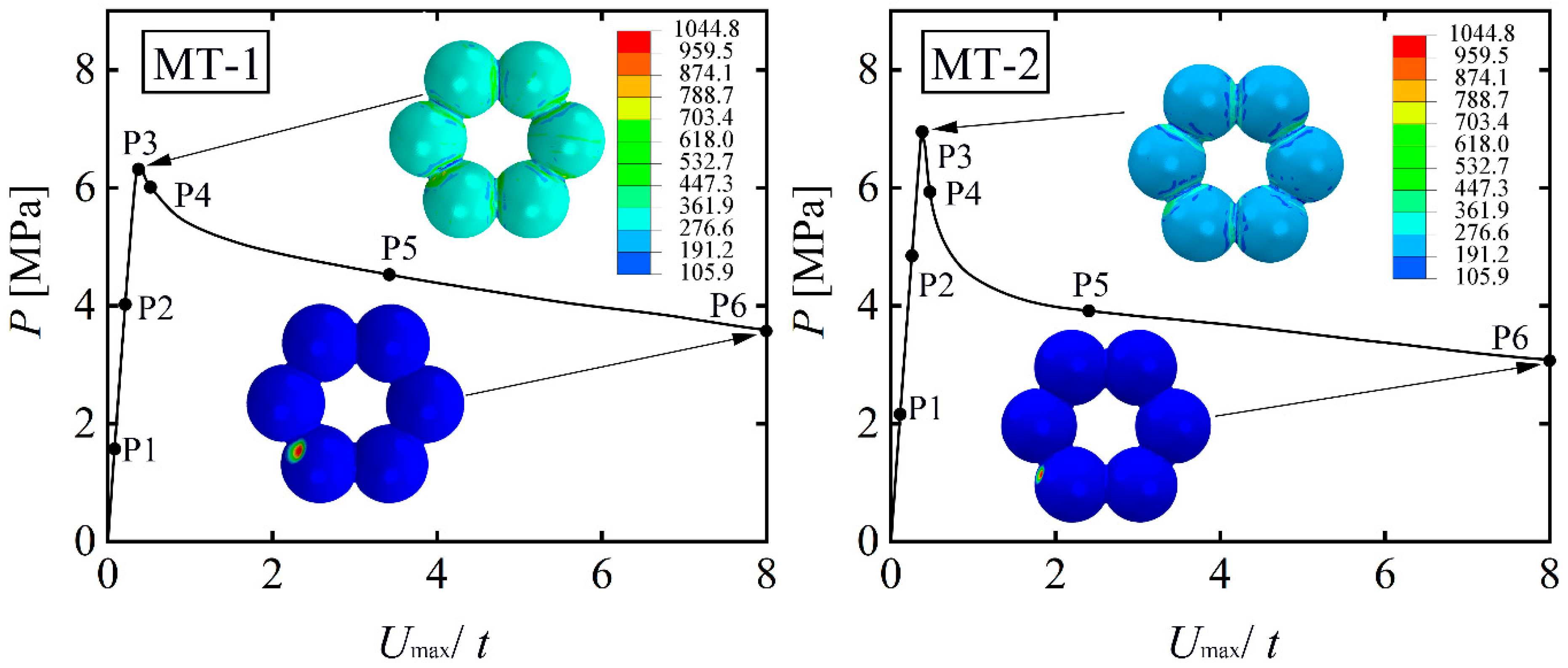
3.2. Numerical Analysis of the Two Manufactured Sphere-Segmented Toroidal Shells
3.3. Experimental Analysis of the Two Sphere-Segmented Toroidal Shells
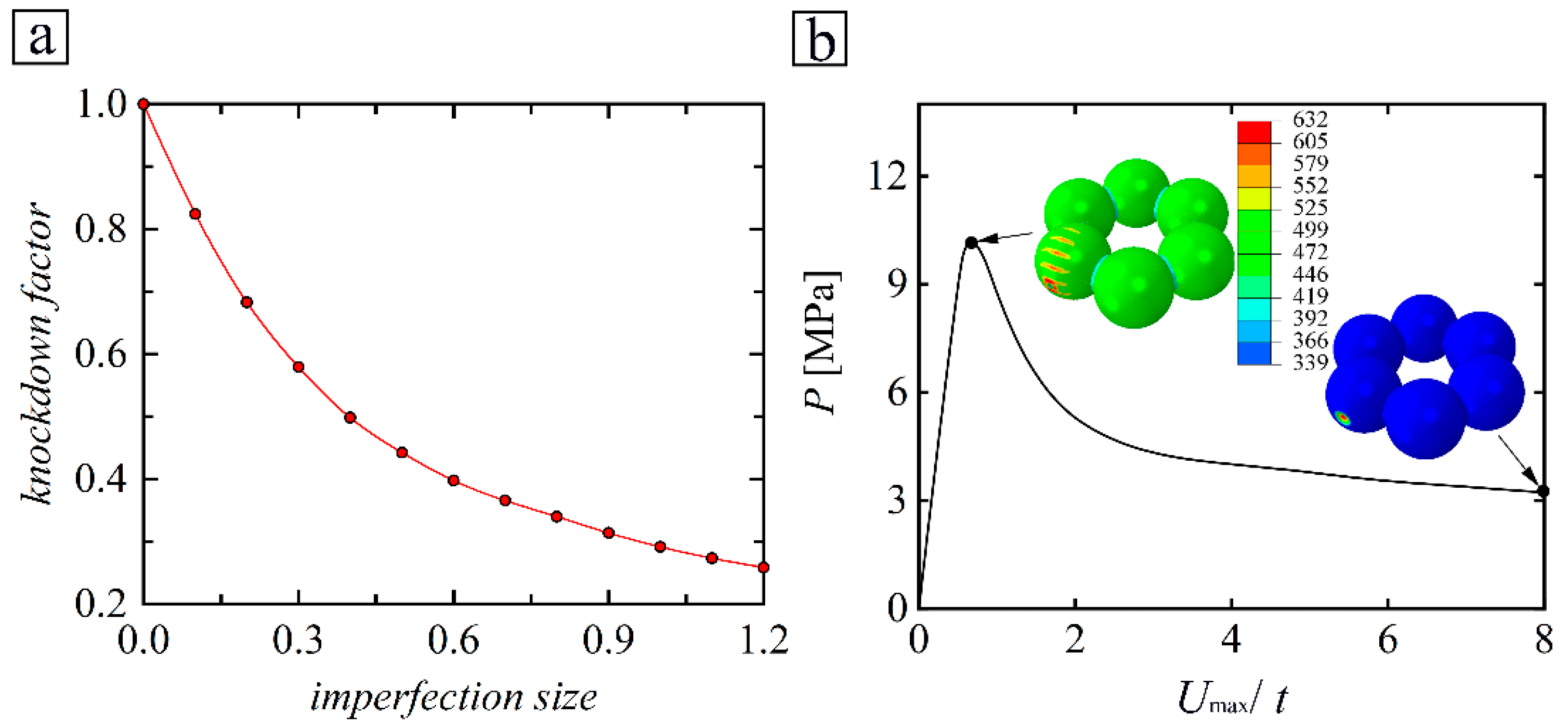
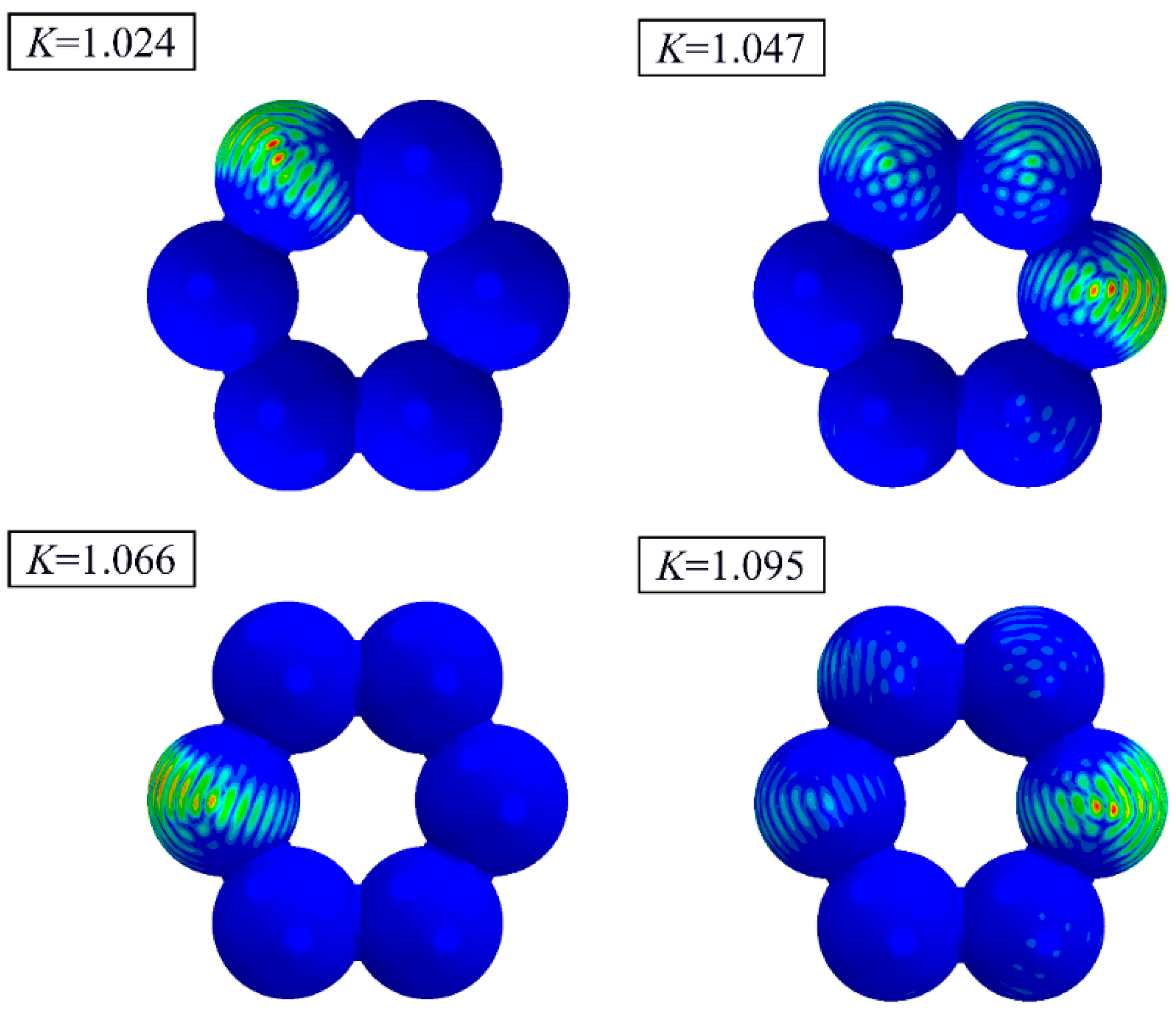
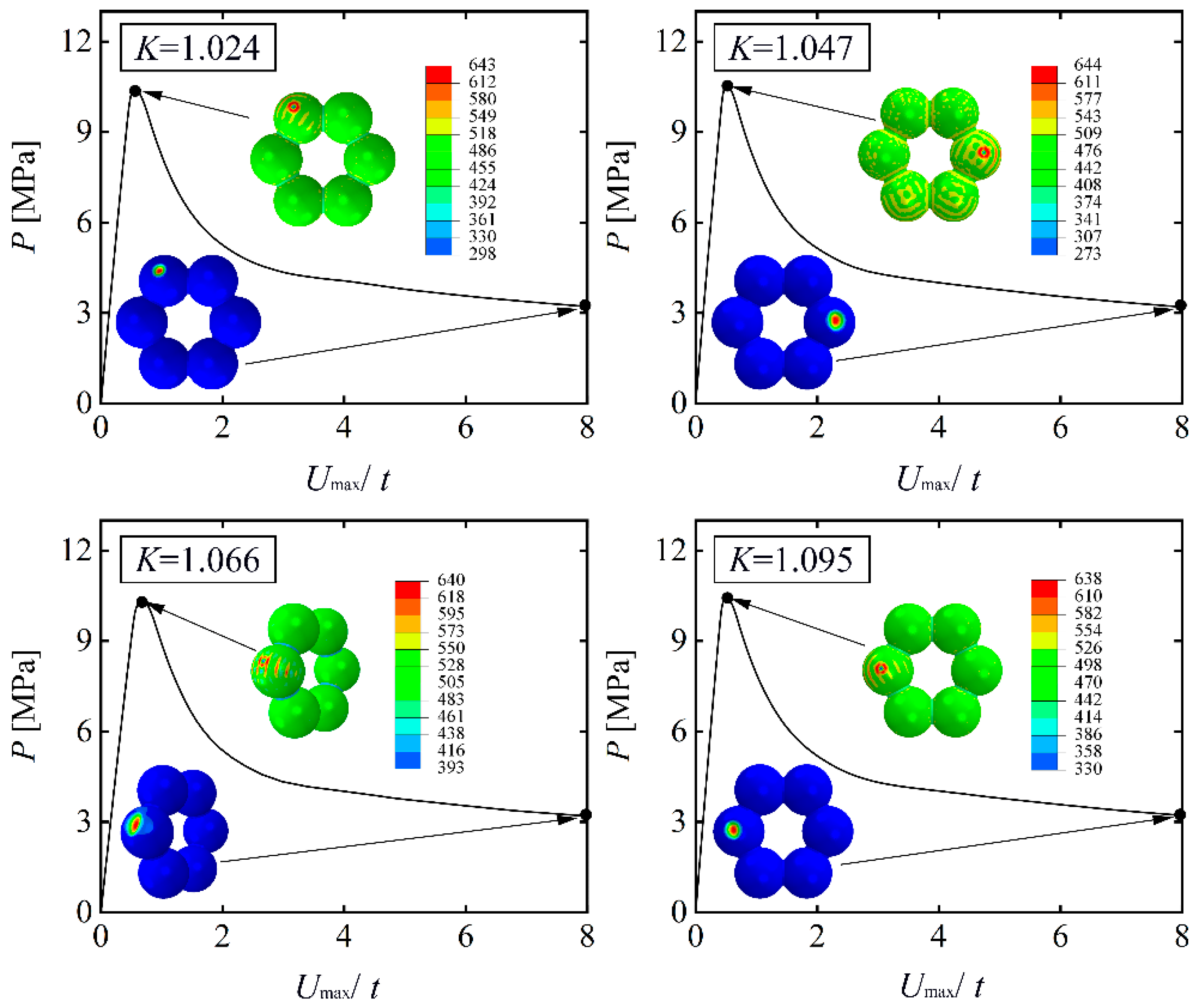
3.4. Effect of Elliptic Imperfections on Sphere-Segmented Toroidal Shells
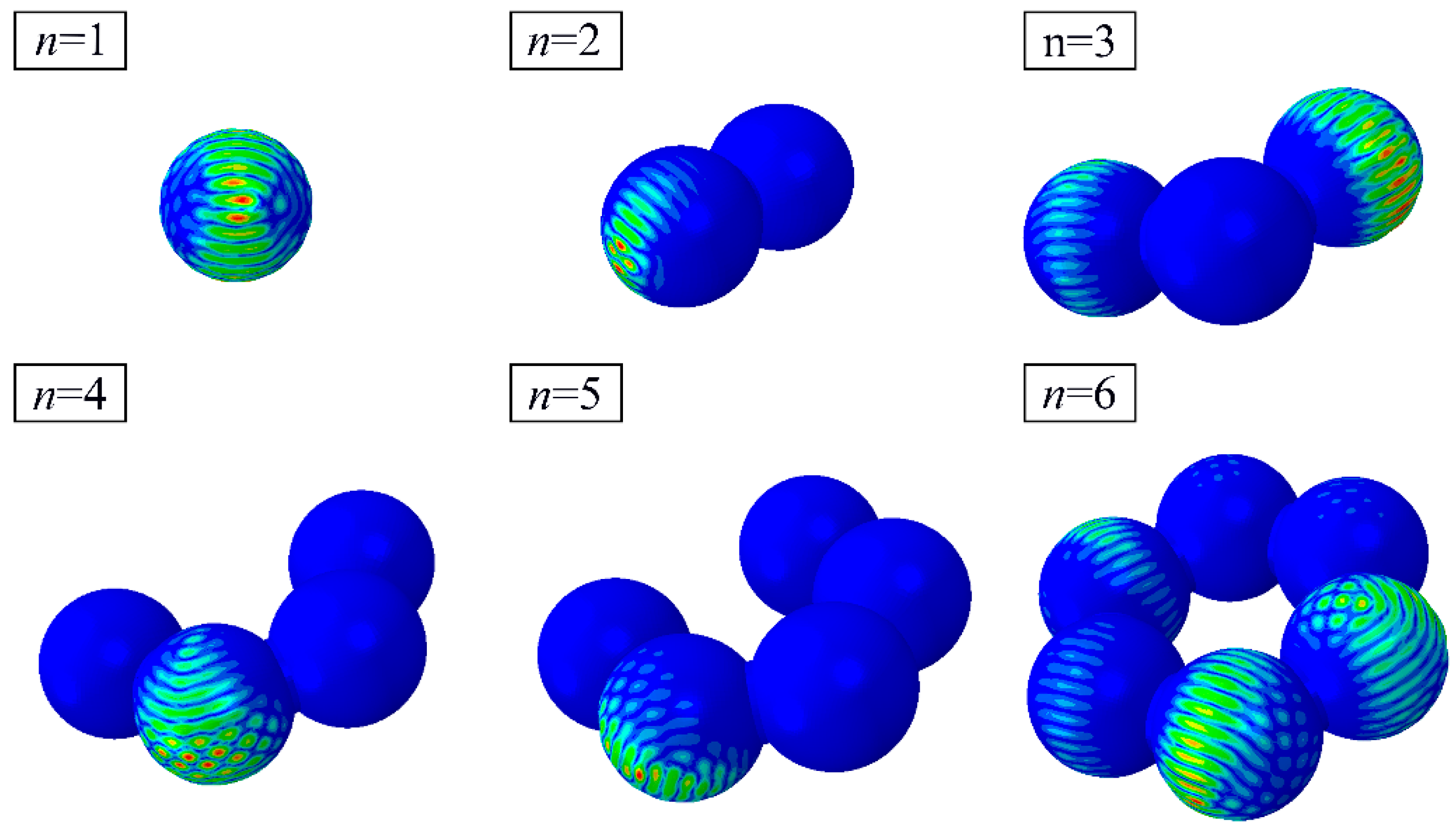
3.5. Effect of Completeness Imperfections on Sphere-Segmented Toroidal Shells
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, Q.; Cui, W.; Zhang, B. Buckling characteristics of a circular toroidal shell with stiffened ribs. Ocean Eng. 2015, 108, 325–335. [Google Scholar] [CrossRef]
- Ross, C. A conceptual design of an underwater missile launcher. Ocean Eng. 2005, 32, 85–99. [Google Scholar] [CrossRef]
- Ross, C. A conceptual design of an underwater vehicle. Ocean Eng. 2006, 33, 2087–2104. [Google Scholar] [CrossRef]
- Błachut, J. Collapse tests on externally pressurized toroids. J. Press. Vessel. Technol. Trans. ASME 2003, 125, 91–96. [Google Scholar] [CrossRef]
- Błachut, J. Buckling and first ply failure of composite toroidal pressure hull. Comput. Struct. 2004, 82, 1981–1992. [Google Scholar] [CrossRef]
- Błachut, J.; Jaiswal, O. Instabilities in torispheres and toroids under suddenly applied external pressure. Int. J. Impact Eng. 1999, 22, 511–530. [Google Scholar] [CrossRef]
- Zingoni, A.; Enoma, N.; Govender, N. Equatorial bending of an elliptic toroidal shell. Thin-Walled Struct. 2015, 96, 286–294. [Google Scholar] [CrossRef]
- Enoma, N.; Zingoni, A. Analytical formulation and numerical modelling for multi-shell toroidal pressure vessels. Comput. Struct. 2020, 232, 105811. [Google Scholar] [CrossRef]
- Du, Q.; Cui, W.; Wan, Z. Nonlinear Finite Element Analysis of a Toroidal Shell with Ring-Stiffened Ribs. OMAE 2010, 21088, 759–765. [Google Scholar] [CrossRef]
- Du, Q.; Zou, G.; Zhang, B.; Wan, Z. Simplified theoretical solution of circular toroidal shell with ribs under uniform external pressure. Thin-Walled Struct. 2015, 96, 49–55. [Google Scholar] [CrossRef]
- Moradi-Dastjerdi, R.; Behdinan, K.; Safaei, B.; Qin, Z. Buckling behavior of porous CNT-reinforced plates integrated between active piezoelectric layers. Eng. Struct. 2020, 222, 111141. [Google Scholar] [CrossRef]
- Civalek, Ö.; Avcar, M. Free vibration and buckling analyses of CNT reinforced laminated non-rectangular plates by discrete singular convolution method. Eng. Comput. 2020, 38, 489–521. [Google Scholar] [CrossRef]
- Zhang, J.; Di, C.; Wang, F.; Tang, W. Buckling of segmented toroids under external pressure. Ocean Eng. 2021, 239, 109921. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, W.; Yuan, S. Research on hydro-forming of spherical shells with different preform types. Int. J. Adv. Manuf. Technol. 2017, 92, 2631–2638. [Google Scholar] [CrossRef]
- Evkin, A.; Lykhachova, O. Design buckling pressure for thin spherical shells: Development and validation. Int. J. Solids Struct. 2019, 156–157, 61–72. [Google Scholar] [CrossRef]
- Cui, W. An Overview of Submersible Research and Development in China. J. Mar. Sci. Appl. 2018, 17, 459–470. [Google Scholar] [CrossRef]
- Yu, C.; Chen, Z.; Chen, C.; Chen, Y. Influence of initial imperfections on ultimate strength of spherical shells. Int. J. Nav. Arch. Ocean Eng. 2017, 9, 473–483. [Google Scholar] [CrossRef]
- Liang, C.; Shiah, S.W.; Jen, C.; Chen, H. Optimum design of multiple intersecting spheres deep-submerged pressure hull. Ocean Eng. 2004, 31, 177–199. [Google Scholar] [CrossRef]
- Gou, P.; Cui, W. Study of structural optimization problem for multiple intersecting spherical pressure hulls. Chuan Bo Li Xue/J. Sh. Mech. 2009, 13, 269–277. [Google Scholar]
- Zhang, M.; Tang, W.; Wang, F.; Zhang, J.; Cui, W.; Chen, Y. Buckling of bi-segment spherical shells under hydrostatic external pressure. Thin-Walled Struct. 2017, 120, 1–8. [Google Scholar] [CrossRef]
- Liu, J.; Yu, B.; Zhou, Y.; Zhang, Y.; Duan, M. The buckling of spherical-cylindrical composite shells by external pressure. Compos. Struct. 2021, 265, 113773. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A. A comprehensive shell approach for vibration of porous nano-enriched polymer composite coupled spheroidal-cylindrical shells. Compos. Struct. 2022, 289, 115464. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.; Ahmadi-Pari, A. Wave frequency responses estimate of the nanocomposite linked hemispherical-conical shell underwater-like bodies with the impacts of two types of graphene-based nanofillers. Ocean Eng. 2022, 262, 112329. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.; Ahmadi-Pari, A. Circumferential vibration analysis of nano-porous-sandwich assembled spherical-cylindrical-conical shells under elastic boundary conditions. Eng. Struct. 2022, 273, 115094. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.; Dimitri, R.; Tornabene, F. Free vibration of porous graphene oxide powder nano-composites assembled paraboloidal-cylindrical shells. Compos. Struct. 2023, 304, 116431. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Masoodi, A. Shell instability analysis by using mixed interpolation. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 419. [Google Scholar] [CrossRef]
- Zingoni, A.; Mokhothu, B.; Enoma, N. A theoretical formulation for the stress analysis of multi-segmented spherical shells for high-volume liquid containment. Eng. Struct. 2015, 87, 21–31. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, H.; Wang, F.; Li, Y.; Tang, W. Buckling of externally pressurized torispheres with uniform and stepwise thickness. Thin-Walled Struct. 2022, 173, 109045. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Wang, F.; Tang, W. Buckling of stainless steel spherical caps subjected to uniform external pressure. Ships Offshore Struct. 2018, 13, 779–785. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Tang, W.; Zhu, Y.; Zhao, X. Buckling of externally pressurised spherical caps with wall-thickness reduction. Thin-Walled Struct. 2019, 136, 129–137. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Wang, F.; Zhu, Y.; Cui, W.; Chen, Y. Experimental and numerical studies on the buckling of the hemispherical shells made of maraging steel subjected to extremely high external pressure. Int. J. Press. Vessel. Pip. 2019, 172, 56–64. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, Z.; Wang, F.; Zhao, T.; Zhu, Y. Ultimate strength of externally pressurised steel spheres containing through-thickness defects. Int. J. Press. Vessel. Pip. 2022, 199, 104750. [Google Scholar] [CrossRef]
- Schalen, A. EN 1993-1.6: 2007.E; Eurocode 3—Design of Steel Structures—Part 1–6: Strength and Stability of Shell Structures. European Committee for Standardisation: Brussels, Belgium, 2004.
- CCS. Rules for Construction and Classification of Diving Systems and Submersibles; China Classification Society: Beijing, China, 2018. [Google Scholar]
- Ricks, E. An Incremental approach to the Solution of snapping and buckling problems. Int. J. Solids Struct. 1979, 15, 529–551. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, M.; Wang, W.; Tang, W. Buckling of egg-shaped shells subjected to external pressure. Thin-Walled Struct. 2017, 113, 122–128. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, J.; Tang, W.; Zhao, X.; Zhu, Y. Experimental and numerical collapse properties of externally pressurized egg-shaped shells under local geometrical imperfections. Int. J. Press. Vessel. Pip. 2019, 175, 103893. [Google Scholar] [CrossRef]
- Zhang, J.; Hua, Z.; Wang, F.; Tang, W.; Zhu, Y. Buckling of an egg-shaped shell with varying wall thickness under uniform external pressure. Ships Offshore Struct. 2019, 14, 559–569. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, M.; Tang, W.; Wang, W.; Wang, M. Buckling of spherical shells subjected to external pressure: A comparison of experimental and theoretical data. Thin-Walled Struct. 2017, 111, 58–64. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, C.; Wagner, H.; Cui, W.; Tang, W. Study on dented hemispheres under external hydrostatic pressure. Mar. Struct. 2020, 74, 102819. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Tang, W.; Wang, F.; Zhu, Y. Non-linear collapse behavior of externally pressurized resin toroidal and cylindrical shells: Numerical and experimental studies. Ships Offshore Struct. 2021, 16, 529–545. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Tang, W.; Wang, F.; Yin, B. Experimental and numerical buckling analysis of toroidal shell segments under uniform external pressure. Thin-Walled Struct. 2020, 150, 106689. [Google Scholar] [CrossRef]
- Reitinger, R.; Ramm, E. Buckling and imperfection sensitivity in the optimization of shell structures. Thin-Walled Struct. 1995, 23, 159–177. [Google Scholar] [CrossRef]
- Deml, M.; Wunderlich, W. Direct evaluation of the “worst” imperfection shape in shell buckling. Comput. Methods Appl. Mech. Eng. 1997, 149, 201–222. [Google Scholar] [CrossRef]
- Lindgaard, E.; Lund, E.; Rasmussen, K. Nonlinear buckling optimization of composite structures considering “worst” shape imperfections. Int. J. Solids Struct. 2010, 47, 3186–3202. [Google Scholar] [CrossRef]
- Dey, T.; Ramachandra, L. Computation of worst geometric imperfection profiles of composite cylindrical shell panels by minimizing the non-linear buckling load. Appl. Math Model. 2019, 74, 483–495. [Google Scholar] [CrossRef]
- Magisano, D.; Garcea, G. Increasing the buckling capacity with modal geometric “imperfections” designed by a reduced order model. Thin-Walled Struct. 2022, 178, 109529. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, S.; Cui, W.; Zhao, X.; Tang, W.; Wang, F. Buckling of circumferentially corrugated cylindrical shells under uniform external pressure. Ships Offshore Struct. 2019, 14, 879–889. [Google Scholar] [CrossRef]
- Lee, A.; Jiménez, F.; Marthelot, J.; Hutchinson, J.; Reis, P. The Geometric Role of Precisely Engineered Imperfections on the Critical Buckling Load of Spherical Elastic Shells. J. Appl. Mech. Trans. ASME 2016, 83, 111005. [Google Scholar] [CrossRef]
- Castro, S.; Zimmermann, R.; Arbelo, M.; Khakimova, R.; Hilburger, M.; Degenhardt, R. Geometric imperfections and lower-bound methods used to calculate knock-down factors for axially compressed composite cylindrical shells. Thin-Walled Struct. 2014, 74, 118–132. [Google Scholar] [CrossRef]
- Hutchinson, J. Buckling of spherical shells revisited. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160577. [Google Scholar] [CrossRef]




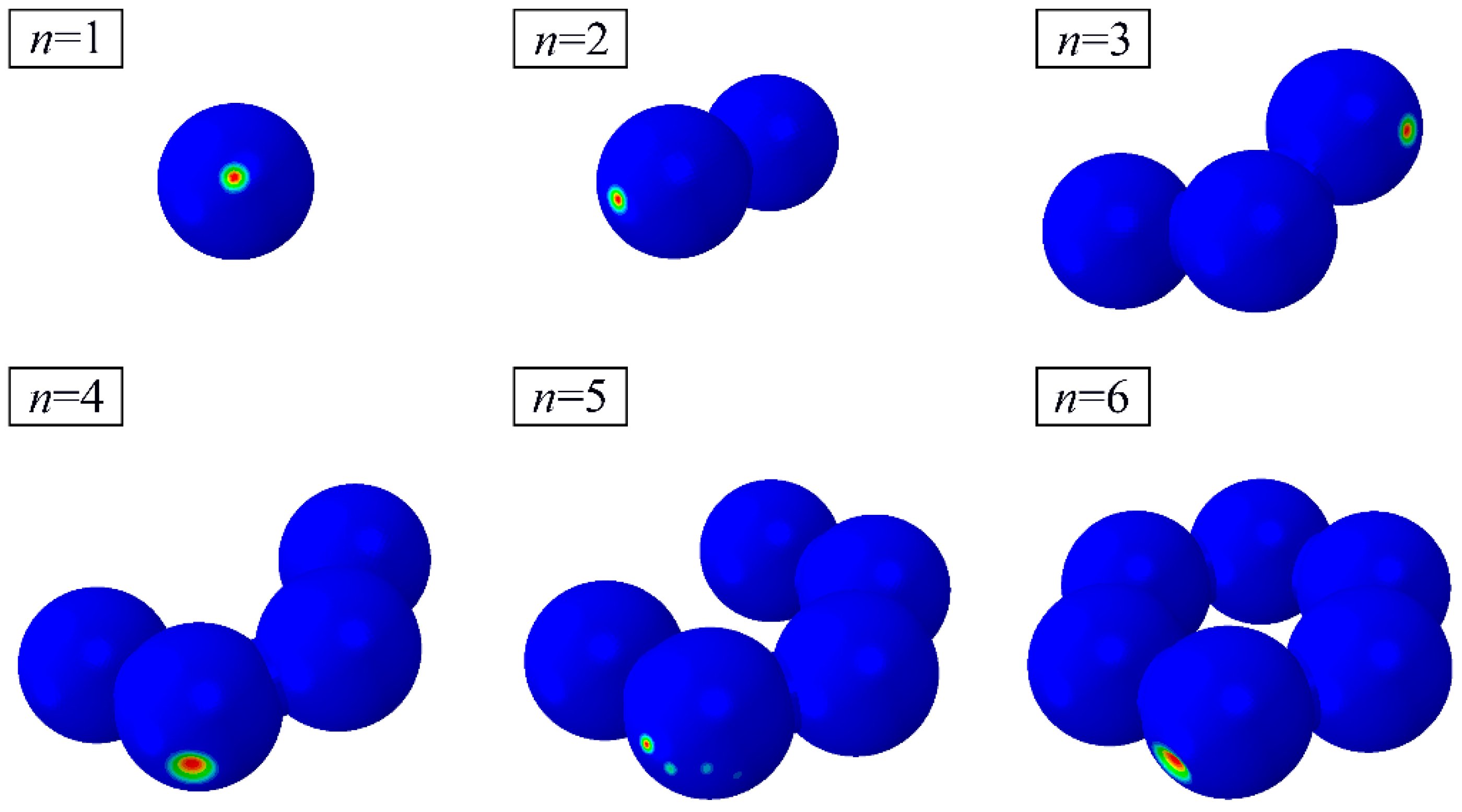
| Model | St. dev. | |||||||
|---|---|---|---|---|---|---|---|---|
| ST-1 | 0.686 | 0.826 | 0.753 | 0.037 | 19.206 | 6.229 | 5.523 | 1.128 |
| ST-2 | 0.688 | 0.818 | 0.746 | 0.031 | 18.452 | 6.292 | 5.525 | 1.139 |
| Order | 1st Mode | 2nd Mode | 3rd Mode | 4th Mode | 5th Mode | 6th Mode | 7th Mode | 8th Mode | 9th Mode |
| Plin | 26.549 | 26.550 | 26.550 | 26.551 | 26.557 | 26.558 | 26.558 | 26.564 | 26.564 |
| Mode |  |  |  |  |  |  |  |  |  |
| Order | 10th Mode | 11th Mode | 12th Mode | 13th Mode | 14th Mode | 15th Mode | 16th Mode | 17th Mode | 18th Mode |
| Plin | 26.577 | 26.579 | 26.586 | 26.586 | 26.586 | 26.594 | 26.594 | 26.595 | 26.601 |
| Mode |  |  |  |  |  |  |  |  |  |
| Order | 19th Mode | 20th Mode | 21st Mode | 22nd Mode | 23rd Mode | 24th Mode | 25th Mode | 26th Mode | 27th Mode |
| Plin | 26.602 | 26.602 | 26.602 | 26.603 | 26.612 | 26.612 | 26.657 | 26.657 | 26.667 |
| Mode |  |  |  |  |  |  |  |  |  |
| Order | 28th Mode | 29th Mode | 30th Mode | 31st Mode | 32nd Mode | 33rd Mode | 34th Mode | 35th Mode | 36th Mode |
| Plin | 26.667 | 26.674 | 26.678 | 26.678 | 26.682 | 26.682 | 26.690 | 26.690 | 26.691 |
| Mode |  |  |  |  |  |  |  |  |  |
| Order | 37th Mode | 38th Mode | 39th Mode | 40th Mode | 41st Mode | 42nd Mode | 43rd Mode | 44th Mode | 45th Mode |
| Plin | 26.691 | 26.694 | 26.708 | 26.708 | 26.713 | 26.714 | 26.727 | 26.732 | 26.737 |
| Mode |  |  |  |  |  |  |  |  |  |
| Order | 46th Mode | 47th Mode | 48th Mode | 49th Mode | 50th Mode | ||||
| Plin | 26.746 | 26.746 | 26.750 | 26.757 | 26.758 | ||||
| Mode |  |  |  |  |  |
| Model | St. dev. | |||
|---|---|---|---|---|
| 26.549 | 26.758 | 26.645 | 0.067 | |
| 9.922 | 10.668 | 10.394 | 0.155 |
| Order | 1st Mode | 2nd Mode | 3rd Mode | 4th Mode | 5th Mode | 6th Mode | 7th Mode | 8th Mode | 9th Mode |
| Pnon | 10.150 | 10.349 | 10.352 | 10.543 | 10.370 | 10.379 | 9.922 | 10.236 | 10.474 |
| Mode |  |  |  |  |  |  |  | 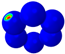 | 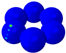 |
| Order | 10th Mode | 11th Mode | 12th Mode | 13th Mode | 14th Mode | 15th Mode | 16th Mode | 17th Mode | 18th Mode |
| Pnon | 10.575 | 10.234 | 10.388 | 10.451 | 10.370 | 10.440 | 10.454 | 10.601 | 10.243 |
| Mode | 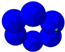 | 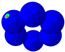 |  | 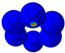 | 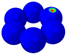 | 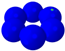 |  |  |  |
| Order | 19th Mode | 20th Mode | 21st Mode | 22nd Mode | 23rd Mode | 24th Mode | 25th Mode | 26th Mode | 27th Mode |
| Pnon | 10.292 | 10.439 | 10.274 | 10.281 | 10.271 | 10.265 | 10.431 | 10.458 | 10.538 |
| Mode |  |  |  |  |  | 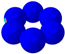 |  |  |  |
| Order | 28th Mode | 29th Mode | 30th Mode | 31st Mode | 32nd Mode | 33rd Mode | 34th Mode | 35th Mode | 36th Mode |
| Pnon | 10.541 | 10.403 | 10.452 | 10.479 | 10.073 | 10.089 | 10.567 | 10.504 | 10.582 |
| Mode |  |  |  |  |  |  |  |  |  |
| Order | 37th Mode | 38th Mode | 39th Mode | 40th Mode | 41st Mode | 42nd Mode | 43rd Mode | 44th Mode | 45th Mode |
| Pnon | 10.521 | 10.342 | 10.509 | 10.283 | 10.584 | 10.489 | 10.668 | 10.534 | 10.367 |
| Mode |  |  |  |  |  |  |  |  |  |
| Order | 46th Mode | 47th Mode | 48th Mode | 49th Mode | 50th Mode | ||||
| Pnon | 10.367 | 10.457 | 10.106 | 10.453 | 10.532 | ||||
| Mode |  |  |  |  |  |
| K | a | b | |||||
|---|---|---|---|---|---|---|---|
| 1 | 60.00 | 60.00 | 126.35 | 126.35 | 11.505 | 12.615 | 10.398 |
| 1.024 | 60.79 | 58.42 | 127.87 | 124.84 | 11.584 | 12.548 | 10.412 |
| 1.047 | 61.50 | 57.01 | 129.22 | 123.44 | 11.582 | 12.666 | 10.540 |
| 1.066 | 62.10 | 55.80 | 130.41 | 122.3 | 11.089 | 12.548 | 10.334 |
| 1.083 | 62.59 | 54.85 | 131.40 | 121.37 | 11.504 | 12.507 | 10.497 |
| 1.095 | 62.96 | 54.07 | 132.12 | 120.61 | 11.682 | 12.669 | 10.446 |
| 1.104 | 63.21 | 53.57 | 132.59 | 120.14 | 11.681 | 12.600 | 10.565 |
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | |
|---|---|---|---|---|---|---|
| 12.007 | 11.635 | 11.362 | 11.491 | 11.651 | 11.505 | |
| Δ = 0 | 12.753 | 12.350 | 12.585 | 12.431 | 12.420 | 12.615 |
| Δ = 0.1 t | 10.483 | 10.381 | 10.244 | 10.186 | 10.492 | 10.398 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di, C.; Zhang, J.; Wang, F.; Zhang, Y. Numerical and Experimental Buckling and Post-Buckling Analyses of Sphere-Segmented Toroidal Shell Subject to External Pressure. Metals 2023, 13, 64. https://doi.org/10.3390/met13010064
Di C, Zhang J, Wang F, Zhang Y. Numerical and Experimental Buckling and Post-Buckling Analyses of Sphere-Segmented Toroidal Shell Subject to External Pressure. Metals. 2023; 13(1):64. https://doi.org/10.3390/met13010064
Chicago/Turabian StyleDi, Chenyang, Jian Zhang, Fang Wang, and Yu Zhang. 2023. "Numerical and Experimental Buckling and Post-Buckling Analyses of Sphere-Segmented Toroidal Shell Subject to External Pressure" Metals 13, no. 1: 64. https://doi.org/10.3390/met13010064
APA StyleDi, C., Zhang, J., Wang, F., & Zhang, Y. (2023). Numerical and Experimental Buckling and Post-Buckling Analyses of Sphere-Segmented Toroidal Shell Subject to External Pressure. Metals, 13(1), 64. https://doi.org/10.3390/met13010064








