Binary Newton Calculation Method of Residual Stress Based on the Indentation Energy Difference Theory

Abstract

Residual stress is a key parameter to evaluate the structural reliability of energy equipment. The indentation method has the characteristics of being nondestructive and easy to operate to calculate the residual stress of test materials, which has a broad application prospect in the field testing of energy equipment. However, because of the effect of preloading and data acquisition delay, the problem of indentation data fluctuation is prominent, and the indentation energy coefficient fitted by the traditional least square method is not consistent with the theoretical law, making it difficult to carry out stable calculations. In this paper, the Newton iteration formula of a binary nonlinear formula is derived based on the univariate Newton iteration formula, which is introduced into the data processing of residual stress, which increases the weight of the data in the stability stage and reduces the influence of the fluctuation data on the fitting results, so that the indentation energy coefficient is accurately calculated. Combined with the basic principle of indentation energy difference theory, the precise and efficient measurement of residual stress is realized.

1. Introduction

Residual stress [1,2] refers to the internal stress that remains in an object to maintain self-phase equilibrium after the disappearance of external force or the action of an inhomogeneous temperature field [3]. The existence of residual stress will not only reduce the structural strength but also cause stress corrosion cracking and fatigue damage, which destroy the integrity of the structure. Therefore, in order to ensure the safety and reliability of the structure, it is necessary to accurately test the magnitude and distribution of residual stress and formulate a pertinent control strategy. At present, the testing methods for residual stress mainly include the mechanical test method and the physical test method [4]. The mechanical testing methods mainly include the drilling method and slotting method, which cause local damage to materials during the measurement process and are difficult to use in service or waiting-for-service equipment; however, physical test methods, such as X-ray diffraction and ultrasound, fluctuate greatly when testing nonuniform tissue and strong stress gradient structures (such as welded structures), and their application in engineering sites is limited [1,5,6]. In contrast, the indentation method has the advantage of convenience without sampling and testing and has a good engineering application potential in the field test of service equipment.

In the early stages, it was found that the hardness value decreased when residual tensile stress existed; when residual compressive stress was present, the hardness value of the test increased. Therefore, by comparing the variation pattern of hardness values, the magnitude and direction of the residual stress can be estimated qualitatively. Subsequently, Tsui and Bolshakov [7] found that the residual stress did not change the true hardness of the material but affected the real indentation area. In 1998, Suresh et al. [8] put forward the indentation method for quantitatively testing residual stress based on the assumption of hardness invariance. However, the test results of this method depend on the indentation topography, and only the equivalent average residual stress can be measured. Aiming at this problem, Peng et al. [9] proposed a new method to calculate the biaxial residual stress by means of the method of indentation energy difference. In this method, the Knoop [10,11] indenter was indented in the direction of biaxial stress, the indentation energy obtained by the integration of the load–depth curve was used as the calculation parameter, and the biaxial stress component was obtained without observing the indentation topography. However, in actual measurement, because of the delay of the control system of the indentation equipment and the large fluctuation of the data points, the original data fitting effect was poor, the residual stress calculation result deviated greatly from the actual result, and sometimes cannot even be calculated.

In view of the above problems, based on the univariate Newton iteration method [12,13], the Newton iteration formula [14] of binary nonlinear formulas was deduced, which is introduced into the fitting process of the indentation data. By increasing the weight of the data in the stability stage, the influence of the fluctuation data on the fitting results is reduced, and the accurate and efficient solution of calculation of the biaxial residual stress based on energy difference theory is realized.

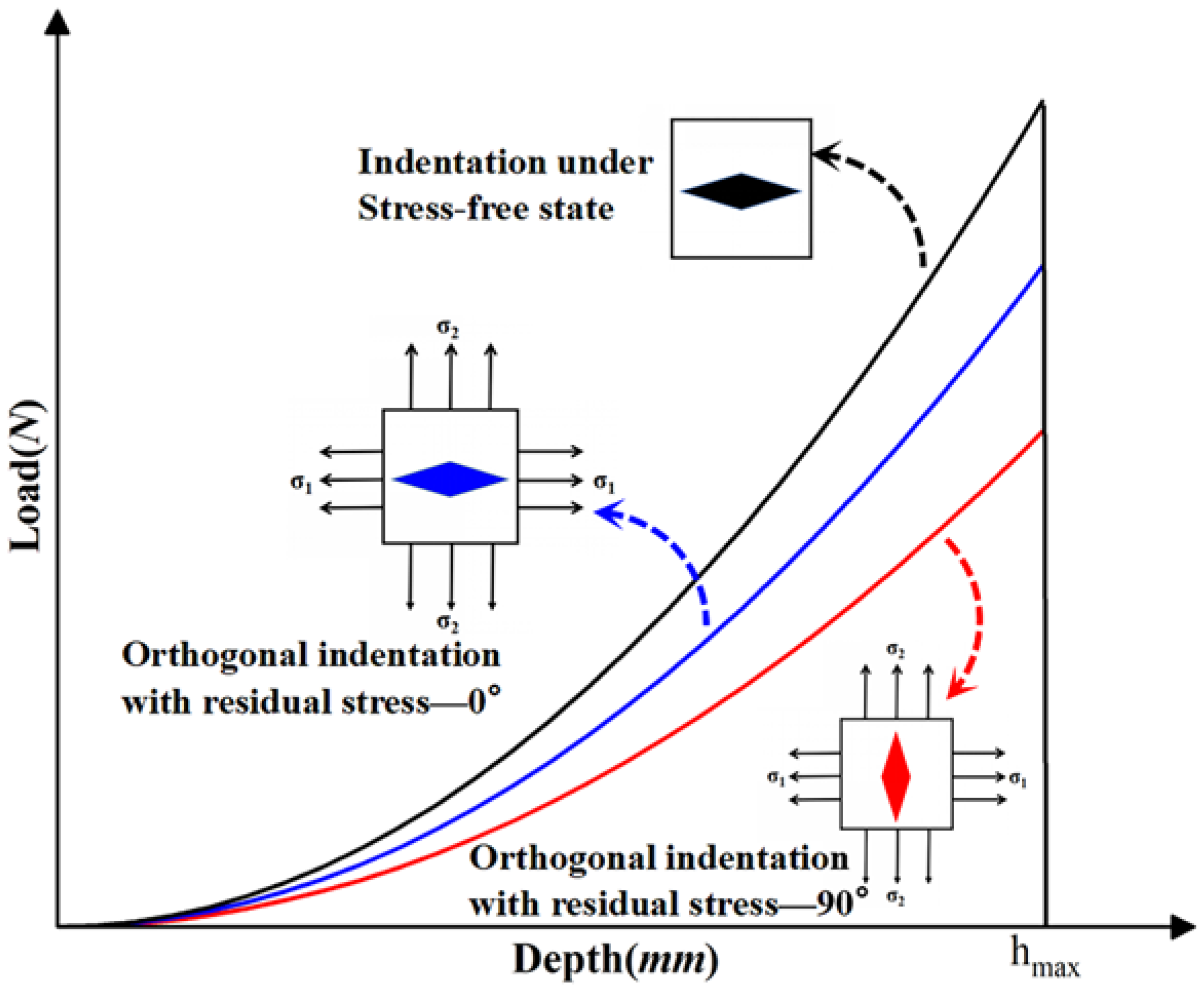
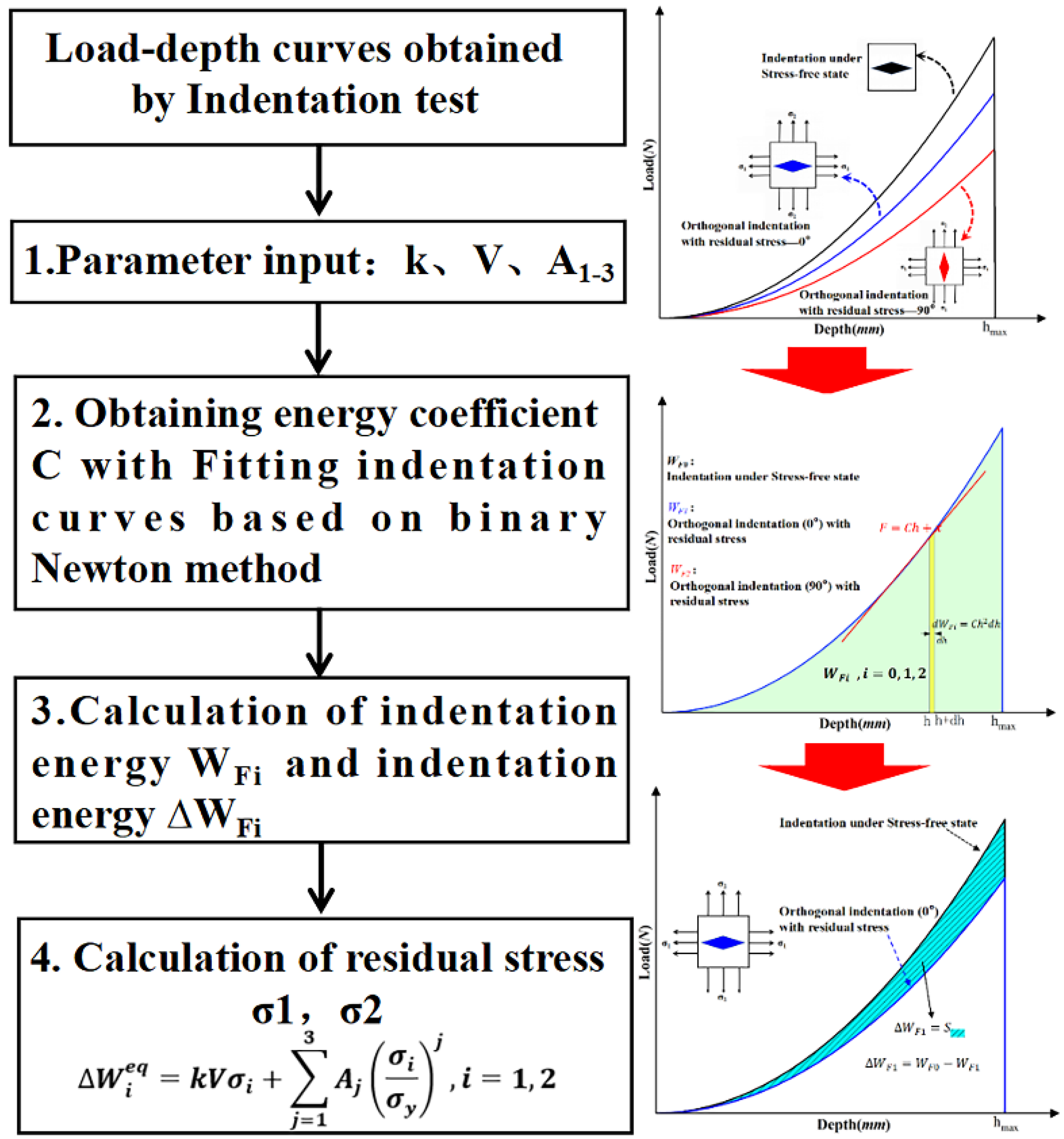
2. Residual Stress Calculation Model Design Based on the Newton Method

According to the theory of indentation energy difference, obtaining the biaxial residual stress of the material requires three indentation tests on the specimen: the first is the test in the stress-free state, and the other two are the orthogonal indentation of the Knoop indenter on the surface of the specimen. The resulting load–depth curve is shown in Figure 1. From an energy point of view, the indentation work and the stress work are all converted into strain energy during each indentation process [15,16,17]. Considering that the stress work cannot be directly solved, the residual stress can be correlated by calculating the indentation energy difference between the stressed and the stress-free states [18].

The calculation of the indentation energy difference at the same indentation depth requires the indentation energy of the three indentation processes, which can be directly obtained by integrating the load–depth curve, as shown in Formula (1) and Figure 2. Since the indentation curve is a quadratic function, the indentation energy can be obtained by substituting the slope of the curve instead of the integral according to the integral solution method of the quadratic function, in which the curve slope is called the indentation energy coefficient, as shown in Formula (2).

$$W_F={{\displaystyle \int }}_0^{h_{max}}Fdh={{\displaystyle \int }}_0^{h_{max}}C{h}^{2}dh$$

(1)

$$W_F=\frac{1}{3}C{h}_{max}^3$$

(2)

It can be seen from Formula (2) that the accurate fitting of the load–depth data is the key to the solution of the indentation energy in the study of welding residual stress measured by the energy difference method [19,20]. In his study, Peng Wei found that due to the deviation of the shape of the equipment indenter and the delay of the control system, the existence of unstable region data caused the curve fitted by Formula (3) to have a large coincidence error with the origin in the initial position, while the fitting with Formula (4) could restrict the original data, and the slope obtained by Formula (3) was compared with that of Formula (3). The fitting curves of the stress-free and the unidirectional stress state do not conform to the theoretical model.

$$F=a{h}^2+bh+c$$

(3)

$$F=C{\left(h+u\right)}^2$$

(4)

In order to fit the indentation data accurately, the author designed an indentation data fitting algorithm based on Newton method. The author first calculated the sum of variance S² of the experimental data and the fitting formula

$$S^2={\displaystyle \sum }_{i=1}^n{\left[F_i-C{\left(h_i+u\right)}^2\right]}^2$$

(5)

When S² is the smallest, the fitting effect is best at this time, i.e., the function must have a unique extremum and a minimum. The basic calculation method based on the extremum of the function should meet the requirements of

$$\begin{array}{c}\left\{\begin{array}{c}\frac{\partial S^2}{\partial C}=2C{\gamma }_{4,0}+8Cu{\gamma }_{3,0}+12C{u}^2{\gamma }_{2,0}+8C{u}^3{\gamma }_{1,0}+2nC{u}^4-2{\gamma }_{2,1}-4u{\gamma }_{1,1}-2u^2{\gamma }_{0,1}=0\\ \frac{\partial S^2}{\partial u}=4C^2{\gamma }_{3,0}+12C^{2}u{\gamma }_{2,0}+12C^2{u}^2{\gamma }_{1,0}+4n{C}^2{u}^3-4C{\gamma }_{1,1}-4Cu{\gamma }_{1,0}=0\end{array}\right.\end{array}$$

(6)

$${\gamma }_{j,k}={\displaystyle \sum }_{i=1}^n{u}_i^j{F}_i^k;k=0,{\gamma }_{j,0}={\displaystyle \sum }_{i=1}^n{u}_i^j;j=0,{\gamma }_{0,k}={\displaystyle \sum }_{i=1}^n{F}_i^k;jandkarenotboth0.$$

Thus, the fit of Formula (3) is transformed into solving a binary nonlinear system of Formula (6).

Based on the Newton iterative formula of nonlinear formulas of binary functions, the author rewrote the abovementioned binary nonlinear formulas into the following functions:

$$\left\{\begin{array}{c}A\left(C,u\right)=C{r}_{4,0}+4Cu{r}_{3,0}+6C{u}^2{r}_{2,0}+4C{u}^3{r}_{1,0}+nC{u}^4-r_{2,1}-2u{r}_{1,1}-u^2{r}_{0,1}\\ B\left(C,u\right)=C^2{r}_{3,0}+3C^{2}u{r}_{2,0}+3C^2{u}^2{r}_{1,0}+n{C}^2{u}^3-C{r}_{1,0}-Cu{r}_{0,1}\end{array}\right.$$

(7)

This function satisfies the basic requirements of Newton method for solving binary nonlinear formulas, so it can be solved by substituting Newton iterative formula.

$$\left\{\begin{array}{c}{C}_{k+1}=C_k+\frac{A\left(C_k,u_k\right)B_h\left(C_k,u_k\right)-B\left(C_k,u_k\right)A_u\left(C_k,u_k\right)}{B_c\left(C_k,u_k\right)A_u\left(C_k,u_k\right)-A_c\left(C_k,u_k\right)B_u\left(C_k,u_k\right)}\\ u_{k+1}=u_k+\frac{B\left(C_k,u_k\right)A_C\left(C_k,u_k\right)-A\left(C_k,u_k\right)B_C\left(C_k,u_k\right)}{B_C\left(C_k,u_k\right)A_u\left(C_k,u_k\right)-A_C\left(C_k,u_k\right)B_u\left(C_k,u_k\right)}\end{array}\right.$$

(8)

$A_c\left(C,u\right)$, $A_u\left(C,u\right)$, $B_c\left(C,u\right)$, $B_u\left(C,u\right)$ is the first-order partial differential of the function $A\left(C,u\right)$ and $B\left(C,u\right)$ for c and u.

The indentation energy coefficient can be accurately fitted by using the binary Newton method, and the three-indentation data are correlated according to the calculated indentation energy to obtain the formula of the biaxial indentation energy difference shown in Figure 3 (when the indentation energy difference is equal to the same depth, the stress-free indentation work minus the stressed indentation work).

$$\left\{\begin{array}{c}\Delta W_{F1}=W_{F0}-W_{F1}\\ \Delta W_{F2}=W_{F0}-W_{F2}\end{array}\right.$$

(9)

Peng found that the energy difference of the Knoop indenter had superposition and directional characteristics after a lot of experimental studies [9,21,22]. The superposition characteristic [23] points out that the indentation energy difference under the biaxial stress is equal to the sum of the two stress components of the biaxial stress as the uniaxial stress, respectively, and the difference in the relative direction is the same as the original biaxial stress, as shown in Formula (10). The directional characteristics show that the difference of the indentation energy produced when the long axis of the Knoop indenter is indented perpendicular to the stress direction is about φ times that in parallel, and φ is the directional coefficient of the Knoop indenter [24], as shown in Formula (11).

$$\Delta W_F=\Delta W_{11}+\Delta W_{12}$$

(10)

$$\Delta W_{21}=\mathsf{\phi }\Delta W_{11}$$

(11)

The combination of the above two formulas immediately converts the indentation energy difference under any biaxial stress to the sum of the difference of the two equivalent uniaxial stresses [25,26] perpendicular to the long axis direction of the indenter to obtain Formula (12)

$$\left\{\begin{array}{c}\Delta W_1^{eq}=\frac{\mathsf{\phi }}{{\mathsf{\phi }}^2-1}\left(\mathsf{\phi }\Delta W_{F1}-\Delta W_{F2}\right)\\ \Delta W_2^{eq}=\frac{\mathsf{\phi }}{{\mathsf{\phi }}^2-1}\left(\mathsf{\phi }\Delta W_{F2}-\Delta W_{F1}\right)\end{array}\right.$$

(12)

Biaxial residual stress components can be calculated according to the relationship between the difference of the indentation energy and residual stress.

$$\Delta W_i^{eq}=kV{\sigma }_i+{\displaystyle \sum }_{j=1}^3{A}_j{\left(\frac{{\sigma }_i}{{\sigma }_y}\right)}^j,i=1,2$$

(13)

At this point, the Knoop indentation method is used to measure biaxial residual stress model. The binary Newton iteration formula commonly used in engineering calculation is used in the above model to process the measured data to obtain the energy coefficient, which avoids the error caused by the error of the specific point in the test data to the calculation results. Combined with the indentation energy difference theory, the problem that the calculation error caused by the traditional fitting method is large or even does not conform to the practical law in the actual calculation process is solved and provides theoretical support for the algorithm design of the residual stress calculation flow automation shown in Figure 4.

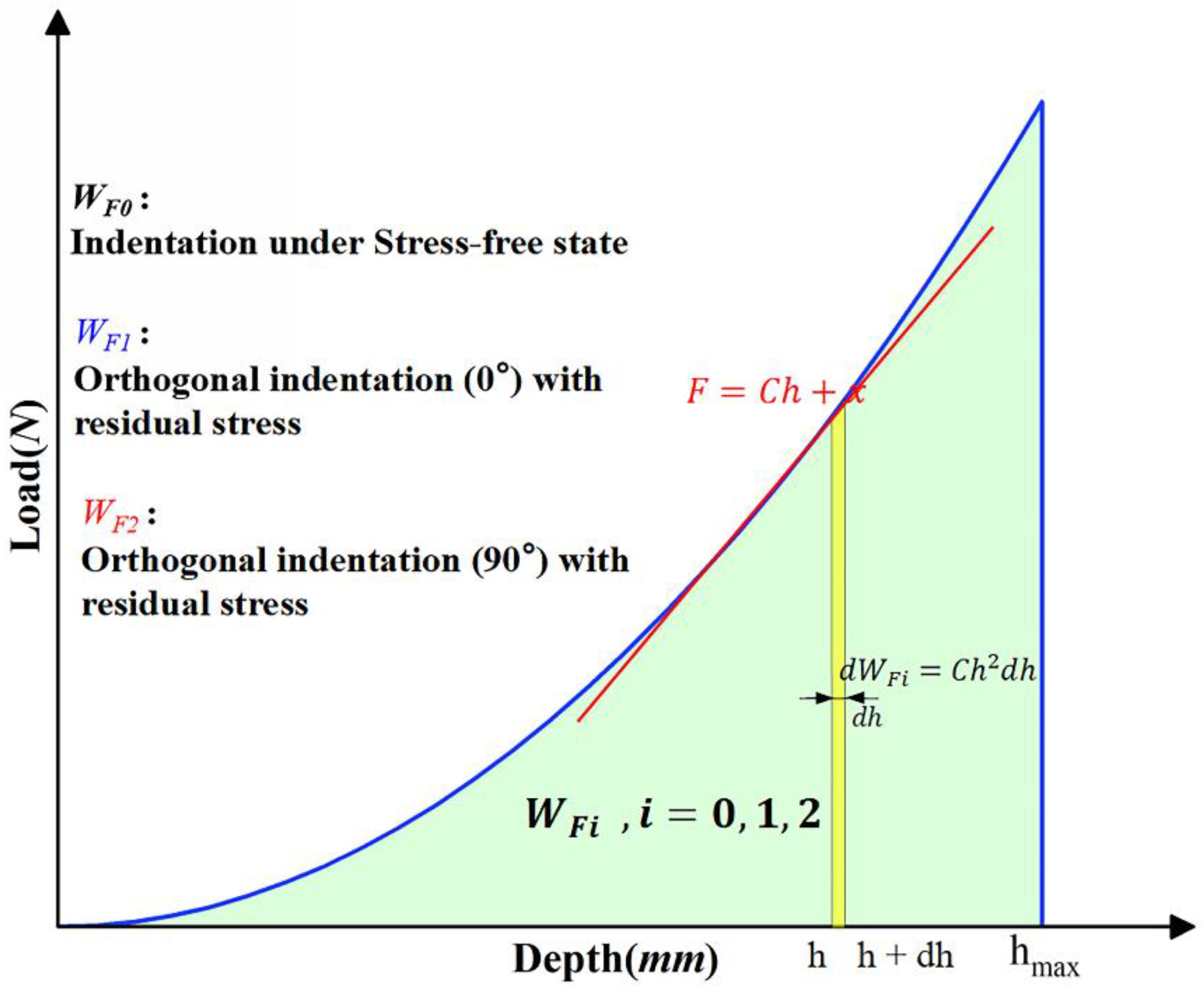
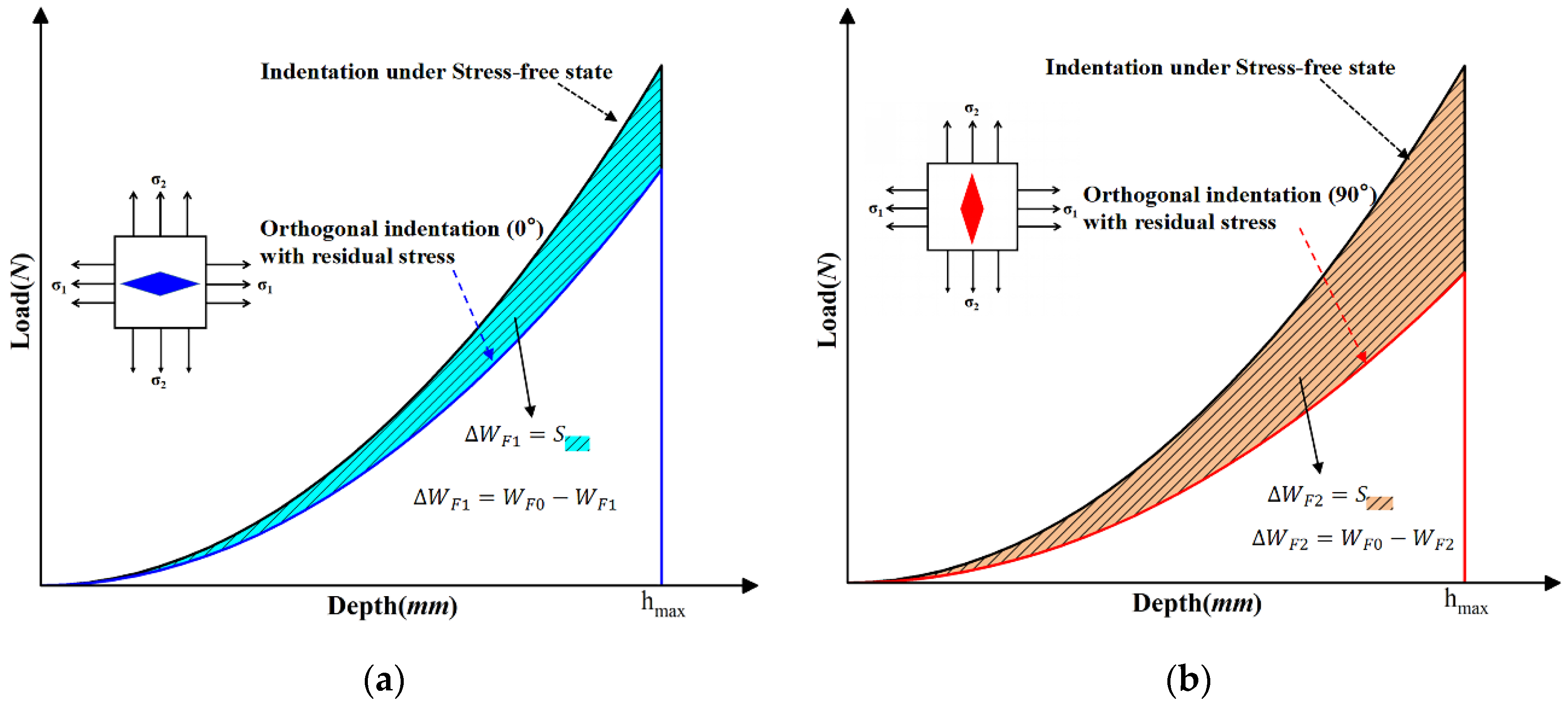
3. Derivation of the Newton Formula for Binary Equation

The Newton iteration method is one of the most powerful techniques to solve the problem of nonlinear equations. In this method, a series of approximate solutions are found to solve the nonlinear equation by selecting an initial estimator and approaching iteratively.

For the univariate equation: f(x) = 0, the Newton iteration formula is as follows

$$x_{n+1}=x_n-\frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}$$

(14)

where n is the number of iterations, $x_n$, $x_{n+1}$ is the approximate root of equation $f\left(x\right)=0,\mathrm{and}{f}^{\prime }\left(x_n\right)$ is the first-order differential of the function $f\left(x\right)$ at $x_n$.

After understanding the iterative solution process of univariate nonlinear equations, the Newton iteration method for binary nonlinear equation can be deduced.

If we have continuous partial derivatives of more than two orders in a certain neighborhood of function $z=f\left(x,y\right)at\left(x_0,y_0\right)$, and $\left(x_0+h,y_0+k\right)$ is at any point within this neighborhood, there is

$$f\left(x_0+h,y_0+k\right)\approx f\left(x_0,y_0\right)+\left(h\frac{\partial }{\partial x}f\left(x,y\right){|}_{x=x_0}+k\frac{\partial }{\partial y}f\left(x,y\right){|}_{y=y_0}\right)$$

(15)

$$\left(h=x-x_0,k=y-y_0\right)$$

If $f\left(x,y\right)=0$, the above equation can be converted to

$$f\left(x_k,y_k\right)+\left(x-x_k\right)f_x\left(x_k,y_k\right)+\left(y-y_k\right)f_y\left(x_k,y_k\right)=0$$

(16)

Similarly, let $z=g\left(x,y\right)$ be continuous in a certain neighborhood at point $\left(x_0,y_0\right)$, and there are continuous partial derivatives up to the 2nd order; then, $\left(x_0+h,y_0+k\right)$ at any point within this neighborhood will also have

$$g\left(x_0+h,y_0+k\right)\approx g\left(x_0,y_0\right)+\left(h\frac{\partial }{\partial x}g\left(x,y\right){|}_{x=x_0}+k\frac{\partial }{\partial y}g\left(x,y\right){|}_{y=y_0}\right)$$

(17)

$$\left(h=x-x_0,k=y-y_0\right)$$

Then, equation $g\left(x,y\right)=0$ can be reduced approximately to

$$g\left(x_0+h,y_0+k\right)\approx g\left(x_0,y_0\right)+\left(h\frac{\partial }{\partial x}g\left(x,y\right){|}_{x=x_0}+k\frac{\partial }{\partial y}g\left(x,y\right){|}_{y=y_0}\right)$$

(18)

Therefore, the equation set can be obtained as follows:

$$\left\{\begin{array}{c}f\left(x_k,y_k\right)+\left(x-x_k\right)f_x\left(x_k,y_k\right)+\left(y-y_k\right)f_y\left(x_k,y_k\right)=0\\ g\left(x_k,y_k\right)+\left(x-x_k\right)g_x\left(x_k,y_k\right)+\left(y-y_k\right)g_y\left(x_k,y_k\right)=0\end{array}\right.$$

(19)

For the above equation, when $g_x\left(x_k,y_k\right)f_y\left(x_k,y_k\right)-f_x\left(x_k,y_k\right)g_y\left(x_k,y_k\right)\ne 0$, it can be converted to

$$\left\{\begin{array}{c}x=x_k+\frac{f\left(x_k,y_k\right)g_y\left(x_k,y_k\right)-g\left(x_k,y_k\right)f_y\left(x_k,y_k\right)}{g_x\left(x_k,y_k\right)f_y\left(x_k,y_k\right)-f_x\left(x_k,y_k\right)g_y\left(x_k,y_k\right)}\\ y=y_k+\frac{g\left(x_k,y_k\right)f_x\left(x_k,y_k\right)-f\left(x_k,y_k\right)g_x\left(x_k,y_k\right)}{g_x\left(x_k,y_k\right)f_y\left(x_k,y_k\right)-f_x\left(x_k,y_k\right)g_y\left(x_k,y_k\right)}\end{array}\right.$$

(20)

The Newton iteration method for nonlinear equations of binary functions can be used to obtain approximate values by the iteration method when k is taken as a non-zero natural number $\left(x_k,y_k\right)$. $\delta$ are the error controls required for data processing; when $\left|\left(x_{k+1},y_{k+1}\right)\right|\le \delta \left(\delta >0\right)$, the root of the original equation is $\left(x_k,y_k\right)$. Then, the Newton iteration formula of the nonlinear equation of the binary function is as follows:

$$\left\{\begin{array}{c}{x}_{k+1}=x_k+\frac{f\left(x_k,y_k\right)g_y\left(x_k,y_k\right)-g\left(x_k,y_k\right)f_y\left(x_k,y_k\right)}{g_x\left(x_k,y_k\right)f_y\left(x_k,y_k\right)-f_x\left(x_k,y_k\right)g_y\left(x_k,y_k\right)}\\ y_{k+1}=y_k+\frac{g\left(x_k,y_k\right)f_x\left(x_k,y_k\right)-f\left(x_k,y_k\right)g_x\left(x_k,y_k\right)}{g_x\left(x_k,y_k\right)f_y\left(x_k,y_k\right)-f_x\left(x_k,y_k\right)g_y\left(x_k,y_k\right)}\end{array}\right.$$

(21)

4. Results and discussion

4.1. Analysis of Newton Fitting Effect of Indentation Data

In order to verify the accuracy of the calculation results, the indentation data were obtained by multiple tests using the indentation equipment in the adjacent area of Q345 weldless sample steel plate. After the unloading stage was removed by data processing, the indentation data were fitted according to the above algorithm and compared with the fitting results of the traditional one-dimensional binary equation. The fitting results are shown in

Table 1. Comparison of The Compression Energy Coefficient C between the Newton Method and the Conventional Method.

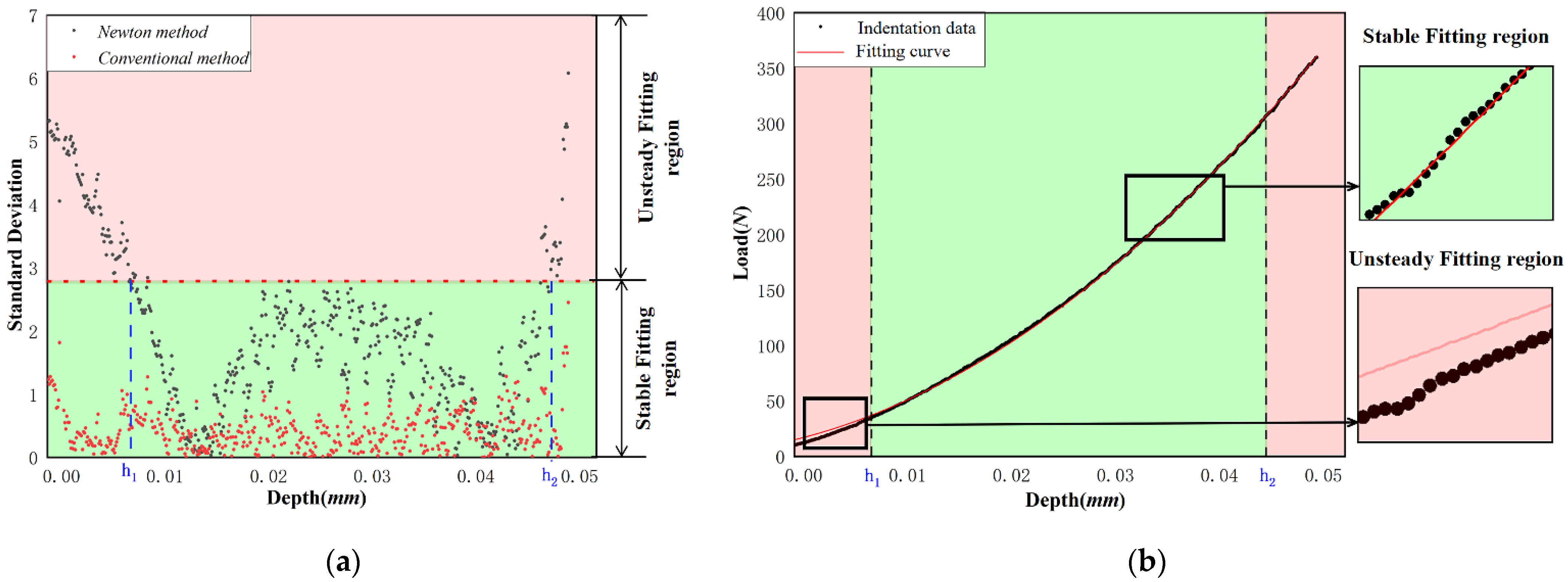
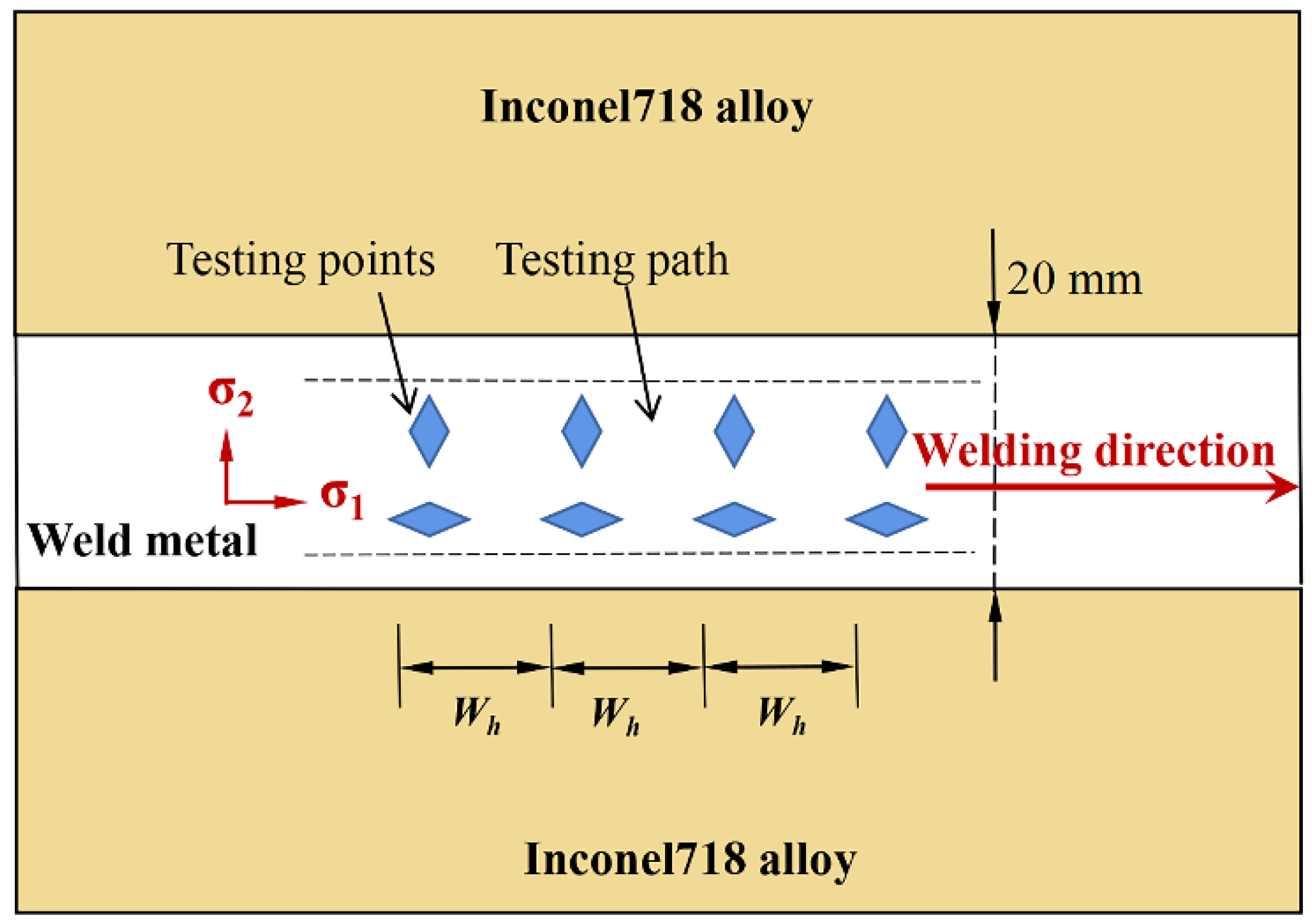
	Standard Value	1	2	3	4	5	6	7	8	9	10
Newton method	75,000 ± 5000	73,765	73,037	78,771	72,175	78,049	77,507	79,446	75,198	73,727	72,405
Conventional method		68,195	65,268	70,139	65,398	63,502	72,918	75,668	65,640	62,379	62,375

. The indentation energy coefficient results of the traditional fitting method were 66,400 ± 9000 and the Newton fitting method were 75,200 ± 3000. This indicates that the repeatability of the energy coefficient C obtained by the Newton method was very high, while the numerical error obtained by the traditional one-dimensional binary equation fitting method was large. In contrast, the residual stress data fitting method designed by Newton method was accurate, fast, and stable, which can meet the requirements of data processing.

The standard deviation analysis of the indentation curve obtained by the binary Newton fitting method and the raw data is shown in Figure 5. The indentation data can be divided into a stable fitting area and an unstable fitting area according to the maximum error of data fitting in the middle stage of the acquisition process. Most of the indentation data can meet the requirements of residual stress measured by indentation method, so it is in the stable fitting area. Since the preloading process and the delay of the sensor during the measurement with the indentation instrument will cause errors in the data at the initial and end of loading phases of the indentation, these values must be removed during the calculation of the end of measurement as “noise”, as they are in the unstable fitting region because they do not conform to the measurement law.

Because of the large amount of data and the difficulty of analyzing the error data, it is almost impossible to remove the “noise” manually. While this issue was not considered in the traditional fitting process, as all data were fitted with the same weight, and with this method, although the degree of fit was high, the results deviated to a large extent, which was an overfitting. It can be seen from the graph that the Newton fitting algorithm had a good fitting effect in the middle stage of the curve, indicating that the middle stage data (stable fitting area) occupied a significant weight in the fitting process, while the standard deviation of the initial stage and the end stage (unstable fitting area) with more error data was large, and the fitting weight was small. Therefore, the binary Newton fitting method increased the weight of the steady-phase data in the fitting process and reduced the influence of fluctuating data on the fitting results.

4.2. Measurement and Analysis of Biaxial Residual Stress

Because X-ray diffraction (XRD) has the advantage of high measurement accuracy, the accuracy of the Newton method in calculating residual stress was verified by comparing X-ray diffraction and the indentation method.

The testing material was an Inconel718 alloy welded plate. The width of the fusion zone was 20 mm, and the residual stress was measured by the X-ray diffraction method and the indentation method in the weld metal, as shown in Figure 6. The nonuniform temperature field caused by the welding process was the essential reason for the residual stress. The higher the temperature, the greater the thermal expansion. However, the thermal expansion will be constrained by the surrounding material subjected to relatively low temperature and vice versa. The uneliminated stress is called the welding residual stress. The measurement results are shown in Figure 7, where σ₁ is the residual stress parallel to the welding direction, and σ₂ is the residual stress perpendicular to the welding direction.

It can be seen from the test results that the residual stress measured by the indentation method was more stable than that by X-ray diffraction. The average error between the indentation method and the X-ray diffraction method was within 10%, and the fluctuation of the calculation result was small, which proves that the test result was stable and reliable and has good engineering applicability.

5. Conclusions

Indentation equipment is poorly fitted to the original data due to the delay of its control system and the large fluctuation of data points. The traditional fitting method does not conform to the theoretical law due to its overfitting of the loading slope (also called the indentation energy coefficient), which leads to large deviation of the measurement results from the actual results, and subsequent calculations cannot be performed. Therefore, in this paper, starting from the Newtonian solution of the nonlinear binary system of equation and combining it with the fitting of indentation data, the solution formula of the residual stress indentation energy coefficient was derived, and the interference of the non-stable zone data was excluded by the binary Newton iteration. The main work was as follows.

(1) The Newton iterative formula for the root of the binary nonlinear equation was deduced through the relationship between the univariate Taylor formula and the Newton iteration method for solving the univariate nonlinear equation. The indentation energy coefficient problem was transformed into the root problem of the binary nonlinear equation. The Newton iterative formula was introduced, and the fast calculation formula of the indentation energy coefficient was established.

(2) The fitting effects of the traditional least squares method and the binary Newton method were compared and analyzed. It was found that the traditional least squares method fitted all data with the same weight, the influence of the data fluctuation could not be ruled out, and the resulting deviation was too large due to overfitting. The binary Newton method improved the fitting weight of the indentation curve in the stable fitting region, and the fitting result was more stable and accurate.

(3) The stability of the binary Newton method for calculating the energy coefficient was verified by using the Q345 weldless sample steel plate test, and the accuracy of the binary Newton calculation method of residual stress based on the theory of indentation energy difference was verified by comparison with the X-ray method.