Quenching Stress of Hot-Rolled Seamless Steel Tubes under Different Cooling Intensities Based on Simulation
Abstract
1. Introduction
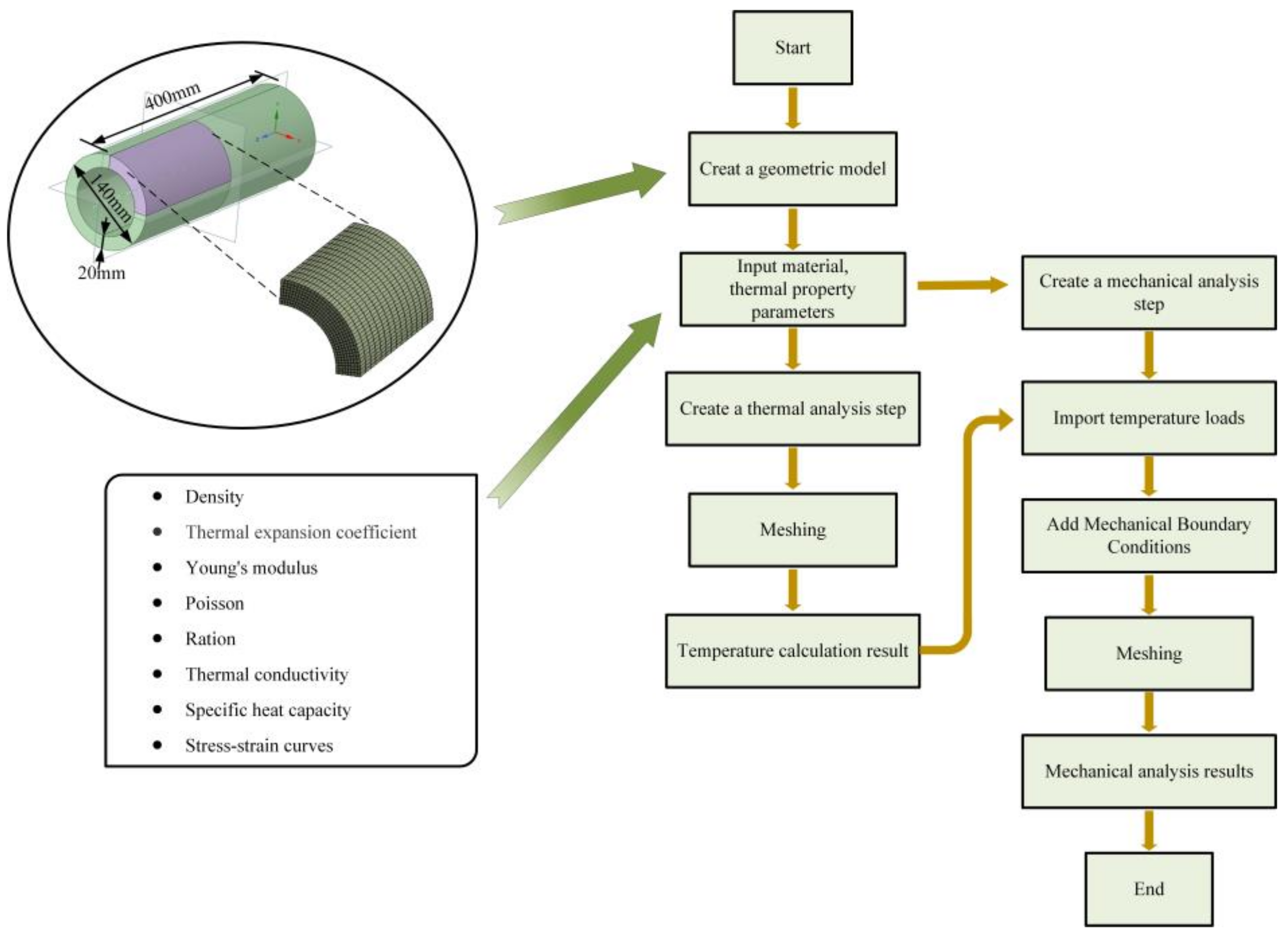
2. FEM Model of Quenching Process
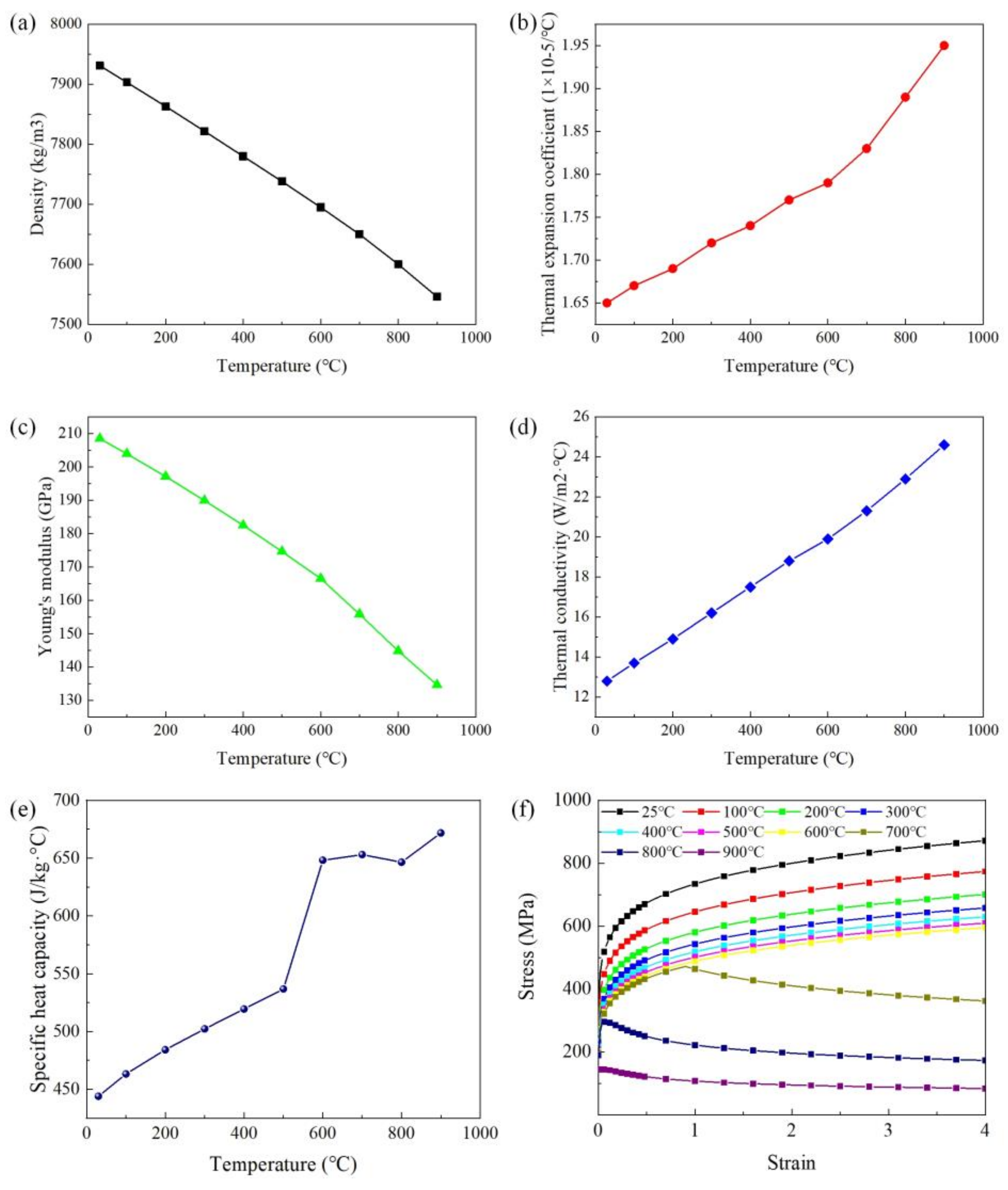
2.1. Materials and Methods
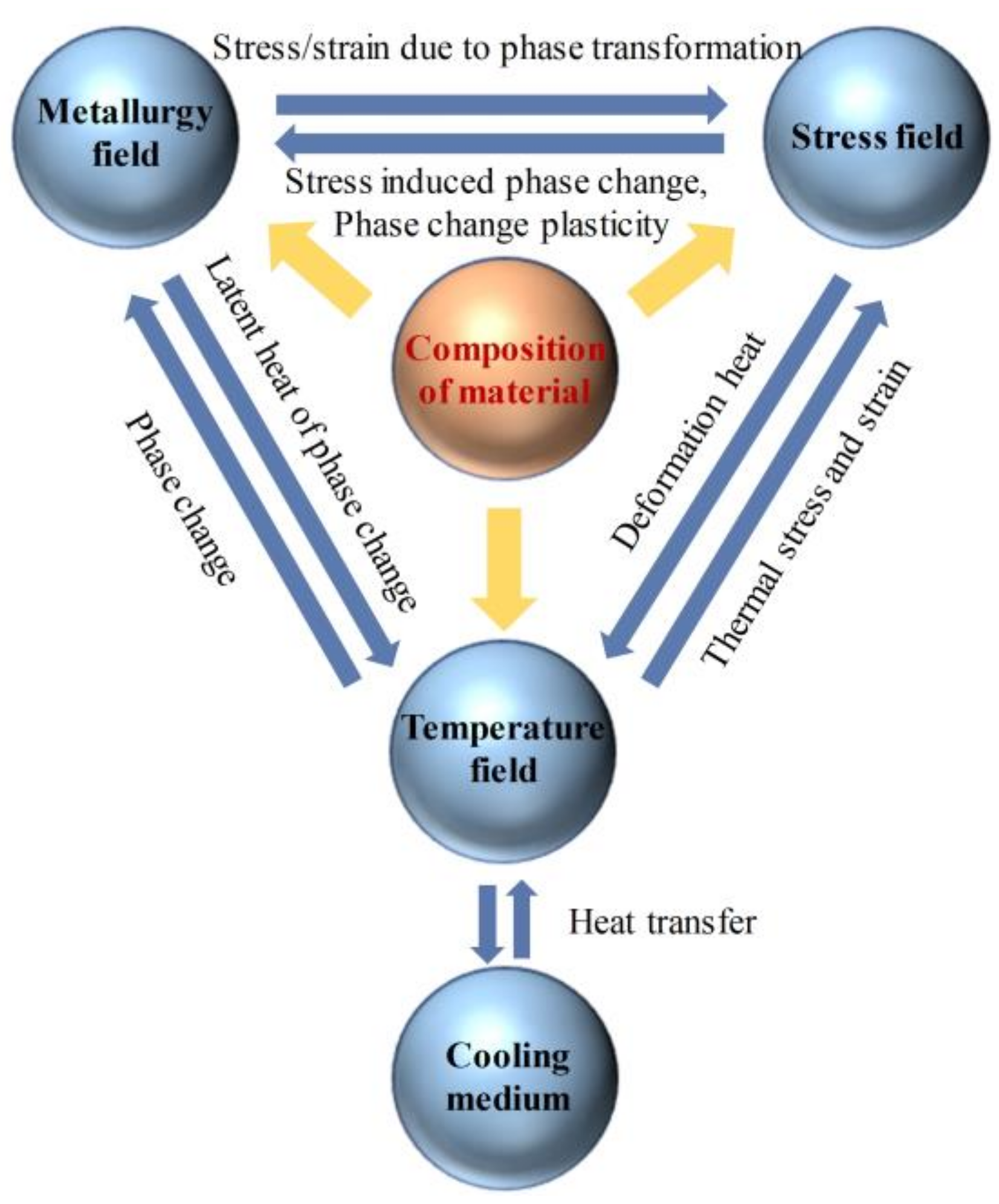
2.2. Mathematical Model
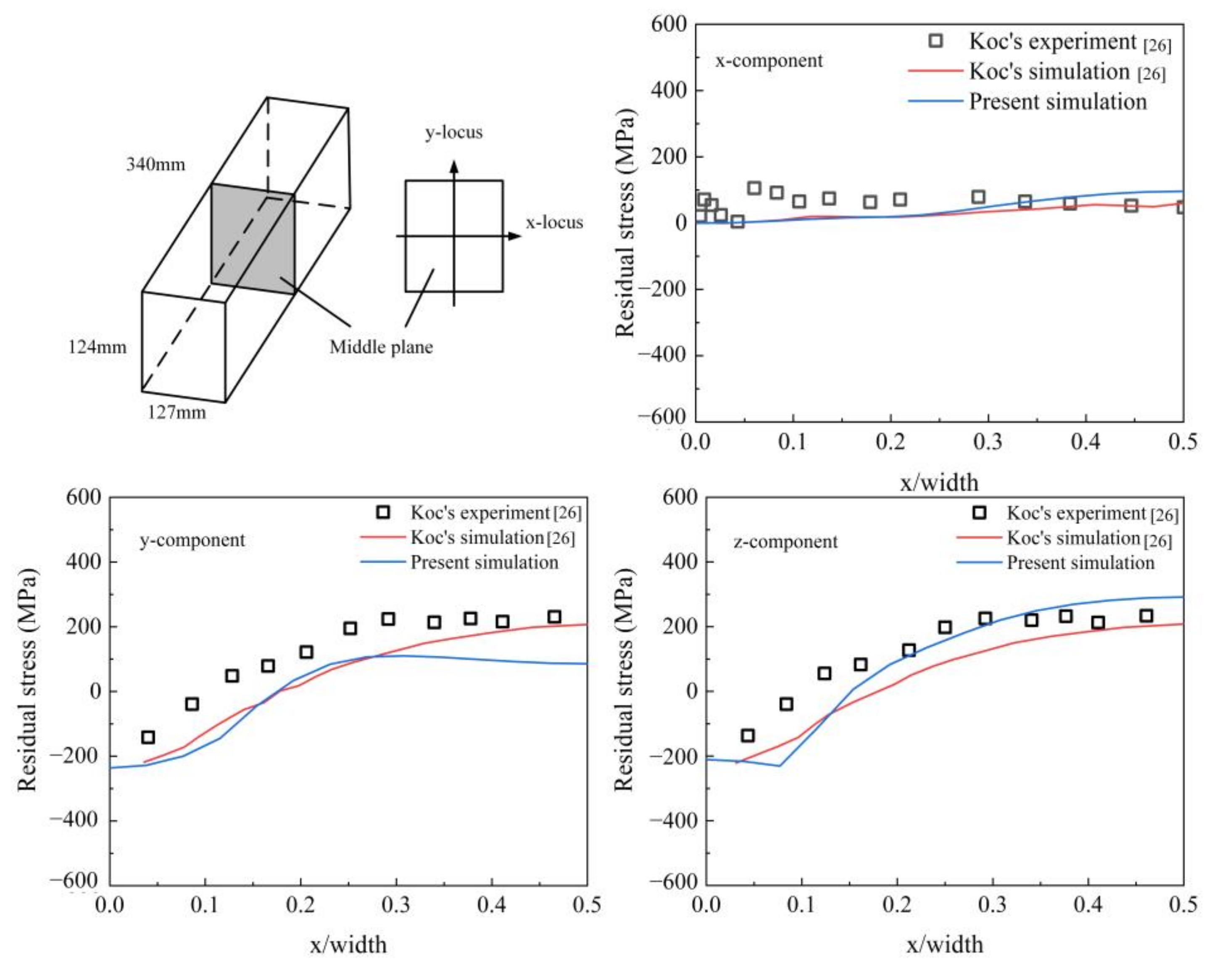
2.3. Verification of Other Finite Element Simulation Cases
3. Results and Discussion
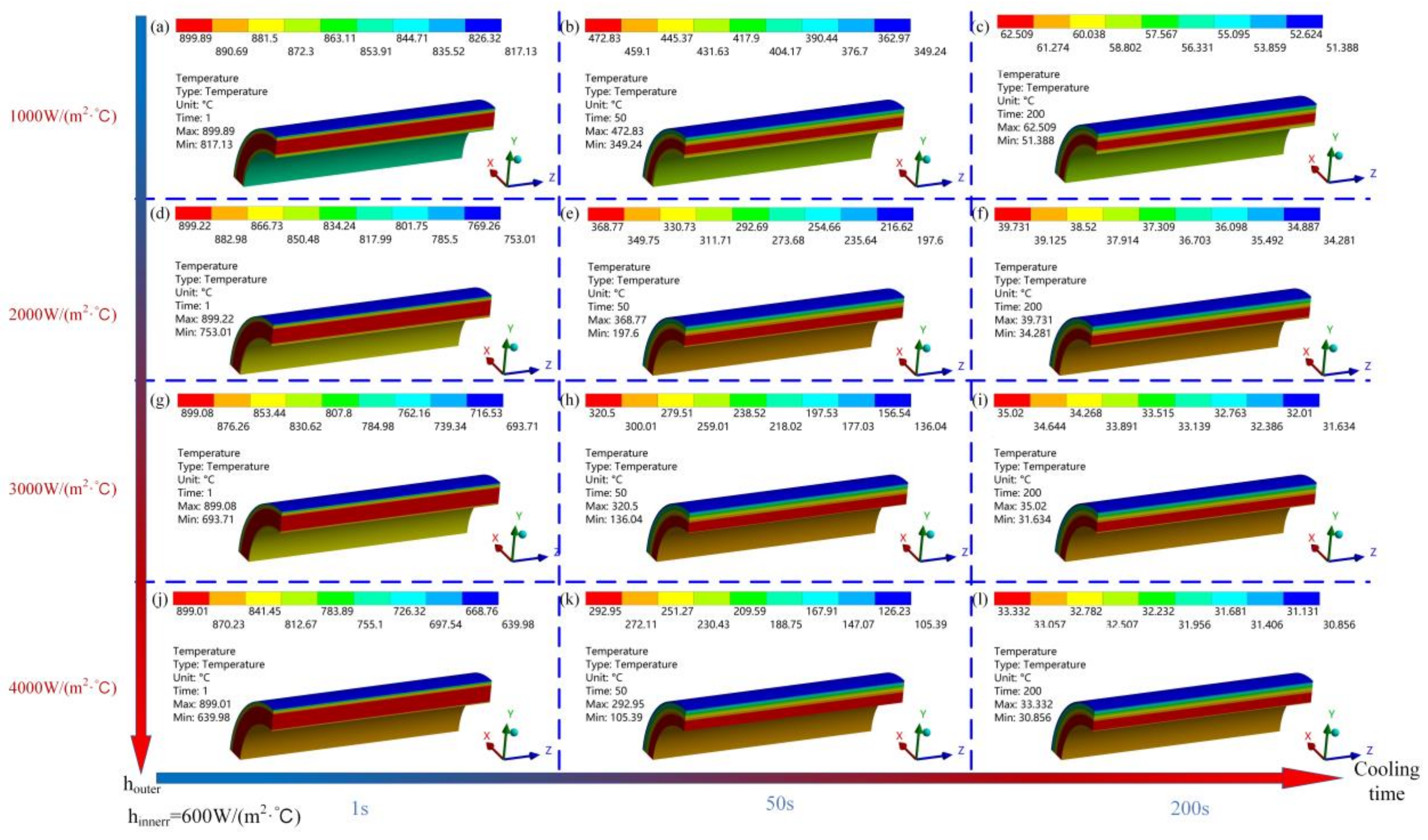
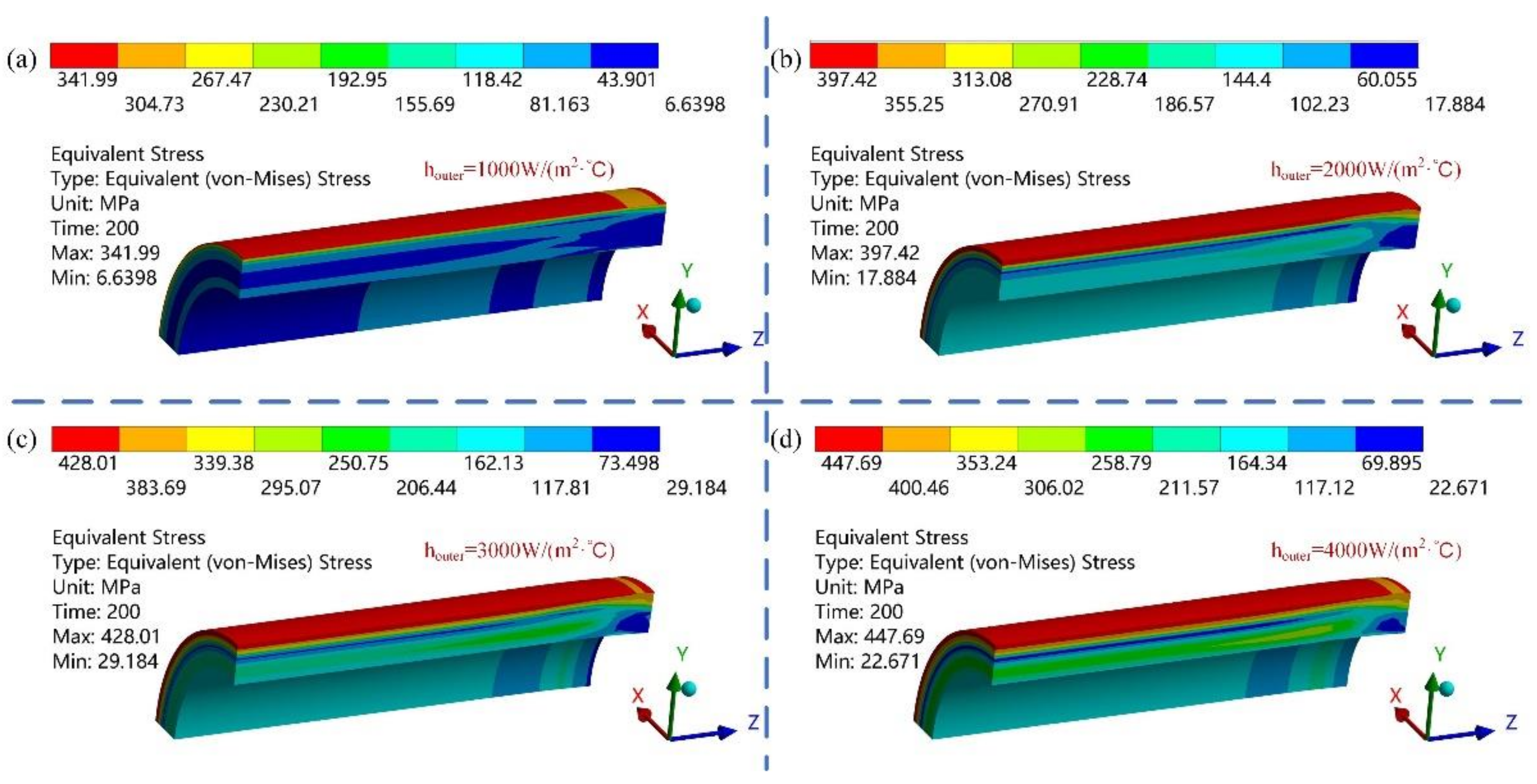
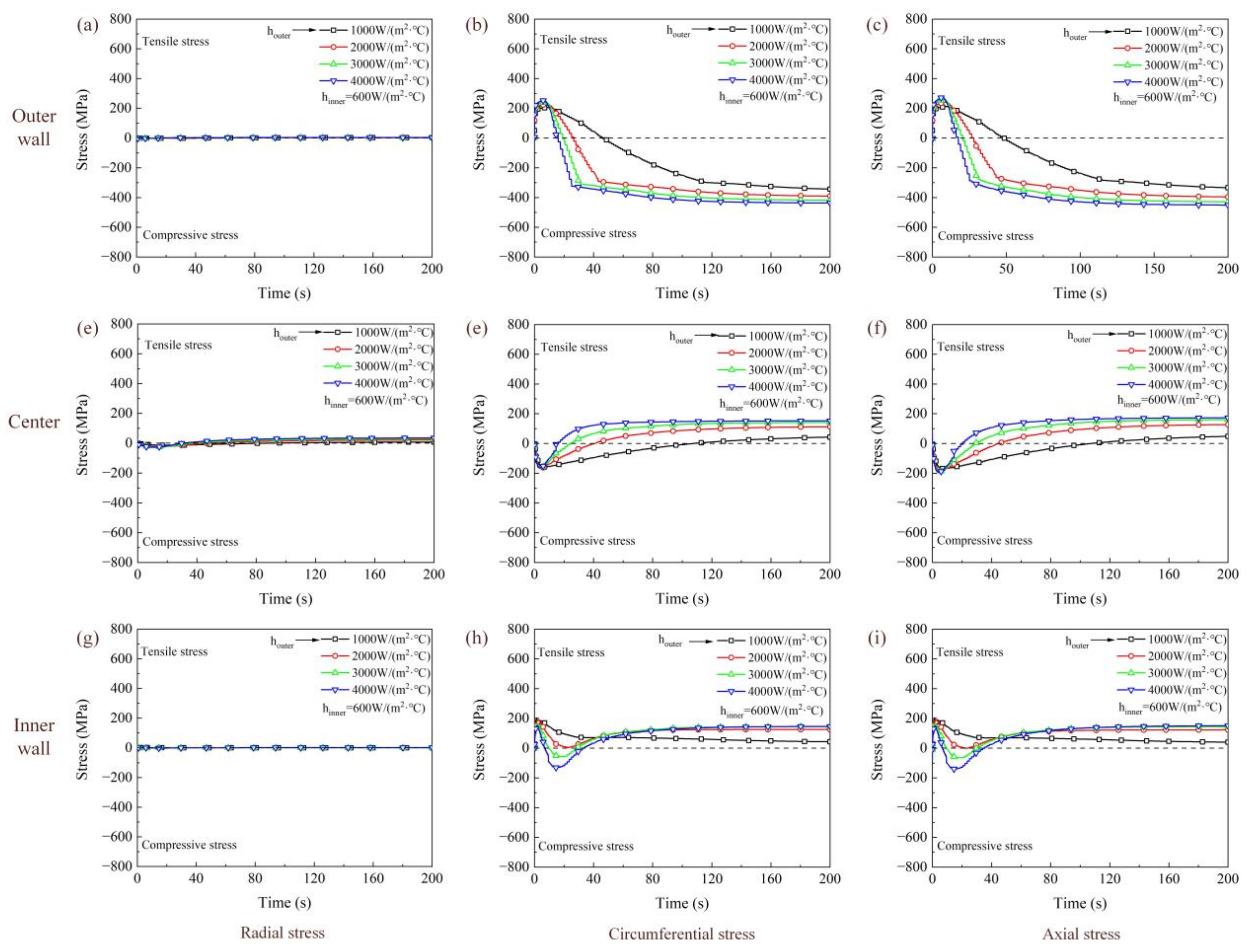
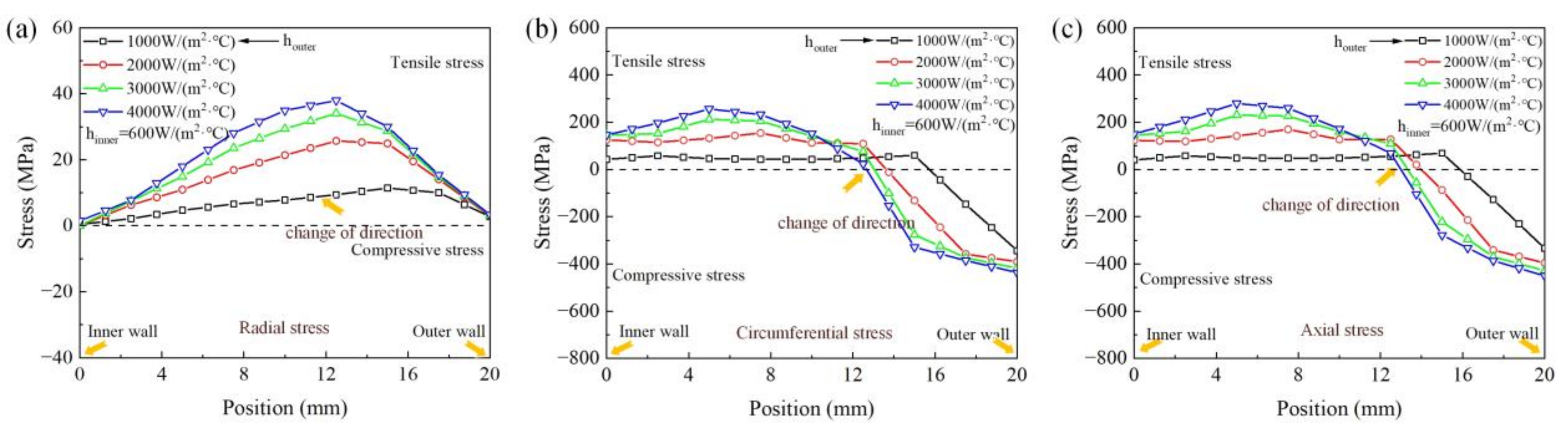
3.1. Different Cooling Intensities of the Outer Wall
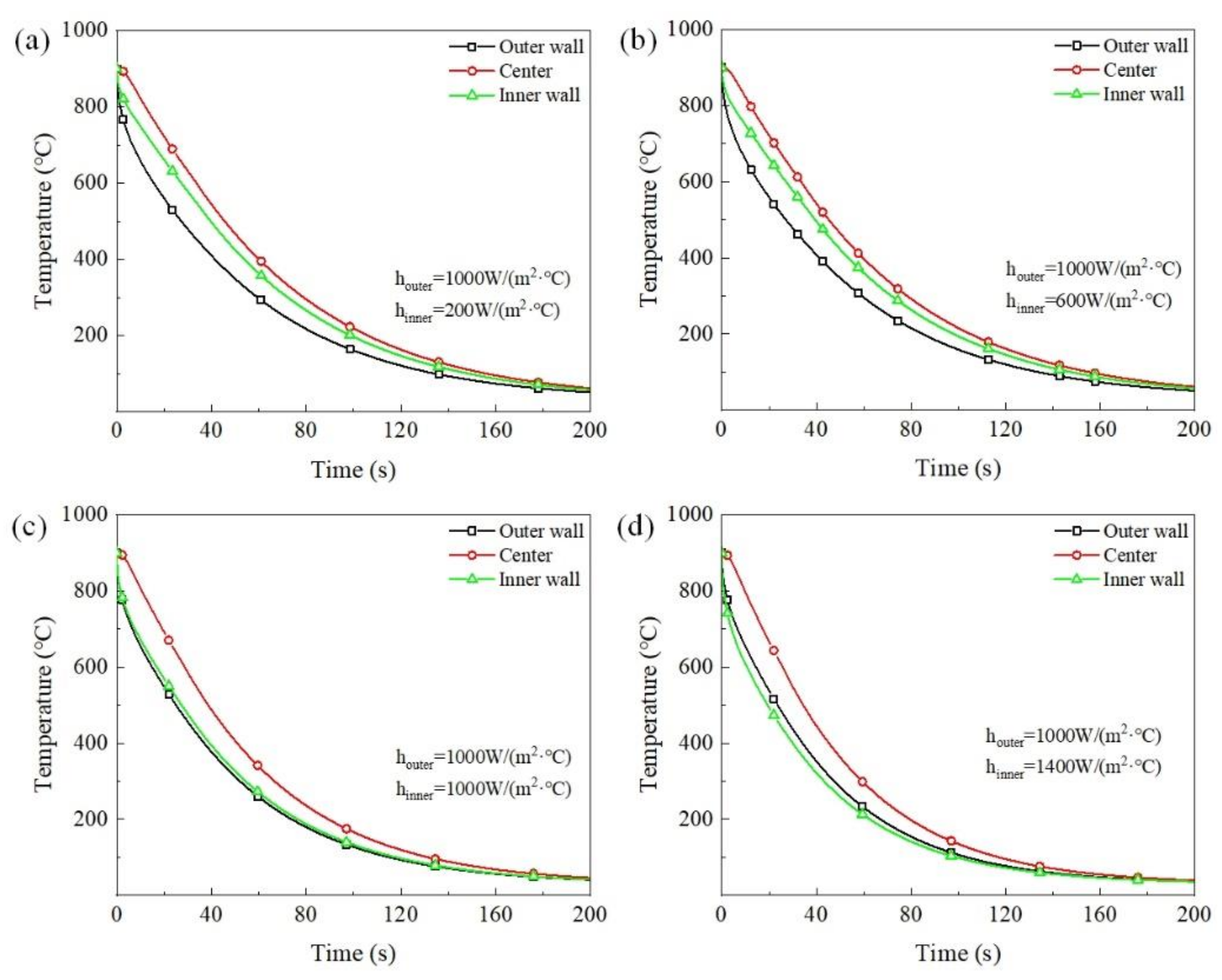
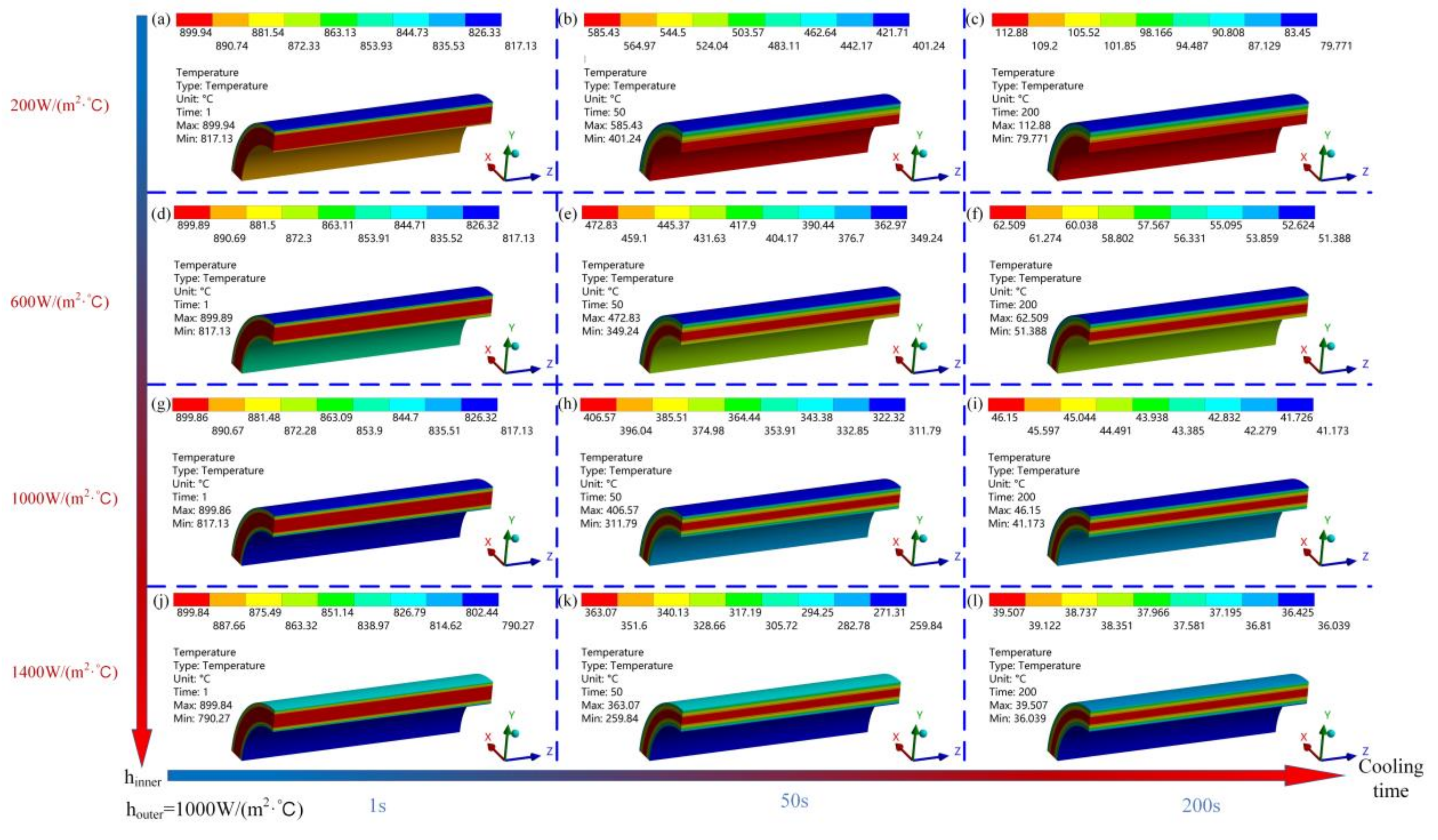
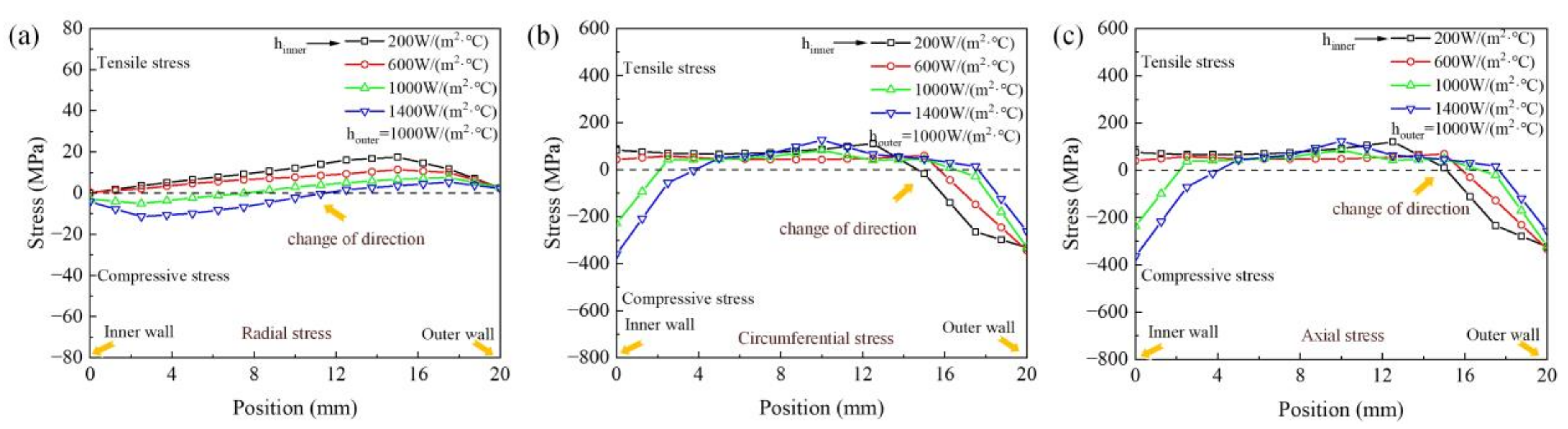
3.2. Different Cooling Intensities of the Inner Wall
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, H.T.; Yan, R. Development progress and reflections of seamless tube industry in China. Steel Roll 2014, 31, 41–44. [Google Scholar]
- Wang, H.H.; Sang, W.; Chen, J.D.; Chen, D. Summary of Domestic Development of Seamless Steel Tube of for Large-capacity Gas Cylinder Service. Steel Tube 2019, 47, 7–13. [Google Scholar]
- Yuan, G.; Kang, J.; Li, Z.L.; Wang, G.D. Development of Technology for Microstructure Control during On-line Heat Treatment Process for Hot-rolled Seamless Steel Tube. Steel Tube 2018, 47, 30–34. [Google Scholar]
- Chen, Z.; Chen, X.; Zhou, T. Microstructure and Mechanical Properties of J55 ERW Steel Tube Processed by On-Line Spray Water Cooling. Metals 2017, 7, 150. [Google Scholar] [CrossRef]
- Liu, Y.; Zuo, X.-w.; Chen, N.-l.; Rong, Y.-h.; Liu, S.-j. Finite element simulation of longitudinal quenching crack. Trans. Mater. Heat Treat. 2019, 40, 160–167. [Google Scholar]
- Zhao, Y.-F.; Liu, H.-S. Analysis of thermal stress in inhomogeneous long cylindrical superconductor. J. Lanzhou Univ. Technol. 2018, 44, 167–172. [Google Scholar]
- Souza, J.L.F.; Ziviani, M.; Vitor, J.F.A. Mathematical modeling of tube cooling in a continuous bed. Appl. Therm. Eng. 2015, 89, 80–89. [Google Scholar] [CrossRef]
- Raič, J.; Landfahrer, M.; Klarner, J.; Zmek, T.; Hochenauer, C. Modelling of the cooling process of steel tubes in a rake type cooling bed. Appl. Therm. Eng. 2020, 169, 114895. [Google Scholar] [CrossRef]
- Raič, J.; Landfahrer, M.; Klarner, J.; Zmek, T.; Hochenauer, C. Coupled CFD simulation for the cooling process of steel tubes in a rake type cooling bed. Appl. Therm. Eng. 2020, 171, 115068. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, R.; Li, Y.; Li, Z.; Yuan, G. Online Cooling System and Improved Similar Self-adaptive Strategy for Hot-rolled Seamless Steel Tube. ISIJ Int. 2021, 61, 2135–2142. [Google Scholar] [CrossRef]
- Mascarenhas, N.; Mudawar, I. Methodology for predicting spray quenching of thick-walled metal alloy tubes. Int. J. Heat Mass Transf. 2012, 55, 2953–2964. [Google Scholar] [CrossRef]
- Ali, M.A.; Hasan, S.T.; Myriounis, D.P. A Method of Analysis to Estimate Thermal Down-Shock Stress Profiles in Hollow Cylinders when Subjected to Transient Heat/Cooling Cycle. In Advanced Materials Research; Trans Tech Publications, Ltd.: Freienbach, Switzerland, 2012; pp. 893–898. [Google Scholar]
- Schemmel, M.; Prevedel, P.; Schöngrundner, R.; Ecker, W.; Antretter, T. Size Effects in Residual Stress Formation during Quenching of Cylinders Made of Hot-Work Tool Steel. Adv. Mater. Sci. Eng. 2015, 2015, 678056. [Google Scholar] [CrossRef]
- Hata, T.; Sumi, N. Thermal stress-focusing effect in a cylinder with phase transformation. Acta Mech. 2008, 195, 69–80. [Google Scholar] [CrossRef]
- De Oliveira, W.P.; Savi, M.A.; Pacheco, P.M.C.L.; de Souza, L.F.G. Thermomechanical analysis of steel cylinders quenching using a constitutive model with diffusional and non-diffusional phase transformations. Mech. Mater. 2010, 42, 31–43. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, K.; Chen, G.; Luo, G. Multiple axial cracks in a coated hollow cylinder due to thermal shock. Int. J. Solids Struct. 2006, 43, 6424–6435. [Google Scholar] [CrossRef][Green Version]
- Devynck, S.; Denis, S.; Bellot, J.P.; Bénard, T.; Gradeck, M. Influence of boiling heat transfer and phase transformations on the deformation of a steel tube during quenching by impinging water jets. Materialwiss. Werkst. 2016, 47, 755–761. [Google Scholar] [CrossRef]
- Leitner, S.; Winter, G.; Klarner, J.; Antretter, T.; Ecker, W. Model-based Residual Stress Design in Multiphase Seamless Steel Tubes. Materials 2020, 13, 439. [Google Scholar] [CrossRef]
- Yang, X.W.; Zhu, J.C.; Lai, Z.H.; Yong, L.I.U.; Dong, H.E.; Nong, Z.S. Finite element analysis of quenching temperature field, residual stress and distortion in A357 aluminum alloy large complicated thin-wall workpieces. Trans. Nonferr. Met. Soc. China 2013, 23, 1751–1760. [Google Scholar] [CrossRef]
- Brunbauer, S.; Winter, G.; Antretter, T.; Staron, P.; Ecker, W. Residual stress and microstructure evolution in steel tubes for different cooling conditions—Simulation and verification. Mat. Sci. Eng. A Struct. 2019, 747, 73–79. [Google Scholar] [CrossRef]
- Gao, J.N.; Gao, Y.; Xu, Q.R.; Wang, G.; Li, Q. Simulation on flow, heat transfer and stress characteristics of large-diameter thick-walled gas cylinders in quenching process under different water spray volumes. J. Cent. South Univ. 2020, 26, 3188–3199. [Google Scholar] [CrossRef]
- Xie, J.B.; He, T.C.; Cheng, H.M. Study on the Thermal Stress Field of Steel 1045 Quenched by Water. Adv. Mater. Res. 2011, 255, 3568–3572. [Google Scholar] [CrossRef]
- Wang, X.; Li, F.; Yang, Q.; He, A. FEM analysis for residual stress prediction in hot rolled steel strip during the run-out table cooling. Appl. Math. Model. 2013, 37, 586–609. [Google Scholar] [CrossRef]
- Şimşir, C.; Gür, C.H. 3D FEM simulation of steel quenching and investigation of the effect of asymmetric geometry on residual stress distribution. J. Mater. Process. Technol. 2008, 207, 211–221. [Google Scholar] [CrossRef]
- Gradeck, M.; Kouachi, A.; Lebouché, M.; Volle, F.; Maillet, D.; Borean, J.L. Boiling curves in relation to quenching of a high temperature moving surface with liquid jet impingement. Int. J. Heat Mass Transf. 2009, 52, 1094–1104. [Google Scholar] [CrossRef]
- Koc, M.; Culp, J.; Altan, T. Prediction of residual stresses in quenched aluminum blocks and their reduction through cold working processes. J. Mater. Process. Technol. 2006, 174, 342–354. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhang, R.; Chen, D.; Xie, Q.; Kang, J.; Yuan, G.; Wang, G. Quenching Stress of Hot-Rolled Seamless Steel Tubes under Different Cooling Intensities Based on Simulation. Metals 2022, 12, 1363. https://doi.org/10.3390/met12081363
Li Z, Zhang R, Chen D, Xie Q, Kang J, Yuan G, Wang G. Quenching Stress of Hot-Rolled Seamless Steel Tubes under Different Cooling Intensities Based on Simulation. Metals. 2022; 12(8):1363. https://doi.org/10.3390/met12081363
Chicago/Turabian StyleLi, Zhenlei, Rui Zhang, Dong Chen, Qian Xie, Jian Kang, Guo Yuan, and Guodong Wang. 2022. "Quenching Stress of Hot-Rolled Seamless Steel Tubes under Different Cooling Intensities Based on Simulation" Metals 12, no. 8: 1363. https://doi.org/10.3390/met12081363
APA StyleLi, Z., Zhang, R., Chen, D., Xie, Q., Kang, J., Yuan, G., & Wang, G. (2022). Quenching Stress of Hot-Rolled Seamless Steel Tubes under Different Cooling Intensities Based on Simulation. Metals, 12(8), 1363. https://doi.org/10.3390/met12081363





