Stir Casting Process Analysis and Optimization for Better Properties in Al-MWCNT-GR-Based Hybrid Composites
Abstract
:1. Introduction
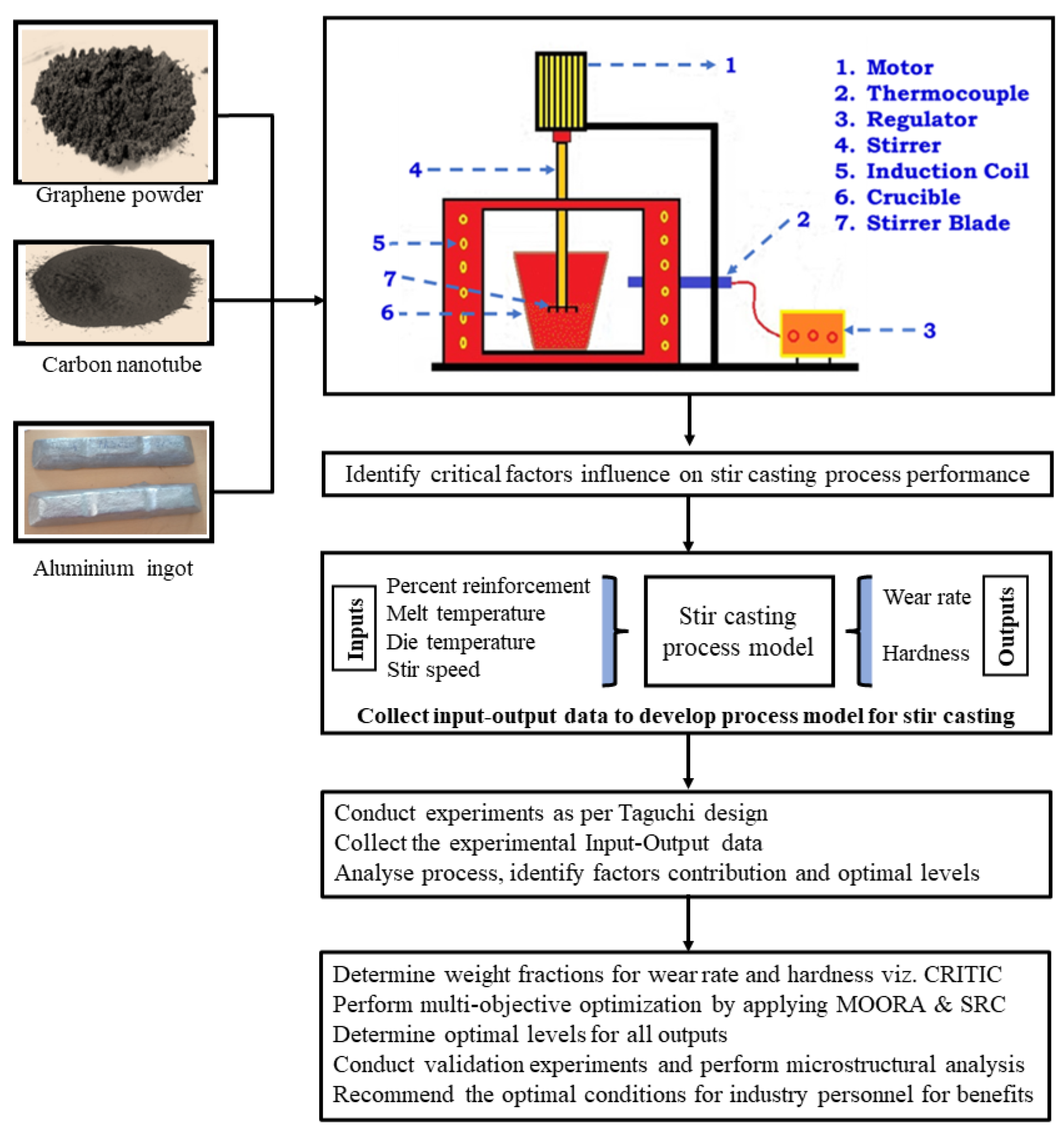
2. Materials and Experimental Set-up
2.1. Materials
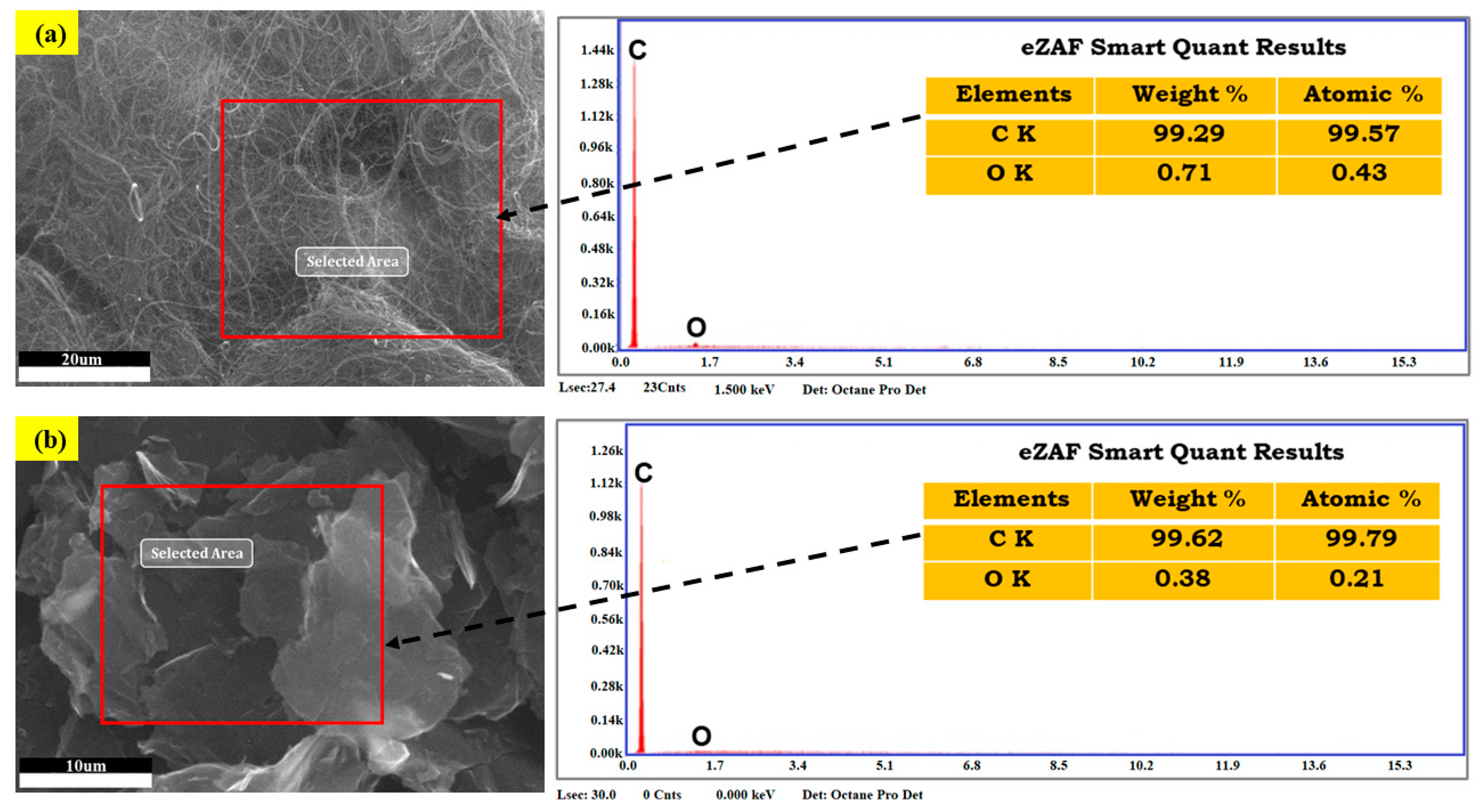
2.2. Powder Morphology Studies
2.3. Experimental Set-Up
Response Measurements and Characterization
2.4. Hybrid Optimization Approach
3. Results
3.1. Response: Hardness
3.2. Response: Wear Rate
3.3. Multiple-Objective Optimization for the Stir Casting Process
3.3.1. CRITIC
3.3.2. Multi-Objective Optimization: Taguchi-CRITIC-GRA
3.3.3. Multi-Objective Optimization: Taguchi-CRITIC-MOORA
3.4. Summary Results of Multiobjective Optimization
Microhardness Indentation Images
4. Wear Track and Wear Debris Analysis
5. Conclusions
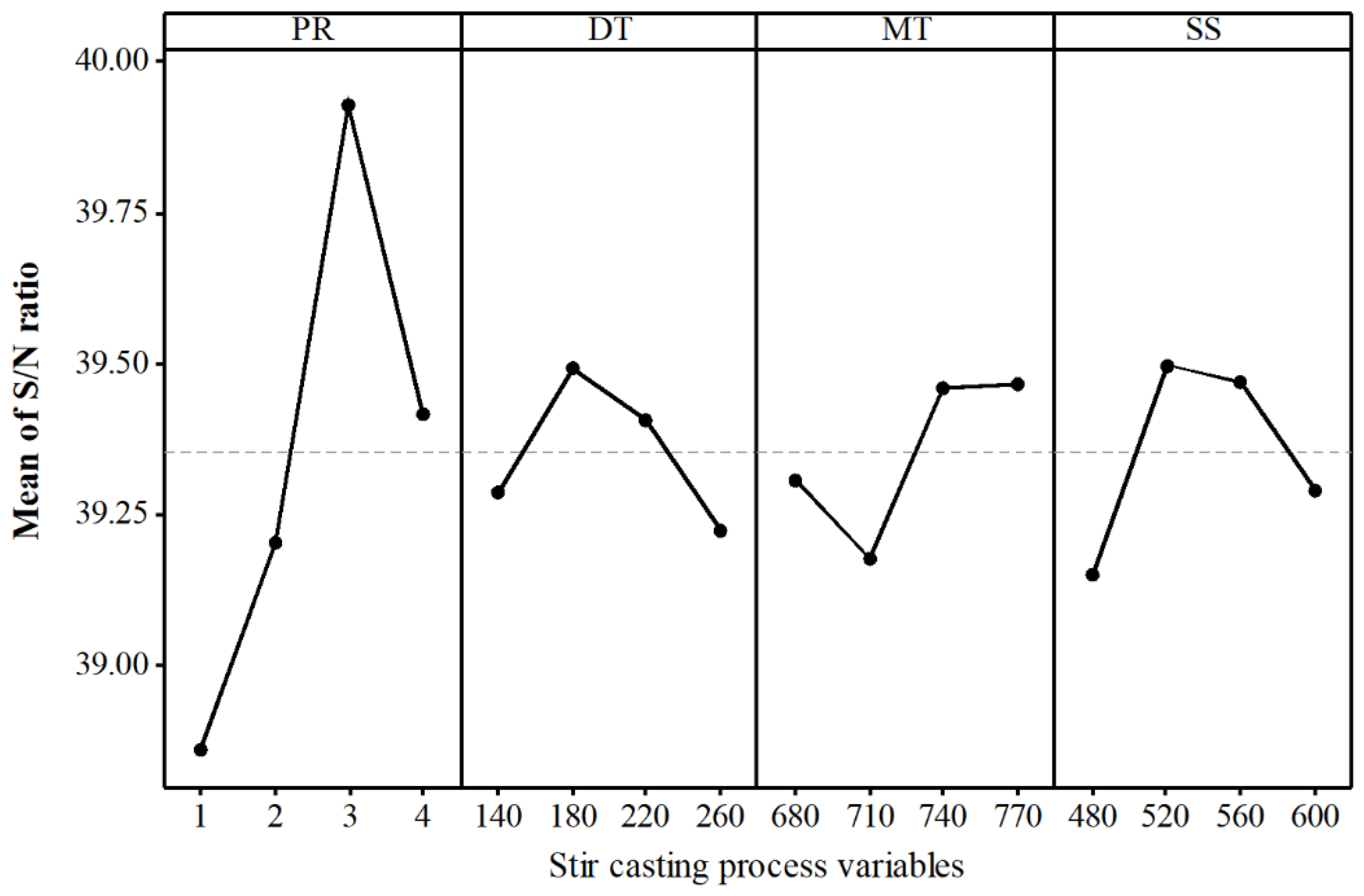
- Taguchi L16 experiments were conducted and collected the experimental output (hardness and wear rate) data. Percent reinforcement of graphene showed the highest effect, whereas die temperature has the least effect on both hardness and wear rate. The optimal factor levels for hardness were found equal to PR3DT2MT4SS2 (percent reinforcement of graphene: 3%, die temperature: 180 °C, melt temperature: 770 °C, stir speed: 520 rpm), whereas PR3DT2MT3SS2 (percent reinforcement of graphene: 3%, die temperature: 180 °C, melt temperature: 740 °C, stir speed: 520 rpm) are the optimal conditions for wear rate.
- SEM analysis of MWCNT resulted in elongated tube-like curl structure and flake-like irregularly shaped structure obtained for graphene nanoparticles. EDS analysis confirms the composition of graphene and carbon nanotube particles.
- The weights corresponding to hardness and wear rate determined viz. CRITIC method were found equal to 0.4752 and 0.5428, respectively. This indicates that the weight fraction for the hardness of stir casting composites is 47.52% and 54.28% for wear rate, respectively.
- Hybrid optimization approaches such as Taguchi-CRITIC-GRA and Taguchi-CRITIC-MOORA determined the optimal factors, and levels were found equal to PR3DT2MT4SS2 and PR3DT2MT3SS2, respectively. Percent reinforcement of graphene is the most dominant effect, followed by melt temperature on the hybrid composites. The Taguchi-CRITIC-MOORA method performs marginally better than Taguchi-CRITIC-GRA in determining optimal conditions (percent reinforcement: 3 wt.%, die temperature: 180 °C, melt temperature: 740 °C, and stir speed: 520 rpm) that could improve the hardness and wear resistance properties with a value equal to the hardness of 112 and wear rate of 1.84 × 10−3 mm3/min. The Taguchi-CRITIC-MOORA method resulted in a 31.77% increase in hardness and a 36.33% decrease in wear rate compared to initial stir casting (percent reinforcement: 1 wt.%, die temperature: 140 °C, melt temperature: 680 °C, and stir speed: 480 rpm) conditions.
- The optimal condition determined viz. the Taguchi-CRITIC-MOORA method ensures a dense microstructure with minimal pores (compared to initial and average conditions) resulting in enhanced properties in composite material.
- The worn-out surface of optimal conditions resulted in a few thin and slender grooves between wear tracks compared to average and initial conditions. Furthermore, less crack propagation on the wear-out surface shows better lubricant formation and causes self-lubrication composites.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| MWCNT | Multiwall carbon nano-tube |
| GR | Graphene |
| CRITIC | Criteria importance through intercriteria correlation |
| MOORA | Multi-objective optimization on the basis of ratio analysis |
| TOPSIS | Technique for order preference by similarity to ideal solution |
| GRA | Grey relational analysis |
| MMCs | Metal matrix composites |
| PR | Percent reinforcement |
| DT | Die temperature |
| MT | Melt temperature |
| SS | Stir speed |
| OL | Optimal level |
| SSD | Sum of squares of differences |
| PC | Percent contribution |
| ANOVA | Analysis of variance |
| GRC | Grey relational coefficient |
| GRG | Grey relational grading |
| WGRG | Weighted grey relational grading |
| Cj | Criterion information |
| Wj | Objective weights |
| SD | Standard deviation |
| SFL | Sum at factor levels |
| S/N ratio | Signal-to-noise ratio |
| HV | Hardness value |
| WR | Wear rate |
References
- Swamy, P.K.; Mylaraiah, S.; Gowdru Chandrashekarappa, M.P.; Lakshmikanthan, A.; Pimenov, D.Y.; Giasin, K.; Krishna, M. Corrosion Behaviour of High-Strength Al 7005 Alloy and Its Composites Reinforced with Industrial Waste-Based Fly Ash and Glass Fibre: Comparison of Stir Cast and Extrusion Conditions. Materials 2021, 14, 3929. [Google Scholar] [CrossRef]
- Ramanathan, A.; Krishnan, P.K.; Muraliraja, R. A review on the production of metal matrix composites through stir casting—Furnace design, properties, challenges, and research opportunities. J. Manuf. Processes 2019, 42, 213–245. [Google Scholar] [CrossRef]
- Bhoi, N.K.; Singh, H.; Pratap, S. Developments in the aluminum metal matrix composites reinforced by micro/nano particles—A review. J. Compos. Mater. 2020, 54, 813–833. [Google Scholar] [CrossRef]
- Chawla, K.K. Metal Matrix Composites. In Composite Materials; Springer: New York, NY, USA, 2012; pp. 197–248. [Google Scholar] [CrossRef]
- Altenbach, H.; Altenbach, J.; Kissing, W. Classification of Composite Materials. In Mechanics of Composite Structural Elements; Springer: Berlin/Heidelberg, Germany, 2004; pp. 1–14. [Google Scholar] [CrossRef]
- Rajan, T.P.D.; Pillai, R.M.; Pai, B.C. Reinforcement coatings and interfaces in aluminium metal matrix composites. J. Mater. Sci. 1998, 33, 3491–3503. [Google Scholar] [CrossRef]
- Yigezu, B.S.; Jha, P.K.; Mahapatra, M.M. The key attributes of synthesizing ceramic particulate reinforced Al-based matrix composites through stir casting process: A review. Mater. Manuf. Processes 2013, 28, 969–979. [Google Scholar] [CrossRef]
- Imran, M.; Khan, A.A. Characterization of Al-7075 metal matrix composites: A review. J. Mater. Res. Technol. 2019, 8, 3347–3356. [Google Scholar] [CrossRef]
- Hayat, M.D.; Singh, H.; He, Z.; Cao, P. Titanium metal matrix composites: An overview. Compos. Part A Appl. Sci. Manuf. 2019, 121, 418–438. [Google Scholar] [CrossRef]
- Gay, D. Composite Materials: Design and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Suthar, J.; Patel, K.M. Processing issues, machining, and applications of aluminum metal matrix composites. Mater. Manuf. Processes 2018, 33, 499–527. [Google Scholar] [CrossRef]
- Prasad, S.V.; Asthana, R. Aluminum metal-matrix composites for automotive applications: Tribological considerations. Tribol. Lett. 2004, 17, 445–453. [Google Scholar] [CrossRef]
- Safri, S.N.A.; Sultan, M.T.H.; Jawaid, M.; Jayakrishna, K. Impact behaviour of hybrid composites for structural applications: A review. Compos. B Eng. 2018, 133, 112–121. [Google Scholar] [CrossRef]
- Vinayaka, N.; Lakshmikanthan, A.; Patel, G.M.; Pon, C. Mechanical, Microstructure and Wear properties of Al 6113 Fly Ash reinforced Composites: Comparison of as-cast and Heat-treated Conditions. Adv. Mater. Processing Technol. 2021, 1–16. [Google Scholar] [CrossRef]
- Avinash, L.; Kumar, H.; Parthasarathy, A.; Kumar, K.N.V.; Sajjan, B. The Effect of Ceramic Reinforcement on the Microstructure, Mechanical Properties and Tribological Behavior of Al-7.5%Si-0.5%Mg alloy. Appl. Mech. Mater. 2017, 867, 39. [Google Scholar] [CrossRef]
- Kareem, A.; Qudeiri, J.A.; Abdudeen, A.; Ahammed, T.; Ziout, A. A review on AA 6061 metal matrix composites produced by stir casting. Materials 2021, 14, 175. [Google Scholar] [CrossRef] [PubMed]
- Nturanabo, F.; Masu, L.; Kirabira, J.B. Novel applications of aluminium metal matrix composites. In Aluminium Alloys and Composites; Cooke, K.O., Ed.; IntechOpen: London, UK, 2019; pp. 1–25. [Google Scholar] [CrossRef] [Green Version]
- Sharma, D.K.; Mahant, D.; Upadhyay, G. Manufacturing of metal matrix composites: A state of review. Mater. Today Proc. 2020, 26, 506–519. [Google Scholar] [CrossRef]
- Minasyan, T.; Hussainova, I. Laser Powder-Bed Fusion of Ceramic Particulate Reinforced Aluminum Alloys: A Review. Materials 2022, 15, 2467. [Google Scholar] [CrossRef] [PubMed]
- Abbasipour, B.; Niroumand, B.; Vaghefi, S.M.M.; Abedi, M. Tribological behavior of A356—CNT nanocomposites fabricated by various casting techniques. Trans. Nonferrous Met. Soc. China 2019, 29, 1993–2004. [Google Scholar] [CrossRef]
- Ayyanar, S.; Gnanavelbabu, A.; Rajkumar, K.; Loganathan, P. Studies on high temperature wear and friction behaviour of AA6061/B 4 C/hBN hybrid composites. Met. Mater. Int. 2020, 27, 3040–3057. [Google Scholar] [CrossRef]
- Singh, R.K.; Dixit, A.R.; Sharma, A.K.; Tiwari, A.K.; Mandal, V.; Pramanik, A. Influence of graphene and multi-walled carbon nanotube additives on tribological behaviour of lubricants. Int. J. Surf. Sci. Eng. 2018, 12, 207–227. [Google Scholar] [CrossRef] [Green Version]
- Moghadam, A.D.; Omrani, E.; Menezes, P.L.; Rohatgi, P.K. Mechanical and tribological properties of self-lubricating metal matrix nanocomposites reinforced by carbon nanotubes (CNTs) and graphene—A review. Compos. B Eng. 2015, 77, 402–420. [Google Scholar] [CrossRef]
- Johnson, P.J.; Setsuda, D.J.; Williams, R.S. Carbon Materials for Advanced Technology; Pergamon: Amsterdam, The Netherlands, 1999; pp. 235–268. [Google Scholar]
- Güler, Ö.; Bağcı, N. A short review on mechanical properties of graphene reinforced metal matrix composites. J. Mater. Res. Technol. 2020, 9, 6808–6833. [Google Scholar] [CrossRef]
- Merino, C.A.I.; Sillas, J.L.; Meza, J.M.; Ramirez, J.H. Metal matrix composites reinforced with carbon nanotubes by an alternative technique. J. Alloys Compd. 2017, 707, 257–263. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z.; Fan, G.; Pan, H.; Chen, Z.; Zhang, D. Reinforcement with graphene nanosheets in aluminum matrix composites. Scr. Mater. 2012, 66, 594–597. [Google Scholar] [CrossRef] [Green Version]
- Khanna, V.; Kumar, V.; Bansal, S.A. Mechanical properties of aluminium-graphene/carbon nanotubes (CNTs) metal matrix composites: Advancement, opportunities, and perspective. Mater. Res. Bull. 2021, 138, 111224. [Google Scholar] [CrossRef]
- Tumnantong, D.; Poompradub, S.; Prasassarakich, P. Poly (methyl methacrylate)-graphene emulsion prepared via RAFT polymerization and the properties of NR/PMMA-graphene composites. Eur. Polym. J. 2020, 139, 109983. [Google Scholar] [CrossRef]
- Sharma, A.; Belokar, R.M.; Kumar, S. Optimization of gas protected stir casting process using GRA and TOPSIS. Indian J. Eng. Mater. Sci. 2017, 24, 437–446. Available online: http://nopr.niscair.res.in/handle/123456789/43712 (accessed on 15 May 2022).
- Samal, P.; Vundavilli, P.R.; Meher, A.; Mahapatra, M.M. Recent progress in aluminum metal matrix composites: A review on processing, mechanical and wear properties. J. Manuf. Process. 2020, 59, 131–152. [Google Scholar] [CrossRef]
- Aqida, S.N.; Ghazali, M.I.; Hashim, J. Effect of porosity on mechanical properties of metal matrix composite: An overview. J. Teknol. 2004, 40, 17–32. [Google Scholar] [CrossRef] [Green Version]
- Ambhai, K.G. Study on Machinability of Al-SiC Particulate Metal Matrix Composite. Ph.D. Thesis, Metallurgical Engineering Department, IIT Roorkee, Roorkee, India, 2007. [Google Scholar]
- Hashim, J.; Looney, L.; Hashmi, M.S.J. Metal matrix composites: Production by the stir casting method. J. Mater. Process. Technol. 1999, 92, 1–7. [Google Scholar] [CrossRef]
- Soltani, S.; Khosroshahi, R.A.; Mousavian, R.T.; Jiang, Z.Y.; Boostani, A.F.; Brabazon, D. Stir casting process for manufacture of Al–SiC composites. Rare Metals 2017, 36, 581–590. [Google Scholar] [CrossRef] [Green Version]
- Kumar, U.K.A.V. Method of stir casting of aluminum metal matrix composites: A review. Mater. Today Proc. 2017, 4, 1140–1146. [Google Scholar] [CrossRef]
- Srinivas, V.; Jayaraj, A.; Venkataramana, V.S.N.; Avinash, T.; Dhanyakanth, P. Effect of ultrasonic stir casting technique on mechanical and tribological properties of aluminium–multi-walled carbon nanotube nanocomposites. J. Bio-Tribo-Corros 2020, 6, 30. [Google Scholar] [CrossRef]
- Coyal, A.; Yuvaraj, N.; Butola, R.; Tyagi, L. An experimental analysis of tensile, hardness and wear properties of aluminium metal matrix composite through stir casting process. SN Appl. Sci. 2020, 2, 892. [Google Scholar] [CrossRef] [Green Version]
- Jena, P.C.; Parhi, D.R.; Pohit, G.; Samal, B.P. Crack assessment by FEM of AMMC beam produced by modified stir casting method. Mater. Today Proc. 2015, 2, 2267–2276. [Google Scholar] [CrossRef]
- Su, H.; Gao, W.; Zhang, H.; Liu, H.; Lu, J.; Lu, Z. Optimization of stirring parameters through numerical simulation for the preparation of aluminum matrix composite by stir casting process. J. Manuf. Sci. Eng. 2010, 132, 061007. [Google Scholar] [CrossRef]
- George, J.; Janardhanan, S.; Sijo, T.M. A numerical study on stir casting process in a metal matrix composite using CFD approach. Adv. Mater. Res. 2015, 1119, 533–541. [Google Scholar] [CrossRef]
- Rangaswamy, H.; Sogalad, I.; Basavarajappa, S.; Acharya, S.; Manjunath Patel, G.C. Experimental analysis and prediction of strength of adhesive-bonded single-lap composite joints: Taguchi and artificial neural network approaches. SN Appl. Sci. 2020, 2, 1055. [Google Scholar] [CrossRef]
- Patel, G.C.M.; Krishna, P.; Parappagoudar, M.B. Optimization of squeeze cast process parameters using Taguchi and grey relational analysis. Proc. Technol. 2014, 14, 157–164. [Google Scholar] [CrossRef] [Green Version]
- Patel, G.C.M.; Pradeep, N.B.; Harsha, H.M.; Shettigar, A.K. Experimental analysis and optimization of plasma spray parameters on microhardness and wear loss of Mo-Ni-Cr coated super duplex stainless steel. Aust. J. Mech. Eng. 2020, 1–13. [Google Scholar] [CrossRef]
- Arulraj, M.; Palani, P.K.; Venkatesh, L. Optimization of process parameters in stir casting of hybrid metal matrix (LM25/SiC/B4C) composite using taguchi method. J. Adv. Chem. 2017, 13, 6475–6479. [Google Scholar] [CrossRef]
- Hanizam, H.; Salleh, M.S.; Omar, M.Z.; Sulong, A.B. Optimisation of mechanical stir casting parameters for fabrication of carbon nanotubes–aluminium alloy composite through Taguchi method. J. Mater. Res. Technol. 2019, 8, 2223–2231. [Google Scholar] [CrossRef]
- Rajeswari, B.; Amirthagadeswaran, K.S.; Anbarasu, K.G. Investigation on mechanical properties of aluminium 7075-silicon carbide-alumina hybrid composite using Taguchi method. Aust. J. Mech. Eng. 2015, 13, 127–135. [Google Scholar] [CrossRef]
- Gurusami, K.; Shalini, S.; Sathish, T. Optimization of stir casting parameters for corrosion rate analysis of AA7068–Boron carbide composites. Mater. Today Proc. 2020, 33, 4650–4655. [Google Scholar] [CrossRef]
- Udaya Prakash, J.; Jebarose Juliyana, S.; Saleem, M.; Moorthy, T.V. Optimisation of dry sliding wear parameters of aluminium matrix composites (356/B4C) using Taguchi technique. Int. J. Ambient. Energy 2018, 42, 140–142. [Google Scholar] [CrossRef]
- Iacob, G.; Ghica, V.G.; Buzatu, M.; Buzatu, T.; Petrescu, M.I. Studies on wear rate and micro-hardness of the Al/Al2O3/Gr hybrid composites produced via powder metallurgy. Compos. B Eng. 2015, 69, 603–611. [Google Scholar] [CrossRef]
- David Raja Selvam, J.; Dinaharan, I.; Rai, R.S.; Mashinini, P.M. Dry sliding wear behaviour of in-situ fabricated TiC particulate reinforced AA6061 aluminium alloy. Tribol.—Mater. Surf. Interfaces 2019, 13, 1–11. [Google Scholar] [CrossRef]
- Tansel, İ.Y.; Yıldırım, S. MOORA-based Taguchi optimisation for improving product or process quality. Int. J. Prod. Res. 2013, 51, 3321–3341. [Google Scholar] [CrossRef]
- Arunachalam, R.; Piya, S.; Krishnan, P.K.; Muraliraja, R.; Christy, J.V.; Mourad, A.H.I.; Al-Maharbi, M. Optimization of stir–squeeze casting parameters for production of metal matrix composites using a hybrid analytical hierarchy process—Taguchi-Grey approach. Eng. Optim. 2020, 52, 1166–1183. [Google Scholar] [CrossRef]
- Patel, J.D.; Maniya, K.D. Application of AHP/MOORA method to select wire cut electrical discharge machining process parameter to cut EN31 alloys steel with brasswire. Mater. Today: Proc. 2015, 2, 2496–2503. [Google Scholar] [CrossRef]
- Luthra, S.; Mangla, S.K.; Xu, L.; Diabat, A. Using AHP to evaluate barriers in adopting sustainable consumption and production initiatives in a supply chain. Int. J. Prod. Econ. 2016, 181, 342–349. [Google Scholar] [CrossRef]
- Kumar, R.; Bilga, P.S.; Singh, S. Multi objective optimization using different methods of assigning weights to energy consumption responses, surface roughness and material removal rate during rough turning operation. J. Clean. Prod. 2017, 164, 45–57. [Google Scholar] [CrossRef]
- Rangaswamy, H.; Sogalad, I.; Basavarajappa, S.; Chandrashekarappa, M.P.G. A comprehensive modelling, analysis and optimisation of adhesive bonded single lap glass fibre reinforced composite joints. Int. J. Mater. Eng. Innov. 2019, 10, 286–309. [Google Scholar] [CrossRef]
- Chate, G.R.; Patel, G.C.M.; Bhushan, S.B.; Parappagoudar, M.B.; Deshpande, A.S. Comprehensive modelling, analysis and optimization of furan resin-based moulding sand system with sawdust as an additive. J. Braz. Soc. Mech. Sci 2019, 41, 183. [Google Scholar] [CrossRef]
- Patel, G.C.M.; Jagadish; Kumar, R.S.; Naidu, N.S. Optimization of Abrasive Water Jet Machining for Green Composites Using Multi-Variant Hybrid Techniques. In Optimization of Manufacturing Processes; Springer: Cham, Switzerland, 2020; pp. 129–162. [Google Scholar] [CrossRef]
- Chate, G.R.; Patel, G.C.M.; Kulkarni, R.M.; Vernekar, P.; Deshpande, A.S.; Parappagoudar, M.B. Study of the effect of nano-silica particles on resin-bonded moulding sand properties and quality of casting. Silicon 2018, 10, 1921–1936. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R. A novel plithogenic TOPSIS-CRITIC model for sustainable supply chain risk management. J. Clean. Prod. 2020, 247, 119586. [Google Scholar] [CrossRef]
- Arunagiri, K.S.; Radhika, N. Studies on adhesive wear characteristics of heat treated aluminium LM25/AlB2 composites. Tribol. Ind. 2016, 38, 277. [Google Scholar]
- Mukherjee, I.; Ray, P.K. A review of optimization techniques in metal cutting processes. Comput. Ind. Eng. 2006, 50, 15–34. [Google Scholar] [CrossRef]
- Park, S.H. Robust Design and Analysis for Quality Engineering; Chapman & Hall: London, UK, 1996. [Google Scholar] [CrossRef]
- Raj, R.R.; Yoganandh, J.; Saravanan, M.S.; Kumar, S.S. Effect of graphene addition on the mechanical characteristics of AA7075 aluminium nanocomposites. Carbon Lett. 2021, 31, 125–136. [Google Scholar] [CrossRef]
- Patel, G.C.M.; Krishna, P.; Parappagoudar, M.B. Squeeze casting process modeling by a conventional statistical regression analysis approach. Appl. Math. Model. 2016, 40, 6869–6888. [Google Scholar] [CrossRef]
- Patel, G.C.M.; Shettigar, A.K.; Parappagoudar, M.B. A systematic approach to model and optimize wear behaviour of castings produced by squeeze casting process. J. Manuf. Processes 2018, 32, 199–212. [Google Scholar] [CrossRef]
- Prasad, K.V.; Jayadevan, K.R. Simulation of stirring in stir casting. Proc. Technol. 2016, 24, 356–363. [Google Scholar] [CrossRef] [Green Version]
- Campbell, J. Castings Practice: The Ten Rules of Castings; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Allison, J.E.; Cole, G.S. Metal-matrix composites in the automotive industry: Opportunities and challenges. JoM 1993, 45, 19–24. [Google Scholar] [CrossRef]
- Sheshadri, R.; Nagaraj, M.; Lakshmikanthan, A.; Chandrashekarappa, M.P.G.; Pimenov, D.Y.; Giasin, K.; Prasad, R.V.S.; Wojciechowski, S. Experimental investigation of selective laser melting parameters for higher surface quality and microhardness properties: Taguchi and super ranking concept approaches. J. Mater. Res. Technol. 2021, 14, 2586–2600. [Google Scholar] [CrossRef]
- Chate, G.R.; Kulkarni, R.M.; Chandrashekarappa, M.P.G.; Lakshmikanthan, A.; Harsha, H.M.; Tophakhane, S.; Shaikh, N.; Kongi, S.; Iranava, P. Synthesis and Characterization of Fe2O3 Nanoparticles Reinforced to Recycled Industrial Aluminium Scrap & Waste Aluminium Beverage Cans for Preparing Metal Matrix Nanocomposites. Frat. E Integrita Strutt. 2022, 16, 229–242. [Google Scholar] [CrossRef]
- Raghuvaran, P.; Baskaran, J.; Aagash, C.; Ganesh, A.; Krishna, S.G. Evaluation of mechanical properties of Al7075-SiC composites fabricated through stir casting technique. Mater. Today Proc. 2021, 45, 1914–1918. [Google Scholar] [CrossRef]
- Chandrashekarappa, M.P.G.; Kumar, S.; Pimenov, D.Y.; Giasin, K.; Jagadish, J. Experimental analysis and optimization of EDM parameters on HcHcr steel in context with different electrodes and dielectric fluids using hybrid taguchi-based PCA-utility and CRITIC-utility approaches. Metals 2021, 11, 419. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Lu, P.; Rosenbaum, M.S. Artificial neural networks and grey systems for the prediction of slope stability. Nat. Hazards 2003, 30, 383–398. [Google Scholar] [CrossRef]
- Brauers, W.K.; Zavadskas, E.K. The MOORA method and its application to privatization in a transition economy. Control Cybern 2006, 35, 445–469. [Google Scholar]
- Singh, J.; Chauhan, A. A review of microstructure, mechanical properties and wear behavior of hybrid aluminium matrix composites fabricated via stir casting route. Sādhanā 2019, 44, 16. [Google Scholar] [CrossRef] [Green Version]
- Jebeen Moses, J.; Joseph Sekhar, S. Investigation on the tensile strength and microhardness of AA6061/TiC composites by stir casting. Trans. Indian Inst. Met. 2017, 70, 1035–1046. [Google Scholar] [CrossRef]
- Liao, J.; Tan, M.J. A simple approach to prepare Al/CNT composite: Spread–Dispersion (SD) method. Mater. Lett. 2011, 65, 2742–2744. [Google Scholar] [CrossRef]
- Singla, D.; Amulya, K.; Murtaza, Q. CNT reinforced aluminium matrix composite-a review. Mater. Today Proc. 2015, 2, 2886–2895. [Google Scholar] [CrossRef]
- Naik, M.H.; Manjunath, L.H.; Koti, V.; Lakshmikanthan, A.; Koppad, P.G.; Kumaran, S.P. Al/Graphene/CNT hybrid composites: Hardness and sliding wear studies. FME Trans. 2021, 49, 414–421. [Google Scholar] [CrossRef]
- Naik, H.R.; Manjunath, L.H.; Malik, V.; Patel, G.C.M.; Saxena, K.K.; Lakshmikanthan, A. Effect of microstructure, mechanical and wear on Al-CNTs/graphene hybrid MMC’S. Adv. Mater. Process. Technol. 2021, 1–14. [Google Scholar] [CrossRef]
- Singh Yadav, S.P.; Lakshmikanthan, A.; Ranganath, S.; Gowdru Chandrashekarappa, M.P.; Anand, P.B.; Shankar, V.K.; Avvari, M. Effect of Pin Geometry and Orientation on Friction and Wear Behavior of Nickel-Coated EN8 Steel Pin and Al6061 Alloy Disc Pair. Adv. Mater. Sci. Eng. 2022, 2022, 327467. [Google Scholar] [CrossRef]
- Suresha, S.; Sridhara, B.K. Wear characteristics of hybrid aluminium matrix composites reinforced with graphite and silicon carbide particulates. Compos. Sci. Technol. 2010, 70, 1652–1659. [Google Scholar] [CrossRef]
- Babu, J.S.S.; Kang, C.A.; Kim, H.H. Dry sliding wear behavior of aluminum-based hybrid composites with graphite nanofiber–alumina fiber. Mater. Des. 2011, 32, 3920–3925. [Google Scholar] [CrossRef]
- Lakshmikanthan, A.; Udayagiri, S.B.; Koppad, P.G.; Gupta, M.; Munishamaiah, K.; Bontha, S. The effect of heat treatment on the mechanical and tribological properties of dual size SiC reinforced A357 matrix composites. J. Mater. Res. Technol. 2020, 9, 6434–6452. [Google Scholar] [CrossRef]
- Lakshmikanthan, A.; Bontha, S.; Krishna, M.; Koppad, P.G.; Ramprabhu, T. Microstructure, mechanical and wear properties of the A357 composites reinforced with dual sized SiC particles. J. Alloys Compd. 2019, 786, 570–580. [Google Scholar] [CrossRef]






| Control Variables | Units | Range (1, 2, 3, 4) |
|---|---|---|
| Percent reinforcement, PR | 1, 2, 3 & 4 | |
| Die temperature, DT | °C | 140, 180, 220 & 260 |
| Melt temperature, MT | °C | 680, 710, 740 & 770 |
| Stir speed, SS | rpm | 480, 520, 560, 600 |
| Exp. No. | Designation | Control Variables | Output Variables | S/N Ratio (dB) | |||||
|---|---|---|---|---|---|---|---|---|---|
| PR, % | DT, °C | MT, °C | SS, rpm | HV | WR (×10−3), mm3/min | HV | WR | ||
| E1 | PR1DT1MT1SS1 | 1 | 140 | 680 | 480 | 85 | 2.89 | 38.59 | −9.22 |
| E2 | PR1DT2MT2SS2 | 1 | 180 | 710 | 520 | 88 | 2.76 | 38.89 | −8.82 |
| E3 | PR1DT3MT3SS3 | 1 | 220 | 740 | 560 | 91 | 2.59 | 39.18 | −8.27 |
| E4 | PR1DT4MT4SS4 | 1 | 260 | 770 | 600 | 87 | 2.84 | 38.79 | −9.07 |
| E5 | PR2DT1MT2SS3 | 2 | 140 | 710 | 560 | 90 | 2.63 | 39.08 | −8.4 |
| E6 | PR2DT2MT1SS4 | 2 | 180 | 680 | 600 | 92 | 2.47 | 39.28 | −7.85 |
| E7 | PR2DT3MT4SS1 | 2 | 220 | 770 | 480 | 90 | 2.68 | 39.08 | −8.56 |
| E8 | PR2DT4MT3SS2 | 2 | 260 | 740 | 520 | 93 | 2.38 | 39.37 | −7.53 |
| E9 | PR3DT1MT3SS4 | 3 | 140 | 740 | 600 | 98 | 2.26 | 39.82 | −7.08 |
| E10 | PR3DT2MT4SS3 | 3 | 180 | 770 | 560 | 104 | 2.05 | 40.34 | −6.24 |
| E11 | PR3DT3MT1SS2 | 3 | 220 | 680 | 520 | 101 | 2.14 | 40.09 | −6.61 |
| E12 | PR3DT4MT2SS1 | 3 | 260 | 710 | 480 | 94 | 2.26 | 39.46 | −7.08 |
| E13 | PR4DT1MT4SS2 | 4 | 140 | 770 | 520 | 96 | 2.17 | 39.65 | −6.73 |
| E14 | PR4DT2MT3SS1 | 4 | 180 | 740 | 480 | 94 | 2.22 | 39.46 | −6.93 |
| E15 | PR4DT3MT2SS4 | 4 | 220 | 710 | 600 | 92 | 2.51 | 39.28 | −7.99 |
| E16 | PR4DT4MT1SS3 | 4 | 260 | 680 | 560 | 92 | 2.55 | 39.28 | −8.13 |
| Factors | Levels | PR | DT | MT | SS | Total |
|---|---|---|---|---|---|---|
| SFL | 1 | 155.45 | 157.14 | 157.24 | 156.59 | 629.4 |
| 2 | 156.81 | 157.97 | 156.71 | 158.00 | ||
| 3 | 159.71 | 157.63 | 157.83 | 157.88 | ||
| 4 | 157.67 | 156.90 | 157.86 | 157.17 | ||
| SSD | 38.24 | 2.78 | 3.59 | 5.20 | 49.80 | |
| PC | 76.77 | 5.58 | 7.22 | 10.43 | 100 | |
| Factors | Levels | PR | DT | MT | SS | Total |
|---|---|---|---|---|---|---|
| SFL | 1 | −35.38 | −31.43 | −31.81 | −31.79 | −124.5 |
| 2 | −32.34 | −29.84 | −32.29 | −29.69 | ||
| 3 | −27.01 | −31.43 | −29.81 | −31.04 | ||
| 4 | −29.78 | −31.81 | −30.6 | −31.99 | ||
| SSD | 153.30 | 9.23 | 15.33 | 13.03 | 190.87 | |
| PC | 80.31 | 4.83 | 8.03 | 6.83 | 100 | |
| Exp. No. | Hardness | Wear Rate |
|---|---|---|
| E1 | 0.0000 | 0.0000 |
| E2 | 0.1579 | 0.1548 |
| E3 | 0.3158 | 0.3571 |
| E4 | 0.1053 | 0.0595 |
| E5 | 0.2632 | 0.3095 |
| E6 | 0.3684 | 0.5000 |
| E7 | 0.2632 | 0.2500 |
| E8 | 0.4211 | 0.6071 |
| E9 | 0.6842 | 0.7500 |
| E10 | 1.0000 | 1.0000 |
| E11 | 0.8421 | 0.8929 |
| E12 | 0.4737 | 0.7500 |
| E13 | 0.5789 | 0.8571 |
| E14 | 0.4737 | 0.7976 |
| E15 | 0.3684 | 0.4524 |
| E16 | 0.3684 | 0.4048 |
| SD | 0.2617 | 0.3108 |
| Responses | Hardness | Wear Rate |
|---|---|---|
| Hardness | 1.0000 | 0.9333 |
| Wear rate | 0.9333 | 1.0000 |
| Responses | Hardness | Wear Rate | Summation |
|---|---|---|---|
| Hardness | 0.0000 | 0.0677 | 0.0677 |
| Wear rate | 0.0667 | 0.0000 | 0.0677 |
| Responses | Cj | Wj |
|---|---|---|
| Hardness | 0.017462 | 0.457118 |
| Wear rate | 0.020738 | 0.542883 |
| Exp. No. | S/N ratio | Normalization | GRC | GRG | |||
|---|---|---|---|---|---|---|---|
| HV | WR | HV | WR | HV | WR | ||
| E1 | 38.59 | −9.22 | 0.000 ‡ | 0.000 | 0.333 ‡ | 0.333 | 0.333 ‡ |
| E2 | 38.89 | −8.82 | 0.171 | 0.134 | 0.376 | 0.366 | 0.371 |
| E3 | 39.18 | −8.27 | 0.337 | 0.319 | 0.430 | 0.423 | 0.426 |
| E4 | 38.79 | −9.07 | 0.114 | 0.050 | 0.361 | 0.345 | 0.352 |
| E5 | 39.08 | −8.4 | 0.280 | 0.275 | 0.410 | 0.408 | 0.409 |
| E6 | 39.28 | −7.85 | 0.394 | 0.460 | 0.452 | 0.481 | 0.468 |
| E7 | 39.08 | −8.56 | 0.280 | 0.221 | 0.410 | 0.391 | 0.400 |
| E8 | 39.37 | −7.53 | 0.446 | 0.567 | 0.474 | 0.536 | 0.508 |
| E9 | 39.82 | −7.08 | 0.703 | 0.718 | 0.627 | 0.639 | 0.634 |
| E10 | 40.34 | −6.24 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| E11 | 40.09 | −6.61 | 0.857 | 0.876 | 0.778 | 0.801 | 0.790 |
| E12 | 39.46 | −7.08 | 0.497 | 0.718 | 0.499 | 0.639 | 0.575 |
| E13 | 39.65 | −6.73 | 0.606 | 0.836 | 0.559 | 0.753 | 0.664 |
| E14 | 39.46 | −6.93 | 0.497 | 0.768 | 0.499 | 0.683 | 0.599 |
| E15 | 39.28 | −7.99 | 0.394 | 0.413 | 0.452 | 0.460 | 0.456 |
| E16 | 39.28 | −8.13 | 0.394 | 0.366 | 0.452 | 0.441 | 0.446 |
| Max. | 40.34 | −6.24 | |||||
| Min. | 38.59 | −9.22 | |||||
| ‡ | Normalization computation: (38.59 − 38.59)/(40.34 − 38.59) = 0.000 | ||||||
| ‡ | Computation of GRC: [0 + (0.5 × 1)]/[(1 − 0.000) + 0.5] = 0.333 | ||||||
| ‡ | Computation of WGRG: [(0.333 × 0.4572) + (0.333 × 0.5428)] = 0.333 | ||||||
| Factors | Levels | PR | DT | MT | SS | Total |
|---|---|---|---|---|---|---|
| SFL | 1 | 1.482 | 2.04 | 2.037 | 1.907 | 8.431 |
| 2 | 1.785 | 2.438 | 1.811 | 2.333 | ||
| 3 | 2.999 | 2.072 | 2.167 | 2.281 | ||
| 4 | 2.165 | 1.881 | 2.416 | 1.91 | ||
| SSD | 5.17 | 0.66 | 0.77 | 0.64 | 7.25 | |
| PC | 71.36 | 9.18 | 10.57 | 8.84 | 100 | |
| Exp. No. | S/N Ratio | Sum of Squares | Normalization | Weighted Normalization | MOORA Index | ||||
|---|---|---|---|---|---|---|---|---|---|
| HV | WR | HV | WR | HV | WR | HV | WR | ||
| E1 | 38.59 | −9.22 | 1489.2 ‡ | 85.0 | 0.000 ‡ | 0.000 | 0.333 ‡ | 0.333 | 0.333 ‡ |
| E2 | 38.89 | −8.82 | 1512.4 | 77.8 | 0.171 | 0.134 | 0.376 | 0.366 | 0.371 |
| E3 | 39.18 | −8.27 | 1535.1 | 68.4 | 0.337 | 0.319 | 0.430 | 0.423 | 0.426 |
| E4 | 38.79 | −9.07 | 1504.7 | 82.3 | 0.114 | 0.050 | 0.361 | 0.345 | 0.352 |
| E5 | 39.08 | −8.4 | 1527.2 | 70.6 | 0.280 | 0.275 | 0.410 | 0.408 | 0.409 |
| E6 | 39.28 | −7.85 | 1542.9 | 61.6 | 0.394 | 0.460 | 0.452 | 0.481 | 0.468 |
| E7 | 39.08 | −8.56 | 1527.2 | 73.3 | 0.280 | 0.221 | 0.410 | 0.391 | 0.400 |
| E8 | 39.37 | −7.53 | 1550.0 | 56.7 | 0.446 | 0.567 | 0.474 | 0.536 | 0.508 |
| E9 | 39.82 | −7.08 | 1585.6 | 50.1 | 0.703 | 0.718 | 0.627 | 0.639 | 0.634 |
| E10 | 40.34 | −6.24 | 1627.3 | 38.9 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| E11 | 40.09 | −6.61 | 1607.2 | 43.7 | 0.857 | 0.876 | 0.778 | 0.801 | 0.790 |
| E12 | 39.46 | −7.08 | 1557.1 | 50.1 | 0.497 | 0.718 | 0.499 | 0.639 | 0.575 |
| E13 | 39.65 | −6.73 | 1572.1 | 45.3 | 0.606 | 0.836 | 0.559 | 0.753 | 0.664 |
| E14 | 39.46 | −6.93 | 1557.1 | 48.0 | 0.497 | 0.768 | 0.499 | 0.683 | 0.599 |
| E15 | 39.28 | −7.99 | 1542.9 | 63.8 | 0.394 | 0.413 | 0.452 | 0.460 | 0.456 |
| E16 | 39.28 | −8.13 | 1542.9 | 66.1 | 0.394 | 0.366 | 0.452 | 0.441 | 0.446 |
| ‡ | Sum of squares: 38.59 × 38.59 = 1489.2 | ||||||||
| ‡ | Normalization value for HV: S/N ratio/√(Total sum of squares) = 38.59/√ (1489.2 + … 1542.9) = 0.245 | ||||||||
| ‡ | Computation of weighted normalization: 0.112 × 0.4572 = 0.112 | ||||||||
| ‡ | Computation of MOORA Index: 0.112 − 0.160 = −0.048 | ||||||||
| Factors | Levels | PR | DT | MT | SS | Total |
|---|---|---|---|---|---|---|
| SFL | 1 | −0.161 | −0.088 | −0.095 | −0.096 | −0.327 |
| 2 | −0.105 | −0.058 | −0.104 | −0.055 | ||
| 3 | −0.004 | −0.086 | −0.057 | −0.079 | ||
| 4 | −0.057 | −0.095 | −0.071 | −0.097 | ||
| SSD | 0.0539 | 0.0032 | 0.0056 | 0.0046 | 0.06733 | |
| PC | 80.08 | 4.73 | 8.31 | 6.88 | 100 | |
| Models | Optimal Factor Levels | Experimental Output Values | Percent Improvement |
|---|---|---|---|
| Initial Condition | PR1DT1MT1SS1 | HV = 85; WR = 2.89 × 10−3 mm3/min | |
| Taguchi-CRITIC- GRA | PR3DT2MT4SS2 | HV = 108; WR = 1.95 × 10−3 mm3/min | 27.06% increase in HV; 32.53% decrease in WR |
| Taguchi-CRITIC- MOORA | PR3DT2MT3SS2 | HV = 112; WR = 1.84 × 10−3 mm3/min | 31.77% increase in HV; 36.33% decrease in WR |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shivalingaiah, K.; Nagarajaiah, V.; Selvan, C.P.; Kariappa, S.T.; Chandrashekarappa, N.G.; Lakshmikanthan, A.; Chandrashekarappa, M.P.G.; Linul, E. Stir Casting Process Analysis and Optimization for Better Properties in Al-MWCNT-GR-Based Hybrid Composites. Metals 2022, 12, 1297. https://doi.org/10.3390/met12081297
Shivalingaiah K, Nagarajaiah V, Selvan CP, Kariappa ST, Chandrashekarappa NG, Lakshmikanthan A, Chandrashekarappa MPG, Linul E. Stir Casting Process Analysis and Optimization for Better Properties in Al-MWCNT-GR-Based Hybrid Composites. Metals. 2022; 12(8):1297. https://doi.org/10.3390/met12081297
Chicago/Turabian StyleShivalingaiah, Kanchiraya, Vinayaka Nagarajaiah, Chithirai Pon Selvan, Smitha Thothera Kariappa, Nandini Gowdru Chandrashekarappa, Avinash Lakshmikanthan, Manjunath Patel Gowdru Chandrashekarappa, and Emanoil Linul. 2022. "Stir Casting Process Analysis and Optimization for Better Properties in Al-MWCNT-GR-Based Hybrid Composites" Metals 12, no. 8: 1297. https://doi.org/10.3390/met12081297
APA StyleShivalingaiah, K., Nagarajaiah, V., Selvan, C. P., Kariappa, S. T., Chandrashekarappa, N. G., Lakshmikanthan, A., Chandrashekarappa, M. P. G., & Linul, E. (2022). Stir Casting Process Analysis and Optimization for Better Properties in Al-MWCNT-GR-Based Hybrid Composites. Metals, 12(8), 1297. https://doi.org/10.3390/met12081297









