1. Introduction
Nowadays, family cars are widely used in daily life. For this modern mechanical equipment, various dynamic loads are applied to the parts [
1,
2]. Thus, a special surface strengthening method is necessary to ensure that the parts can fulfil the corresponding service life requirements. Among these methods, the electromagnetic induction quenching approach is considered to be an effective choice [
3,
4]. This technique can effectively improve the fatigue strength of the metal parts, such as the steel crankshafts, to make them applicable to the high-power engine, thus corresponding technique parameters are necessary to be reasonably planned during the design stage.
In recent years, some experts focused on researching this problem. Among them, Cajner proposed a 2D simplified axial symmetrical model to conduct the numerical simulation of the electromagnetic induction quenching approach on a 42CrMo steel crankshaft; the experimental verification showed that this model can provide accurate surface hardness and hardness layer-depth results [
5]. Dmitry conducted a technological parameter influence analysis of this approach and proposed a corresponding model to accurately simulate the process [
6]. Mohan proposed a new optimal design method based on a satisfactory function, which was established during the electromagnetic induction quenching process [
7]. Stephanie compared the mechanical and microstructure properties of the 42CrMo steel after electromagnetic induction quenching and conventional heat treatment process through the standard tensile experiment and pyramid hardness test. The result showed that yield strength and hardness of the steel after electromagnetic induction quenching were a little lower than those of the steel after a conventional heat treatment process, which can be attributed to the size effect [
8]. Dietmar applied the adaptive finite element analysis approach in simulating the electromagnetic induction quenching of the gear and obtained accuracy for the temperature and hardening curve [
9]. Umberto researched the microstructure and mechanical property of the hardening layer and proposed that the main influence factors were the heating and cooling speeds during the electromagnetic induction quenching, as well as the peak value of the temperature [
10]. Akram proposed novel alternate magnetic field treatments in EN8 steel and discovered that this approach could improve the wear resistance and reduce the coefficient of the friction of the material, which could be explained by the increase in the compressive residual stress and the microhardness. This method can also be applied to the fatigue property research of similar metal materials [
11].
Nowadays, the turbocharging technique has been widely applied for improving the engine power, which results in the more critical demand for the fatigue strength of some key metal parts, such as the crankshaft. As a result of this, a more accurate assessment of the strengthening effect of this approach is necessary. However, the strengthening effect of this approach has not been quantitatively evaluated. In addition, the heat-up process of the electromagnetic induction quenching approach is usually no more than 20 s and corresponding components are surrounded by the coil. This situation makes the real-time experiment verification difficult to conduct.
In a previous study, we evaluated the strengthening effect of this technique by considering the residual stress as the mean stress and applied corresponding mean stress models to the prediction of the fatigue limit load of a given type of steel crankshaft [
12,
13]. The theoretical foundation of this approach is that both the mean and alternating stresses are uniaxial and in the same direction; whereas, for the parts with complicated shapes, the state of the alternating stress is usually multi-axial, even though the load applied to it is the uniaxial type [
14,
15]. This situation makes the application of the mean stress models unreasonable to some degree.
In this paper, a comprehensive assessment of the strengthening effect of the electromagnetic induction quenching technique is conducted. First, the whole process of this approach is simulated by a finite element model to provide the basic stress and temperature information. Then, a combination of the residual stress field obtained in a previous chapter and a verified multi-axial fatigue model are chosen to predict the fatigue limit load of the crankshaft. Finally, the predictions based on different models are checked by the corresponding experiment verification. The results show that, when compared to the usual modified models based on the mean stress, the modified McDiarmid multi-axial fatigue model can exhibit higher accuracy in this prediction, thus possessing practicability and value of popularization in actual engineering applications.
Author Contributions
Conceptualization: S.S.; methodology: S.S.; software: X.Z.; validation: S.S., X.Z.; formal analysis: S.S.; investigation: S.S., X.Z.; resources: S.S.; data curation: S.S.; writing—original draft preparation: S.S.; writing—review and editing: X.G., M.W.; visualization: None; supervision: X.X.; funding acquisition: X.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data generated or analyzed during this study are included in this published article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jie, T.; Tong, J.; Shi, L. Differential steering control of four-wheel independent-drive electric vehicles. Energies 2018, 11, 2892. [Google Scholar]
- Tian, J.; Wang, Q.; Ding, J.; Wang, Y.; Ma, Z. Integrated Control with DYC and DSS for 4WID Electric Vehicles. IEEE Access 2019, 7, 124077–124086. [Google Scholar] [CrossRef]
- Zhu, Y.; Luo, Y.; Ma, N. Relationship between equivalent surface heat source and induction heating parameters for analysis of thermal conduction in thick plate bending. Ships Offshore Struct. 2019, 14, 921–928. [Google Scholar] [CrossRef]
- Asadzadeh, M.Z.; Raninger, P.; Prevedel, P.; Ecker, W.; Mücke, M. Inverse Model for the Control of Induction Heat Treatments. Materials 2019, 12, 2826. [Google Scholar] [CrossRef] [Green Version]
- Cajner, F.; Smoljan, B.; Landek, D. Computer simulation of induction hardening. J. Mater. Process. Technol. 2004, 157, 55–60. [Google Scholar] [CrossRef]
- Ivanov, D.; Markegård, L.; Asperheim, J.I.; Kristoffersen, H. Simulation of Stress and Strain for Induction-Hardening Applications. J. Mater. Eng. Perform. 2013, 22, 3258–3268. [Google Scholar] [CrossRef] [Green Version]
- Misra, M.K.; Bhattacharya, B.; Singh, O.; Chatterjee, A. Multi response Optimization of Induction Hardening Process—A New Approach. IFAC Proc. Vol. 2014, 47, 862–869. [Google Scholar] [CrossRef]
- Sackl, S.; Leitner, H.; Zuber, M.; Clemens, H.; Primig, S. Induction Hardening vs Conventional Hardening of a Heat Treatable Steel. Met. Mater. Trans. A 2014, 45, 5657–5666. [Google Scholar] [CrossRef]
- Hömberg, D.; Liu, Q.; Montalvo-Urquizo, J.; Nadolski, D.; Petzold, T.; Schmidt, A.; Schulz, A. Simulation of multi-frequency-induction-hardening including phase transitions and mechanical effects. Finite Elem. Anal. Des. 2016, 121, 86–100. [Google Scholar] [CrossRef]
- Prisco, U. Case microstructure in induction surface hardening of steels: An overview. Int. J. Adv. Manuf. Technol. 2018, 98, 2619–2637. [Google Scholar] [CrossRef]
- Akram, S.; Babutskyi, A.; Chrysanthou, A.; Montalvão, D.; Whiting, M.J.; Modi, O.P. Improvement of the wear resistance of EN8 steel by application of alternating magnetic field treatment. Wear 2021, 484–485, 203926. [Google Scholar] [CrossRef]
- Wu, C.; Sun, S. Crankshaft High Cycle Bending Fatigue Research Based on a 2D Simplified Model and Different Mean Stress Models. J. Fail. Anal. Prev. 2021, 21, 1396–1402. [Google Scholar] [CrossRef]
- SongSong, S.; Xingzhe, Z.; Chang, W.; Maosong, W.; Fengkui, Z. Crankshaft high cycle bending fatigue research based on the simulation of electromagnetic induction quenching and the mean stress effect. Eng. Fail. Anal. 2021, 122, 105214. [Google Scholar] [CrossRef]
- Sun, S.; Yu, X.; Liu, Z.; Chen, X. Component HCF Research Based on the Theory of Critical Distance and a Relative Stress Gradient Modification. PLoS ONE 2016, 11, e0167722. [Google Scholar] [CrossRef]
- Sun, S.-S.; Yu, X.-L.; Chen, X.-P.; Liu, Z.-T. Component structural equivalent research based on different failure strength criterions and the theory of critical distance. Eng. Fail. Anal. 2016, 70, 31–43. [Google Scholar] [CrossRef]
- Li, J. Numerical Studies on the Induction Quenching Process of Crankshaft; Beijing Institute of Technology: Beijing, China, 2015. [Google Scholar]
- Zhang, X. Simulation of Electromagnetic Induction Quenching of Crankshaft and Study on Prediction Method of Fatigue Property; Nanjing Forestry University: Nanjing, China, 2020. [Google Scholar]
- Sun, S.S.; Wan, M.S.; Wang, H. Crankshaft fatigue research based on modified multi-axial fatigue model. J. Mech. Electr. Eng. 2019, 797–802. [Google Scholar]
- Böhm, M.; Głowacka, K. Fatigue Life Estimation with Mean Stress Effect Compensation for Lightweight Structures—The Case of GLARE 2 Composite. Polymers 2020, 12, 251. [Google Scholar] [CrossRef] [Green Version]
- Xun, Z.; Xiaoli, Y. Failure criterion in resonant bending fatigue test for crankshafts. Chin. Intern. Combust. Engine Eng. 2007, 28, 45–47. [Google Scholar]
- Xun, Z.; Xiaoli, Y. Error analysis and load calibration technique investigation of resonant loading fatigue test for crankshaft. Trans. Chin. Soc. Agric. Mach. 2007, 38. [Google Scholar]
- Zhang, Y.; Wang, A. Remaining Useful Life Prediction of Rolling Bearings Using Electrostatic Monitoring Based on Two-Stage Information Fusion Stochastic Filtering. Math. Probl. Eng. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, Y.; Yu, Y. Joint estimation of SOC of lithium battery based on dual kalman filter. Processes 2021, 9, 1412. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, Y.; Yu, Y. Lithium-ion battery SOC estimation based on adaptive forgetting factor least squares online identification and unscented kalman filter. Mathematics 2021, 9, 1733. [Google Scholar] [CrossRef]
- Zhou, W.; Zheng, Y.; Pan, Z.; Lu, Q. Review on the Battery Model and SOC Estimation Method. Processes 2021, 9, 1685. [Google Scholar] [CrossRef]
- Chang, C.; Zheng, Y.; Sun, W.; Ma, Z. LPV estimation of SOC based on electricity conversion and hysteresis characteristic. J. Energy Eng. 2019, 145, 04019026. [Google Scholar] [CrossRef]
- Chang, C.; Zheng, Y.; Yu, Y. Estimation for battery state of charge based on temperature effect and fractional extended kalman filter. Energies 2020, 13, 5947. [Google Scholar] [CrossRef]
- Chen, X.; Yu, X.; Hu, R.; Li, J. Statistical distribution of crankshaft fatigue: Experiment and modeling. Eng. Fail. Anal. 2014, 42, 210–220. [Google Scholar] [CrossRef]
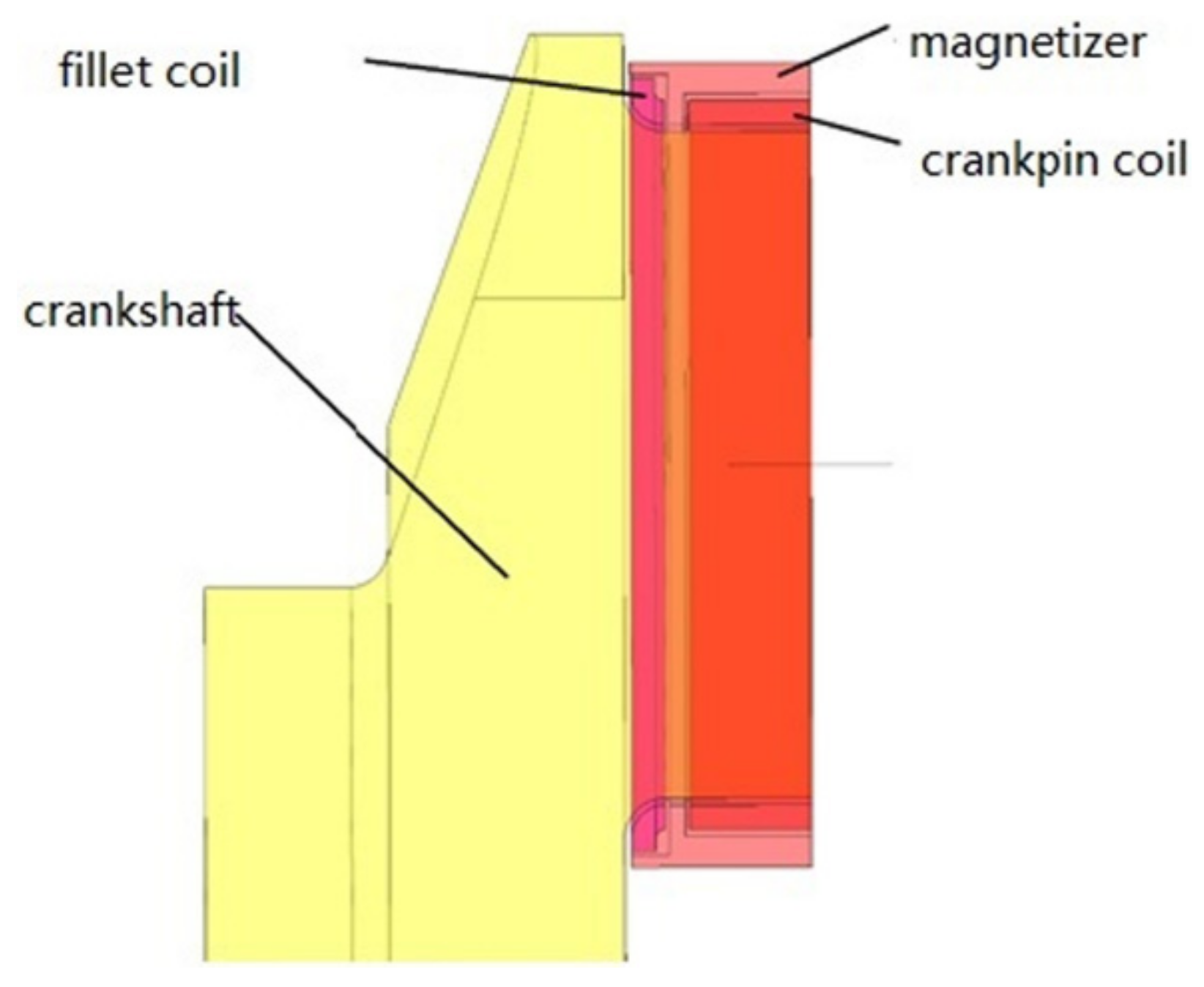
Figure 1.
The structure diagram of the electromagnetic induction quenching equipment.
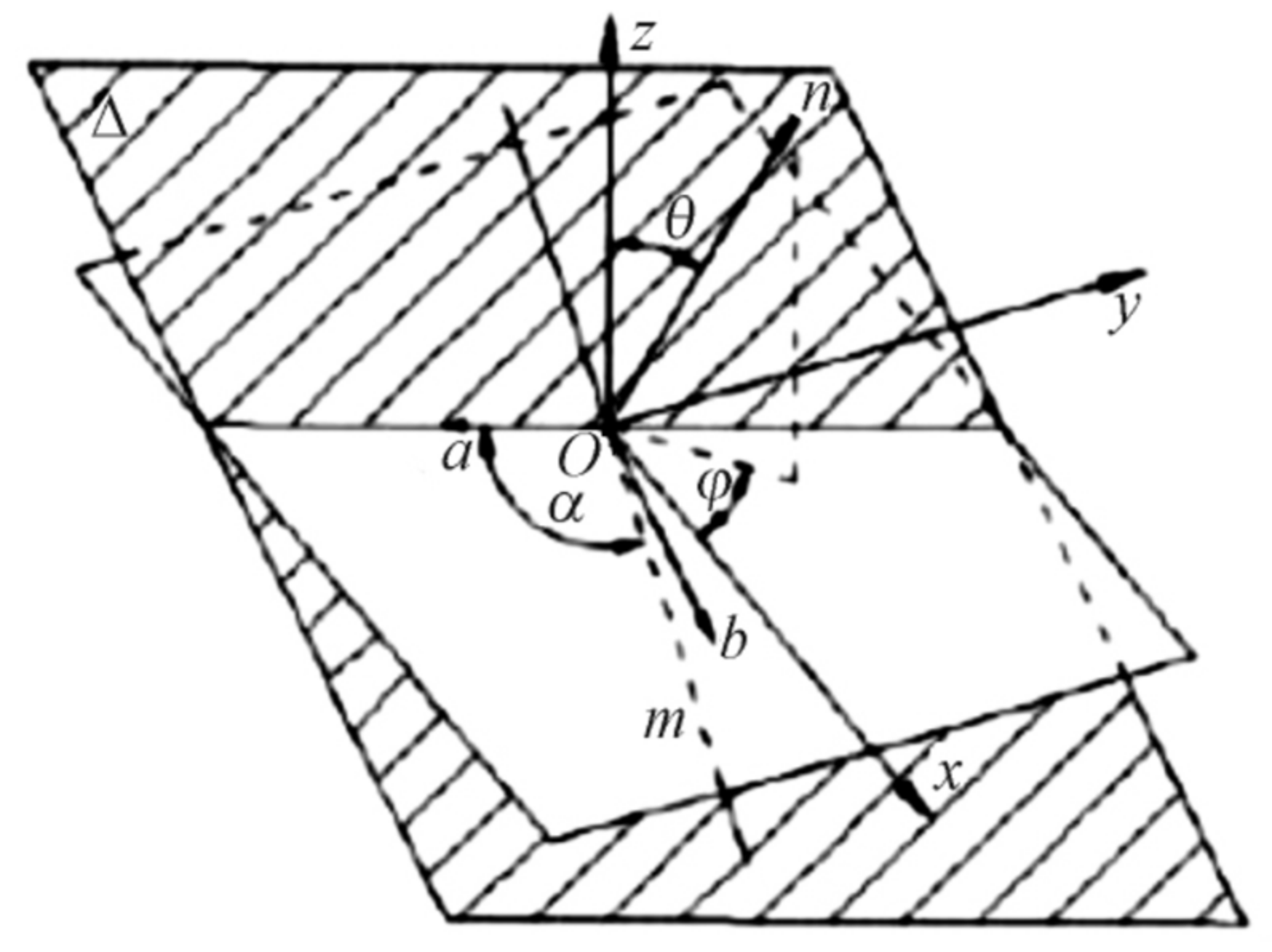
Figure 2.
A random plane crossing the calculation point.
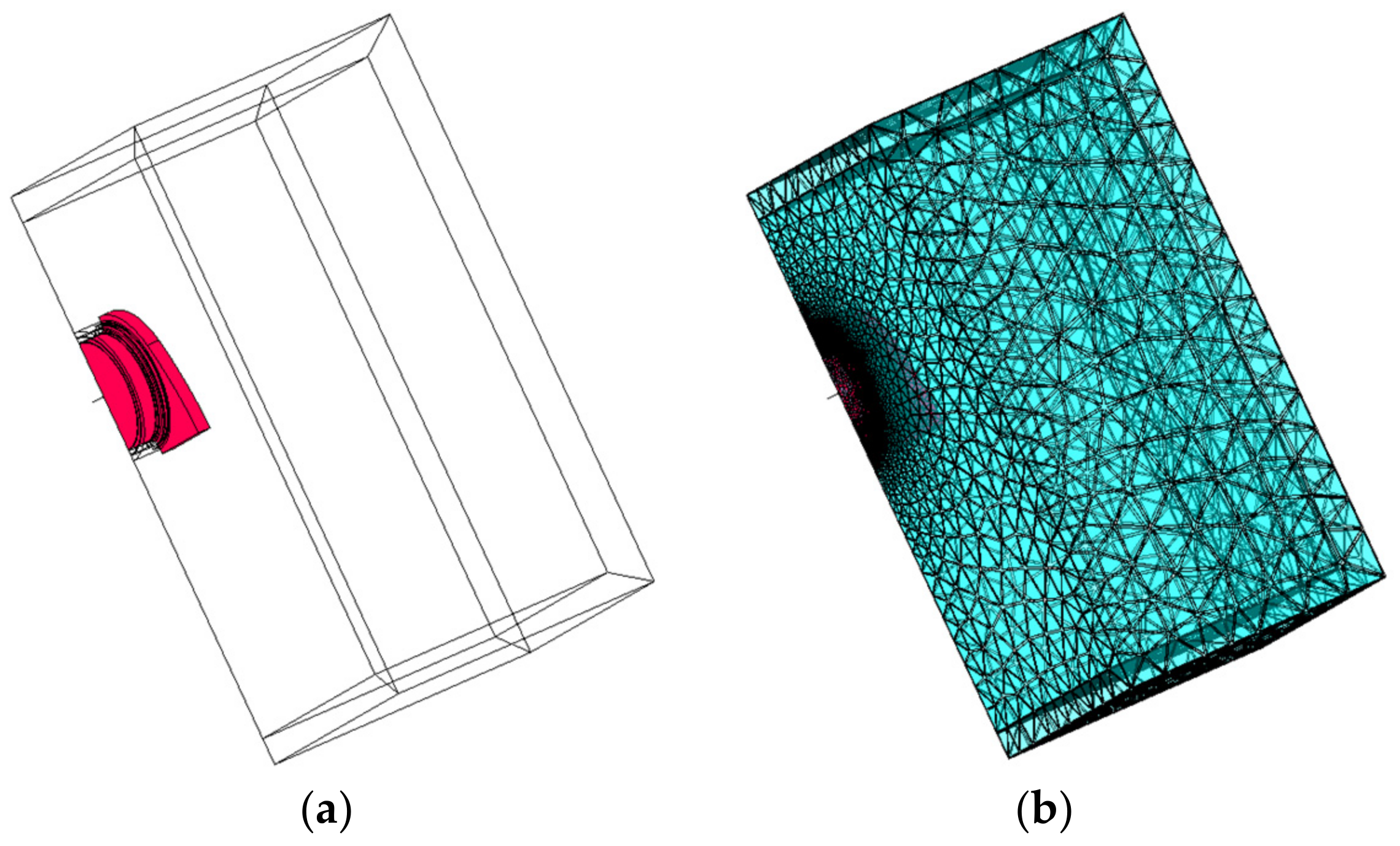
Figure 3.
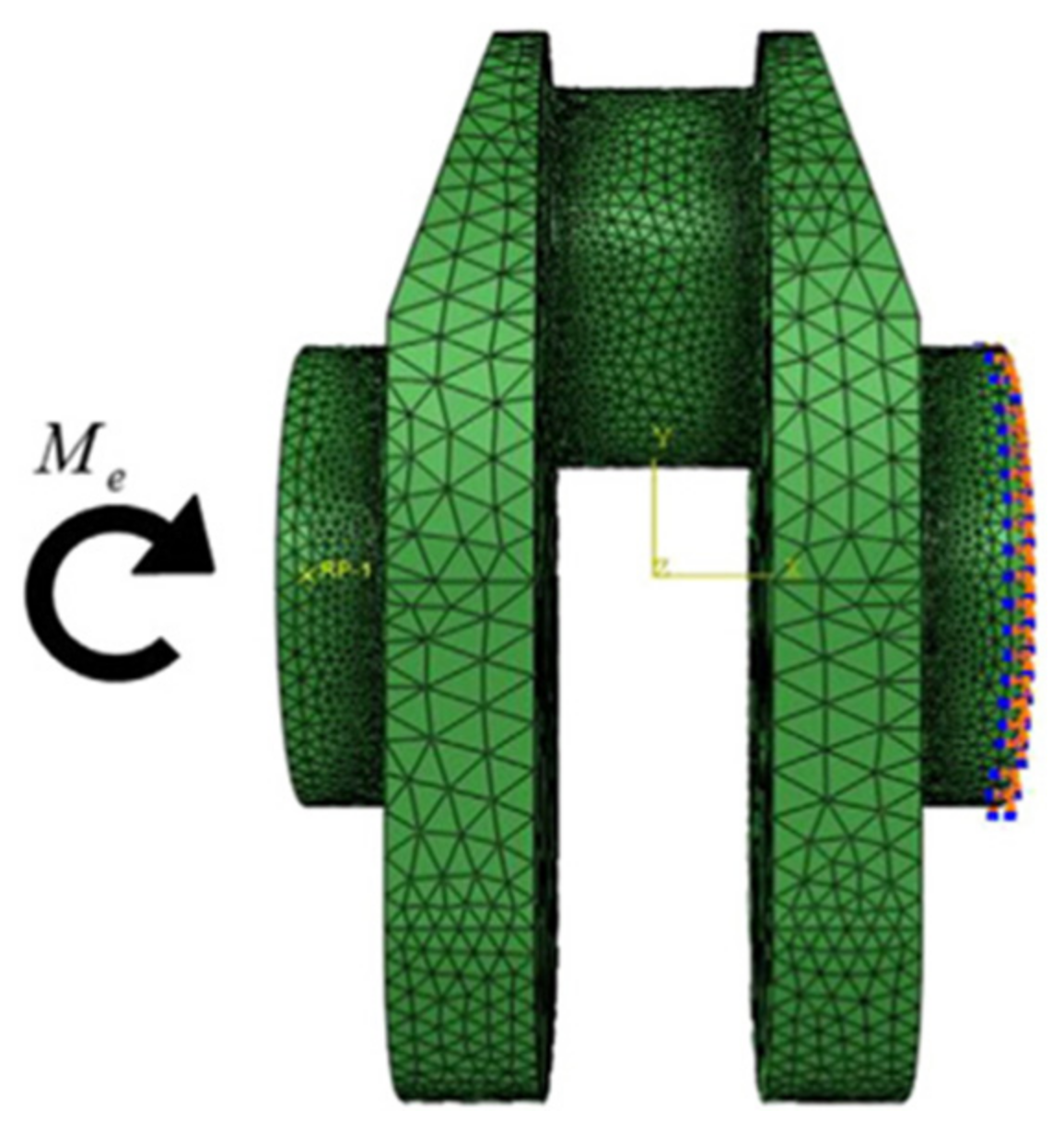
A quarter-pin model in the electromagnetic field ((a) Geometric model; (b) mesh model).
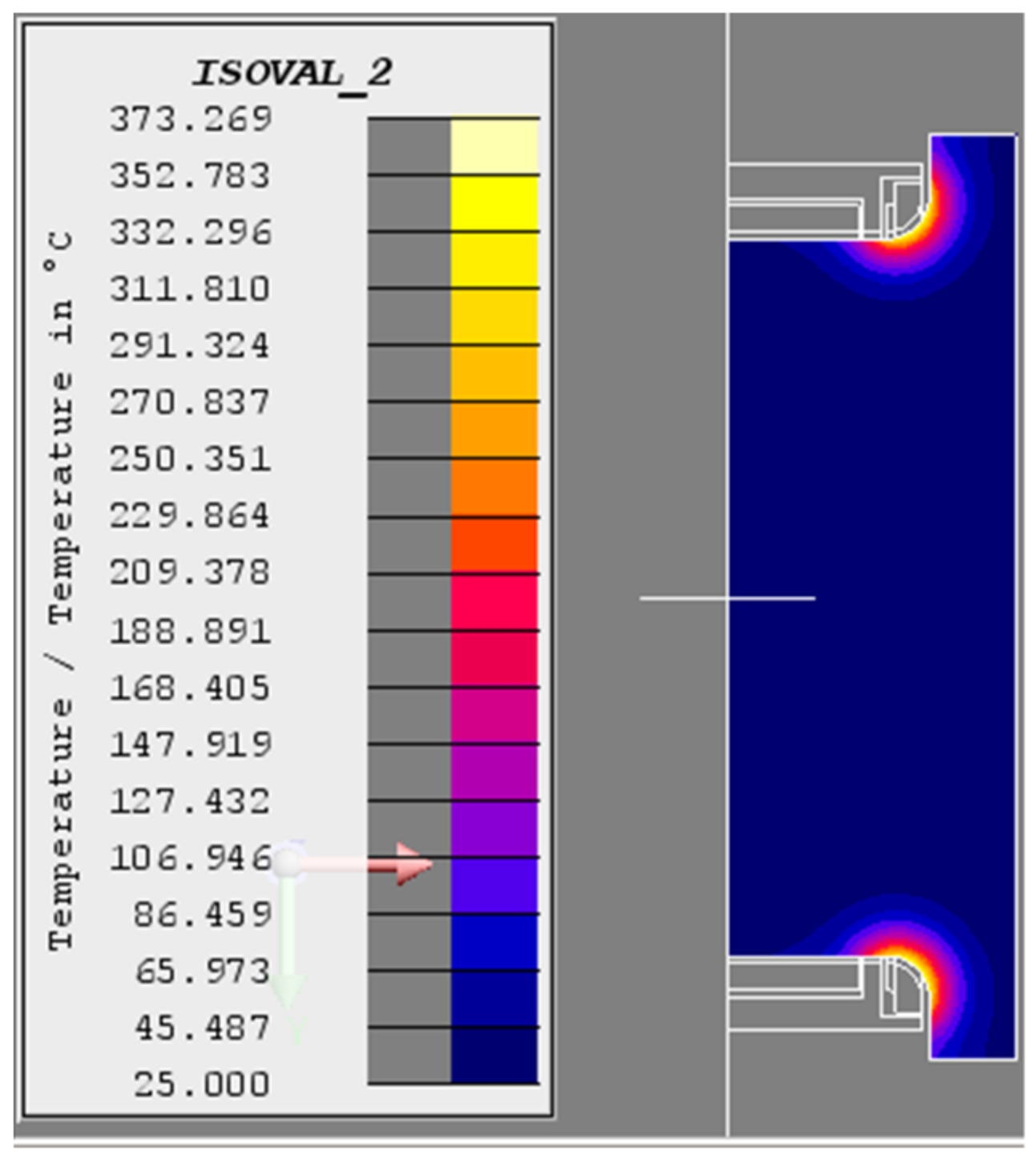
Figure 4.
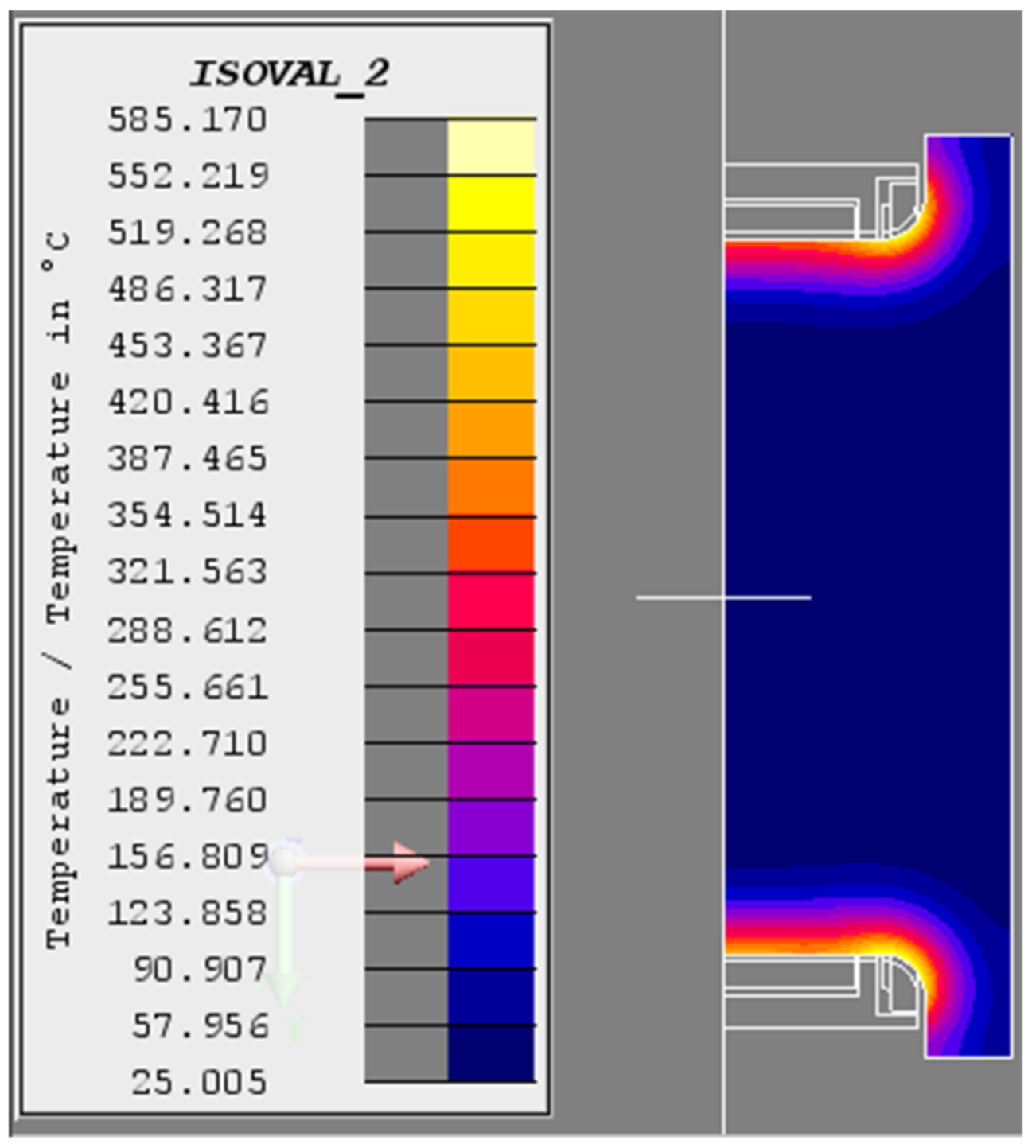
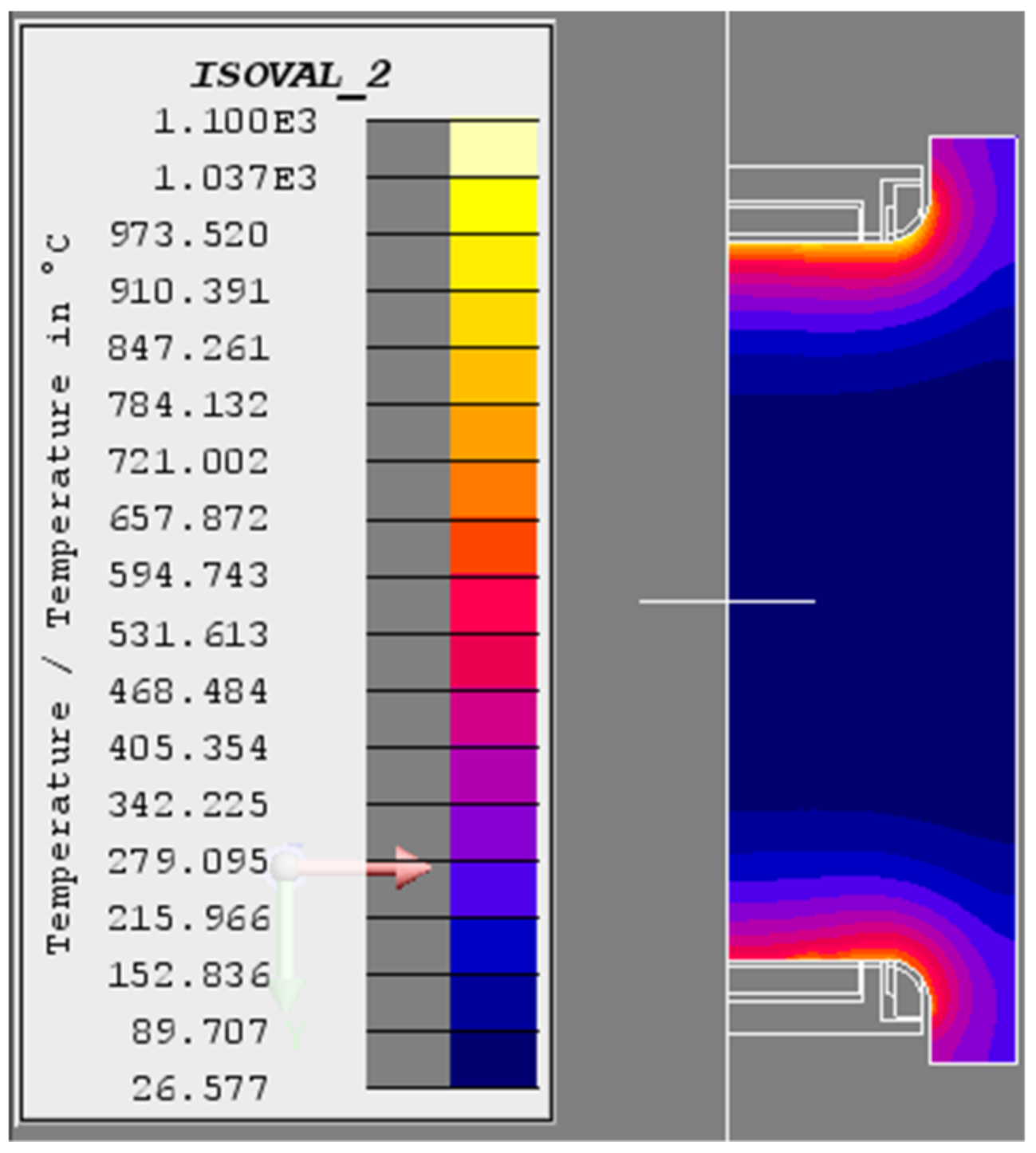
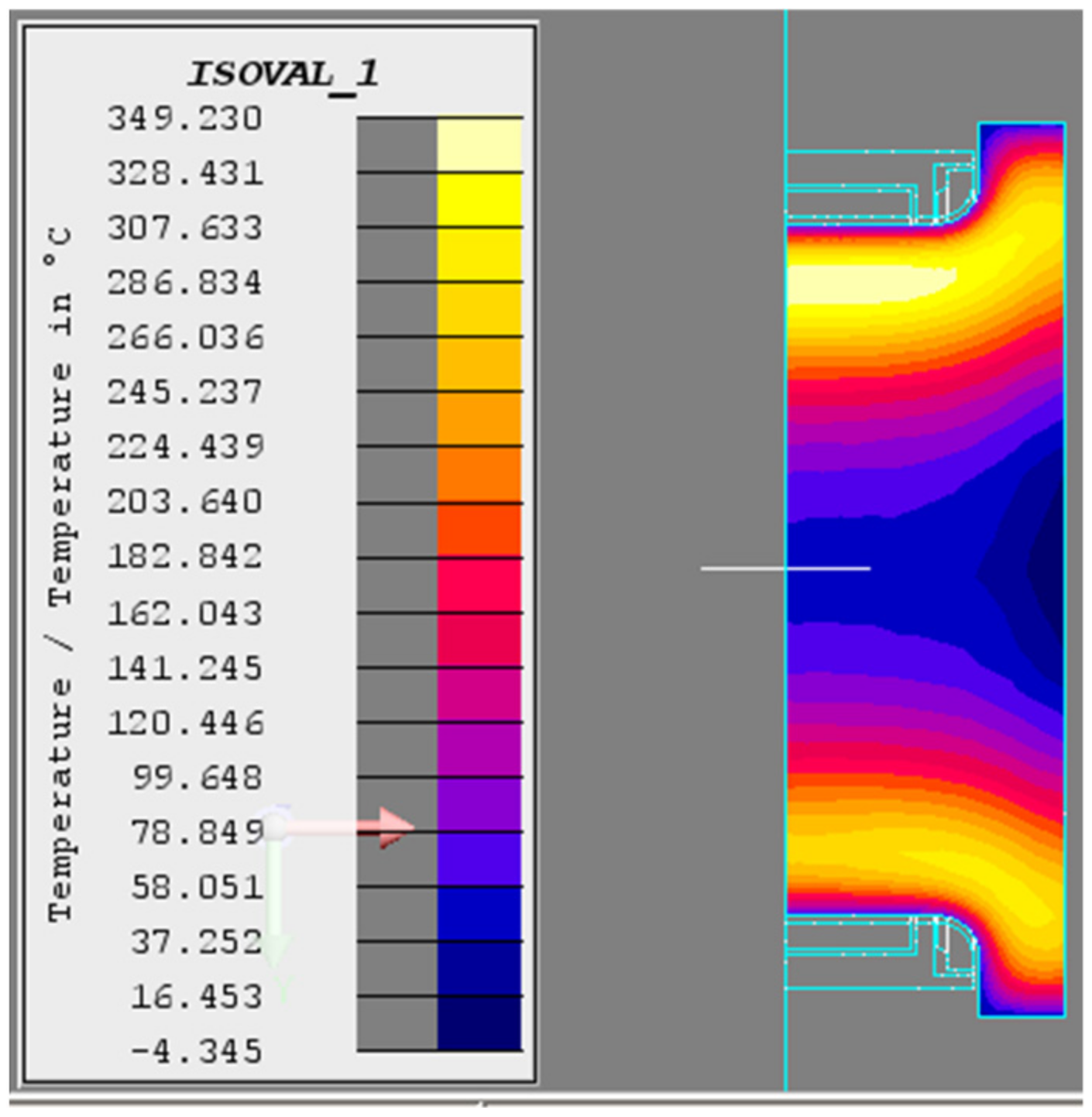
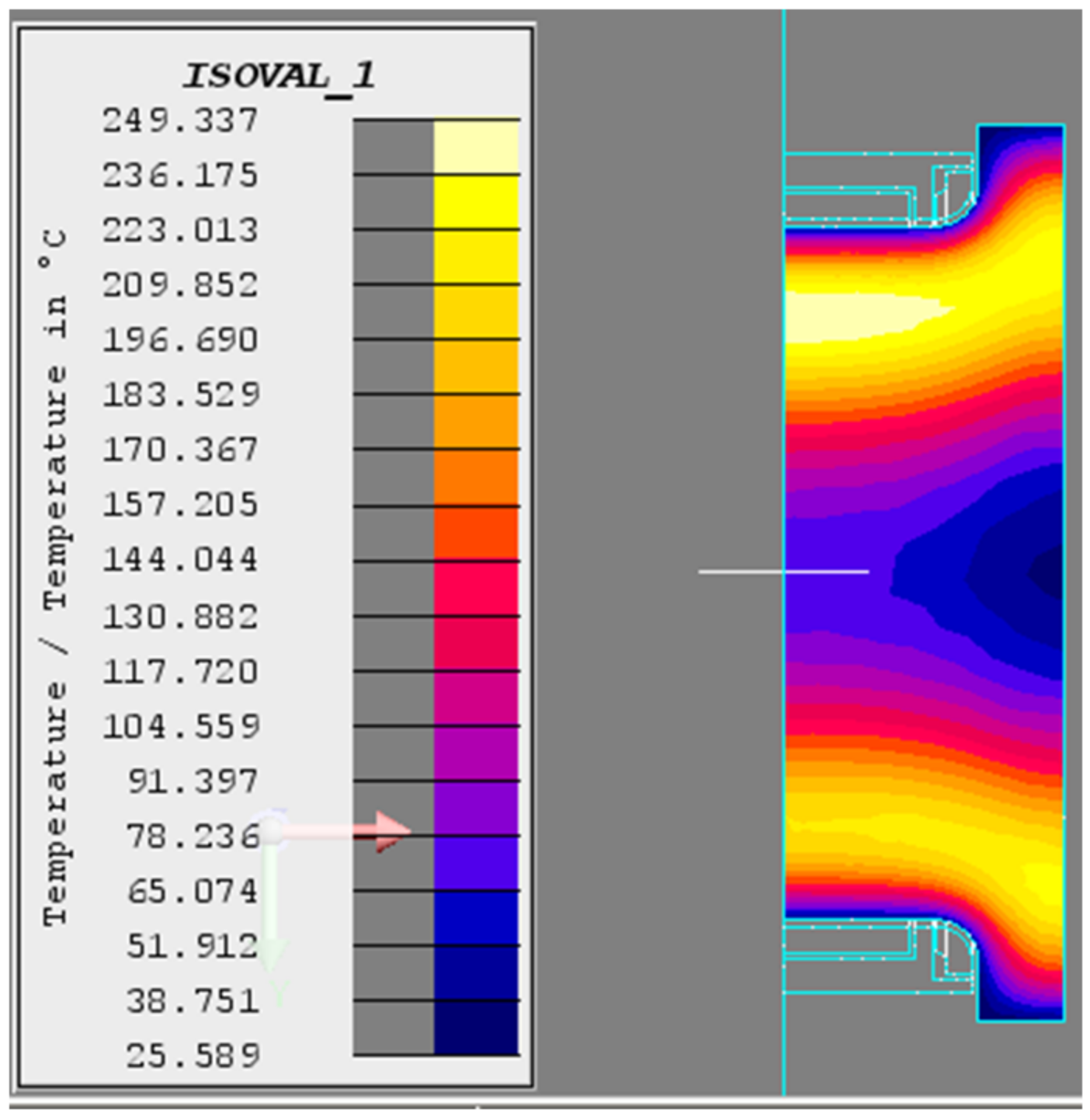
Temperature field of the crankshaft (T = 3 s).
Figure 5.
Temperature field of the crankshaft (T = 6 s).
Figure 6.
Temperature field of the crankshaft (T = 9 s).
Figure 7.
Temperature field of the crankshaft (T = 12 s).
Figure 8.
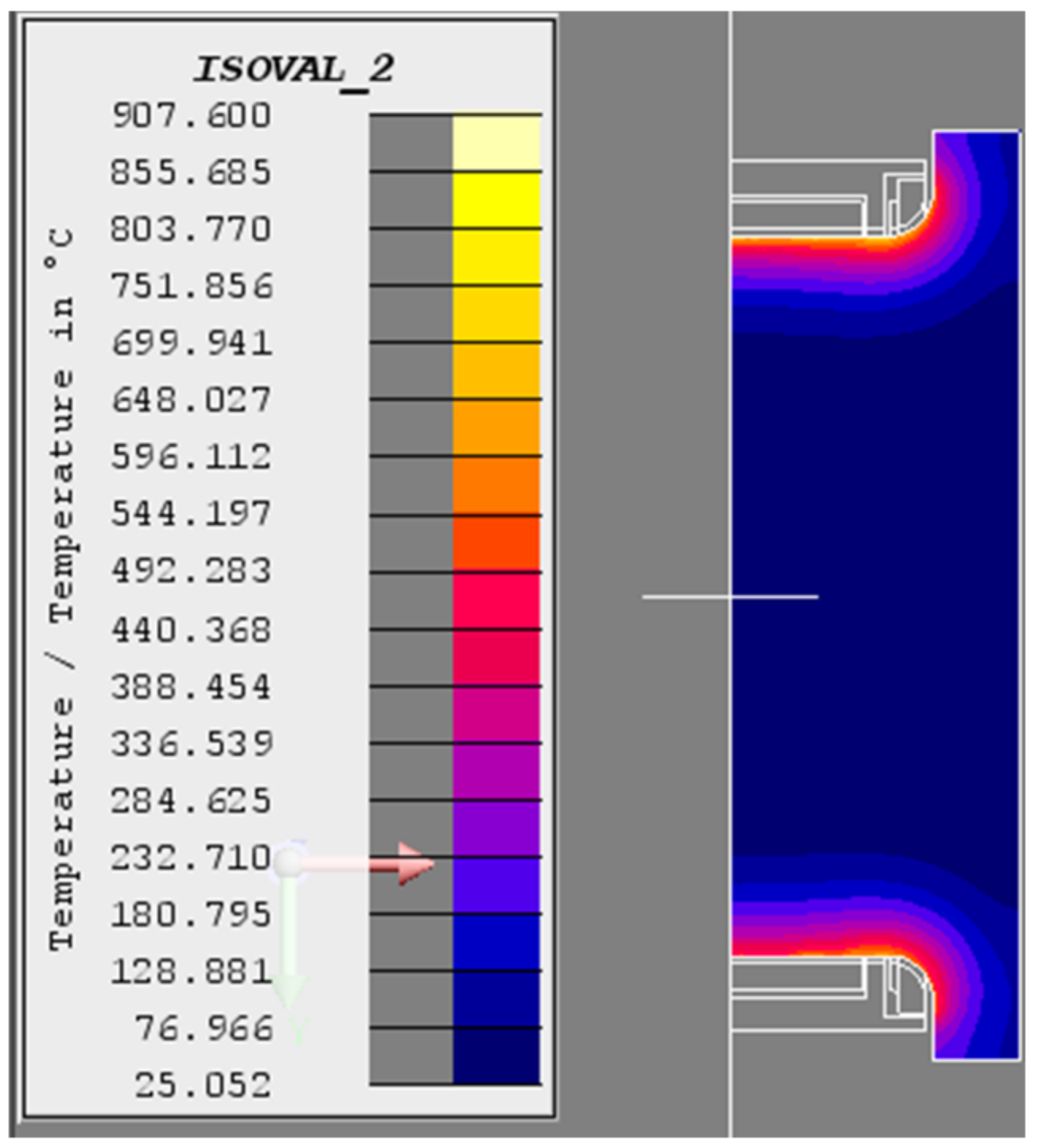
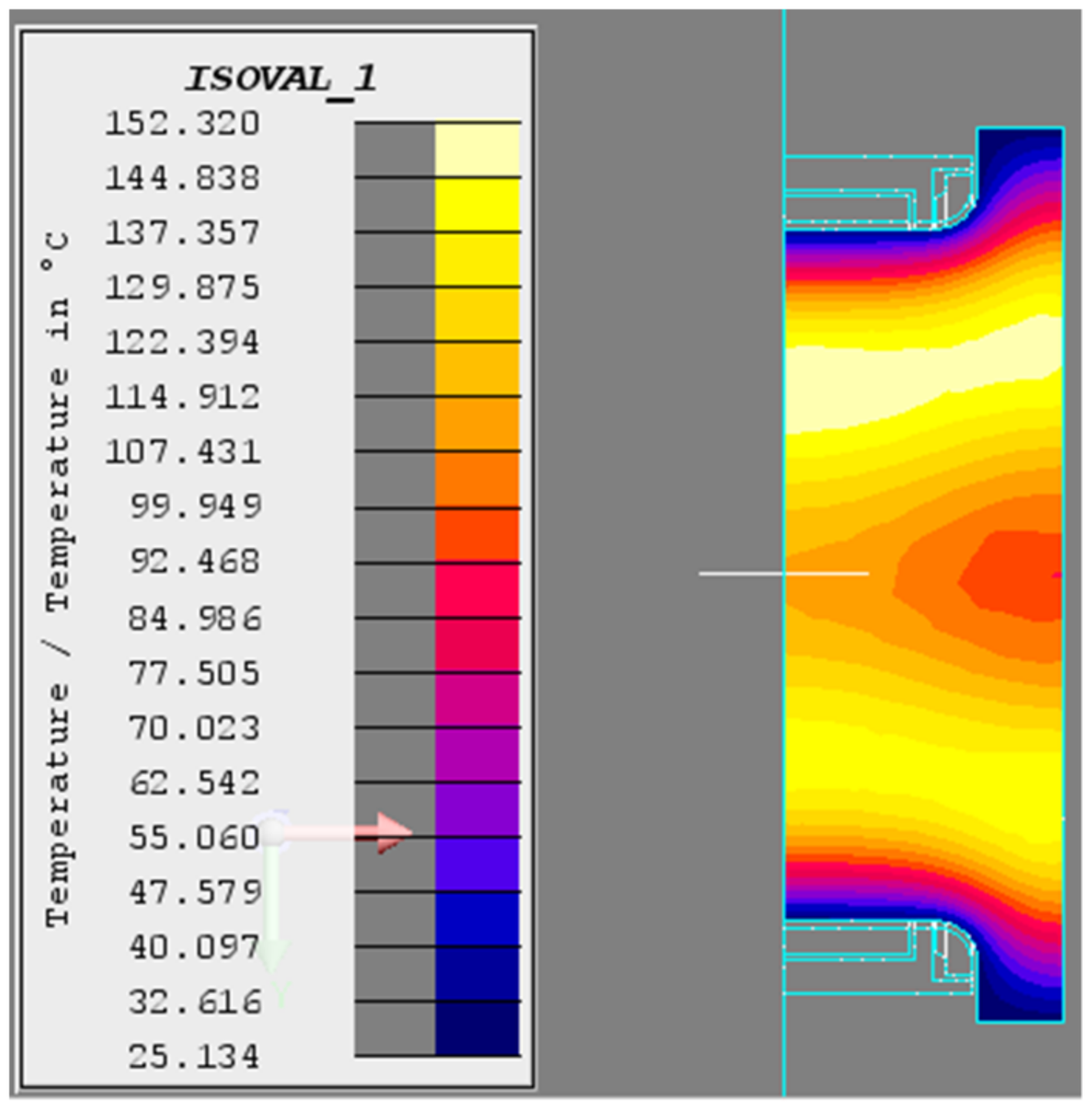
Temperature field of the crankshaft (T = 1 s).
Figure 9.
Temperature field of the crankshaft (T = 4 s).
Figure 10.
Temperature field of the crankshaft (T = 7 s).
Figure 11.
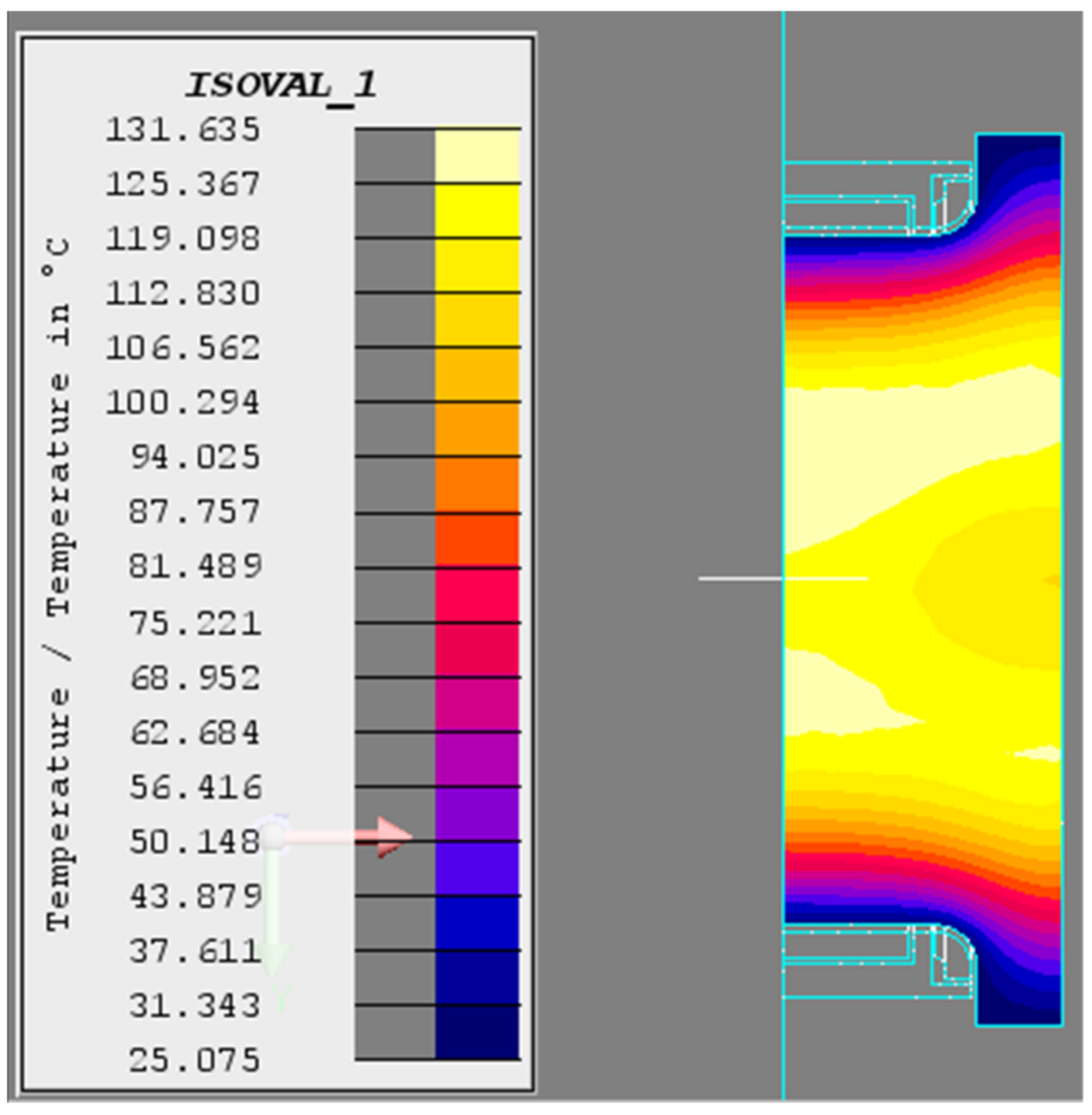
Temperature field of the crankshaft (T = 10 s).
Figure 12.
Displacement boundary conditions of the crankshaft.
Figure 13.
The residual stress field distribution of the crankshaft.
Figure 14.
The finite element model of the crankshaft.
Figure 15.
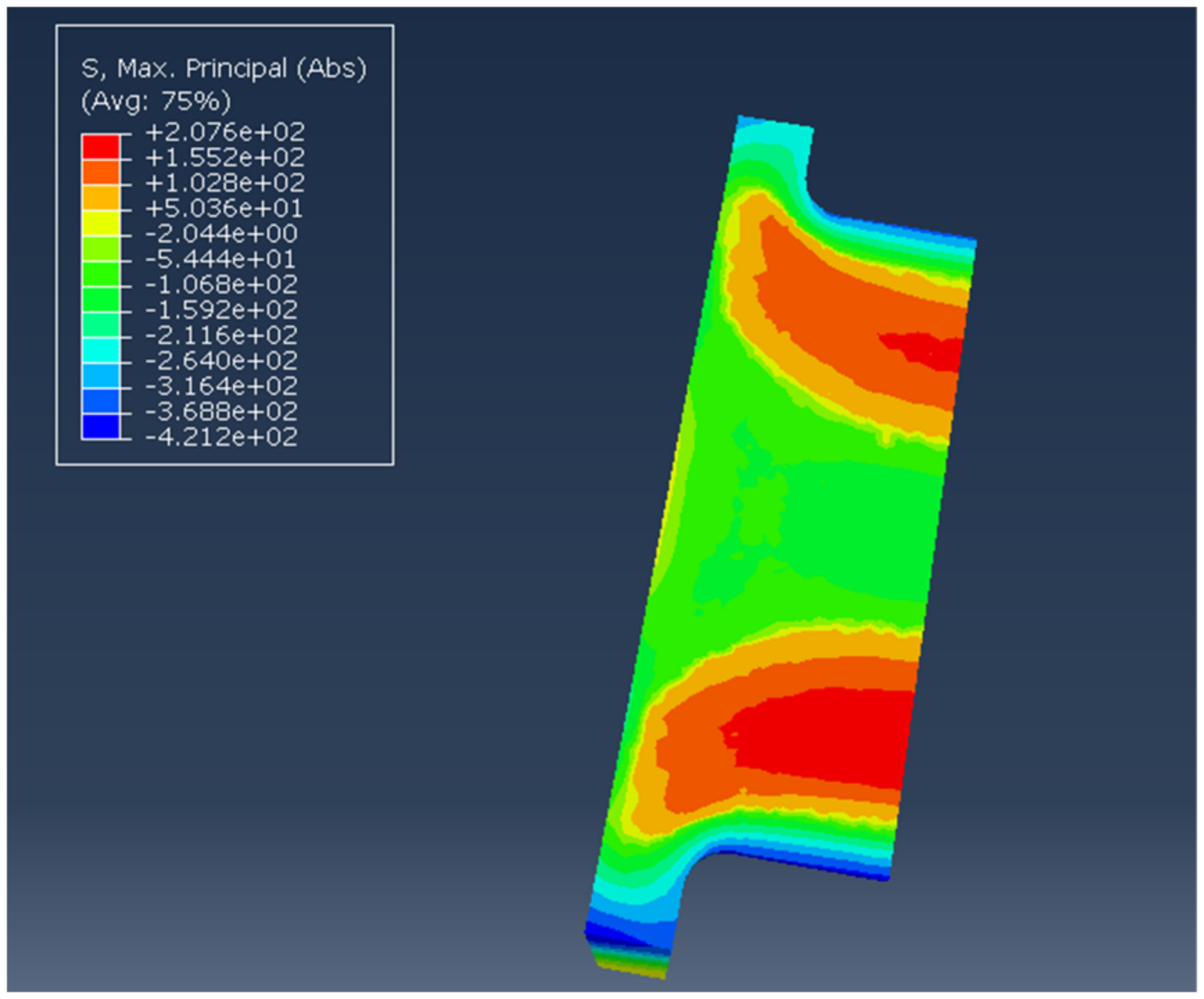
The Von Mises stress distribution of the crankshaft (under the given load).
Figure 16.
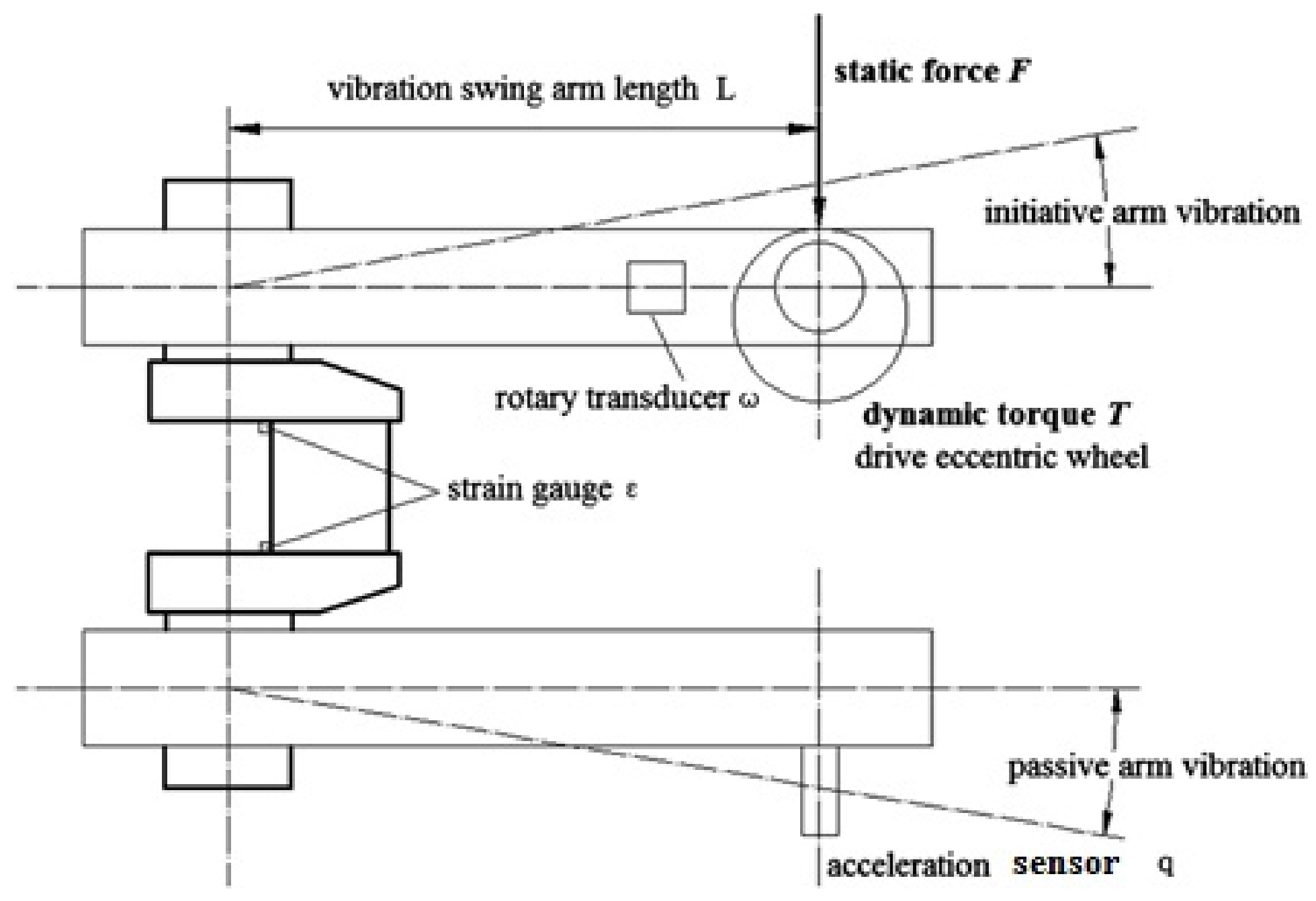
The bending fatigue experiment equipment.
Figure 17.
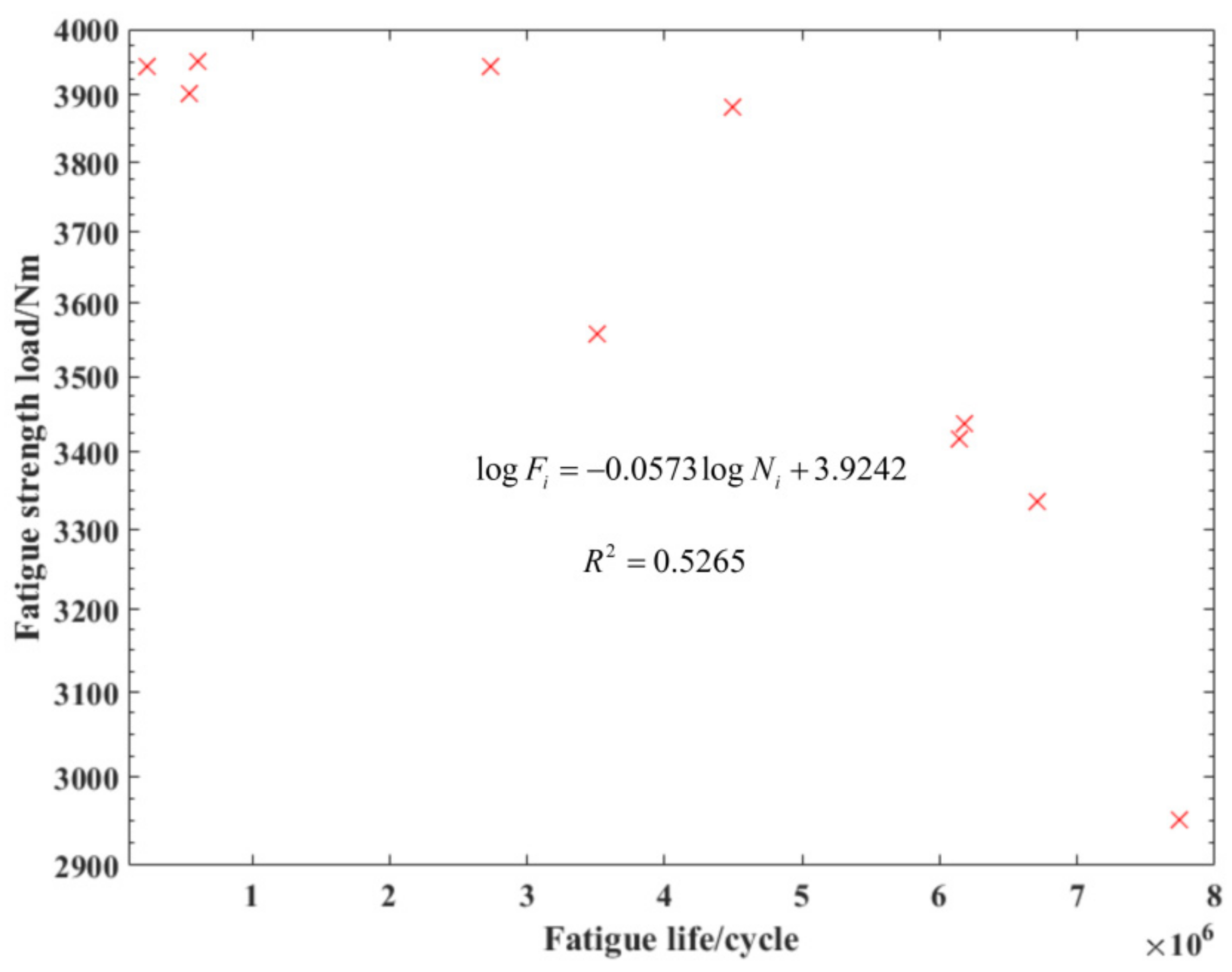
Fatigue test results of the crankshaft.
Table 1.
Basic parameters of the material.
| Temperature (°C) | Relative Permeability (Mur) | Volumetric Heat Capacity (J·m3·°C) | Heat Conductivity (m·°C) | Electrical
Resistivity (Ω·m) |
|---|
| 25 | 200 | 3,685,270 | 38.5 | 1.8 × 10−7 |
| 100 | 194 | 3,795,044 | 35.5 | 2.0 × 10−7 |
| 200 | 188 | 4,085,161 | 35.0 | 3.2 × 10−7 |
| 300 | 181 | 4,390,960 | 33.5 | 4.2 × 10−7 |
| 400 | 170 | 4,759,487 | 32.5 | 5.0 × 10−7 |
| 500 | 158 | 5,237,788 | 31.0 | 6.2 × 10−7 |
| 600 | 141 | 5,842,545 | 28.0 | 7.7 × 10−7 |
| 700 | 100 | 6,845,193 | 24.5 | 9.7 × 10−7 |
| 760 | 1 | 8,429,075 | 20.0 | 1.0 × 10−6 |
| 800 | 1 | 6,241,436 | 21.0 | 1.2 × 10−6 |
| 900 | 1 | 5,363,244 | 23.0 | 1.2 × 10−6 |
| 1000 | 1 | 5,308,357 | 22.5 | 1.2 × 10−6 |
Table 2.
Parameters of the load.
| Detailed Parameter | Value |
|---|
| Current frequency | 8000 Hz |
| Fillet working time | 12 s |
| Crankpin working time | 4 s |
| Current intensity | 350 A |
| Current density (fillet coil) | 9.9 × 107 A/m2 |
| Current density (crankpin coil) | 1.15 × 108 A/m2 |
Table 3.
Parameters of the boundary condition.
| Parameter | Value |
|---|
| Convective heat transfer coefficient | 150.00 W/(m2·°C) |
| Radiative heat transfer coefficient | 0.8 |
| Young’s modulus | 210,000 MPa |
| Poisson’s ratio | 1.35 × 10−6/K |
| Coefficient of thermal expansion | 1.35 |
| Stefan–Boltzmann constant | 5.67 × 10−8 W/(m−2·K−4) |
Table 4.
Stress components of the maximum stress point from different sources.
| Parameter | From the Given Load | From the Residual Stress Field |
|---|
| S11 | 70.5 MPa | −72.5 MPa |
| S22 | 123 MPa | −75.1 MPa |
| S33 | 117 MPa | −323.8 MPa |
| S12 | 1.5 MPa | 75.4 MPa |
| S13 | −2.9 MPa | −1.6 MPa |
| S23 | −118 MPa | 2.03 MPa |
Table 5.
The stress components of the critical plane from the residual stress and the given load.
| Parameter | Residual Stress Field | Given Load |
|---|
| Shear stress | −24.4 MPa | 119.2 MPa |
| Normal stress | −157.3 MPa | −118.6 MPa |
Table 6.
The expressions of the commonly used mean stress models.
| Model Type | Expression | Model Type | Expression |
|---|
| Goodman | | Haigh | |
| Gerbera | | Soderberg | |
Table 7.
Predictions based on some other methods.
| Model Name | Results (N·m) |
|---|
| Goodman | 2494 |
| Haigh | 2956 |
| Soderberg | 2082 |
| Gerbera | 2683 |
Table 8.
The median rank (failure rate) estimation of the fatigue limit load.
| Load Value/N·m | Media Rank |
|---|
| 2893 | 0.067308 |
| 3025 | 0.163462 |
| 3255 | 0.259615 |
| 3280 | 0.355769 |
| 3321 | 0.451923 |
| 3343 | 0.548077 |
| 3352 | 0.644231 |
| 3386 | 0.740385 |
| 3738 | 0.836538 |
| 3759 | 0.932692 |
Table 9.
Errors of the predictions.
| Model Name | Error |
|---|
| Goodman | 32% |
| Haigh | 22.8% |
| Soderberg | 24.8% |
| Gerbera | 43.2% |
| McDiarmid | 1.1% |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).