Abstract
In modern engineering, electromagnetic induction quenching is usually adopted in improving the fatigue performance of steel engine parts such as crankshafts. In order to provide the theoretical basis for the design of the process, correct evaluation of the strengthening effect of this technique is necessary. In this paper, the research aim is the strengthening effect of this technique on a given type of steel crankshaft. First the magnetic-thermal coupling process was simulated by a 3D finite element model to obtain information on the temperature field during the heating and cooling stages. Then the residual stress field after cooling was simulated based on the same model. At last, the fatigue property of this crankshaft was predicted based on the combination of three parameters: the KBM (Kandil–Brown–Miller) multi-axial fatigue model, the residual stress field and the fatigue strength of the material. The experimental results showed that this method can achieve a much more reasonable prediction than the traditional strengthening factor, and thus can be applied in guiding the design of the quenching process.
1. Introduction
In modern engineering applications, for critical steel such as crankshafts, various dynamic loads will be applied to them during the working period [1,2]. Thus, it is necessary to determine the fatigue property of the crankshafts in order to provide a basic safety guarantee [3,4].
In recent years, many studies focused on fatigue properties were and are still being developed. According to the emphases of these jobs, the works can be divided into two types. The first type was focused on analyzing the failure features of the fatigue damaged crankshaft; in this way a corresponding damage mechanism could be proposed for a further improved design. Based on this assumption, Gomes analyzed a broken crankshaft from a maritime V12 diesel engine and modified the geometric profile based on the Soderberg criterion to improve the strength of the part [5]. Wang conducted the fracture surface analysis of a broken crankshaft from a fracturing pump and discovered that the main cause of insufficient fatigue strength may be due to the absence of a surface hardening treatment, and the stress concentration became much higher with the transition of thread root from smooth to sharp fillet [6]. Macek researched the feature of the fracture face and proposed a new fatigue loading parameter that depended on the ratio of maximum stresses and the fatigue life. The results showed that a very good correlation in a 4th degree type of fit can be obtained [7]. Aliakbari analyzed the unusual failure in the crankshaft of the heavy-duty truck engine. The results showed that although the stress field in stress concentration zones with the lubricating hole was much less than the web-crankpin fillet, the presence of cluster impurities, low hardness, and downshifting has caused the growth of primary cracks [8]. Fonte analyzed a failed crankshaft from a diesel motor engine and discovered that the main reason for the failure may not be attributed to the part itself, but to the misalignment of the main journals and a weakness of design close to the gear at the region where the crack was initiated [9]. Infante analyzed a failure crankshaft from a helicopter engine based on various kinds of professional test. The results showed that the crankshaft itself had no obvious surface or inside initiation of the crack. However, the damaged shell bearings applied to the main journal revealed significant damage, which was considered to be the main reason [10]. Karim Aliakbari conducted the fatigue failure analysis of a ductile iron crankshaft based on different experiments and tests. The result showed that the main reasons for the failure may be attributed to the low nodularity of the material and the low crankpin hardness [11]. For the second type, the aim of the research was to discover one or more effective models to predict the fatigue property (such as the fatigue life under a given load condition, the fatigue strength under a specified fatigue life, or the fatigue safety factor) of a given type of crankshaft. Among these works, M. Leitner investigated the fatigue strength of multi-axially loaded gas engine crankshafts and pointed out that the model proposed by Spagnoli provided the best accuracy in both fatigue strength and crack angle [12]. Venicius also applied multi-axial fatigue criteria to motor crankshafts in thermoelectric power plants to provide guidance for the selection of the material in the production [13]. Bulut proposed a new fatigue safety factor model to analyze the fatigue life of the crankshaft from a single cylinder diesel engine under variable forces and speeds; in this way, the comprehensive evaluation of the safety of the crankshaft during the whole working period can be achieved [14]. Khameneh extracted the standard specimens from the crankshaft and examined them with a four-point rotary-bending high-cycle fatigue testing machine; the results indicated that the high-cycle fatigue lifetimes were lower than the S-N curve from the FEMFAT data bank, and that the standard specimens extracted from the crankshaft could be used to consider the manufacturing effects [15]. Singh conducted the fatigue life analysis of a diesel locomotive crankshaft and proposed a 3D finite element model to research the relationship between the fillet radius and the least life of the crankshaft. Based on this, the optimum structural design of the crankshaft can be proposed [16]. Fonseca analyzed the influence of the manufacturing process on the residual stress, which was caused by deep rolling with the combination of the finite element analysis and the corresponding fatigue tests. The research results could provide the theoretical basis for the optimization design of the process [17,18]. Antunes analyzed the finite element meshes for optimal modeling of plasticity-induced crack closure and proposed the analytical expression of the most refined region along the crack propagation area. The results showed that there may be an optimum value for the plasticity-induced crack closure [19]. At present, most of the crankshafts applied in powerful engines are made of high strength steel and are treated with surface strengthening techniques before being arranged in the engine. One of the most commonly used techniques is electromagnetic induction quenching [20,21]. Stephanie compared the mechanical and microstructure property of the 42CrMo steel after electromagnetic induction quenching and conventional heat treatment processes through the standard tensile experiment and pyramid hardness test. The result showed that yield strength and hardness of the steel after electromagnetic induction quenching were a little lower than those of the steel after conventional heat treatment processes, which can be attributed to the size effect [22]. Umberto researched the microstructures and mechanical properties of the hardening layer and proposed that the main influencing factors were the heating and cooling speeds during the electromagnetic induction quenching, as well as the peak value of the temperature [23]. Cajner proposed a 2D simplified axial symmetrical model to conduct the numerical simulation of the electromagnetic induction quenching approach on a 42CrMo steel crankshaft. The experimental verification showed that this model can provide accurate surface hardness and hardness layer depth results [24]. Dietmar applied the adaptive finite element analysis approach in simulating the electromagnetic induction quenching of the gear and got accuracy in the temperature and hardening curve [25]. Dmitry carried out the technological parameter influence analysis of this approach and proposed a corresponding model to accurately simulate the process [26]. Akram proposed the novel alternate magnetic field treatments in EN8 steel and discovered that this approach could improve the wear resistance and reduce the coefficient of friction of the material, which could be explained by the increase of the compressive residual stress and the microhardness. This method can also be applied in fatigue property research of similar metal materials [27]. Mohan proposed a new optimal design method based on a satisfactory function, which was established during the electromagnetic induction quenching process [28].
According to previous research, this approach can improve the fatigue strength of a steel crankshaft by generating the compressive residual stress at the stress concentrate surface. However, the comprehensive evaluation of the strengthening effect of this approach has rarely been studied. In modern engineering applications, this effect is usually evaluated by the strengthening factor. The definition of this parameter can be expressed as [29]:
where is the strengthening factor of a given surface treatment approach, and are the median values of the fatigue limit load of the crankshaft after and before the surface treatment, respectively. This parameter can provide an easy means to evaluate the strengthening effect of this approach, but according to previous studies, the key technological parameters during the quenching process (for example, the frequency of the electric current, the durations of the heating and cooling stage, the element of the cooling liquid and so on) will affect the temperature field and the residual stress field obviously. As a result of this, the strengthening effect of the approach will also be affected. How to directly predict the fatigue strength of a given type of treated part based on the known fabrication process is a problem that is yet to be solved.
In previous studies, we evaluated the strengthening effect of this technique by considering the residual stress as the mean stress and applied corresponding mean stress models in the prediction of the fatigue limit load of a given type of steel crankshaft [30]. The theoretical foundation of this approach is that both the mean stress and the alternating stress are uniaxial and go in the same direction. For the parts with complicated shapes, the state of the alternating stress is usually multi-axial, even though the load applied to it are of a uniaxial type [31]. This situation makes the application of the mean stress models unreasonable in some degrees.
In this paper, a new fatigue strength prediction method of the quenched crankshaft was proposed based on multi-physic coupling numerical simulation approaches. First, a 3D finite element model was built to carry out the magnetic-thermal coupling process during the heating-up stage. In this way, the evolutionary process of the temperature field during this stage can be presented. Next, the thermo-mechanical coupling process during the cooling stage was also proposed based on the same mesh model to obtain the residual stress field at the end of the stage. In the end, the fatigue limit load of this quenched crankshaft was predicted based on a combination of three elements: the KBM multi-axial fatigue model, the residual stress field and the fatigue strength of the material. The subsequent experiment results showed that compared with the traditional strengthening factor, this method can provide an obviously higher accuracy in this application, and is thus valuable and can be popularized in the design of key technological parameters during the quenching process.
2. Materials and Methods
2.1. Research Object and Material
Figure 1 shows the electromagnetic induction quenching equipment (Tianrun crankshaft Co., Ltd., Weifang, China). According to this photograph, the whole equipment can be divided into three parts: the steel crankshaft at the center of the equipment, the induction coils around the crankshaft, and the magnetizer between them. During the heating-up stage, an intermediate or high frequency alternating current will pass through the coils. In this way, the surface temperature of the steel crankshaft will rise rapidly due to the skin effect. Then, the cooling liquid is sprayed to the surface to cool down the surface temperature and raise the inner temperature. In the end all the equipment is placed in the air condition until it is completely cooled. In this way, different types of residual stress will be generated in different areas.
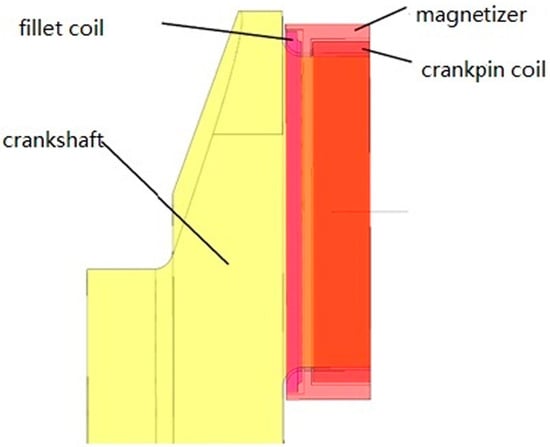
Figure 1.
The induction coils and the crankshaft.
The material of the crankshaft in this paper is 42CrMo. The chemical component of this material is shown in Table 1. The information is provided by the manufacturer and fulfills the standard demands.

Table 1.
The chemical component of the material 42CrMo.
2.2. The Prediction Method
At present, the strengthening effect of the electromagnetic induction quenching approach is usually considered to be achieved by generating compressive residual stress at the stress concentration point. On the other hand, according to previous study, the fatigue damage mode of the crankshaft under an alternating bending moment is shear fatigue failure. Based on the two preconditions above, the fatigue property of a quenched steel crankshaft depends on the combination of the equivalent stress–strain state caused by the residual stress field and the alternating stress field. The relationship can be expressed as:
In this equation, and are the equivalent shear strains caused by the residual stress field and the alternating stress field, respectively; and is the total value of the equivalent shear strain. According to the fatigue damage theory, the fatigue property of a given component depends on two parameters: the equivalent stress or strain state based on a proposed model and the fatigue property of the material. In other words, for two components made by the same material under the fatigue limit condition, the equivalent stress or strain of them should be the same if the fatigue damage models were the same. Therefore, in this paper, the equivalent strain of the quenched steel crankshaft under the fatigue limit load is the same as that in the material under the fatigue strength.
For the left side of the equation, the stress and strain information caused by the residual stress field can also be provided through a finite element analysis. In this way, the fatigue limit load prediction can be expressed as:
In this equation, and are the predictions of the fatigue limit load and a known given load applied on the crankshaft, respectively; and is the equivalent strain caused by the given load.
2.3. The Experiment Method
In order to check the accuracy of the prediction, corresponding experiment verification is necessary. Figure 2 shows the bending fatigue test bed that consists of the electromagnetic vibration exciter, the master arm, the slave arm, the acceleration transducer, and the foundation bed. The crankshaft and the connected arms are vertically supported by springs, and the excitation force is generated by rotating the eccentric with the motor. In this way, a cyclic bending moment is applied on the crankshaft for fatigue testing. During the experiment process, a crack is expected to appear at the fillet of the crankshaft and the stiffness of the system decreases. As a result of this, the responsive acceleration and the amplitude of the load may increase if the frequency of the exciter remains unchanged. To avoid this unwanted situation, the rotation speed of the exciter will decrease accordingly. When the speed decreases to a certain level, the crankshaft is considered broken [32,33]. In this paper, the value of the decrement of the rotate speed is 60 rpm. The serial number of the experiment standard used in this paper is QC-T637-2000.

Figure 2.
The bending fatigue experiment equipment.
Based on this equipment and the analysis method above, the whole research process of this paper can be determined. Detailed information is shown in Figure 3.
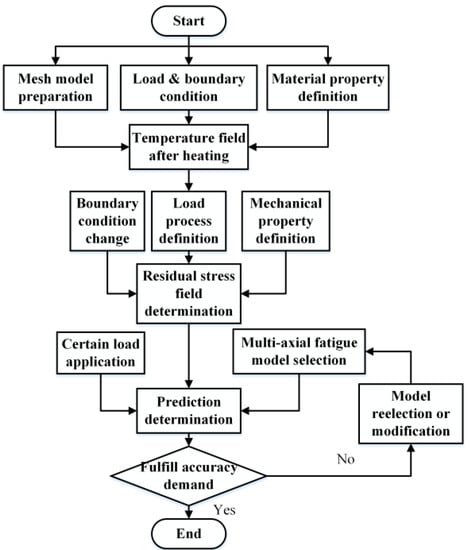
Figure 3.
The research process of the paper.
3. Results
3.1. Heating Stage Analysis
3.1.1. Mesh Model and Material Parameter
In this paper, the research is carried out on a steel crankshaft from a six-cylinder diesel engine. Figure 4 shows the structure features of this crankshaft. From this figure, it can be discovered that each of the six crankpins has the same structure. In addition, during the course of the induction, all of the six crankpins were selected to be surrounded by the coil for heating and cooling based on the same process. In order to reduce the computation amount, a crankpin is selected to replace the whole crankshaft for the analysis in this paper; the result is shown in Figure 5.
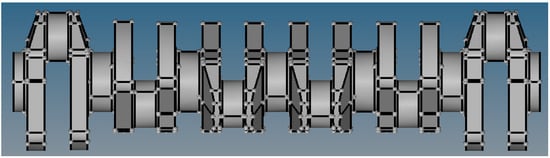
Figure 4.
The structure feature of the six-cylinder engine crankshaft.
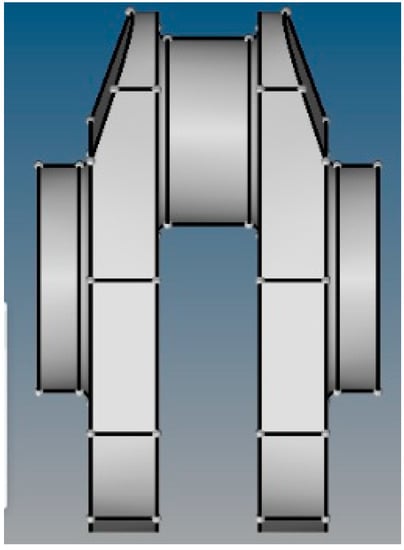
Figure 5.
The crankpin of the crankshaft.
As shown in Figure 5, the crankpin has a bilateral symmetry in both the front–back and the left–right directions. During the quenching process, the coil around the crankpin is also symmetrical in these directions. Therefore, the whole crankpin and the coil can be simplified to a quarter model. Figure 6 shows the finite element model of this analysis.
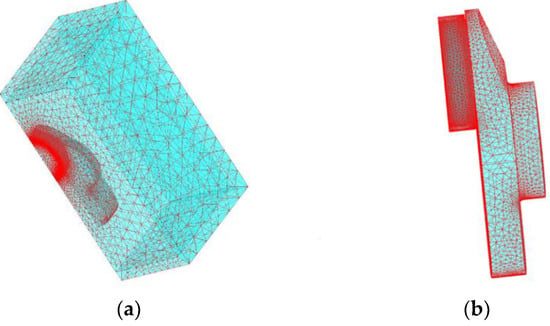
Figure 6.
The finite element model of the crankshaft; (a) the quarter model in the far field; (b) the quarter model of the crankpin and the coil.
The Figure contains 290,074 nodes and 207,423 elements. In addition, the crankpin was placed in a far field, which can fulfil the demands of the electromagnetic field dissipation. The type of element applied in this model is tetrahedron with 10 nodes. Among the whole model, 61,376 elements belong to the crankpin and the coil. The whole model was built based on the software Flux.
3.1.2. Load and Boundary Conditions
During the heating stage, the heat source is the eddy flow under the surface of the crankshaft. The function of the boundary condition at this stage can be expressed as [30]:
As shown in this equation, h is the equivalent heat transfer coefficient, λ is the thermal conductivity, TS is the temperature of the crankshaft surface, and Tf is the temperature of the air. During the heating stage, the main styles of heat transfer on the surface are convective and radiative heat transfer. The corresponding transfer coefficients are 100 W/(m2∙°C) and 0.8. The symmetrically cut planes are the thermal insulation.
In this paper, the load during this process is just the high frequency alternating current inside the induction coils. The electric current density and time length in different coils are not the same. For the fillet coil, the current density is 1.0 × 108 A/m2 and the heating time is 9 s. While for the crankpin, the values of these two parameters are 6.5 × 107 A/m2 and 3 s.
3.1.3. Temperature Field Results
For this high strength steel, some of the mechanical properties will change with the temperature. The detailed information is shown in Table 2.

Table 2.
Material properties of the crankshaft.
Based on the material properties, the load and boundary conditions, and the mesh model above, the magnetic–thermal coupling process can be carried out based on the above mesh model. The corresponding results are shown in Figure 7 and Figure 8.
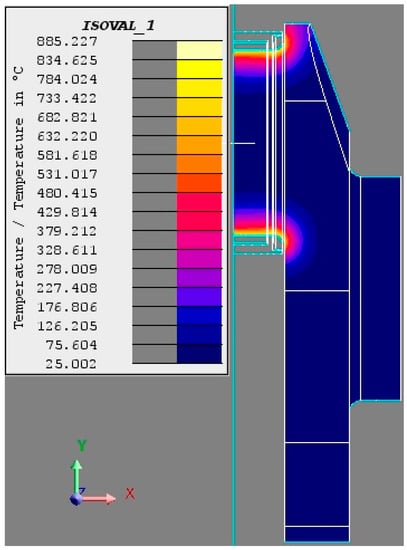
Figure 7.
The evolution process of the temperature field during the heating stage (T = 3 s).
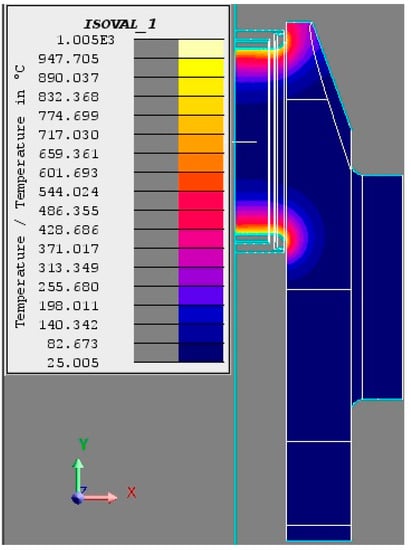
Figure 8.
The evolution process of the temperature field during the heating stage (T = 9 s).
As shown in the figures above, it can be discovered easily that the heating temperature and depth has increased steadily during the heating stage. In addition, the heating depth of the fillet is much larger than that of the crankpin at the early stage (t = 3 s). The primary cause of this phenomenon is the longer effective heating time of the former area. With the passage of heating time, the surface temperature has gradually increased to the austenite transformation point. In this way, the surface austenite layer can be generated. At the end of the heating stage, the heating depth of both the fillet and the crankpin are nearly the same. This can be explained by the longer effective heating time and the heat capacity of the fillet. After this heating process, the surface temperature has increased to 1005 °C.
3.2. Cooling Process Analysis
According to the standard process flow, the cooling liquid is sprayed on the surface of the hot steel crankshaft after the heating stage. This process lasts 10 s. As a result of this, the surface temperature of the crankshaft will drop down rapidly and the inner temperature will rise by some degrees. In this way, the residual stress will occur based on the temperature field after cooling. In addition, the heat transfer during this stage happens between the steel crankshaft and the cooling liquid. The convective heat transfer coefficient between them is 15,000 W/(m2∙°C). Based on these parameters and the temperature field obtained in the previous step, the evolution process of the temperature field during the cooling stage can be carried out based on the same mesh model. Figure 9 shows the cooling result of this crankshaft. It can be discovered that the location of the maximum temperature point has moved from the surface to the central part of the crankpin. The value of the maximum temperature is 212 °C.
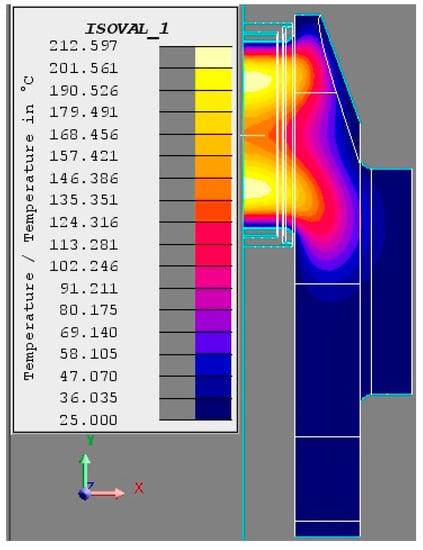
Figure 9.
The temperature field after liquid cooling.
After liquid cooling, the whole crankshaft will be placed in air conditions until completely cool. During this stage, the temperature field after rapid heating and cooling will create a corresponding internal stress to the residual stress. In other words, the evolution process of the temperature field after liquid cooling is just the thermal load of the residual stress. On the other hand, for the metal solid parts, such as crankshafts, there are corresponding geometry constraints which will affect the transformation results caused by the thermal expansion. Figure 10 shows the finite element model during this thermo–mechanical coupling process. For this model, the symmetrical freedom of the nodes on the symmetrical cut planes is fixed. In this way, an evolution process of the internal stress can be carried out. The whole model was built based on the software Abaqus. The final result is shown in Figure 11.
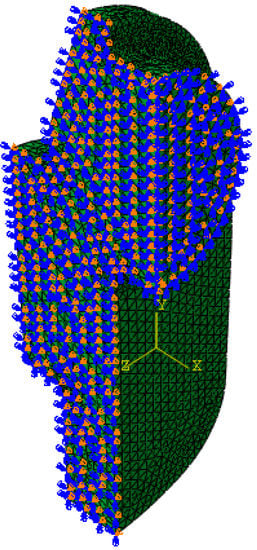
Figure 10.
Displacement boundary conditions of the crankshaft for the residual stress analysis.
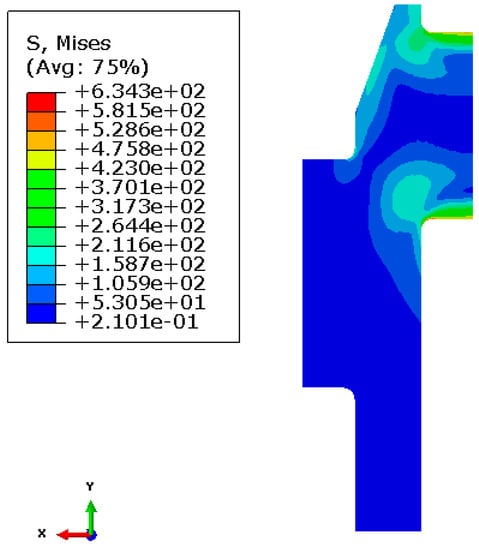
Figure 11.
The residual stress field of the crankshaft.
3.3. Prediction and Experimental Verification
According to the theory of elastic mechanics, for the parts with complicated shapes, the state of the alternating stress is usually multi-axial, even though the load applied to it is of a uniaxial type. As a matter of experience based on our previous study, the KBM multi-axial fatigue model is an effective choice in researching the high cycle bending fatigue properties of the crankshaft. The expression of this model in this research field is shown as follows [34]:
In this equation, and are the maximum shear strain and the amplitude of the normal strain in the critical plane, is the normal stress in this plane, is the yield strength of the material, is the fatigue life of the component, and the other parameters are all material constants. The values of the parameters are shown in Table 3.

Table 3.
The model parameters of the KBM model.
As shown in Table 3, the values of the model parameters are from the fatigue analysis software Femfat.
At present, the definition of the fatigue limit load of the steel crankshaft is defined according to the fatigue life of 107. In this paper, the shear fatigue strength of the material under this condition is 226 MPa, and the shear modulus of the material is 80,000 MPa.
The key parameters of the model such as the direction of the critical plane, and the shear and normal stress strain on this plane can be proposed by a coordinate transition method. The detailed process of this method is shown in Figure 12.
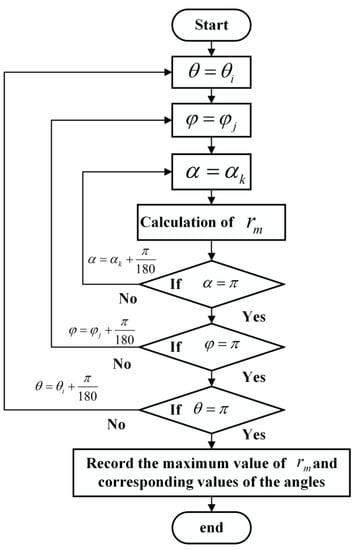
Figure 12.
The process of the coordinate transition method.
As shown in Figure 12, the substantive theory of this approach is to compare the values of the alternating shear strain from different planes. In this paper, the strain tensor of the crankshaft under the bending moment load is also proposed by the finite element method. The corresponding finite element model is shown in Figure 13.
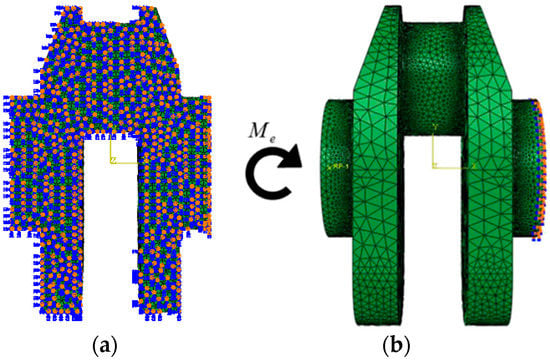
Figure 13.
The finite element model of the crankpin. (a) The boundary condition on the symmetrical plane; (b) the load and boundary condition on the right face.
As shown in Figure 13, in this model a bending moment is applied on a node that is coupled with the left face of the crankshaft. The right face of the crankshaft is fixed [34]. In order to reduce the computation amount, this model is composed of half of the crankpin with the corresponding freedoms on the plane of symmetry also being fixed. Based on this model, the stress and strain conditions under a given bending moment (1000 N·m) can be exhibited. The result is shown in Figure 14 and Table 4.
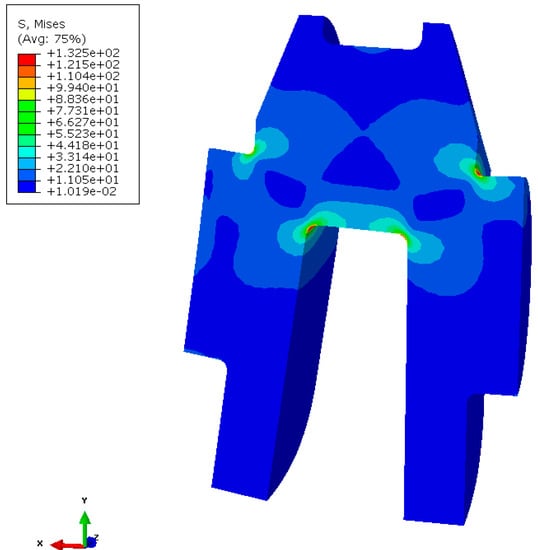
Figure 14.
The Von Mises stress distribution of the crankshaft (under the given load).

Table 4.
The stress and strain components of the crankshaft (under the given load).
As shown in Figure 14, the maximum stress point of the crankshaft under this given load is located at the fillet of the crankshaft, which is in accordance with the fatigue damage point of the crankshaft. Table 5 shows the stress and strain components from the maximum stress point. In addition, the Von mises stress at the same point from the residual stress field is 494 MPa. Based on these parameters and the coordinate transition method, the shear and normal stress and strain from different sources in the critical plane can be determined. Corresponding results are shown in Table 5.

Table 5.
The stress and strain components of the critical plane.
Based on the parameters and the KBM multi-axial fatigue model, the fatigue limit load and, according to previous studies, the stress ratio of the bending fatigue experiment, is −1, so the expression of the prediction can be proposed as:
Based on the professional computing software matlab, the value of the fatigue limit load of this crankshaft can be determined to be 4825 N·m.
As mentioned in the introduction part, in modern engineering applications, the strengthening effect of the commonly used surface treatment techniques are usually evaluated by the strengthening factor. For the electromagnetic induction quenching, this parameter is about 1.5. In addition, the fatigue strength of the material under this fatigue life is 396 MPa. Therefore, the prediction based on this parameter can be expressed as:
In a comparison between Equations (5) and (6), it is obvious that the predictions based on these two approaches are quite different from each other. In order to make a comprehensive comparison, it is necessary to conduct a professional experimental verification. The experimental results are shown in Table 6.

Table 6.
The fatigue test results of the crankshaft.
As shown in Table 6, the sample size of this experiment is 10. At present, most of the engineering equipment must be able to work normally during the designed working period [35,36]. In addition, the service life of a crankshaft is limited to a certain number of cycles depending on the demand of the travelling distance. As a result of this, compared with the common fatigue property evaluation parameter (usually the fatigue life under a given load) [37,38], it is more important to correctly evaluate the high-cycle fatigue load of a crankshaft under a specified fatigue life [39,40]. According to previous studies, the SAFL (Statistical Analysis for Fatigue Limit) approach is considered to be an effective method for analyzing the distribution property of the fatigue limit load [41]. In addition, the fatigue limit load of the crankshaft obeys normal distribution. As a result of this, the fatigue limit load of this crankshaft under a 50% survival rate is 5045 N·m.
As shown in Figure 15, an obvious conclusion can be discovered that the fitting results based on the Gaussian distribution function is quite near to the original experimental results. For the strengthening factor, the error between the prediction and the experimental result is 11.1%. For the KBM model, the error is 4.3%. This comparison clearly shows the superiority of the model proposed in this paper in the crankshaft fatigue limit load prediction. The main reason for this phenomenon may be attributed to the multi-axial fatigue property of the part. As mentioned in the introduction, the fatigue damage type of the steel crankshaft under the alternating bending moment is shear fatigue damage. While the KBM model is considered to be effective in researching the shear fatigue damage component, this model is more suitable for analyzing the fatigue property of such steel crankshafts.
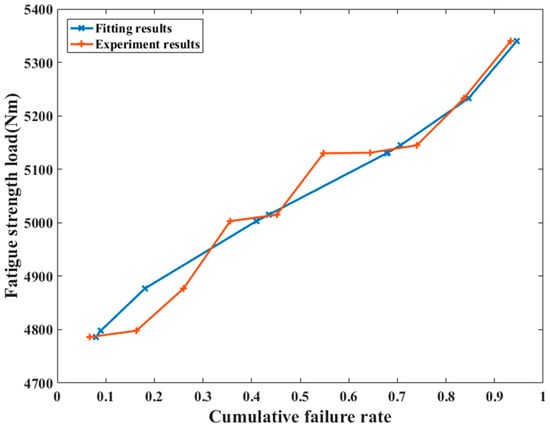
Figure 15.
The fitting results of the fatigue limit load based on the Gaussian distribution function.
On the other hand, according to previous studies, the strengthening effect of this approach was influenced by the technological parameters (such as the frequency of the current, the coolant composition, and so on). Therefore, research into the applicability of this method in other kinds of steel crankshafts is still needed.
4. Conclusions and Further Work Plans
In this paper, a new fatigue property prediction approach for quenched metal crankshafts was proposed. First, a quarter model composed of the crankpin was built to simulate the magnetic–thermal coupling process during the heating and cooling stages. Next, the residual stress field was conducted by the subsequent thermal–mechanical coupling analysis. Finally, the fatigue limit load prediction of the treated crankshaft was achieved based on three factors: the parameters obtained above, the KBM multi-axial fatigue damage model, and the material property. The results show that this manufacturing procedure can generate uniform temperature fields at the surface of the crankpin area during the heating stage, which is beneficial for the forming of the uniform layer. In addition, compared to the commonly used strengthening factor, the KBM multi-axial fatigue model can provide a high enough accuracy in predicting the fatigue limit load of the quenched crankshaft, which makes this model valuable in guiding the design of the manufacturing procedure.
During our study, we discovered that the levels of the technological parameters during the quenching approach (such as the frequency of the current, the heating time of the coil and so on) would affect the temperature field, as well as the residual stress field. In addition, for the purpose of an anti-fatigue design, high residual stress is useful, especially at the fillet location. For the wear-resistant design, a uniform temperature field is helpful in the generation of the surface layer. Therefore, in our further work, we will focus on the multi-objective optimization design method in this field.
Author Contributions
Conceptualization, S.S.; methodology, S.S.; software, S.S.; validation, S.S.; formal analysis, S.S.; investigation, S.S.; resources, S.S.; data curation, S.S.; writing—original draft preparation, S.S.; writing—review and editing, X.G.; visualization, none.; supervision, none.; project administration, X.X.; funding acquisition, X.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data generated or analyzed during this study are included in this published article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| the strengthening factor of a given surface treatment approach | |
| the median value of the fatigue limit load of the crankshaft after the surface treatment | |
| the median value of the fatigue limit load of the crankshaft before the surface treatment | |
| the equivalent shear strain caused by the residual stress field | |
| the equivalent shear strain caused by the alternating stress field | |
| the total amount of the equivalent shear strain | |
| the applied bending moment load on the crankshaft | |
| the prediction of the fatigue limit load | |
| the equivalent heat transfer coefficient | |
| the thermal conductivity | |
| the temperature of the crankshaft surface | |
| the temperature of the crankshaft surface | |
| the maximum shear strain in the critical plane | |
| the amplitude of the normal strain in the critical plane | |
| the normal stress in the critical plane | |
| the yield strength of the material | |
| the fatigue life of the component |
References
- Jie, T.; Tong, J.; Shi, L. Differential steering control of four-wheel independent-drive electric vehicles. Energies 2018, 11, 2892. [Google Scholar]
- Tian, J.; Wang, Q.; Ding, J.; Wang, Y.; Ma, Z. Integrated control with DYC and DSS for 4wid electric vehicles. IEEE Access. 2019, 7, 124077–124086. [Google Scholar] [CrossRef]
- Valjan, V.; Raspudic, V. Stress and Fatigue Analysis of a Single Cylinder Engine Crankshaft. In Proceedings of the 31st DAAAM International Symposium on Intelligent Manufacturing and Automation, Mostar, Bosnia and Herzegovina, 19–25 October 2020; pp. 692–700. [Google Scholar]
- Marchesi, T.; Trindade, W. Use of Staircase Method to Validate a New Design of Engine Pulley; 2019 SAE Brasil Congress & Exhibition; SAE International: Warrendale, PA, USA, 2020. [Google Scholar]
- Gomes, J.; Gaivotab, N.; Martinsc, R.F. Failure analysis of crankshafts used in maritime V12 diesel engines. Eng. Fail. Anal. 2018, 92, 466–479. [Google Scholar] [CrossRef]
- Wang, H.; Yang, S.; Han, L.; Fan, H.; Jiang, Q. Failure analysis of crankshaft of fracturing pump. Eng. Fail. Anal. 2020, 109, 104378. [Google Scholar] [CrossRef]
- Macek, W. Fracture areas quantitative investigating of bending-torsion fatigued low-alloy high-strength steel. Metals 2021, 11, 1620. [Google Scholar] [CrossRef]
- Aliakbari, K.; Imanparast, M.; Nejad, R.M. Microstructure and fatigue fracture mechanism for a heavy-duty truck diesel engine crankshaft. Sci. Iran. 2019, 26, 3313–3324. [Google Scholar]
- Fonte, M.; Infante, V.; Reis, L.; Freitas, M. Failure mode analysis of a diesel motor crankshaft. Eng. Fail. Anal. 2017, 82, 681–686. [Google Scholar] [CrossRef]
- Infante, V.; Freitas, M.; Fonte, M. Failure analysis of a crankshaft of a helicopter engine. Eng. Fail. Anal. 2019, 100, 49–59. [Google Scholar] [CrossRef]
- Aliakbari, K. Failure analysis of ductile iron crankshaft in four-cylinder diesel engine. Int. J. Met. 2021, 5, 1223–1237. [Google Scholar] [CrossRef]
- Leitner, M.; Tuncali, Z.; Steiner, R. Multiaxial fatigue strength assessment of electroslag remelted 50CrMo4 steel crankshafts. Int. J. Fatigue 2017, 100, 159–175. [Google Scholar] [CrossRef]
- Pereira, M.V.S.; Darwish, F.A.; Feiferis, A.; Lima Castro, T.; Palin-Luc, T.; Morel, F.; Carpinteri, A. Multiaxial fatigue criteria applied to motor crankshaft in thermoelectric power plants. MATEC Web Conf. 2019, 300, 04003. [Google Scholar] [CrossRef] [Green Version]
- Bulut, M.; Cihan, M.; Temizer, L. Fatigue Life and Stress Analysis of the crankshaft of a single cylinder diesel engine under variable forces and speeds. Mater. Test. 2021, 63, 770–777. [Google Scholar] [CrossRef]
- Khameneh, M.J.; Azadi, M. Evaluation of high-cycle bending fatigue and fracture behaviors in EN-GJS700-2 ductile cast iron of crankshafts. Eng. Fail. Anal. 2018, 85, 189–200. [Google Scholar] [CrossRef]
- Singh, T.; Sengar, S.S. Least life analysis of diesel locomotive crankshaft. Mater. Today Proc. 2021, 44, 4369–4374. [Google Scholar] [CrossRef]
- Fonseca, L.G.A.; de Faria, A.R.; Batalha, M.H.F.; Jahed, H. Manufacturing processes’ role over the residual stress state evolution of crankshafts. Int. J. Adv. Manuf. Technol. 2021, 112, 2425–2433. [Google Scholar] [CrossRef]
- Fonseca, L.G.A.; Cantisano, A.; Faria, A.R. Numerical modelling of deep rolling influence over crankshaft bending and correlation with fatigue behavior. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 672–683. [Google Scholar] [CrossRef]
- Antunes, F.V.; Camas, D.; Correia, L.; Branco, R. Finite element meshes for optimal modelling of plasticity induced crack closure. Eng. Fract. Mech. 2015, 142, 184–200. [Google Scholar] [CrossRef] [Green Version]
- Asadzadeh, M.Z.; Raninger, P.; Prevedel, P.; Ecker, W.; Mücke, M. Inverse Model for the Control of Induction Heat Treat-ments. Metals 2019, 12, 2826. [Google Scholar]
- Prochazka, J.; Pokorny, Z.; Dobrocky, D. Service behavior of nitride layers of steels for military applications. Coating 2020, 10, 975. [Google Scholar] [CrossRef]
- Sackl, S.; Leitner, H.; Zuber, M.; Clemens, H.; Primig, S. Induction hardening vs conventional hardening of a heat treatable steel. Metall. Mater. Trans. A 2014, 45, 5657–5666. [Google Scholar] [CrossRef]
- Prisco, U. Case microstructure in induction surface hardening of steels: An overview. Int. J. Adv. Manuf. Technol. 2018, 98, 2619–2637. [Google Scholar] [CrossRef]
- Cajner, F.; Smoljan, B.; Landek, D. Computer simulation of induction hardening. J. Mater. Process. Tech. 2004, 157, 55–60. [Google Scholar] [CrossRef]
- Homberg, D.; Liu, Q. Simulation of multi-frequency-induction-hardening including phase transitions and mechanical effects. Finite Elem. Anal. Des. 2016, 121, 86–100. [Google Scholar] [CrossRef]
- Ivanov, D.; Leif, M. Simulation of stress and strain for induction-hardening applications. J. Mater. Eng. Perform. 2013, 22, 3258–3268. [Google Scholar] [CrossRef] [Green Version]
- Akram, S.; Babutskyi, A.; Chrysanthou, A.; Montalvão, D.; Whiting, M.J.; Modi, O.P. Improvement of the wear resistance of EN8 steel by application of alternating magnetic field treatment. Wear 2021, 484–485, 203926. [Google Scholar] [CrossRef]
- Misra, M.K.; Bhattacharya, B.; Singh, O.; Chatterjee, A. Multi response optimization of induction hardening process -a new approach. IFAC Proc. Vol. 2014, 47, 862–869. [Google Scholar] [CrossRef]
- Sun, S. A new stress field intensity model and its application in component high cycle fatigue research. PLoS ONE 2020, 15, e0235323. [Google Scholar] [CrossRef]
- Sun, S.S.; Zhang, X.; Wu, C.; Wan, M.; Zhao, F. Crankshaft high cycle bending fatigue research based on the simulation of electromagnetic induction quenching and the mean stress effect. Eng. Fail. Anal. 2021, 122, 105214. [Google Scholar]
- Sun, S.S.; Yu, X.-L.; Li, J. A study on the equivalent fatigue of crankshaft structure based on the theory of multi-axial fatigue. Automot. Eng. 2016, 38, 1001–1005. [Google Scholar]
- Xun, Z.; Xiaoli, Y. Failure criterion in resonant bending fatigue test for crankshafts. Chin. Intern. Combust. Engine Eng. 2007, 28, 45–47. [Google Scholar]
- Zhou, X.; Yu, X. Error analysis and load calibration technique investigation of resonant loading fatigue test for crankshaft. Trans. Chin. Soc. Agric. Mach. 2007, 4, 35–38. [Google Scholar]
- Brown, M.W.; Miller, K.J. A theory for fatigue failure under multiaxial stress-strain conditions. ARCHIVE: Proc. Inst. Mech. Eng. 1973, 187, 1847–1982. [Google Scholar]
- Zhang, Y.; Wang, A. Remaining useful life prediction of rolling bearings using electrostatic monitoring based on two-stage information fusion stochastic filtering. Math. Probl. Eng. 2020, 2020, 2153235. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, Y.; Yu, Y. Joint estimation of SOC of lithium battery based on dual kalman filter. Processes 2021, 9, 1412. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, Y.; Yu, Y. Lithium-ion battery SOC estimation based on adaptive forgetting factor least squares online identification and unscented kalman filter. Mathematics 2021, 9, 1733. [Google Scholar] [CrossRef]
- Zhou, W.; Zheng, Y.; Pan, Z.; Lu, Q. Review on the Battery model and SOC estimation method. Processes 2020, 9, 1685. [Google Scholar] [CrossRef]
- Chang, C.; Zheng, Y.; Sun, W.; Ma, Z. LPV estimation of SOC based on electricity conversion and hysteresis characteristic. J. Energy Eng. 2019, 145, 04019026. [Google Scholar] [CrossRef]
- Chang, C.; Zheng, Y.; Yu, Y. Estimation for battery state of charge based on temperature effect and frac-tional extended kalman filter. Energies 2020, 13, 5947. [Google Scholar] [CrossRef]
- Chen, X.; Yu, X.; Hu, R.; Li, J. Statistical distribution of crankshaft fatigue: Experiment and modeling. Eng. Fail. Anal. 2014, 42, 210–220. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).