Predicting the Irradiation Swelling of Austenitic and Ferritic/Martensitic Steels, Based on the Coupled Model of Machine Learning and Rate Theory
Abstract
1. Introduction
2. Materials and Methods
2.1. Machine Learning of Steady-State Swelling Onset Dose
2.2. Rate Theory of the Swelling Behavior after Incubation Period
3. Results
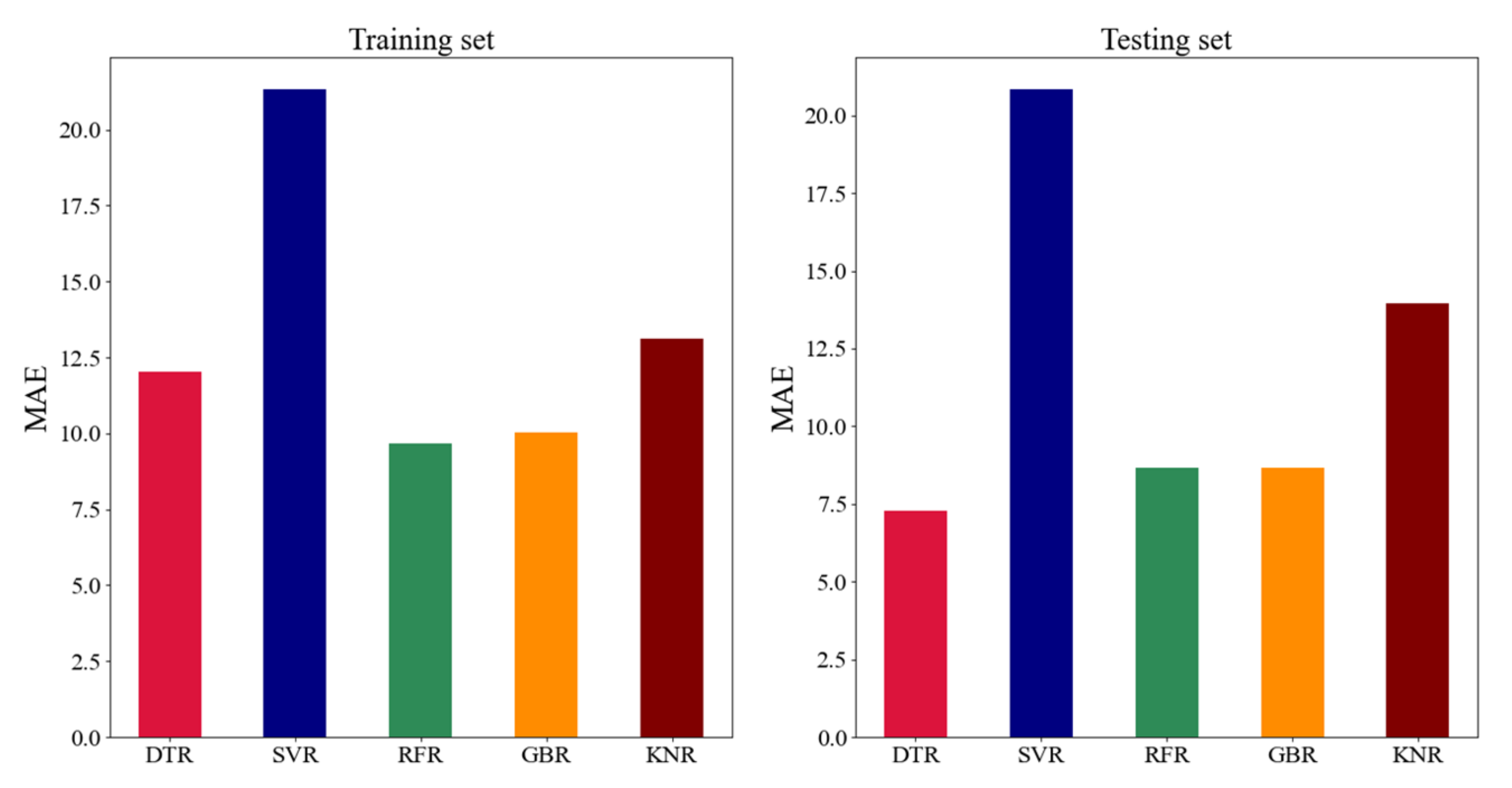
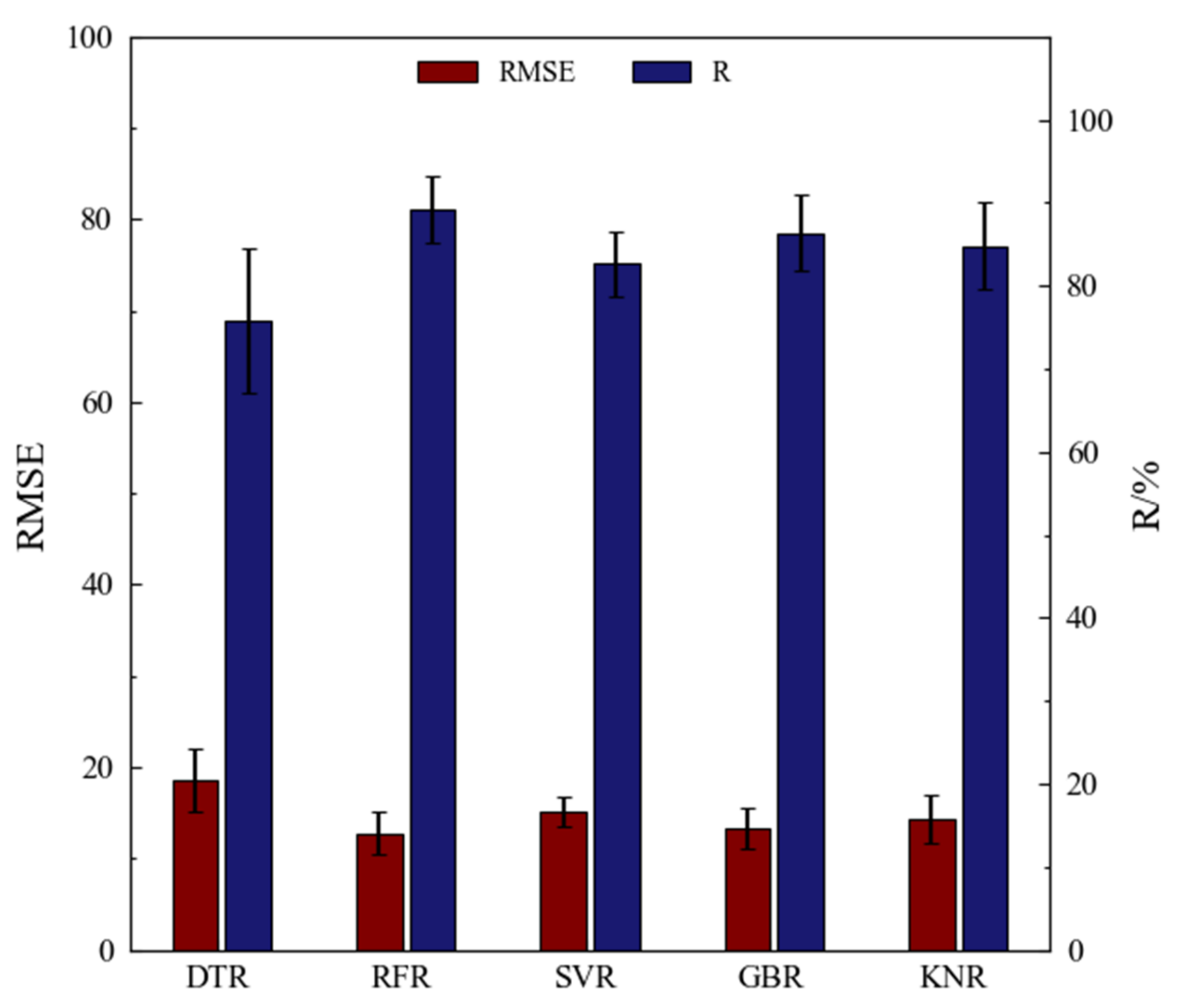
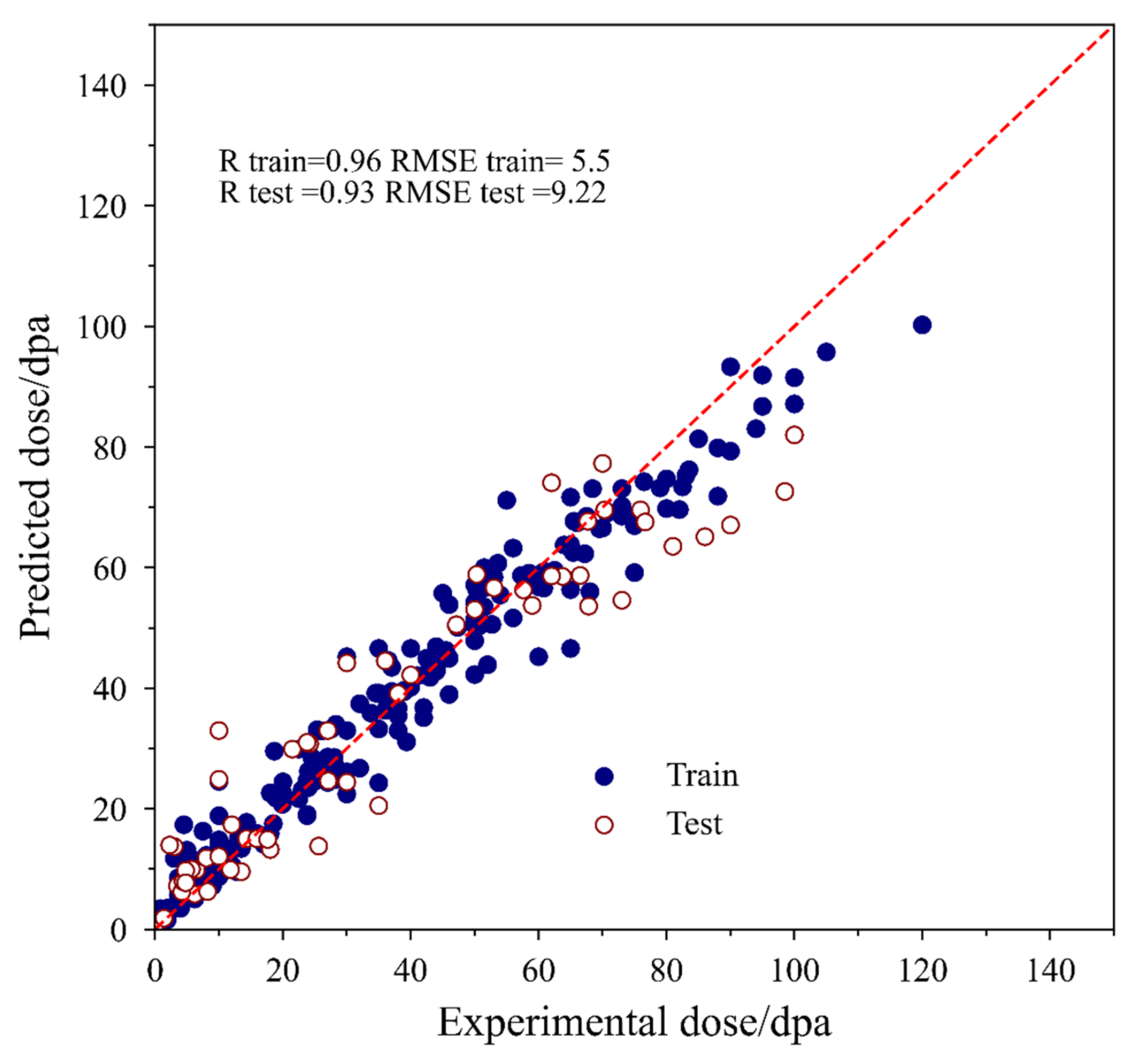
3.1. Prediction of the Onset Dose of Swelling
3.2. Simulation of Irradiation Swelling
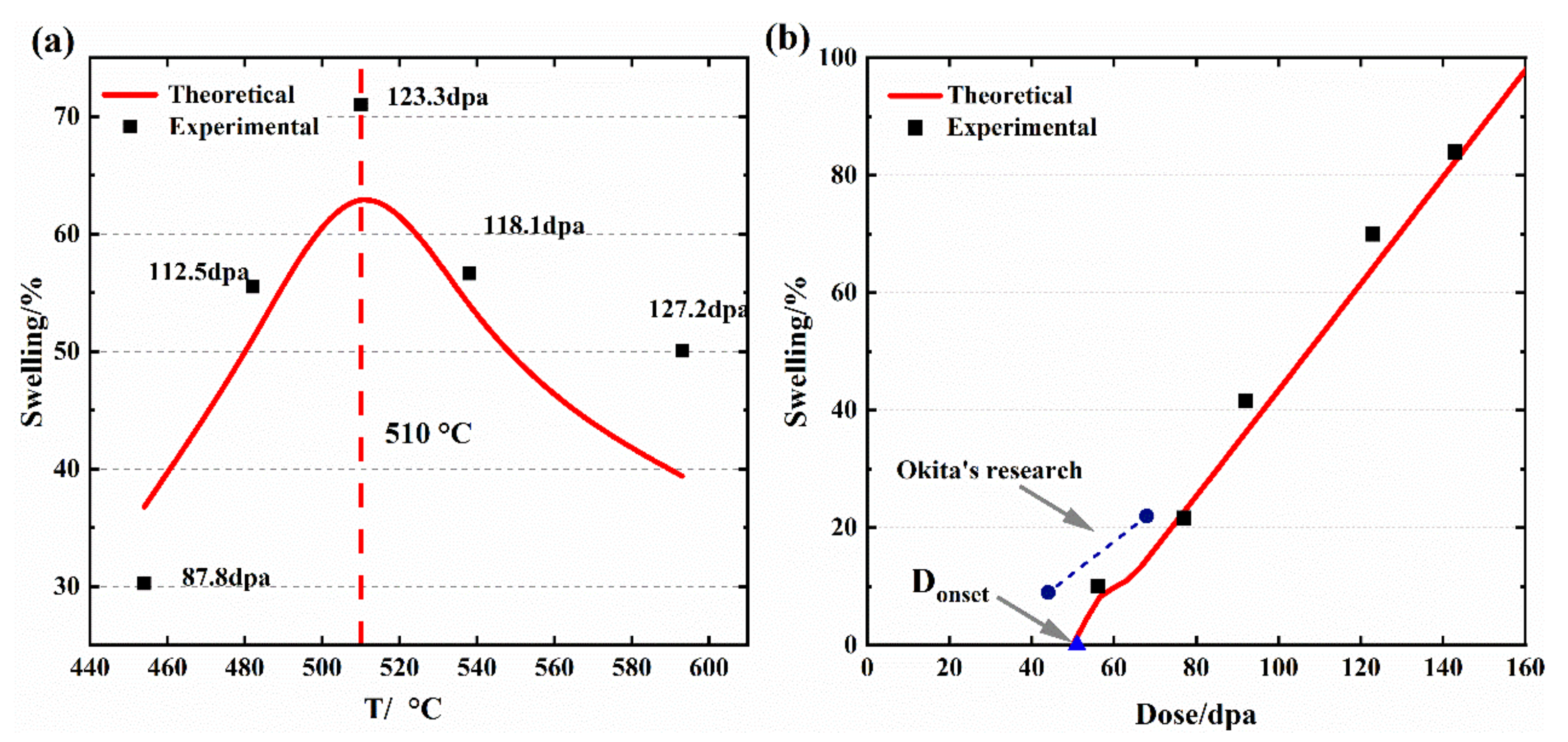
3.2.1. Irradiation Swelling of Austenitic Steels
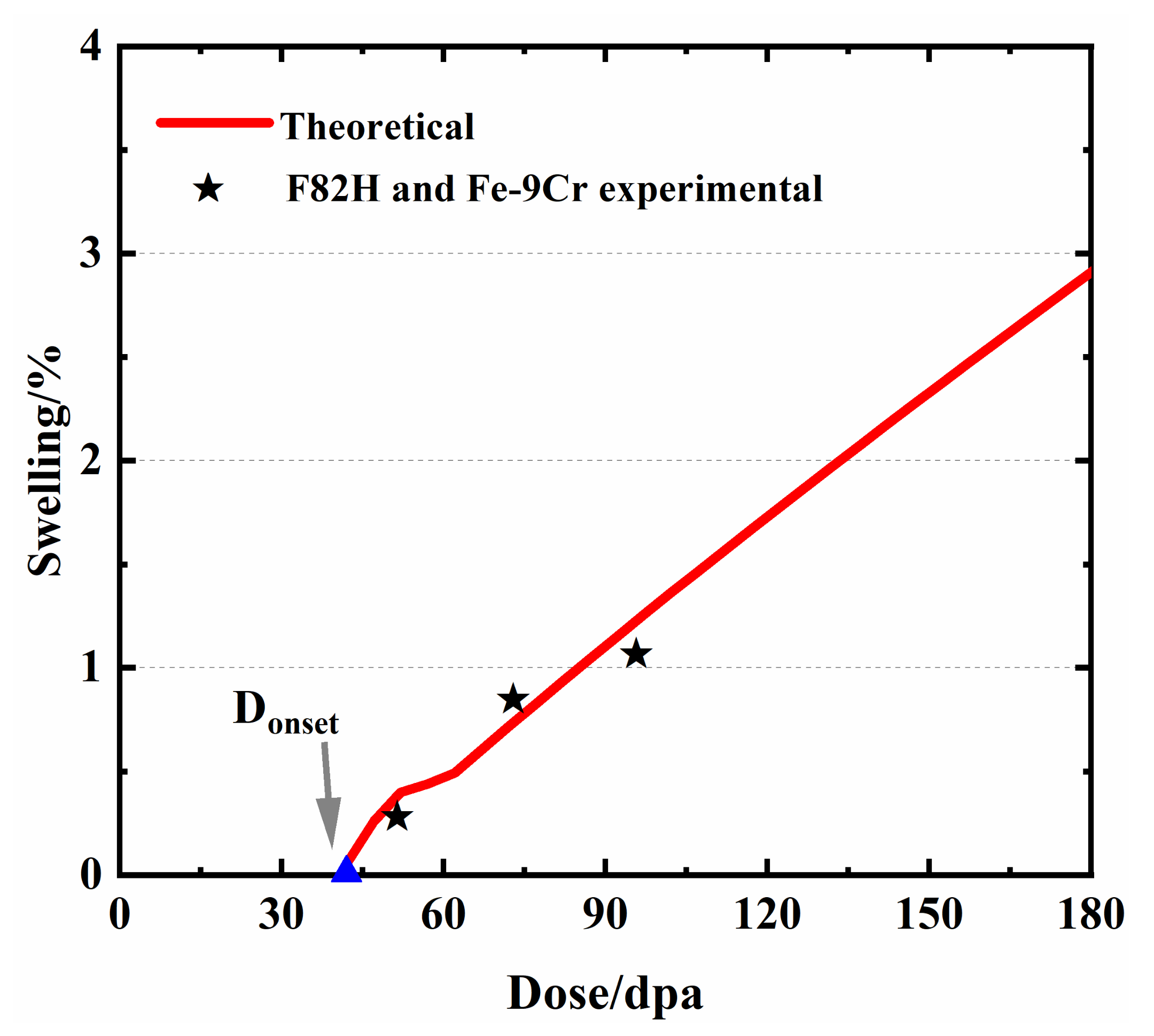
3.2.2. Irradiation Swelling of F/M Steels
3.2.3. Prediction of Irradiation Swelling in CLAM Steel
4. Discussion
4.1. Steady-State Swelling Onset Dose
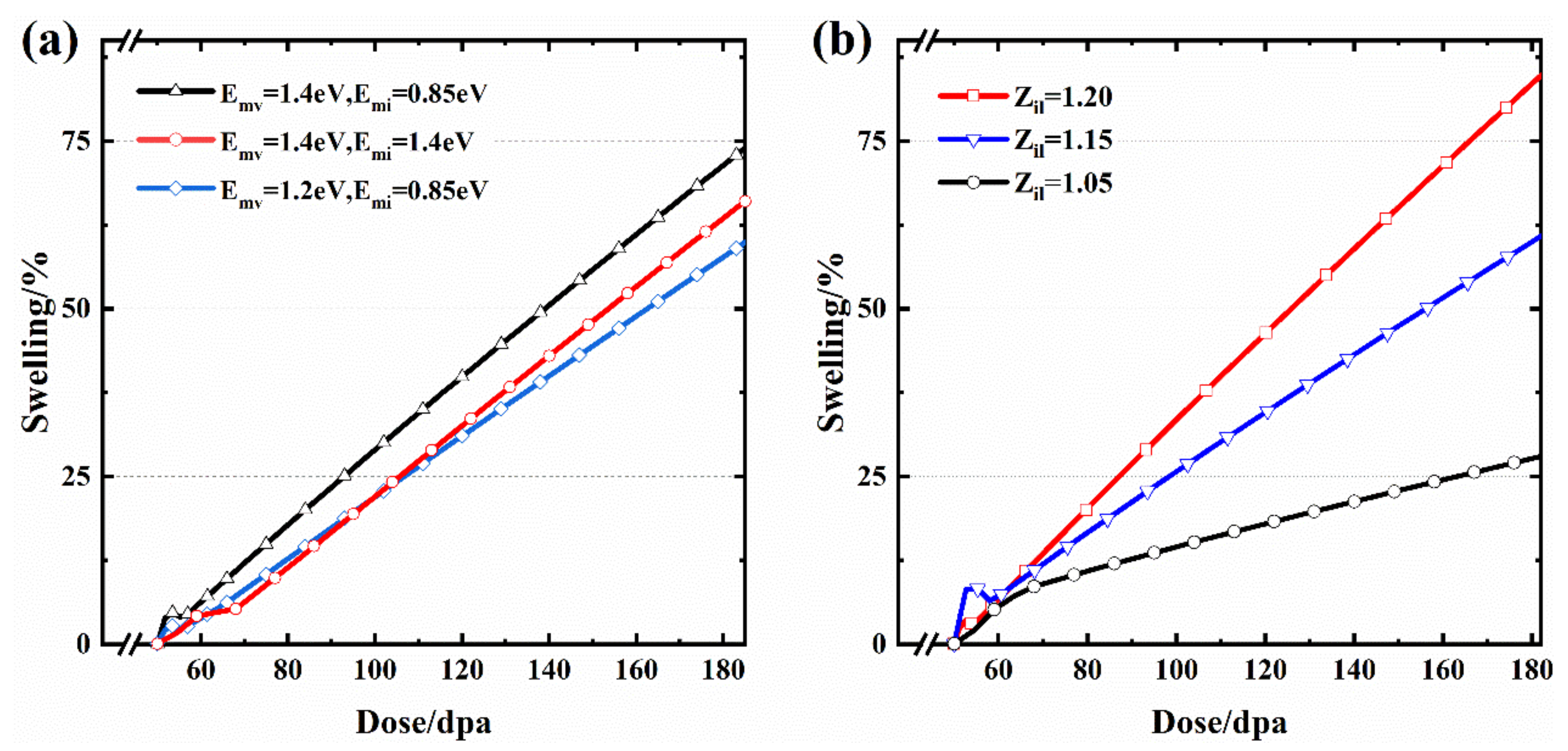
4.2. Cascade Efficiency
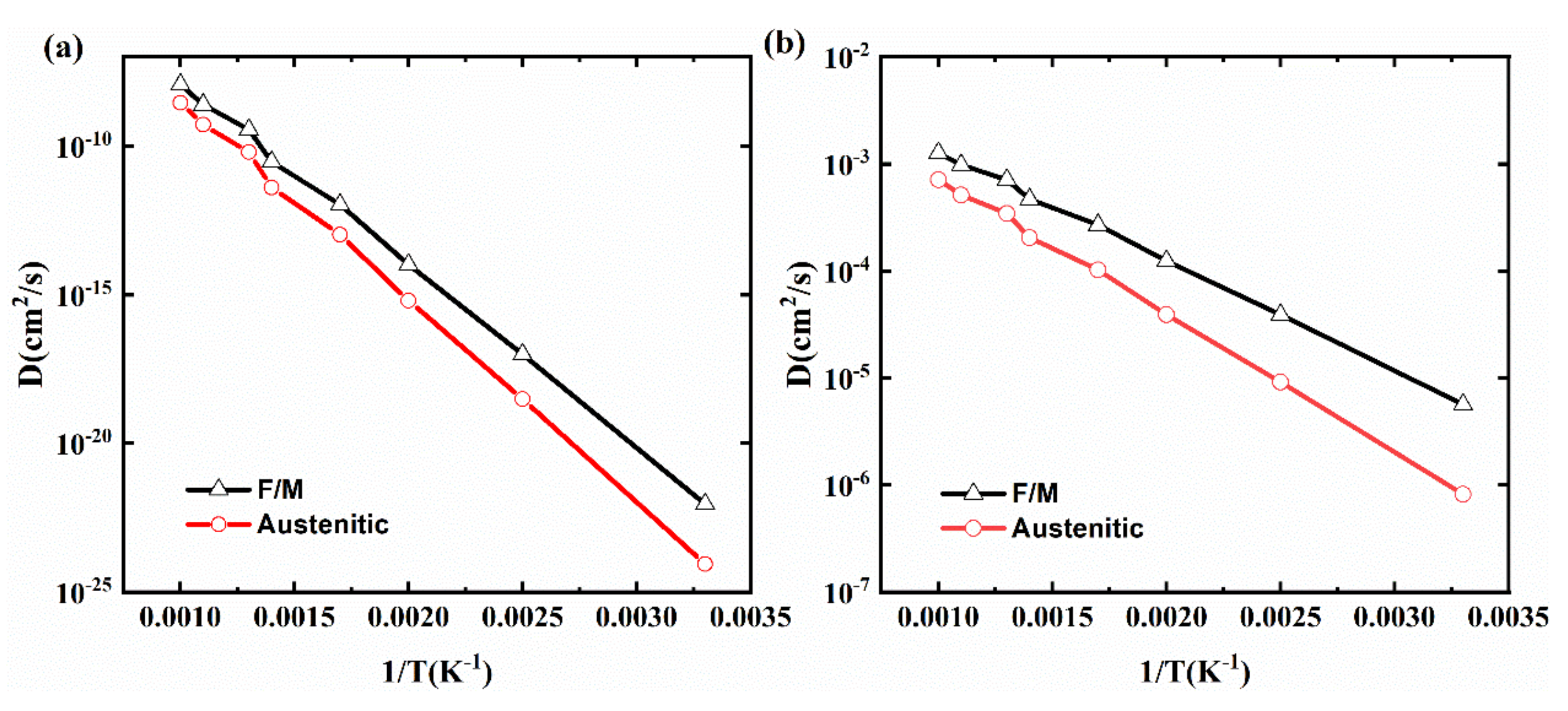
4.3. Point Defect Diffusion
4.4. Sink Strength
4.5. Helium Effects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Konobeev, Y.V.; Dvoriashin, A.M.; Porollo, S.I.; Garner, F.A. Swelling and microstructure of pure Fe and Fe–Cr alloys after neutron irradiation to ~26 dpa at 400 °C. J. Nucl. Mater. 2006, 355, 124–130. [Google Scholar] [CrossRef]
- Garner, F. Void swelling and irradiation creep in light water reactor (LWR) environments. In Understanding and Mitigating Ageing in Nuclear Power Plants; Elsevier: Amsterdam, The Netherlands, 2010; pp. 308–356. [Google Scholar]
- Bullough, R.; Eyre, B.L.; Krishan, K.; Marshall, W.C. Cascade damage effects on the swelling of irradiated materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 1975, 346, 81–102. [Google Scholar] [CrossRef]
- Cottrell, G.A. Void migration, coalescence and swelling in fusion materials. Fusion Eng. Des. 2003, 66–68, 253–257. [Google Scholar] [CrossRef]
- Surh, M.P.; Sturgeon, J.B.; Wolfer, W.G. Radiation swelling behavior and its dependence on temperature, dose rate, and dislocation structure evolution. J. Nucl. Mater. 2005, 336, 217–224. [Google Scholar] [CrossRef]
- Kohnert, A.A.; Wirth, B.D.; Capolungo, L. Modeling microstructural evolution in irradiated materials with cluster dynamics methods: A review. Comput. Mater. Sci. 2018, 149, 442–459. [Google Scholar] [CrossRef]
- Golubov, S.I.; Ovcharenko, A.M.; Barashev, A.V.; Singh, B.N. Grouping method for the approximate solution of a kinetic equation describing the evolution of point-defect clusters. Philos. Mag. A 2001, 81, 643–658. [Google Scholar] [CrossRef]
- Jin, M.; Cao, P.; Short, M.P. Predicting the onset of void swelling in irradiated metals with machine learning. J. Nucl. Mater. 2019, 523, 189–197. [Google Scholar] [CrossRef]
- Foreman, A.; Makin, M. The effect of vacancy loops on the swelling of irradiated materials. J. Nucl. Mater. 1979, 79, 43–57. [Google Scholar] [CrossRef]
- Kwon, J.; Toyama, T.; Kim, Y.M.; Kim, W.; Hong, J.H. Effects of radiation-induced defects on microstructural evolution of Fe–Cr model alloys. J. Nucl. Mater. 2009, 386–388, 165–168. [Google Scholar] [CrossRef]
- Turkin, A.; Bakai, A. Formation of steady state size distribution of precipitates in alloys under cascade-producing irradiation. J. Nucl. Mater. 2006, 358, 10–25. [Google Scholar] [CrossRef]
- Okita, T.; Wolfer, W.G. A critical test of the classical rate theory for void swelling. J. Nucl. Mater. 2004, 327, 130–139. [Google Scholar] [CrossRef]
- Diaz de la Rubia, T.; Caturla, M.J.; Alonso, E.; Fluss, M.J.; Perlado, J.M. Self-decay-induced damage production and micro-structure evolution in fcc metals: An atomic-scale computer simulation approach. J. Comput.-Aided Mater. Des. 1998, 5, 243–264. [Google Scholar] [CrossRef]
- Ghoniem, N.M.; Sharafat, S. A numerical solution to the fokker-planck equation describing the evolution of the interstitial loop microstructure during irradiation. J. Nucl. Mater. 1980, 92, 121–135. [Google Scholar] [CrossRef]
- Zinkle, S.J.; Singh, B.N. Analysis of displacement damage and defect production under cascade damage conditions. J. Nucl. Mater. 1993, 199, 173–191. [Google Scholar] [CrossRef]
- Bacon, D.J.; Gao, F.; Osetsky, Y.N. The primary damage state in fcc, bcc and hcp metals as seen in molecular dynamics simulations. J. Nucl. Mater. 2000, 276, 1–12. [Google Scholar] [CrossRef]
- Osetsky, Y.N.; Bacon, D.J.; Serra, A.; Singh, B.N.; Golubov, S.I. Stability and mobility of defect clusters and dislocation loops in metals. J. Nucl. Mater. 2000, 276, 65–77. [Google Scholar] [CrossRef]
- Garner, F.A. Radiation Damage in Austenitic Steels. In Comprehensive Nuclear Materials; Elsevier: Amsterdam, The Netherlands, 2012; pp. 33–95. [Google Scholar]
- Garner, F. Recent insights on the swelling and creep of irradiated austenitic alloys. J. Nucl. Mater. 1984, 122, 459–471. [Google Scholar] [CrossRef]
- Garner, F.A.; Perrin, J. Effects of Radiation on Materials: Twelfth International Symposium: A Symposium; Astm International: West Conshohocken, PA, USA, 1985; Volume 870. [Google Scholar]
- Surh, M.P.; Sturgeon, J.B.; Wolfer, W.G. Void nucleation, growth, and coalescence in irradiated metals. J. Nucl. Mater. 2008, 378, 86–97. [Google Scholar] [CrossRef]
- Wolfer, W.G.; Si-Ahmed, A. On the coefficient for bulk recombination of vacancies and interstitials. J. Nucl. Mater. 1981, 99, 117–123. [Google Scholar] [CrossRef]
- Wu, F.; Zhu, Y.; Wu, Q.; Li, X.; Wang, P.; Wu, H. Helium bubbles aggravated defects production in self-irradiated copper. J. Nucl. Mater. 2017, 496, 265–273. [Google Scholar] [CrossRef]
- Pokor, C.; Brechet, Y.; Dubuisson, P.; Massoud, J.P.; Barbu, A. Irradiation damage in 304 and 316 stainless steels: Experimental investigation and modeling. Part I: Evolution of the microstructure. J. Nucl. Mater. 2004, 326, 19–29. [Google Scholar] [CrossRef]
- Wolfer, W.G. Fundamental Properties of Defects in Metals. In Comprehensive Nuclear Materials; Elsevier: Amsterdam, The Netherlands, 2012; pp. 1–45. [Google Scholar]
- Kiritani, M.; Takata, H.; Moriyama, K.; Fujita, F.E. Mobility of lattice vacancies in iron. Philos. Mag. A 1979, 40, 779–802. [Google Scholar] [CrossRef]
- Katoh, Y.; Muroga, T. Characterization of cascade-induced defect production by microstructural analysis based on rate theory modeling. J. Nucl. Mater. 1996, 233, 1029–1034. [Google Scholar] [CrossRef][Green Version]
- Sniegowski, J.; Wolfer, W. On the physical basis for the swelling resistance of ferritic steels. In Proceedings of the Topical Conference on Ferritic Alloys for Use in Nuclear Energy Technologies, Snowbird, UT, USA, 19–23 June 1983. [Google Scholar]
- Garner, F.A. Comparison of swelling and irradiation creep behavior of fcc-austenitic and bcc-ferritic/martensitic alloys at high neutron exposure. J. Nucl. Mater. 2000, 276, 123–142. [Google Scholar] [CrossRef]
- Gelles, D.S. Microstructural examination of neutron-irradiated simple ferritic alloys. J. Nucl. Mater. 1982, 108–109, 515–526. [Google Scholar] [CrossRef]
- Morimura, T.; Kimura, A.; Matsui, H. Void swelling of Japanese candidate martensitic steels under FFTF/MOTA irradiation. J. Nucl. Mater. 1996, 239, 118–125. [Google Scholar] [CrossRef]
- Wakai, E.; Hashimoto, N.; Miwa, Y.; Robertson, J.P.; Klueh, R.L.; Shiba, K.; Jistukawa, S. Effect of helium production on swelling of F82H irradiated in HFIR. J. Nucl. Mater. 2000, 283–287, 799–805. [Google Scholar] [CrossRef]
- Kohno, Y.; Gelles, D.S.; Kohyama, A.; Tamura, M.; Hishinuma, A. Irradiation response of a reduced activation Fe-8Cr-2W martensitic steel (F82H) after FFTF irradiation. J. Nucl. Mater. 1992, 191–194, 868–873. [Google Scholar] [CrossRef]
- Allen, T.R.; Cole, J.I.; Trybus, C.L.; Porter, D.L.; Tsai, H.; Garner, F.; Kenik, E.A.; Yoshitake, T.; Ohta, J. The effect of dose rate on the response of austenitic stainless steels to neutron radiation. J. Nucl. Mater. 2006, 348, 148–164. [Google Scholar] [CrossRef]
- Gelles, D. Void swelling resistance in Fe-Cr alloys at 200 dpa. MRS Online Proc. Libr. 1994, 373, 69–74. [Google Scholar] [CrossRef]
- Huang, Q. Status and improvement of CLAM for nuclear application. Nucl. Fusion 2017, 57, 086042. [Google Scholar] [CrossRef]
- Little, E.A.; Bullough, R.; Wood, M.H. On the swelling resistance of ferritic steel. Proc. R. Soc. Lond. A Math. Phys. Sci. 1997, 372, 565–579. [Google Scholar] [CrossRef]
- Gelles, D.; Meinecke, R. Alloy Development for Irradiation Performance Semiannual Progress Report; DOE/ER-045/11; Oak Ridge National Lab.: Oak Ridge, TN, USA, 1984.
- Pasianot, R.C.; Monti, A.M.; Simonelli, G.; Savino, E.J. Computer simulation of SIA migration in bcc and hcp metals. J. Nucl. Mater. 2000, 276, 230–234. [Google Scholar] [CrossRef]
- Hashimoto, N.; Sakuraya, S.; Tanimoto, J.; Ohnuki, S. Effect of impurities on vacancy migration energy in Fe-based alloys. J. Nucl. Mater. 2014, 445, 224–226. [Google Scholar] [CrossRef]
- Woo, C.H.; Singh, B.N. Production bias due to clustering of point defects in irradiation-induced cascades. Philos. Mag. A 1992, 65, 889–912. [Google Scholar] [CrossRef]
- Dai, Y.; Krsjak, V.; Kuksenko, V.; Schäublin, R. Microstructural changes of ferritic/martensitic steels after irradiation in spallation target environments. J. Nucl. Mater. 2018, 511, 508–522. [Google Scholar] [CrossRef]
- Krsjak, V.; Shen, T.; Degmova, J.; Sojak, S.; Korpas, E.; Noga, P.; Egger, W.; Li, B.; Slugen, V.; Garner, F.A. On the helium bubble swelling in nano-oxide dispersion-strengthened steels. J. Mater. Sci. Technol. 2022, 105, 172–181. [Google Scholar] [CrossRef]

| Variables | Min | Max | Variables | Min | Max |
|---|---|---|---|---|---|
| Fe/(wt %) | 8.0 | 97.0 | V/(wt %) | 0 | 2 |
| Cr/(wt %) | 3 | 24.7 | W/(wt %) | 0 | 2.1 |
| Ni/(wt %) | 0.0 | 74.9 | Temperature/(K) | 500 | 1013 |
| Si/(wt %) | 0.0 | 1.3 | Dose rate/(dpa/s) | 8 × 10−9 | 0.06 |
| Mn/(wt %) | 0.0 | 15 | Dislocation density/(m−2) | 5 × 1013 | 8.5 × 1015 |
| Mo/(wt %) | 0.0 | 2.8 | Cascade efficiency | 0.01 | 0.3 |
| Ta/(wt %) | 0.0 | 0.36 | Dose(dpa) | 0.2 | 120 |
| Material Parameters | AISI 316 | Fe-9Cr |
|---|---|---|
| V-formation energy (eV) | 1.8 [21] | 1.9 [25] |
| SIA-formation energy (eV) | 1.8 [21] | 4.1 [25] |
| V-migration energy (eV) | 1.4 [24] | 1.1 [26] |
| SIA-migration energy (eV) | 0.85 [24] | 0.2 [26] |
| Dv0 (cm2·s−1) | 1.29 × 10−2 [21] | 4.5 × 10−3 [25] |
| Di0 (cm2·s−1) | 1.29 × 10−2 [21] | 3.0 × 10−5 [25] |
| Recombination coefficient | 5.69 × 1026 | 5.48 × 1027 |
| Recombination radius (cm) | 1.27 × 10−7 | 1.1 × 10−7 |
| Dislocation density (cm−2) | 1.5 × 1010 [27] | 1.1 × 1011 [27] |
| Dislocation bias | 1.20 [24] | 1.05 [28] |
| Loop bias | 1.20 [24] | 1.05 [28] |
| Loop initial radius (cm) | 10−7 | 10−7 |
| Burger’s vector (cm) | 2.0 × 10−8 | 2.86 × 10−8 |
| Lattice parameter (cm) | 3.64 × 10−8 | 2.8 × 10−8 |
| Poisson’s ratio | 0.264 | 0.3 |
| Parameters | AISI 316 [29] | Fe-9Cr [30] | JLF-1 [31] | CLAM [32,33] |
|---|---|---|---|---|
| Dose rate (dpa/s) | 10−6 | 10−6 | 10−6 | 10−6 |
| Cascade efficiency | 0.2 | 0.25 | 0.25 | 0.25 |
| Interstitial loop density (cm−3) | 2.2 × 104 exp (1.7/) | 6.5 × 1016 at 425 °C | 1.8 × 103 exp (1.8/) | 1.1 × 1016 |
| Void concentration (cm−3) | 3.0 × 1016 exp {−[(1/ × 1.2]2} | 8.7 × 1015 at 425 °C | 7.45 × 1013 at 390 °C 2.2 × 1014 at 430 °C | 5.0 × 1014 |
| Irradiation type | neutron | neutron | neutron | neutron |
| Neutron fluence (n m−2) | 10 × 1026–25 × 1026 | 19 × 1026 | 5.8 × 1026 | 7.7 × 1026 |
| T (°C) | 427–593 | 420 | 390–460 | 400 |
| Dose/(dpa) | Swelling/% 510 °C | T/(°C) | Dose/(dpa) | Swelling/% |
|---|---|---|---|---|
| 123.3 | 71.1 | 427 | 87.8 | 16.9 |
| 141.3 | 87.5 | 482 | 112.5 | 46.4 |
| 89.7 | 41.5 | 510 | 123.3 | 51.6 |
| 71.8 | 23.6 | 538 | 118.1 | 41.5 |
| 56.1 | 11.5 | 593 | 127.2 | 29.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Li, X.; Zheng, M. Predicting the Irradiation Swelling of Austenitic and Ferritic/Martensitic Steels, Based on the Coupled Model of Machine Learning and Rate Theory. Metals 2022, 12, 651. https://doi.org/10.3390/met12040651
Zhu X, Li X, Zheng M. Predicting the Irradiation Swelling of Austenitic and Ferritic/Martensitic Steels, Based on the Coupled Model of Machine Learning and Rate Theory. Metals. 2022; 12(4):651. https://doi.org/10.3390/met12040651
Chicago/Turabian StyleZhu, Xiaohan, Xiaochen Li, and Mingjie Zheng. 2022. "Predicting the Irradiation Swelling of Austenitic and Ferritic/Martensitic Steels, Based on the Coupled Model of Machine Learning and Rate Theory" Metals 12, no. 4: 651. https://doi.org/10.3390/met12040651
APA StyleZhu, X., Li, X., & Zheng, M. (2022). Predicting the Irradiation Swelling of Austenitic and Ferritic/Martensitic Steels, Based on the Coupled Model of Machine Learning and Rate Theory. Metals, 12(4), 651. https://doi.org/10.3390/met12040651






