Effect of Corrugated Sheet Diameter on Structural Behavior under Cryogenic Temperature and Hydrodynamic Load
Abstract
1. Introduction
2. Finite Element Analysis
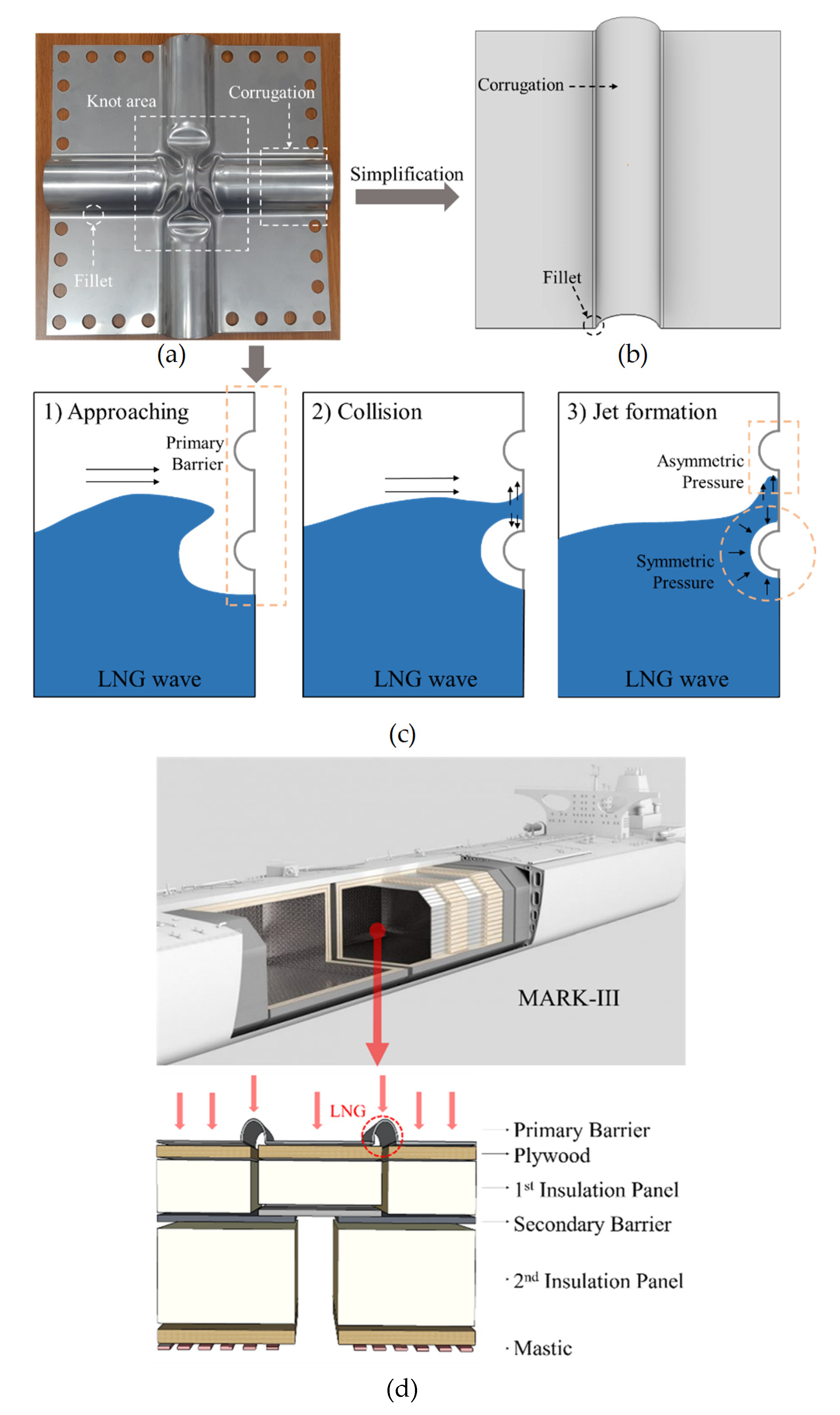
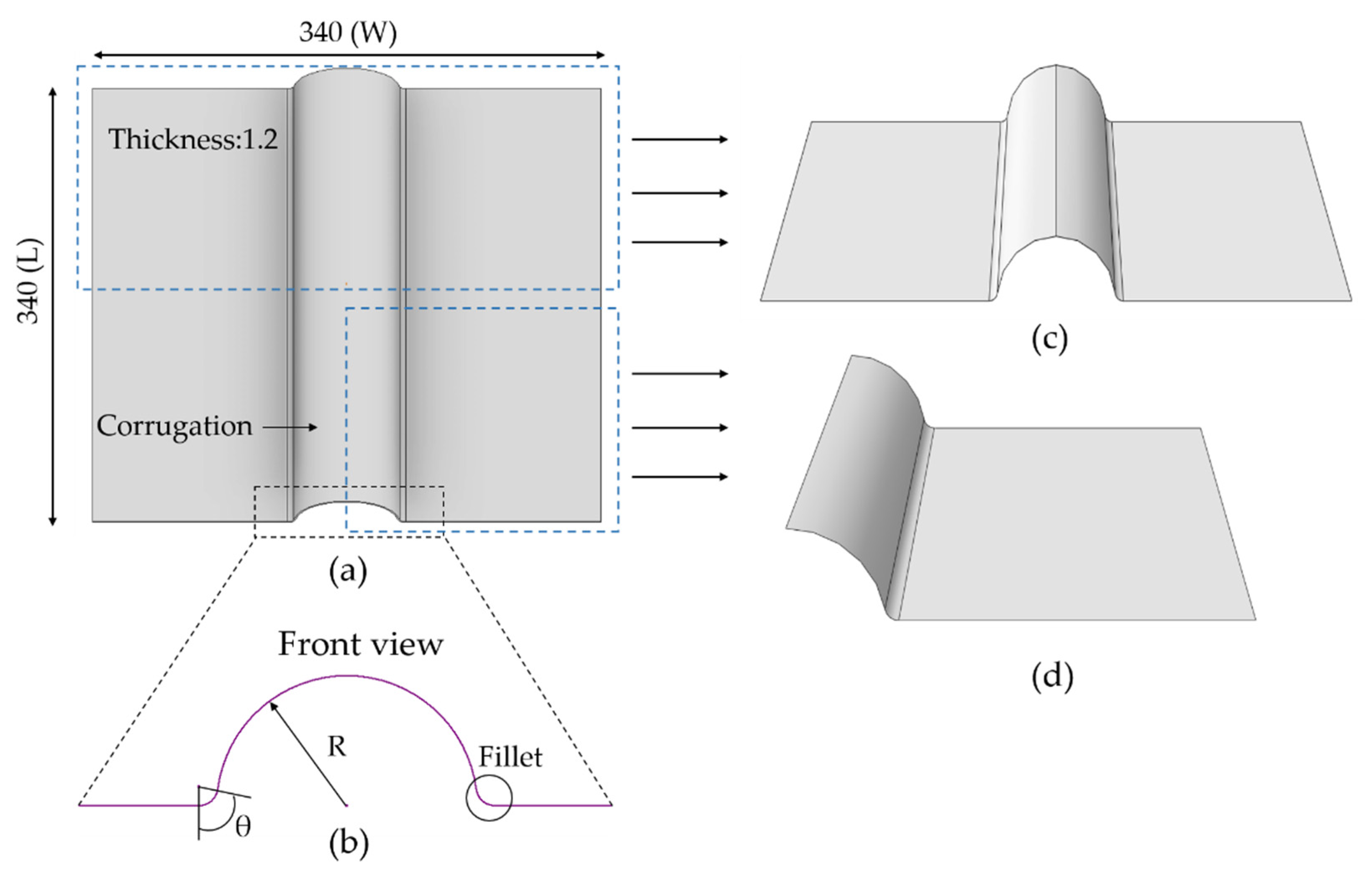
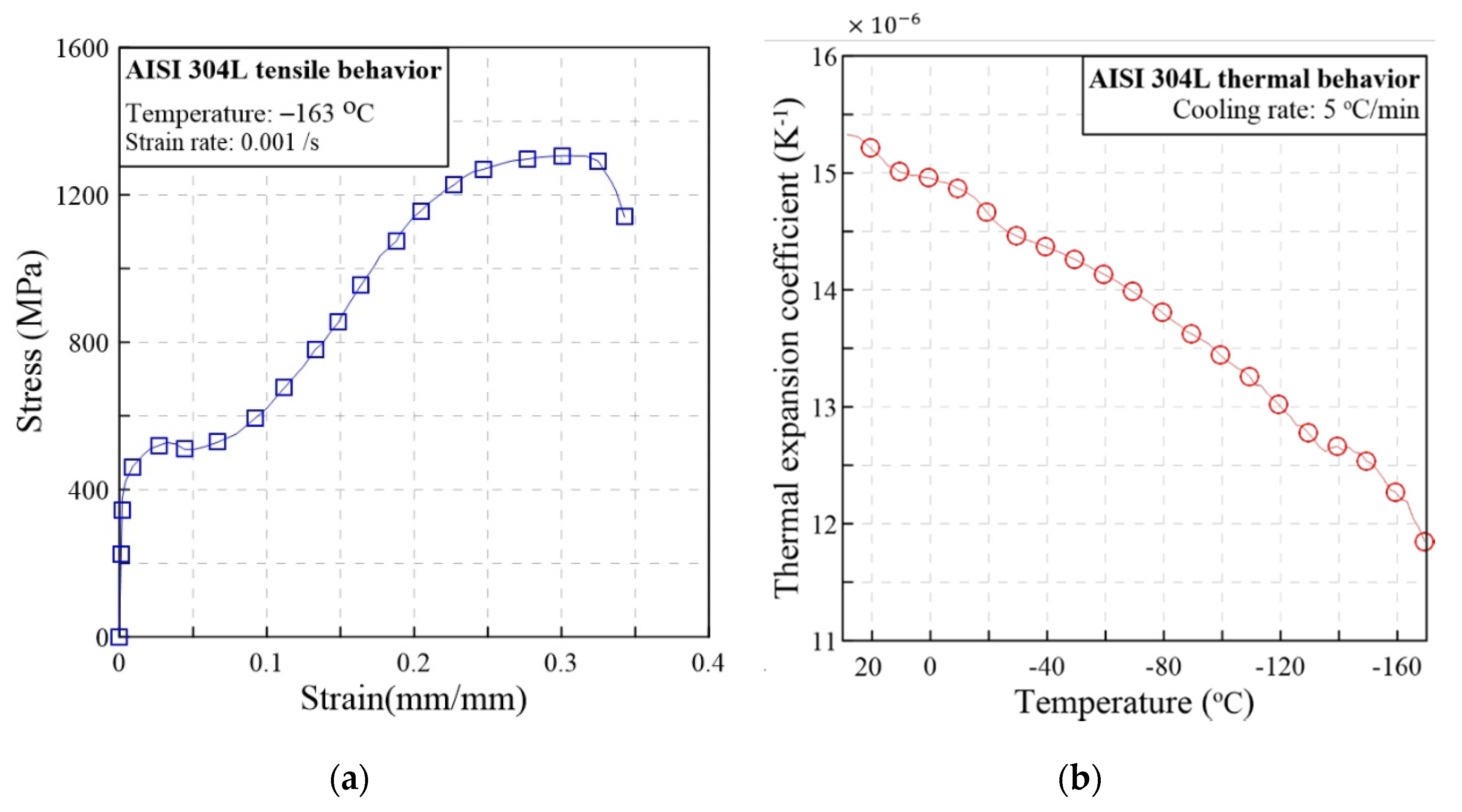
2.1. Scenario and Material Properties
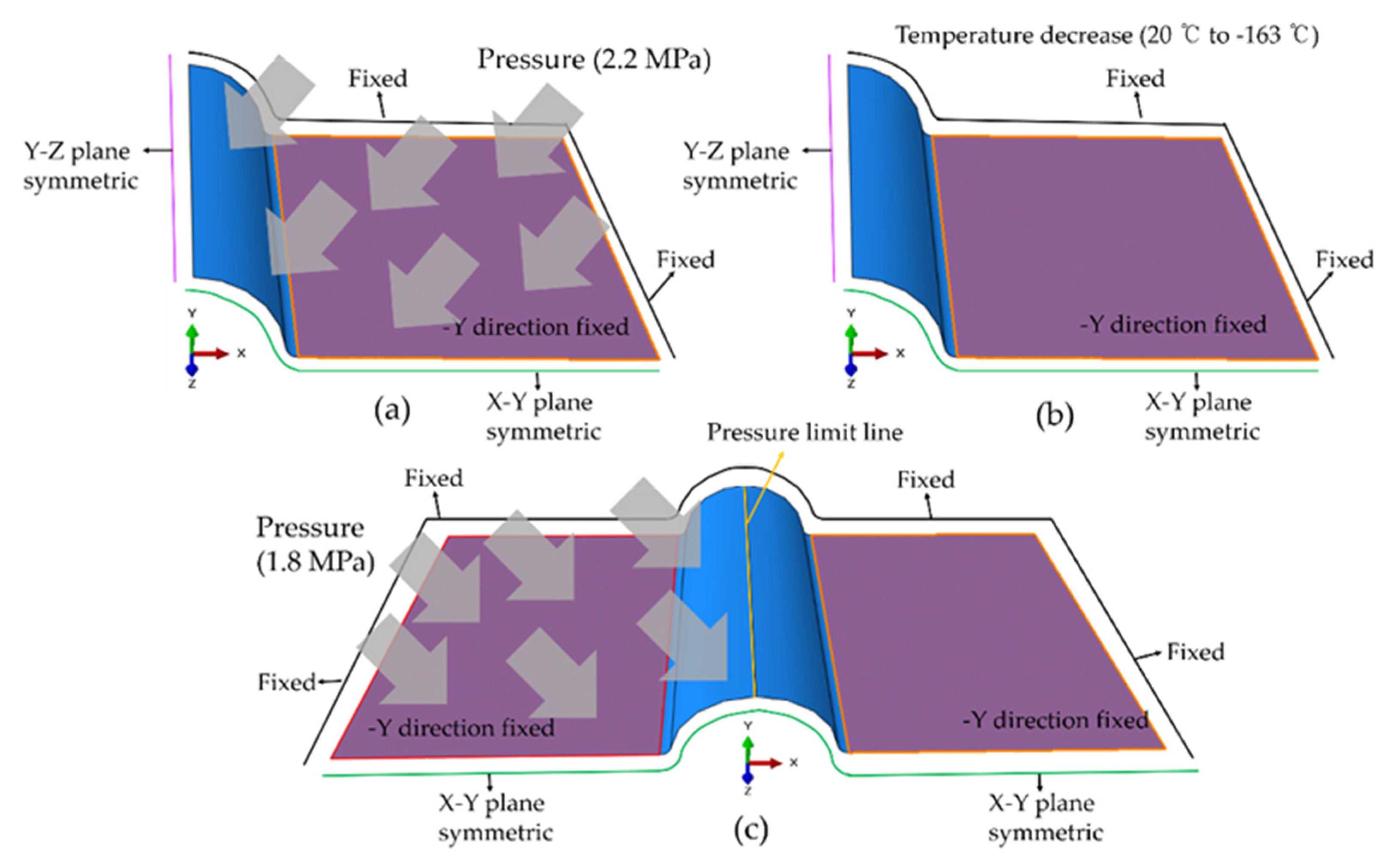
2.2. Loading and Boundary Conditions
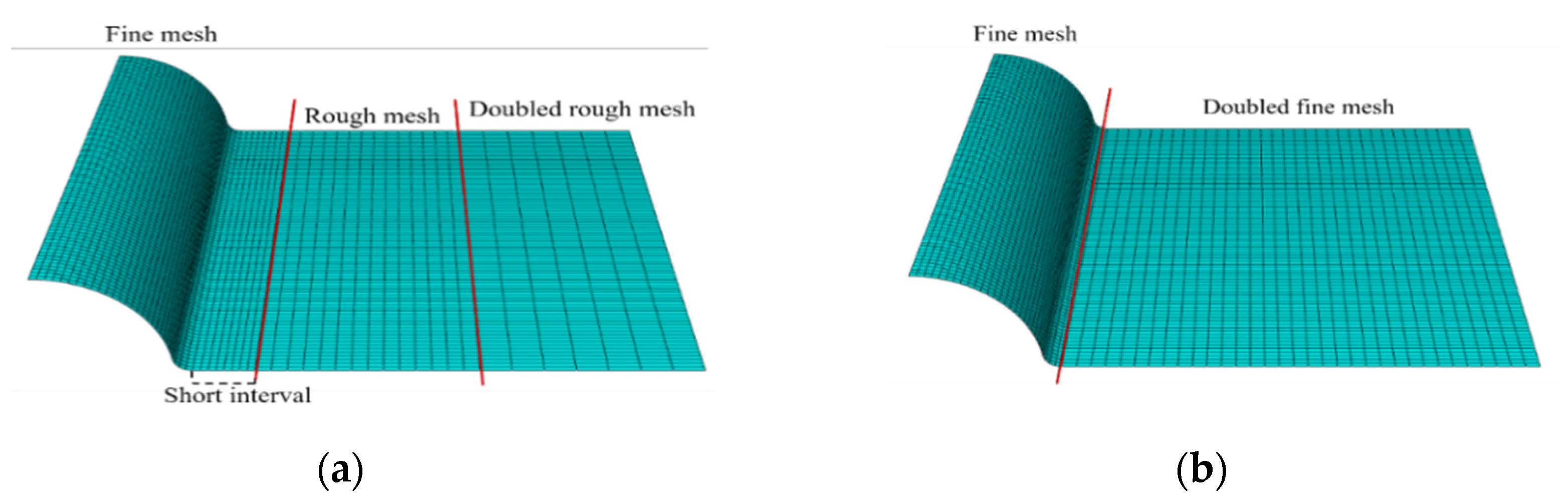
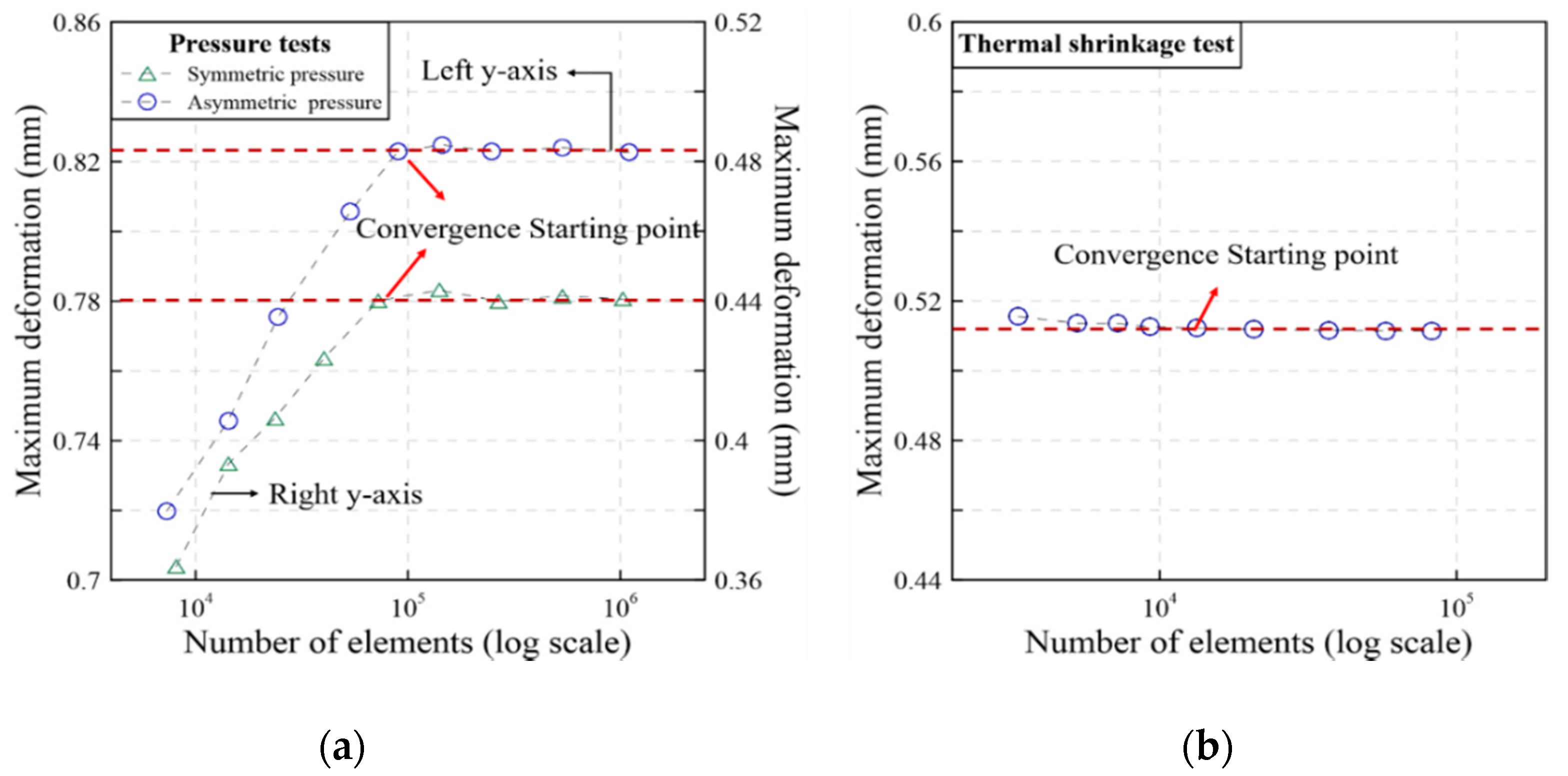
2.3. Mesh Convergence Study
3. Result and Discussion
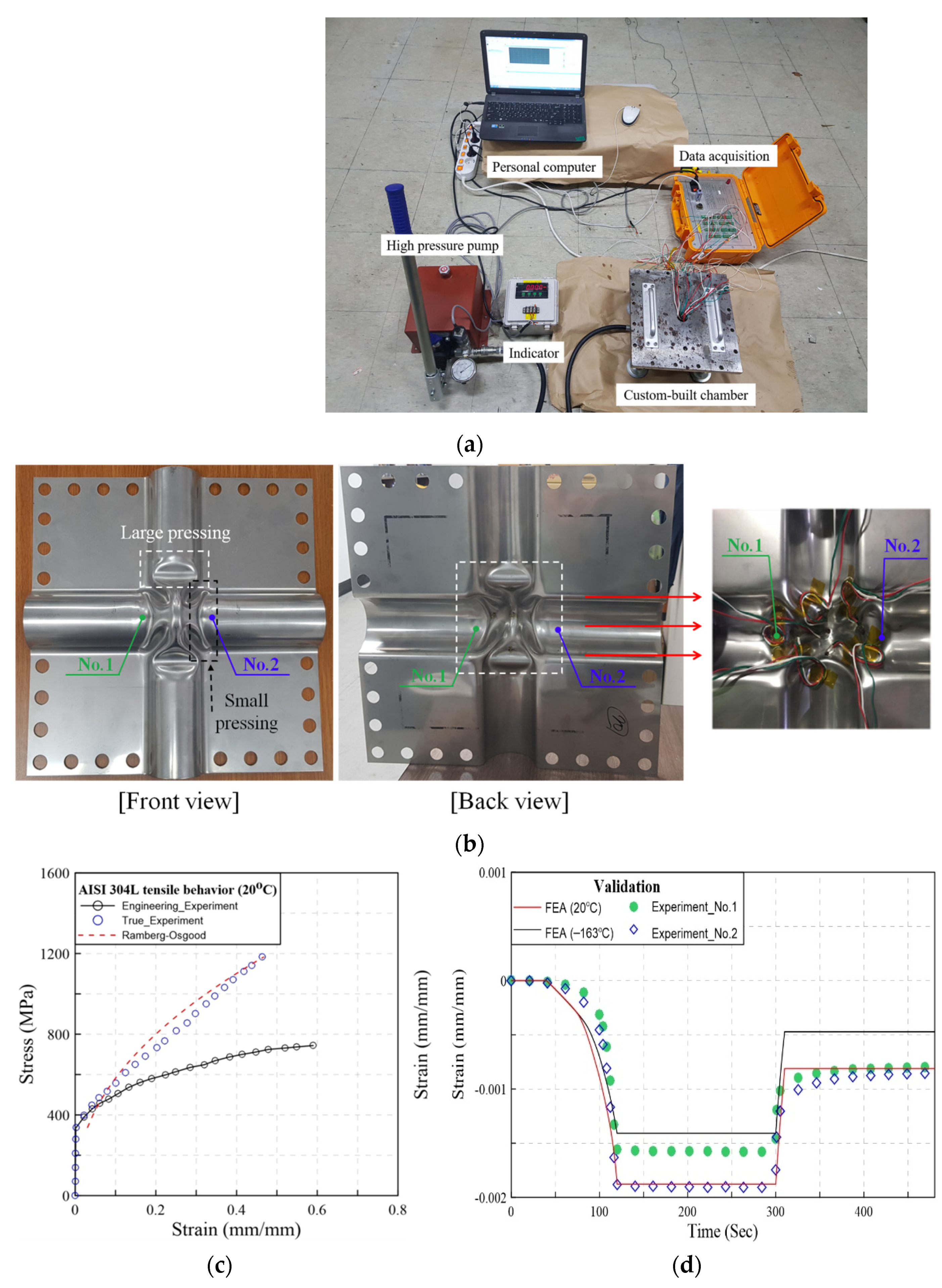
3.1. Validation
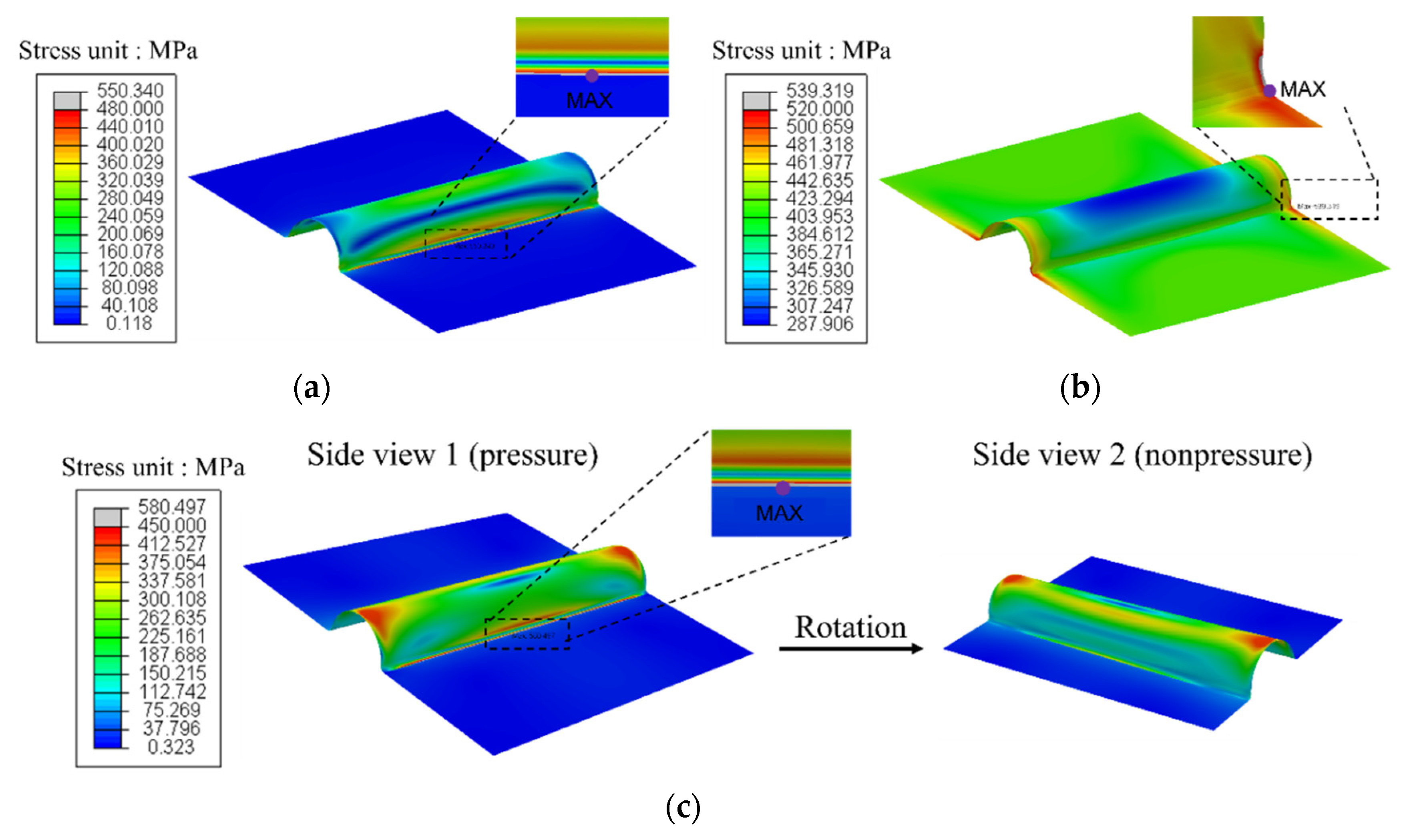
3.2. Overall Structural Behavior
3.3. Effect of Corrugation Shape under Pressure
3.3.1. Effect of Corrugation Radius
3.3.2. Effect of Fillet Angle
3.4. Effect of Corrugated Dimension under Temperature Gradient
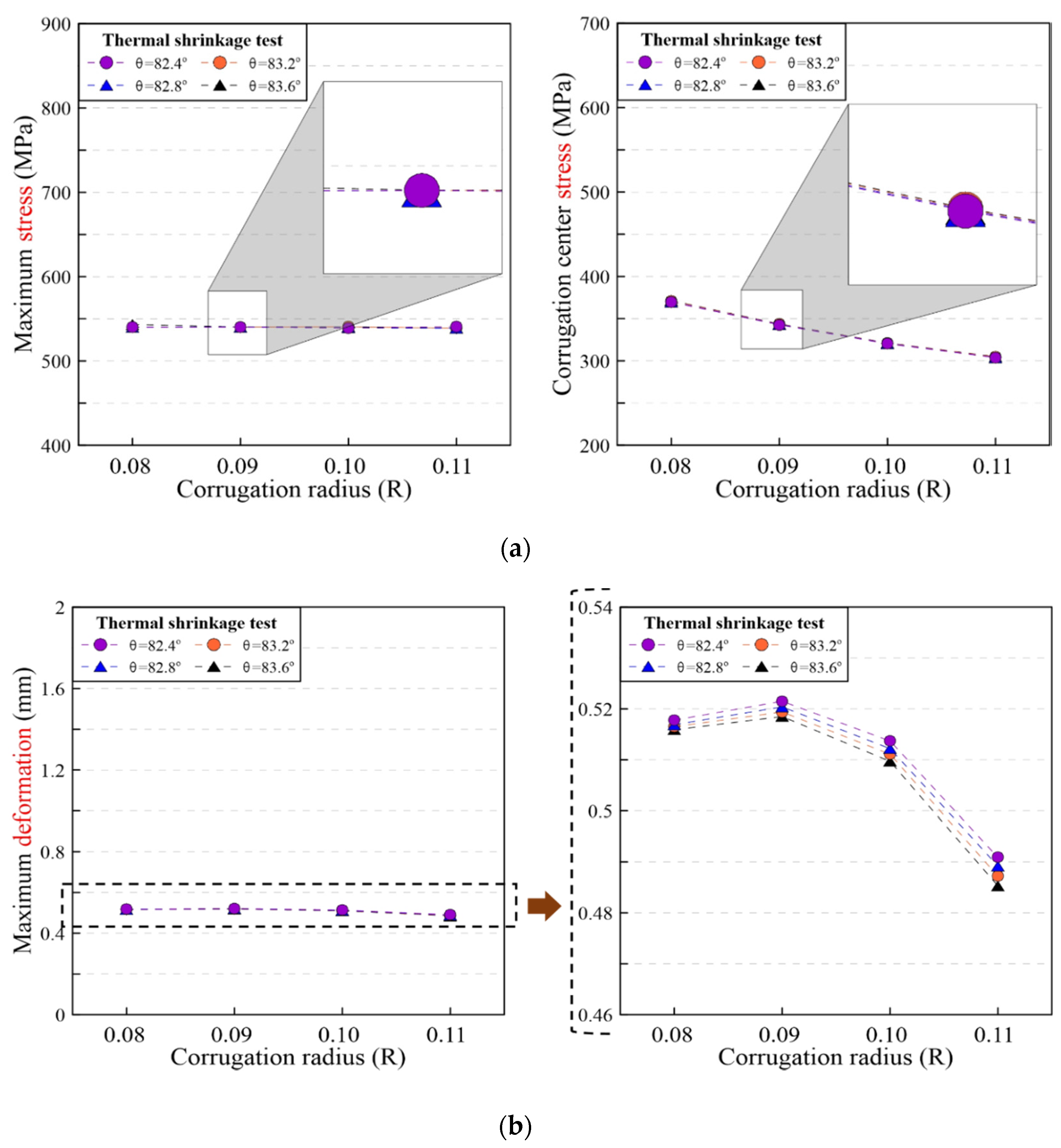
3.4.1. Effect of Corrugation Radius
3.4.2. Effect of Fillet Angle
4. Conclusions
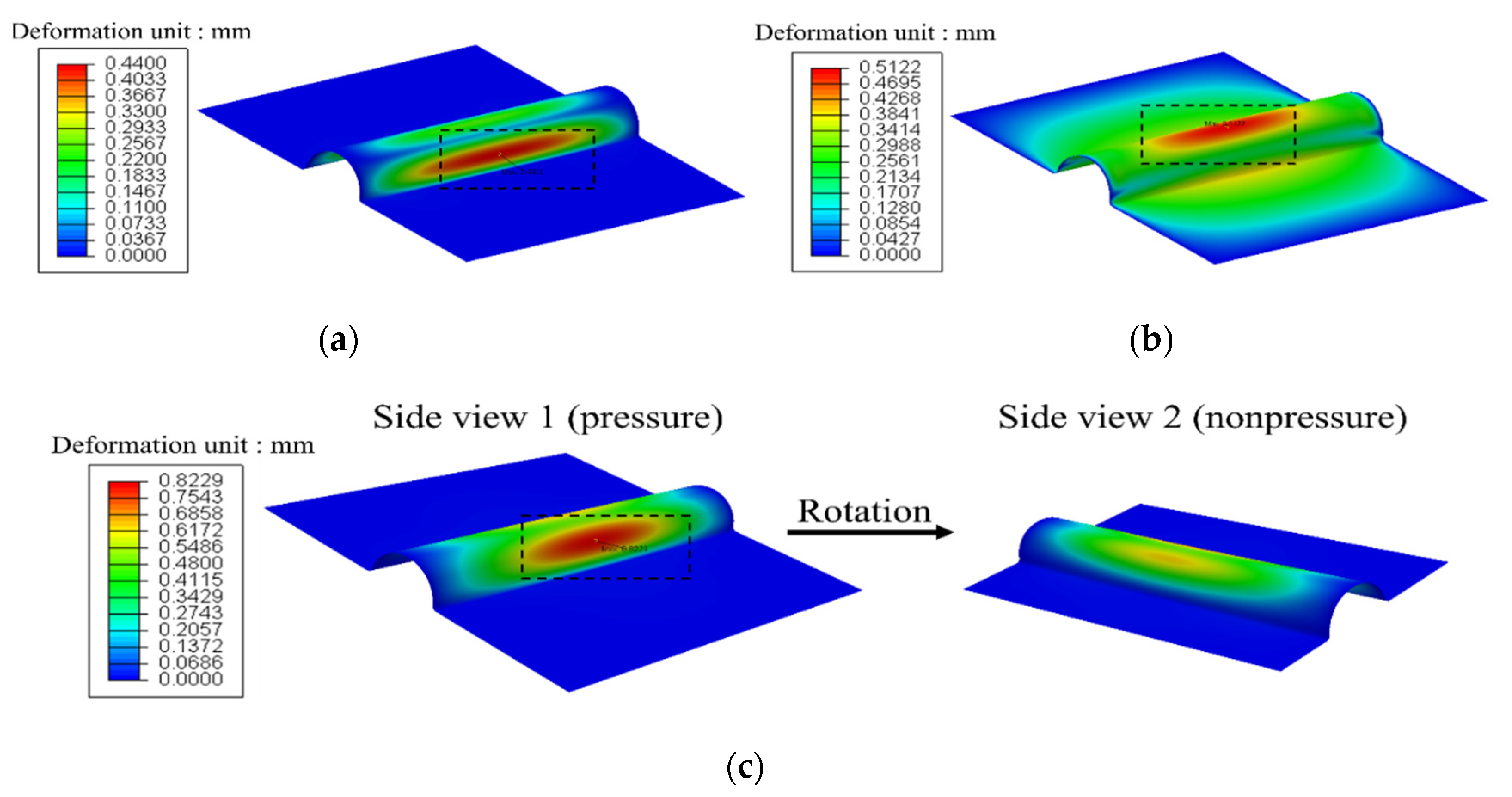
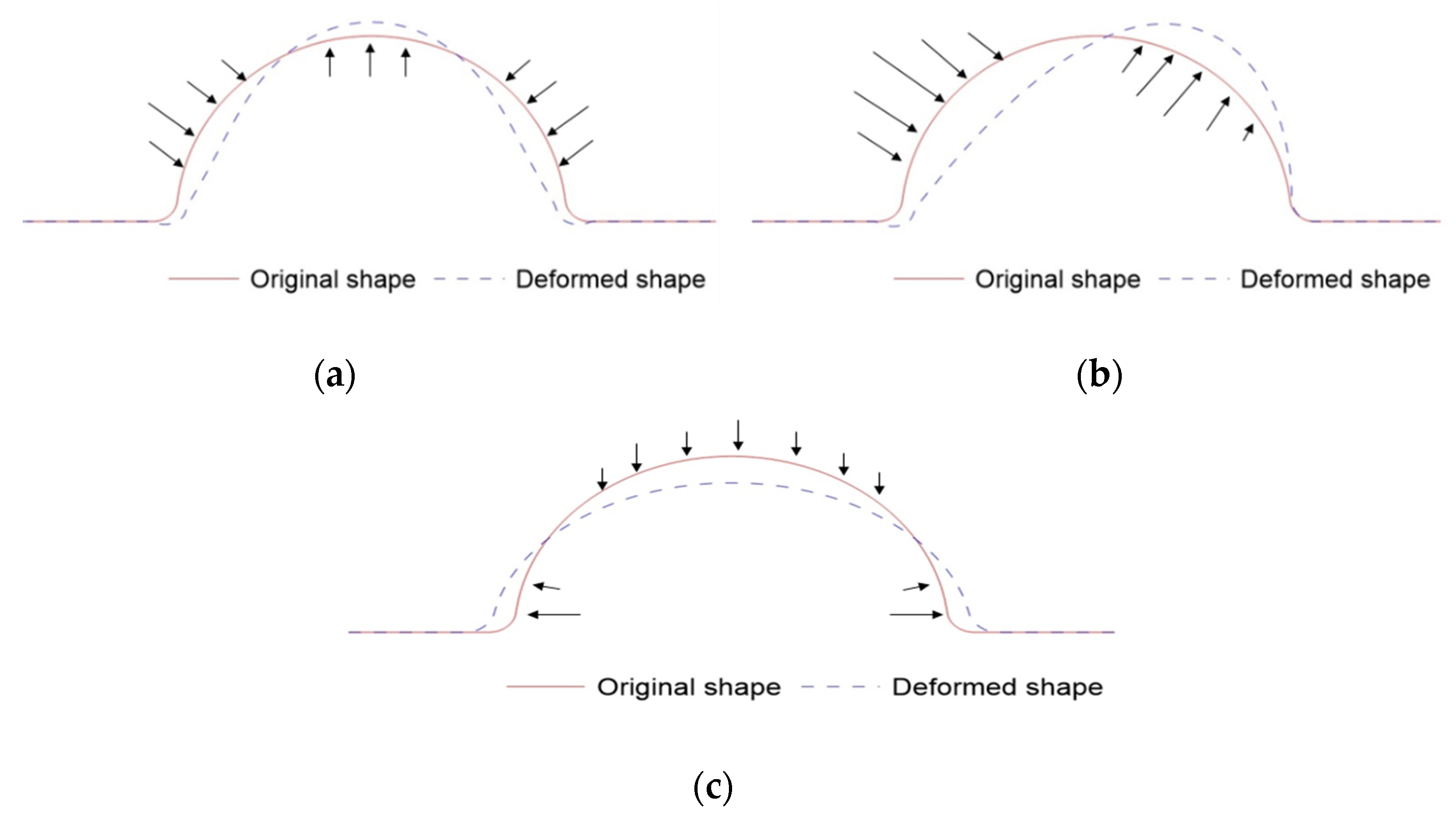
- In the pressure analysis, the maximum stress occurs at the intersection of the fillet along the middle of the longitudinal direction. In addition, the maximum deformation occurs at the center of the corrugation for different heights based on the load conditions.
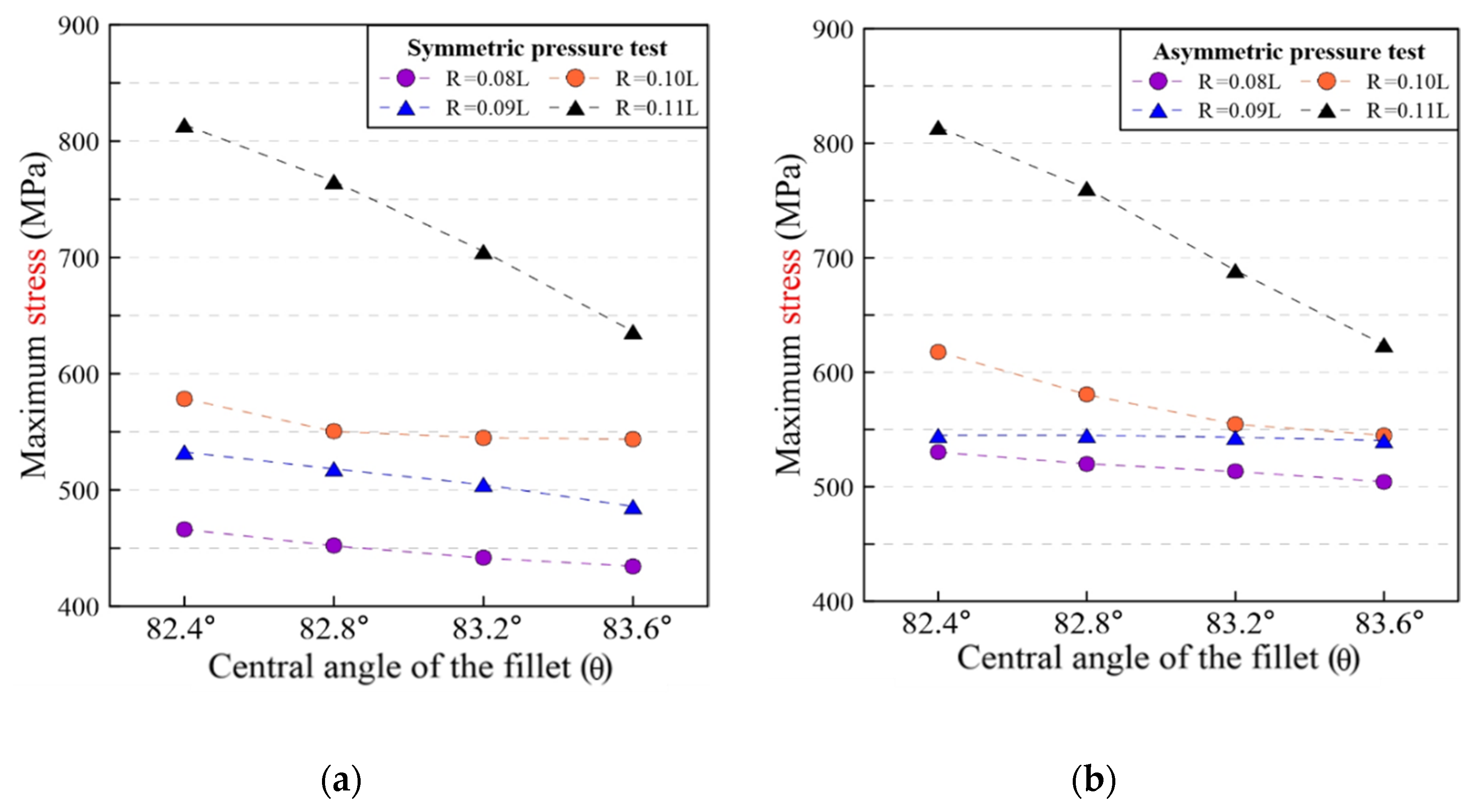
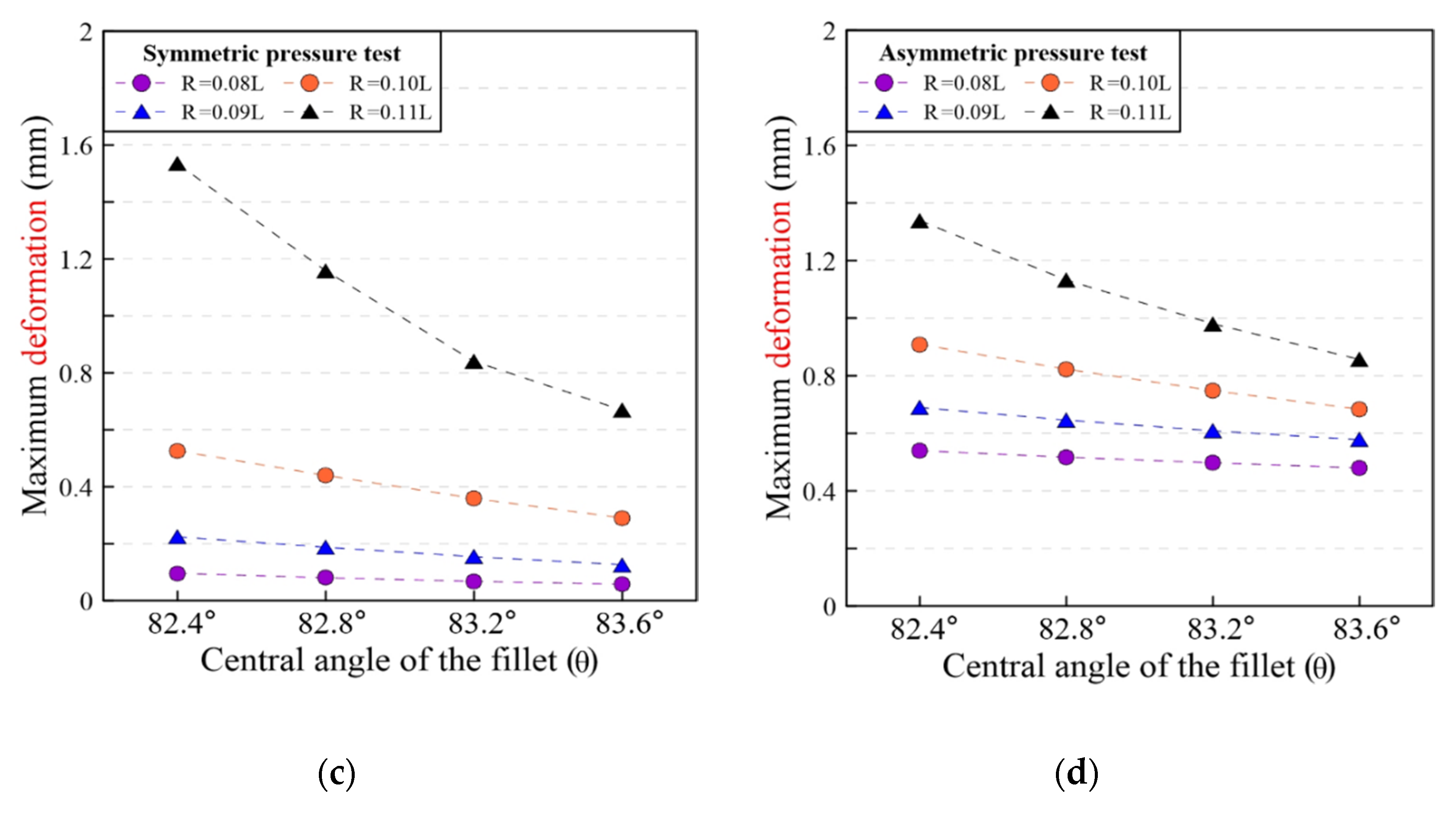
- In the hydrodynamic pressure analysis, the maximum stress and deformation increase as the radius of the corrugation increases. In particular, the corrugation radius should not exceed 0.11 L because it would induce severe deformation compared to that of the 0.1 L corrugation radius.
- In the pressure load condition, the maximum stress and deformation decrease with increasing fillet angle. The sensitivity is greater in the symmetric pressure analysis, where the maximum deformation decreases by 15% to 25% based on the fillet angle.
- In the thermal contraction condition, the effect of the fillet angle on the structural behavior is less than 1%. However, there exists an inflection point at which the maximum deformation increases or decreases depending on the corrugation radius. Furthermore, a short corrugation radius induces more residual stress in the corrugation.
- From the analysis results, the optimum corrugation radius and fillet angle were determined as 0.09 L and 82.4°, respectively. The fillet angle is a more important factor under hydrodynamic loading than thermal contraction conditions. Therefore, a larger fillet angle is recommended for reducing corrugation deformation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, S.; Kwon, H.T.; Choi, K.H.; Lim, W.; Cho, J.H.; Tak, K.; Moon, I. LNG: An eco-friendly cryogenic fuel for sustainable development. Appl. Energy 2011, 88, 4264–4273. [Google Scholar] [CrossRef]
- Kim, J.H.; Park, D.H.; Lee, C.S.; Park, K.J.; Lee, J.M. Effects of cryogenic thermal cycle and immersion on the mechanical characteristics of phenol-resin bonded plywood. Cryogenics 2015, 72, 90–102. [Google Scholar] [CrossRef]
- Kim, T.W.; Kim, S.K.; Kim, J.H.; Lee, J.M. Effects of Environmental Conditions on the Mechanical and Degradation Behavior of Polyurethane Foam Subjected to Various Deformation Histories. J. Mater. Eng. Perform. 2019, 28, 5063–5075. [Google Scholar] [CrossRef]
- Lee, D.H.; Ha, M.K.; Kim, S.Y.; Shin, S.C. Research of design challenges and new technologies for floating LNG. Int. J. Nav. Archit. Ocean Eng. 2014, 6, 307–322. [Google Scholar] [CrossRef]
- Hasan, M.M.F.; Zheng, A.M.; Karimi, I.A. Minimizing boil-off losses in liquefied natural gas transportation. Ind. Eng. Chem. Res. 2009, 48, 9571–9580. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, C.S.; Kim, M.H.; Lee, J.M. Prestrain-dependent viscoplastic damage model for austenitic stainless steel and implementation to ABAQUS user-defined material subroutine. Comput. Mater. Sci. 2013, 67, 273–281. [Google Scholar] [CrossRef]
- Choe, J.H.; Kim, K.H.; Lee, D.Y.; Bang, C.S.; Lee, D.G. Glass composite vibration isolating structure for the LNG cargo containment system. Compos. Struct. 2014, 107, 469–475. [Google Scholar] [CrossRef]
- Park, S.B.; Choi, S.W.; Kim, J.H.; Bang, C.S.; Lee, J.M. Effect of the blowing agent on the low-temperature mechanical properties of CO2- and HFC-245fa-blown glass-fiber-reinforced polyurethane foams. Compos. Part B Eng. 2016, 93, 317–327. [Google Scholar] [CrossRef]
- Lee, D.Y.; Kim, K.H.; Choi, I.B.; Lee, D.G. Pressure-resisting capability of the knot area of the primary barrier for a LNG containment system. Ocean Eng. 2015, 95, 128–133. [Google Scholar] [CrossRef]
- Jeong, Y.J.; Kim, H.T.; Kim, S.K.; Kim, J.H.; Kim, Y.T.; Heo, W.S.; Lee, J.M. Evaluation of the pressure-resisting capability of membrane-type corrugated sheet under hydrodynamic load. Thin-Walled Struct. 2021, 106, 107388. [Google Scholar] [CrossRef]
- Kim, M.S.; Kim, J.H.; Kim, S.K.; Lee, J.M. Experimental investigation of structural response of corrugated steel sheet subjected to repeated impact loading: Performance of LNG cargo Containment System. Appl. Sci. 2019, 9, 1558. [Google Scholar] [CrossRef]
- Brosset, L.; Lafeber, W.; Bogaert, H.; Marhem, M.; Carden, P.; Maguire, J. A mark III panel subjected to a flip-through wave impact: Results from the Sloshel project. In Proceedings of the Twenty-First International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Wang, B.; Shin, Y. Full-scale test and FE analysis of LNG MK III containment system under sloshing loads. In Proceedings of the Twenty-First International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Kwon, S.B.; Kim, M.S.; Lee, J.M. A numerical study on the fatigue evaluation of mark-III LNG primary barrier. J. Korean Soc. Mar. Eng. 2017, 4, 337–344. [Google Scholar] [CrossRef]
- Xiong, J.; Feng, L.; Ghosh, R.; Wu, H.; Wu, L.; Ma, L.; Vaziri, A. Fabrication and mechanical behavior of carbon fiber composite sandwich cylindrical shells with corrugated cores. Compos. Struct. 2016, 156, 307–319. [Google Scholar] [CrossRef]
- Bogaert, H.; Kaminski, M.L.; Brosset, L. Full and large scale wave impact tests for a better understanding of sloshing—Results of the Sloshel project. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011. [Google Scholar]
- Kim, B.C.; Yoon, S.H.; Lee, D.G. Pressure resistance of the corrugated stainless steel membranes of LNG carriers. Ocean Eng. 2011, 38, 592–608. [Google Scholar]
- Abaqus, Version 6.14 Documentation; Dassault Systemes Simulia Corporation: Providence, RI, USA, 2014.
- Song, C.Y.; Cho, D.Y. Cryogenic compressive strength and thermal deformation of reinforced polyurethane foam material for membrane type LNG carrier. Key Eng. Mater. 2018, 773, 30–39. [Google Scholar] [CrossRef]
- Sorohan, S.; Constantinescu, D.M.; Sandu, M.; Sandu, A. Using point symmetry in finite element analyses. Mater. Today Proc. 2020, 32, 139–147. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, S.K.; Kim, M.H.; Lee, J.M. Numerical model to predict deformation of corrugated austenitic stainless steel sheet under cryogenic temperatures for design of liquefied natural gas insulation system. Mater. Des. 2014, 57, 26–39. [Google Scholar] [CrossRef]
- Kim, J.H.; Park, W.S.; Chun, M.S.; Kim, J.J.; Bae, J.H.; Kim, M.H.; Lee, J.M. Effect of pre-straining on low-temperature mechanical behavior of AISI 304L. Mater. Sci. Eng. A 2012, 543, 50–57. [Google Scholar] [CrossRef]
- Kim, S.K.; Kim, J.H.; Kim, J.H.; Lee, J.M. Numerical model for mechanical nonlinearities of high manganese steel based on the elastoplastic damage model. Metals 2018, 8, 680. [Google Scholar] [CrossRef]
- Sadok, L.; Luksza, J.; Majta, J. Inhomogeneity of mechanical properties in stainless steel rods after drawing. J. Mater. Process. Technol. 1994, 44, 129–141. [Google Scholar] [CrossRef]
- Chieslar, J.D.; Ghali, A. Solid to shell element geometric transformation. Comput. Struct. 1987, 25, 451–455. [Google Scholar] [CrossRef]
- Ehlers, S.; Guiard, M.; Kubiczek, J.; Höderath, A.; Sander, F.; Sopper, R.; Charbonnier, P.; Marhem, M.; Darie, I.; von Selle, H.; et al. Experimental and numerical analysis of a membrane cargo containment system for liquefied natural gas. Ships Offshore Struct. 2017, 12, S257–S267. [Google Scholar] [CrossRef]
- Choi, S.W.; Li, M.; Lee, W.I.; Kim, H.S. Analysis of buckling load of glass fiber/epoxy-reinforced plywood and its temperature dependence. J. Compos. Mater. 2014, 48, 2191–2206. [Google Scholar] [CrossRef]
- Turon, A.; Dávila, C.G.; Camanho, P.P.; Costa, J. An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Eng. Fract. Mech. 2007, 74, 1665–1682. [Google Scholar] [CrossRef]
- Cichanski, A. Mesh size dependency on notch radius for FEM analysis of notched round bars under tension. AIP Conf. Proc. 2017, 1822, 020004. [Google Scholar]
- Kim, S.K.; Lee, C.S.; Kim, J.H.; Kim, M.H.; Lee, J.M. Computational evaluation of resistance of fracture capacity for SUS304L of liquefied natural gas insulation system under cryogenic temperatures using ABAQUS user-defined material subroutine. Mater. Des. 2013, 50, 522–532. [Google Scholar] [CrossRef]
- Patwardhan, P.S.; Nalavde, R.A.; Kujawski, D. An estimation of Ramberg-Osgood constants for materials with and without luder’s strain using yield and ultimate strengths. Procedia Struct. Integr. 2019, 17, 750–757. [Google Scholar] [CrossRef]
- Li, T.; Zheng, J.; Chen, Z. Description of full-range strain hardening behavior of steels. Springerplus 2016, 5, 1316. [Google Scholar] [CrossRef]
- Lee, C.S.; Yoo, B.M.; Kim, M.H.; Lee, J.M. Viscoplastic damage model for austenitic stainless steel and its application to the crack propagation problem at cryogenic temperatures. Int. J. Damage Mech. 2012, 22, 95–115. [Google Scholar] [CrossRef]
- Sohn, J.M.; Bae, D.M.; Bae, S.Y.; Paik, J.K. Nonlinear structural behaviour of membrane-type LNG carrier cargo containment systems under impact pressure loads at −163 °C. Ships Offshore Struct. 2017, 12, 722–733. [Google Scholar] [CrossRef]
- Sano, H.; Wakabayashi, I.; Itoi, E. Stress distribution in the supraspinatus tendon with partial-thickness tears: An analysis using two-dimensional finite element model. J. Shoulder Elb. Surg. 2006, 15, 100–105. [Google Scholar] [CrossRef]
- Martín-Martín, A.; Avella, M.; Iiguez, M.P.; Jiménez, J.; Oudart, M.; Nagle, J. Thermomechanical model for the plastic deformation in high power laser diodes during operation. J. Appl. Phys. 2009, 106, 073105. [Google Scholar] [CrossRef]
- El-Mahdy, G.M. Parametric study of the structural and in-plane buckling analysis of ogee arches. HBRC J. 2014, 10, 108–116. [Google Scholar] [CrossRef][Green Version]
- Wibawa, L.A.N. Numerical Study of The Effect of Wall Thickness and Internal Pressure on Von Mises Stress and Safety Factor of Thin-Walled Cylinder for Rocket Motor Case. JST 2020, 9, 30–38. [Google Scholar] [CrossRef]

| R/L | Case No. | θ (°) |
|---|---|---|
| 0.08 | 11 | 82.4 |
| 12 | 82.8 | |
| 13 | 83.2 | |
| 14 | 83.6 | |
| 0.09 | 21 | 82.4 |
| 22 | 82.8 | |
| 23 | 83.2 | |
| 24 | 83.6 | |
| 0.10 | 31 | 82.4 |
| 32 | 82.8 | |
| 33 | 83.2 | |
| 34 | 83.6 | |
| 0.11 | 41 | 82.4 |
| 42 | 82.8 | |
| 43 | 83.2 | |
| 44 | 83.6 |
| Yield Stress | Young’s Modulus (E, MPa) | Strength Coefficient (H, MPa) | Strain Hardening Exponent (n) |
|---|---|---|---|
| 331.3 | 206,387 | 1678.8 | 0.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.-S.; Kim, J.-H.; Jeong, Y.-C.; Kim, H.-T.; Kim, S.-K.; Lee, J.-M. Effect of Corrugated Sheet Diameter on Structural Behavior under Cryogenic Temperature and Hydrodynamic Load. Metals 2022, 12, 521. https://doi.org/10.3390/met12030521
Park J-S, Kim J-H, Jeong Y-C, Kim H-T, Kim S-K, Lee J-M. Effect of Corrugated Sheet Diameter on Structural Behavior under Cryogenic Temperature and Hydrodynamic Load. Metals. 2022; 12(3):521. https://doi.org/10.3390/met12030521
Chicago/Turabian StylePark, Jin-Seok, Jeong-Hyeon Kim, Yong-Cheol Jeong, Hee-Tae Kim, Seul-Kee Kim, and Jae-Myung Lee. 2022. "Effect of Corrugated Sheet Diameter on Structural Behavior under Cryogenic Temperature and Hydrodynamic Load" Metals 12, no. 3: 521. https://doi.org/10.3390/met12030521
APA StylePark, J.-S., Kim, J.-H., Jeong, Y.-C., Kim, H.-T., Kim, S.-K., & Lee, J.-M. (2022). Effect of Corrugated Sheet Diameter on Structural Behavior under Cryogenic Temperature and Hydrodynamic Load. Metals, 12(3), 521. https://doi.org/10.3390/met12030521






