Plastic Deformation Behavior of Metal Materials: A Review of Constitutive Models
Abstract
1. Introduction
2. Phenomenological Model
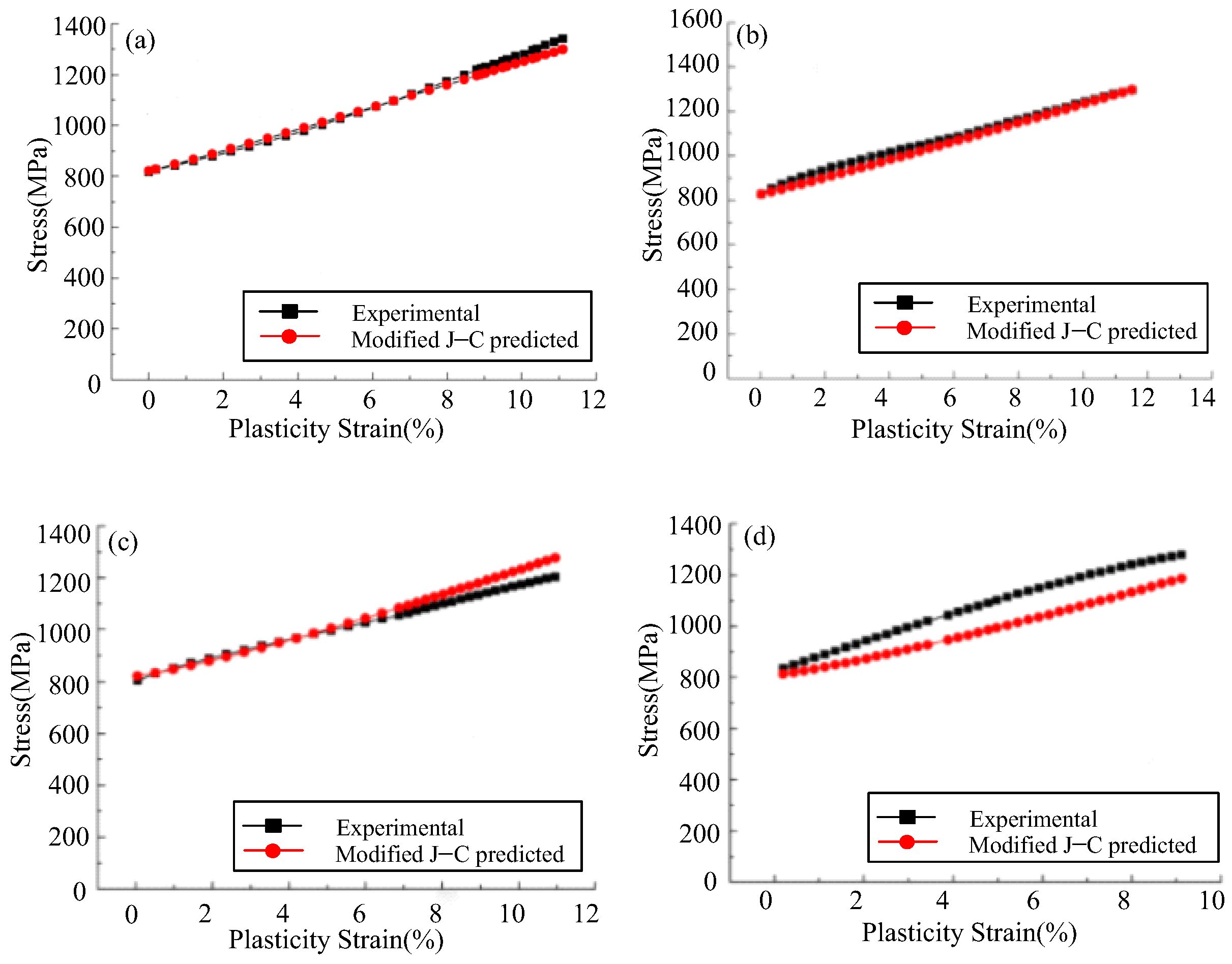
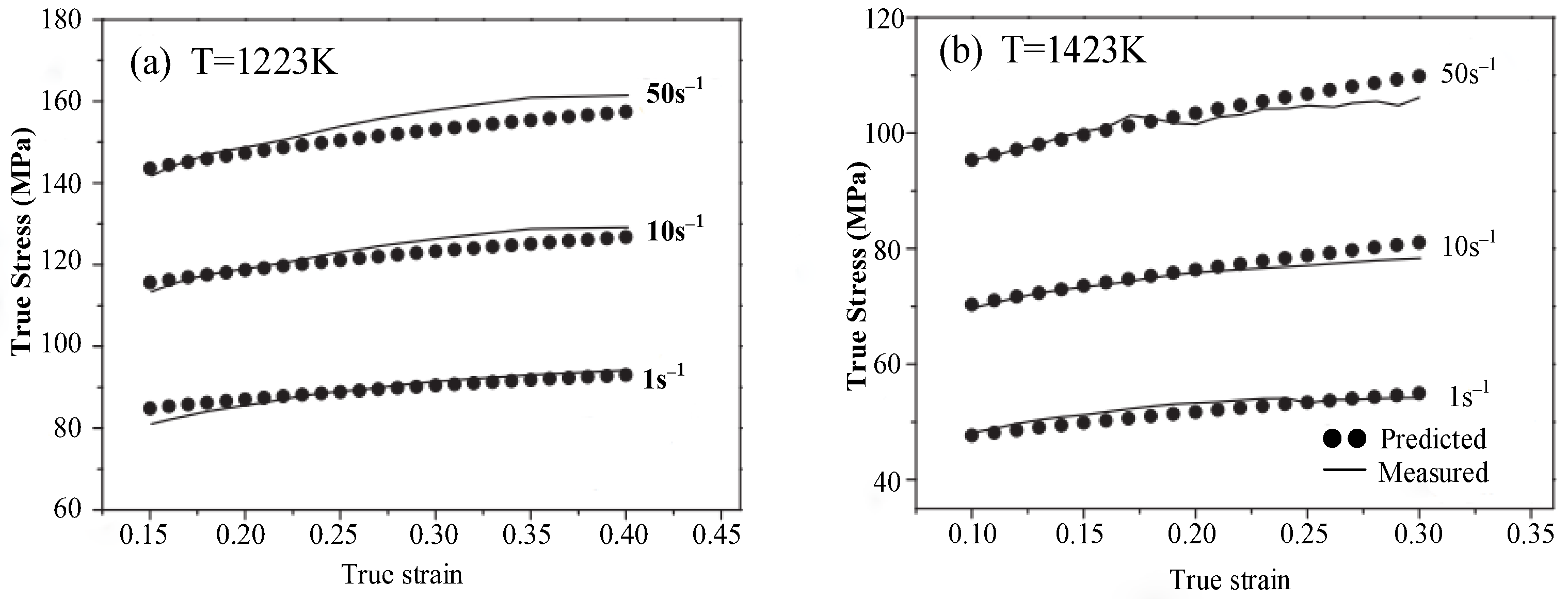
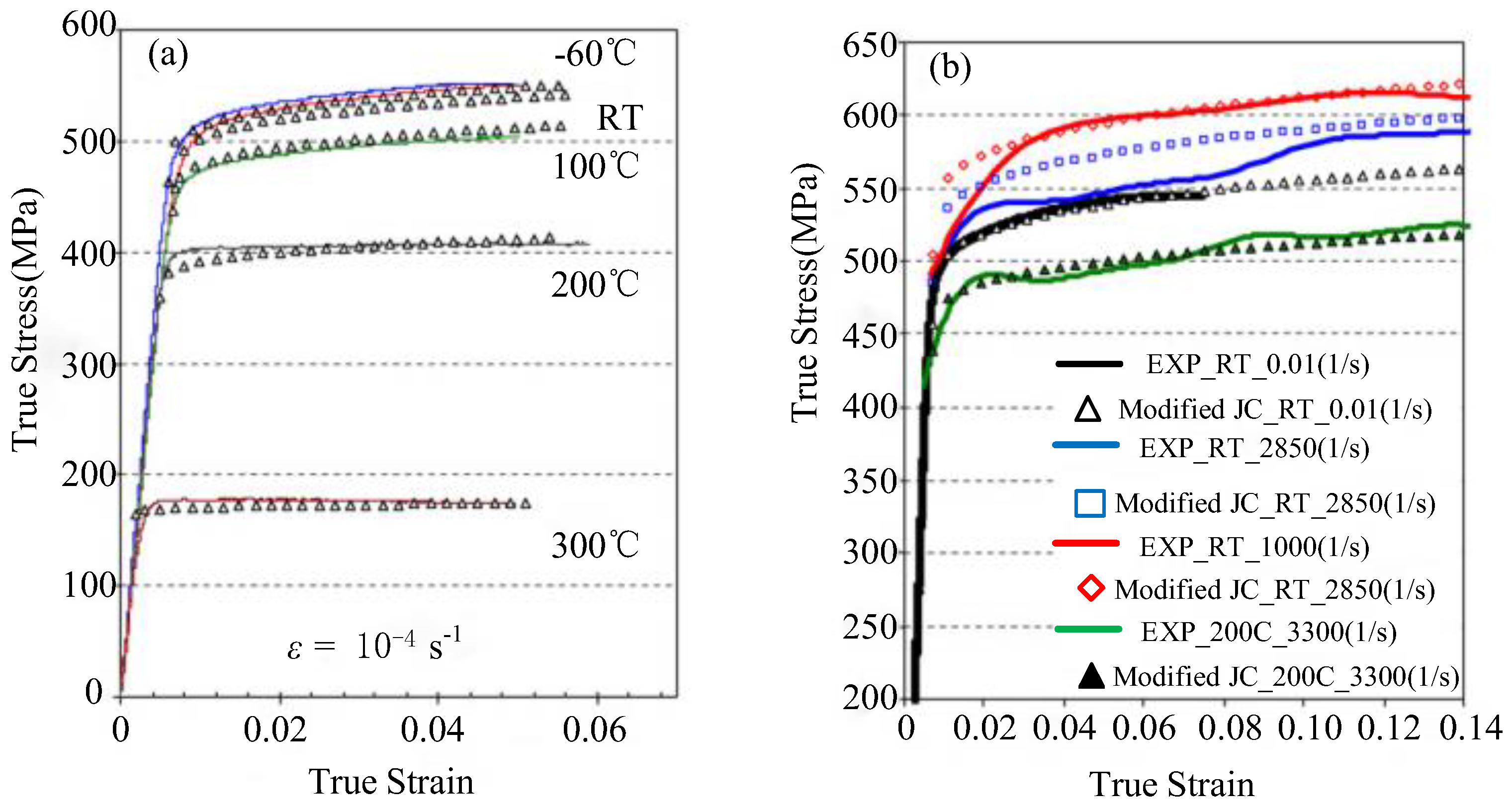
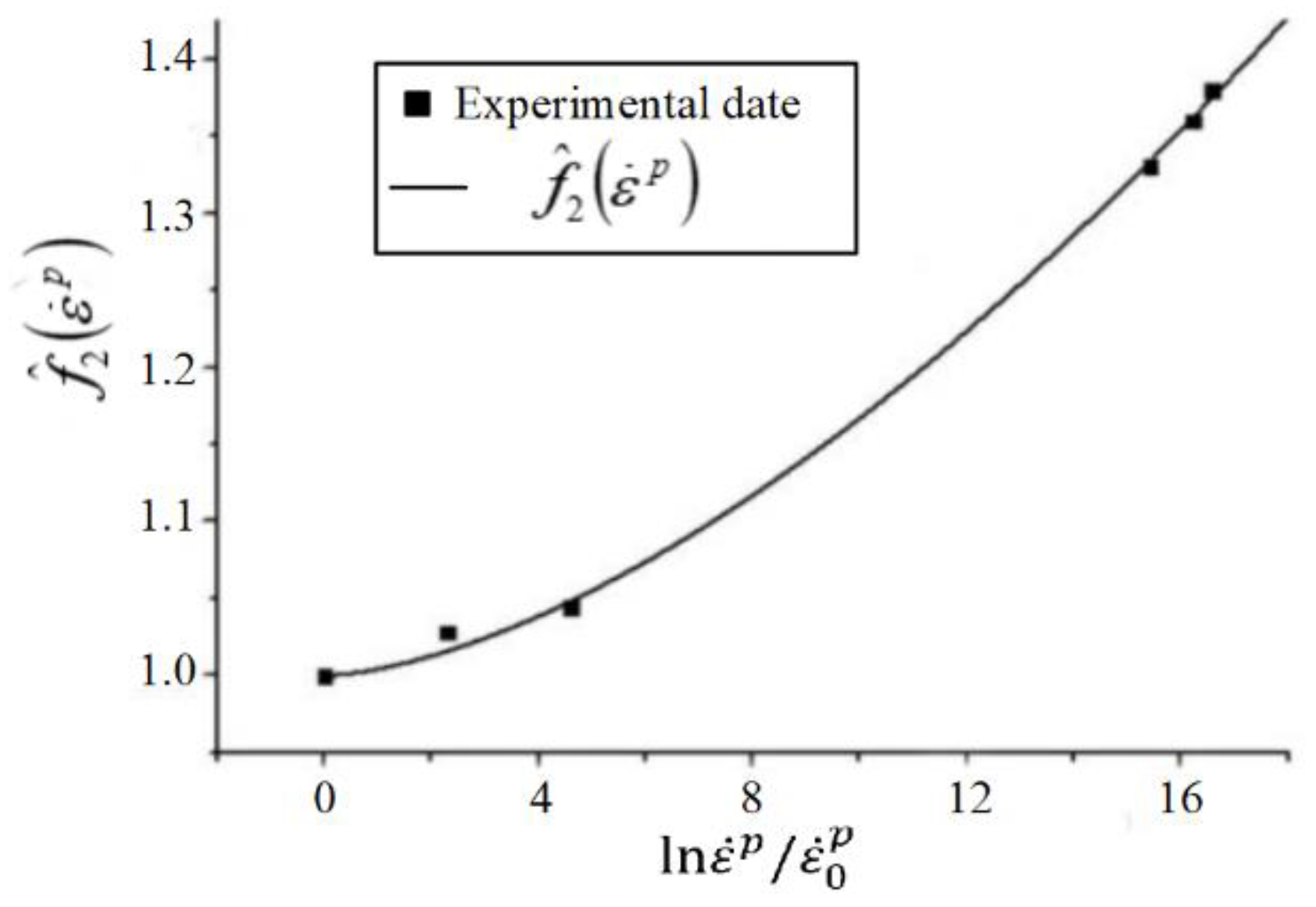
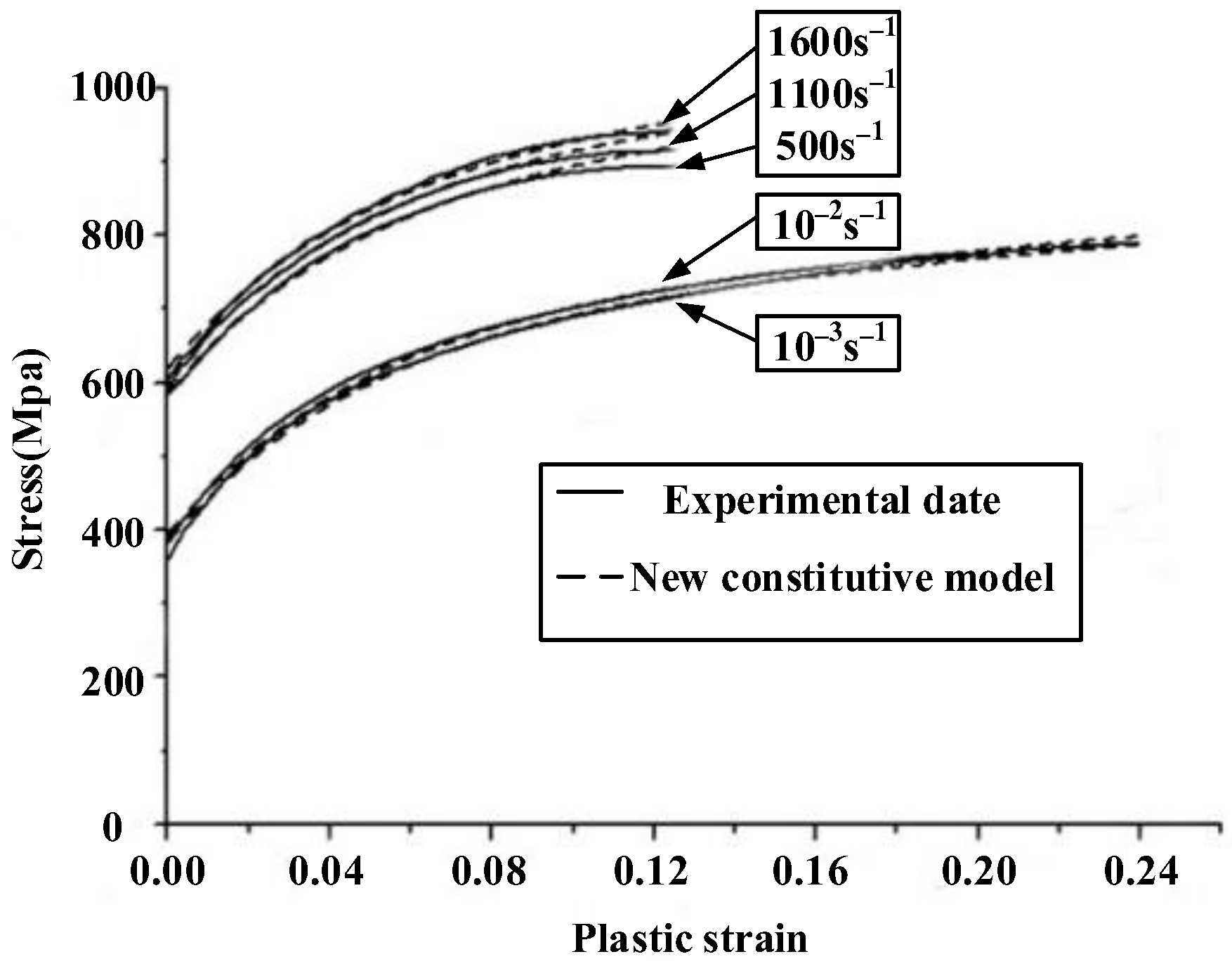
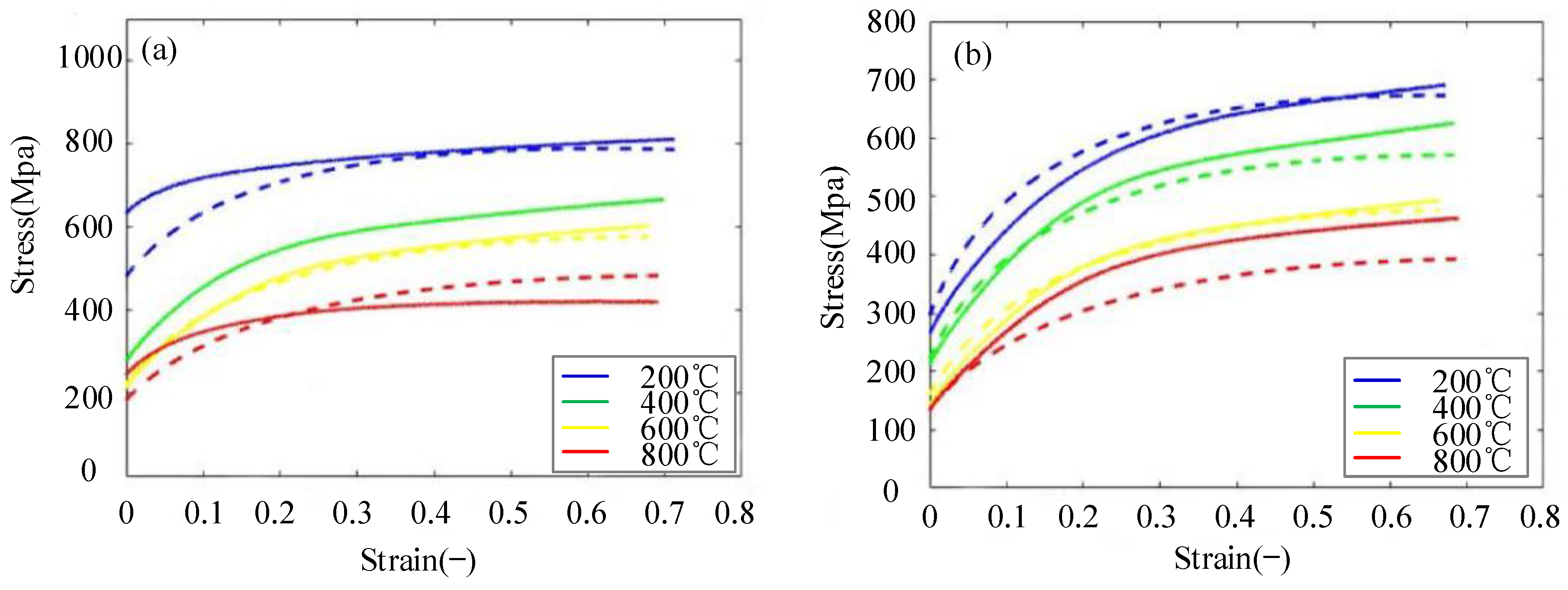
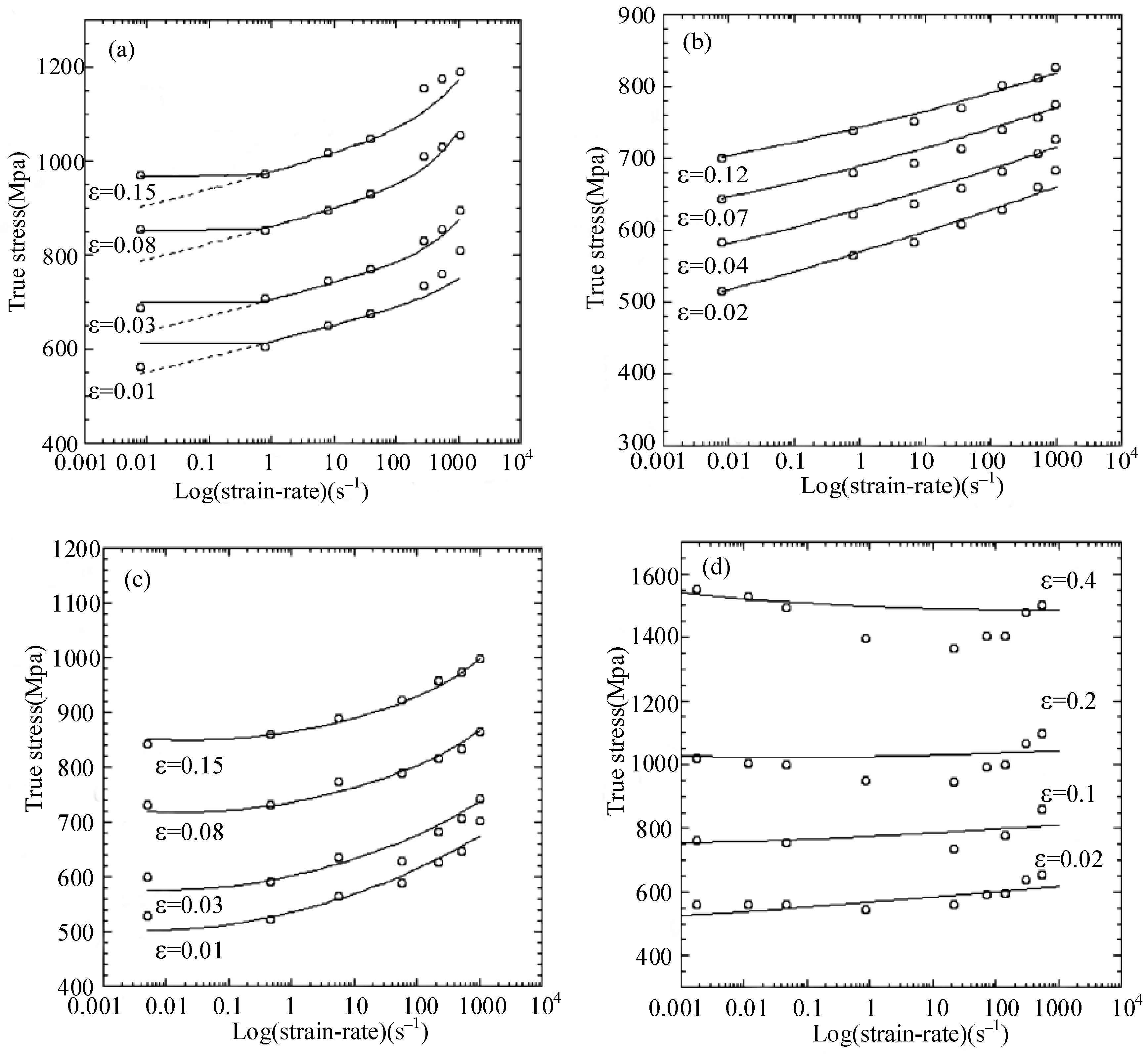
2.1. Johnson–Cook (J–C) Model
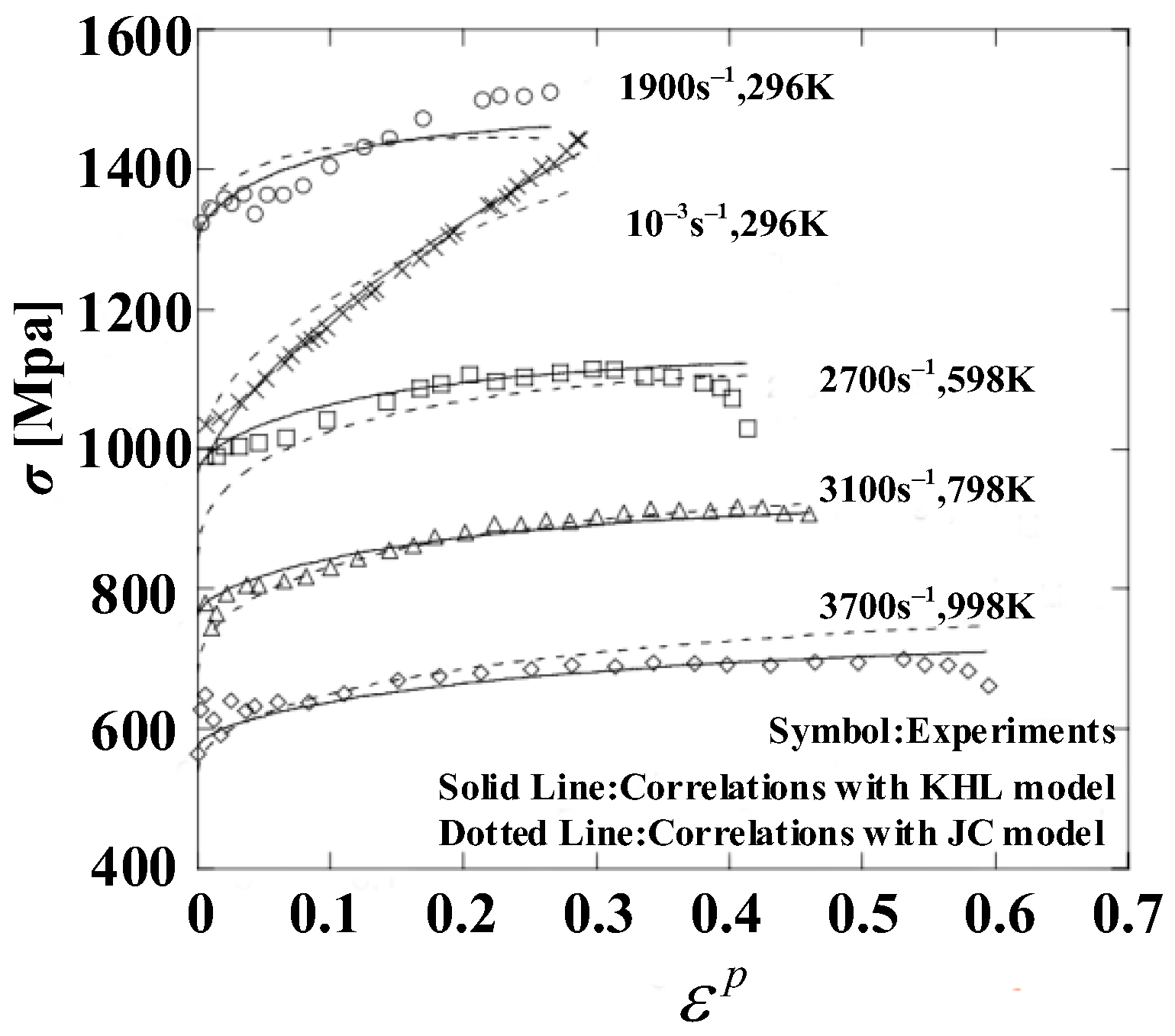
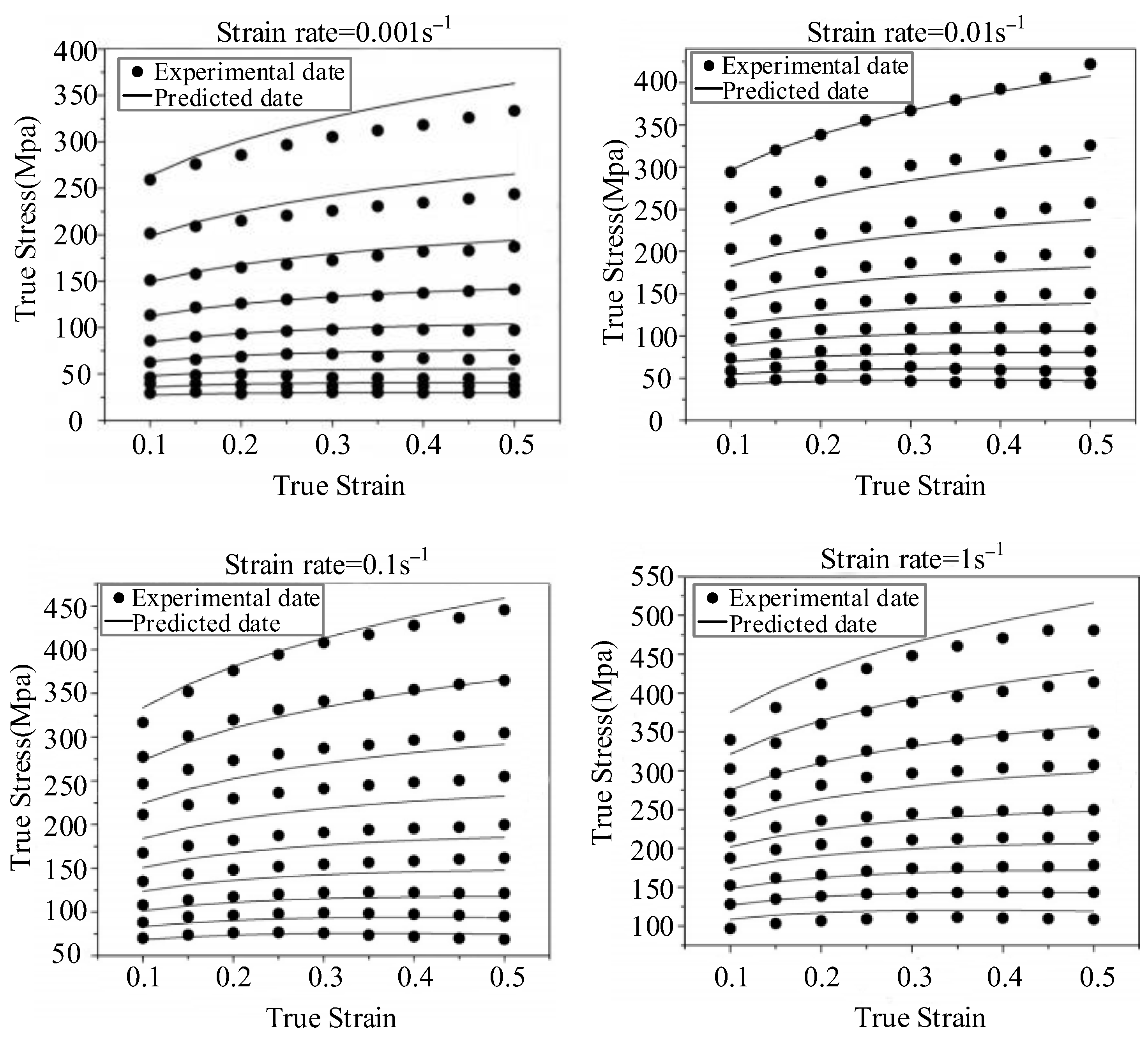
2.2. Khan–Huang (KH), Khan–Huang–Liang (KHL), Khan–Liang–Farrokh (KLF) Models
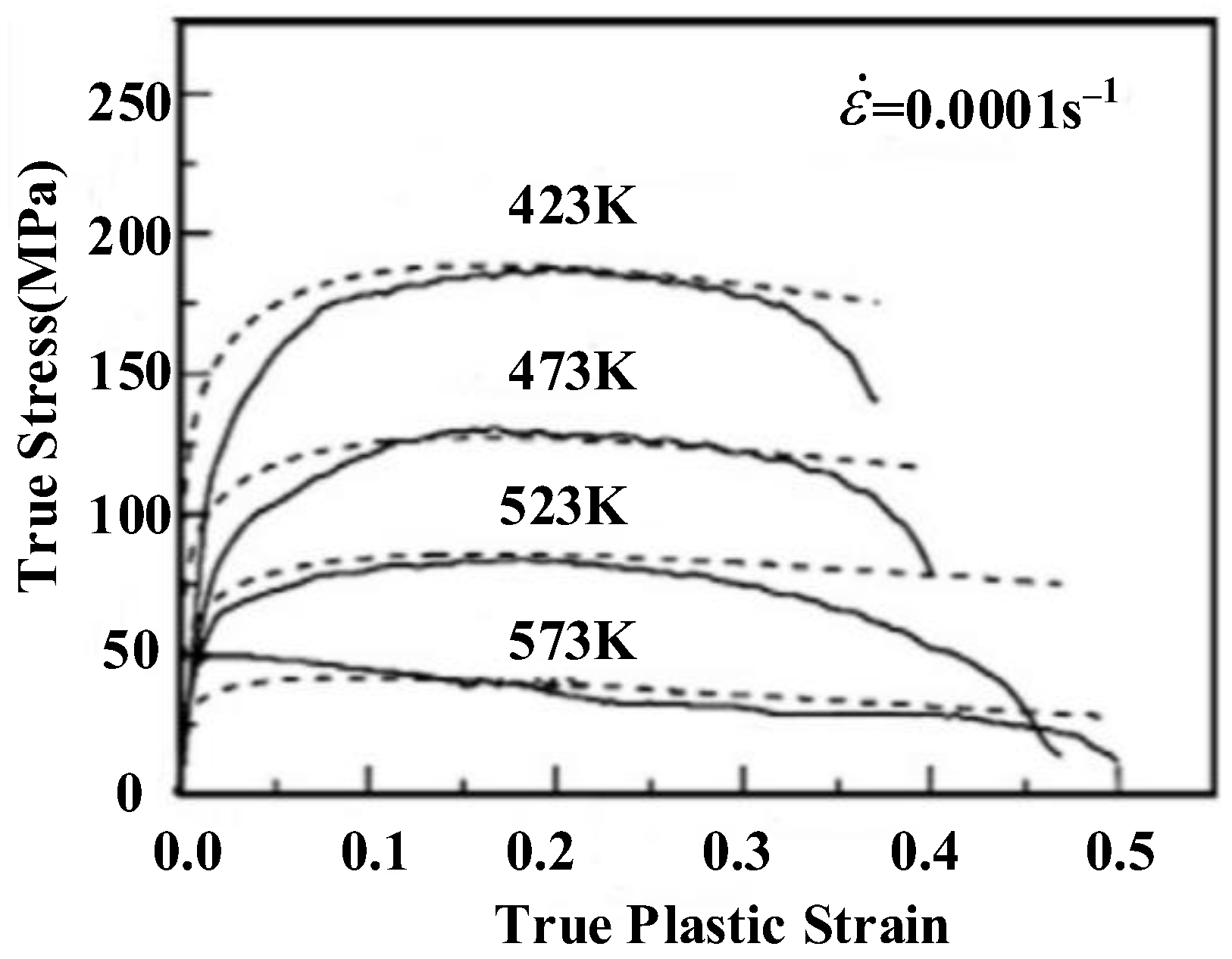
2.3. Fields–Backofen (FB) Model
2.4. Hansel–Spittel Model
2.5. Arrhenius Model
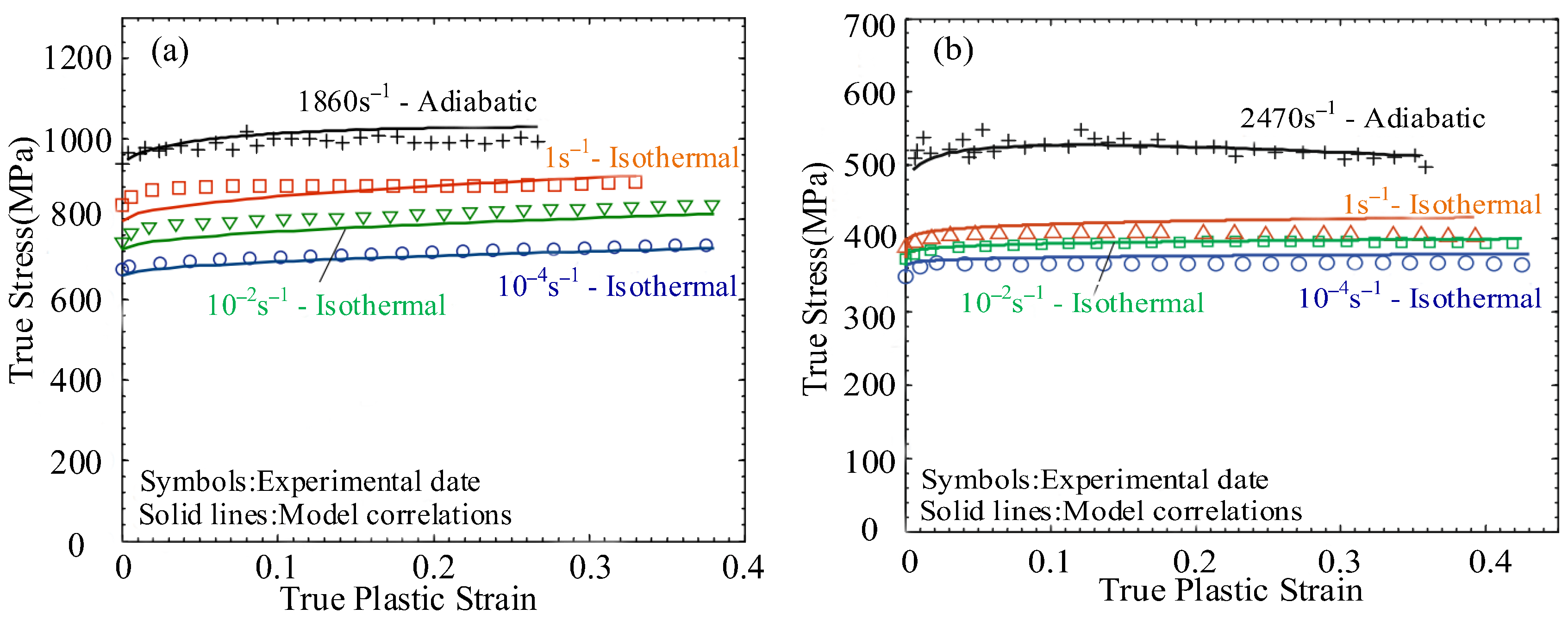
2.6. Molinari–Ravichandran Model
2.7. Comparison and Analysis of Phenomenological Models
3. Constitutive Model Based on Microscopic Characteristics
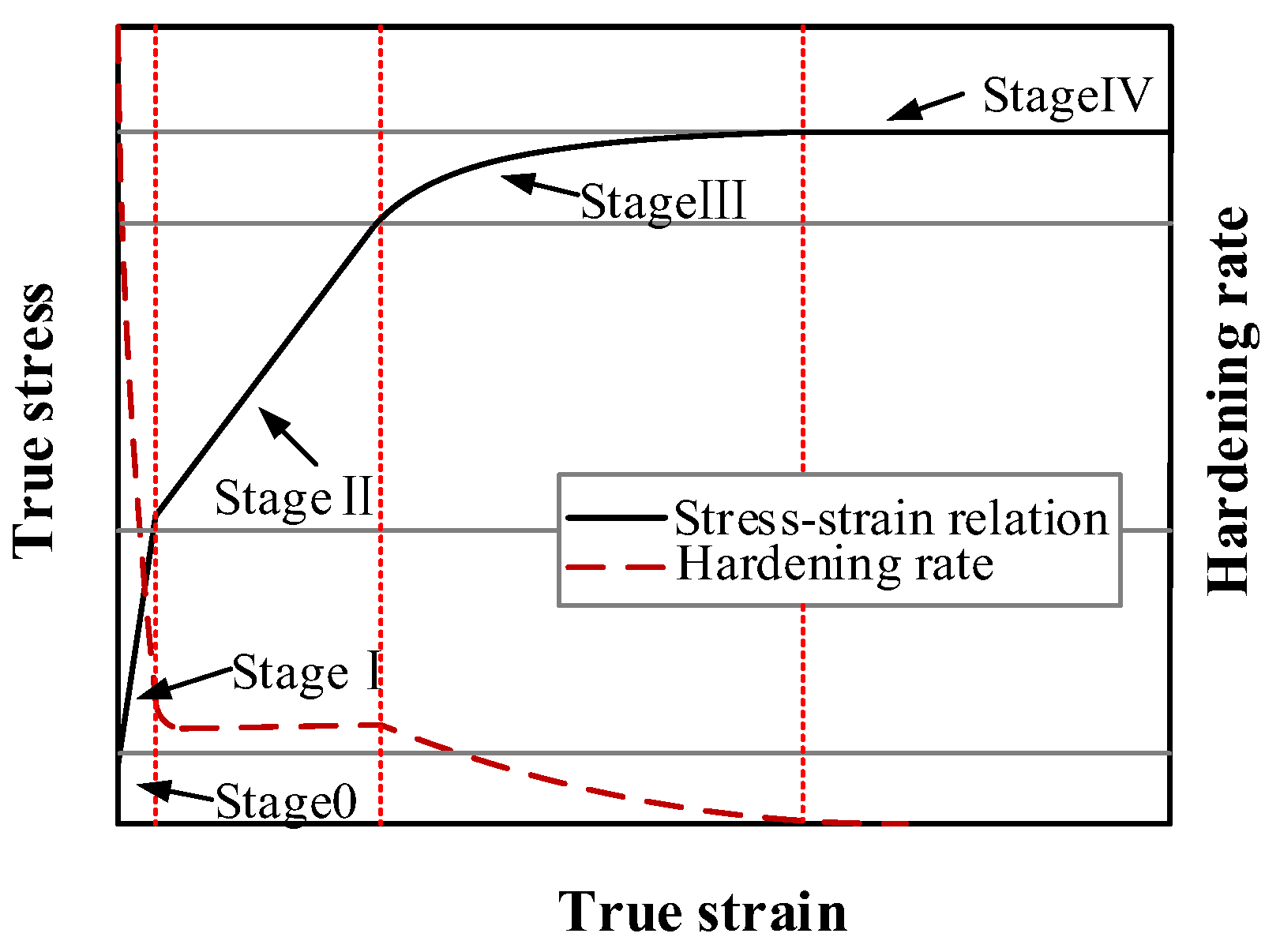
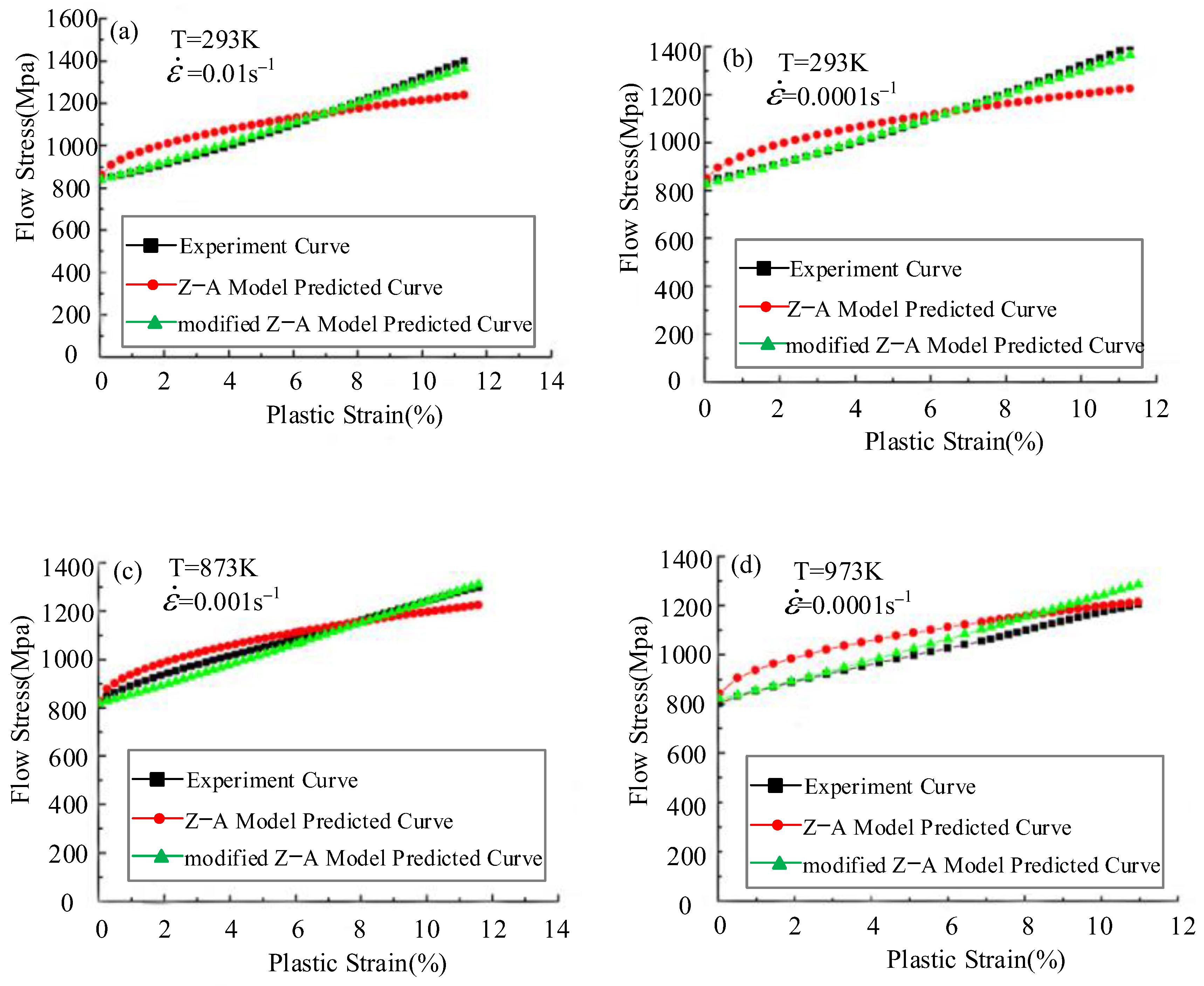
3.1. Zerilli–Armstrong Model (ZA Model)
3.2. Preston–Tonks–Wallace (PTW) Model
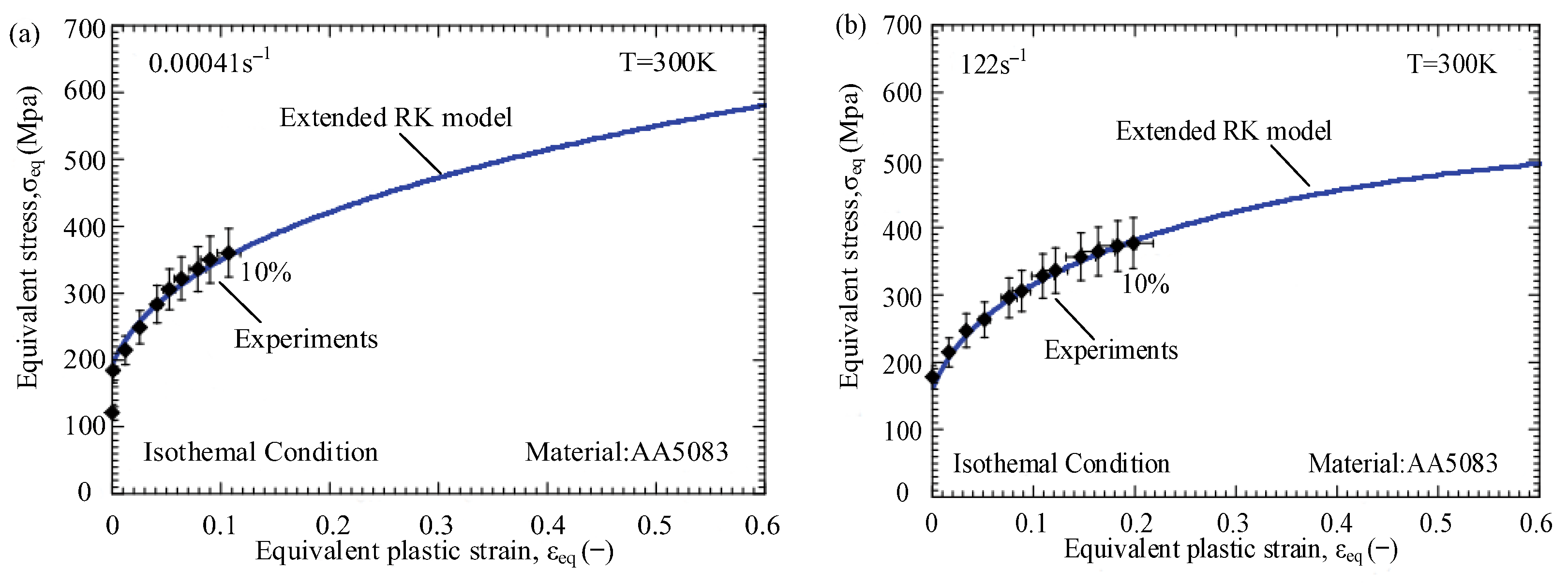
3.3. Rusinek–Klepaczko (RK) Model
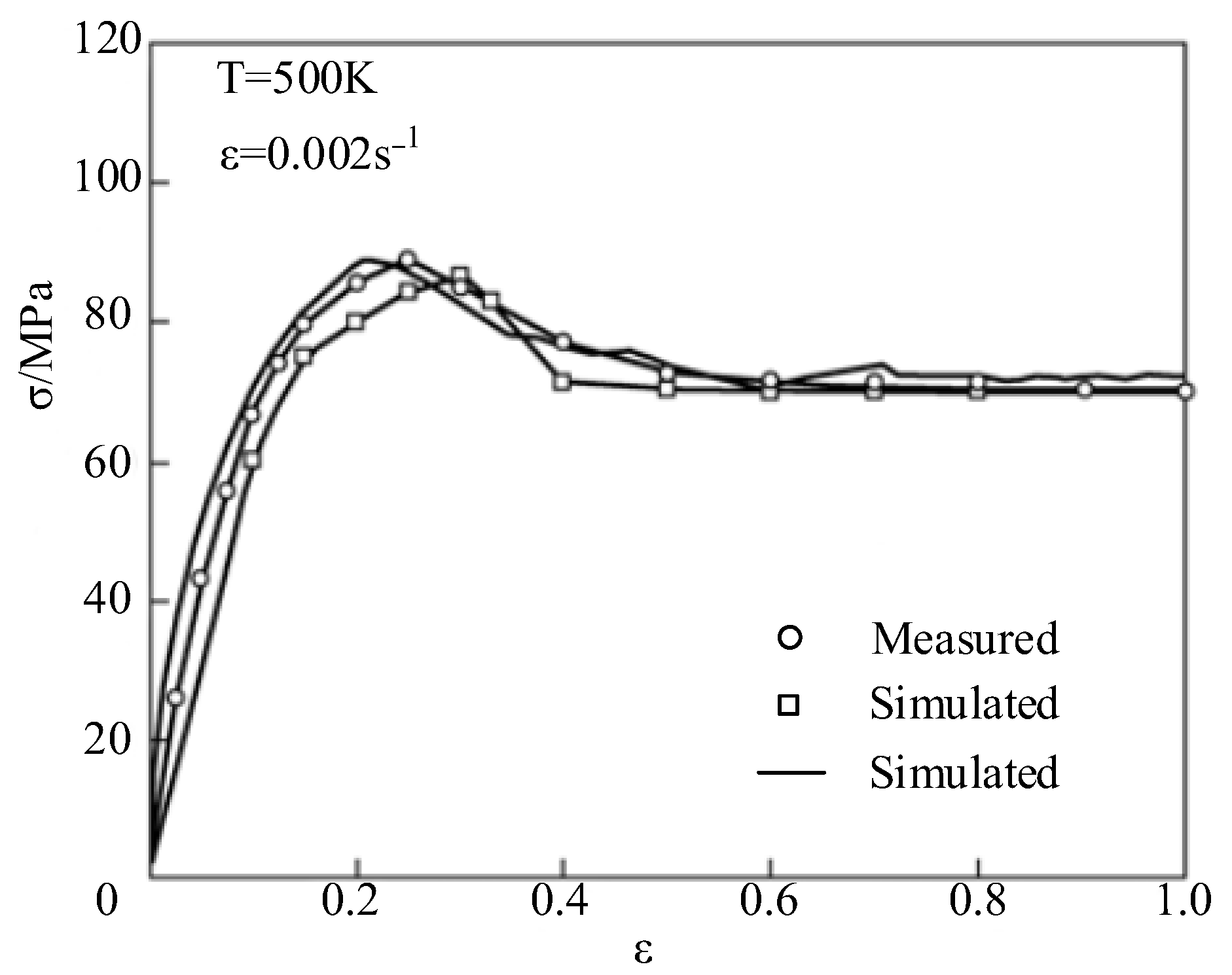
3.4. Cellular Automaton (CA) Model
3.5. Steinberg–Guinan (SG) Model and Steinberg–Lund (SL) Model
3.6. Comparison and Analysis of Microscopic Constitutive Models
4. Artificial Neural Network Model (ANN Model)
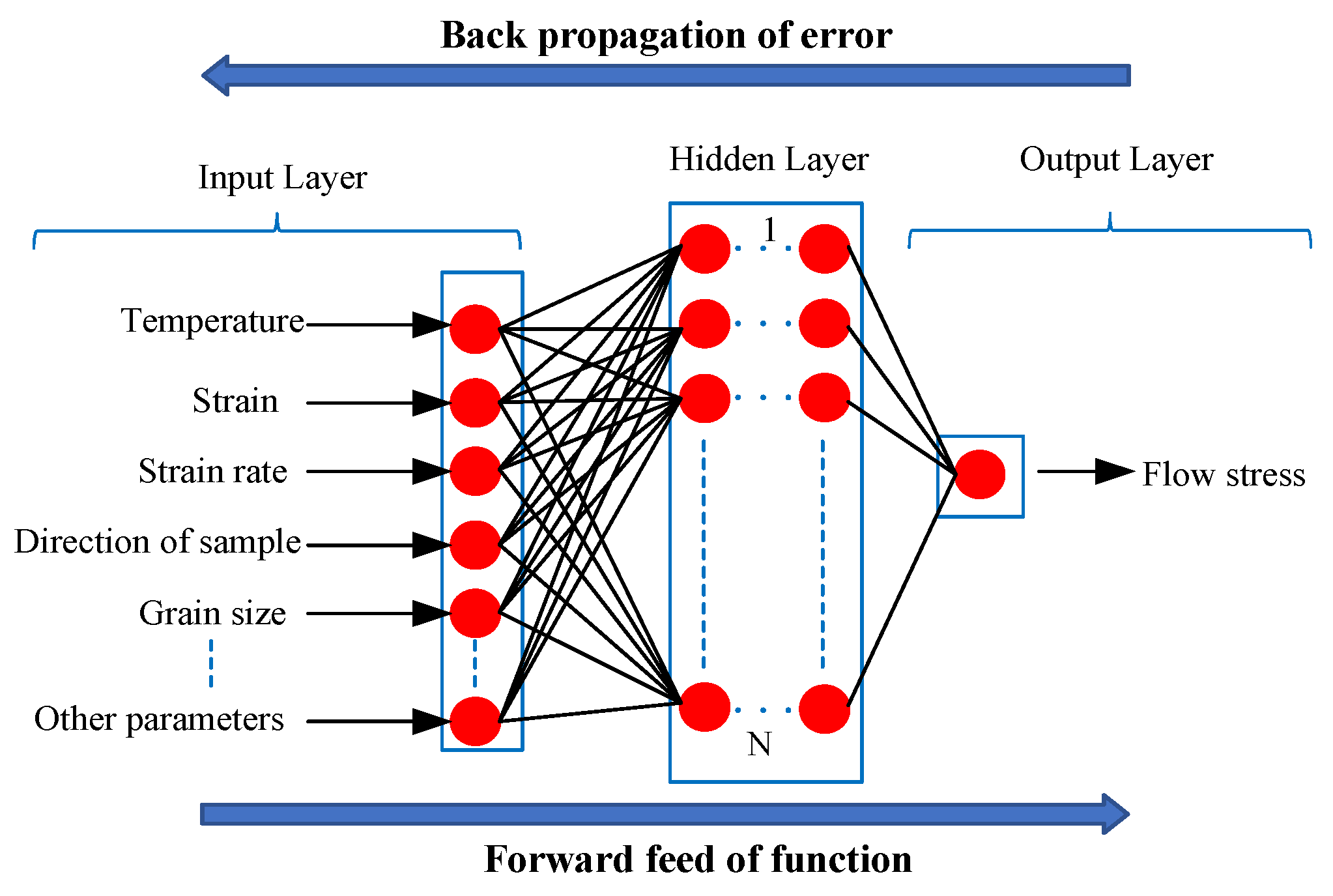
4.1. Back-Propagation (BP) Neural Network
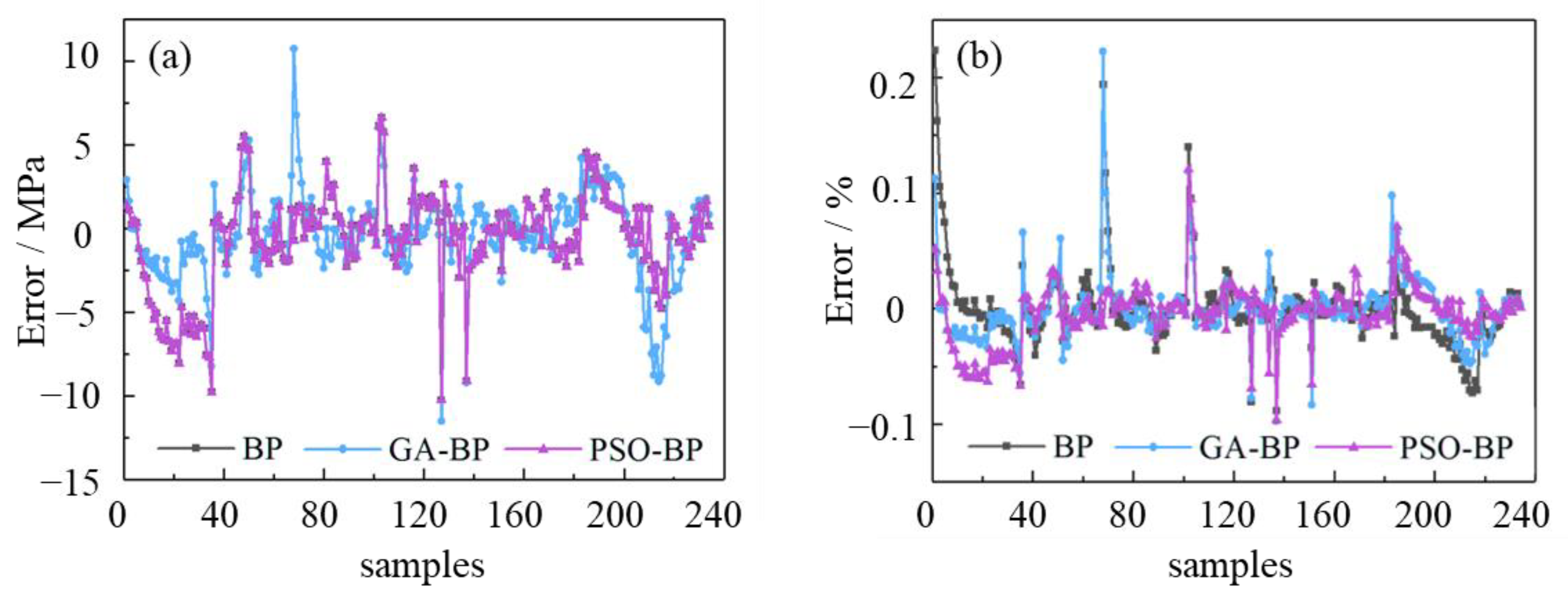
4.2. Applications of (BP) Neural Network
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xiao, J.; Li, D.S.; Li, X.Q.; Deng, T.S. Constitutive modeling and microstructure change of Ti–6Al–4V during the hot tensile deformation. J. Alloys Compd. 2012, 541, 346–352. [Google Scholar] [CrossRef]
- Ashtiani, H.R.R.; Parsa, M.H.; Bisadi, H. Constitutive equations for elevated temperature flow behavior of commercial purity aluminum. Mater. Sci. Eng. A 2012, 545, 61–67. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Study of metadynamic recrystallization behaviors in a low alloy steel. J. Mater. Process. Technol. 2008, 209, 2477–2482. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Effects of deformation temperatures on stress/strain distribution and microstructural evolution of deformed 42CrMo steel. Mater. Des. 2008, 30, 908–913. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel. Comput. Mater. Sci. 2007, 42, 470–477. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Study of static recrystallization kinetics in a low alloy steel. Comput. Mater. Sci. 2008, 44, 316–321. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S. Study of microstructural evolution during static recrystallization in a low alloy steel. J. Mater. Sci. 2009, 44, 835–842. [Google Scholar] [CrossRef]
- Pu, B.; Song, P.; Li, W.B.; Yao, W.J.; Wang, X.M. Plastic deformation behavior and constitutive modeling of Cu-50Ta alloy during hot compression. Mater. Res. Express 2022, 9, 016517. [Google Scholar] [CrossRef]
- Shin, H.; Kim, J.B. A Phenomenological Constitutive Equation to Describe Various Flow Stress Behaviors of Materials in Wide Strain Rate and Temperature Regimes. J. Eng. Mater. Technol. 2010, 132, 021009. [Google Scholar] [CrossRef]
- Rusinek, A.; Rodriguez-Martinez, J.A.; Arias, A. A thermo-viscoplastic constitutive model for FCC metals with application to OFHC copper. Int. J. Mech. Sci. 2009, 52, 120–135. [Google Scholar] [CrossRef]
- Gao, Y.L.; Sun, X.M. On the parameters of dynamic deformation and damage models of aluminum alloy 6008-T4 used for high-speed railway vehicles. Explos. Shock. Waves 2021, 41, 118–129. [Google Scholar]
- Ru, Y.F.; Zhang, L.L.; Liu, W.; Chen, G.; Dou, W.Y. Inverse Determination Method of Johnson-Cook Model Parameters Based on the Stress State Test of Notched Specimens. J. Mech. Eng. 2021, 57, 60–70. [Google Scholar]
- Zhang, H.J.; Wen, W.D.; Cui, H.T. Behaviors of IC10 alloy over a wide range of strain rates and temperatures: Experiments and modeling. Mater. Sci. Eng. A 2008, 504, 99–103. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M. A combined Johnson–Cook and Zerilli–Armstrong model for hot compressed typical high-strength alloy steel. Comput. Mater. Sci. 2010, 49, 628–633. [Google Scholar] [CrossRef]
- Vural, M.; Caro, J. Experimental analysis and constitutive modeling for the newly developed 2139-T8 alloy. Mater. Sci. Eng. A 2009, 520, 56–65. [Google Scholar] [CrossRef]
- Khan, A.S.; Huang, S.J. Experimental and theoretical study of mechanical behavior of 1100 aluminum in the strain rate range 10-5-104s-1. Int. J. Plast. 1992, 8, 397–424. [Google Scholar] [CrossRef]
- Yu, H.D.; Guo, Y.J.; Zhang, K.Z. Constitutive model on the description of plastic behavior of DP600 steel at strain rate from 10−4 to 103s−1. Comput. Mater. Sci. 2009, 46, 36–41. [Google Scholar] [CrossRef]
- Khan, A.S.; Liang, R.Q. Behaviors of three BCC metal over a wide range of strain rates and temperatures: Experiments and modeling. International Journal of Plasticity, 1999, 1 A combined Johnson–Cook and Zerilli–Armstrong model for hot compressed typical high-strength alloy steel. Int. J. Plast. 1999, 5, 1089–1109. [Google Scholar] [CrossRef]
- Khan, A.S.; Suh, Y.S.; Kazmi, R. Quasi-static and dynamic loading responses and constitutive modeling of titanium alloys. Int. J. Plast. 2004, 20, 2233–2248. [Google Scholar] [CrossRef]
- Khan, A.S.; Suh, Y.S.; Chen, X.; Takacs, L.; Zhang, H. Nanocrystalline aluminum and iron: Mechanical behavior at quasi-static and high strain rates, and constitutive modeling. Int. J. Plast. 2006, 22, 195–209. [Google Scholar] [CrossRef]
- Farrokh, B.; Khan, A.S. Grain size, strain rate, and temperature dependence of flow stress in ultra-fine grained and nanocrystalline Cu and Al: Synthesis, experiment, and constitutive modeling. Int. J. Plast. 2008, 25, 715–732. [Google Scholar] [CrossRef]
- Fields, D.S.; Bachofen, W.A. Determination of strain hardening characteristics by torsion testing. ASTM Proc. Am. Soc. Test. Mater. 1957, 57, 1259–1272. [Google Scholar]
- Cheng, Y.Q.; Zhang, H.; Chen, Z.H. Flow stress equation of AZ31 magnesium alloy sheet during warm tensile deformation. J. Mater. Process. Technol. 2008, 208, 29–34. [Google Scholar] [CrossRef]
- Zhang, X.H. Experimental and Numerical Study of Magnesium Alloy during Hot Working Process. PhD Thesis, Shanghai Jiaotong University, Shanghai, China, 2003. [Google Scholar]
- Chen, Y.Y.; Li, M.Q.; Li, L. Kinetic variables based constitutive model for high temperature deformation of Ti-46.5Al–2Nb–2Cr. J. Mater. Res. Technol. 2021, 15, 3525–3537. [Google Scholar] [CrossRef]
- Yoo, J.D.; Kim, M.C.; Kim, E.J.; Razali, M.K.; Joun, M.S. Flow stress characterization of magnesium alloys at elevated temperatures: A review. J. Phys. Conf. Ser. 2021, 2047, 012002. [Google Scholar] [CrossRef]
- Spigarelli, S.; El Mehtedi, M. A New Constitutive Model for the Plastic Flow of Metals at Elevated Temperatures. J. Mater. Eng. Perform. 2014, 23, 658–665. [Google Scholar] [CrossRef]
- Brown, C.; McCarthy, T.; Chadha, K.; Rodrigues, S.; Aranas, C., Jr.; Saha, G.C. Constitutive modeling of the hot deformation behavior of CoCrFeMnNi high-entropy alloy. Mater. Sci. Eng. A 2021, 826, 141940. [Google Scholar] [CrossRef]
- Shi, H.; McLaren, A.J.; Sellars, C.M.; Shahani, R.; Bolingbroke, R. Constitutive equations for high temperature flow stress of aluminium alloys. Mater. Sci. Technol. 1997, 13, 210–216. [Google Scholar] [CrossRef]
- Guan, S.K.; Wu, L.H.; Wang, L.G. Flow stress and microstructure evolution of semi-continuous casting AZ70 Mg-alloy during hot compression deformation. Trans. Nonferrous Met. Soc. China 2008, 18, 315–320. [Google Scholar] [CrossRef]
- Chae, D.; Koss, D.A. Damage Accumulation and Failure of HY-100 Steel.Metallurgical and Materials Transactions, A. Phys. Metall. Mater. Sci. 2001, 32, 2985–2994. [Google Scholar]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Effect of temperature and strain rate on the compressive deformation behavior of 42CrMo steel. J. Mater. Process. Technol. 2007, 205, 308–315. [Google Scholar] [CrossRef]
- Molinari, A.; Ravichandran, G. Constitutive modeling of high-strain-rate deformation in metals based on the evolution of an effective microstructural length. Mech. Mater. 2005, 37, 737–752. [Google Scholar] [CrossRef]
- Naderi, M.; Durrenberger, L.; Molinari, A.; Bleck, W. Constitutive relationships for 22MnB5 boron steel deformed isothermally at high temperatures. Mater. Sci. Eng. A 2007, 478, 130–139. [Google Scholar] [CrossRef]
- Durrenberger, L.; Molinari, A. Modeling of Temperature and Strain-Rate Effects in Metals Using an Internal Variable Model. Exp. Mech. 2009, 49, 247–255. [Google Scholar] [CrossRef]
- Durrenberger, L.; Molinari, A.; Rusinek, A. Internal variable modeling of the high strain-rate behavior of metals with applications to multiphase steels. Mater. Sci. Eng. A 2008, 478, 297–304. [Google Scholar] [CrossRef]
- Cerik, B.C.; Choung, J. Rate-dependent combined necking and fracture model for predicting ductile fracture with shell elements at high strain rates. Int. J. Impact Eng. 2020, 146, 103697. [Google Scholar] [CrossRef]
- He, X.; Liu, L.; Zeng, T.; Yao, Y. Micromechanical modelling of work hardening for coupling microstructure evolution, dynamic recovery and recrystallization: Application to high entropy alloys. Int. J. Mech. Sci. 2020, 177, 105567. [Google Scholar] [CrossRef]
- Zerilli, F.J.; Armstrong, R.W. Dislocation-mechanics-based constitutive relations for material dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef]
- Zhang, H.; Wen, W.; Cui, H.; Xu, Y. A modified Zerilli–Armstrong model for alloy IC10 over a wide range of temperatures and strain rates. Mater. Sci. Eng. A 2009, 527, 328–333. [Google Scholar] [CrossRef]
- Samantaray, D.; Mandal, S.; Borah, U.; Bhaduri, A.K.; Sivaprasad, P.V. A thermo-viscoplastic constitutive model to predict elevated-temperature flow behaviour in a titanium-modified austenitic stainless steel. Mater. Sci. Eng. A 2009, 526, 1–6. [Google Scholar] [CrossRef]
- Preston, D.L.; Tonks, D.L.; Wallace, D.C. Model of plastic deformation for extreme loading conditions. J. Appl. Phys. 2002, 93, 211. [Google Scholar] [CrossRef]
- Kim, J.B.; Shin, H.H. Comparison of plasticity models for tantalum and a modification of the PTW model for wide ranges of strain, strain rate, and temperature. Int. J. Impact Eng. 2009, 36, 746–753. [Google Scholar] [CrossRef]
- Rusinek, A.; Klepaczko, J.R. Shear testing of a sheet steel at wide range of strain rates and a constitutive relation with strain-rate and temperature dependence of the flow stress. Int. J. Plast. 2001, 17, 87–115. [Google Scholar] [CrossRef]
- Rusinek, A.; Rodríguez-Martínez, J.A. Thermo-viscoplastic constitutive relation for aluminium alloys, modeling of negative strain rate sensitivity and viscous drag effects. Mater. Des. 2009, 30, 4377–4390. [Google Scholar] [CrossRef]
- Goetz, R.L.; Seetharaman, V. Modeling Dynamic Recrystallization Using Cellular Automata. Scr. Mater. 1998, 38, 405–413. [Google Scholar] [CrossRef]
- Jin, Z.Y.; Juan, L.; Cui, Z.S.; Wei, D.L. Identification of nucleation parameter for cellular automaton model of dynamic recrystallization. Trans. Nonferrous Met. Soc. China 2010, 20, 458–464. [Google Scholar] [CrossRef]
- Ren, Z.; Pu, Z.P.; Liu, D.R. Prediction of grain-size transition during solidification of hypoeutectic Al-Si alloys by an improved three-dimensional sharp-interface model. Comput. Mater. Sci. 2022, 203, 111131. [Google Scholar] [CrossRef]
- Zhao, Y.; Pu, Z.; Wang, L.; Liu, D.R. Modeling of Grain Refinement and Nucleation Behavior of Mg-4Y-0.5Zr (wt.%) Alloy via Cellular Automaton Model. Int. J. Met. 2021, 16, 945–961. [Google Scholar] [CrossRef]
- Song, Y.; Jiang, H.; Zhang, L.; He, J.; Zhao, J. Integrated model for describing the microstructure evolution of the inoculated Al-Zn-Mg-Cu alloys in continuous solidification. Results Phys. 2021, 26, 104465. [Google Scholar] [CrossRef]
- Gu, C.; Lu, Y.; Ridgeway, C.D.; Cinkilic, E.; Luo, A.A. Three-dimensional cellular automaton simulation of coupled hydrogen porosity and microstructure during solidification of ternary aluminum alloys. Sci. Rep. 2019, 9, 13099. [Google Scholar] [CrossRef]
- Steinberg, D.J.; Cochran, S.G.; Guinan, M.W. A constitutive model for metals applicable at high-strain rate. J. Appl. Phys. 1980, 51, 1498–1504. [Google Scholar] [CrossRef]
- Steinberg, D.J.; Lund, C.M. A constitutive model for strain rates from 10-4 to10-6S-1. J. Appl. Phys. 1989, 65, 1528. [Google Scholar] [CrossRef]
- Zaretsky, E.B.; Frage, N.; Ratzker, B.; Kalabukhov, S.; Mayseless, M. Impact response of a tungsten heavy alloy over 23–1100 °C temperature range. J. Appl. Phys. 2021, 129, 125902. [Google Scholar] [CrossRef]
- Brown, J.L.; Knudson, M.D.; Alexander, C.S.; Asay, J.R. Shockless compression and release behavior of beryllium to 110 GPa. J. Appl. Phys. 2014, 116, 411. [Google Scholar] [CrossRef]
- Li, W.; Kou, H.; Zhang, X.; Ma, J.; Li, Y.; Geng, P.; Wu, X.; Chen, L.; Fang, D. Temperature-dependent elastic modulus model for metallic bulk materials. Mech. Mater. 2019, 139, 103194. [Google Scholar] [CrossRef]
- Yang, X.; Zeng, X.; Wang, F.; Zhao, H.; Chen, J.; Wang, Y. A modified Steinberg-Cochran-Guinan model applicable to solid-liquid mixed zone along the principle Hugoniot. Mech. Mater. 2021, 155, 103775. [Google Scholar] [CrossRef]
- Mishra, S.K.; Brahma, A.; Dutta, K. Prediction of mechanical properties of Al-Si-Mg alloy using artificial neural network. Sādhanā 2021, 46, 139. [Google Scholar] [CrossRef]
- Singh, K.; Rajput, S.K.; Mehta, Y. Modeling of the hot deformation behavior of a high phosphorus steel using artificial neural network. Mater. Discov. 2017, 6, S2352924517300078. [Google Scholar] [CrossRef]
- Zhong, M.J.; Wang, K.L.; Lu, S.Q. Study on high temperature deformation behavior and BP neural network constitutive model of MoNb alloy. J. Plast. Eng. 2020, 27, 177–182. [Google Scholar]
- Jain, R.; Jain, A.; Rahul, M.R.; Kumar, A.; Dubey, M.; Sabat, R.K.; Samal, S.; Phanikumar, G. Development of ultrahigh strength novel Co–Cr–Fe–Ni–Zr quasi-peritectic high entropy alloy by an integrated approach using experiment and simulation. Materialia 2020, 14, 100896. [Google Scholar] [CrossRef]
- Lin, Q.Q.; Peng, D.S.; Zhu, Y.Z. Establishment of constitutive relationship model for 2519 aluminum alloy based on BP artificial neural network. J. Cent. South Univ. Technol. 2005, 12, 380–384. [Google Scholar] [CrossRef]
- Yu, Y.; Pan, Q.; Wang, W.; Huang, Z.; Xiang, S.; Lin, G.; Yan, J.; Liu, B. Microstructure Evolution and Constitutive Analysis of Al-Mg-Si-Ce-B Alloy during Hot Deformation. J. Mater. Eng. Perform. 2022, 31, 4707–4720. [Google Scholar] [CrossRef]
- Mi, X.; Tian, L.; Tang, A.; Kang, J.; Peng, P.; She, J.; Wang, H.; Chen, X.; Pan, F. A reverse design model for high-performance and low-cost magnesium alloys by machine learning. Comput. Mater. Sci. 2022, 201, 110881. [Google Scholar] [CrossRef]
- Sheikh, H.; Serajzadeh, S. Estimation of flow stress behavior of AA5083 using artificial neural networks with regard to dynamic strain ageing effect. J. Mater. Process. Technol. 2008, 196, 115–119. [Google Scholar] [CrossRef]
- Yan, J.; Pan, Q.L.; Li, A.D.; Song, W.B. Flow behavior of Al–6.2Zn–0.70Mg–0.30Mn–0.17Zr alloy during hot compressive deformation based on Arrhenius and ANN models. Trans. Nonferrous Met. Soc. China 2017, 27, 638–647. [Google Scholar] [CrossRef]
- Sabokpa, O.; Zarei-Hanzaki, A.; Abedi, H.R.; Haghdadi, N. Artificial neural network modeling to predict the high temperature flow behavior of an AZ81 magnesium alloy. Mater. Des. 2012, 39, 390–396. [Google Scholar] [CrossRef]
- Li, H.Y.; Wei, D.D.; Li, Y.H.; Wang, X.F. Application of artificial neural network and constitutive equations to describe the hot compressive behavior of 28CrMnMoV steel. Mater. Des. 2012, 35, 557–562. [Google Scholar] [CrossRef]
- Haghdadi, N.; Zarei-Hanzaki, A.; Khalesian, A.R.; Abedi, H.R. Artificial neural network modeling to predict the hot deformation behavior of an A356 aluminum alloy. Mater. Des. 2013, 49, 386–391. [Google Scholar] [CrossRef]
- Rao, K.P.; Prasad, Y.K.D.V. Neural network approach to flow stress evaluation in hot deformation. J. Mater. Process. Technol. 1995, 53, 552–566. [Google Scholar] [CrossRef]
- Wang, Y.J.; Wang, K.L.; Liu, S.Q. Hot Deformation Behavior and Forging Process Optimization of MoLa Alloy Based on Polar Reciprocity Model. Rare Met. Mater. Eng. 2018, 47, 2225–2231. [Google Scholar]
- Zhang, J.P.; Gao, P.F.; Fang, F. An ATPSO-BP neural network modeling and its application in mechanical property prediction. Comput. Mater. Sci. 2019, 163, 262–266. [Google Scholar] [CrossRef]
- Wan, P.; Wang, K.L.; Lu, S.Q. Constitutive modeling of Ti-2.7Cu alloy based on strain compensation and PSO-BP neural network. J. Eng. 2019, 47, 113–119. [Google Scholar]
- Ding, F.j.; Jia, X.D.; Hong, T.J.; Xu, Y.L. Flow Stress Prediction Model of 6061 Aluminum Alloy Sheet Based on GA-BP and PSO-BP Neural Networks. Rare Met. Mater. Eng. 2020, 49, 1840–1853. [Google Scholar]
- Gao, T.J.; Zhao, D.; Zhang, T.W.; Jin, T.; Ma, S.G.; Wang, Z.H. Strain-rate-sensitive mechanical response, twinning, and texture features of NiCoCrFe high-entropy alloy: Experiments, multi-level crystal plasticity and artificial neural networks modeling. J. Alloys Compd. 2020, 845, 155911. [Google Scholar] [CrossRef]
- Yuan, D.; Chen, J.; Yang, Y.; Zhang, L.; Liu, S.; Jiang, H.; Qian, N. Thermal Performance of the Thin Heat Pipe for Cooling of Solid-State Drives. Metals 2022, 12, 1786. [Google Scholar] [CrossRef]
- Stoffel, M.; Bamer, F.; Markert, B. Neural network based constitutive modeling of nonlinear viscoplastic structural response. Mech. Res. Commun. 2019, 95, 85–88. [Google Scholar] [CrossRef]
- Bonnili, R.; Madhu, V. Constitutive modeling and fracture behavior of a biomedical Ti-13Nb-13Zr alloy. Mater. Sci. Eng. A 2017, 700, 82–91. [Google Scholar]








| Model Name | Characteristics and Application Conditions |
|---|---|
| Johnson–Cook (J–C) Model |
|
| Khan–Huang (KH) Model |
|
| Khan–Huang–Liang (KHL) Model |
|
| Khan–Liang–Farrokh (KLF) Model |
|
| Fields–Backofen (FB) Model |
|
| Hansel–Spittel Model |
|
| Arrhenius Model |
|
| Molinari–Ravichandran Model |
|
| Model Name | Characteristics and Application Conditions |
|---|---|
| Zerilli–Armstrong Molde (ZA Model) |
|
| Preston–Tonks–Wallace (PTW) Model |
|
| Rusinek–Klepaczko Model (RK Model) |
|
| Cellular Automaton Model (CA Model) |
|
| Steinberg-Guinan Model (SG Model) |
|
| Steinberg-Lund Model (SL Model) |
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, X.; Hao, K.; Luo, Z.; Fan, Z. Plastic Deformation Behavior of Metal Materials: A Review of Constitutive Models. Metals 2022, 12, 2077. https://doi.org/10.3390/met12122077
Jia X, Hao K, Luo Z, Fan Z. Plastic Deformation Behavior of Metal Materials: A Review of Constitutive Models. Metals. 2022; 12(12):2077. https://doi.org/10.3390/met12122077
Chicago/Turabian StyleJia, Xiangdong, Kunming Hao, Zhan Luo, and Zhenyu Fan. 2022. "Plastic Deformation Behavior of Metal Materials: A Review of Constitutive Models" Metals 12, no. 12: 2077. https://doi.org/10.3390/met12122077
APA StyleJia, X., Hao, K., Luo, Z., & Fan, Z. (2022). Plastic Deformation Behavior of Metal Materials: A Review of Constitutive Models. Metals, 12(12), 2077. https://doi.org/10.3390/met12122077





