Structural Phase Transformation of Rail Steel in Compression
Abstract
1. Introduction
2. Materials and Methods
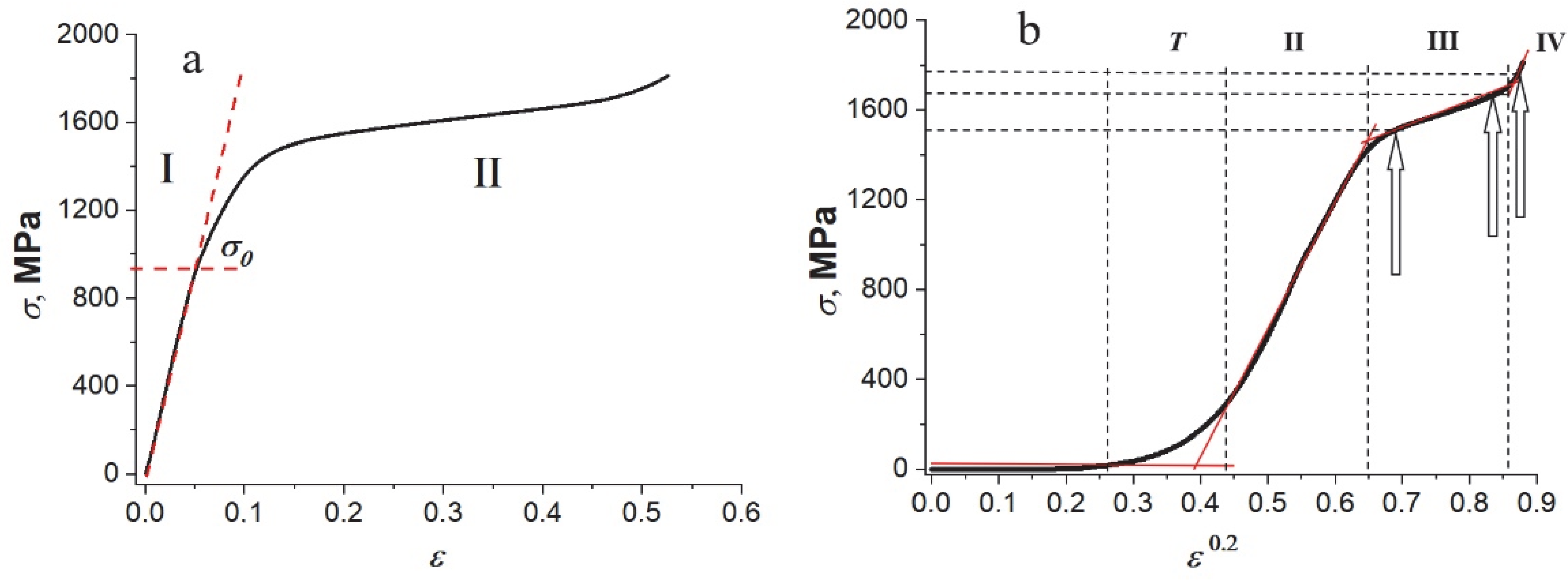
3. Results
4. Conclusions
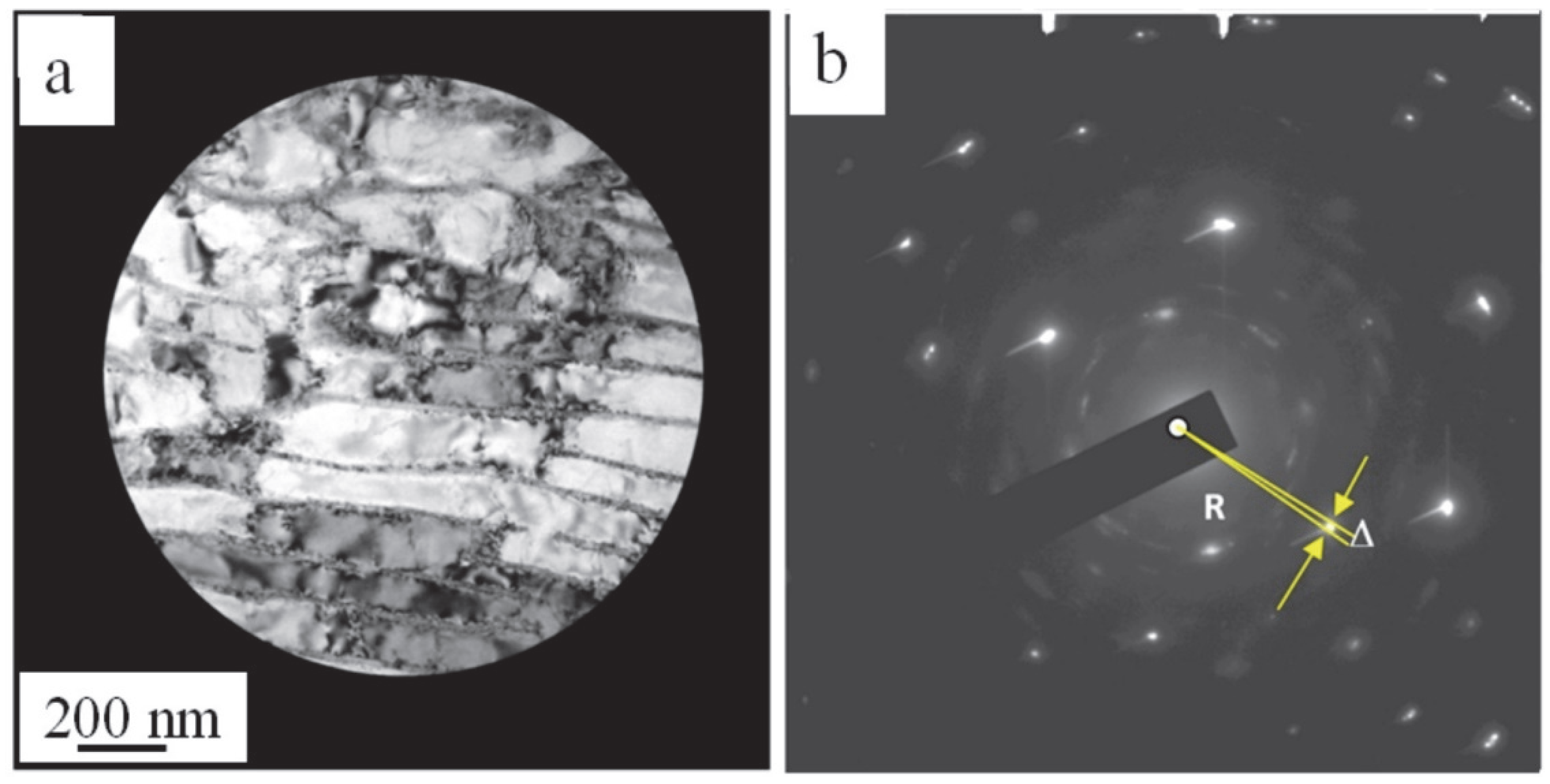
- The analysis of the defective substructure evolution of rail steel has revealed that cold hardening has a multi-stage character. Steel deformation is accompanied by a fragmentation of pearlite grains which intensifies as the degree of deformation increases and reaches ≈ 0.4 of the material volume at ε = 50%. With the increase in the degree of deformation, the average size of the fragments of the ferrite plates decreases, from 240 nm at ε = 15% to 200 nm at ε = 50%.
- The fragmentation of cementite plates has been detected. It is established that fragment sizes vary in a range between 15 and 20 nm and depend weakly on the degree of steel deformation. It is found that the failure of cementite plates is proceeded by the mechanisms of their dissolution and cut with mobile dislocations. It is shown that carbon atoms, having gone from the cementite crystal lattice, are carried out to an interplanar space and form the particles of tertiary cementite whose sizes are between 2 to 4 nm.
- A formation of the non-uniform dislocation substructure due to a deceleration of dislocations by cementite particles is revealed in the process of steel deformation. The increase in the degree of deformation is accompanied by a decrease in the scalar and excess dislocation density, which may be caused by the escape of dislocation to low-angle boundaries in addition to their annihilation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuriev, A.A.; Ivanov, Y.F.; Gromov, V.E.; Rubannikova, Y.A.; Starostenkov, M.D.; Tabakov, P.Y. Structure and Properties of Lengthy Rails after Extreme Long-Term Operation; Materials Research Forum LLC: Millersville, PA, USA, 2021; p. 190. [Google Scholar]
- Ivanov, Y.F.; Gromov, V.E.; Nikitina, E.N. Bainite Constructional Steel: Structure and Properties; CISP Ltd.: Cambridge, UK, 2016; p. 179. [Google Scholar]
- Vinogradov, A.; Estrin, Y. Analytical and numerical approaches to modelling severe plastic deformation. Prog. Mater. Sci. 2018, 95, 172–242. [Google Scholar] [CrossRef]
- Pan, R.; Ren, R.; Chen, C.; Zhao, X. Formation of nanocrystalline structure in pearlitic steels by dry sliding wear. Mater. Charact. 2017, 132, 397–404. [Google Scholar] [CrossRef]
- Kapp, M.W.; Hohenwarter, A.; Wurster, S.; Yang, B.; Pippan, R. Anisotropic deformation characteristics of an ultrafine- and nanolamellar pearlitic steel. Acta Mater. 2016, 106, 239–248. [Google Scholar] [CrossRef]
- Raabe, D.; Kumar, R. Tensile deformation characteristics of bulk ultrafine-grained austenitic stainless steel produced by thermal cycling. Scr. Mater. 2012, 66, 634–637. [Google Scholar]
- Skakov, M.K.; Uazyrkhanova, G.K.; Popova, N.A.; Scheffler, M. Influence of heat treatment and deformation on the phase-structural state of steel 30CrMnSiA. Key Eng. Mater. 2013, 531, 13–17. [Google Scholar] [CrossRef]
- Zrnik, J.; Dobatkin, S.; Raab, G.; Fujda, M.; Kraus, L. Ultrafine grain structure development in steel with different initial structure by severe plastic deformation. Rev. Mater. 2010, 15, 240–246. [Google Scholar]
- Takahashi, T.; Ochiai, I.; Tashiro, H.; Ohashi, S.; Nishida, S.; Tarui, T. Strenghening of steel wire for tire cord. Nippon. Steel Tech. Rep. 1995, 64, 45–49. [Google Scholar]
- Zhao, Y.; Tan, Y.; Ji, X.; Xiang, Z.; Xiang, S. In situ study of cementite deformation and its fracture mechanism in pearlitic steel. Mater. Sci. Eng. A 2018, 731, 93–101. [Google Scholar] [CrossRef]
- Yahyaoui, H.; Sidhom, H.; Braham, C.; Baczmanski, A. Effect of interlamellar spacing on the elastoplastic behavior of C70 pearlitic steel: Experimental results and self-consistent modeling. Mater. Des. 2014, 55, 888–897. [Google Scholar] [CrossRef]
- Ekh, M.; Larijani, N.; Dartfeldt, E.; Kapp, M.; Pippan, R. Prediction of the mechanical behaviour of pearlitic steel based on microcompression tests, micromechanical models and homogenization approaches. Eur. J. Mech. A. Solids 2018, 67, 272–279. [Google Scholar] [CrossRef]
- Veter, V.V.; Zhuleikin, S.G.; Ignatenko, L.N. Gradient structures arising during plastic deformation of pearlitic steel. Proc. Russ. Acad. Sci. Phys. Ser. 2003, 67, 1375–1379. [Google Scholar]
- Wang, Y.; Tomota, Y.; Harjo, S.; Gong, W.; Ohmuraa, T. In-situ neutron diffraction during tension-compression cyclic deformation of a pearlite steel. Mater. Sci. Eng. A 2016, 676, 522–530. [Google Scholar] [CrossRef]
- Li, Y.J.; Choi, P.; Borchers, C.; Westerkamp, S.; Goto, S.; Raabe, D.; Kirchheim, R. Atomic-scale mechanisms of deformation-induced cementite decomposition in pearlite. Acta Mater. 2011, 59, 3965–3977. [Google Scholar] [CrossRef]
- Tung, P.-Y.; Zhou, X.; Mayweg, D.; Morsdorf, L.; Herbig, M. Under-stoichiometric cementite in decomposing binary Fe-C pearlite exposed to rolling contact fatigue. Acta Mater. 2021, 216, 117144. [Google Scholar] [CrossRef]
- Egerton, F.R. Physical Principles of Electron Microscopy; Springer International Publishing: Basel, Switzerland, 2016; p. 196. [Google Scholar]
- Kumar, C.S.S.R. Transmission Electron Microscopy. In Characterization of Nanomaterials; Springer: New York, NY, USA, 2014; p. 717. [Google Scholar]
- Carter, C.B.; Williams, D.B. Transmission Electron Microscopy; Springer International Publishing: Berlin, Germany, 2016; p. 518. [Google Scholar]
- Koneva, N.A.; Kozlov, E.V. Nature of substructural strengthening. Proc. High Schools Phys. 1982, 8, 3–14. [Google Scholar]
- Trefilov, V.I.; Moiseev, V.F.; Pechkovsky, E.P.; Gornaya, I.D. Cold Hardening and Failure of Polycrystalline Materials; Naukova Dumka: Kiev, Ukraine, 1989; p. 256. [Google Scholar]
- Kocks, U.F.; Mesking, H. Physics and phenomenology of strain hardening: The FCC case. Prog. Mater. Sci. 2003, 48, 171–279. [Google Scholar] [CrossRef]
- Koneva, N.A. The nature of the stages of plastic deformation. Soros Educ. J. 1998, 10, 99–105. [Google Scholar]
- Podrezov, Y.N.; Firstov, S.A. Two approaches to analysis of curves of cold gardening. Phys. Technol. High Press. 2006, 16, 37–48. [Google Scholar]
- Gavriljuk, V.G. Effect of interlamellar spacing on cementite dissolution during wire drawing of pearlitic steel wires. Scr. Mater. 2001, 45, 1469–1472. [Google Scholar] [CrossRef]
- Gavriljuk, V.G. Decomposition of cementite in pearlite steel due to plastic deformation. Mater. Sci. Eng. A 2003, 345, 81–89. [Google Scholar] [CrossRef]
- Gromov, V.E.; Yuriev, A.B.; Morozov, K.V.; Ivanov, Y.F. Microstructure of Quenched Rails; CISP Ltd.: Cambridge, UK, 2016; p. 152. [Google Scholar]
- Koneva, N.A.; Kozlov, E.V.; Popova, N.A. Effect of grain and fragment sizes on dislocation density in metallic materials. Fundam. Probl. Mod. Mater. Sci. 2010, 7, 64–70. [Google Scholar]
- Kozlov, E.V.; Popova, N.A.; Koneva, N.A. Scalar density of dislocations in fragments with different types of substructures. Lett. About Mater. 2011, 1, 15–18. [Google Scholar] [CrossRef]






| Mass Fraction of Chemical Elements, % (the Rest is Fe) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| C | Mn | Si | P | S | Cr | Ni | Cu | Ti | Mo | V | Al |
| 0.73 | 0.75 | 0.58 | 0.012 | 0.007 | 0.42 | 0.07 | 0.13 | 0.003 | 0.006 | 0.04 | 0.003 |
| Dislocation Density, 1010, cm−2 | Degree of Deformation, ε, % | |||
|---|---|---|---|---|
| 0 | 15 | 30 | 50 | |
| 〈〉 | 2.5 | 2.1 | 1.6 | 0.6 |
| ρ± | 1.8 | 1.6 | 1.0 | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aksenova, K.; Gromov, V.; Ivanov, Y.; Qin, R.; Vashchuk, E. Structural Phase Transformation of Rail Steel in Compression. Metals 2022, 12, 1985. https://doi.org/10.3390/met12111985
Aksenova K, Gromov V, Ivanov Y, Qin R, Vashchuk E. Structural Phase Transformation of Rail Steel in Compression. Metals. 2022; 12(11):1985. https://doi.org/10.3390/met12111985
Chicago/Turabian StyleAksenova, Krestina, Victor Gromov, Yurii Ivanov, Rongshan Qin, and Ekaterina Vashchuk. 2022. "Structural Phase Transformation of Rail Steel in Compression" Metals 12, no. 11: 1985. https://doi.org/10.3390/met12111985
APA StyleAksenova, K., Gromov, V., Ivanov, Y., Qin, R., & Vashchuk, E. (2022). Structural Phase Transformation of Rail Steel in Compression. Metals, 12(11), 1985. https://doi.org/10.3390/met12111985







