Assessment of the Effect of Residual Stresses Arising in the HAZ of Welds on the Fatigue Life of S700MC Steel
Abstract
1. Introduction
2. Materials and Methods
3. Experiments and Results
- (1)
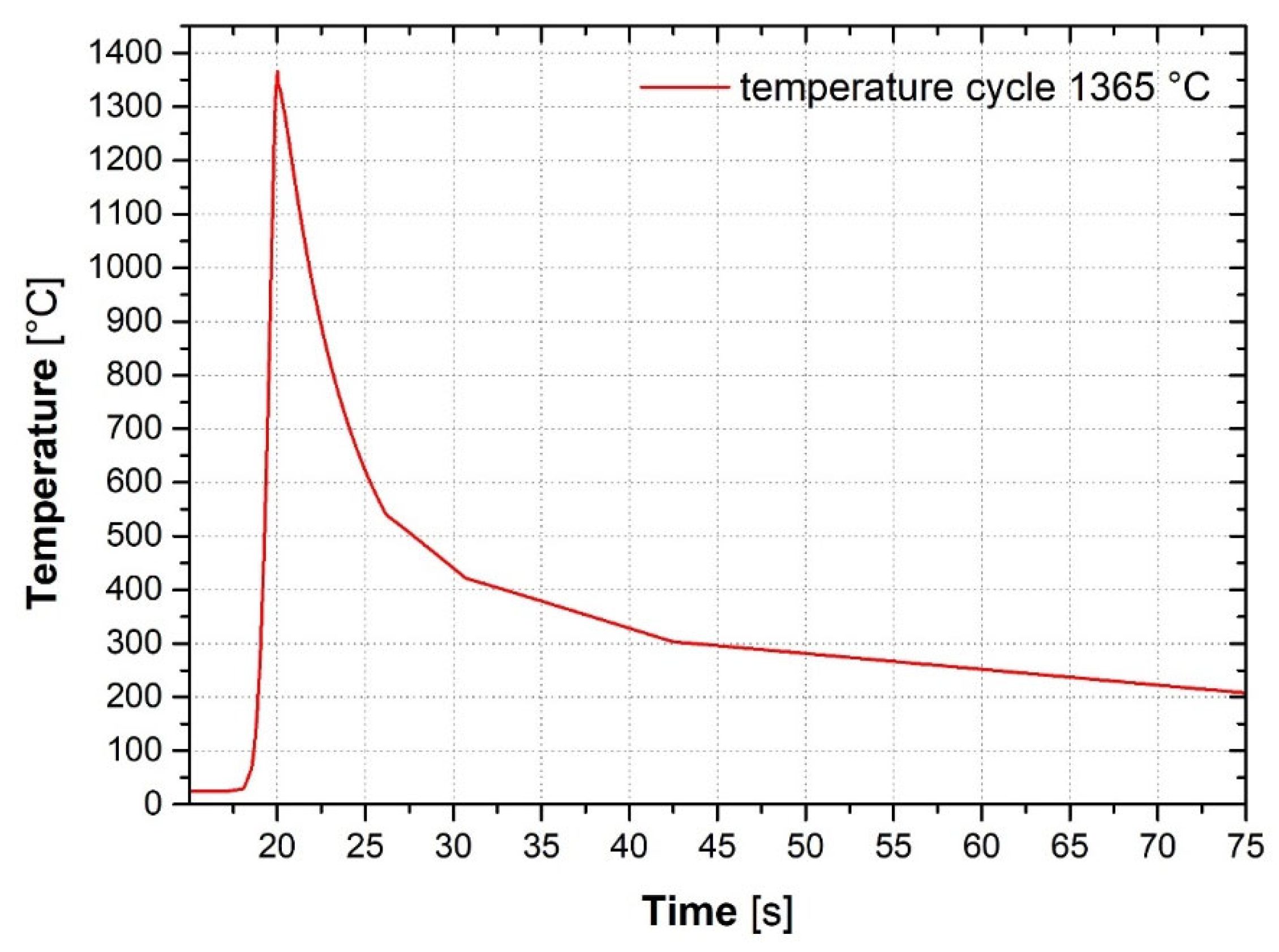
- Obtaining a real temperature cycle corresponding to MAG welding with heat input up to 10 kJ·cm−1;
- (2)
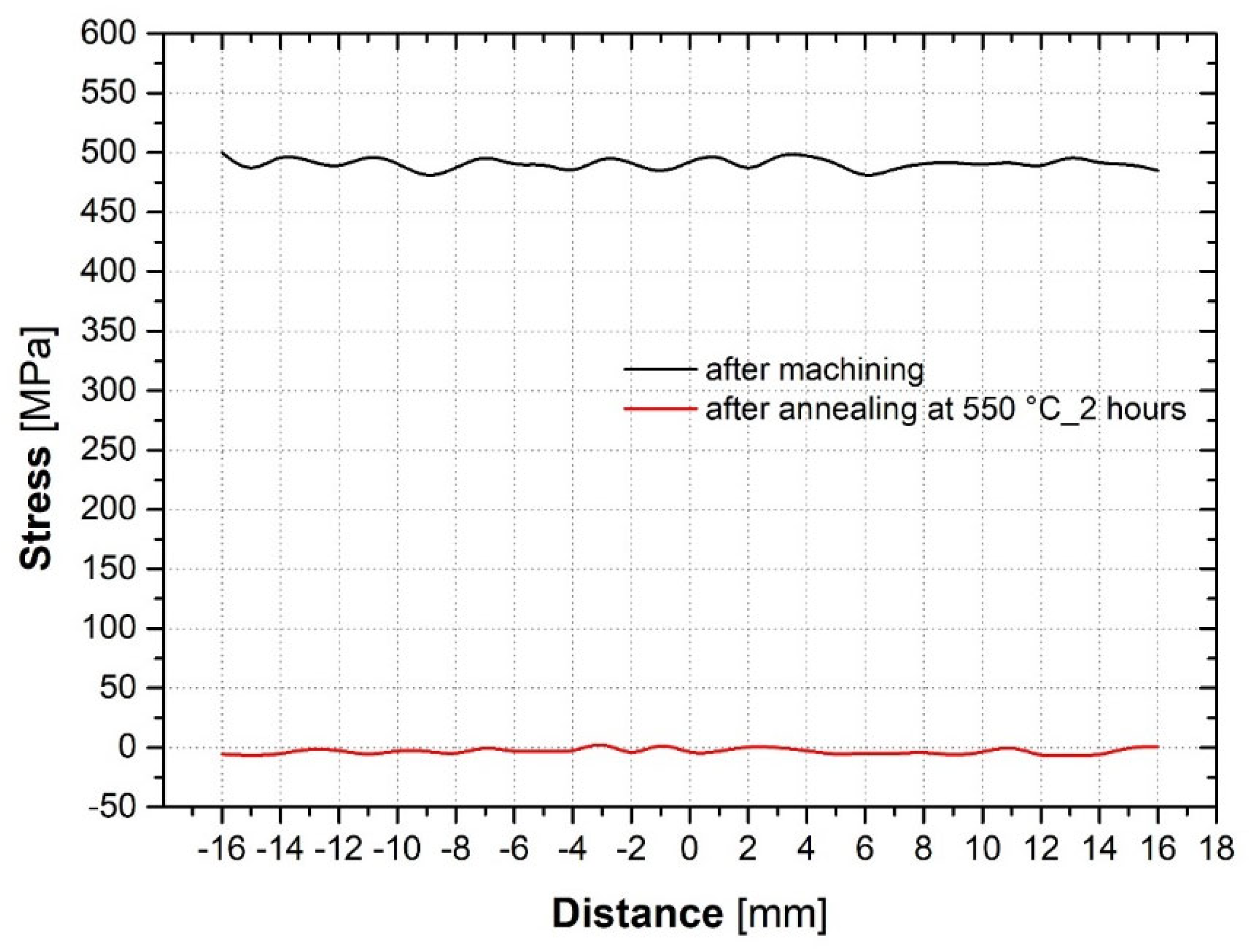
- Experimental setting of the annealing conditions (T = 550 °C; t = 2 h) at which the surface residual stresses created during the machining of the test samples are reduced;
- (3)
- Determination of mechanical properties and S–N curves for the base and annealed materials;
- (4)
- Application of a temperature–stress cycle to annealed samples (produced in accordance with Figure 2) in a Gleeble 3500;
- (5)
- Determination of the residual stresses in the samples using the XRD method;
- (6)
- Annealing to reduce residual stresses after application of temperature–stress cycle in device Gleeble 3500 realized for some samples;
- (7)
- Determination of S–N curves for the state corresponding to the influence of the temperature–stress cycle (with residual stresses) and also for the state after application of the temperature–stress cycle but with subsequent annealing to reduce residual stresses.
3.1. Measurement and Application of Temperature Cycles
3.2. Analysis of Residual Stresses after Machining and after Annealing
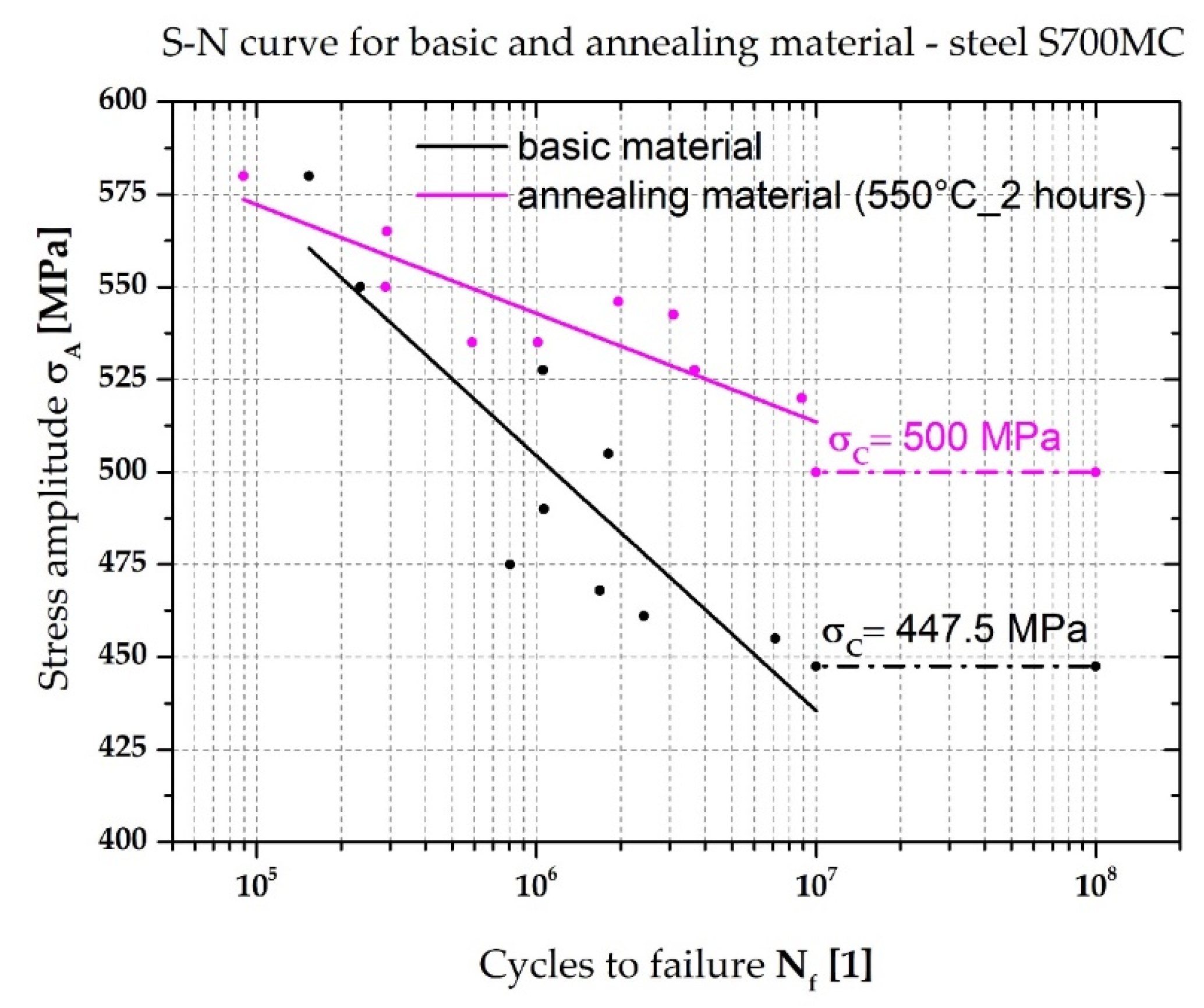
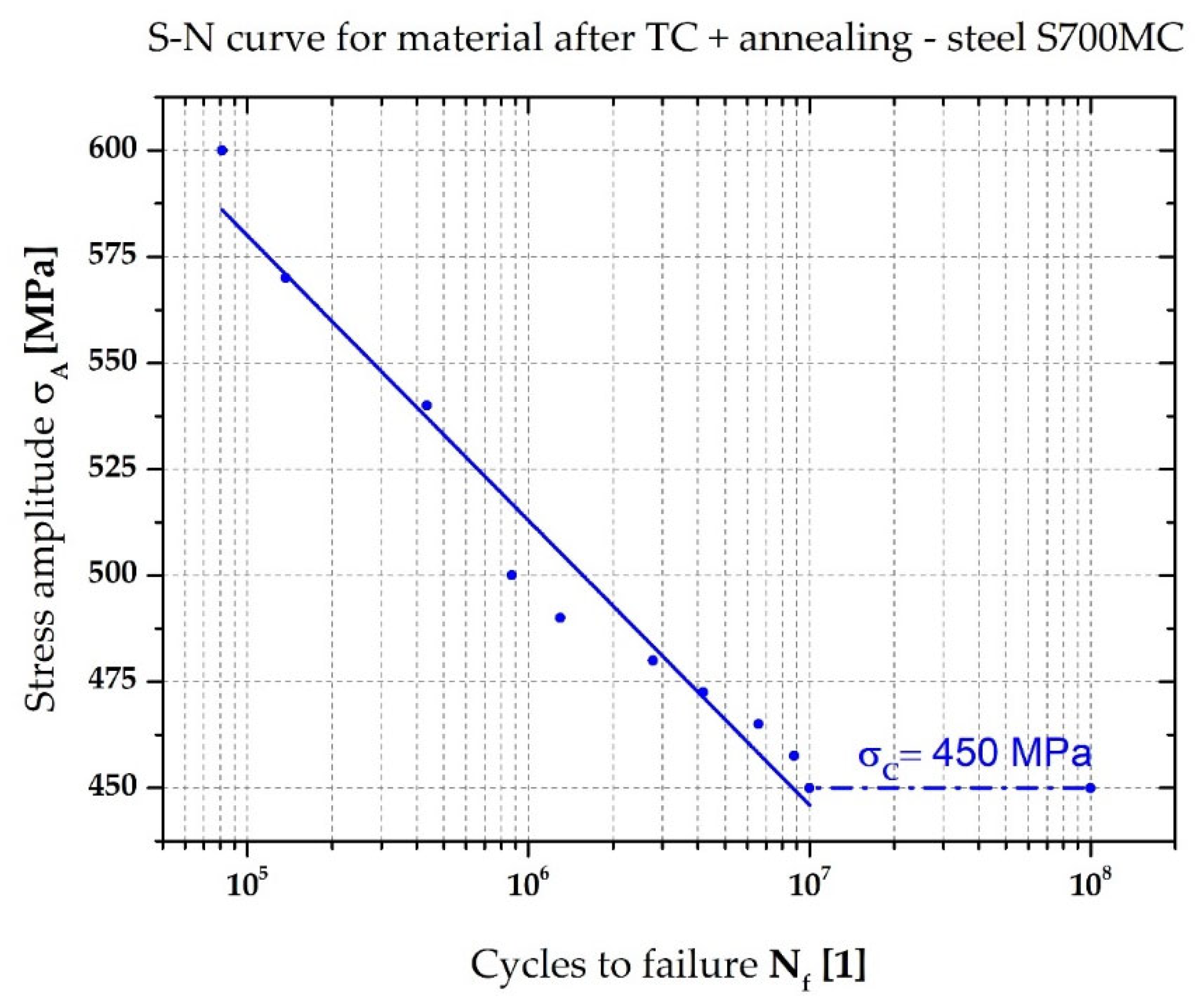
3.3. Determination of S–N Curve for Base Material S700MC and Annealed Material
3.4. Application of Temperature Cycles in the Gleeble 3500
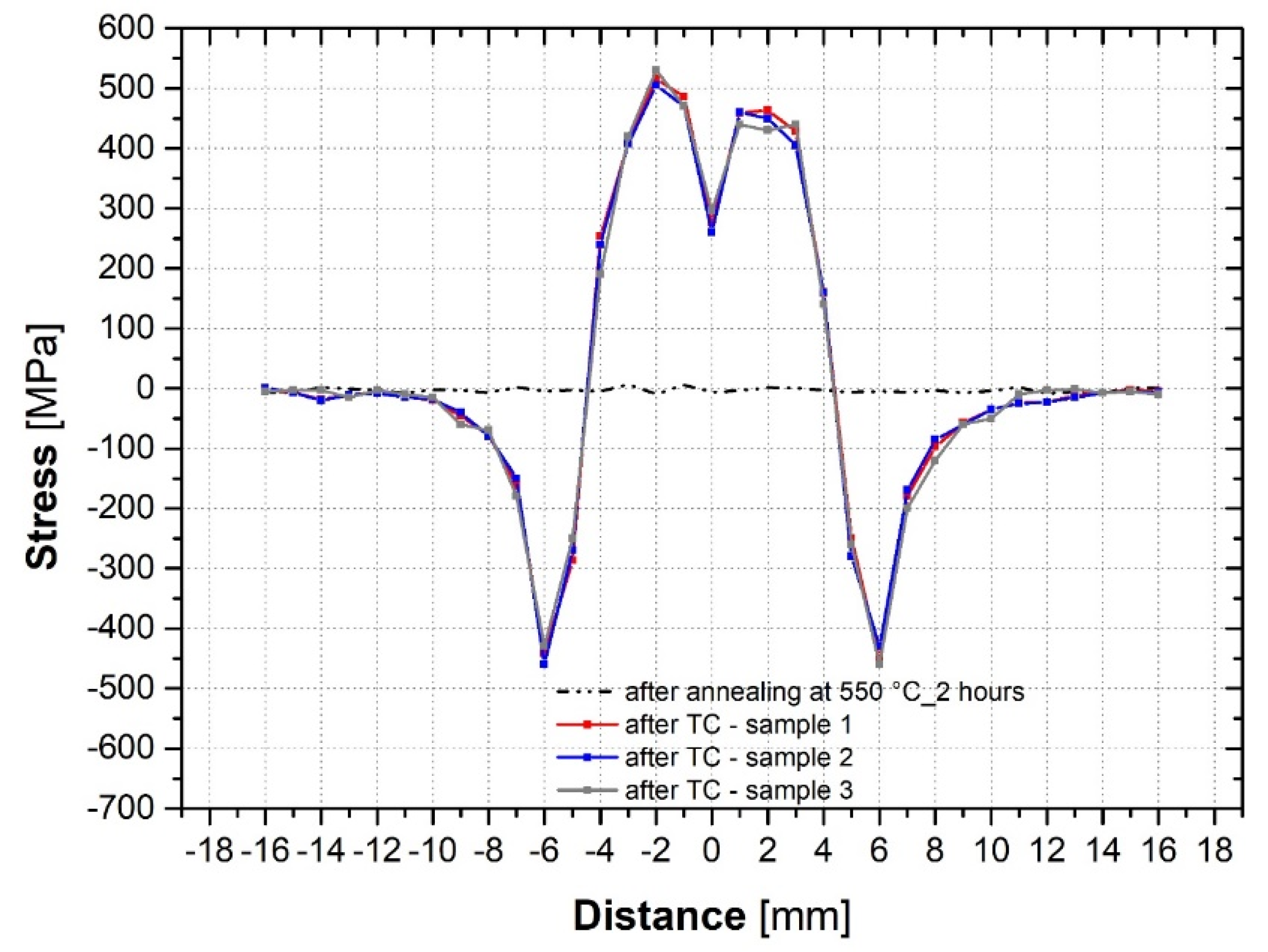
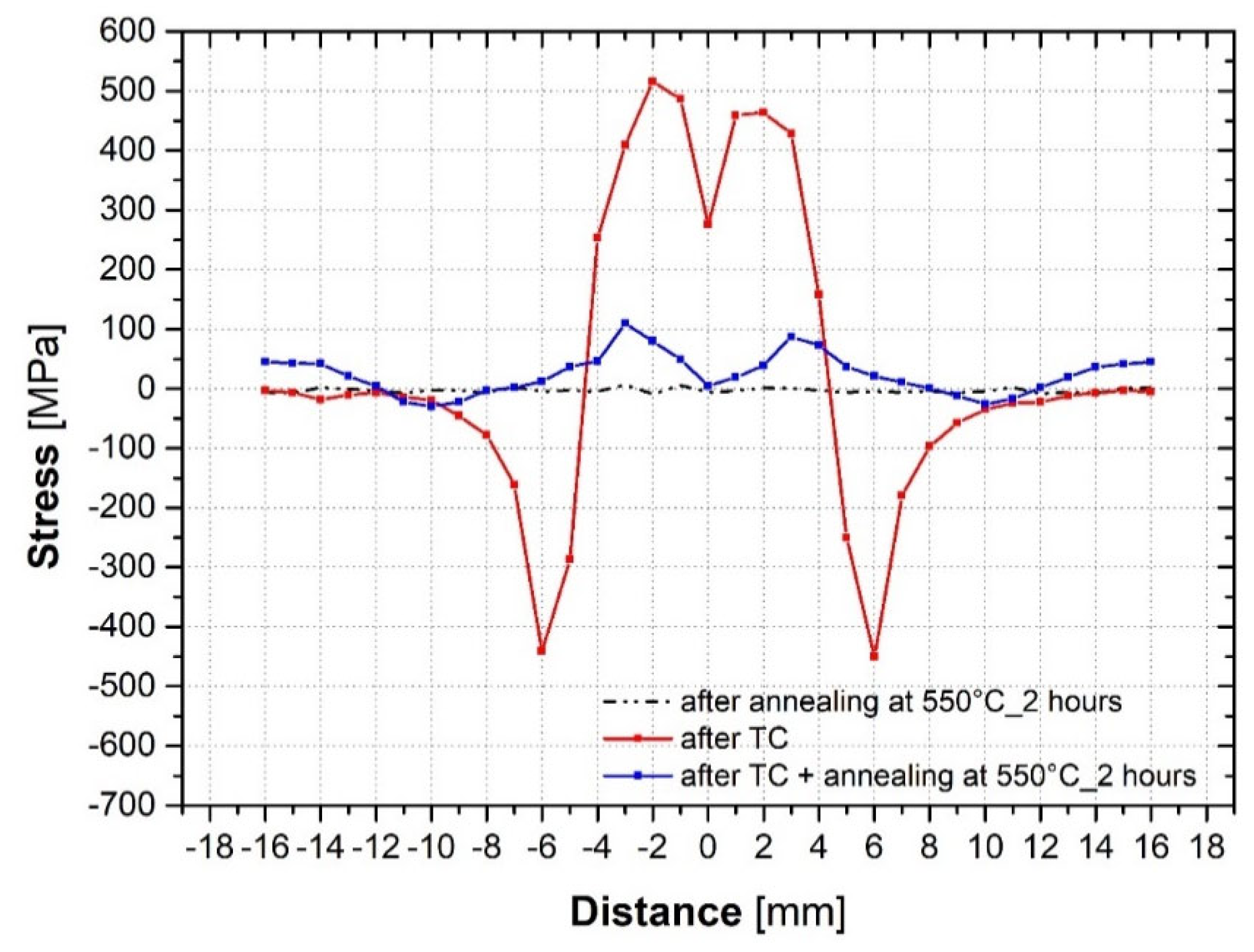
3.5. Analysis of Residual Stresses after Application of the Temperature–Stress Cycle
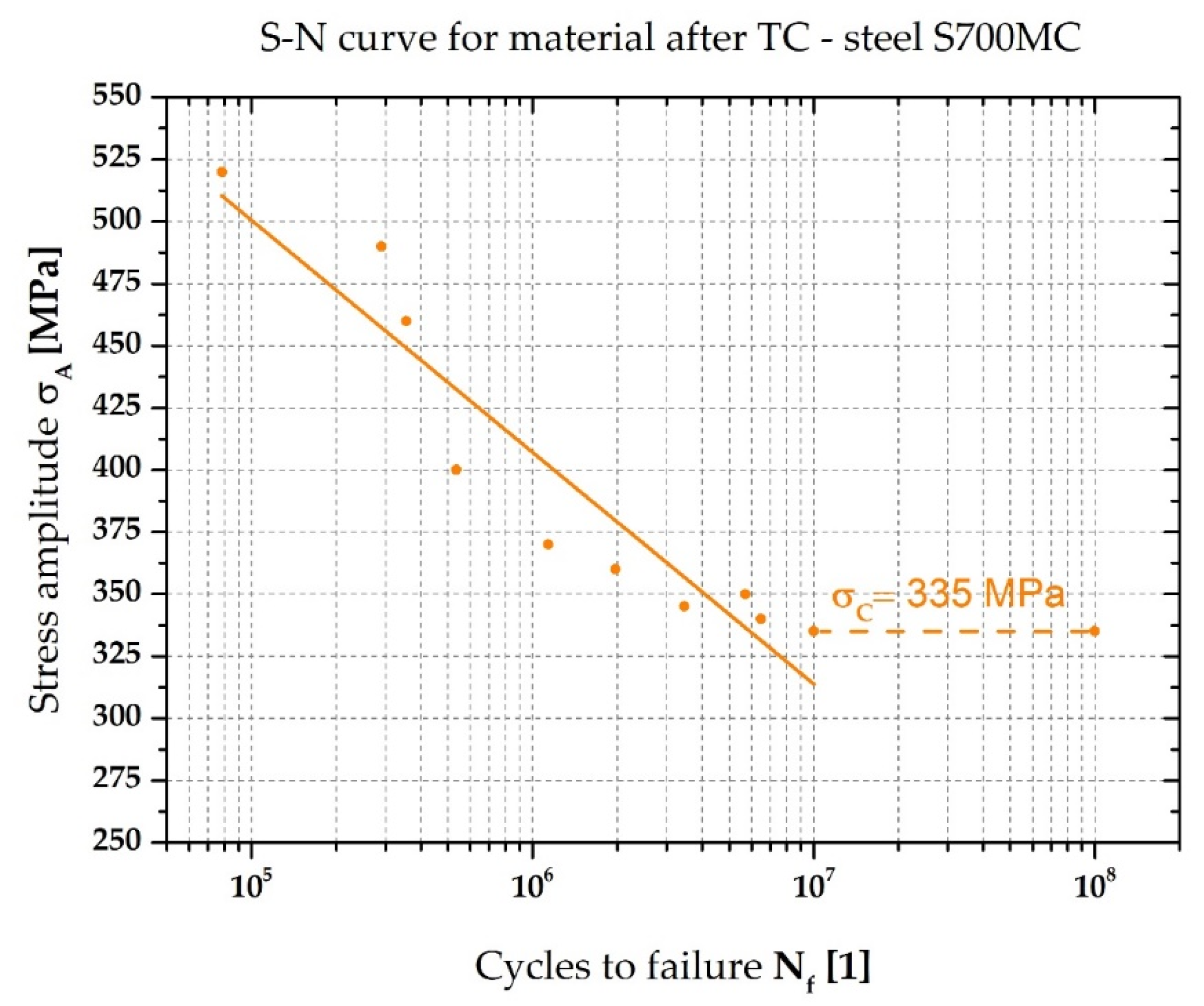
3.6. Fatigue Life Determination of Samples with Residual Stresses
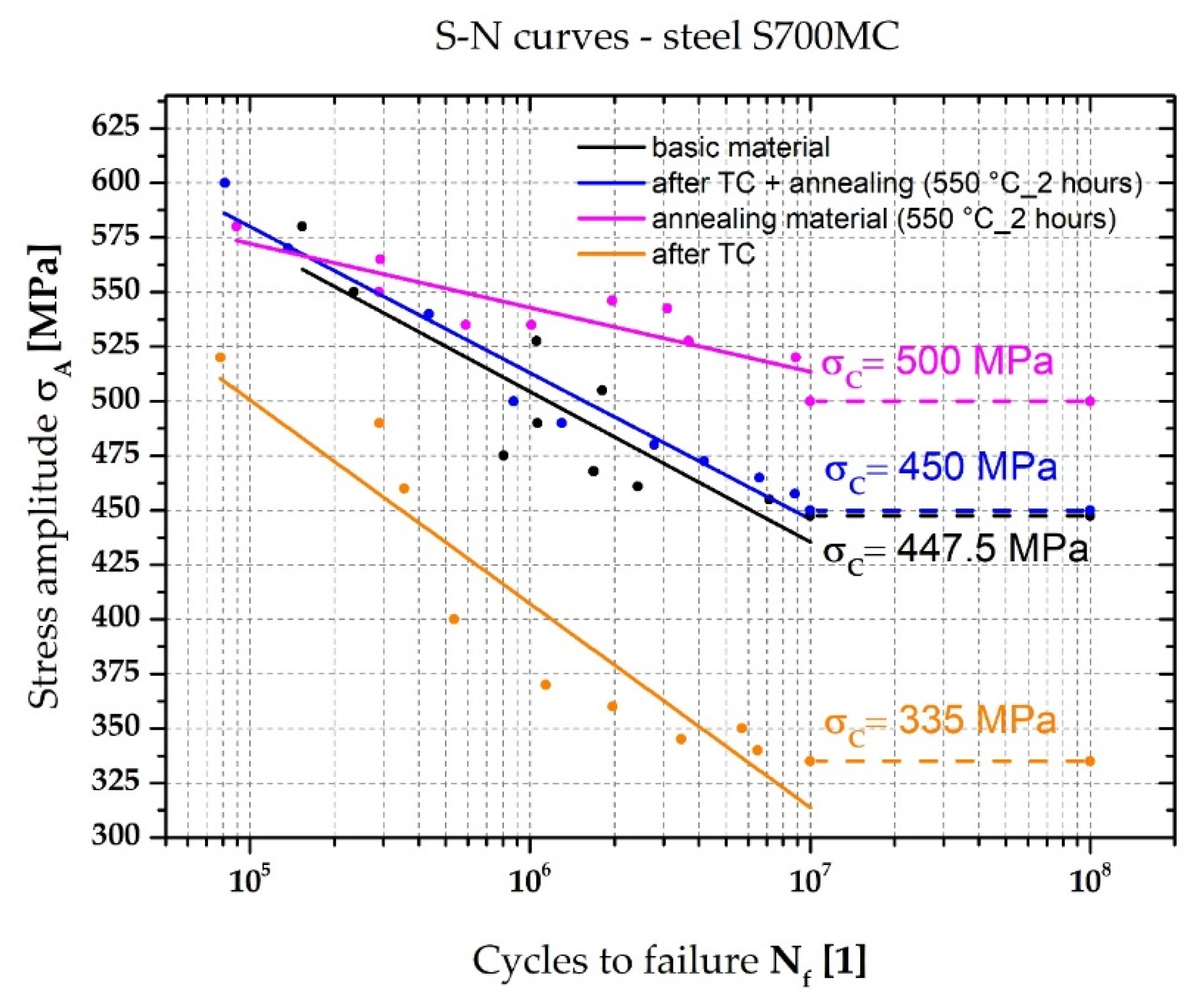
4. Discussion
5. Conclusions
- (1)
- After annealing the S700MC steel samples (550 °C_2 h), the YS value remained unchanged but the UTS value decreased by 7.8%. At the same time, the fatigue strength increased by 10%, from 447.5 MPa to 500 Mpa;
- (2)
- Application of the temperature–stress cycle caused residual tensile stresses in the sample with a maximum value of 507 MPa and compressive residual stresses with a maximum value of 471 Mpa;
- (3)
- The application of the temperature–stress cycle also caused a decrease in the fatigue strength σc from 500 MPa to 335 MPa, i.e., a decrease of 33%;
- (4)
- Annealing at 550 °C for 2 h caused the complete elimination of compressive residual stresses and a significant 80% reduction in tensile residual stresses in the samples subjected to the temperature–stress cycle. As a result, the fatigue strength of the samples increased from 335 MPa to 450 Mpa;
- (5)
- According to the above, residual stresses contribute to 69% of the fatigue strength reduction. The residue is due to material changes;
- (6)
- The samples with residual stresses fractured at a point 3.7 mm from the center of the sample, thus up to the tensile stress peaks. This is probably related to the redistribution of residual stresses that occur during cyclic loading.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- De Meester, B. The Weldability of Modern Structural TMCP Steels. ISIJ Int. 1997, 37, 537–551. [Google Scholar] [CrossRef]
- Ufuah, E.; Ikhayere, J. Elevated Temperature Mechanical Properties of Butt-Welded Connections Made with High Strength Steel Grades S355 and S460M. In Design, Fabrication and Economy of Metal Structures; Springer: Berlin/Heidelberg, Germany, 2013; pp. 407–412. [Google Scholar]
- Lee, C.-H.; Shin, H.-S.; Park, K.-T. Evaluation of High Strength TMCP Steel Weld for Use in Cold Regions. J. Constr. Steel Res. 2012, 74, 134–139. [Google Scholar] [CrossRef]
- Zavdoveev, A.; Poznyakov, V.; Baudin, T.; Rogante, M.; Kim, H.S.; Heaton, M.; Demchenko, Y.; Zhukov, V.; Skoryk, M. Effect of Heat Treatment on the Mechanical Properties and Microstructure of HSLA Steels Processed by Various Technologies. Mater. Today Commun. 2021, 28, 102598. [Google Scholar] [CrossRef]
- Illescas Fernandez, S.; Fernández, J.; Asensio, J.; Sánchez Soto, M.; Guilemany Casadamon, J.M. Study of the Mechanical Properties of Low Carbon Content HSLA Steels. Rev. Metal. 2009, 45, 424–431. [Google Scholar] [CrossRef]
- Fernández, J.; Illescas, S.; Guilemany, J. Effect of Microalloying Elements on the Austenitic Grain Growth in a Low Carbon HSLA Steel. Mater. Lett. 2007, 61, 2389–2392. [Google Scholar] [CrossRef]
- Barbaro, F.; Kuzmikova, L.; Zhu, Z.; Li, H. Weld HAZ Properties in Modern High Strength Niobium Pipeline Steels. In Energy Materials 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 657–664. [Google Scholar]
- Nazarov, A.; Yakushev, E.; Shabalov, I.; Morozov, Y.D.; Kireeva, T. Comparison of Weldability of High-Strength Pipe Steels Microalloyed with Niobium, Niobium and Vanadium. Metallurgist 2014, 57, 911–917. [Google Scholar] [CrossRef]
- Schaupp, T.; Schroepfer, D.; Kromm, A.; Kannengiesser, T. Welding Residual Stresses in 960 MPa Grade QT and TMCP High-Strength Steels. J. Manuf. Process. 2017, 27, 226–232. [Google Scholar] [CrossRef]
- Laitila, J.; Larkiola, J. Effect of Enhanced Cooling on Mechanical Properties of a Multipass Welded Martensitic Steel. Weld. World 2019, 63, 637–646. [Google Scholar] [CrossRef]
- Branco, R.; Berto, F. Mechanical Behavior of High-Strength, Low-Alloy Steels. Metals 2018, 8, 610. [Google Scholar] [CrossRef]
- Taavitsainen, J.; da Silva, P.S.V.; Porter, D.; Suikkanen, P. Weldability of Direct-Quenched Steel with a Yield Stress of 960 MPa. In Proceedings of the 10th International Conference on Trends in Welding Research and 9th International Welding Symposium of Japan Welding Society (9WS), Tokyo, Japan, 11–14 October 2016; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 11–14. [Google Scholar]
- Njock Bayock, F.; Kah, P.; Mvola, B.; Layus, P. Effect of Heat Input and Undermatched Filler Wire on the Microstructure and Mechanical Properties of Dissimilar S700MC/S960QC High-Strength Steels. Metals 2019, 9, 883. [Google Scholar] [CrossRef]
- Górka, J. Microstructure and Properties of the High-Temperature (HAZ) of Thermo-Mechanically Treated S700MC High-Yield-Strength Steel. Mater. Tehnol. 2016, 50, 617–621. [Google Scholar] [CrossRef]
- Moravec, J.; Novakova, I.; Sobotka, J.; Neumann, H. Determination of Grain Growth Kinetics and Assessment of Welding Effect on Properties of S700MC Steel in the HAZ of Welded Joints. Metals 2019, 9, 707. [Google Scholar] [CrossRef]
- Mičian, M.; Harmaniak, D.; Nový, F.; Winczek, J.; Moravec, J.; Trško, L. Effect of the T8/5 Cooling Time on the Properties of S960MC Steel in the HAZ of Welded Joints Evaluated by Thermal Physical Simulation. Metals 2020, 10, 229. [Google Scholar] [CrossRef]
- Jambor, M.; Ulewicz, R.; Nový, F.; Bokůvka, O.; Trško, L.; Mičian, M.; Harmaniak, D. Evolution of Microstructure in the Heat Affected Zone of S960MC GMAW Weld. Mater. Res. Proc. 2018, 5, 78–83. [Google Scholar]
- Kik, T. Computational Techniques in Numerical Simulations of Arc and Laser Welding Processes. Materials 2020, 13, 608. [Google Scholar] [CrossRef]
- Kik, T. Heat Source Models in Numerical Simulations of Laser Welding. Materials 2020, 13, 2653. [Google Scholar] [CrossRef]
- Nassiraei, H.; Rezadoost, P. Stress Concentration Factors in Tubular X-Connections Retrofitted with FRP under Compressive Load. Ocean Eng. 2021, 229, 108562. [Google Scholar] [CrossRef]
- Nassiraei, H.; Rezadoost, P. Stress Concentration Factors in Tubular T/Y-Connections Reinforced with FRP under in-Plane Bending Load. Mar. Struct. 2021, 76, 102871. [Google Scholar] [CrossRef]
- Nassiraei, H.; Rezadoost, P. SCFs in Tubular X-Connections Retrofitted with FRP under in-Plane Bending Load. Compos. Struct. 2021, 274, 114314. [Google Scholar] [CrossRef]
- Nassiraei, H.; Rezadoost, P. Parametric Study and Formula for SCFs of FRP-Strengthened CHS T/Y-Joints under out-of-Plane Bending Load. Ocean Eng. 2021, 221, 108313. [Google Scholar] [CrossRef]
- Lahtinen, T.; Vilaça, P.; Infante, V. Fatigue Behavior of MAG Welds of Thermo-Mechanically Processed 700MC Ultra High Strength Steel. Int. J. Fatigue 2019, 126, 62–71. [Google Scholar] [CrossRef]
- Kim, Y.; Hwang, W. Effect of Weld Seam Orientation and Welding Process on Fatigue Fracture Behaviors of HSLA Steel Weld Joints. Int. J. Fatigue 2020, 137, 105644. [Google Scholar] [CrossRef]
- Lago, J.; Trško, L.; Jambor, M.; Nový, F.; Bokůvka, O.; Mičian, M.; Pastorek, F. Fatigue Life Improvement of the High Strength Steel Welded Joints by Ultrasonic Impact Peening. Metals 2019, 9, 619. [Google Scholar] [CrossRef]
- Šebestová, H.; Hornik, P.; Mrňa, L.; Jambor, M.; Hornik, V.; Pokorný, P.; Hutař, P.; Ambrož, O.; Doležal, P. Fatigue Properties of Laser and Hybrid Laser-TIG Welds of Thermo-Mechanically Rolled Steels. Mater. Sci. Eng. A 2020, 772, 138780. [Google Scholar] [CrossRef]
- Moravec, J.; Sobotka, J.; Solfronk, P.; Thakral, R. Heat Input Influence on the Fatigue Life of Welds from Steel S460MC. Metals 2020, 10, 1288. [Google Scholar] [CrossRef]
- Hong, J.K.; Dong, P.; Brust, F.; Forte, T. Effect of Welding Induced Residual Stresses on the Fatigue Behavior of T-Joints; SAE Technical Paper: Warrendale, PA, USA, 1998. [Google Scholar]
- Webster, G.; Ezeilo, A. Residual Stress Distributions and Their Influence on Fatigue Lifetimes. Int. J. Fatigue 2001, 23, 375–383. [Google Scholar] [CrossRef]
- James, M.; Hughes, D.; Chen, Z.; Lombard, H.; Hattingh, D.; Asquith, D.; Yates, J.; Webster, P. Residual Stresses and Fatigue Performance. Eng. Fail. Anal. 2007, 14, 384–395. [Google Scholar] [CrossRef]
- Lee, C.-H.; Chang, K.-H. Comparative Study on Girth Weld-Induced Residual Stresses between Austenitic and Duplex Stainless Steel Pipe Welds. Appl. Therm. Eng. 2014, 63, 140–150. [Google Scholar] [CrossRef]
- Harati, E.; Karlsson, L.; Svensson, L.-E.; Dalaei, K. The Relative Effects of Residual Stresses and Weld Toe Geometry on Fatigue Life of Weldments. Int. J. Fatigue 2015, 77, 160–165. [Google Scholar] [CrossRef]
- Kang, H.T.; Lee, Y.-L.; Sun, X.J. Effects of Residual Stress and Heat Treatment on Fatigue Strength of Weldments. Mater. Sci. Eng. A 2008, 497, 37–43. [Google Scholar] [CrossRef]
- Jandera, M.; Machacek, J. Residual Stresses and Strength of Hollow Stainless Steel Sections. 2007, pp. 262–263. Available online: https://www.researchgate.net/profile/Michal-Jandera/publication/268358021_RESIDUAL_STRESSES_AND_STRENGTH_OF_HOLLOW_STAINLESS_STEEL_SECTIONS/links/54b78e070cf2bd04be33a1f3/RESIDUAL-STRESSES-AND-STRENGTH-OF-HOLLOW-STAINLESS-STEEL-SECTIONS.pdf (accessed on 2 November 2022).
- Dakhlaoui, R.; Braham, C.; Baczmański, A. Mechanical Properties of Phases in Austeno-Ferritic Duplex Stainless Steel—Surface Stresses Studied by X-Ray Diffraction. Mater. Sci. Eng. A 2007, 444, 6–17. [Google Scholar] [CrossRef]
- Johansson, J.; Odén, M. Load Sharing between Austenite and Ferrite in a Duplex Stainless Steel during Cyclic Loading. Metall. Mater. Trans. A 2000, 31, 1557–1570. [Google Scholar] [CrossRef]
- Jang, D.; Watkins, T.; Kozaczek, K.; Hubbard, C.; Cavin, O. Surface Residual Stresses in Machined Austenitic Stainless Steel. Wear 1996, 194, 168–173. [Google Scholar] [CrossRef]
- Ragavendran, M.; Vasudevan, M.; Hussain, N. Study of the Microstructure, Mechanical Properties, Residual Stresses, and Distortion in Type 316LN Stainless Steel Medium Thickness Plate Weld Joints. J. Mater. Eng. Perform. 2022, 31, 5013–5025. [Google Scholar] [CrossRef]
- ČSN EN 10027-1; Systémy Označování Ocelí–Část 1: Stavba Značek Ocelí. Praha: Úřad pro Technickou Normalizaci, Metrologii a Státní Zkušebnictví, 2017; 40 s. Třídící Znak 42 0011.
- ČSN EN 10027-2; Systémy Označování Ocelí–Část 2: Systém Číselného Označování. Praha: Úřad pro Technickou Normalizaci, Metrologii a Státní Zkušebnictví, 2016; 24 s. Třídící Znak 42 0011.
- Moravec, J.; Sobotka, J.; Novakova, I.; Bukovska, S. Assessment the Partial Welding Influences on Fatigue Life of S700MC Steel Fillet Welds. Metals 2021, 11, 334. [Google Scholar] [CrossRef]

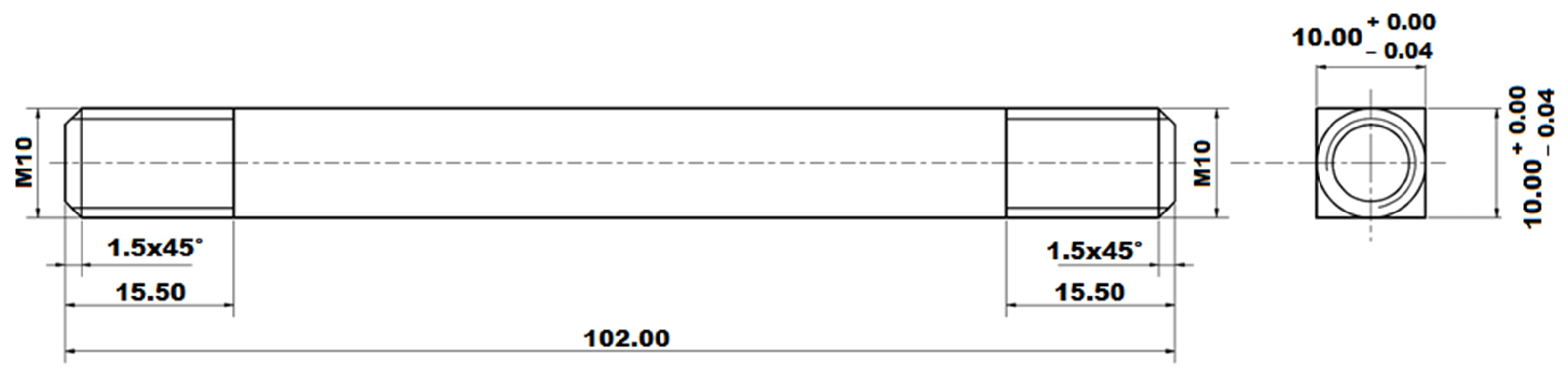
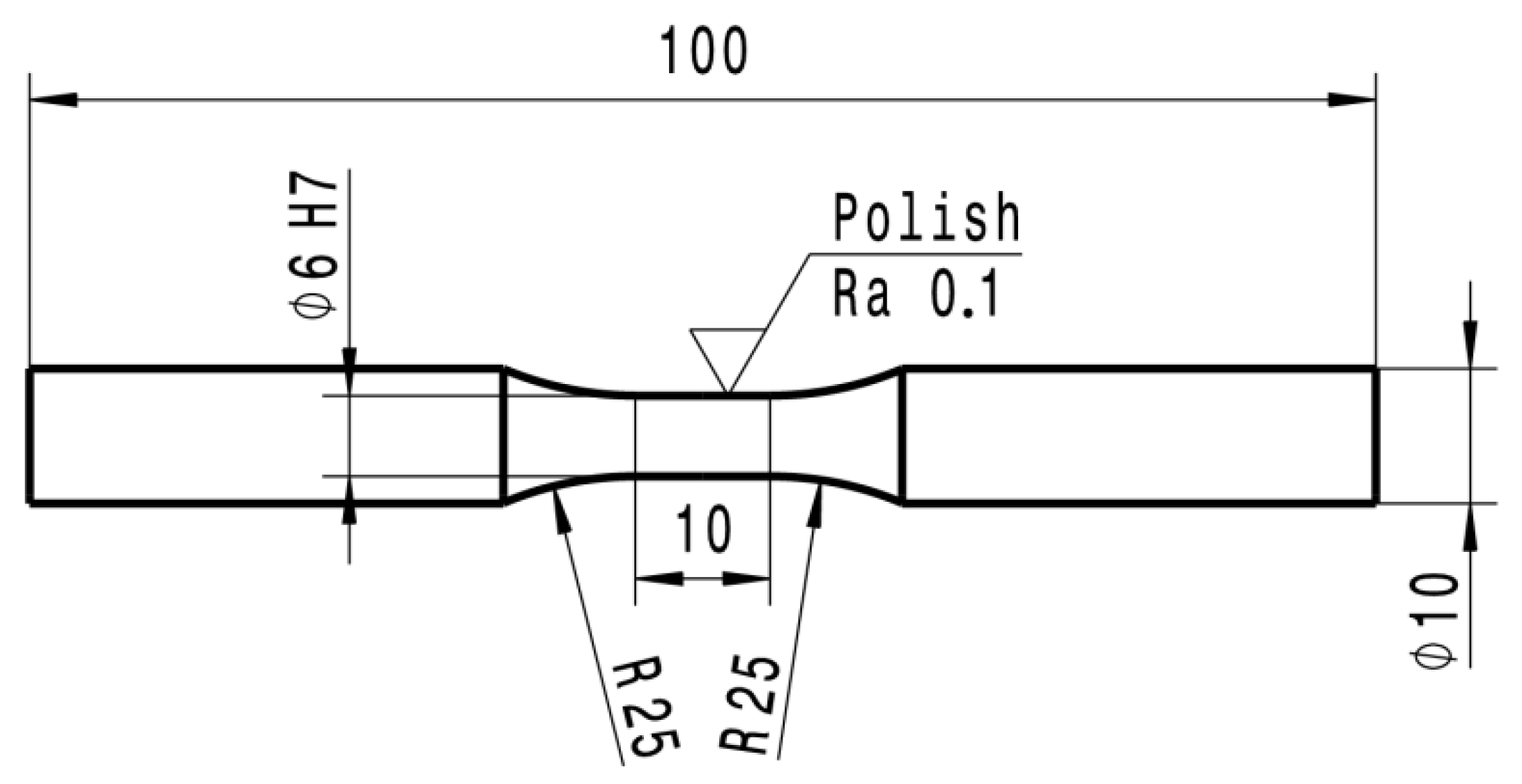

| C | Si | Mn | P | S | Al | Nb | V | |
| ČSN EN 10149-2 | max. 0.12 | max. 0.6 | max. 2.2 | max. 0.025 | max. 0.010 | min. 0.015 | max. 0.09 | max. 0.2 |
| Experiment | 0.050 | 0.196 | 1.914 | 0.006 | 0.006 | 0.037 | 0.063 | 0.072 |
| Ti | Mo | B | N | Ni | Cr | W | ||
| ČSN EN 10149-2 | max. 0.25 | max. - | max. 0.005 | - | - | - | - | |
| Experiment | 0.056 | 0.112 | 0 | 0.013 | 0.153 | 0.035 | 0.035 |
| Sample No. | YS [MPa] | UTS [MPa] | Ag [%] | A30 [%] |
|---|---|---|---|---|
| Basic material | 748 ± 9 | 851 ± 1 | 11.08 ± 0.62 | 24.03 ± 0.62 |
| Annealing material (550 °C_2 h) | 745 ± 3 | 785 ± 3 | 9.69 ± 0.12 | 21.16 ± 0.29 |
| Basic material | σA [MPa] | 580 | 550 | 527.5 | 505 | 490 |
| Nf [1] | 153,695 | 234,942 | 1,056,376 | 1,804,894 | 1,063,721 | |
| σA [MPa] | 475 | 468 | 461 | 455 | 447.5 | |
| Nf [1] | 804,513 | 1,687,452 | 2,420,822 | 7,153,698 | 107 | |
| 550 °C 2 h | σA [MPa] | 580 | 565 | 550 | 546 | 542.5 |
| Nf [1] | 89,479 | 292,247 | 288,898 | 1,964,321 | 3,083,698 | |
| σA [MPa] | 535 | 535 | 527,5 | 520 | 500 | |
| Nf [1] | 589,138 | 1,011,574 | 3,680,777 | 8,881,583 | 107 |
| After TC | σA [MPa] | 520 | 490 | 460 | 400 | 370 |
| Nf [1] | 78,412 | 290,364 | 354,888 | 536,242 | 1,138,628 | |
| σA [MPa] | 360 | 350 | 345 | 340 | 335 | |
| Nf [1] | 1,968,348 | 5,698,176 | 3,458,265 | 6,483,620 | 107 |
| After TC + annealing | σA [MPa] | 600 | 570 | 540 | 500 | 490 |
| Nf [1] | 81,275 | 136,846 | 436,195 | 874,693 | 1,297,314 | |
| σA [MPa] | 480 | 472.5 | 465 | 457.5 | 450 | |
| Nf [1] | 2,769,674 | 4,181,239 | 6,583,912 | 8,826,743 | 107 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bukovská, Š.; Moravec, J.; Solfronk, P.; Pekárek, M. Assessment of the Effect of Residual Stresses Arising in the HAZ of Welds on the Fatigue Life of S700MC Steel. Metals 2022, 12, 1890. https://doi.org/10.3390/met12111890
Bukovská Š, Moravec J, Solfronk P, Pekárek M. Assessment of the Effect of Residual Stresses Arising in the HAZ of Welds on the Fatigue Life of S700MC Steel. Metals. 2022; 12(11):1890. https://doi.org/10.3390/met12111890
Chicago/Turabian StyleBukovská, Šárka, Jaromír Moravec, Pavel Solfronk, and Milan Pekárek. 2022. "Assessment of the Effect of Residual Stresses Arising in the HAZ of Welds on the Fatigue Life of S700MC Steel" Metals 12, no. 11: 1890. https://doi.org/10.3390/met12111890
APA StyleBukovská, Š., Moravec, J., Solfronk, P., & Pekárek, M. (2022). Assessment of the Effect of Residual Stresses Arising in the HAZ of Welds on the Fatigue Life of S700MC Steel. Metals, 12(11), 1890. https://doi.org/10.3390/met12111890







