Influence of Nonmetallic Interstitials on the Phase Transformation between FCC and HCP Titanium: A Density Functional Theory Study

Abstract

In addition to the common stable and metastable phases in titanium alloys, the face-centered cubic phase was recently observed under various conditions; however, its formation remains largely unclarified. In this work, the effect of nonmetallic interstitial atoms O, N, C and B on the formation of the face-centered cubic phase of titanium was investigated with the density functional theory. The results indicate that the occupancy of O, N, C and B on the octahedral interstitial sites reduces the energy gap between the hexagonal-close-packed (HCP) and face-centered cubic (FCC) phases, thus assisting the formation of FCC-Ti under elevated temperature or plastic deformation. Such a gap further decreases with the increase in the interstitial content, which is consistent with the experimental observation of FCC-Ti under high interstitial content. The relative stability of the interstitial-containing HCP-Ti and FCC-Ti was studied against the physical and chemical origins, e.g., the lattice distortion and the electronic bonding. Interstitial O, N, C and B also reduce the stacking fault energy, thus further benefiting the formation of FCC-Ti.

1. Introduction

Because of their excellent comprehensive mechanical properties, preeminent corrosion resistance and biological compatibility, titanium alloys are widely used in aerospace, automobile manufacturing, medical equipment [1,2,3], etc. Under ambient conditions, pure titanium stabilizes at the hexagonal-close-packed (HCP) α phase, which transforms into the body-centered cubic structure (BCC) β phase above the β transus temperature. Previous investigations also suggest the existence of the metastable face-centered cubic (FCC) phase in various Ti alloys in film or bulk samples [4,5,6,7,8,9,10,11,12,13,14,15], as well as in Zr alloys [16,17], which may also significantly influence the microstructure evolution like other metastable phases, e.g., the hexagonal ω and α’ phases and the tetragonal α” phase [18,19,20,21,22]. However, the formation of FCC-Ti remains largely unclarified, and thus hinders further microstructure control.

The addition of alloying elements either alters the phase β-α transus temperature or introduce other phases, e.g., hexagonal α₂-Ti₃Al, whereas the FCC phase is rarely observed. It was believed that the FCC phase was only a hydride formed by hydrogen contamination during sample preparation [12]. However, in several in situ transmission electron microscope (TEM) observations [8,11,13], the stable FCC phase was found at a high temperature far beyond the decomposition temperature of TiHx (x ≥ 1), where the appearance of FCC-Ti was attributed to the interstitial oxygen [13]. The FCC phase was also found in titanium alloy samples after ball milling, rolling, explosive impact and other mechanical deformation [6,7,14,23]. In particular, the contribution of interstitial carbon to the formation of FCC-Ti in Ti₃₇Nb₂₈Mo₂₈-C₇ alloy under ball milling was proven through the combination of a simulation and experiment [14]. Despite the confirmation of the FCC phase in Ti alloys, its formation mechanism remains unclear. Two types of orientation relationships between HCP-Ti and FCC-Ti have been identified, i.e., P-type (${\left[\overline{1}2\overline{1}0\right]}_{HCP}\left|\right|{\left[1\overline{1}0\right]}_{FCC}$ and ${\left[\overline{1}0\overline{1}0\right]}_{HCP}\left|\right|{\left[110\right]}_{FCC}$) and B-type (${\left[\overline{1}2\overline{1}0\right]}_{HCP}\left|\right|{\left[1\overline{1}0\right]}_{FCC}$ and ${\left[0001\right]}_{HCP}\left|\right|{\left[\overline{11}1\right]}_{FCC}$). Atomic-scale calculations have been performed to analyze the formation conditions and mechanism of FCC-Ti under mechanical deformation [24,25,26], but the results were insufficient to explain the appearance of FCC-Ti in high-temperature in situ TEM observations [13].

Given the fact that interstitial atoms have been proven to have influence on the crystal structure of high-entropy alloys [27] and the results of the increase in interstitial atoms in the previous in situ heating experiments of titanium alloys [13], the present work focuses on the effect of nonmetallic interstitial elements O, N, C and B on the phase transition from HCP-Ti to FCC-Ti based on the density functional theory. Firstly, the stable interstitial sites in HCP-Ti and FCC-Ti and the relationship between the formation energy and the interstitial content were investigated. Secondly, the influence of interstitial elements on the relative stability of HCP-Ti and FCC-Ti was rationalized and attributed to the difference in the electronic structure and lattice distortion by the interstitial solutes. Finally, the possible formation mechanism of FCC-Ti was discussed by investigating the influence of the interstitial atoms on the generalized stacking fault energy of HCP-Ti. The results of the present work will shed light on the impact of phase transformation on the thermal and mechanical processing and additive manufacturing of titanium alloys for better properties.

2. Method

All calculations were based on density functional theory using VASP (Vienna Ab-inito Simulation Package 5.4.4, Hafner Research Group, University of Vienna) [28]. The interaction between nucleus and electron was described by projecting plane waves, and the generalized gradient approximation function in the form of PBE was used to estimate the exchange correlation energy. The plane wave cutoff energy was set to 450 eV, the energy tolerance for the electronic minimization was set as 10⁻⁶ eV/atom, and the Hellman–Feynman force tolerance was set as 0.01 eV/Å.

To verify the accuracy of the calculation parameter setting, we compared the results of lattice relaxation with the literature. The results are shown in

Table 1. Comparison of DFT results.

Phase	a (Å)	c/a	C11 (GPa)	C12 (GPa)	C13 (GPa)	C33 (GPa)	C44 (GPa)
HCP a	2.935	1.585	175	87.9	76.8	189	42.0
FCC a	4.109	/	127	101	/	/	60.3
HCP b	2.931	1.584	177	84.5	77.0	190	41.5
HCP c	2.930	/	172	85.0	78.6	188	39.0
FCC d	4.109	/	123	99.0	/	/	55.0

^a This work; ^b Ref. [29]; ^c Ref. [30]; ^d Ref. [31].

.

In the calculation of the interstitial formation energy in HCP-Ti and FCC-Ti, the unit cells oriented as $u_X^{HCP}=\frac{1}{3}\left[2\overline{1}\overline{1}0\right]$, $u_Y^{HCP}=\frac{1}{3}\left[\overline{1}2\overline{1}0\right]$, $u_Z^{HCP}=\left[0001\right]$ and $u_X^{FCC}=\left[100\right]$, $u_Y^{FCC}=\left[010\right]$, $u_Z^{FCC}=\left[001\right]$ were employed. One single interstitial atom was added in the HCP-Ti boxes expanded as $4u_X^{HCP}\times 4u_Y^{HCP}\times 2u_Z^{HCP}$, $4u_X^{HCP}\times 2u_Y^{HCP}\times 2u_Z^{HCP}$, $2u_X^{HCP}\times 2u_Y^{HCP}\times 2u_Z^{HCP}$ and $2u_X^{HCP}\times 2u_Y^{HCP}\times u_Z^{HCP}$, while in the FCC-Ti boxes, it was expanded as $4u_X^{FCC}\times 2u_Y^{FCC}\times 2u_Z^{FCC}$, $2u_X^{FCC}\times 2u_Y^{FCC}\times 2u_Z^{FCC}$, $2u_X^{FCC}\times 2u_Y^{FCC}\times u_Z^{FCC}$ and $2u_X^{FCC}\times u_Y^{FCC}\times u_Z^{FCC}$. As such, the atomic fractions of 1.54 at.%, 3.03 at.%, 5.88 at.% and 11.11 at.% were achieved, with the corresponding mass fraction of 0.52~4.01 wt.% (O), 0.45~3.53 wt.% (N), 0.39~3.04 wt.% (C) and 0.35~2.75 wt.% (B). The vaspkit [32] was used to generate a k-point mesh with the same precision (fine = 0.02) centered on the Gamma point. For the geometry optimizations and elastic constant calculations, the supercell shape and all atoms are allowed to relax.

In the calculation of the generalized stacking fault energy of α-Ti, the unit cells oriented as $u_{X2}^{HCP}=\frac{1}{3}[11\overline{2}$0], $u_{Y2}^{HCP}=\frac{\surd 3}{3}[1\overline{1}$00], $u_{Z2}^{HCP}=\left[0001\right]$, boxes expanded as $2u_{X2}^{HCP}\times 1u_{Y2}^{HCP}\times 7u_{Z2}^{HCP}$, each cell containing 56 titanium atoms and 1 interstitial atom, as well as a vacuum layer of 20 Å [33], were employed. The Г-point-centered Monkhorst–Pack grids [34] of 6 × 7 × 1 were used. The upper half box slid along <11$\overline{2}$0> and <1$\overline{1}$00> relative to the lower half, while the interstitial atoms were placed in the octahedral interstitials adjacent to the sliding plane. A full periodic boundary was employed with atoms only allowed to relax in the z direction.

3. Results and Discussion

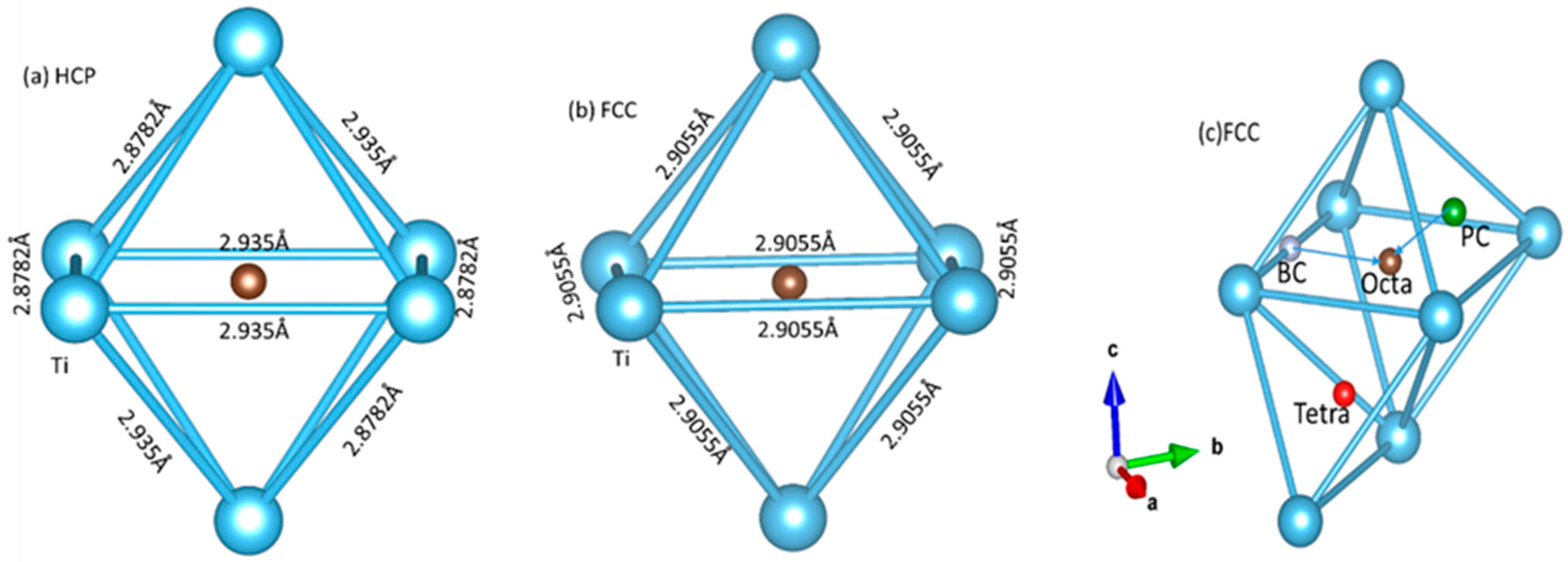
3.1. Stable Interstitial Site

Single B, C, N and O atoms are placed at various interstitial sites to determine the stable interstitial sites in HCP-Ti and FCC-Ti. The interstitial formation energy is defined as [35,36]:

$${}_{}{}^{M}E{}_f^{}={}_{}{}^{M}E{}_{tot}^{}-N\times {}_{}{}^{M}E{}_{host}^{}-{}_{}{}^{M}E{}_{}^{}$$

(1)

where N is the number of atoms in the Ti matrix, ${}_{}{}^{M}E{}_{tot}^{}$ is the total energy of the system with N Ti atoms and an interstitial atom M (M = B, C, N or O), ${}_{}{}^{M}E{}_{host}^{}$ is the energy per atom in pure HCP-Ti or FCC-Ti, and ${}_{}{}^{M}E{}_{}^{}$ is the energy per atom of pure element M (−6.679, −9.22, −8.336 and −4.948 eV/atom for B, C, N and O, respectively, from the Material Project database [37]). Both octahedral (Octa) and tetrahedral (Tetra) interstitial sites are considered in HCP-Ti and in FCC-Ti, as well as the plane-centered (PC) and bond-centered (BC) sites in FCC-Ti (Figure 1).

As shown in Figure 2a, in HCP-Ti, the atoms in the initial tetrahedral position enter the nearest hexahedral position after relaxation, while the octahedral gap is stable and the formation energy is the lowest. This is consistent with previous investigations, which indicated that the octahedral interstitial is stable in α-Ti, and it is difficult for interstitial atoms to exist in the tetrahedral interstitial site [35,38,39]. In FCC-Ti, interstitial atoms are further sited at the face-centered and bond-centered sites, as shown in Figure 1c. However, interstitial atoms in BC and PC interstitial sites automatically move to the nearest octahedral position after relaxation. The present result indicates that in HCP-Ti and FCC-Ti, the most stable interstitial site is the octahedral site. This is also consistent with previous investigations, which indicated that the stable interstice is the octahedral site [40,41]; however, unlike α-Ti, its atoms in the tetrahedral interstice do not escape under relaxation. Interstitials are exclusively placed in the octahedral sites in the following calculations. Figure 2b shows that when the interstitial atoms are located in a stable octahedral interstitial, the interstitial atom formation energy of the four kinds of interstitial atoms changes slightly with the change in content. However, all interstitial atoms still prefer to stay in the octahedral interstitial of FCC-Ti; that is, the stable structure composed of interstitial atoms and interstitial vertex atoms (Ti) is the octahedral structure in FCC-Ti.

3.2. Stability against Interstitial Content

According to the method of Jiang et al. [14], the interstitial effect is further studied against the interstitial content and the B, C, N and O species. In addition to the formation energy employed in Equation (1), we further define the average cohesive energy as follows for comparison between different interstitial species:

$${}_{}{}^{M}E{}_{coh}^{}=\frac{{}_{}{}^{M}E{}_{tot}^{}-N{E}_{mh}-{}_{}{}^{M}E{}_{mi}}{N_{tot}}$$

(2)

where $N_{tot}$ is the total number of atoms, and the modified values E_mh and ^ME_mi of titanium atoms and interstitial atoms were calculated according to the VASP manual. Then, the relative stability of HCP-Ti and FCC-Ti containing the same number of interstitials is determined by the difference in their cohesive energies:

$$∆{}_{}{}^{M}E{}_{coh}^{}={}_{}{}^{M}E{}_{coh}^{FCC}-{}_{}{}^{M}E{}_{coh}^{HCP}$$

(3)

Figure 3a shows the effect of interstitial atoms on the average cohesive energy. Consistent with the results in Figure 2a, B atoms are not easy to be solubilized in titanium, while the other three types of atoms can increase the stability of the two structures, but the stability of FCC-Ti is increased more significantly. As shown in the Figure 3b, $∆{}_{}{}^{M}E{}_{coh}^{}$ is closely relevant to both the interstitial content and specie within the range investigated. The leftmost point indicates the cohesive energy difference in HCP-Ti and FCC-Ti without interstitial, i.e., $∆E_{coh}^{}$. = 58 meV/atom. As the interstitial content increases, $∆{}_{}{}^{M}E{}_{coh}^{}$ exclusively decrease, indicating the enhanced stability of FCC-Ti relative to HCP-Ti. At the largest interstitial content of 11 at.%, $∆{}_{}{}^{M}E{}_{coh}^{}$ amounts to 20, 20, 30 and 43 meV/atom for B, C, N and O, respectively, with reductions of 38, 38, 28 and 15 meV/atom.

Despite the larger energy decrease with interstitial B, C and N compared with O, FCC-Ti is seldom observed in Ti-B, Ti-C and Ti-N systems, as intermetallic compounds TiB, Ti₂N and TiC [42,43,44] are extremely easy to form with significantly smaller solid solubility compared with O, especially at a high temperature. Nevertheless, with C addition, FCC-Ti was observed in a BCC-type Ti₃₇Nb₂₈Mo₂₈-C₇ alloy [14]. It is worth noting that interstitial atoms may have a more pronounced effect on in situ heating. In the experiment where FCC-Ti formation was observed by in situ heating, the initial sample was Ti-0.1 wt% O. During heating, the oxygen content in the sample increased from 0.05 at.% to 7.77 at.%, and the carbon content increased from 0.03 at.% to 1.44 at.% [13]. It can be seen from the calculation that the increase in the content of C and O has an important influence on the reduction in the phase transition energy barrier, so it is not difficult to understand why the formation of FCC-Ti is easier to be observed in these in situ heating experiments [8,11,13].

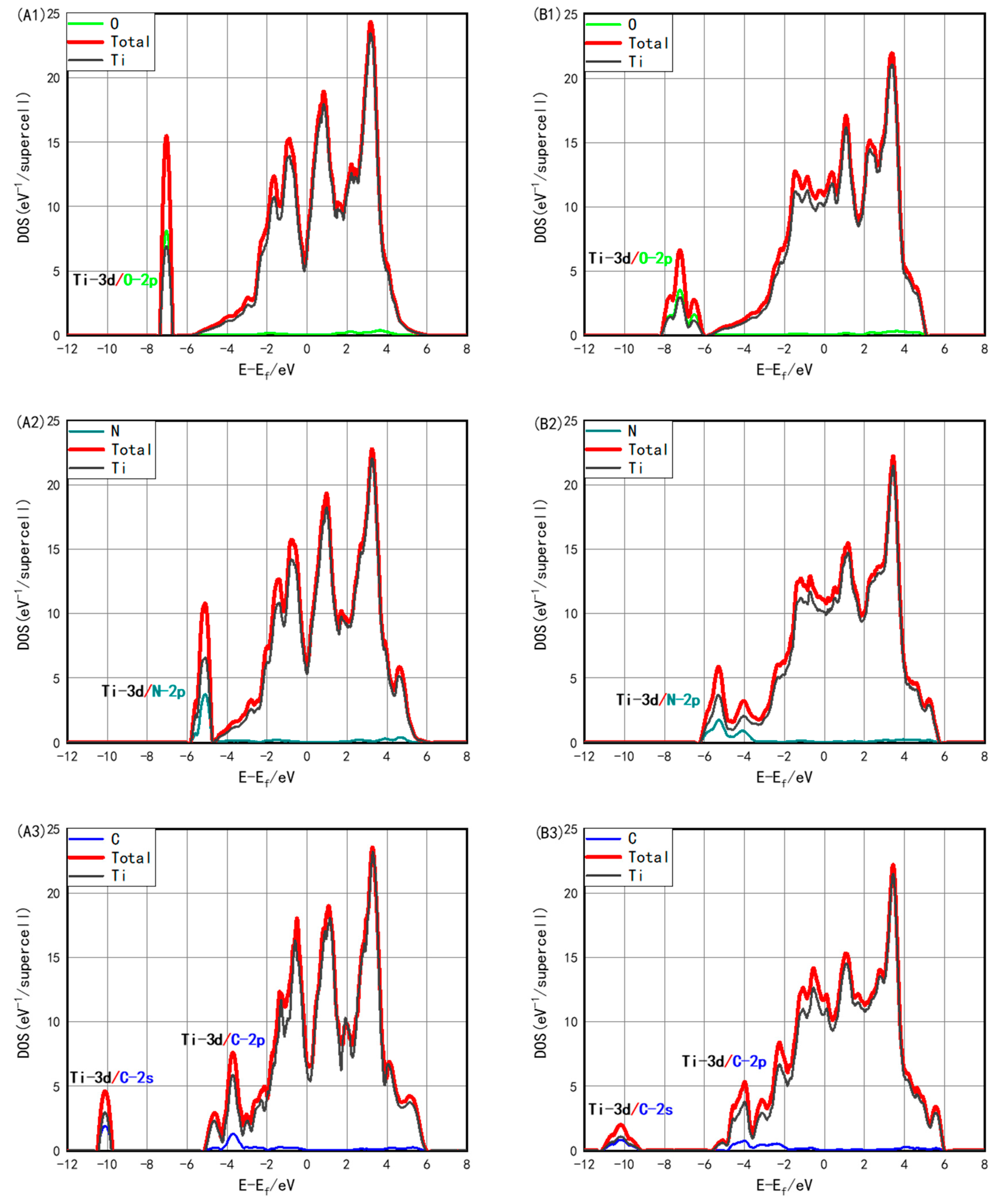
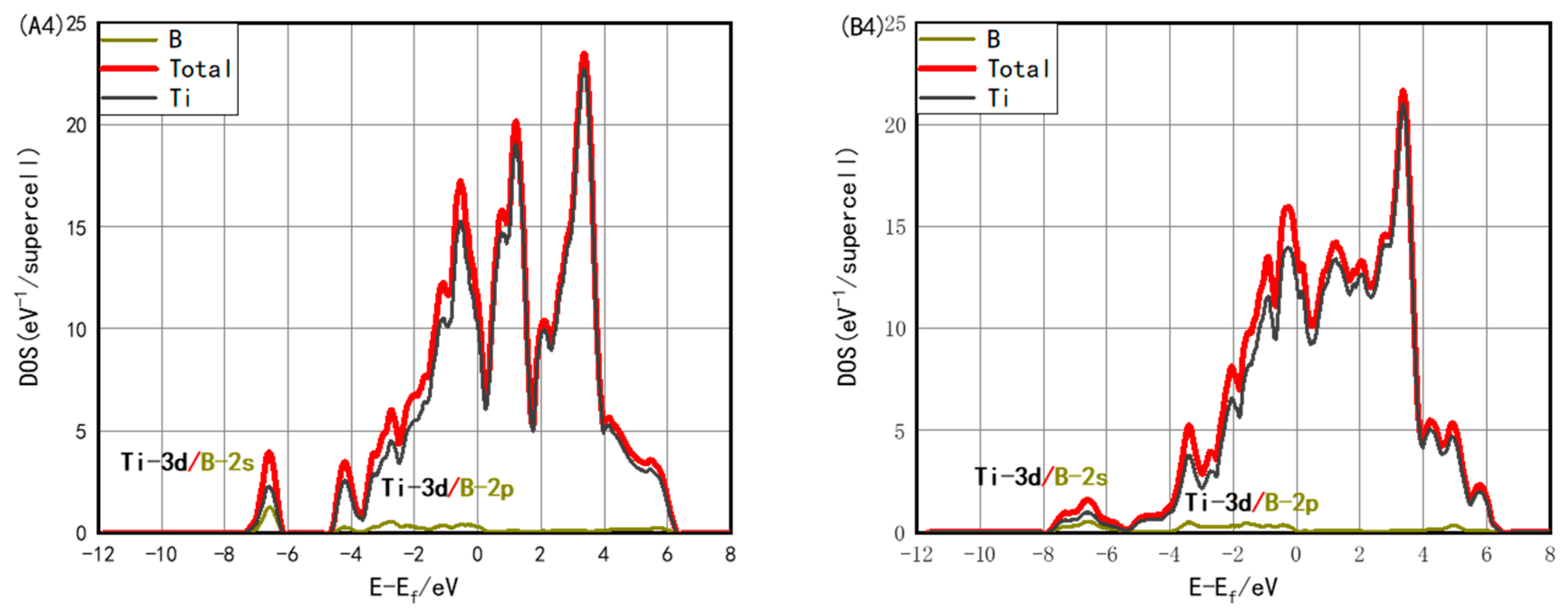
3.3. Electronic Structure with Interstitials

To understand the above influence of nonmetallic interstitials on the phase stability, the electron density of states (DOSs) of HCP-Ti and FCC-Ti with interstitial B, C, N and O were calculated at the content of 11.11 at.% regarding the 3s, 3p, 4s and 3d electrons of Ti, as well as the 2s and 2p electrons of the interstitial atoms [39]. The total DOS and projected DOS are shown in Figure 4. For O and N, mainly the 2p orbitals interact with the 3d orbitals of Ti, while for C and B, both the 2p and 2s orbitals interact with the 3d orbitals of Ti. The electron density states of the orbital interaction between solute atoms and interstitial atoms in FCC-Ti are more dispersed in energy levels compared with those in HCP-Ti, indicating that Ti atoms and the interstitial atoms are more likely to form covalent bonds in FCC-Ti. In addition, it can be seen from Figure 4 that the orbital interaction between interstitial atoms and titanium atoms will shift to a lower energy level after more covalent bonding. On the other hand, the results of integral crystal orbital Hamilton populations (ICOHP) [45] analysis also prove that interstitial atoms exhibit stronger bonding with Ti atoms in FCC-Ti (

Table 2. Integral of crystal orbital Hamilton populations analysis.

System	Ti-O	Ti-N	Ti-C	Ti-B
ICOHPFCC(eV)	−2.338	−2.864	−3.156	−3.450
ICOHPHCP(eV)	−2.000	−2.674	−2.999	−3.001

).

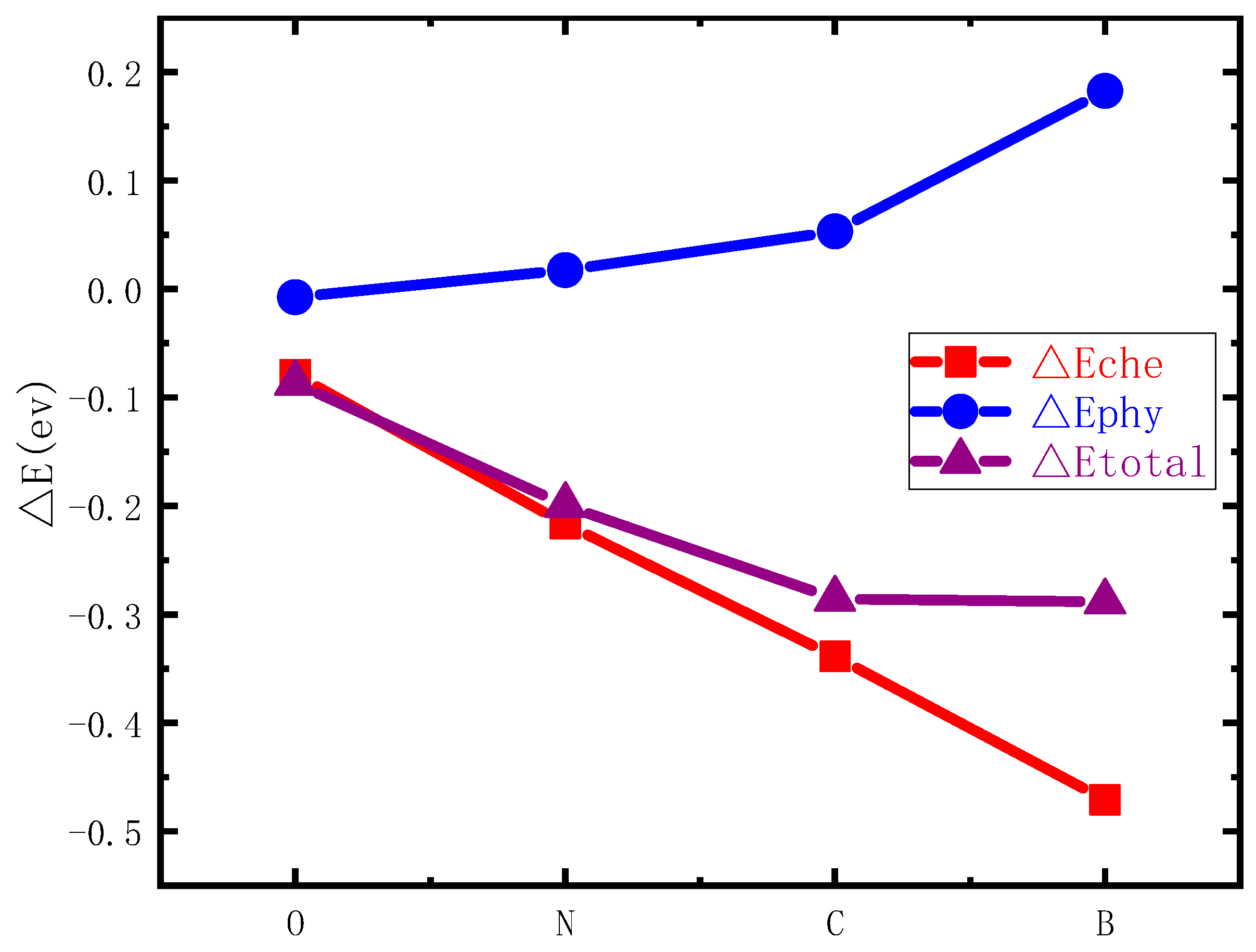
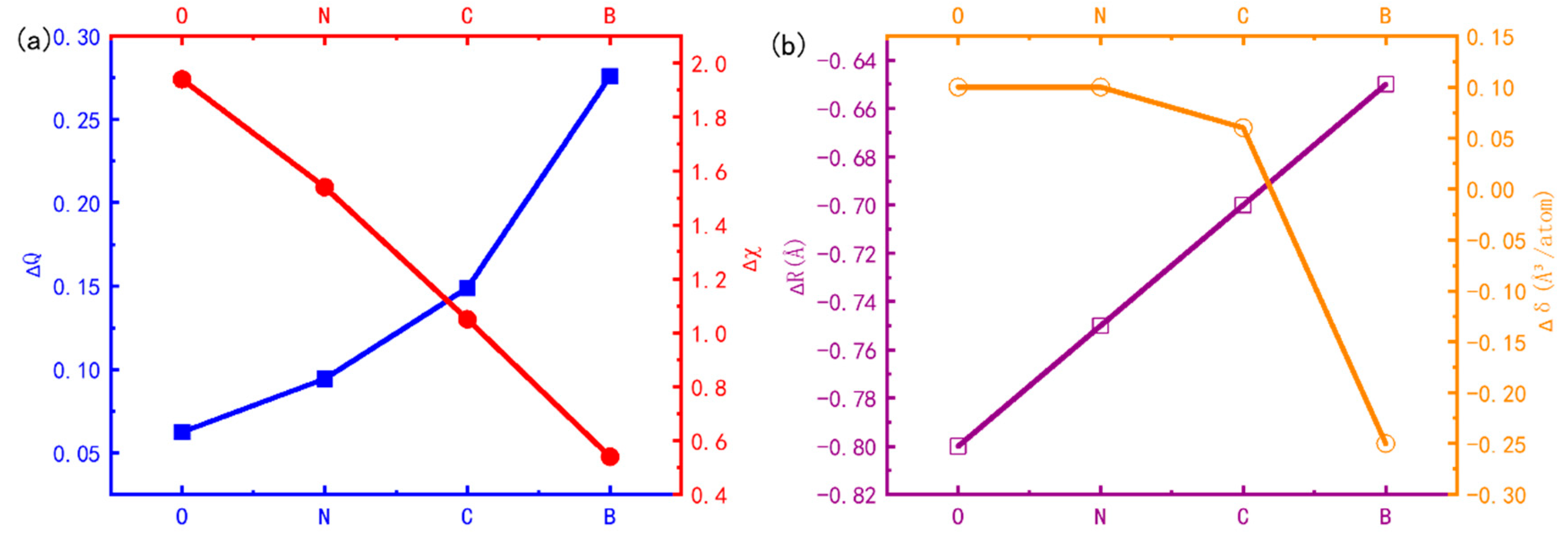
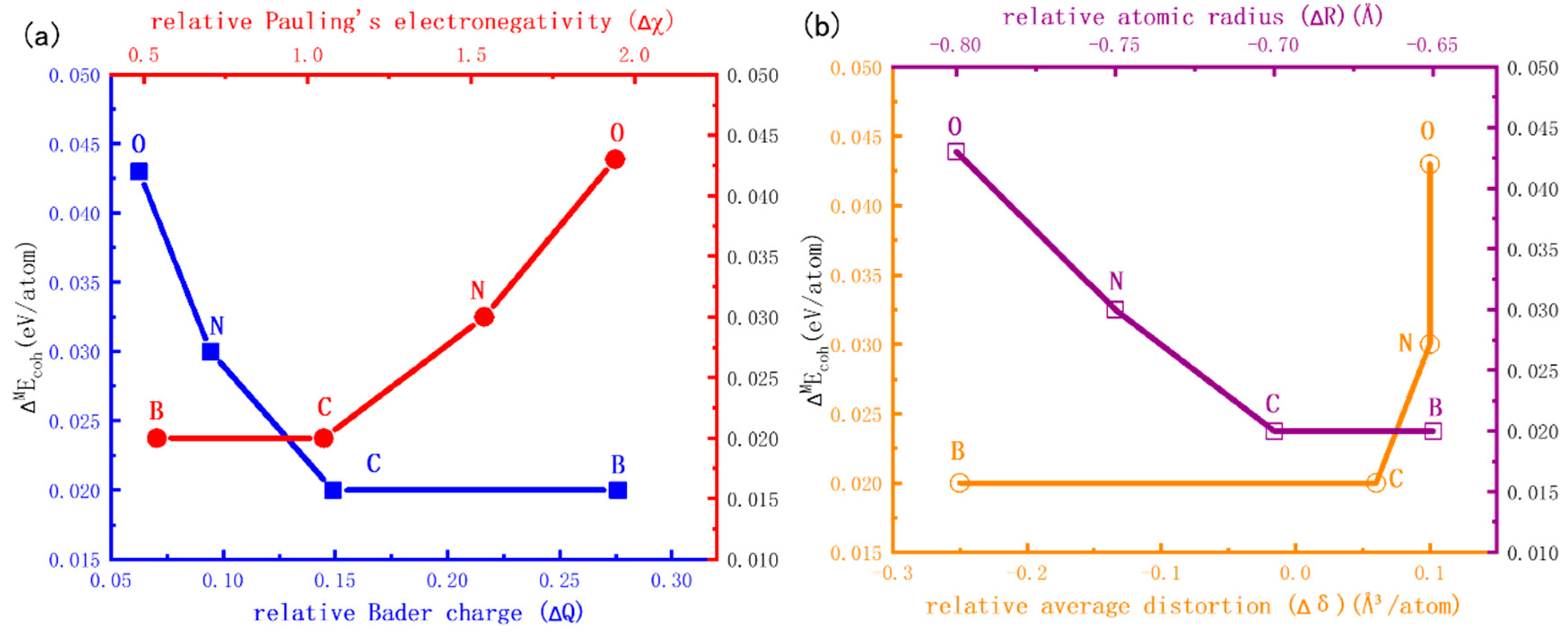
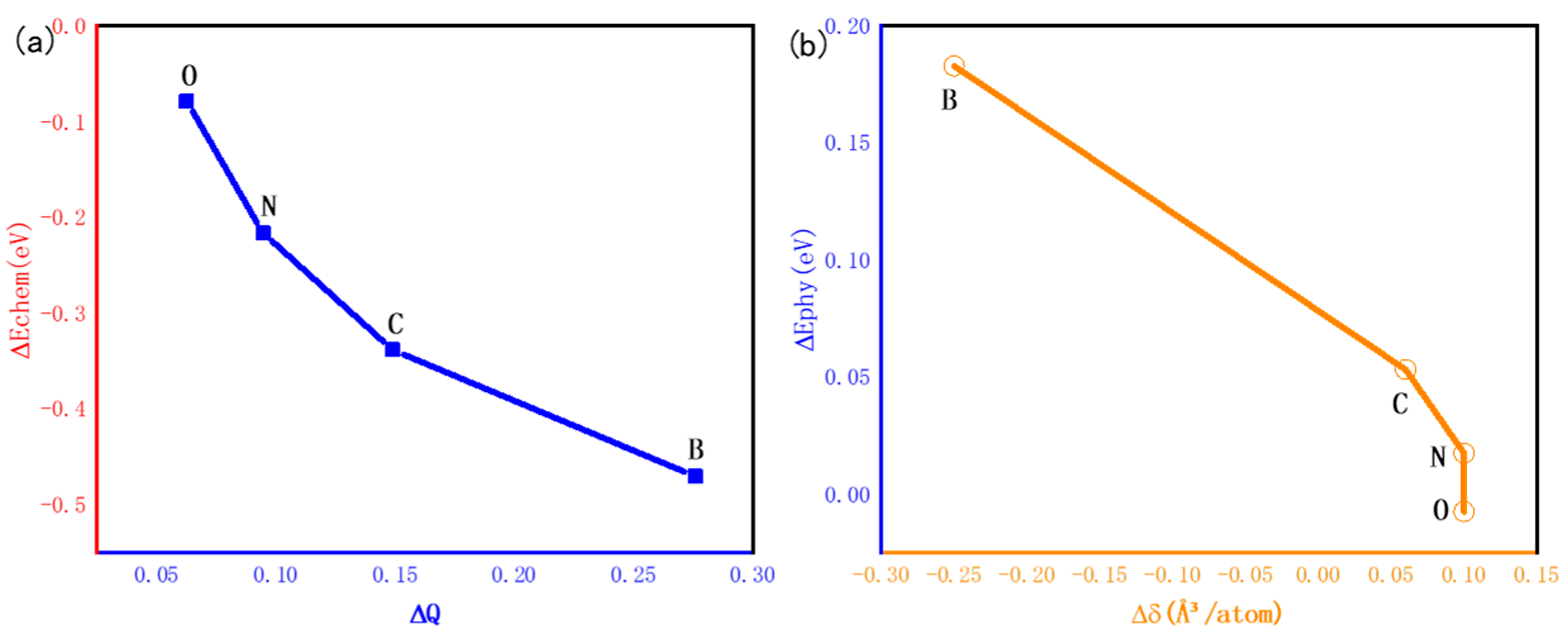
3.4. Influencing Factors of HCP-FCC Phase Transition

Since the relative stability of the interstitial-containing HCP-Ti and FCC-Ti is relevant to the interstitial species, we pursue the study from the physical and chemical aspects, which are determined by the lattice distortion and the electronic structure, respectively, to further clarify the atomic-scale influencing parameters of the HCP-FCC phase transition in Ti alloys. The solution of interstitial atoms causes the energy of the two systems to be close, and this contribution is represented by ΔE_total.

$$△Etotal=({}_{}{}^{M}E{}_{hcp }^{}-{}_{}{}^{M}E{}_{fcc}^{}) - ({}_{}{}^{}E{}_{hcp }^{}-{}_{}{}^{}E{}_{fcc}^{})$$

(4)

where ${}_{}{}^{}E{}_{hcp}^{}$ and ${}_{}{}^{}E{}_{fcc}^{}$ are the energy of a pure titanium perfect cell with an HCP structure and FCC structure, respectively. ${}_{}{}^{M}E{}_{hcp}^{}$ and ${}_{}{}^{M}E{}_{fcc}^{}$ are the energy of the crystal cell containing interstitial atom M (M = B, C, N, O; one interstitial atom was solidly dissolved in these systems, and the content was 11.11 at.%.) with an HCP structure and FCC structure, respectively. After the solid solution of interstitial atoms, the energy of the two systems is close because of the difference in the physical and chemical energy introduced by interstitial atoms in the two systems.

△E_total = △E_phy + △E_chem

(5)

We delete the interstitial atoms in these systems after solid solution relaxation and perform a single-point energy calculation for the system with lattice distortion. The energy obtained is denoted as ${}_{}{}^{M}E{}_{hcp}^d$ and ${}_{}{}^{M}E{}_{hcp}^d$, respectively.

$$△E_{\mathit{phy}}=({}_{}{}^{M}E{}_{hcp}^d -{}_{}{}^{M}E{}_{fcc}^d)-({}_{}{}^{}E{}_{hcp}^{} -{}_{}{}^{}E{}_{fcc}^{})$$

(6)

Finally, as shown in Figure 5, the reduction in the phase transition energy barrier is mainly caused by the difference in the chemical energy introduced by interstitial atoms in the solid solution of the two systems. For example, the C atom reduces the energy barrier of the two systems by 0.286 eV, in which chemical energy contributes −0.339 eV and physical energy contributes 0.053 eV.

To determine electronic bonding and the lattice distortion, Pauling’s electronegativity (χ) [46], the Bader charge (Q) [39,47], the atomic radius (R) [48] and the average distortion (δ), which significantly vary among the interstitial elements, are used. For convenience, we define the relative values as Δχ: the difference in Pauling’s electronegativity between the interstitial atoms and Ti; ΔQ: the difference in the Bader charges acquired by the interstitial atoms between FCC-Ti and HCP-Ti; ΔR: the difference in the atomic radii between the interstitial atoms and Ti; and Δδ: the difference in the average distortion between interstitial-containing HCP-Ti and FCC-Ti. Figure 6 shows the values of Δχ, ΔQ, ΔR and Δδ of interstitial atoms O, N, C and B, where Δχ and Δδ decrease, while ΔQ and ΔR increase in the order of O, N, C, B. Δχ and ΔQ are strongly inversely intercorrelated, while ΔR and Δδ weakly inversely intercorrelate.

Lattice distortion is defined as

$$\delta =\frac{V_e-V_s}{N_h}$$

(7)

where N_h is the number of titanium atoms in a system, and vs and V_e are the volume of crystal cells before and after solid solution distortion, respectively. Accordingly, we define $∆$δ to reflect the difference in cell aberration caused by interstitial atoms in the two crystal structures.

$$∆\delta ={\delta }^{HCP}-{\delta }^{FCC}$$

(8)

Hence, the relative phase stability, $∆{}_{}{}^{M}E{}_{coh}^{}$, can exist. Figure 7 shows the dependence of relative phase stability, $∆{}_{}{}^{M}E{}_{coh}^{}$, on the relative Pauling’s electronegativity (Δχ), the relative Bader charge (ΔQ), the relative atomic radius (ΔR) and the relative average distortion (Δδ) of the interstitial atoms O, N, C and B at the content of 11.11 at.%.

For O, N and C atoms, the difference in solution distortion between the two systems is small. The relative stability of the interstitial-containing HCP-Ti and FCC-Ti is more relevant to electronic bonding than the local lattice distortion. A large Δχ favors ionic bonding between atoms; hence, the bonding covalency of the intestinal atom with the Ti atoms decreases in the order of C, N and O. Since Δχ and ΔQ are inversely intercorrelated, the increase in Δχ and the decrease in ΔQ are relevant to $∆{}_{}{}^{M}E{}_{coh}^{}$ (Figure 7a). On the other hand, $∆{}_{}{}^{M}E{}_{coh}^{}$ is weakly dependent on ΔR and almost independent on Δδ. For these systems containing B atoms, the difference in solution distortion is not negligible. On the one hand, a B atom has stronger bond cooperation with Ti atoms in the FCC-Ti system, which reduces the energy difference between the two systems; on the other hand, it causes greater solid solution distortion in the FCC-Ti system (Figure 7b), which increases $∆{}_{}{}^{M}E{}_{coh}^{}$. Therefore, it has a larger ΔQ value but contributes almost as much to phase stability as carbon (Figure 5 and Figure 7b).

In this study, the value of $∆{}_{}{}^{M}E{}_{coh}^{}$ is affected by two aspects. One is the difference in chemical energy caused by different bonding states of interstitial atoms in the two systems. The other is the difference in strain energy introduced by interstitial atoms in different systems. A comprehensive comparison of the four interstitial atoms shows that charge transfer and lattice distortion affect the relative phase stability of the two systems, and charge transfer plays a major role (Figure 5 and Figure 8). Of course, we should not ignore that the premise we give is the formation of an interstitial solid solution. For example, a B atom should not be considered as an atom prone to FCC-Ti formation due to its large interstitial atomic formation energy.

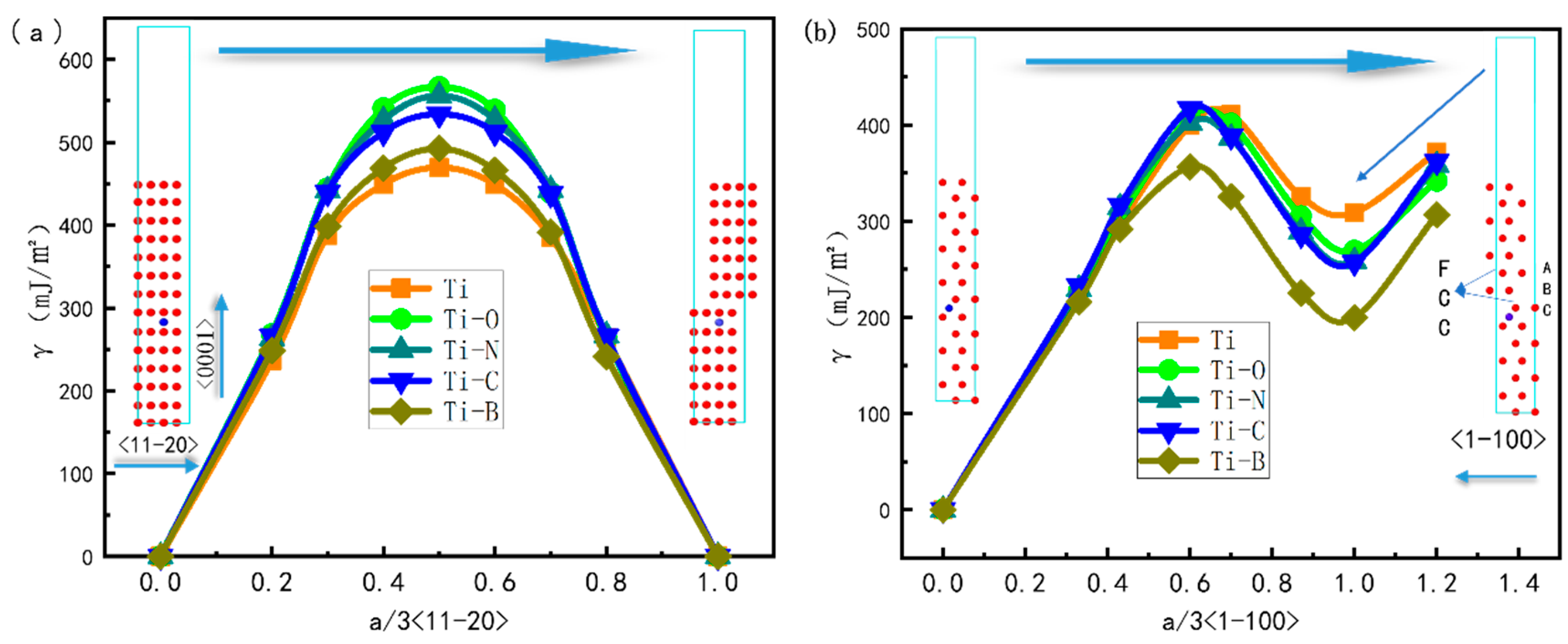
3.5. Stacking Fault Energy

The generalized stacking fault energy is defined as follows [33,49,50]:

$$\gamma =\frac{E_r-E_0}{S}$$

(9)

where E_r is the system energy after the slide of the upper part relative to the lower part at a given distance, E₀ is the initial system energy, and S is the area of the slip surface.

The influence of the interstitial atoms on the slip of HCP-Ti along the <11$\overline{2}$0> and <1$\overline{1}$00> directions is shown in Figure 9. Without interstitial atoms in the system, the intrinsic stacking fault energy (${\gamma }_{ISF}^2$) is 309 mJ/m², while the unstable stacking fault energy of pure HCP-Ti along <11$\overline{2}$0> and <1$\overline{1}$00> (${\gamma }_{USF}^1$ and ${\gamma }_{USF}^2$) are 470 mJ/m² and 411 mJ/m², respectively. This is consistent with previous results on ${\gamma }_{ISF}^2$ i.e., 287 mJ/m² in Ref. [51], 307 mJ/m² in Ref. [33] and 310 mJ/m² in Ref. [52]. With interstitial atoms O, N, C and B, ${\gamma }_{ISF}^{}$ reduces to 269 mJ/m², 258 mJ/m², 257 mJ/m² and 200 mJ/m², respectively, whereas ${\gamma }_{USF}^1$ increases to 567 mJ/m², 556 mJ/m², 534 mJ/m² and 492 mJ/m², respectively. In addition, B significantly reduces ${\gamma }_{USF}^2$, the other three atoms have no obvious effect on ${\gamma }_{USF}^2$.The increase in ${\gamma }_{USF}^1$/${\gamma }_{USF}^2$ and the decrease in ${\gamma }_{ISF}^2$ favor the following dislocation dissociation [29]:

$$1/3<11\overline{2}0>\to 1/3<10\overline{1}0>+1/3<01\overline{1}0>$$

which further facilitates the formation of FCC-Ti through the slip of Shockley partial dislocations [14].

4. Conclusions

In the present work, the effect of nonmetallic interstitial atoms B, C, N and O on the hexagonal-close-packed (HCP) to face-centered cubic (FCC) phase transition of titanium was investigated with the density functional theory. The following conclusions can be drawn:

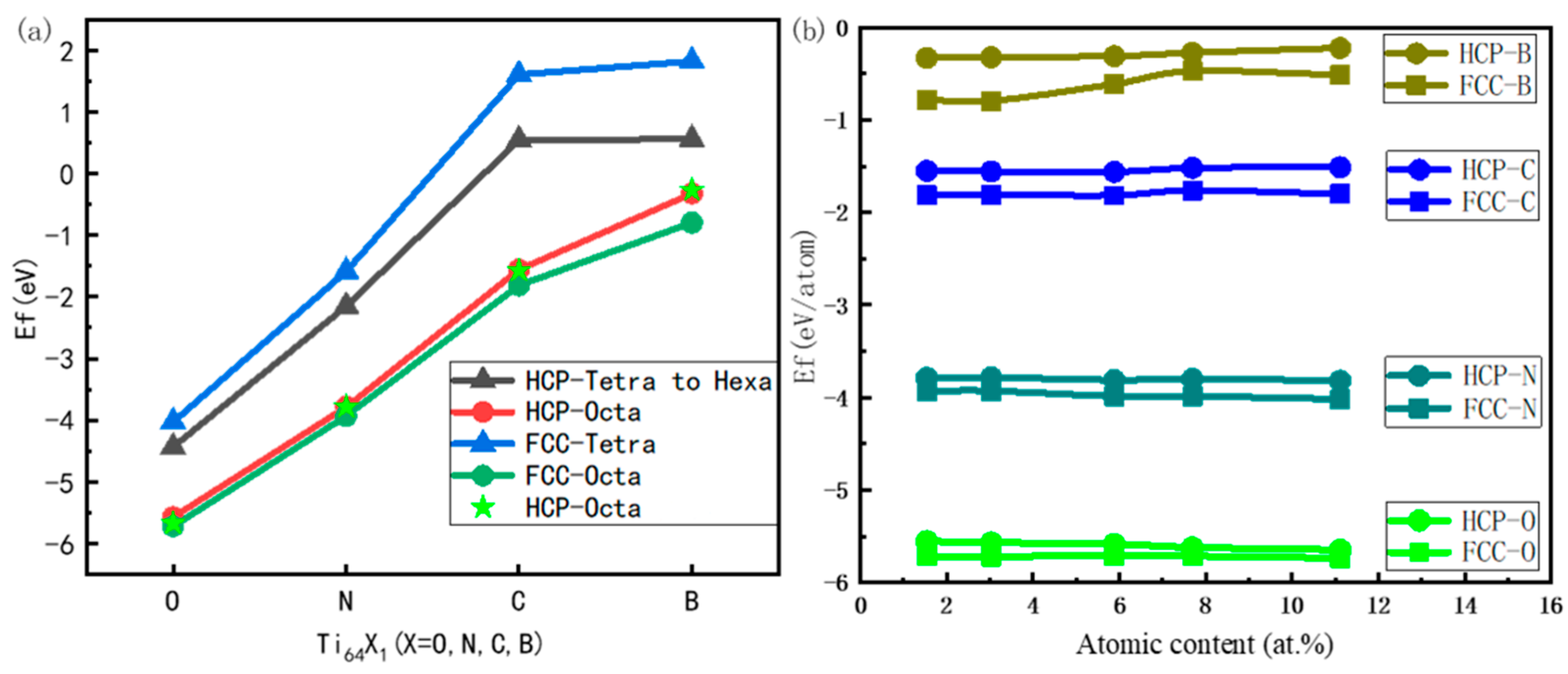
• In both HCP-Ti and FCC-Ti, the nonmetallic atoms B, C, N and O favor the octahedral interstitial site rather than the tetrahedral site. The octahedral B, C, N and O interstitials decrease the energy gap between FCC-Ti and HCP-Ti, and the gap further decreases with the increase in the interstitial content.
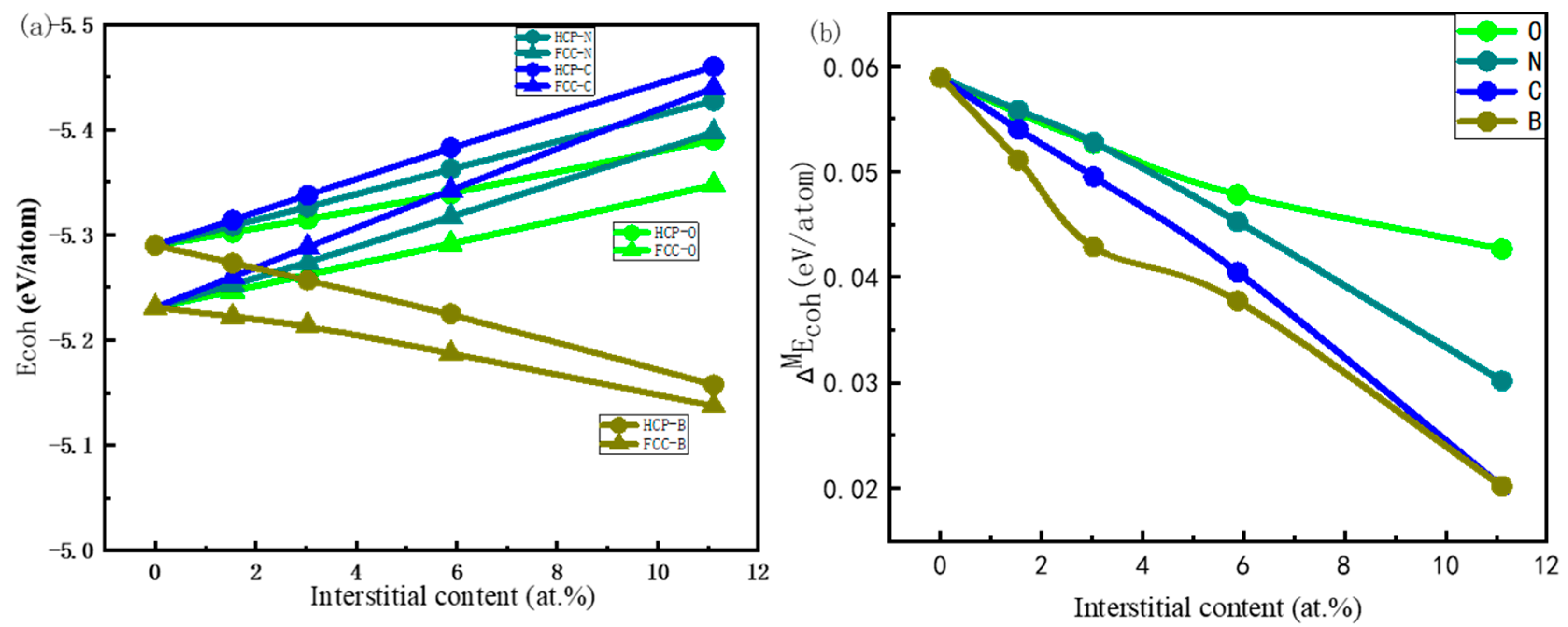
• The relative stability of the interstitial-containing HCP-Ti and FCC-Ti is strongly relevant to the electronic structure, while it is weakly relevant to the lattice distortion. The relative stability of FCC-Ti decreases with the relative Pauling’s electronegativity, while it increases with the relative Bader charge.
• The existence of interstitial atoms reduces the intrinsic stacking fault energy of HCP-Ti, which is conducive to the decomposition of perfect dislocation into partial dislocations and is further beneficial to the formation of FCC-Ti.