Two-Stage Model for Fatigue Life Assessment of High Frequency Mechanical Impact (HFMI) Treated Welded Steel Details
Abstract
:1. Introduction
2. Materials and Methods
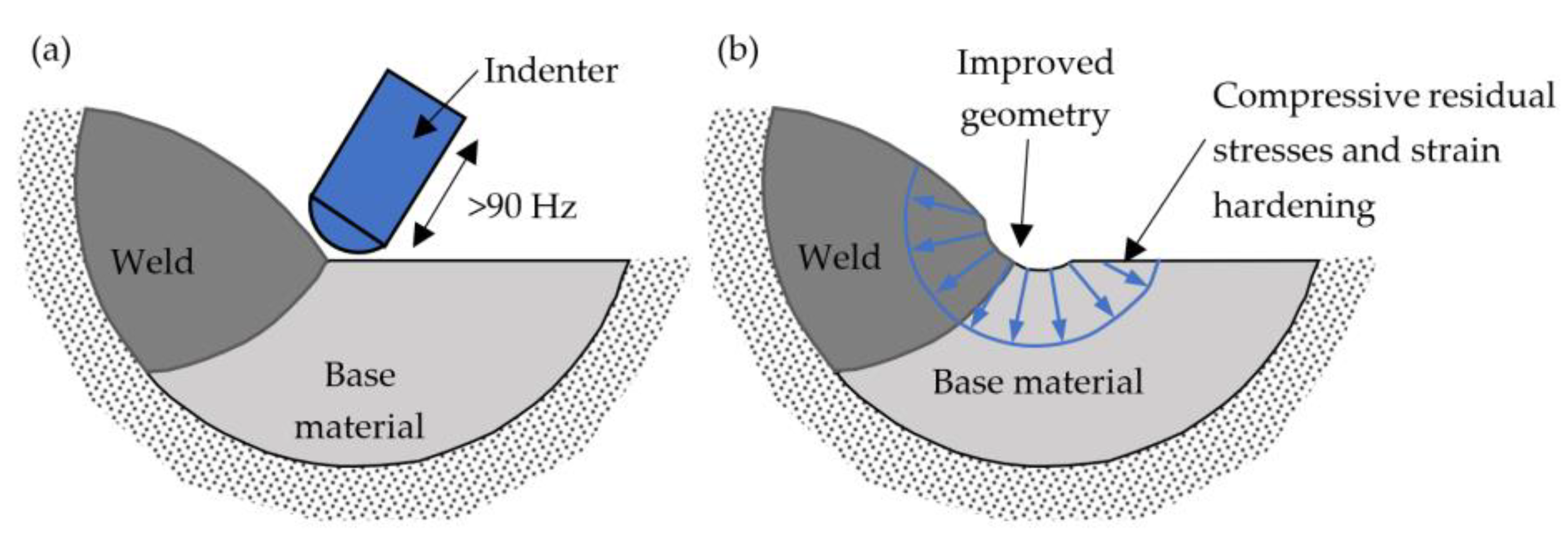
2.1. High-Frequency Mechanical Impact (HFMI) Treatment
2.2. Two-Stage Model (TSM)
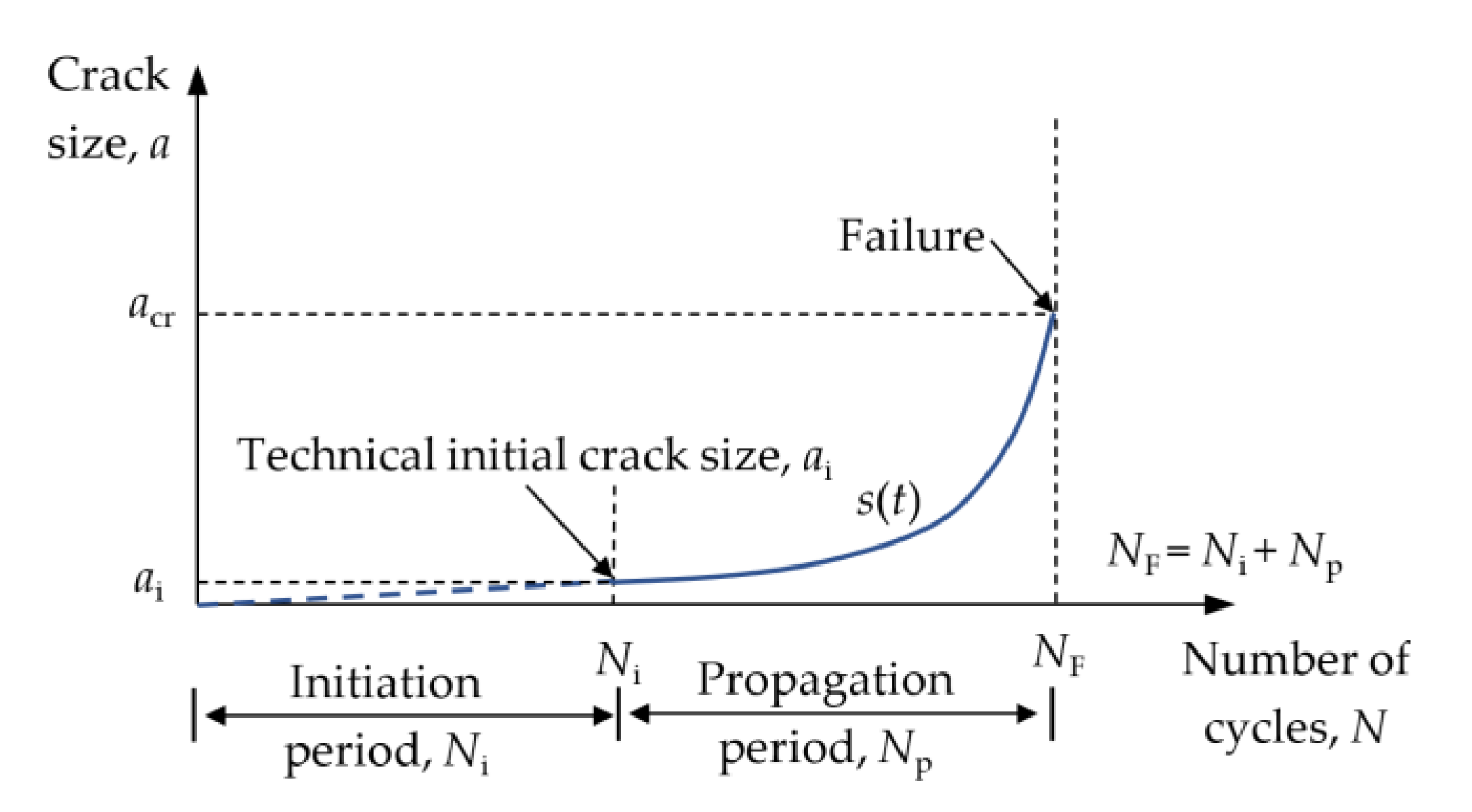
2.2.1. General
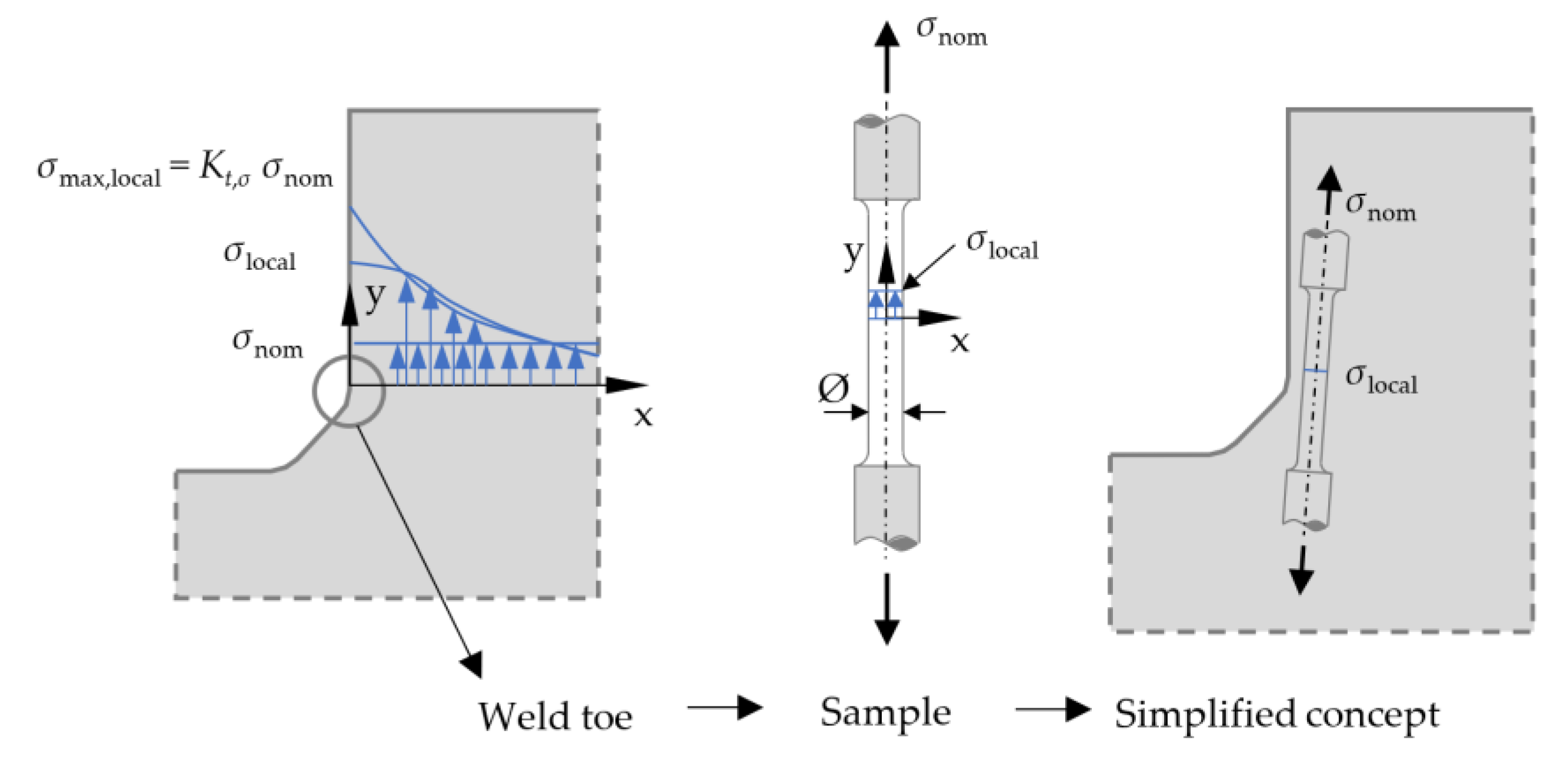
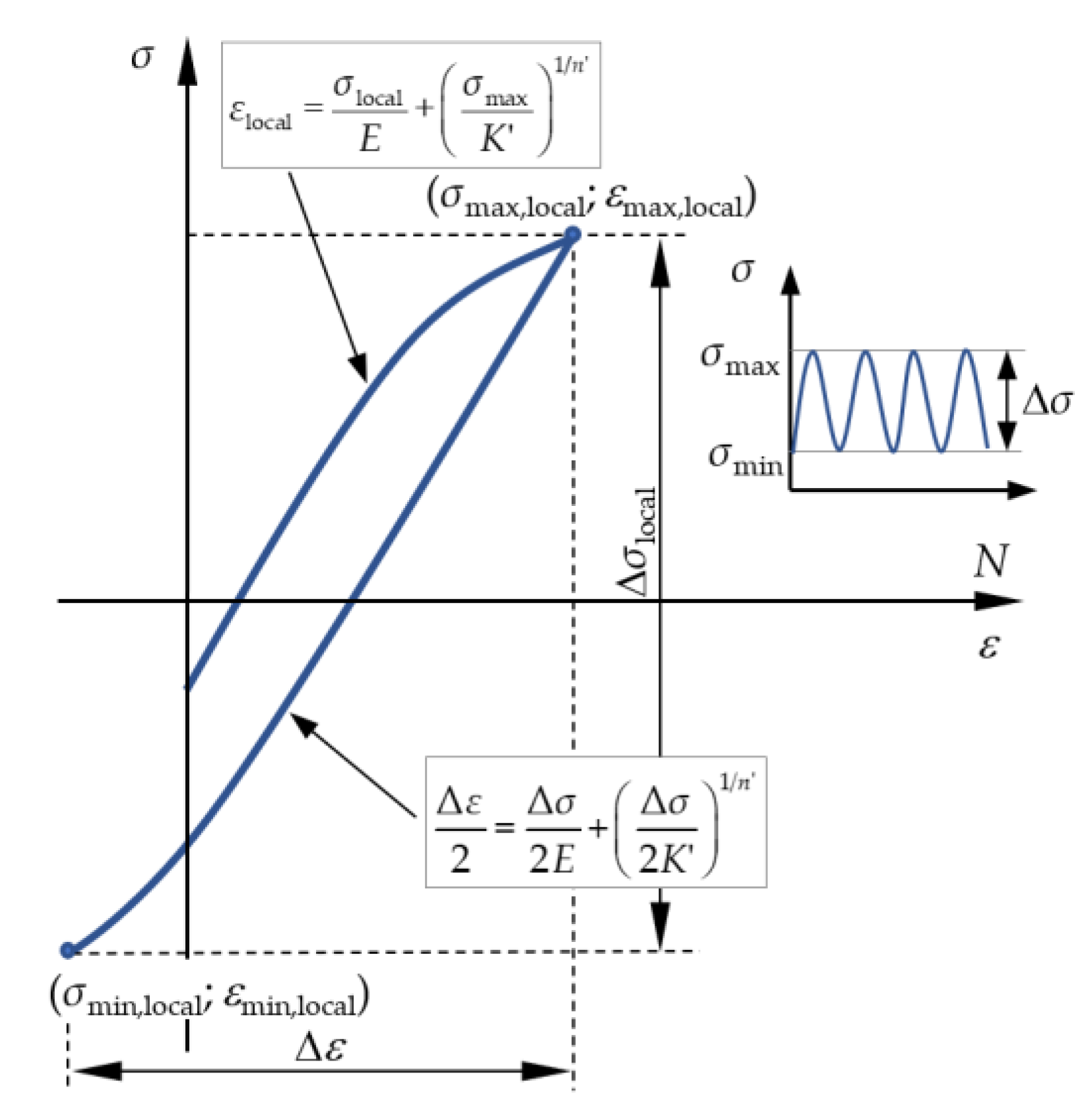
2.2.2. Crack Initiation Period—Notch Strain Approach (NS)
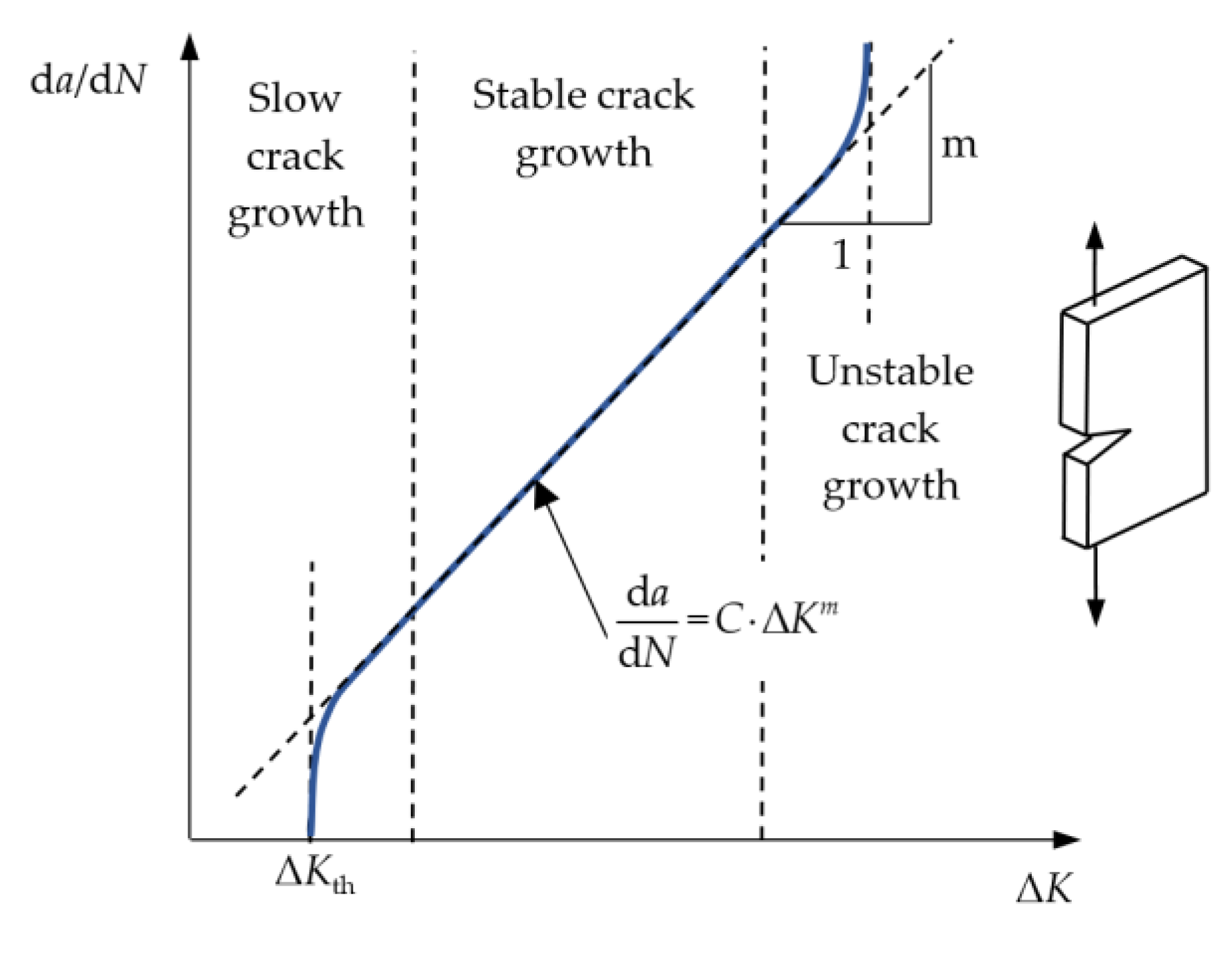
2.2.3. Crack Propagation Period–Linear Elastic Fracture Mechanics (LEFM)
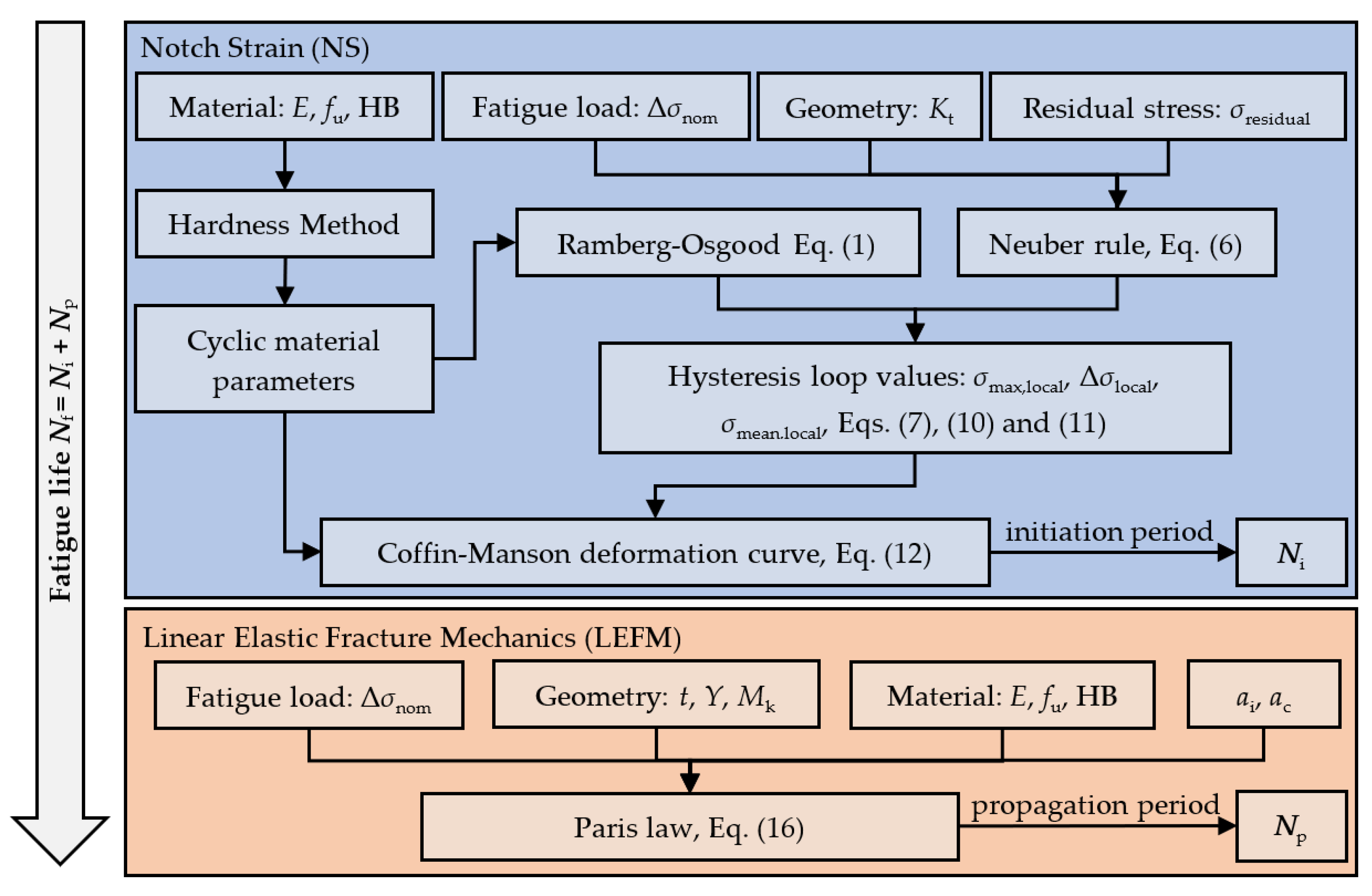
2.2.4. Flowchart of the Two-Stage Model (TSM)
3. Results and Discussion
3.1. Calibration of the TSM
3.1.1. General
3.1.2. Material Parameters for NS Approach
3.1.3. Material and Geometry Parameters for the LEFM Approach
3.1.4. HFMI Parameters for TSM
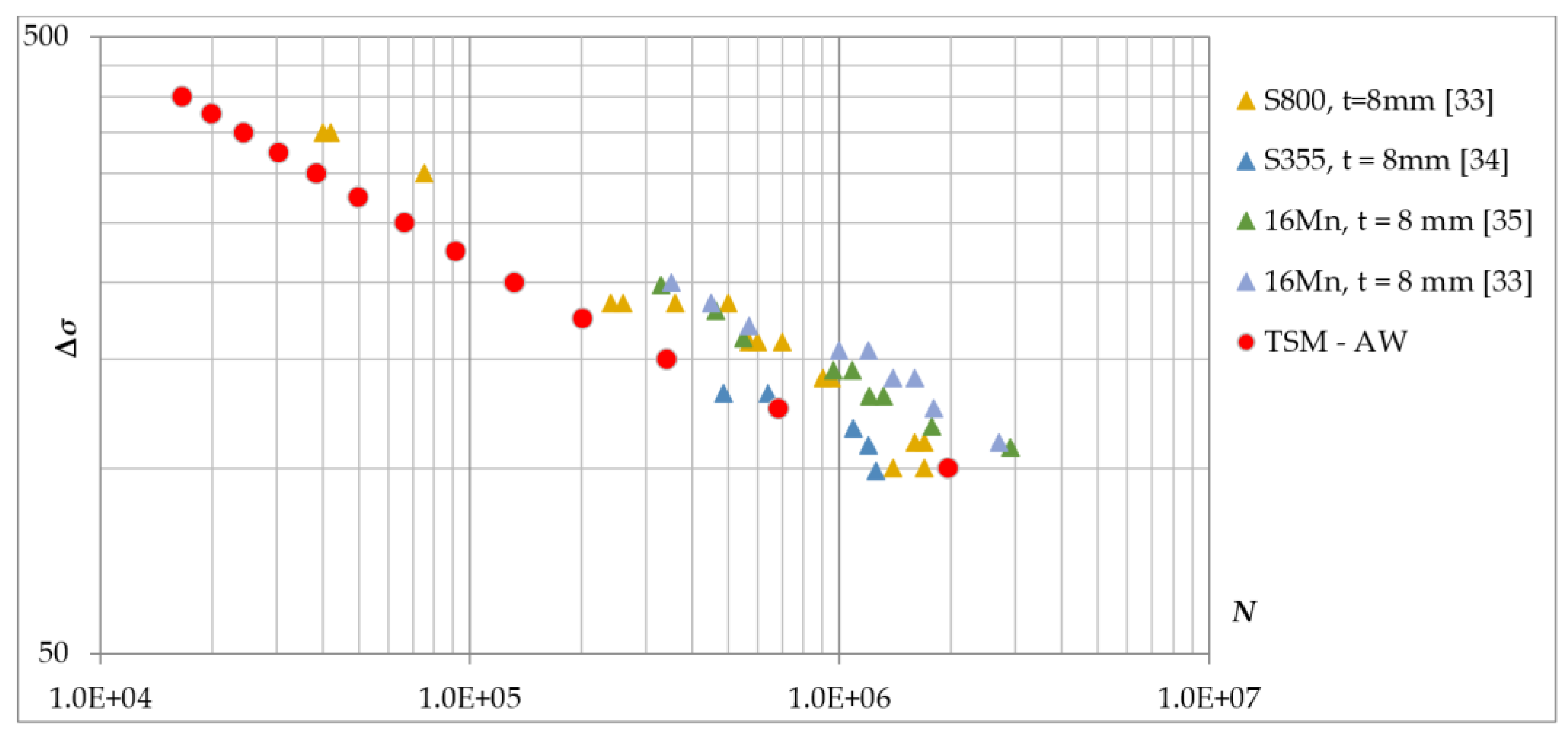
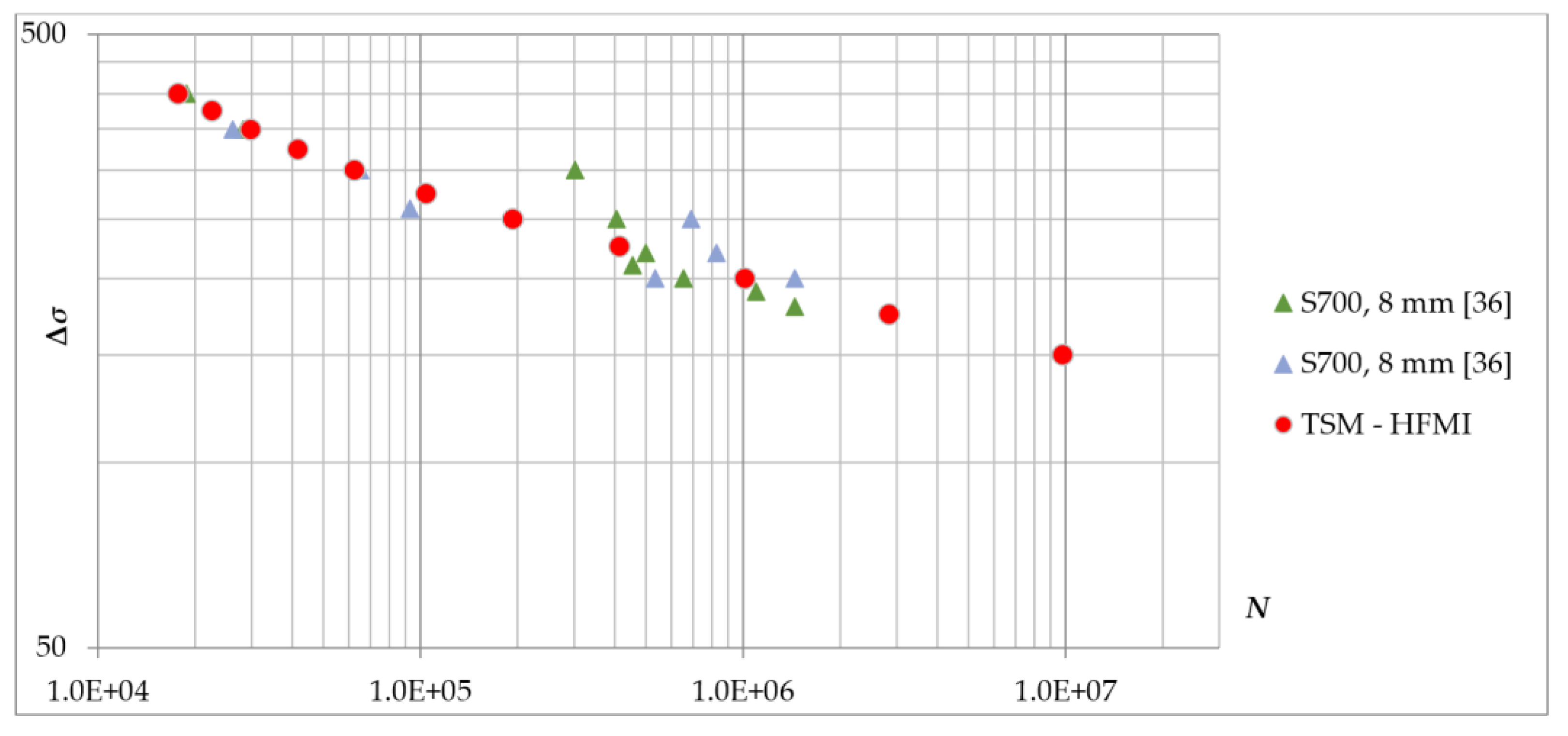
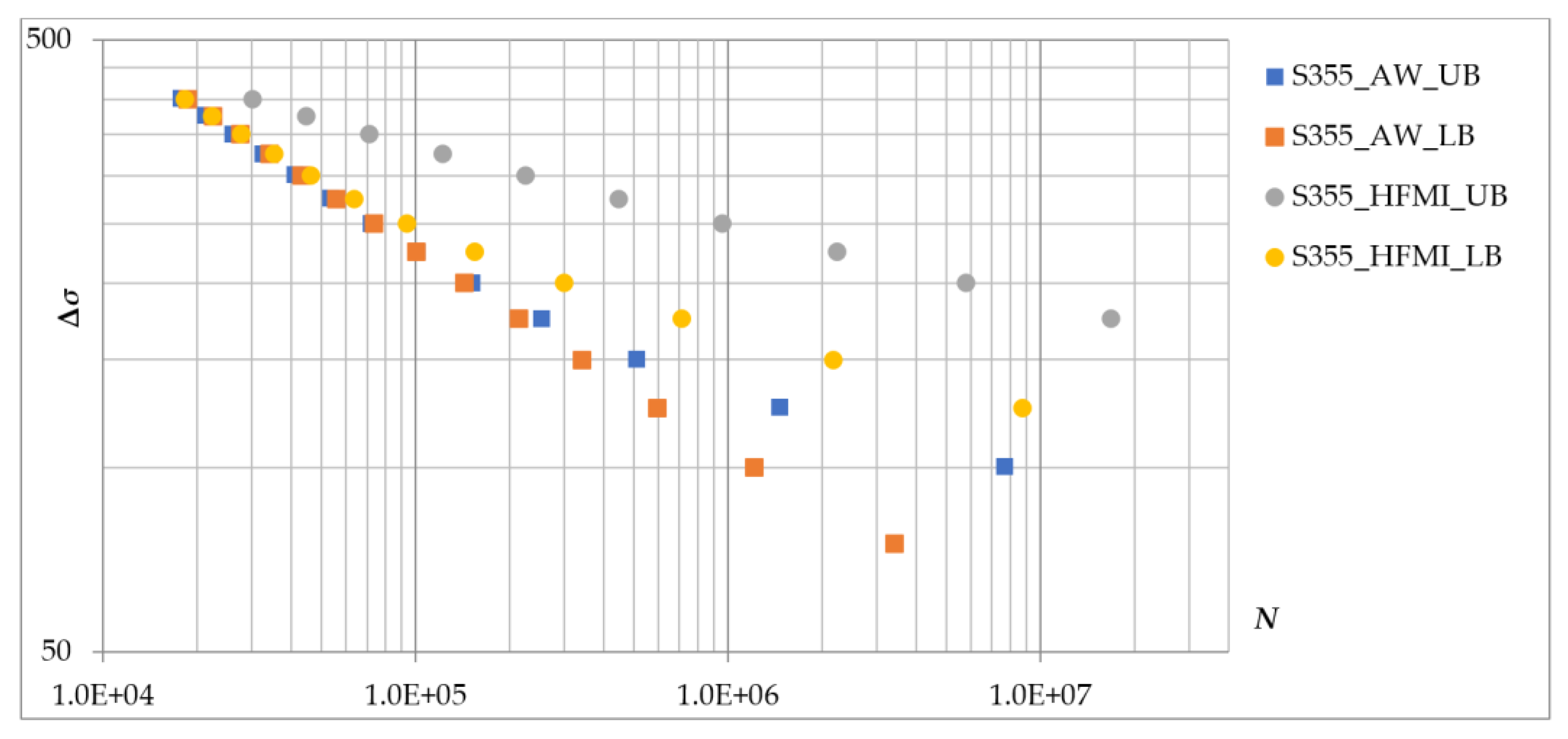
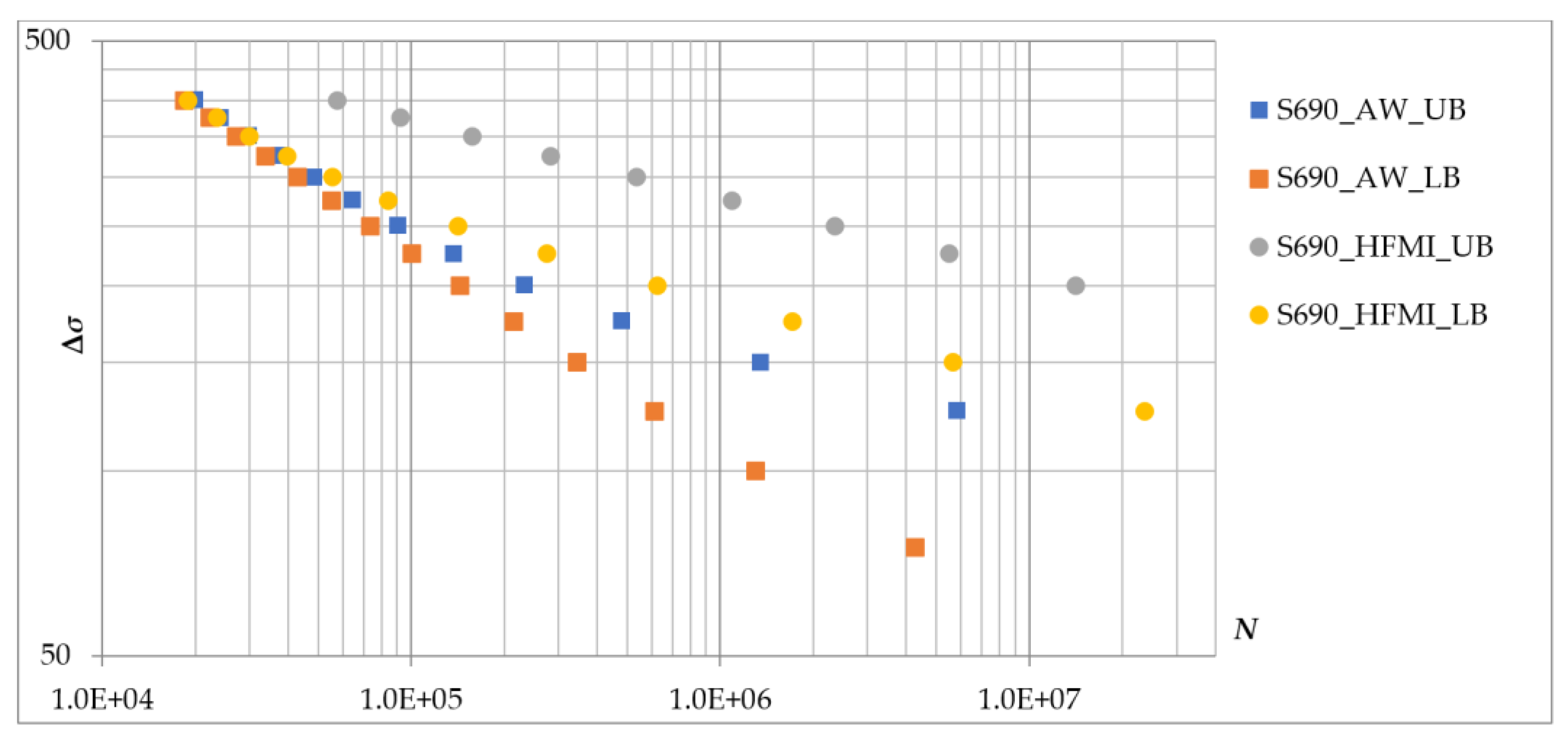
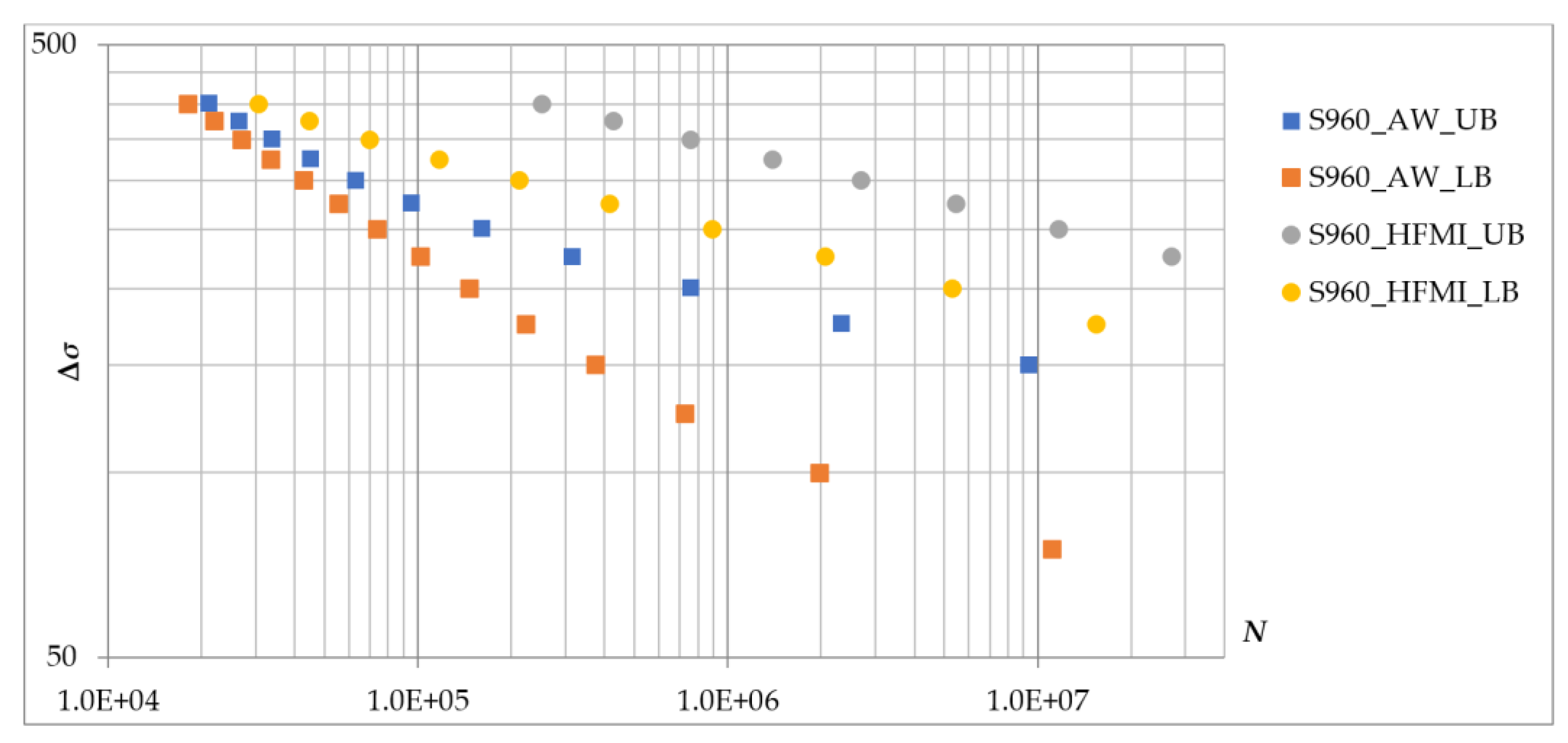
3.1.5. Results of the TSM
3.2. Parametric Study
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schijve, J. Fatigue as a Phenomenon in the Material. In Fatigue of Structures and Materials; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004; pp. 7–44. [Google Scholar]
- Maddox, S.J. Fatigue Strength of Welded Structures, 2nd ed.; Abington Publishing: Cambridge, UK, 1991. [Google Scholar]
- Haagensen, P.J.; Maddox, S.J. IIW Recommendations on Methods for Improving the Fatigue Strength of Welded Joints: IIW-2142-110; Woodhead Publishing: Cambridge, UK, 2013; ISBN 978-1-78242-065-1. [Google Scholar]
- Marquis, G.B.; Barsoum, Z. IIW Recommendations for the HFMI Treatment for Improving the Fatigue Strength of Welded Joints; Springer Science & Business Media: Singapore, 2016; ISBN 978-981-10-2503-7. [Google Scholar]
- Mikkola, E. A study on effectiveness limitations of high-frequency mechanical impact. Doctoral Dissertation, Aalto University, Espoo, Finland, 2016. [Google Scholar]
- Fuštar, B.; Lukačević, I.; Dujmović, D. High-Frequency mechanical impact treatment of welded joints. Gradjevinar 2020, 72, 421–436. [Google Scholar] [CrossRef]
- European Committee for Standardization (CEN). Eurocode 3: Design of steel structures, Part 1–9: Fatigue (EN 1993-1-9:2005); CEN: Brussels, Belgium, 2005.
- European Committee for Standardization—Technical Committee 250 (CEN/TC 250). Eurocode 3: Design of Steel Structures (prEN 1993-1-9 Final Draft: 2020); CEN/TC 250: Brussels, Belgium, 2020.
- Fuštar, B.; Lukačević, I.; Dujmović, D. Review of fatigue assessment methods for welded steel structures Fatigue of welded joints. Adv. Civ. Eng. 2018, 2018, 3597356. [Google Scholar] [CrossRef] [Green Version]
- Radaj, D.; Sonsino, C.M.; Fricke, W. Fatigue Assessment of Welded Joints by Local Approaches, 2nd ed.; Woodhead Publishing and Maney Publishing: Cambridge, UK, 2006. [Google Scholar] [CrossRef]
- Hobbacher, A.F. Erratum to: Recommendations for Fatigue Design of Welded Joints and Components; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef] [Green Version]
- Ottersböck, M.J.; Leitner, M.; Stoschka, M.; Maurer, W. Crack Initiation and Propagation Fatigue Life of Ultra High-Strength Steel Butt Joints. Appl. Sci. 2019, 9, 4590. [Google Scholar] [CrossRef] [Green Version]
- Leitner, M.; Simunek, D.; Shah, S.F.; Stoschka, M. Numerical fatigue assessment of welded and HFMI-treated joints by notch stress/strain and fracture mechanical approaches. Adv. Eng. Softw. 2016, 120, 96–106. [Google Scholar] [CrossRef]
- Röscher, S.; Knobloch, M. Towards a prognosis of fatigue life using a Two-Stage-Model: Application to butt welds. Steel Constr. 2019, 12, 198–208. [Google Scholar] [CrossRef]
- Baptista, C.; Reis, A.; Nussbaumer, A. Probabilistic S-N curves for constant and variable amplitude. Int. J. Fatigue 2017, 101, 312–327. [Google Scholar] [CrossRef]
- Yıldırım, H.C. Recent results on fatigue strength improvement of high-strength steel welded joints. Int. J. Fatigue 2017, 101, 408–420. [Google Scholar] [CrossRef]
- Yıldırım, H.C.; Marquis, G.B. A round robin study of high-frequency mechanical impact (HFMI)-treated welded joints subjected to variable amplitude loading. Weld. World 2013, 57, 437–447. [Google Scholar] [CrossRef]
- Marquis, G.; Barsoum, Z. Fatigue strength improvement of steel structures by high-frequency mechanical impact: Proposed procedures and quality assurance guidelines. Weld. World 2014, 58, 19–28. [Google Scholar] [CrossRef]
- Peterson, R.E. Notch sensitivity. In Metal Fatigue; McGraw-Hill: New York, NY, USA, 1959; pp. 293–306. [Google Scholar]
- Neuber, H. Über die Berücksichtigung der Spannungskonzentration bei Festigkeitsberechnungen. Konstruktion 1968, 20, 245–251. [Google Scholar]
- Radaj, D. Design and Analysis of Fatigue Resistant Welded Structures; Woodhead Publishing: Cambridge, UK, 1990. [Google Scholar]
- Seeger, T. Grundlagen für Betriebsfestigkeitsnachweise (Stahlbau Handbuch); Stahlbau-Verlagsges: Köln, Germany, 1996. [Google Scholar]
- Lihavainen, V.M.; Marquis, G. Estimation of fatigue life improvement for ultrasonic impact treated welded joints. Steel Res. Int. 2006, 77, 896–900. [Google Scholar] [CrossRef]
- Atzori, B.; Lazzarin, P. Notch sensitivity and defect sensitivity under fatigue loading: Two sides of the same medal. Int. J. Fract. 2001, 107, 1–8. [Google Scholar] [CrossRef]
- Glinka, G. Energy density approach to calculation of inelastic strain-stress near notches and cracks. Eng. Fract. Mech. 1985, 22, 485–508. [Google Scholar] [CrossRef]
- Hobbacher, A. The use of fracture mechanics in the fatigue analysis of welded joints. In Fracture Fatigue Welded Joints Struct; Elsevier Ltd.: Amsterdam, The Netherlands, 2011; pp. 91–112. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress–Strain Curves by Three Parameters; National Advisory Comittee for Aeronautics, Rep. 902; University of Washington Libraries: Washington, DC, USA, 1943. [Google Scholar]
- Neuber, H. Kerbspannungslehre: Grundlagen für Genaue Spannungsrechnung; Springer: Berlin/Heidelberg, Germany, 1937. [Google Scholar] [CrossRef]
- Masing, G. Eigenspannungen und Verfestigung beim Messing. In Proceedings of the 2nd International Congress for Applied Mechanics, Zurich, Switzerland, 12–17 September 1926; pp. 332–335. [Google Scholar]
- Chattopadhyay, A.; Glinka, G.; El-Zein, M.; Qian, J.; Formas, R. Stress analysis and fatigue of welded structures. Weld. World 2011, 55, 2–21. [Google Scholar] [CrossRef]
- Hou, C.Y.; Charng, J.J. Models for the Estimation of Weldemnt Fatigue Crack Initiation Life. Int. J. Fatigue 1997, 19, 537–541. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A critical analysis of crack propagation laws. J. Fluids. Eng. Trans. Am. Soc. Mech. Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Wang, T.; Wang, D.; Huo, L.; Zhang, Y. Discussion on fatigue design of welded joints enhanced by ultrasonic peening treatment (UPT). Int. J. Fatigue 2009, 31, 644–650. [Google Scholar] [CrossRef]
- Lihavainen, V.M.; Marquis, G.; Statnikov, E.S. Fatigue strength of a longitudinal attachment improved by ultrasonic impact treatment. Weld. World 2004, 48, 67–73. [Google Scholar] [CrossRef]
- Huo, L.; Wang, D.; Zhang, Y. Investigation of the fatigue behaviour of the welded joints treated by TIG dressing and ultrasonic peening under variable-amplitude load. Int. J. Fatigue 2005, 27, 95–101. [Google Scholar] [CrossRef]
- Haagensen, P.J.; Alnes, Ø. Progress Report on IIW WG2 Round Robin Fatigue Testing Program on 700 MPa and 350 MPa YS Steels. IIW Doc, XIII-2081-05; International Institute of Welding: Paris, France, 2005. [Google Scholar]
- Leitner, M.; Ottersböck, M.; Pußwald, S.; Remes, H. Fatigue strength of welded and high frequency mechanical impact (HFMI) post-treated steel joints under constant and variable amplitude loading. Eng Struct 2018, 163, 215–223. [Google Scholar] [CrossRef]
- Leitner, M.; Barsoum, Z.; Schäfers, F. Crack propagation analysis and rehabilitation by HFMI of pre-fatigued welded structures. Weld. World 2016, 60, 581–592. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.S.; Chen, X.; Han, C.; Lee, H.W. Estimation methods for fatigue properties of steels under axial and torsional loading. Int. J. Fatigue 2002, 24, 783–793. [Google Scholar] [CrossRef]
- Bäumel, A.; Seeger, T.; Boller, C. Materials Data for Cyclic Loading. Supplement 1. Materials science monographs; Elsevier: Amsterdam, The Netherlands, 1990; Volume 3. [Google Scholar]
- Korkmaz, S. Extension of the Uniform Material Law for High Strength Steels. Master’s Thesis, Bauhaus University Graduate School of Structural Engineering, Weimar, Germany, 2008. [Google Scholar]
- Roessle, M.L.; Fatemi, A. Strain-controlled fatigue properties of steels and some simple approximations. Int. J. Fatigue 2000, 22, 495–511. [Google Scholar] [CrossRef]
- Dowling, N.E. Notched Member Fatigue Life Predictions Combining Crack Initiation and Propagation. Fatigue Fract. Eng. Mater. Struct. 1979, 2, 129–138. [Google Scholar] [CrossRef]
- Yıldırım, H.C.; Marquis, G.; Sonsino, C.M. Lightweight design with welded high-frequency mechanical impact (HFMI) treated high-strength steel joints from S700 under constant and variable amplitude loadings. Int. J. Fatigue 2016, 91, 466–474. [Google Scholar] [CrossRef]
- Suominen, L.; Khurshid, M.; Parantainen, J. Residual stresses in welded components following post-weld treatment methods. Procedia Eng. 2013, 66, 181–191. [Google Scholar] [CrossRef] [Green Version]
- Schubnell, J.; Eichheimer, C.; Ernould, C.; Maciolek, A.; Rebelo-Kornmeier, J.; Farajian, M. The influence of coverage for high frequency mechanical impact treatment of different steel grades. J. Mater. Process. Technol. 2020, 277, 116437. [Google Scholar] [CrossRef]
- Schubnell, J.; Pontner, P.; Wimpory, R.C.; Farajian, M.; Schulze, V. The influence of work hardening and residual stresses on the fatigue behavior of high frequency mechanical impact treated surface layers. Int. J. Fatigue 2020, 134, 105450. [Google Scholar] [CrossRef]
- METINVEST. Available online: https://metinvestholding.com/en/products/steel-grades/s690q (accessed on 12 May 2021).
- Wohlfahrt, H. Auswirkungen mechanischer Oberflächenbehandlungen auf das Dauerschwingverhalten unter Einschluss von Rissbildung und Rissausbreitung. In Mechanische Oberflächenbehandlungen; Wohlfahrt, H., Krull, P., Eds.; Wiley-VCH: Weinheim, Germany, 2000; pp. 56–85. [Google Scholar]



| Parameter | UML [10] | Extended UML [41] | HM [42] |
|---|---|---|---|
| K′ | 1.61 fu | σf’/(εf’)n′ | 1.65 fu |
| n′ | 0.15 | b/c | 0.15 |
| σf’ | 1.5 fu | fu (1 + ψ) | 4.25 HB + 225 |
| εf’ | 0.59 ψ | 0.58 ψ + 0.01 | 1/E(0.32 (HB)2 − 487 (HB) + 191,000 |
| b | −0.087 | −log (σf’/σE)/6 | −0.057 to −0.14 |
| σE * | 0.45 fu | fu(0.32 + ψ)/6 | - |
| c | −0.58 | −0.58 | −0.39 to 1.04 |
| ψ ** | 1.0 for (fu/E) ≤ 3 × 10−3 1.375 − 125 (fu/E) for (fu/E) > 3 × 10−3 and ≥0 | 0.5(cos(π(fu − 400)/2200) + 1) | - |
| Steel Grade | S355 | S690 | S960 | ||||
|---|---|---|---|---|---|---|---|
| Parameter | Condition | min | max | min | max | min | max |
| Stress concentration | AW | 2.6 | 4.0 | 2.6 | 4.0 | 2.6 | 4.0 |
| HFMI | 1.8 | 2.2 | 1.8 | 2.2 | 1.8 | 2.2 | |
| Residual stress (at surface) (MPa) | AW | 25 | 250 | 25 | 400 | 25 | 600 |
| HFMI | −350 | −200 | −650 | −400 | −800 | −600 | |
| Hardness (at surface) (HB) | AW | 146 | 187 | 230 | 240 | 320 | 320 |
| HFMI | 240 | 290 | 240 | 270 | 320 | 340 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuštar, B.; Lukačević, I.; Skejić, D.; Lukić, M. Two-Stage Model for Fatigue Life Assessment of High Frequency Mechanical Impact (HFMI) Treated Welded Steel Details. Metals 2021, 11, 1318. https://doi.org/10.3390/met11081318
Fuštar B, Lukačević I, Skejić D, Lukić M. Two-Stage Model for Fatigue Life Assessment of High Frequency Mechanical Impact (HFMI) Treated Welded Steel Details. Metals. 2021; 11(8):1318. https://doi.org/10.3390/met11081318
Chicago/Turabian StyleFuštar, Boris, Ivan Lukačević, Davor Skejić, and Mladen Lukić. 2021. "Two-Stage Model for Fatigue Life Assessment of High Frequency Mechanical Impact (HFMI) Treated Welded Steel Details" Metals 11, no. 8: 1318. https://doi.org/10.3390/met11081318
APA StyleFuštar, B., Lukačević, I., Skejić, D., & Lukić, M. (2021). Two-Stage Model for Fatigue Life Assessment of High Frequency Mechanical Impact (HFMI) Treated Welded Steel Details. Metals, 11(8), 1318. https://doi.org/10.3390/met11081318








