Abstract
The ability of a metal to be subjected to forming processes depends mainly on its plastic behavior and, thus, the mechanical properties belonging to this region of the stress–strain curve. Forming techniques are among the most widespread metalworking procedures in manufacturing, and aluminum alloys are of great interest in fields as diverse as the aerospace sector or the food industry. A precise characterization of the mechanical properties is crucial to estimate the forming capability of equipment, but also for a robust numerical modeling of metal forming processes. Characterizing a material is a very relevant task in which large amounts of resources are invested, and this paper studies how to optimize a multilayer neural network to be able to make, through machine learning, precise and accurate predictions about the mechanical properties of wrought aluminum alloys. This study focuses on the determination of the ultimate tensile strength, closely related to the strain hardening of a material; more precisely, a methodology is developed that, by randomly partitioning the input dataset, performs training and prediction cycles that allow estimating the average performance of each fully-connected topology. In this way, trends are found in the behavior of the networks, and it is established that, for networks with at least 150 perceptrons in their hidden layers, the average predictive error stabilizes below . Beyond this point, no really significant improvements are found, although there is an increase in computational requirements.
1. Introduction
Aluminum alloys are among the most widely used materials in the industry, and, although their use is still far from being as widespread as that of steel, they have many advantages that make them a very interesting material whose use is growing regularly [1]. There is a huge number of aluminum alloys, but few of them are typically used in the industrial field [2], sometimes because it is difficult to find new solutions and, sometimes, because they are special materials with optimized properties to fulfill their requirements, according to their application [3].
Aluminum alloys are manufactured by different techniques [4]. Among its many properties of industrial interest, it can be noted that it is a material with a high formability, so it is especially suitable for metal forming processes. Moreover, a precise characterization of the mechanical properties is crucial to estimate the forming capability of equipment but also for a robust numerical modeling of metal forming processes. Among all the mechanical properties, the ultimate tensile strength () plays a key role in the definition of the onset of the plastic instability by tensile tension [3]. This mechanical property is closely related to the strain hardening of the metal and, therefore, to its forming capacity under metal forming processes. In uniaxial tension, the plastic deformation is limited by the value of since, once it is exceeded, the onset of the plastic instability takes place, and from then on, the behavior of the material is almost unpredictable until fracture [5].
Therefore, it is well known that aluminum alloys present a high ductility [6] because they can withstand a lot of plastic deformation before fracture and, so, they are widely used in metal forming operations [7]; such metals can be manufactured by metal sheet operations and bulk forming processes, such as forging, rolling, extrusion and/or drawing [2]. Ductile materials are able to absorb a great amount of energy before failing, otherwise known as toughness [8].
The design and production of some industrial components rely on the knowledge of the mechanical properties obtained and tensile testing [9]. The may serve to determine the beginning of the plastic instability and provides an insight into the initiation of the fracture or the necking [10]. It also can be used as an input to estimate the forming force in the conventional forming procedures such as stretch-bending or deep-drawing [10].
Metal forming is frequently employed to manufacture components. The microstructure and the mechanical properties of these parts are modified by these processes [2]. For example, the increase in the ultimate stress and hardness observed during the A-6063 extrusion is attributed to the grain size reduction and the temperature increase [11].
In addition to , the strain hardening exponent, the yield strength (), the process-induced residual stresses, and the hardness are also important mechanical characteristics [1,3,10]. These properties offer an idea of the in-service behavior of the formed part. Furthermore, their correlations help to understand the response of the component [12], i.e., knowing the difference between and can help the designer to predict how much additional stress a component can withstand before failure [5] because defines the onset of plastic deformation, and defines the onset of plastic instability.
Knowing the expected behavior of the materials used in industrial designs is critical; however, obtaining these data frequently requires accessing large amounts of resources, which are normally not accessible [1]. Many tests are required to obtain relevant information, which entail having enough time, personnel and facilities be available [13]. Characterizing a metal comprises many tests that require non-trivial quantities of resources [8].
Although it is a relatively new technology and not as widespread in materials science and manufacturing as in other areas [13], artificial intelligence (AI) and machine learning (ML) techniques have been successfully used to make predictions about the metallurgical properties of some materials [1,3,14,15,16].
Over recent years, AI and ML have received much attention in the field of materials modeling, due to their outstanding ability to analyze a huge amount of data and expose correlations between complex interrelated properties [17]. ML is, perhaps, the most relevant branch of AI, and is the science of making computers learn and act like humans without being explicitly programmed [18,19]. It is often used to discover hidden patterns in complex systems through a training process in which a great amount of noisy data is furnished as input [20,21]. ML can be classified into supervised learning (the machine learns from labeled data) and unsupervised learning (the machine finds patterns in the data without any external help) [20,22,23].
Among the most challenging topics in this field is the search for the best representation of input variables in ML models, which is commonly called feature engineering and comprises a set of activities, such as feature extraction, feature construction and feature selection [23,24]. Feature engineering research is crucial to the application of the ML.
Within current materials science, the scale and speed of data acquisition, the accuracy of the data and the volatility of the data are additional challenges for researchers [3]. It raises the question of how to use and analyze these data in a useful way that supports the decisions of developers and designers [18,23]. Material data tend to be wide in scope and, often, shallow in depth. Here, depth should be understood as the number of observations of the state of a system. The lack of observations is due not only to the cost and difficulty of acquiring data (especially through experimentation), but also to the nature of the data itself. However, fully employing the data is a key part of advanced design systems [23,25].
In recent years, an incipient trend in materials science research is the combination of existing experimental and numerical modeling methodologies with AI techniques [26,27,28]. In general, materials science advances thanks to accumulated experience and already established rules [29,30]. New advances in numerical modeling facilitate the methodical acquisition of large amounts of data, while complicating analysis, hypothesis formulation and pattern prediction. The rise of AI techniques makes up for this deficiency to a great extent [31].
Multilayer artificial neural networks (ANN) can be considered the most remarkable methodology of those that are included into the field of AI because they have demonstrated their capabilities in almost all branches of knowledge and because they are currently receiving a lot of attention from investigators [32]. A multilayer network is able to learn a function by training on a labeled dataset that can be used to perform regressions [33]. ANN are made up of perceptrons (neurons) that regroup forming layers (clusters of neurons) that communicate with each other (in general, perceptrons do not communicate with their own layer companions) [13]. For a fully connected multilayer neural network, the time complexity of the backpropagation training is given by Equation (1). So, it is highly recommended to minimize the number of hidden nodes to reduce the training time [1].
where n is the size of the training dataset, m is the number of features, o is the number of output perceptrons, N is the number of iterations and k is the number of hidden layers (each of them containing nodes).
The main objective of this work is to develop a working methodology that allows optimizing the topology of a multilayer neural network in such a way that it is capable of making predictions about the of wrought aluminum alloys [34], maximizing the precision and accuracy of the estimation and minimizing the computational resources [20]. Although this paper only takes into account the , this same approach could be applied to other properties that have already been mentioned, such as the or the elongation at break (A).
2. Methodology
This work is developed following a three-stage scheme, and the data generated in each of them are used as input for the subsequent one [13]. This workflow guarantees that the data that reach each phase are correctly prepared and processed, and are ready to be employed. Therefore, the information resulting from the entire process is a consequence of the initial dataset.
Figure 1 schematically shows the three stages that compose the methodology of this work: in the first stage, an initial input dataset is created; in the second stage, the optimization process is carried out through training-prediction cycles; and in the third phase, all available information is analyzed.
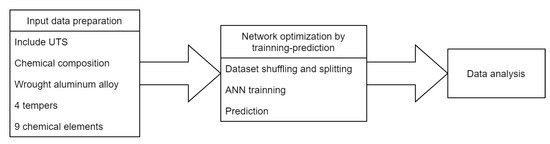
Figure 1.
Overview of the methodology.
2.1. Input Dataset Preparation
All initial data on the properties of the materials were obtained from Matmatch GmbH (Munich, Germany) [35]. It is an online library that contains freely accessible specification sheets about material properties [13]. These include a large number of aluminum alloys with very heterogeneous information. The volume of data initially obtained comprises more than 5000 materials and more than 350 properties [1,3].
After obtaining these data, each record must be read and interpreted in an automated way. Each specification sheet contains much more information than is used during this study, so it is necessary to discard the irrelevant data [35]. The following considerations are taken into account to select the records that are found to be useful:
- Only datasheets that contain the value of the ultimate tensile stress () at 20 °C are considered.
- Only alloys whose chemical composition is defined at more than are taken into account [13] (note that some datasheets are poorly defined).
- Only 9 chemical elements are considered to define the chemical composition of the alloys [29]: Al, Zn, Cu, Si, Fe, Mn, Mg, Ti and Cr. The mass contribution of all other chemical elements is regrouped as ”Other”.
- Only wrought alloys are considered in this study.
- Only the specification sheets that include the temper of the alloy are considered. This study only considers the following tempers: F (as fabricated), O (annealed), H (strain hardening) and T (thermally treated) [7].
After taking all these considerations into account, only 2671 materials (the obviated records do not meet the aforementioned conditions), 11 input properties and the are considered. These alloys constitute the initial dataset on which the entire study is developed. One of these properties is categorical (temper) and must be mapped as an integer, while the other 11 are numerical ( and chemical composition) and must be normalized to avoid bias [20,22]. Normalization is carried out using Equation (2).
where is each of the non-normalized input values, is the related normalized value , is the minimum value for that parameter and is the maximum value.
2.2. Network Optimization by Training-Prediction
The ANN topology denotes the way in which perceptrons are associated and is an essential characteristic in the performance of the network [19]. Layers are shapeless in the sense that all of its nodes are equally relevant, connected the same way, and lack differentiators [22]. Only the initialization step and the following training make its importance change [25].
In this study, the neural network is defined as a fully connected multilayer feedforward topology [33], which comprises an input layer, two hidden layers and an output layer. In this topology, all the perceptrons in each layer are only connected to all ones in the next layer so that the information only flows in one direction, from the input layer to the output layer [22].
The neural network receives an input vector of 11 elements (chemical composition and temper) and returns a prediction about the value of the expected [3]. Therefore, the input layer is made up of 11 nodes, and the output layer only contains a single node. Additionally, the network topology contains two hidden layers whose number of nodes is to be optimized [19]. Figure 2 shows a schematic representation of the network in which the hidden layers are represented as squares.
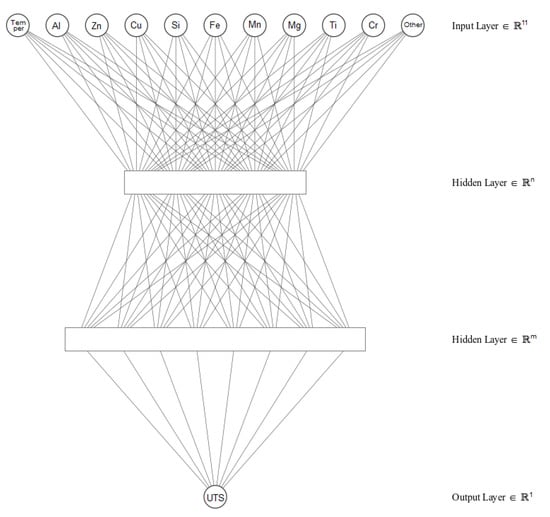
Figure 2.
Multilayer artificial neural network scheme.
Different topologies are tested to carry out the network optimization: the number of nodes in both hidden layer changes in increments of 10 nodes (from 10 to 200). In this way, 400 topologies are obtained with a number of nodes that varies between 32 and 412. For each of these networks, 10 independent training and prediction iterations are carried out [1,3].
Each iteration consists of four phases:
- Dataset shuffling and splitting to create a training subset ( of records, so 2137) and a testing subset (remaining , so 534).
- ANN training, using the data contained in the training subset.
- Prediction of the properties for the records in the testing subset.
- Results and data storage for further analysis.
The training is configured as follow [1]:
- Calculation of the learning rate for each parameter using adaptive moment estimation (ADAM) with , (algorithm parameters), (step size) and (stability factor) [36].
- Early stopping after 20 iterations without significant changes.
- Training stops when a training error of less than is reached.
- Maximum of 100,000 training epochs to avoid infinite loops.
2.3. Data Analysis
The optimization process generates a large amount of data that must be processed to generate information that allows to draw conclusions about the network performance [3,13]. For each of the considered 400 topologies, the predictive performance of the 10 iterations is calculated and stored.
With the information obtained about the tests on these topologies, it is possible to build a performance map of 20 × 20 cells; each of these cells represents a topology described by the number of nodes in the two hidden layers. In each position of this data structure, it is possible to store statistical information that allows making comparisons between the different topologies.
Network topologies with the lowest average predictive error (highest accuracy), lowest standard deviation of predictive error (highest precision), and shortest training time (lowest resource usage) are preferred [20].
3. Results and Discussion
Table 1 contains some statistical metrics about the information contained in the input dataset. It is interesting to highlight the wide range of values associated with the .

Table 1.
Statistical information about the input dataset.
As expected, more complex topologies tend to have higher precision than those with fewer perceptrons and, in fact, the lowest error is related to a network with 160 and 200 nodes in its two hidden layers (). Moreover, the highest error rate () occurs for the simplest network of those that are considered (10 and 10 nodes). More detailed information can be found on Table A1.
Figure 3 graphically shows the average predictive error (values above are trimmed to avoid scale-related issues). A region with a very low precision (error greater than ) can be seen for topologies with less than 150 perceptrons, while for more complex networks, the error remains lower (less than ). It is interesting to note that, as can be seen in the three-dimensional figure, the transition between both regions is quite abrupt, and a step (yellow zone) is formed. This transition zone (yellow) separates an almost flat area from a steep one.
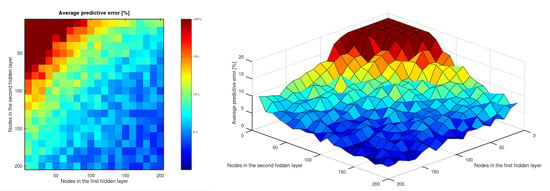
Figure 3.
Average predictive error [%] (trimmed above ).
This transition can be interpreted as a frontier before which the predictions cannot be trusted because the error is excessive and the model is very unstable (small changes in the network produce large differences).
Figure 4 shows the value of the mean predictive error as a function of the number of nodes in the hidden layers. It can be seen that the error asymptotically tends to a value close to . Note that the number of nodes in the hidden layers is the sum of the number of perceptrons in both layers.
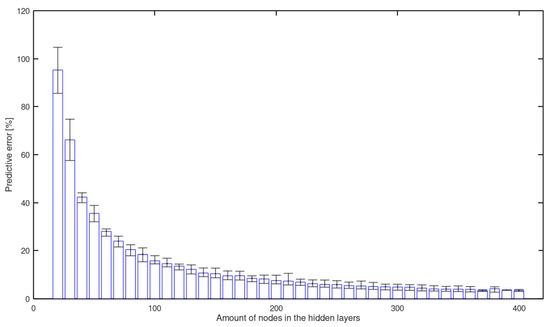
Figure 4.
Predictive error [%] as a function of the amount of nodes in both hidden layers.
It is interesting to highlight that, for neural networks with more than 300 nodes, the average predictive error remains, in all cases, approximately stable at around . It is a very interesting result since it establishes a boundary beyond which no significant improvement can be seen, although there is an increase in computational requirements.
In view of these results, it is clear that complex topologies should be privileged over simpler ones; however, it should also be considered that, as the number of nodes increases, achieving significant improvements becomes very expensive in computational terms and, in fact, it is found that a more complex topology does not always guarantee better accuracy.
On the other hand, it is not only necessary to take into account the accuracy (related to the average predictive error) of the results, but also the precision (related to the predictive error standard deviation).
The standard deviation of the error gives an idea of the repeatability of the estimates, and, together with the average error, allow to identify the confidence range in which a prediction is. In a similar way to what happened in the case of the average error, the more complex networks are more precise (the minimum is reached for a network with 180 and 160 perceptrons, respectively), whereas the simpler ones obtain a higher standard deviation value (the maximum is reached for a network with 30 and 10 nodes, respectively). More detailed information can be found on Table A2.
Figure 5 graphically shows the standard deviation of the predictive error (values above are trimmed to avoid scale-related issues). The distribution of values is much more irregular than in the case of the average error. However, three areas can be seen: for networks with less than 150 perceptrons, the standard deviation is high (mostly above ); for topologies with between 150 and 250 nodes, a very irregular transition zone is produced with scattered high values; and, for the more complex networks (more than 250 nodes), the values are mostly kept below .
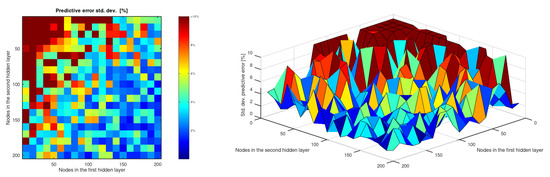
Figure 5.
Standard deviation of the predictive error [%] (trimmed above ).
As can be seen by comparing Figure 3 and Figure 5, although the standard deviation is distributed in a much more irregular way, the trends of both statistical metrics are similar. For networks whose hidden layers contain 150 or more perceptrons, the accuracy and precision stabilize, and there are hardly any significant differences in the performance of these topologies.
4. Conclusions and Future Work
This paper studies how to optimize the topology of a multilayer artificial neural network to carry out predictions about mechanical properties of aluminum alloys, such as , using machine learning. It is a contribution of great industrial interest since it allows exploring how to obtain sufficiently precise estimates with minimal computational cost and, therefore, using fewer resources. Therefore, the main conclusions of this work are presented as follows:
- An artificial neural network with two hidden layers can predict the of wrought aluminum alloys by taking its chemical composition and temper as input. The accuracy of this prediction stabilizes below and even reaches in this study.
- The predictive ability of an ANN with two hidden layers to estimate the of aluminum alloys is stabilized for topologies that include 150 or more perceptrons in both hidden layers. The precision and accuracy of these networks do not show significant differences that allow us to affirm that one topology is really better than the others.
- A multilayer ANN can be used as a tool to, through machine learning, make predictions about the mechanical behavior of a piece of aluminum alloy subjected to forming processes. In theory, these networks can learn to approximate any nonlinear function if the input data set is large enough and has enough perceptrons [37].
This study presents a methodology that allows optimizing the topology of a neural network whose task is to make predictions about the using techniques based on machine learning. In the same way, it would be possible to use this same approach with other properties and even with other materials.
Since this scheme of work is shown to work adequately, a similar method could be applied to test other more complex network architectures. There are a multitude of architectures related to machine learning that allow different problems to be addressed [33].
Author Contributions
Conceptualization, D.M., A.R.-P. and A.M.C.; methodology, D.M.; software, D.M.; validation, D.M., A.R.-P. and A.M.C.; formal analysis, D.M.; investigation, D.M.; resources, A.R.-P. and A.M.C.; data curation, D.M.; writing—original draft preparation, D.M.; writing—review and editing, D.M., A.R.-P. and A.M.C.; visualization, D.M.; supervision, A.R.-P. and A.M.C.; project administration, A.R.-P. and A.M.C.; funding acquisition, A.R.-P. and A.M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was developed within the framework of the Doctorate Program in Industrial Technologies of the UNED and was funded by the Annual Grants Call of the E.T.S.I.I. of the UNED via the projects of reference 2021-ICF07 and 2021-ICF08, as well as by the Innovation Teaching Project of the GID2016-28 focused on “Reliability and Advanced Failure Prognosis in industrial applications applied to the teaching of Materials Technology and Processing”.
Data Availability Statement
All data can be found in Appendix A.
Acknowledgments
We extend our acknowledgments to the Research Group of the UNED “Industrial Production and Manufacturing Engineering (IPME)” and the Industrial Research Group “Advanced Failure Prognosis (AFP) for Engineering Applications”. We also thank Matmatch GmbH for freely supplying all the material data employed to accomplish this study.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations and symbols are used in this manuscript:
| ADAM | Adaptive moment estimation |
| AI | Artificial intelligence |
| ANN | Artificial neural networks |
| ADAM algorithm parameter | |
| ADAM stability factor | |
| ADAM step size | |
| m | ADAM first moment estimate |
| ML | Machine learning |
| Ultimate tensile strength | |
| Standard deviation | |
| ADAM second moment estimate | |
| Average | |
| Yield strength |
Appendix A. Numerical Results
Table A1 shows the average predictive error after testing each of the 400 topologies through 10 independent training–prediction iterations.

Table A1.
Average predictive error (%) for each topology as a function of the amount of nodes in the hidden layers.
Table A1.
Average predictive error (%) for each topology as a function of the amount of nodes in the hidden layers.
| Nodes in the First Hidden Layer | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | ||
| Nodes in the second hidden layer | 10 | 95.28 | 74.79 | 44.11 | 34.89 | 28.74 | 23.07 | 20.56 | 19.26 | 17.96 | 13.79 | 13.98 | 12.86 | 12.55 | 11.70 | 11.60 | 10.48 | 8.68 | 9.42 | 9.86 | 10.62 |
| 20 | 57.57 | 39.99 | 36.42 | 29.08 | 22.67 | 21.50 | 16.95 | 15.34 | 15.52 | 14.29 | 12.68 | 11.64 | 10.31 | 9.29 | 8.84 | 9.57 | 8.33 | 8.30 | 9.07 | 6.79 | |
| 30 | 42.92 | 32.07 | 26.03 | 25.78 | 17.93 | 21.18 | 14.82 | 14.81 | 13.20 | 10.38 | 10.37 | 9.57 | 10.06 | 11.14 | 7.34 | 8.08 | 7.89 | 6.37 | 7.00 | 7.13 | |
| 40 | 38.87 | 28.11 | 21.55 | 20.78 | 15.44 | 14.82 | 13.33 | 12.82 | 11.55 | 9.26 | 12.81 | 9.13 | 9.02 | 8.56 | 8.56 | 8.27 | 8.43 | 6.51 | 7.19 | 5.98 | |
| 50 | 28.26 | 24.81 | 19.79 | 18.44 | 16.25 | 15.39 | 14.40 | 12.23 | 9.71 | 10.05 | 9.91 | 7.86 | 9.37 | 8.64 | 9.63 | 6.74 | 7.10 | 7.23 | 6.11 | 5.38 | |
| 60 | 26.05 | 22.47 | 19.38 | 16.83 | 14.03 | 13.50 | 11.19 | 10.70 | 10.86 | 8.80 | 9.88 | 9.54 | 7.88 | 6.84 | 5.93 | 6.97 | 7.58 | 7.84 | 6.62 | 4.57 | |
| 70 | 20.21 | 18.32 | 14.56 | 13.78 | 14.48 | 12.19 | 10.22 | 10.15 | 8.95 | 7.93 | 7.88 | 7.48 | 7.53 | 5.79 | 7.67 | 7.12 | 6.13 | 6.05 | 4.50 | 5.42 | |
| 80 | 18.73 | 16.20 | 16.92 | 14.03 | 10.41 | 10.17 | 8.79 | 7.96 | 10.60 | 8.24 | 9.34 | 6.65 | 8.23 | 6.88 | 6.14 | 4.94 | 4.89 | 6.91 | 4.35 | 5.01 | |
| 90 | 15.90 | 13.50 | 13.71 | 12.51 | 9.33 | 10.43 | 10.02 | 11.50 | 8.80 | 8.42 | 6.31 | 6.61 | 5.62 | 5.11 | 5.77 | 5.78 | 4.36 | 6.28 | 4.35 | 5.51 | |
| 100 | 15.52 | 13.30 | 14.13 | 9.33 | 11.15 | 9.13 | 9.85 | 8.45 | 7.53 | 6.23 | 5.99 | 7.45 | 5.54 | 4.87 | 5.55 | 4.41 | 4.20 | 4.94 | 5.77 | 3.66 | |
| 110 | 12.05 | 13.74 | 12.86 | 9.58 | 9.39 | 8.33 | 8.94 | 6.42 | 8.33 | 6.91 | 8.19 | 5.26 | 5.82 | 6.77 | 6.43 | 5.26 | 3.94 | 5.08 | 6.09 | 5.51 | |
| 120 | 13.69 | 12.34 | 10.69 | 10.43 | 10.48 | 7.33 | 7.60 | 8.60 | 6.01 | 6.86 | 7.89 | 6.78 | 4.87 | 4.39 | 6.54 | 6.04 | 5.30 | 5.77 | 5.57 | 4.12 | |
| 130 | 11.45 | 9.94 | 10.87 | 9.45 | 7.13 | 8.46 | 6.68 | 6.78 | 6.49 | 5.03 | 4.85 | 4.52 | 6.30 | 5.10 | 5.17 | 3.74 | 3.60 | 3.54 | 3.66 | 4.19 | |
| 140 | 10.57 | 8.26 | 9.72 | 8.36 | 8.62 | 7.70 | 6.71 | 6.83 | 6.01 | 6.82 | 5.56 | 6.65 | 6.45 | 5.09 | 6.05 | 5.63 | 4.51 | 4.30 | 3.89 | 3.49 | |
| 150 | 10.13 | 10.59 | 8.20 | 8.53 | 7.54 | 6.26 | 5.77 | 6.43 | 6.93 | 6.59 | 6.98 | 5.13 | 5.06 | 5.76 | 3.64 | 5.47 | 3.31 | 4.23 | 5.18 | 3.08 | |
| 160 | 8.28 | 9.58 | 8.06 | 7.28 | 7.99 | 6.88 | 6.05 | 7.30 | 6.21 | 5.48 | 7.41 | 5.68 | 5.27 | 5.62 | 3.54 | 5.48 | 3.28 | 4.06 | 3.02 | 3.96 | |
| 170 | 9.19 | 7.77 | 6.65 | 7.98 | 7.59 | 7.16 | 5.01 | 7.28 | 6.32 | 4.14 | 6.29 | 6.13 | 5.38 | 4.24 | 5.82 | 5.23 | 3.31 | 5.39 | 3.03 | 3.78 | |
| 180 | 9.88 | 7.68 | 8.91 | 7.66 | 6.36 | 5.04 | 6.65 | 4.53 | 5.18 | 3.98 | 3.78 | 5.03 | 4.53 | 5.42 | 3.35 | 3.15 | 4.41 | 4.95 | 3.74 | 2.77 | |
| 190 | 7.01 | 8.05 | 6.31 | 5.50 | 5.01 | 7.55 | 4.65 | 4.24 | 3.95 | 3.89 | 4.87 | 5.72 | 3.72 | 5.47 | 4.10 | 4.05 | 5.12 | 3.22 | 5.01 | 3.64 | |
| 200 | 8.72 | 7.92 | 5.30 | 7.15 | 4.74 | 5.73 | 5.26 | 6.82 | 3.79 | 4.90 | 5.90 | 4.45 | 3.25 | 5.07 | 4.27 | 2.88 | 3.07 | 4.81 | 3.67 | 3.49 | |
Table A2 shows the standard deviation of the predictive error for each of the topologies that are tested.

Table A2.
Standard deviation of the predictive error (%) for each topology as a function of the amount of nodes in the hidden layers.
Table A2.
Standard deviation of the predictive error (%) for each topology as a function of the amount of nodes in the hidden layers.
| Nodes in the First Hidden Layer | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | ||
| Nodes in the second hidden layer | 10 | 58.96 | 28.75 | 61.09 | 41.95 | 13.42 | 23.40 | 6.31 | 9.94 | 14.81 | 13.57 | 13.25 | 13.00 | 12.76 | 3.60 | 3.21 | 5.28 | 5.72 | 5.05 | 4.87 | 4.62 |
| 20 | 19.33 | 47.56 | 13.39 | 16.32 | 8.62 | 18.35 | 6.16 | 5.14 | 7.12 | 11.86 | 4.15 | 5.40 | 8.93 | 8.26 | 3.32 | 2.75 | 5.08 | 8.61 | 2.39 | 3.99 | |
| 30 | 22.01 | 16.41 | 26.93 | 10.95 | 22.21 | 17.56 | 8.28 | 4.40 | 12.88 | 4.23 | 10.87 | 4.80 | 8.39 | 8.28 | 8.64 | 2.87 | 6.43 | 7.93 | 2.21 | 2.53 | |
| 40 | 17.07 | 31.23 | 24.15 | 20.37 | 8.87 | 7.79 | 6.70 | 6.03 | 3.40 | 3.28 | 3.88 | 4.19 | 11.49 | 4.30 | 2.86 | 7.13 | 2.30 | 3.65 | 3.23 | 7.03 | |
| 50 | 9.52 | 11.56 | 9.35 | 7.92 | 6.87 | 6.95 | 6.25 | 5.54 | 5.34 | 9.62 | 4.03 | 7.33 | 8.89 | 3.87 | 6.29 | 6.88 | 3.23 | 2.39 | 3.70 | 4.72 | |
| 60 | 22.65 | 10.43 | 7.95 | 4.66 | 4.46 | 12.15 | 12.45 | 9.26 | 11.20 | 3.04 | 2.95 | 3.99 | 8.77 | 8.28 | 2.87 | 2.18 | 7.99 | 3.06 | 3.33 | 2.24 | |
| 70 | 22.05 | 18.31 | 4.78 | 13.17 | 12.53 | 4.21 | 4.64 | 10.87 | 5.03 | 4.91 | 2.94 | 3.79 | 2.70 | 6.73 | 3.78 | 5.19 | 7.10 | 1.97 | 6.82 | 4.71 | |
| 80 | 17.48 | 21.58 | 4.26 | 6.41 | 6.29 | 3.91 | 5.55 | 5.11 | 3.36 | 3.97 | 2.53 | 4.49 | 1.90 | 2.50 | 2.32 | 1.78 | 5.58 | 1.82 | 2.17 | 1.97 | |
| 90 | 17.69 | 16.30 | 4.24 | 12.62 | 9.19 | 5.24 | 10.07 | 2.52 | 4.04 | 2.64 | 7.91 | 3.56 | 1.94 | 2.66 | 2.29 | 2.82 | 2.84 | 6.09 | 1.79 | 5.04 | |
| 100 | 4.50 | 12.01 | 4.13 | 12.25 | 11.17 | 7.81 | 4.86 | 8.29 | 7.72 | 3.51 | 6.66 | 3.55 | 7.05 | 2.39 | 1.64 | 1.47 | 2.65 | 3.20 | 3.82 | 1.23 | |
| 110 | 6.31 | 11.91 | 9.64 | 4.32 | 5.36 | 4.71 | 2.59 | 6.47 | 6.06 | 7.08 | 2.10 | 3.62 | 2.27 | 2.59 | 2.23 | 2.13 | 2.02 | 4.48 | 1.26 | 3.52 | |
| 120 | 5.57 | 11.89 | 2.95 | 8.35 | 7.60 | 2.90 | 3.01 | 2.70 | 6.68 | 1.82 | 3.50 | 4.76 | 5.99 | 4.37 | 2.14 | 5.54 | 4.87 | 2.35 | 4.48 | 1.12 | |
| 130 | 3.80 | 9.36 | 8.35 | 9.85 | 7.08 | 3.39 | 3.90 | 6.64 | 5.35 | 2.09 | 1.59 | 5.57 | 1.44 | 1.84 | 2.71 | 1.92 | 2.39 | 1.19 | 1.79 | 1.70 | |
| 140 | 11.68 | 2.80 | 4.81 | 8.22 | 2.50 | 3.56 | 3.93 | 3.52 | 2.45 | 5.78 | 5.55 | 4.94 | 4.24 | 3.92 | 2.51 | 1.89 | 3.45 | 4.52 | 4.18 | 1.53 | |
| 150 | 10.64 | 3.94 | 3.58 | 7.68 | 7.39 | 2.30 | 2.57 | 6.58 | 3.49 | 6.99 | 7.12 | 2.16 | 2.55 | 4.93 | 1.68 | 1.18 | 4.50 | 2.60 | 4.16 | 2.29 | |
| 160 | 3.19 | 9.65 | 7.71 | 6.33 | 8.70 | 5.79 | 3.60 | 2.45 | 1.63 | 2.27 | 2.08 | 1.52 | 3.94 | 4.45 | 1.37 | 1.44 | 1.59 | 1.05 | 1.70 | 2.45 | |
| 170 | 5.24 | 9.33 | 3.48 | 3.42 | 3.28 | 7.52 | 3.63 | 2.18 | 3.25 | 4.41 | 3.99 | 3.95 | 2.81 | 2.44 | 3.32 | 3.50 | 5.10 | 2.95 | 1.34 | 2.77 | |
| 180 | 10.02 | 3.72 | 2.33 | 4.27 | 6.64 | 5.74 | 5.60 | 2.10 | 6.98 | 5.18 | 1.97 | 1.55 | 1.77 | 5.35 | 1.63 | 2.55 | 4.05 | 1.94 | 1.59 | 1.90 | |
| 190 | 2.29 | 2.30 | 3.78 | 5.29 | 2.60 | 7.36 | 2.21 | 2.18 | 2.72 | 5.01 | 4.60 | 5.89 | 1.78 | 2.59 | 1.07 | 4.19 | 2.14 | 4.17 | 4.71 | 1.38 | |
| 200 | 2.83 | 2.29 | 5.43 | 7.18 | 6.58 | 2.21 | 1.55 | 3.09 | 2.05 | 1.21 | 2.77 | 5.38 | 5.40 | 1.64 | 2.58 | 2.01 | 1.48 | 2.00 | 2.62 | 1.74 | |
References
- Merayo, D.; Rodríguez-Prieto, A.; Camacho, A.M. Prediction of the Bilinear Stress-Strain Curve of Aluminum Alloys Using Artificial Intelligence and Big Data. Metals 2020, 10, 904. [Google Scholar] [CrossRef]
- Alam, T.; Ansari, A.H. Review on Aluminium and Its Alloys for automotive applications. Int. J. Adv. Technol. Eng. Sci. 2017, 5, 278–294. [Google Scholar]
- Merayo, D.; Rodríguez-Prieto, A.; Camacho, A.M. Prediction of mechanical properties by artificial neural networks to characterize the plastic behavior of aluminum alloys. Materials 2020, 13, 5227. [Google Scholar] [CrossRef]
- Ashkenazi, D. How aluminum changed the world: A metallurgical revolution through technological and cultural perspectives. Technol. Forecast. Soc. Chang. 2019, 143, 101–113. [Google Scholar] [CrossRef]
- Hahn, G.; Rosenfield, A. Metallurgical factors affecting fracture toughness of aluminum alloys. Metall. Trans. A 1975, 6, 653–668. [Google Scholar] [CrossRef]
- Yogo, Y.; Sawamura, M.; Iwata, N.; Yukawa, N. Stress-strain curve measurements of aluminum alloy and carbon steel by unconstrained-type high-pressure torsion testing. Mater. Des. 2017, 122, 226–235. [Google Scholar] [CrossRef]
- Kaufman, J.G. Introduction to Aluminum Alloys and Tempers; ASM international: Russell Township, Geauga County, OH, USA, 2000. [Google Scholar]
- Kamaya, M.; Kawakubo, M. A procedure for determining the true stress–strain curve over a large range of strains using digital image correlation and finite element analysis. Mech. Mater. 2011, 43, 243–253. [Google Scholar] [CrossRef]
- Hu, J.; Marciniak, Z.; Duncan, J. Mechanics of Sheet Metal Forming; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Hosford, W.F.; Caddell, R.M. Metal Forming: Mechanics and Metallurgy; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Zhao, Y.; Song, B.; Pei, J.; Jia, C.; Li, B.; Linlin, G. Effect of deformation speed on the microstructure and mechanical properties of AA6063 during continuous extrusion process. J. Mater. Process. Technol. 2013, 213, 1855–1863. [Google Scholar] [CrossRef]
- Ilyas, M.; Hussain, G.; Rashid, H.; Alkahtani, M. Influence of Forming Parameters on the Mechanical Behavior of a Thin Aluminum Sheet Processed through Single Point Incremental Forming. Metals 2020, 10, 1461. [Google Scholar] [CrossRef]
- Merayo, D.; Rodríguez-Prieto, A.; Camacho, A.M. Prediction of Physical and Mechanical Properties for Metallic Materials Selection Using Big Data and Artificial Neural Networks. IEEE Access 2020, 8, 13444–13456. [Google Scholar] [CrossRef]
- Ghosh, I.; Das, S.K.; Chakraborty, N. An artificial neural network model to characterize porosity defects during solidification of A356 aluminum alloy. Neural Comput. Appl. 2014, 25, 653–662. [Google Scholar] [CrossRef]
- Zhao, D.; Ren, D.; Zhao, K.; Pan, S.; Guo, X. Effect of welding parameters on tensile strength of ultrasonic spot welded joints of aluminum to steel–By experimentation and artificial neural network. J. Manuf. Process. 2017, 30, 63–74. [Google Scholar] [CrossRef]
- Haghdadi, N.; Zarei-Hanzaki, A.; Khalesian, A.; Abedi, H. Artificial neural network modeling to predict the hot deformation behavior of an A356 aluminum alloy. Mater. Des. 2013, 49, 386–391. [Google Scholar] [CrossRef]
- Huang, J.; Liew, J.; Ademiloye, A.; Liew, K. Artificial intelligence in materials modeling and design. Arch. Comput. Methods Eng. 2020, 28, 3399–3413. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Merayo, D.; Rodriguez-Prieto, A.; Camacho, A.M. Comparative analysis of artificial intelligence techniques for material selection applied to manufacturing in Industry 4.0. Procedia Manuf. 2019, 41, 42–49. [Google Scholar] [CrossRef]
- Jackson, P.C. Introduction to Artificial Intelligence; Courier Dover Publications: Mineola, NY, USA, 2019. [Google Scholar]
- Chen, C.T.; Gu, G.X. Machine learning for composite materials. MRS Commun. 2019, 9, 556–566. [Google Scholar] [CrossRef] [Green Version]
- Joshi, P. Artificial Intelligence with Python; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Dimiduk, D.M.; Holm, E.A.; Niezgoda, S.R. Perspectives on the impact of machine learning, deep learning, and artificial intelligence on materials, processes, and structures engineering. Integr. Mater. Manuf. Innov. 2018, 7, 157–172. [Google Scholar] [CrossRef] [Green Version]
- Balachandran, P.V.; Xue, D.; Theiler, J.; Hogden, J.; Gubernatis, J.E.; Lookman, T. Importance of feature selection in machine learning and adaptive design for materials. In Materials Discovery and Design; Springer: Berlin/Heidelberg, Germany, 2018; pp. 59–79. [Google Scholar]
- Feng, S.; Zhou, H.; Dong, H. Using deep neural network with small dataset to predict material defects. Mater. Des. 2019, 162, 300–310. [Google Scholar] [CrossRef]
- Mueller, T.; Kusne, A.G.; Ramprasad, R. Machine learning in materials science: Recent progress and emerging applications. Rev. Comput. Chem. 2016, 29, 186–273. [Google Scholar]
- Lefik, M.; Boso, D.; Schrefler, B. Artificial neural networks in numerical modelling of composites. Comput. Methods Appl. Mech. Eng. 2009, 198, 1785–1804. [Google Scholar] [CrossRef]
- Sha, W.; Edwards, K. The use of artificial neural networks in materials science based research. Mater. Des. 2007, 28, 1747–1752. [Google Scholar] [CrossRef]
- Davis, J.R. Alloying: Understanding the Basics; ASM International: Russell Township, Geauga County, OH, USA, 2001. [Google Scholar]
- Naik, D.L.; Sajid, H.U.; Kiran, R. Texture-based metallurgical phase identification in structural steels: A supervised machine learning approach. Metals 2019, 9, 546. [Google Scholar] [CrossRef] [Green Version]
- Honysz, R. Modeling the Chemical Composition of Ferritic Stainless Steels with the Use of Artificial Neural Networks. Metals 2021, 11, 724. [Google Scholar] [CrossRef]
- Qian, L.; Winfree, E.; Bruck, J. Neural network computation with DNA strand displacement cascades. Nature 2011, 475, 368–372. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- The Aluminum Association. Designations and Chemical Composition Limits for Aluminum Alloys in the Form of Castings and Ingot; The Aluminum Association Inc.: Arlington, VA, USA, 2006. [Google Scholar]
- Matmatch GmbH. Matmatch. 2021. Available online: https://matmatch.com/ (accessed on 15 June 2021).
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference for Learning Representations (ICLR 15), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).